Study on Dynamic Performance Parameters of Laser Tracker Based on Self-Developed Circular Trajectory Generator System
Abstract
:1. Introduction
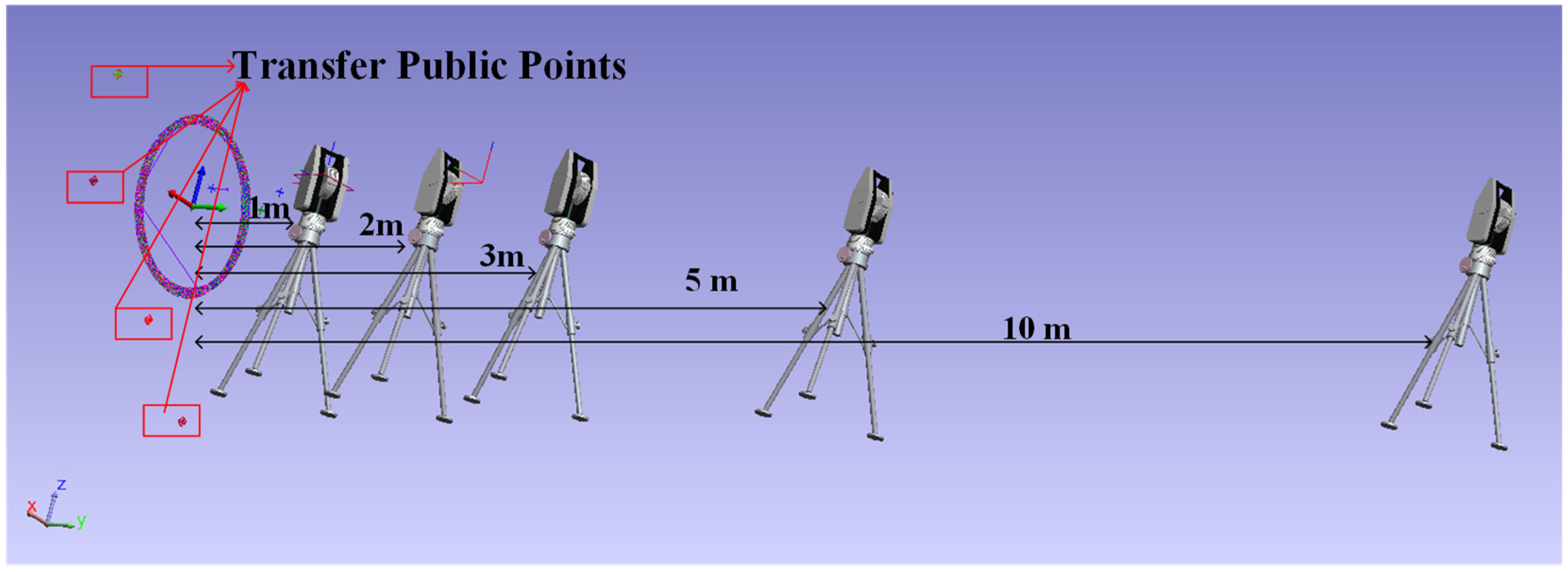
2. Circular Trajectory Generator Measurement System
3. Definition of Performance Test
3.1. Static Measurement
3.2. Dynamic Measurement
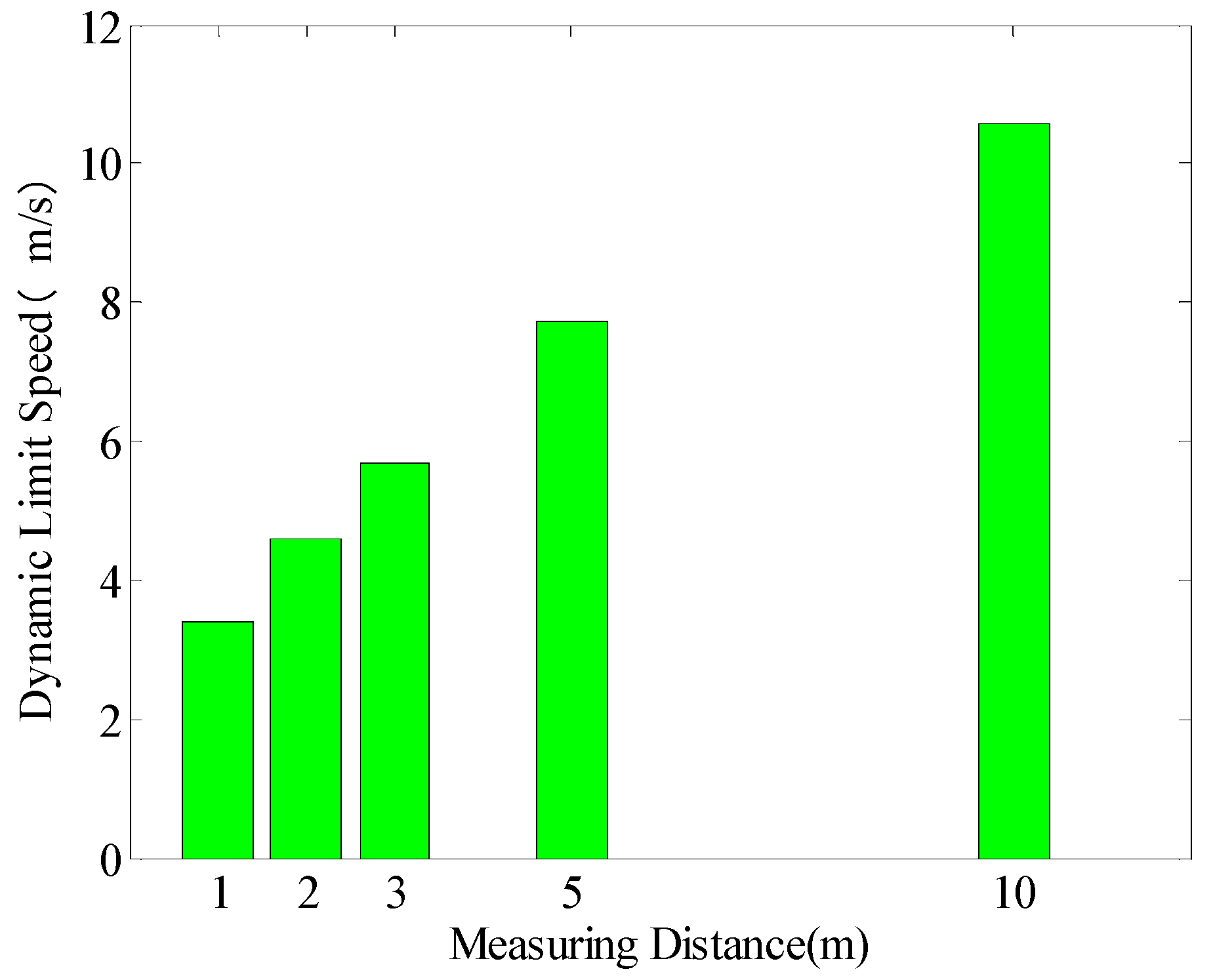
3.2.1. Dynamic Limit Rotational Velocity
3.2.2. Dynamic Indication Error
3.2.3. Dynamic Indication Variable
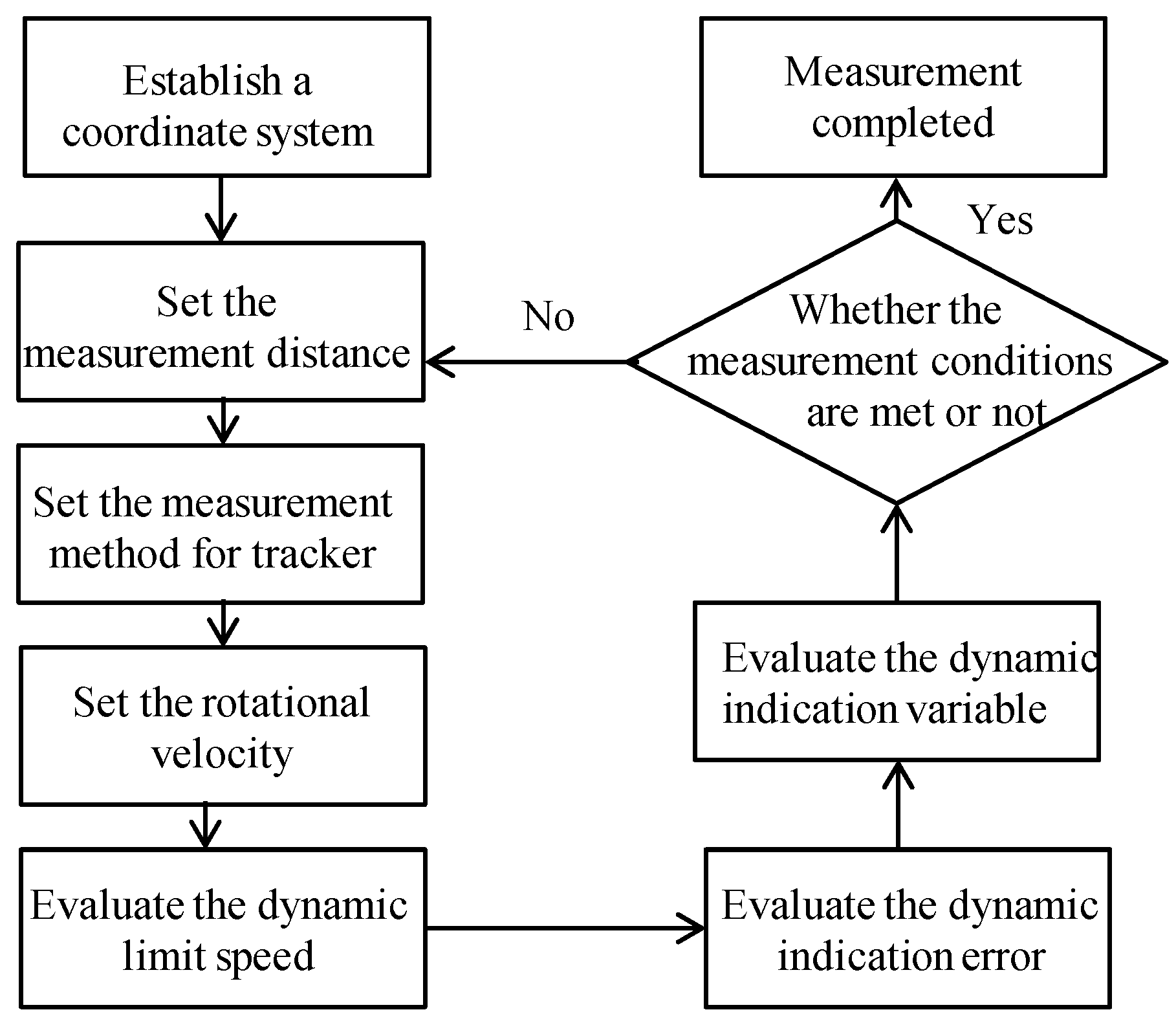
4. Measurement Methods and Data Analysis
4.1. Measurement Methods
4.2. Data Analysis
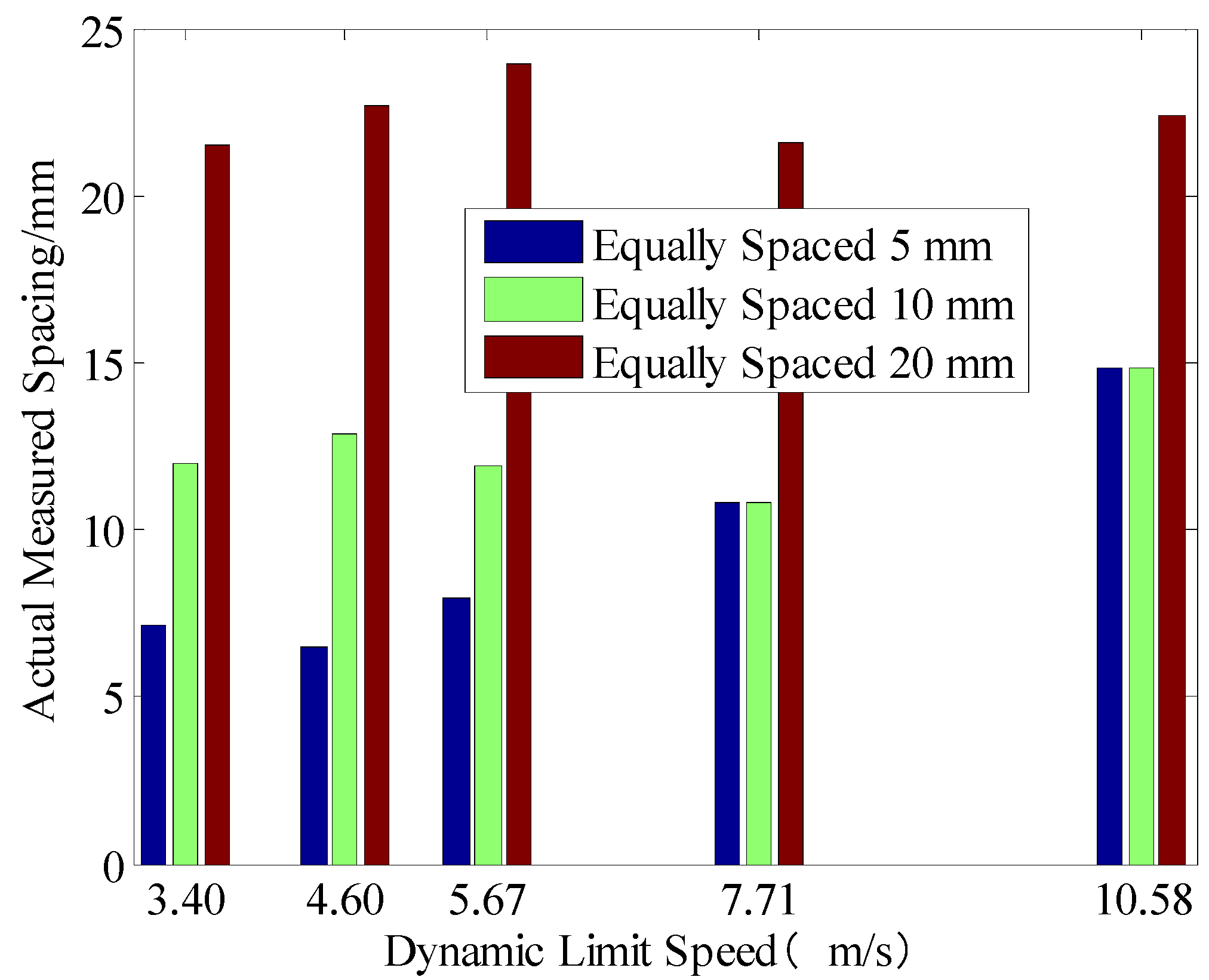
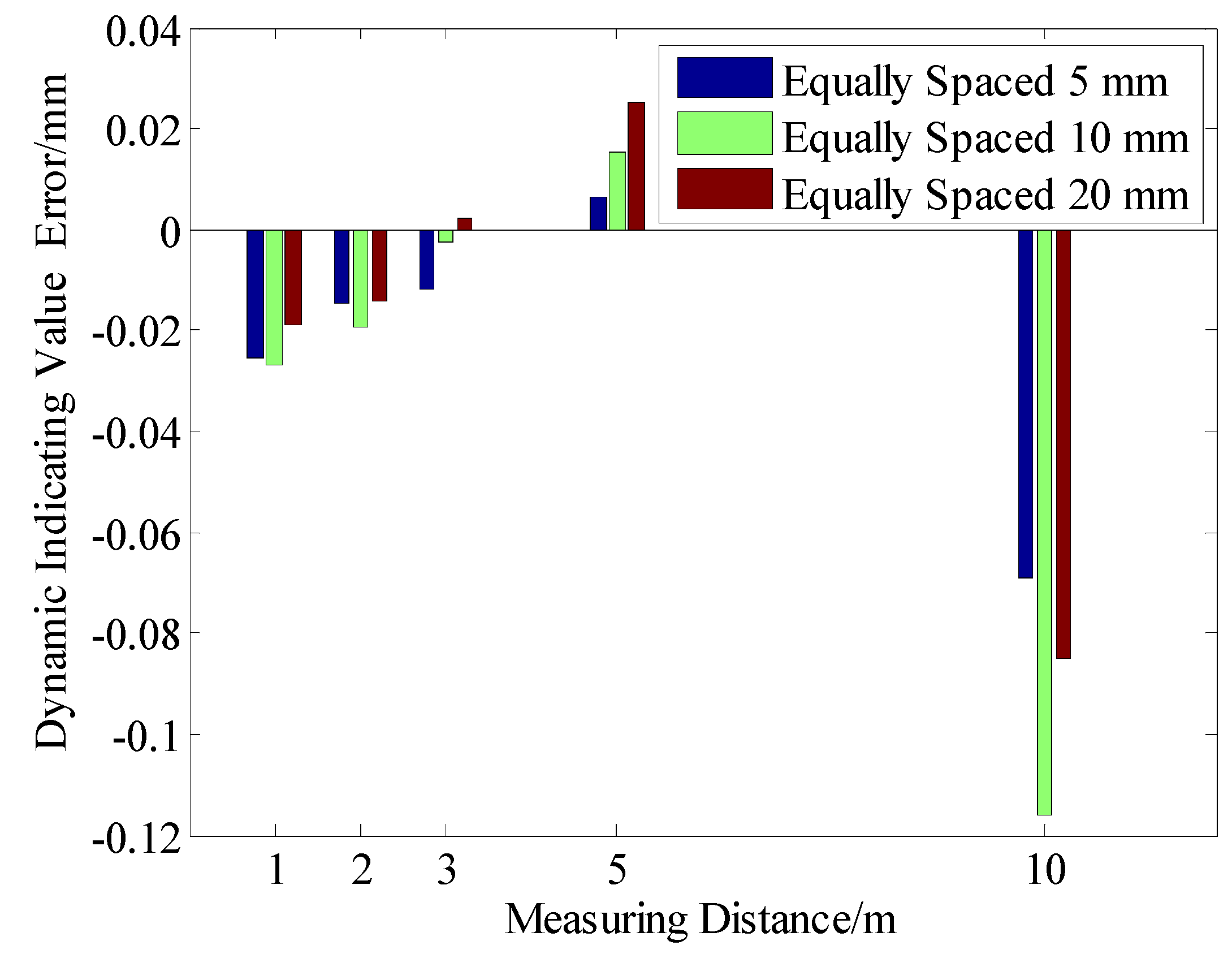
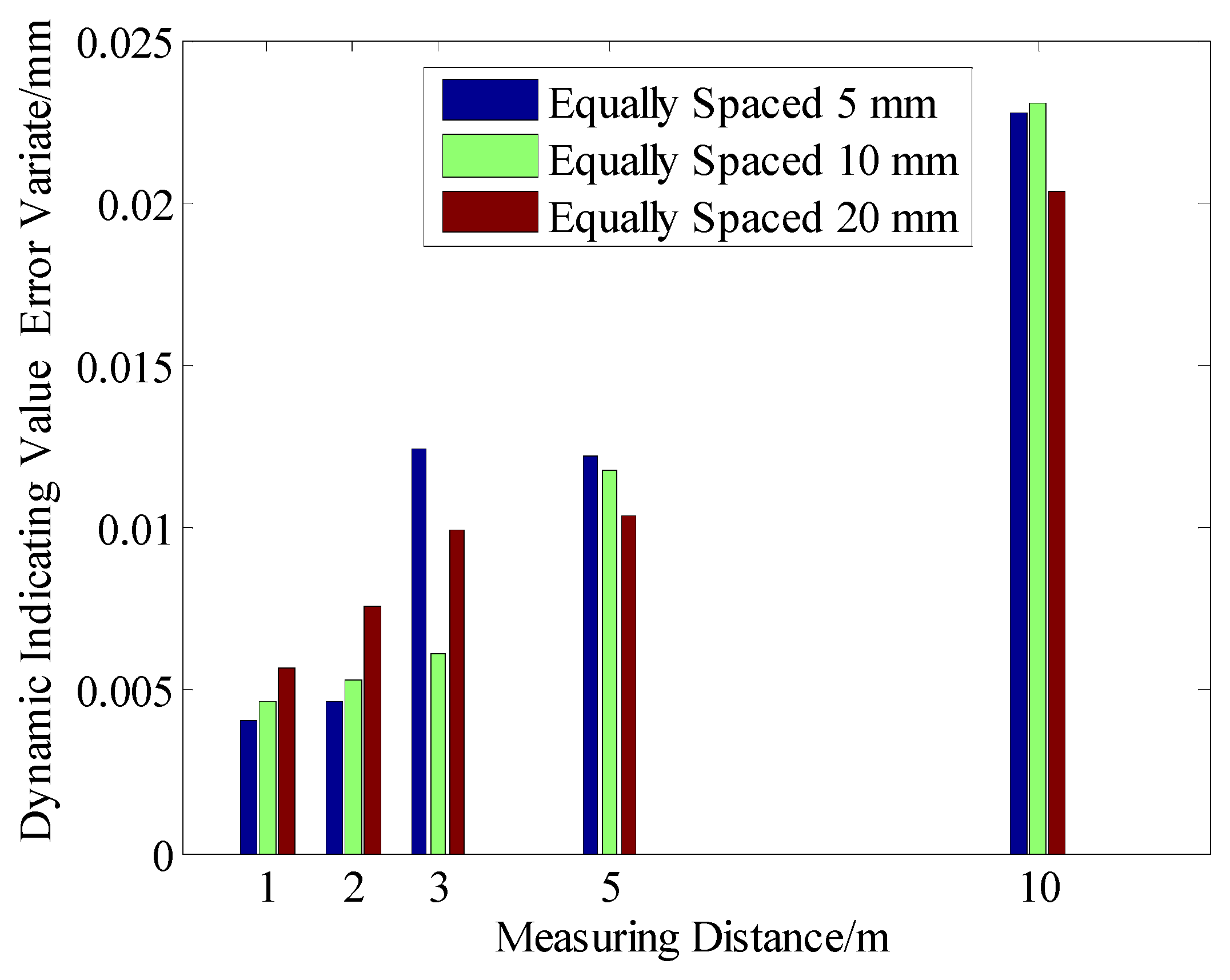
4.2.1. Analysis of the Data Collected at Different Distances with Equal Spacing
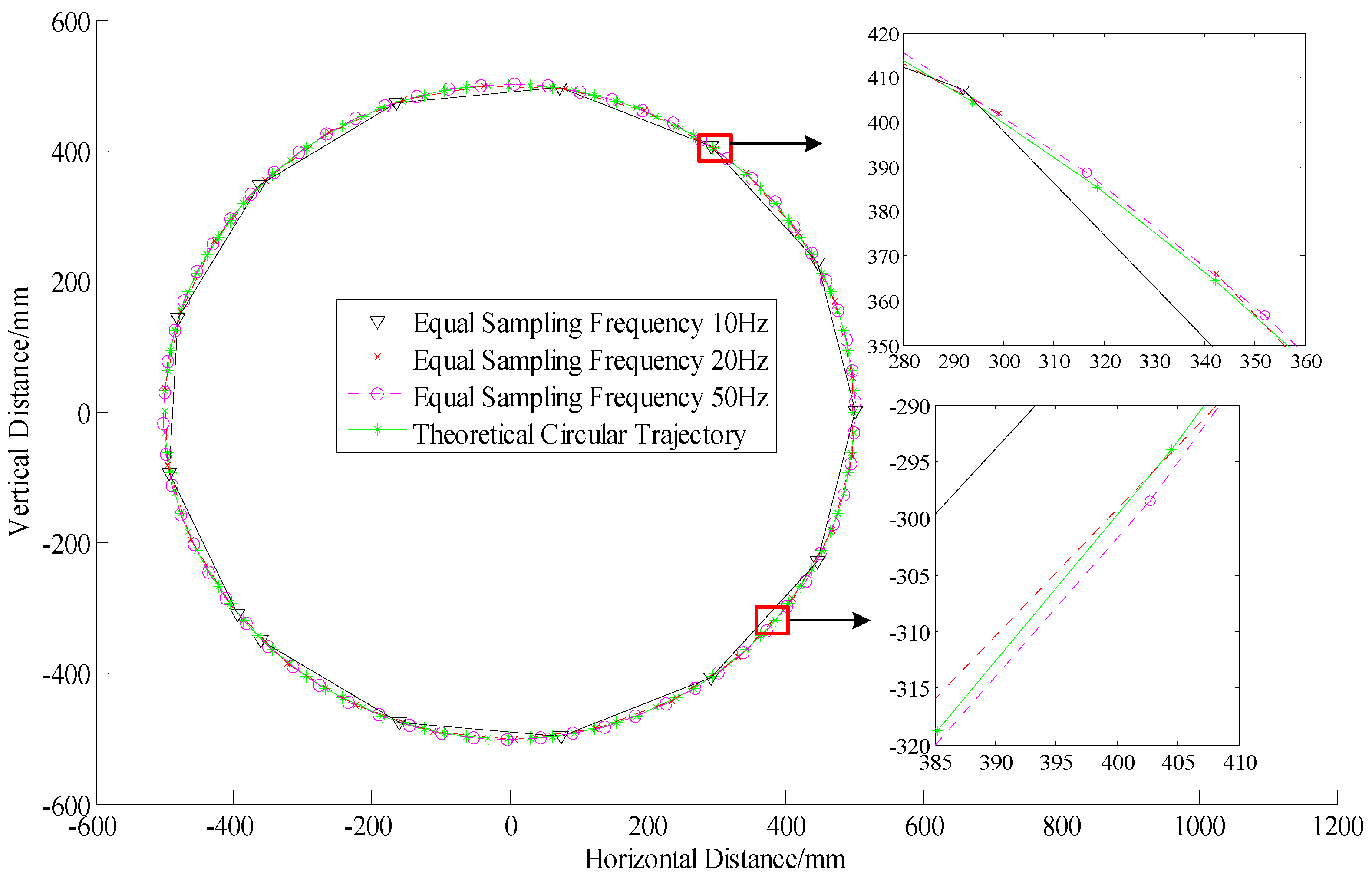
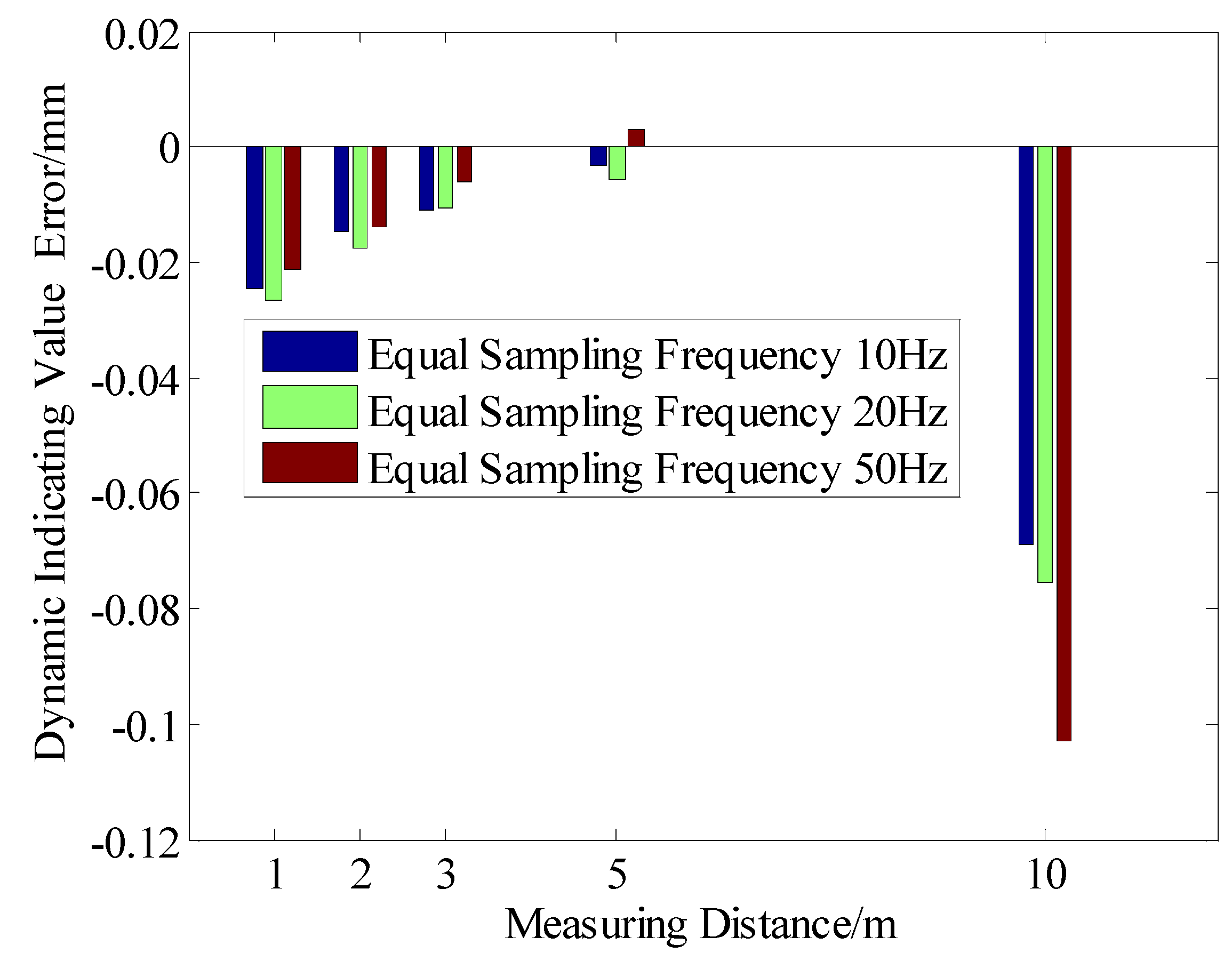
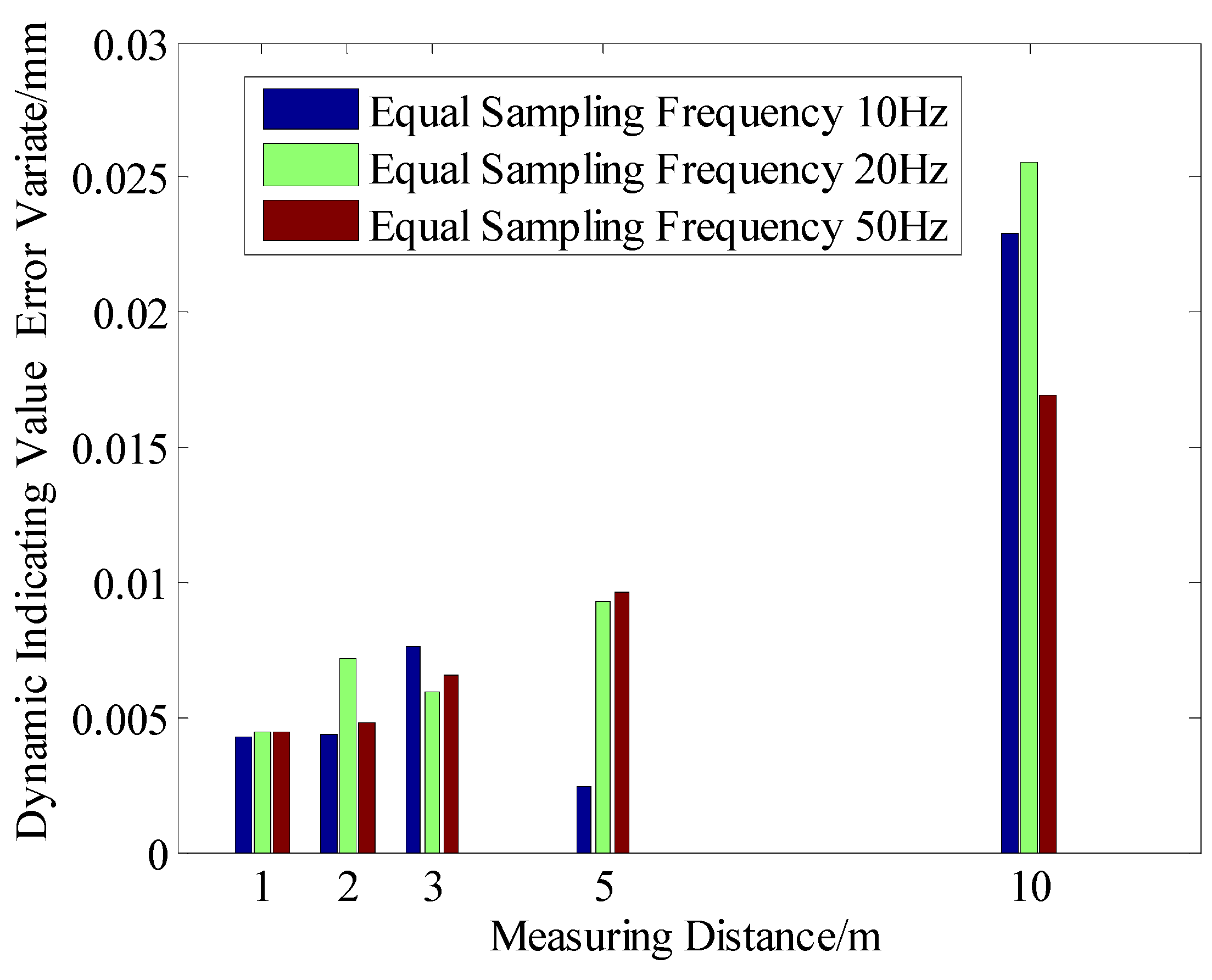
4.2.2. Data Analysis of Equal Sampling Frequency at Different Measurement Distances
4.2.3. Data Analysis at the Same Measurement Distance and Different Rotational Velocities
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, J.; Zhang, L.; Li, X. Several Primary Problems in the Development of Dynamic Metrology. Metrol. Meas. Technol. 2021, 41, 14. [Google Scholar]
- Gan, X.; Zhao, Z.; Ma, L. Calibration Status Analysis of Large Scale Measurement System Measurement Capability for Moving Target. Metrol. Meas. Technol. 2021, 38, 33–38. [Google Scholar]
- ASME B89.4.19; Performance Evaluation of Laser-Based Spherical Coordinate Measurement Systems. The American Society of Mechanical Engineers: New York, NY, USA, 2006.
- Wang, W.; Su, Y.; Ren, G.Y. A Study on Dynamic Character of Laser Tracker. Acta Metrol. Sin. 2007, 28, 36–38. [Google Scholar]
- State Administration for Market Regulation. JJF 1242-2010, Calibration Specification for Laser Tracker 3-Dimensional Measuring System; China Metrology Press: Beijing, China, 2010. [Google Scholar]
- Gan, X.-c.; Sun, A.-b.; Wang, J.-h.; Cao, T.-z.; Ma, L.-q. Calibration Method for Lateral Tracking Speed of Laser Tracker. Acta Metrol. Sin. 2014, 35, 39–44. [Google Scholar]
- Bi, S. Research on the Measurement Method of Target Motion Track Based on Laser Tracker; Shandong University of Science and Technology: Taian, China, 2020. [Google Scholar]
- Ma, Y.; Fan, B.; Huang, J. Research on the evaluation method of the accuracy of combined dynamic position and attitude measurement of multiple laser trackers. Eng. Surv. Map. 2021, 30, 55–59. [Google Scholar]
- Pan, T.; Fan, B.; Yi, W. Research on Evaluation Method of Laser Tracker Dynamic Accuracy. Bull. Surv. Map. 2016, 5, 54–56. [Google Scholar]
- Spiess, S.; Vincze, M. On the calibration of a 6-D laser tracking system for dynamic robot measurements. IEEE Trans. Instrum. Meas. 1998, 47, 270–274. [Google Scholar] [CrossRef]
- Brecher, C.; Ayromiou, M.; Guralnik, A.; Bäumler, S. Measurement of structure dynamics using a tracking-interferometer. Prod. Eng. 2012, 6, 89–96. [Google Scholar] [CrossRef]
- Slamani, M.; Nubiola, A.; Bonev, I. Assessment of the positioning performance of an industrial robot. Ind. Robot 2012, 39, 57–68. [Google Scholar] [CrossRef]
- Morse, E.; Welty, V. Dynamic testing of laser trackers. CIRP Ann. 2015, 64, 475–478. [Google Scholar] [CrossRef]
- Yang, J.; Wang, D.; Zhou, W. Precision laser tracking servo control system for moving target position measurement. Optik 2016, 131, 994–1002. [Google Scholar]
- Yao, L.; Sun, H.; Wang, X.; Zhou, Y. Detection of Track Static Regularities Based on a Laser Tracker. J. Surv. Eng. 2017, 143, 04016026. [Google Scholar] [CrossRef]
- Budzyn, G.; Rzepka, J.; Kaluza, P. Laser interferometer based instrument for 3D dynamic measurements of CNC machines geometry. Opt. Lasers Eng. 2021, 142, 106594. [Google Scholar] [CrossRef]
- Wang, T.; Xi, M.; Liu, H. Research on Evaluation and Experiment of Dynamic Measurement Uncertainty for On-machine Measurement. Modul. Mach. Tool Autom. Manuf. Tech. 2021, 1, 13–18. [Google Scholar]
- Lu, Y.; Zhu, W.; Huang, Y. Development of Dynamic Measuring Circuit of Circular Grating Angle Based on FPGA. Instrum. Tech. Sens. 2021, 3, 35–39. [Google Scholar]
- Huo, Z. Dynamic 3D Measurement Method of Rotating Object Based on Line Structured Light; Xi’an University of Technology: Xi’an, China, 2021. [Google Scholar]
- Yong, S. Research on Dynamic Measuring and Positioning Technology of Accurate Laser Positioning System (ALPS) in Large-scale Space; Xi’an University of Technology: Xi’an, China, 2021. [Google Scholar]
- Fu, Y.; Chen, B.; Yan, K.; Miao, H.; Yu, Q. Engineering-oriented laser interferometric dynamic measurement: A review. J. Exp. Mech. 2021, 36, 1–16. [Google Scholar]

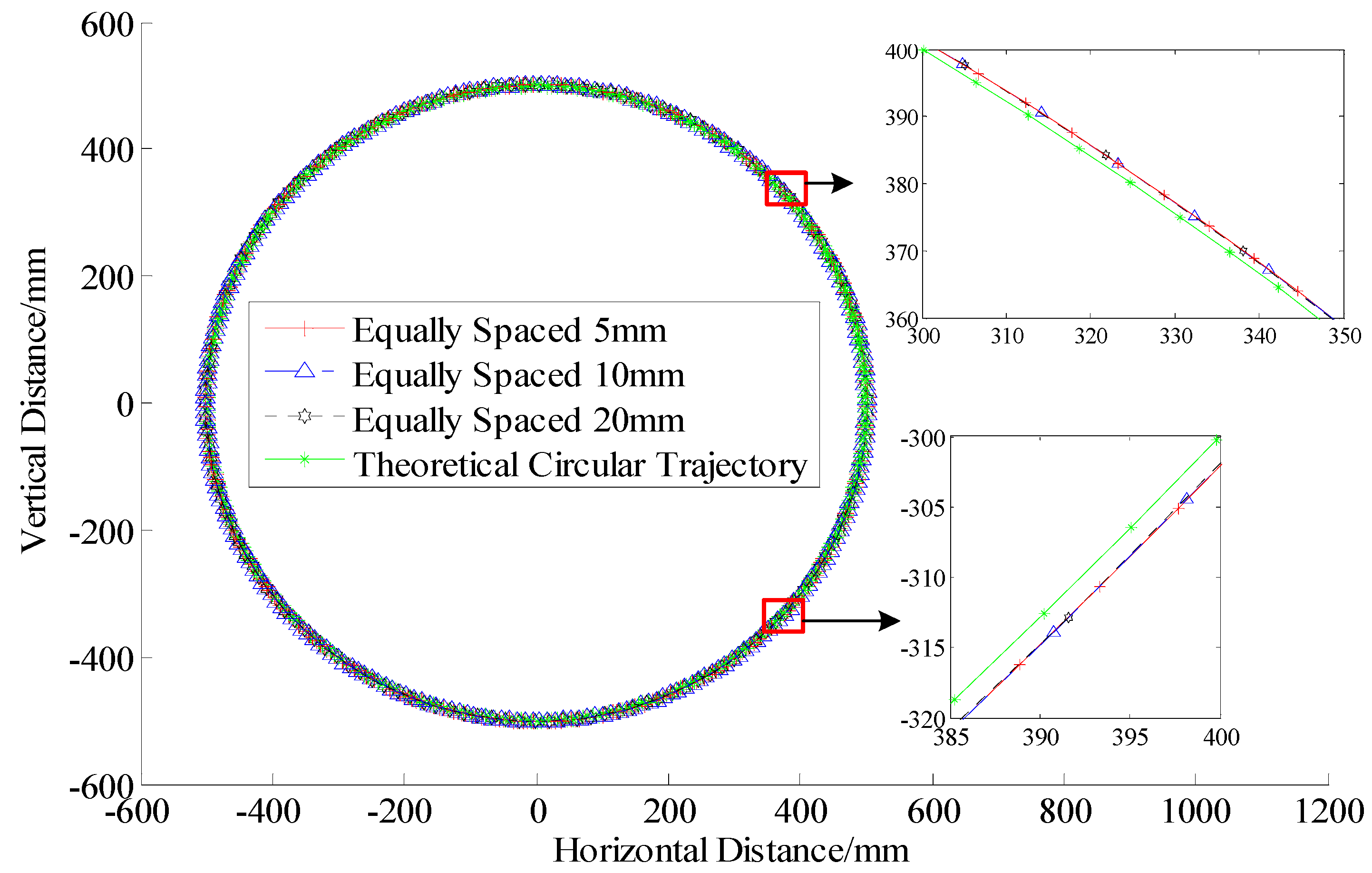


| Measurement Distance | Dynamic limit Rotational Velocity (m/s) | Equal Spacing Measurement (5 mm) | Equal Spacing Measurement (10 mm) | Equal Spacing Measurement (20 mm) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dynamic Indication Error (mm) | Dynamic Indication Variable (mm) | Actual Spacing (mm) | Number of Measurement Points | Dynamic Indication Error (mm) | Dynamic Indication Variable (mm) | Actual Spacing (mm) | Number of Measurement Points | Dynamic Indication Error (mm) | Dynamic Indication Variable (mm) | Actual Spacing (mm) | Number of Measurement Points | ||
| 1 m | 3.40 | −0.0253 | 0.00409 | 7.17 | 440 | −0.0273 | 0.00468 | 11.96 | 265 | −0.0191 | 0.00571 | 21.49 | 147 |
| 2 m | 4.60 | −0.0146 | 0.00462 | 6.47 | 489 | −0.0194 | 0.00535 | 12.84 | 244 | −0.0143 | 0.00762 | 22.67 | 140 |
| 3 m | 5.67 | −0.0117 | 0.01240 | 7.96 | 396 | −0.0026 | 0.00615 | 11.94 | 264 | 0.0020 | 0.00995 | 23.93 | 133 |
| 5 m | 7.71 | 0.0064 | 0.01224 | 10.83 | 292 | 0.0156 | 0.01176 | 10.83 | 292 | 0.0251 | 0.01037 | 21.56 | 147 |
| 10 m | 10.58 | −0.0689 | 0.02275 | 14.81 | 213 | −0.1158 | 0.02309 | 14.82 | 212 | −0.0852 | 0.02035 | 22.37 | 142 |
| Measurement Spacing | Equal Sampling Frequency (10 Hz) | Equal Sampling Frequency (20 Hz) | Equal Sampling Frequency (50 Hz) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Dynamic Indication Error (mm) | Dynamic Indication Variable (mm) | Number of Measurement Points | Dynamic Indication Error (mm) | Dynamic Indication Variable (mm) | Number of Measurement Points | Dynamic Indication Error (mm) | Dynamic Indication Variable (mm) | Number of Measurement Points | |
| 1 m | −0.0244 | 0.00428 | 14 | −0.0266 | 0.00448 | 27 | −0.0214 | 0.00440 | 66 |
| 2 m | −0.0145 | 0.00436 | 10 | −0.0176 | 0.00719 | 20 | −0.0137 | 0.00477 | 49 |
| 3 m | −0.0110 | 0.00796 | 8 | −0.0107 | 0.00596 | 16 | −0.0060 | 0.00659 | 40 |
| 5 m | −0.0034 | 0.00241 | 6 | −0.0056 | 0.00930 | 12 | 0.0029 | 0.00960 | 30 |
| 10 m | −0.0690 | 0.02296 | 5 | −0.0753 | 0.02553 | 9 | −0.1031 | 0.01694 | 22 |
| Rotational Velocity (r/s) | Equal Sampling Frequency (10 Hz) | Equal Sampling Frequency (20 Hz) | Equal Sampling Frequency (50 Hz) | |||
|---|---|---|---|---|---|---|
| Dynamic Indication Error (mm) | Number of Measurement Points | Dynamic Indication Error (mm) | Number of Measurement Points | Dynamic Indication Error (mm) | Number of Measurement Points | |
| 0.2 | −0.0118 | 48 | −0.0097 | 96 | −0.0109 | 240 |
| 0.6 | −0.0085 | 17 | −0.0079 | 33 | −0.0047 | 83 |
| 1.0 | −0.0047 | 10 | −0.0117 | 20 | 0.0058 | 50 |
| 1.4 | −0.0080 | 8 | −0.0148 | 15 | −0.0017 | 36 |
| 1.8 | −0.0335 | 6 | −0.0121 | 12 | −0.0403 | 28 |
| Rotational Velocity (r/s) | Equal Spacing Measurement (5 mm) | Equal Spacing Measurement (10 mm) | Equal Spacing Measurement (5 mm) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Dynamic Indication Error (mm) | Actual Spacing (mm) | Number of Measurement Points | Dynamic Indication Error (mm) | Actual Spacing (mm) | Number of Measurement Points | Dynamic Indication Error (mm) | Actual Spacing (mm) | Number of Measurement Points | |
| 0.2 | −0.0081 | 5.21 | 600 | −0.0067 | 10.47 | 300 | −0.0076 | 20.27 | 155 |
| 0.6 | −0.0066 | 5.75 | 549 | −0.0142 | 11.51 | 274 | −0.0064 | 21.05 | 150 |
| 1.0 | −0.0033 | 6.35 | 497 | −0.0121 | 12.61 | 249 | −0.0065 | 22.12 | 143 |
| 1.4 | −0.0260 | 8.87 | 356 | −0.0179 | 13.28 | 237 | −0.0037 | 22.12 | 143 |
| 1.8 | −0.0310 | 11.33 | 278 | −0.0436 | 11.39 | 278 | −0.0126 | 22.66 | 139 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, F.; Hu, C.; Sun, H.; Li, W. Study on Dynamic Performance Parameters of Laser Tracker Based on Self-Developed Circular Trajectory Generator System. Appl. Sci. 2023, 13, 167. https://doi.org/10.3390/app13010167
Lv F, Hu C, Sun H, Li W. Study on Dynamic Performance Parameters of Laser Tracker Based on Self-Developed Circular Trajectory Generator System. Applied Sciences. 2023; 13(1):167. https://doi.org/10.3390/app13010167
Chicago/Turabian StyleLv, Fei, Chang’an Hu, Haifeng Sun, and Wanze Li. 2023. "Study on Dynamic Performance Parameters of Laser Tracker Based on Self-Developed Circular Trajectory Generator System" Applied Sciences 13, no. 1: 167. https://doi.org/10.3390/app13010167
APA StyleLv, F., Hu, C., Sun, H., & Li, W. (2023). Study on Dynamic Performance Parameters of Laser Tracker Based on Self-Developed Circular Trajectory Generator System. Applied Sciences, 13(1), 167. https://doi.org/10.3390/app13010167






