Experimental Assessment of the Acoustic Performance of Nozzles Designed for Clean Agent Fire Suppression
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup and Procedure
- The first set was aimed at assessing the reliability of the experimental setup and measurements—mostly through statistical analysis—together with evaluating the potential directionality of SPL; these tests were carried out employing an inert gas mixture (i.e., IG55, 50% argon and 50% nitrogen) with a fixed nozzle diameter (5 mm) and pressure at the nozzle outlet; measurements were taken at various values of the distance between the nozzle and the sound level meter, also varying the angle of inclination of the sound level meter with respect to the nozzle.
- The second set was aimed at investigating the discharge of inert gases (nitrogen IG100, in the present case); these tests were carried out at varied orifice diameters, between 5 and 23 mm, while keeping the distance between the nozzle and the sound level meter constant and equal to 1 m (Figure 1).
- The third set was aimed at investigating the discharge of halocarbon compounds (FK-5-1-12, in the present case); these tests were carried out only using nozzles with 6 mm orifice diameter, given the higher cost of the involved substance; the distance between the nozzle and the sound level meter was also kept constant and equal to 1 m (Figure 1).
| Set | Nozzle Type | Clean Agent | Nozzle-to-Sound Meter Level Distance (m) | Nozzle Diameter (mm) |
|---|---|---|---|---|
| I | Silent | IG55 | 2.5 | 5 |
| Silent | IG55 | 1.25 | 5 | |
| Silent | IG55 | 5 | 5 | |
| Silent | IG55 | 1–2–4–8 * | 5 | |
| Standard | IG55 | 1–2–4–8 * | 5 | |
| II | Silent | IG100 | 1 | 5 |
| Standard | IG100 | 1 | 5 | |
| Silent | IG100 | 1 | 10 | |
| Standard | IG100 | 1 | 10 | |
| Silent | IG100 | 1 | 14 | |
| Standard | IG100 | 1 | 14 | |
| Silent | IG100 | 1 | 17 | |
| Standard | IG100 | 1 | 17 | |
| Silent (low ceiling applications) | IG100 | 1 | 17 | |
| Silent | IG100 | 1 | 23 | |
| Standard | IG100 | 1 | 23 | |
| III | Standard | FK-5-1-12 | 1 | 6 |
| Silent (low ceiling applications) | FK-5-1-12 | 1 | 6 |
2.2. Data Processing and Analysis
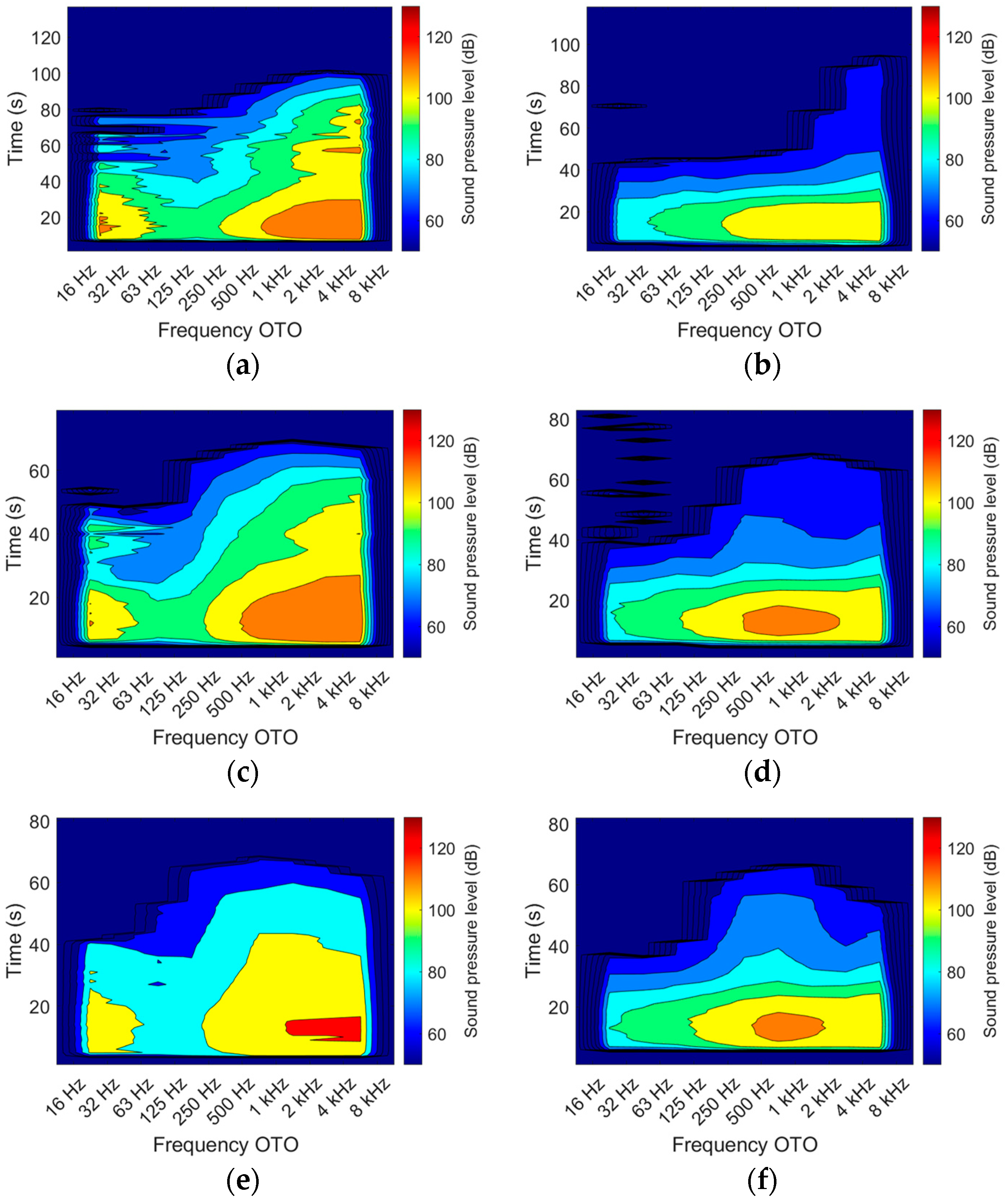
- Determining and comparing the acoustic performance of standard and silent nozzles; to this end, SPL is presented as a function of released flow rate and time for both tested clean agents and for the whole set of investigated orifice diameters; the results from spectral analysis by octave bands are also included.
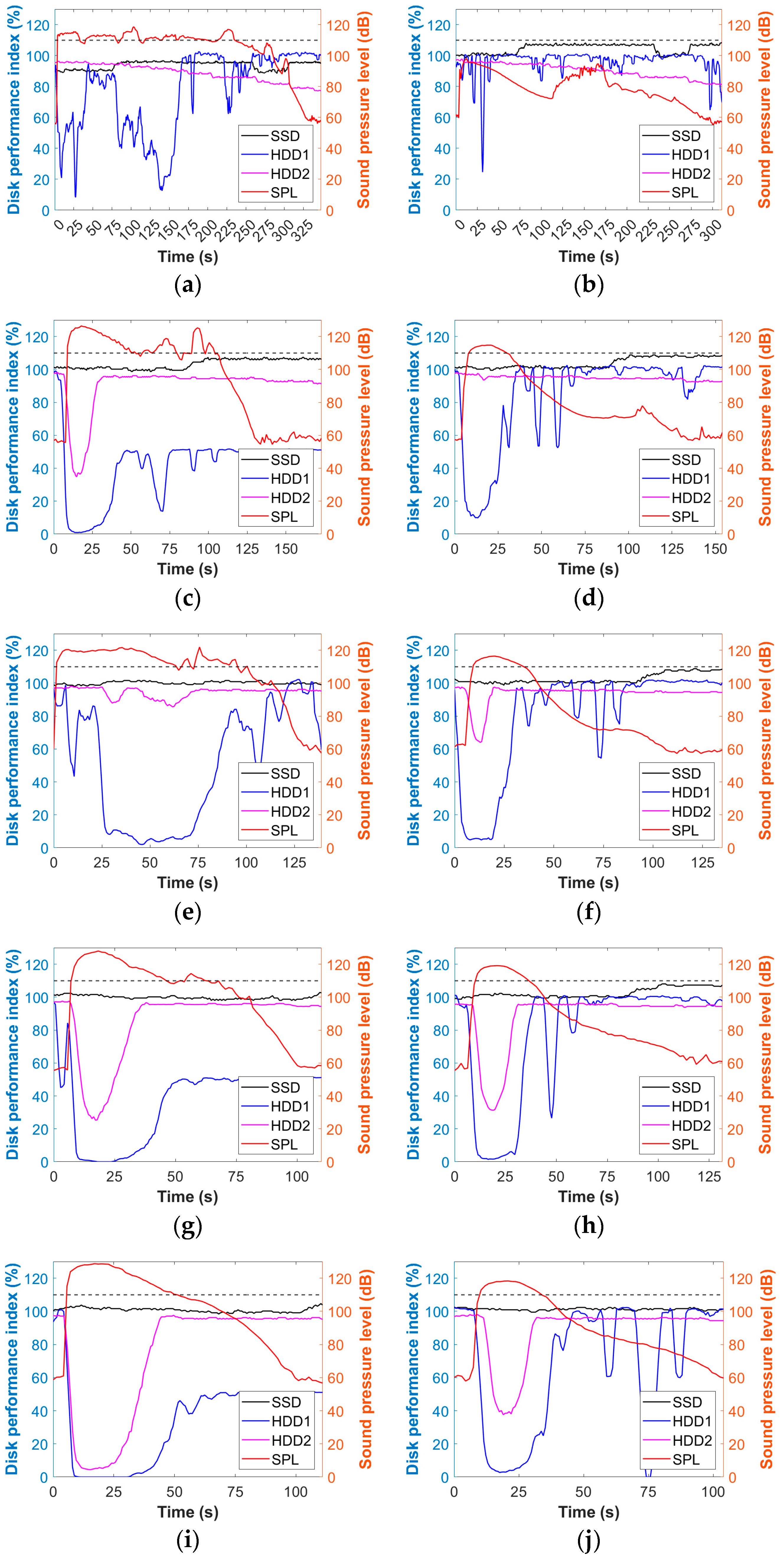
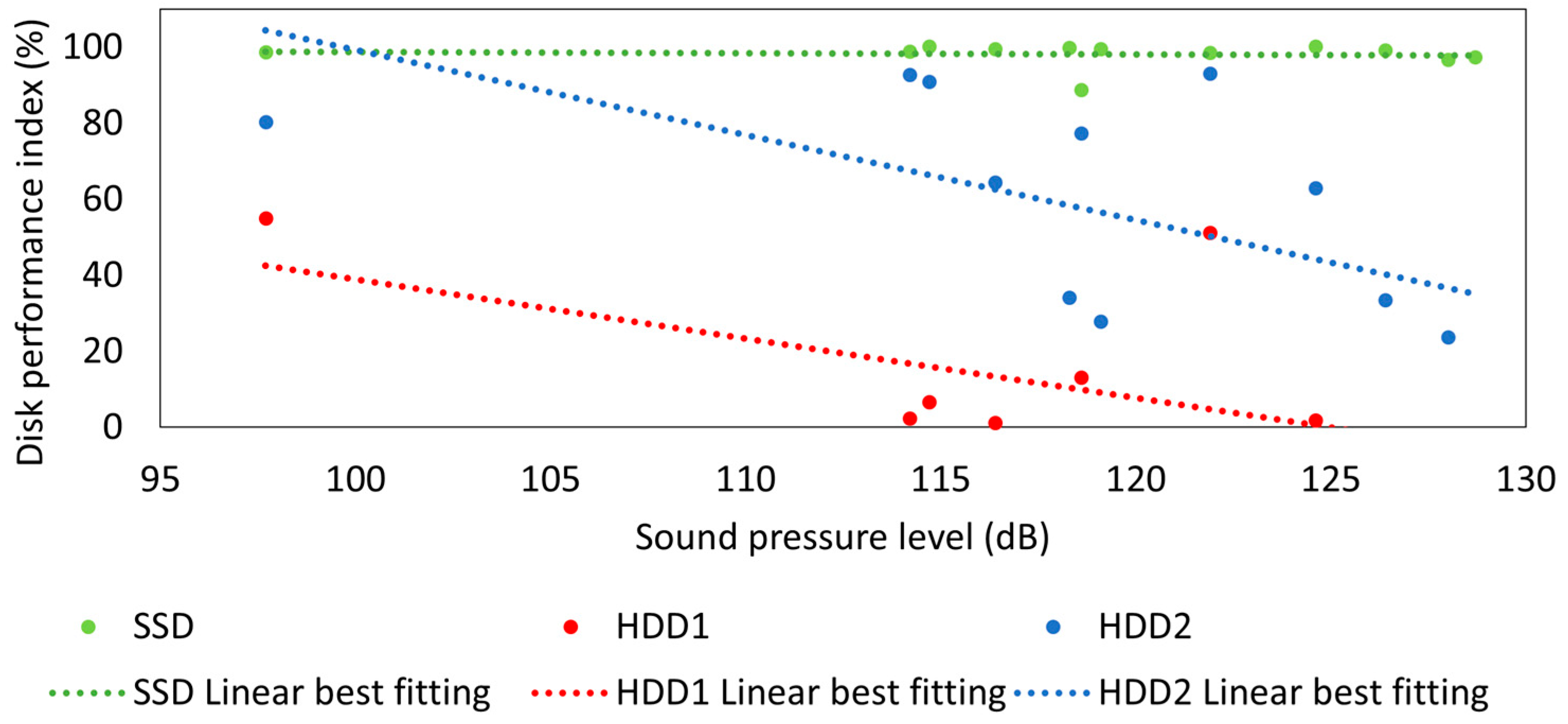
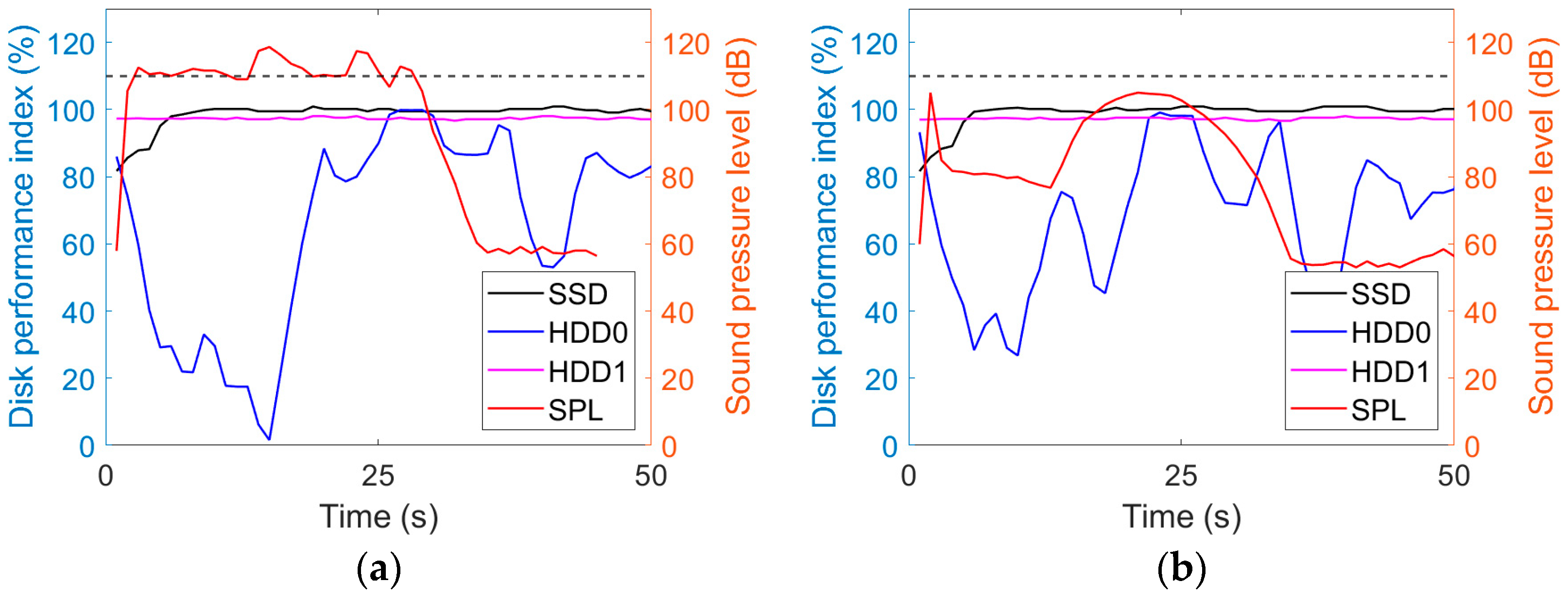
- Evaluating the effect of SPL on the different tested hard drives and highlighting quantitatively the performance loss in the same configuration towards a comparison between standard and silent nozzles; to this end, an index of the disk behavior and performance through the discharge is proposed as inspired by a recent report [20], which produces measurements of read/write speed and includes that under the SPL due to white noise (i.e., baseline speed).
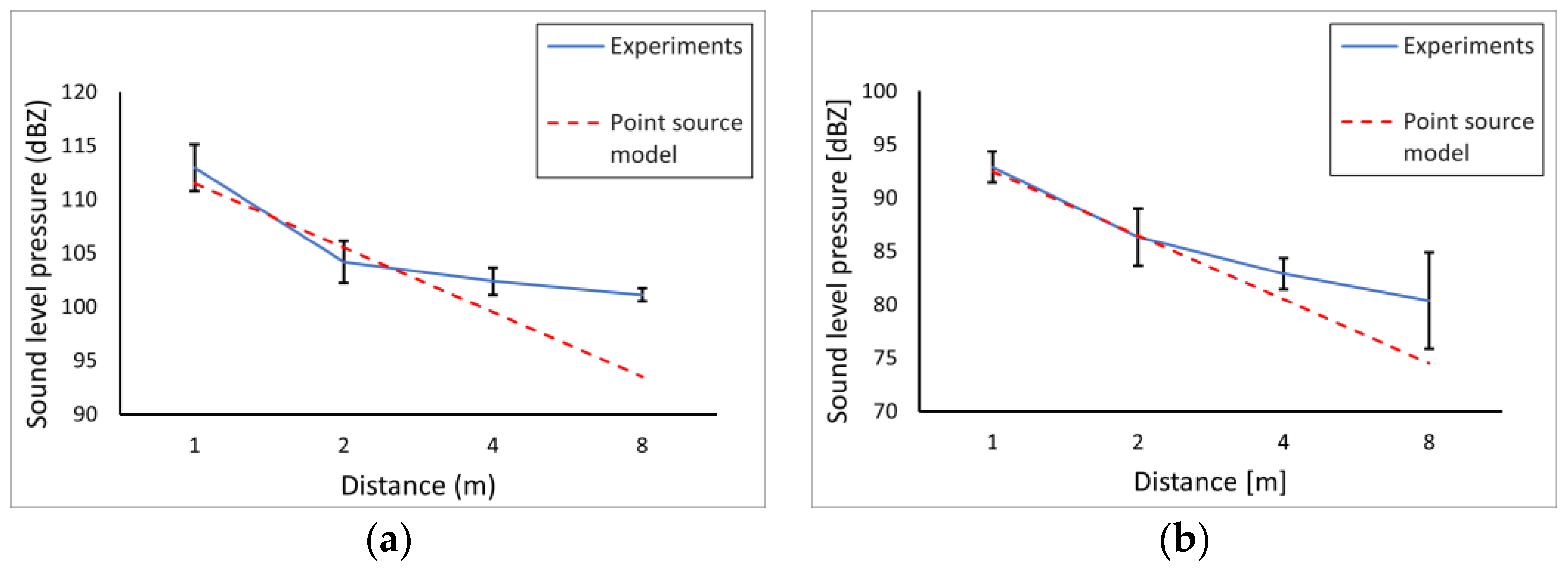
- Checking the applicability of the point source model [22], which supports the proposed design of the experimental setup, where SPL was measured at the location described in Section 2.1 and shown in Figure 1, without resorting to an array of microphones, as in [15]; this preliminary evaluation is included in Section 2.3.
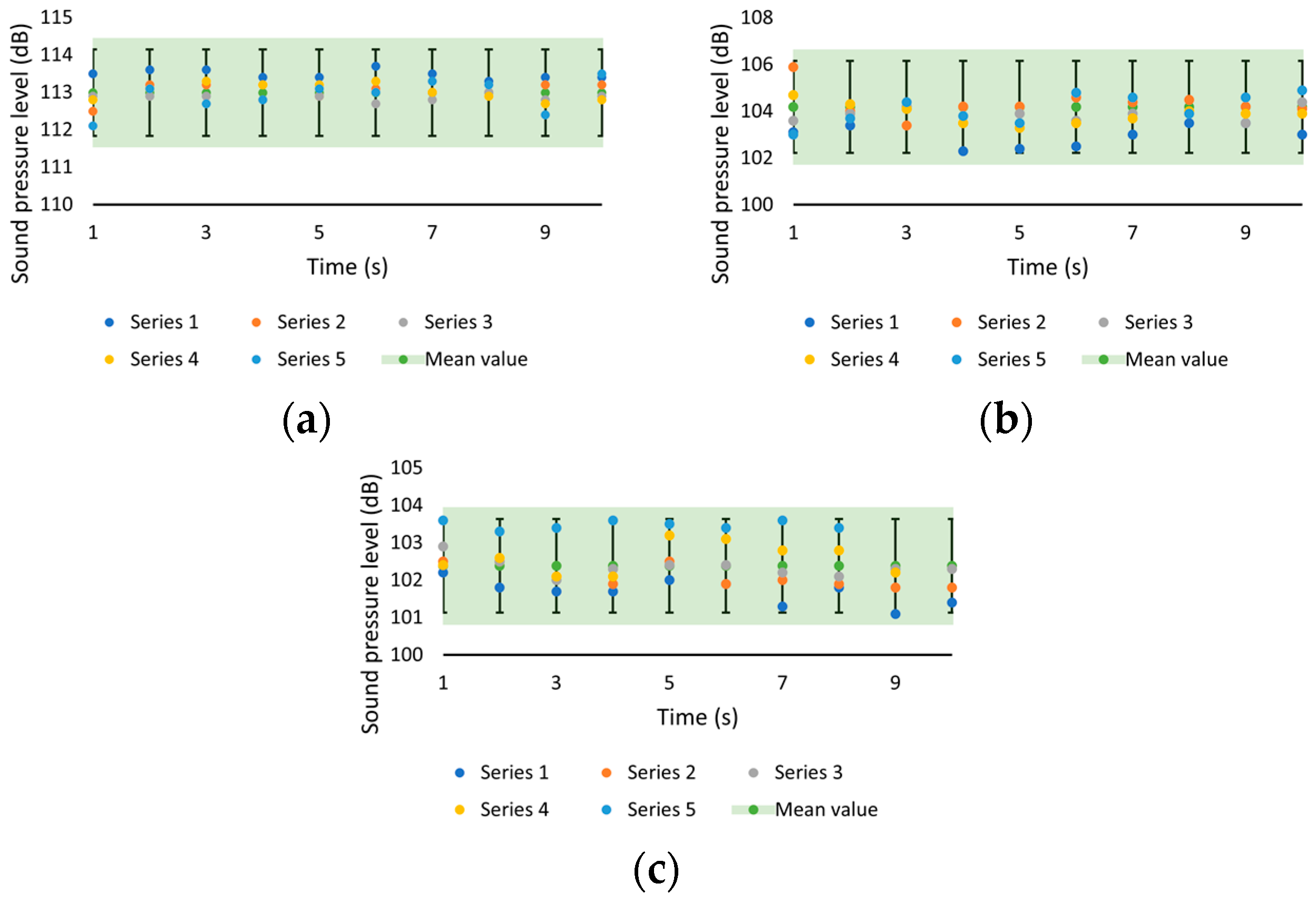
- Evaluating standard deviation [23] of the acquired data—mainly the SPL dataset as a function of time or released flow rate over repeated tests under the same configuration—in order to assess repeatability.
2.3. Applicability of Point Source Model and Statistical Analysis
3. Results and Discussion
3.1. Discharge of Inert Gases: Effect of Generated Noise
3.2. Discharge of Halocarbon Compounds: Effect of Generated Noise
3.3. Overview of the Relationship between Flow Rate and Noise
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grant, C.C. Halon design calculations. In SFPE Handbook of Fire Protection Engineering; DiNenno, P.J., Drysdale, D., Beyler, C.L., Walton, W.D., Custer, R.L.P., Hall, J.R., Jr., Watts, J.M., Jr., Eds.; National Fire Protection Association: Quincy, MA, USA, 2002; Section 4, Chapters 4–6; pp. 149–172. [Google Scholar]
- DiNenno, P.J. Halon replacement clean agent total flooding systems. In SFPE Handbook of Fire Protection Engineering; DiNenno, P.J., Drysdale, D., Beyler, C.L., Walton, W.D., Custer, R.L.P., Hall, J.R., Jr., Watts, J.M., Jr., Eds.; National Fire Protection Association: Quincy, MA, USA, 2002; Section 4, Chapters 4–7; pp. 173–200. [Google Scholar]
- Kim, Y.-H.; Lee, M.; Hwang, I.-J.; Kim, Y.-J. Noise reduction of an extinguishing nozzle using the Response Surface Method. Energies 2019, 12, 4346. [Google Scholar] [CrossRef] [Green Version]
- Mann, M.T.; Coll, M. Potential Problems with Computer Hard Disks When Fire Extinguishing Systems Are Released; Siemens Switzerland: Zug, Switzerland, 2010. [Google Scholar]
- Lilley, G.M. Aerodynamic noise—A review of the contributions to jet noise research at the College of Aeronautics, Cranfield 1949-1961 (together with some recent conclusions). Aeronaut. J. 1984, 88, 213–223. [Google Scholar]
- Tam, C.K.W.; Tanna, H.K. Shock associated noise of supersonic jets from convergent-divergent nozzles. J. Sound Vib. 1982, 81, 337–358. [Google Scholar] [CrossRef]
- Tam, C.K.W. Influence of nozzle geometry on the noise of high-speed jets. AIAA J. 1998, 36, 1396–1400. [Google Scholar] [CrossRef]
- Dutta, T.; Barnard, A.R. Performance of hard disk drives in high noise environments. Noise Control Eng. J. 2017, 65, 386–395. [Google Scholar] [CrossRef] [Green Version]
- Green, K.; Nelson, D.; Pai, N.; Nickerson, M. Hard drive performance degradation due to high level noise in data centers. In Proceedings of the 40th International Congress and Exposition on Noise Control Engineering—Inter-Noise, Osaka, Japan, 4–7 September 2011. [Google Scholar]
- Nickerson, M.L.; Green, K.; Pai, N. Tonal noise sensitivity in hard drives. Proc. Meet. Acoust. 2014, 20, 040006. [Google Scholar]
- Daigle, B. Data Centers around the World: A Quick Look; United States International Trade Commission: Washington, DC, USA, 2021.
- Loureiro, M.A.; Elder, A.; Ahmadzadegan, A. Acoustic nozzle design for fire protection application. In Proceedings of the 2017 Suppression, Detection, and Signaling Research and Applications Conference (SUPDET 2017) and 16th International Conference on Fire Detection (AUBE’17), College Park, MD, USA, 12–14 September 2017. [Google Scholar]
- Kim, Y.-H.; Yoo, H.-S.; Hwang, I.-J.; Kim, Y.-J. Influence of the nozzle contraction angles of gaseous extinguishing systems on discharge noise. Fire Sci. Eng. 2019, 33, 77–82. [Google Scholar] [CrossRef] [Green Version]
- Mihalace, C.-M.; Bigan, C.; Panduru, V.; Tsakiris, C. Modelling of noise reduction for datacentre buildings fire protection with inert gas systems. MATEC Web Conf. 2019, 290, 12006. [Google Scholar] [CrossRef]
- Koushik, S.; McCormick, D.; Cao, C.; Corn, M. Acoustic impact of fire suppression nozzles. In Proceedings of the 2017 Suppression, Detection, and Signaling Research and Applications Conference (SUPDET 2017) and 16th International Conference on Fire Detection (AUBE’17), College Park, MD, USA, 12–14 September 2017. [Google Scholar]
- NFPA 75; Standard for the Fire Protection of Information Technology Equipment. National Fire Protection Association: Quincy, MA, USA, 2020.
- Silence Is Golden—Maintaining the Integrity of HDD’s in a Noisy Situation; Fire Eater: Hillerød, Denmark, 2016.
- Effect of Sound Waves on Data Storage Devices; Fire Suppression Systems Association: Baltimore, MD, USA, 2018.
- Sandahl, D.; Elder, A.; Barnard, A. Impact of Sound on Computer Hard Disk Drives and Risk Mitigation Measures; Form no. T-2016367-01; Johnson Controls: Milwaukee, WI, USA, 2018. [Google Scholar]
- Silent Extinguishing; Siemens Switzerland: Zug, Switzerland, 2022.
- Silva, R.A.; Buiatti, C.M.; Cruz, S.L.; Pereira, J.A.F.R. Pressure wave behaviour and leak detection in pipelines. Comput. Chem. Eng. 1996, 20, 5491–5496. [Google Scholar] [CrossRef]
- Li, K.M.; Waters-Fuller, T.; Attenborough, K. Sound propagation from a point source over extended-reaction ground. J. Acoust. Soc. Am. 1998, 104, 679. [Google Scholar] [CrossRef]
- Coleman, H.W.; Steele, W.G. Experimentation and Uncertainty Analysis for Engineers; Wiley: New York City, NY, USA, 1999. [Google Scholar]
- Tilton, J.N. Fluid and particle dynamics. In Perry’s Chemical Engineers’ Handbook; Perry, R.H., Green, D.W., Eds.; McGraw-Hill: New York City, NY, USA, 1997; Section 6; pp. 1–54. [Google Scholar]
- CoolProp. Available online: http://www.coolprop.org/ (accessed on 24 August 2022).
- Santangelo, P.E.; Jacobs, B.C.; Ren, N.; Sheffel, J.A.; Corn, M.L.; Marshall, A.W. Suppression effectiveness of water-mist sprays on accelerated wood-crib fires. Fire Saf. J. 2014, 70, 98–111. [Google Scholar] [CrossRef]
- Santangelo, P.E.; Tarozzi, L.; Tartarini, P. Full-scale experiments of fire control and suppression in enclosed car parks: A comparison between sprinkler and water-mist systems. Fire Technol. 2016, 52, 1369–1407. [Google Scholar] [CrossRef]
- Cannio, M.; Righi, S.; Santangelo, P.E.; Romagnoli, M.; Pedicini, R.; Carbone, A.; Gatto, I. Smart catalyst deposition by 3D printing for Polymer Electrolyte Membrane Fuel Cell manufacturing. Renew. Energy 2021, 163, 414–422. [Google Scholar] [CrossRef]
- Mi, J.; Xu, M.; Zhou, T. Reynolds number influence on statistical behaviors of turbulence in a circular free jet. Phys. Fluids 2013, 25, 075101. [Google Scholar] [CrossRef]
- White, F.M. Viscous Fluid Flow; McGraw-Hill: New York City, NY, USA, 2006. [Google Scholar]
- Dutta, T. Performance of Hard Disk Drives in High Noise Environments. Master’s Thesis, Michigan Technological University, Houghton, MI, USA, 2017. [Google Scholar]
- Thongchom, C.; Jearsiripongkul, T.; Refahati, N.; Roudgar Saffari, P.; Roodgar Saffari, P.; Sirimontree, S.; Keawsawasvong, S. Sound transmission loss of a honeycomb sandwich cylindrical shell with functionally graded porous layers. Buildings 2022, 12, 151. [Google Scholar] [CrossRef]



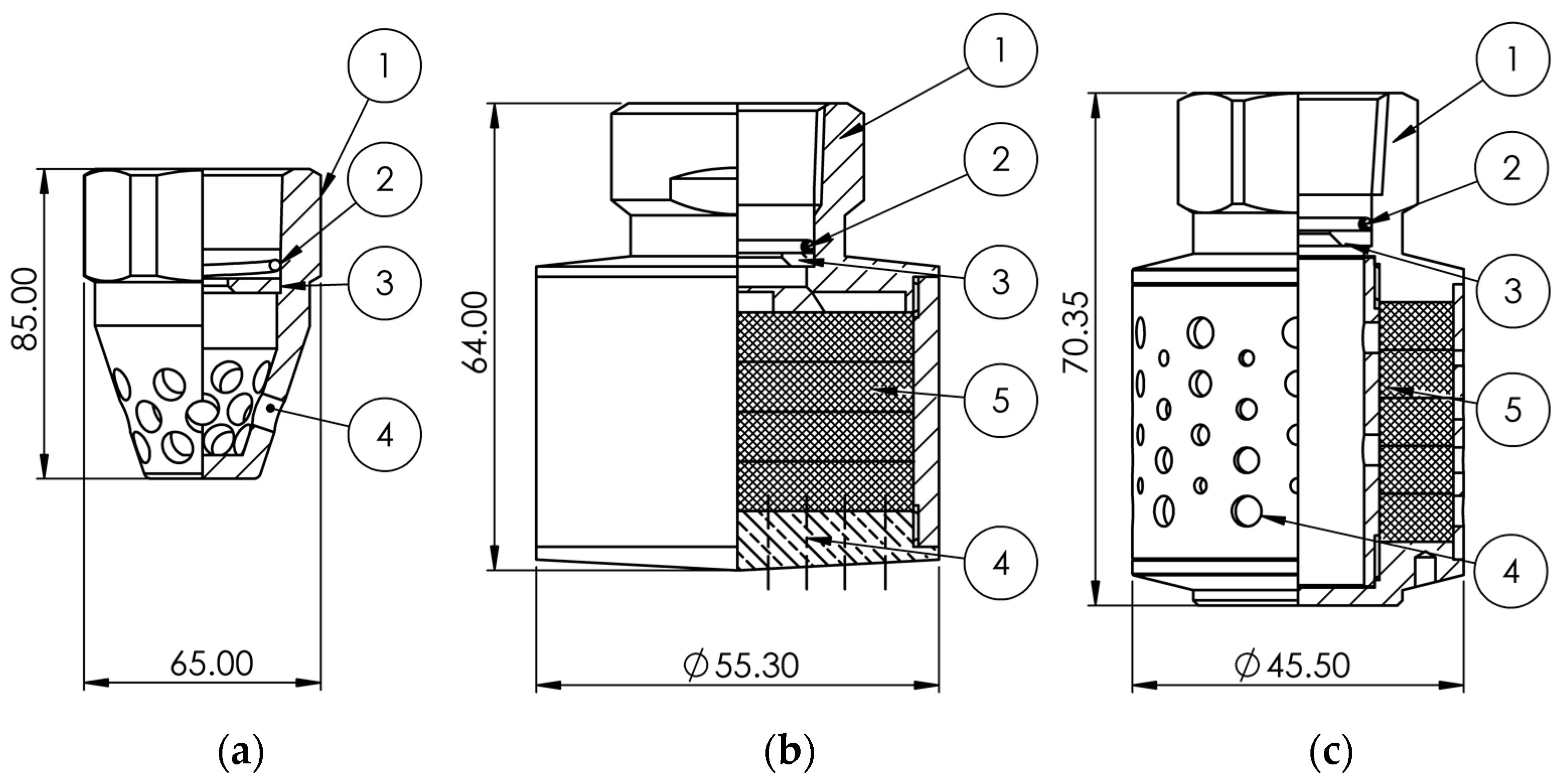


| Measured Parameter | Acquisition Frequency (Hz) | Instrument/ Sensor | Data Acquisition Board |
|---|---|---|---|
| Storage mass (cylinder + clean agent) | 10 | Scale P1250S5 by LAUMAS Elettronica, 1500 kg F.S. | NI 9208 board by National Instruments, 16 channels (current) |
| Pressure | 10 | Pressure transducer 21y by Keller, 400 bar F.S. ± 0.1 bar accuracy | |
| Temperature | 10 | Thermocouple T type, 1.0 mm bead diameter, accuracy in accordance with standard IEC 60584 | NI 9212 board by National Instruments, 8 channels (thermocouple) |
| SPL | 1 | Sound level meter HD2010UC/A by Deltaohm, with spectral analysis by octave bands from 31.5 Hz to 8 kHz | Data stored on the instrument |
| Hard drive performance | 2 | – | Data recorded by HD Speed software, version 1.7 |
| Reference Name | Manufacturer | Model | Type | Rate of Rotation (rpm) | Nominal Speed * (MB/s) |
|---|---|---|---|---|---|
| SSD | Toshiba | OCZ-VERT EX3 MI SCSI | SSD | – | 229 |
| HDD1 | Hitachi | DeskStar 7K160 | HDD | 7200 | 77 |
| HDD2 | Western Digital | WD36 ADFD | HDD | 10,000 | 89 |
| Tested Condition (Nozzle Type, Clean Agent) | Scaling Factor a | Exponent b |
|---|---|---|
| Standard, nitrogen IG100 | 124.4 | 0.06788 |
| Silent, nitrogen IG100 | 112.3 | 0.1873 |
| Standard, FK-5-1-12 | 109 | 0.05422 |
| Silent for low ceiling applications, FK-5-1-12 | 80.49 | 0.2596 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strianese, M.; Torricelli, N.; Tarozzi, L.; Santangelo, P.E. Experimental Assessment of the Acoustic Performance of Nozzles Designed for Clean Agent Fire Suppression. Appl. Sci. 2023, 13, 186. https://doi.org/10.3390/app13010186
Strianese M, Torricelli N, Tarozzi L, Santangelo PE. Experimental Assessment of the Acoustic Performance of Nozzles Designed for Clean Agent Fire Suppression. Applied Sciences. 2023; 13(1):186. https://doi.org/10.3390/app13010186
Chicago/Turabian StyleStrianese, Marco, Nicolò Torricelli, Luca Tarozzi, and Paolo E. Santangelo. 2023. "Experimental Assessment of the Acoustic Performance of Nozzles Designed for Clean Agent Fire Suppression" Applied Sciences 13, no. 1: 186. https://doi.org/10.3390/app13010186
APA StyleStrianese, M., Torricelli, N., Tarozzi, L., & Santangelo, P. E. (2023). Experimental Assessment of the Acoustic Performance of Nozzles Designed for Clean Agent Fire Suppression. Applied Sciences, 13(1), 186. https://doi.org/10.3390/app13010186







