Abstract
Stock price prediction is crucial but also challenging in any trading system in stock markets. Currently, family of recurrent neural networks (RNNs) have been widely used for stock prediction with many successes. However, difficulties still remain to make RNNs more successful in a cluttered stock market. Specifically, RNNs lack power to retrieve discerning features from a clutter of signals in stock information flow. Making it worse, by RNN a single long time cell from the market is often fused into a single feature, losing all the information about time which is essential for temporal stock prediction. To tackle these two issues, we develop in this paper a novel hybrid neural network for price prediction, which is named frequency decomposition induced gate recurrent unit (GRU) transformer, abbreviated to FDGRU-transformer or FDG-trans). Inspired by the success of frequency decomposition, in FDG-transformer we apply empirical model decomposition to decompose the complete ensemble of cluttered data into a trend component plus several informative and independent mode components. Equipped with the decomposition, FDG-transformer has the capacity to extract the discriminative insights from the cluttered signals. To retain the temporal information in the observed cluttered data, FDG-transformer utilizes hybrid neural network of GRU, long short term memory (LSTM) and multi-head attention (MHA) transformers. The integrated transformer network is capable of encoding the impact of different weights from each past time step to the current one, resulting in the establishment of a time series model from a deeper fine-grained level. We appy the developed FDG-transformer model to analyze Limit Order Book data and compare the results with that obtained from other state-of-the-art methods. The comparison shows that our model delivers effective price forecasting. Moreover, an ablation study is conducted to validate the importance and necessity of each component in the proposed model.
1. Introduction
The stock market has been widely recognized as an investment approach with great potential in making profits [1]. Ways have been studied to predict the future prices in order to maximize the returns of the investments and minimize the corresponding risks [2]. However, due to the unpredictable fluctuation of stock market data and complicated trading circumstances in practice [3], it is difficult to interpret the price movement by domain knowledge. Thus, though traditional statistical methods with good interpretation such as auto regressive models [4], hidden Markov models [5] and tree models [6] have been studied, it is still under extensive investigation to train a strong prediction model [7].
In search for powerful prediction models, deep learning techniques have become more and more popular due to the increasing number of available datasets and growing computational power [8,9]. Compared to traditional models, deep learning models are capable of approximating almost all algebra functions [10]. Therefore, they do not have the disadvantage of suffering from model misspecification [11]. Moreover, prior knowledge has been incorporated to the neural networks to improve model performance [12]. Existing methods focus on designing a novel model structure or adaptive loss functions. For example, convolutional neural networks have been proposed to capture the spatially invariant features of the relevant datasets [13]. Resnet has been proposed to guide the process of training the neural networks [14]. Also, loss function has been adjusted according to domain rules to obtain a better network [15].
Meanwhile, recurrent neural networks (RNN) have been established to handle sequential datasets [16]. In RNN family, information is passed recursively along the time axis with a weighted decay, which means, more recent time will have an impact with larger weight. But the importance of the information does not always depend on the happening time in real problems [17]. Hence, in order to store crucial long temporal information, many adaptive RNNs have been proposed for use. For instance, long short-term memory (LSTM) [18], which stores both short and long time information jointly, is considered to further incorporate their interactions with new information. In addition, gated recurrent unit (GRU) has been proposed to supplement LSTM to accelerate the training and mitigate the problem of overfitting [19].
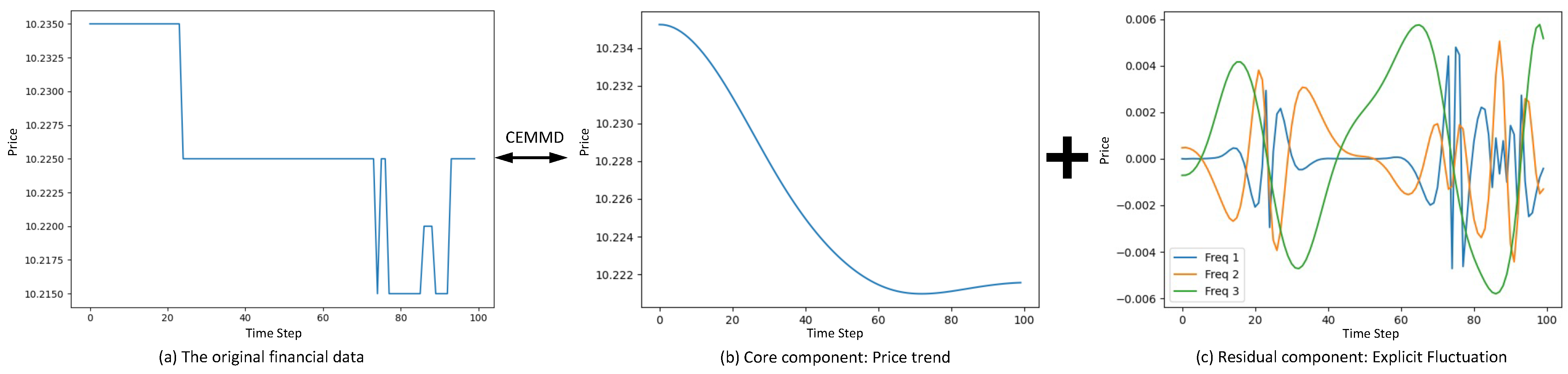
Due to its success in analyzing sequential datasets [20], LSTM and GRU have been extended to perform stock prediction [21,22,23]. But there are two main challenges in this approach. The first challenge is that a subtle change in high frequency financial data may cause a significant increase of difficulty for the neural network to make reliable stock price predictions. As displayed in Figure 1a, the stock price change from 10.235 to 10.215 with a 0.19% fluctuation would be too subtle to be captured. The second challenge lies in that current RNN networks mingle all the past information (from time 0 to time ) into a single long time cell, thus unable to consider the impact of past time on current time from the fine-grained level. At the same time, due to the extremely low signal-to-noise ratio of the stock data in comparison to the other sequential datasets such as speech recognition and text analysis, it is necessary to take certain targeted adjustments to boost this signal-to-noise ratio [24].
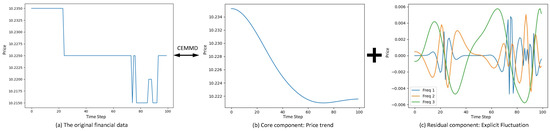
Figure 1.
The illustration of decomposition for complete ensemble empirical mode decomposition (CEEMD): (a) The original financial sequence data is decomposed into: (b) a trend component, and (c) several mode components.
To tackle the first problem, the complete ensemble empirical mode decomposition (CEEMD) [25] will be introduced to decompose the original high-frequency sequential data into several component. As shown in Figure 1, we decompose the signal into one trend component of high frequency data (price trend) and several mode components by frequency revealing explicit fluctuations. The mode components range between and 0.006, where the relative change can be easily captured. To solve the second problem, we consider impact of different weights from each time step to current time, and establish the time series model from a more fine-grained level. Transformers are such functions that have been proved to possess strong modelling abilities to capture long-time dependencies in sequential data [26], thus have been studied to perform the stock prediction as well [27]. In summary, to combine the strong potentials of RNN and transformer in capturing related signals, we propose in this paper a hybrid GRU-based network with a multi-head transformer layer and the complete ensemble empirical mode decomposition (CEEMD) [25]. To the best of our knowledge, this is the first time that a hybrid deep learning model integrating these three great time series techniques is used to forecast the stock price. In our experiments to be detailed later in the paper, it shows our model outperforms the 3 other strong hybrid models in [28,29,30] regarding high-frequency stock price prediction.
There are three major features in our proposed frequency decomposition based GRU transformer (FDG-Trans) neural network:
- We decompose the feature of sequential prices into 4 series using CEEMD. After applying CEEMD, there are 1 trend component and 3 mode components, which are far more inofrmative and greatly alleviates the model training problems caused by subtle change problem. Hence, it is well designed for the highly noisy stock data.
- In the FDG-Trans hybrid network structure, transformer is used first to extract fine-grained information between different time steps, followed by LSTM and GRU to do further analysis. This architecture does a well trade-off between capturing more information and reducing overfitting.
- When applied to high frequency data such as limit order book (LOB), FDG-Trans distinguishes the timely variant features such as prices and volumes and timely invariant features such as open price and yesterday close price. In FDG-Trans, the invariant features will not be put into the RNN networks, which further reduces the overfitting and makes the training process more efficient.
The rest of this paper is organized as following: In Section 2 we review the related work about applying deep neural networks to stock data. In Section 3, our proposed method, as well as the evaluation criterion, is developed in detail. In Section 4, both high frequency trading datasets and their forecasting results using different models are presented. The conclusions and discussions are given in Section 5.
2. Related Work
In the last 5 years there is rich literature on applying the RNN family to do forecasting about the stock price. LSTM is the most well-known and widely-used one. It has a short-term and long-term cell in each step to capture both the instant information and important information. Due to the complexity of the stock data, some hybrid models including LSTM layers have also been proposed. GRU is an adaptive version of LSTM. It involves less number of parameters so it is computationally faster and more applicable even when the size of stock dataset is overly large. Attention is a mechanism which addresses how the current information relates to the previous information, thus has great potential capturing the sequential interactions. The remaining of this section will review the use of LSTM based, GRU based or attention based models for stock market forecasting, respectively.
2.1. LSTM Based Models
Zhuge et al. [31], Srijiranon et al. [32], and Nguyen and Yoon [33] use LSTM to predict the opening price or close price of the stock. In [31], the input consists of normal stock index data and emotional data obtained by a Bayesian classifier. Then the normal stock index data and emotional data will be transformed by a separate fully connected neural network, respectively. In [32], the news and historical data was pre-processed by FinBERT [34] and Principle Component Analysis(PCA) [35], respectively. In [33], some prior knowledge has been used through transfer learning [36]. Experiment shows that the prediction performances have been greatly improved. Selvin et al. [37] integrates LSTM combined with Convolutional Neural Network(CNN) to do the stock price prediction. The data is first inputed into a CNN layer to capture some locational features, and then followed by a LSTM layer. In the experiment, the model is trained on the Infosys dataset and can be applied to TCS and Cipla with good performance. Kim and Won [38] combines LSTM with several GARCH type models to predict the stock price index volatility. The input consists of GARCH parameters, EGARCH parameters and explain variables. After concatenation, the data will be passed in 1 LSTM layer and 2 dense layers to get the final prediction. In the experiment, the proposed model is superior to GARCH models and LSTM under the dataset of KOSPI 200. Sunny et al. [39] applies Bi-Directional LSTM (BI-LSTM) to forecast the stock price trend. The model consists of an activation RELU layer, 2 hidden BI-LSTM layers, 1 drop out layer and 1 dense layer. After some adjustment of hyper-parameters, lower RMSE can be generated compared to LSTM models, which helps the stock traders to get some financial profits with a sustainable strategy. Zhang et al. [28] uses LSTM based model to forecast the stock price trend with limit order book data, which is a snapshot of instant bid and ask information every 3 s. The model (named DeepLOB) consists of 6 CNN layers, 3 parallel inception layers and 1 LSTM layer. Experimental shows that DeepLOB outperforms 10 time-series related models when applied to London Stock Exchange.
2.2. GRU Based Models
Hossain et al. [40] uses GRU based models to do the stock prediction. The model consists of 1 LSTM layer, 1 dropout layer, 1 GRU layer, 1 another dropout layer, and finally followed by a dense layer. In the experiment, S& P 500 historical time series data is used to train and test the model. It is shown that this model out performances former state-of-art methods including RNN, CNN and Ensemble methods. Shahi et al. [23] uses LSTM and GRU to do the stock market forecasting. The model consists of 3 data transformation process, which pre-process the stock and news data, and then concatenate into a time series sequence generator. After the transformation, the output will be put into an LSTM or GRU layer to get the final prediction. In the NEPSE dataset in the experiment, it is showed that news data helps with the prediction and GRU outperforms LSTM. Gao et al. [21] intends to combine GRU with LASSO or PCA to predict the price trend. The model will first use LASSO or PCA to do the dimension reduction and then apply LSTM or GRU layer to get the final prediction. In the experiment, the data of the Shanghai Composite Index with a total of 3481 days are used to do the training and test. It is shown that GRU using LASSO dimension reduction is better. Wu at al [41] uses GRU with a Tree Regularization technique(GRU-Tree) to forecast the price trend. In this method, a GRU based neural network is converted to a decision tree. In the experiment, it is shown that GRU-Tree is with a higher AUC both than the decision tree and GRU network under a dataset of SSE Composite Index in China. Liu et al. [42] proposes a regularized GRU-LSTM neural network to do short-term closing price prediction. The model consists of 1 regularized GRU layer, 1 another GRU layer, 1 LSTM layer and finally 1 dense layer. In the experiment, 2 stock prices with a time range of 10 years in China are used. It is shown that the hybrid model performs better that the existing GRU and LSTM network.
2.3. Attention Based Models
Li et al. [43] incorporates multi input LSTM to attention based neural networks. In this model, there is a multi input LSTM and a attention layer, followed by several ReLU layers to get the final prediction. The multi input consists of a main stream and 3 auxiliary feature groups in order to avoid dimension expansion problems. It is showed that in the dataset of CSI-300 index with a time range of 4 years, there is a significant improvement compared to several LSTM or CNN based methods. Muhammad et al. [44] develops a transformer-based model with 2 input layers, 3 transformers layers, 1 pooling layer, followed by 2 dropout layers and 2 dense layers, which is used to do the forecasting of Dhaka Stock Exchange(DSE), including daily, weekly and monthly stock prices, with a promising results. Liu et al. [45] proposes CapTE (Capsule network based on Transformer Encoder) model to do the stock movements prediction. The transformer encoder is utilized to filter the deep notable features of text in social media. Combined with the stock data, it will be passed into 2 CNN and 2 dense layers to get the final prediction. It shows significant results when applying to a dataset including 47 stocks with a time range of 10 years. Zhang and Zohren [29] combines the aforementioned DeepLOB with an encoder-decoder structure to do the prediction. The encoder part is a DeepLOB model, through which the stock data is transformed into a vector, followed by a decoder to get the final predictions. Experimental shows that it outperforms DeepLOB and other time-series related models when applied to FI-2010 dataset, especially when the prediction time horizon is long. Sridhar and Sanagavarapu [46] integrates transformer with CNN layers to do the stock movement prediction. The structure of the model consists of 2 multi head layers, 1 transformer and 2 CNN layers. In the experiment, it is showed that this model is superior to several CNN or RNN based models under the dataset of the S& P 500 index.
Compared to other papers above, in this paper, FDG-Trans intends to combine GRU and transformer, which can take advantage of the fast-speed GRU, and capture the semantic signals along different timestamps. In addition, the decomposition of the frequency technique has been added to our model. After the decomposition, the fluctuation of the price will be largely reduced, which leads to more stable training data for the training process of the neural network, thus improves the prediction performance.
3. Methods
3.1. Problem Statement
Let y denote the value of target, the predicted value and the values of predictors at different time steps. Then we want to minimize where
is a vector of J predictors at time t, and is the hyper parameter in function . is a customized distance discrepancy to measure how close the estimation is to the true value.
3.2. Problem Analysis and Overview
In Equation (1), when represents the stock data, we hope to capture the inter correlation between and . Hence, it is highly recommended to explicitly model the relationship between and . Another problem of the stock data aforementioned is the subtle change problem. As such, ideally it is preferred that the same features at different time steps are comparatively more stable. To address this, we hope to do some data transformation to the original scattered features.
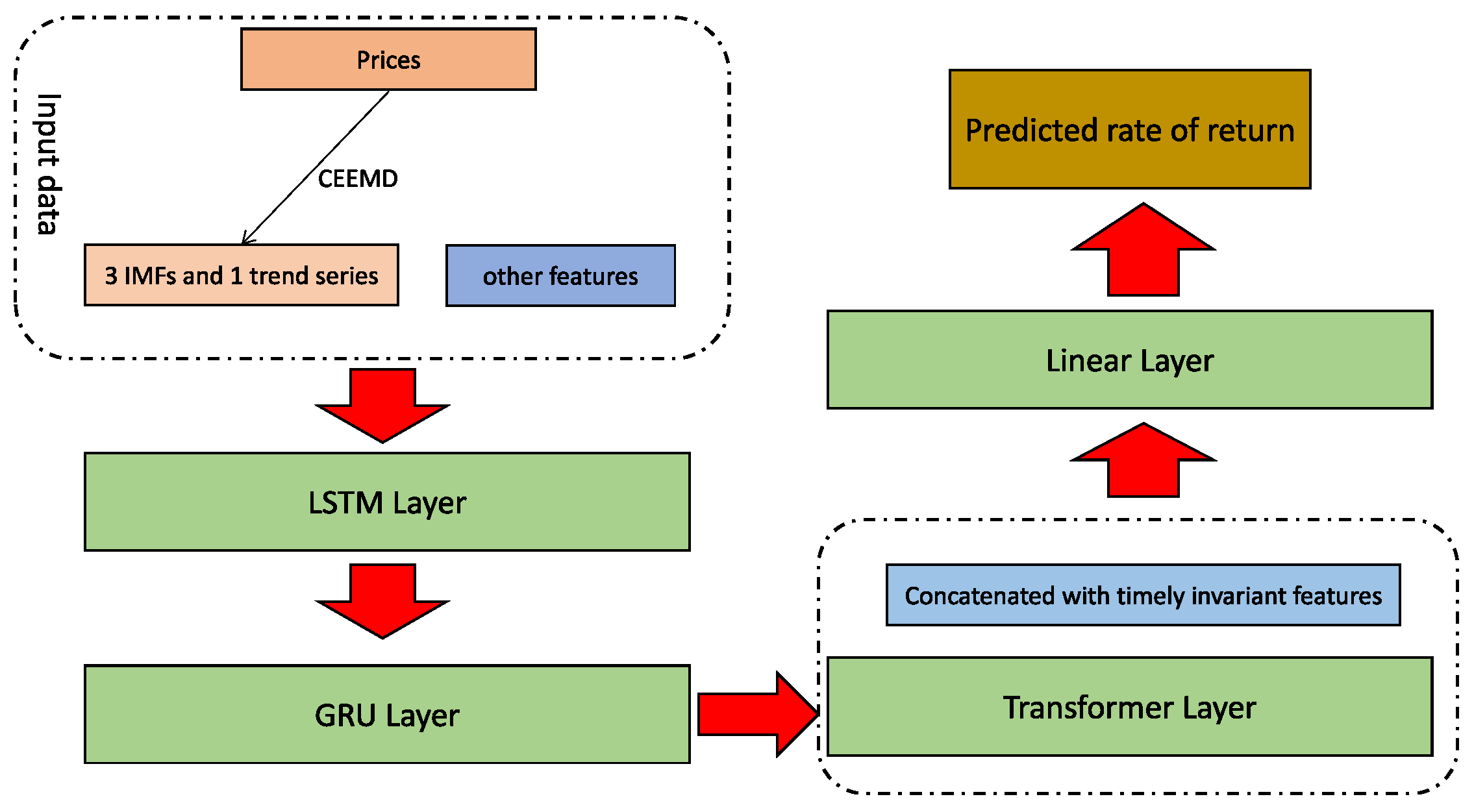
In detail, let denote the feature at time step t, and assume that the column is where the mid price located. We propose frequency decomposition based GRU Transformer (FDG-Trans) framework, consisting of a CEEMD module and a hybrid GRU Transformer. First, we use the CEEMD to do the decomposition for and get . Then, we put the new data matrix into 1 LSTM and 1 GRU, followed by 1 multi-head transformer, finally concatenated with timely invariant features and 1 linear layer. The sketch of our method can be shown in Figure 2.
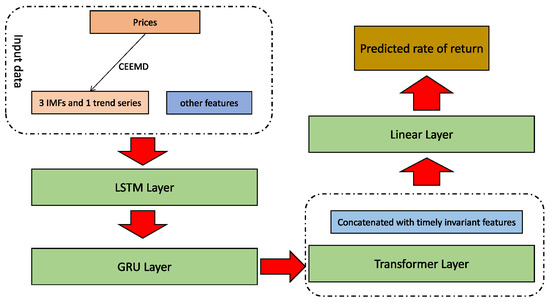
Figure 2.
The overview of architecture of FDG-Trans. The series of prices is first decomposed to 4 more stable series, then concatenated with other futures as the input of the LSTM layer, followed by the GRU layer and transformer layer. Finally, the output of transformer concatenated with timely invariant features is passed by a linear layer to get the predicted rate of return.
3.3. Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMD)
3.3.1. Empirical Mode Decomposition (EMD)
EMD algorithm [47] attends to decompose a complex series data to several basic ones, which is under the assumption that the series data is influenced by several simple factors. The phase of simple factors is composed of Intrinsic Mode Functions (IMFs), which satisfy 2 conditions: (i) in the whole series data, the number of extrema and the number of zero-crossings must be equal or differ by one; and (ii) the mean value of upper and lower envelopes in each signal is zero. The detailed process can be described as following:
- (1)
- Mark all the local minimums and maximums in the series data .
- (2)
- Apply cubic spline method to determine the lower and upper envelops along the time line.
- (3)
- Obtain the local mean according to the lower and upper envelops.
- (4)
- , if the variance of is less than a pre-defined threshold, then . Otherwise, replace by and repeat the above steps.
- (5)
- , repeat the above process to get . The value of K is determined by the termination condition.
- (6)
- In sum, we get where is a term to indicate the overall trend of series.
3.3.2. Ensemble Empirical Mode Decomposition (EEMD)
Although widely used, EMD has its own weakness. In practice the signals are sometimes mixed with variational fluctuations, or white noise, which means . is what we do not know but has significant impact on the decomposition. As such, EEMD [41] has been put up.
In EEMD, , where is the randomly generated Gaussian noise. For each and mode, we apply EMD to get the . Then . From the process we can see, EEMD tries to decompose several similar series of and get the average one.
3.3.3. Complete Ensemble Empirical Mode Decomposition (CEEMD)
EEMD is a further step to do the data analysis, but it is found that the number of experiments n needed to get a satisfactory decomposition is large [25]. To address this problem, Ref. [25] proposed CEEMD. In EEMD, white Gaussian noise has been added to compared to EMD. In CEEMD, white Gaussian noises are added for every mode. In other words, each IMF can be regarded as the original definition plus a Gaussian noise. Overall, we get the following steps:
- (1)
- , where is a white noise series. Decompose by EMD to get .
- (2)
- .
- (3)
- Let . Decompose by EMD to get , then
- (4)
- Repeat the above process K steps. For each , , , where is a bunch of noise series, with the variance decreasing in general.
- (5)
- , where K is determined by a pre-defined stopping criteria.
With the proposed CEEMD, it is easier to capture the signals of the series of prices. The original price series change subtly, which makes it difficult for the neural network to learn how to extract informative information to do the forecasting. After CEEMD, the trend component provides the trend information and 3 mode components indicate the explicit fluctuation of stock price.
Note that after the EEMD is applied several IMFs are generated by the decomposition. Selection of suitable IMFs is always a challenge, Ref. [48] has discussed the selection criteria by calculating the cross-correlation for all the modes considered. However, for RNNs, as the fixed number of input features is required, for simplicity, the price series is decomposed to a certain number of IMFs and all will be chosen.
3.4. Hybrid GRU-Transformer
3.4.1. RNN
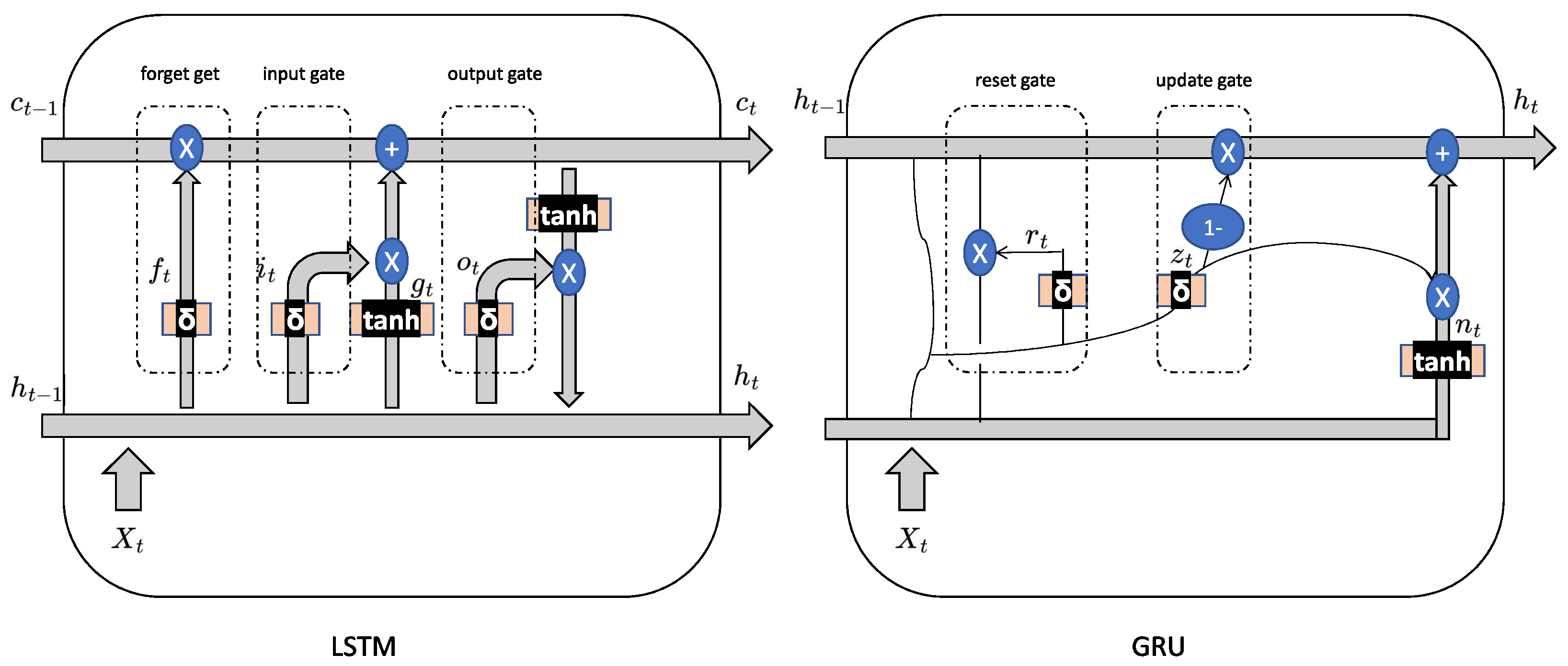
Recurrent neural network(RNN) is a class of neural network where its hidden states are connected to the hidden states of the previous outputs, so its output is affected by the previous states [49]. By retaining a state that can represent information from an arbitrarily long context window, RNN exhibits temporal dynamic behavior. As shown in Figure 3, a typical RNN consists of three parts: input units X, hidden units h and output units Y. Mathematically, the RNN model can be formulated as:
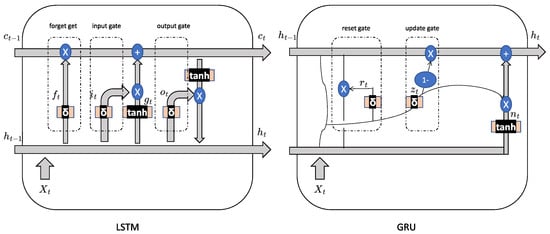
Figure 3.
The structure of LSTM and GRU unit.
- : the hidden state at time t
- : the output state at time t
- : the input state at time t
- U: the weight matrix from input layer to hidden layer
- W: the value of the previous hidden layer is used as the weight matrix for the input of the next layer
- V: the weight matrix from hidden layer to output layer
- f: the activation function, usually nonlinear
3.4.2. LSTM and GRU
Long Short-Term Memory (LSTM) network [18] is a specially designed version of RNN to handle sequential dataset. Previous RNN models only use the past information based on the time line, while gates have been proposed in LSTM to realize the function of capturing the long time important information. In the LSTM unit, there are 1 input gate, 1 forget gate and 1 output gate.
Gate Recurrent Unit (GRU) network [19] is similar to LSTM but with simpler structure. In the GRU unit, there are 1 update gate and 1 reset gate. The structures of LSTM and GRU unit can be visualized in Figure 3.
In the LSTM unit in Figure 3, and can be regarded as the short and long term memories, respectively. The forget gate () determines the importance of information stored in the long term memory after obtaining new data at time step t. The input gate () indicates how the long term memory should be updated. The output gate calculates the new short term memory, taking the new long term memory into consideration. Mathematically, it can be formulated as:
- : the input gate at time t
- : the forget gate at time t
- : the candidate memory state at time t
- : the memory state at time t
- : the hidden state at time t
- : the output gate at time t
- : the activation function
- : the wight matrix from state x to state y, where i, g, f, h, n mean the input state, the candidate memory state, the forget state, the hidden state, the new memory state, respectively
- : the bias term from state x to state y
In the GRU unit, compared to LSTM, contains integrate information of both long and short terms. The reset gate is similar to the function of the input gate in LSTM, while the update gate realizes the functions of the forget and output gates simultaneously. In practice, it is widely accepted that GRU performs more or less the same as LSTM with less computational burden [50]. The mathematical update process is:
- : the update gate at time t
- : the reset gate at time t
- : the new memory state at time t
- : the hidden state at time t
- : the activation function
- : the wight matrix from state x to state y, where i, z, h, n mean the input state, the update state, the hidden state, the new memory state, respectively.
- : the bias term from state x to state y
3.4.3. Transformer
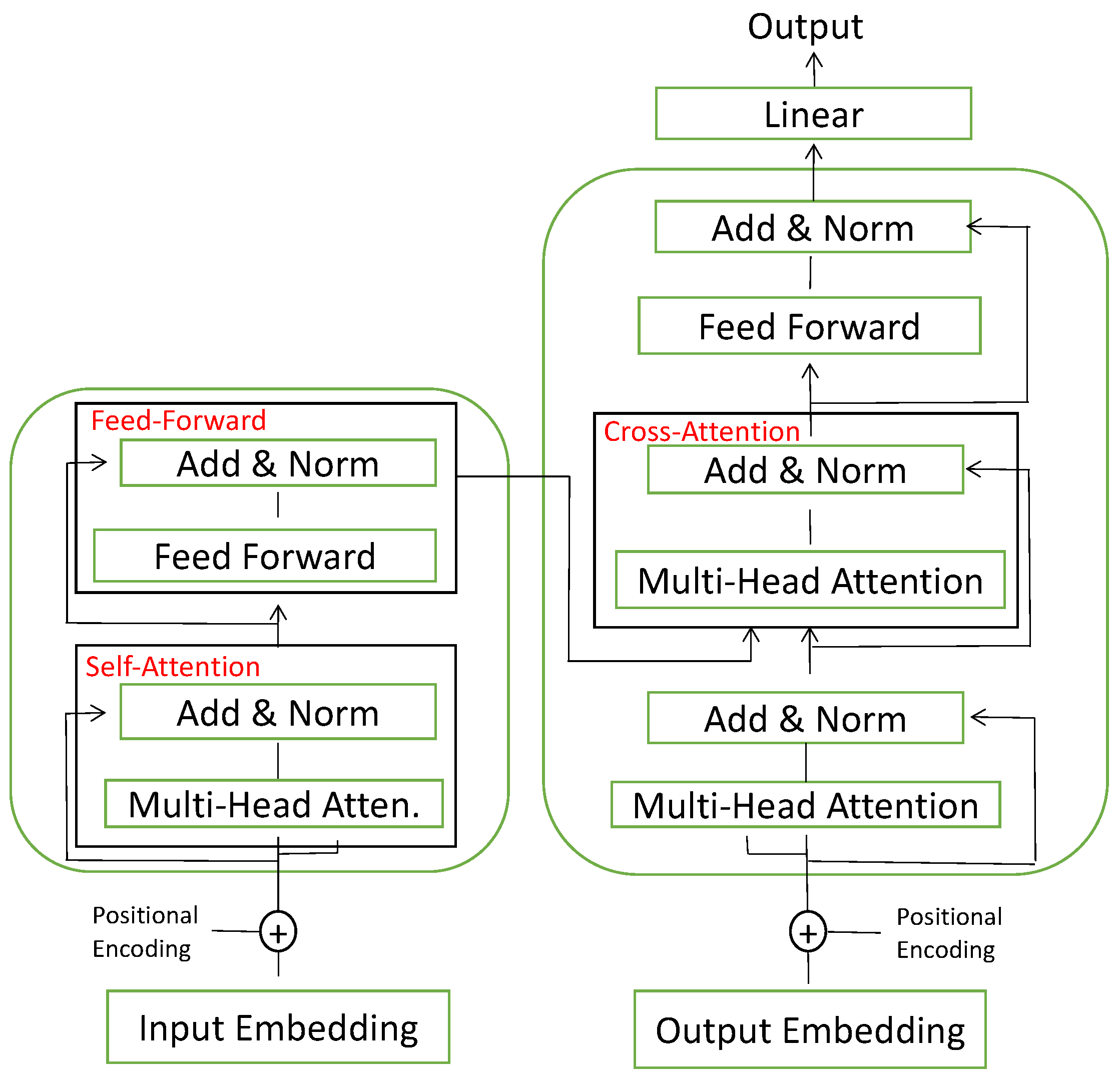
Transformer is designed to have a more fine-grained process of sequential data. It adopts the self-attention mechanism [51], which is used to capture the interaction information between any pair of time step i and j. Compared to LSTM and GRU, it is stronger to make use of long term information at the expense of more parameters.
As sketched in Figure 4, the input at each time step will first be transfered by a Embedding layer to a vector, which is a representation of information a high-dimensional space. Then the vector is combined with the positional information to be the input of the multi-head attention unit. For each head of attention unit, there are 3 matrix parameters for the transformer to learn: the key weights , the query to be keyed weights , and the value weights . The embedding X is multiplied with the above 3 matrix to get the key matrix K, query matrix Q and value matrix V. Denote the dimension of K, then
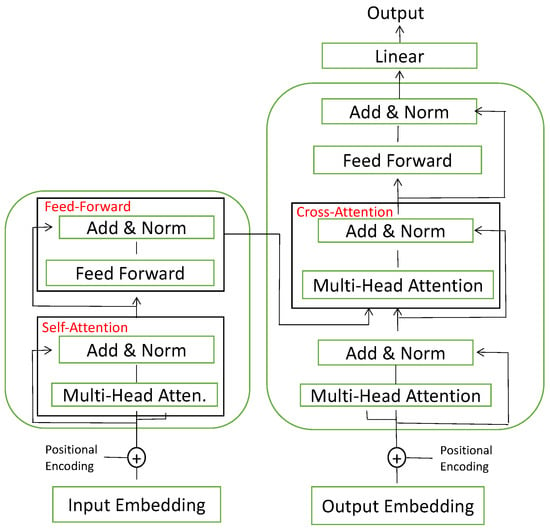
Figure 4.
The overview sketch of transformer.
One tuple of weight matrix is named an attention head, and in a multi-head attention layer there exist several heads. The outcomes of each attention head are added and normalized to be passed into the next layer. The feed-forward layer is the weight matrix which is trained during training and is applied to every respective time step position.
Transformer is originally designed for and widely used in the natural language process (NLP) field [52]. In the stock price prediction and FDG-Trans, we make use of the multi-head self-attention mechanism. After the process by LSTM and GRU, multi-head transformer helps with extract useful information about interactions between different time steps.
3.5. Training Objective
The training objective is to minimize the loss function which measures the discrepancy between the predicted and true values on the training or validation dataset. Some widely used loss functions are:
- Mean Absolute Error (MAE):
- Mean Squared Error (MSE):
- Root Mean Squared Error (RMSE):
- Huber Loss:where y is the real value, is the predicted value, n is the number of samples, is a pre-defined threshold.
Among the losses, MAE is the simplest one. It calculates the mean of absolute differences between the predicted and actual values. MDPE can be regarded as a normalized version of MAE, as large scale values will not have a key impact. Meanwhile, MAE and MDPE can be biased. MSE is unbiased and computationally efficient, but it is sensitive to outliers. RMSE is a less extreme loss function for large values compared to MSE but the gradient is less smooth near the extreme point. Huber loss function [53] is more smooth and robust, but with a greater training burden.
4. Experiment
4.1. Dataset
4.1.1. Limit Order Book (LOB)
Limit order book (LOB) is a key dataset for doing research about high frequency trading as a mechanism to match buy and sell orders in the market. The key information of an order consists of price, volume and direction (buy or sell). In most stock markets there are two kinds of orders: limit order and market order. Limit order is the order with fixed price, volume and direction for a specific stock. It is also the object to be stored by LOB. The limit orders will be added to the order queue according to the price level and direction, offering market liquidity. Market order is the order with fixed volume and direction, which will be executed immediately on the best prices in the opposite direction. Hence, market orders can be executed immediately but may with disadvantageous prices. Limit orders will only be executed at the limit price but the execution time cannot be guaranteed. Meanwhile, limit orders extend the information stored by LOB while market orders or cancellations of limit orders shorten the LOB.
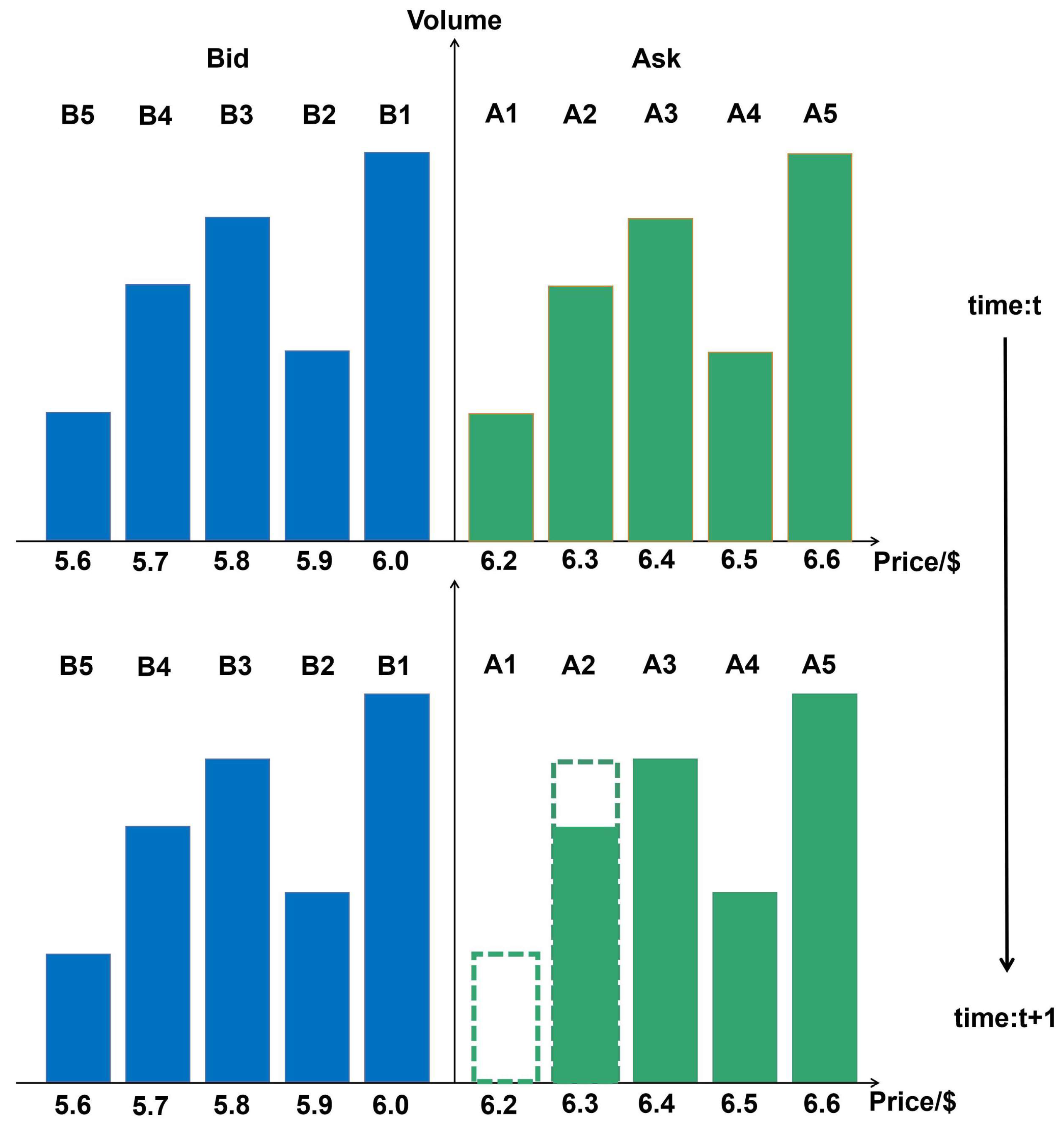
LOB contains cumulative information of current limit orders. For high frequency trading analysis, usually at least 5 queues of each direction are recorded, which means, the best 5 five selling prices (Ask), the best 5 five buying prices (Bid) and their corresponding volumes are used. Figure 5 is a snapshot example of LOB.
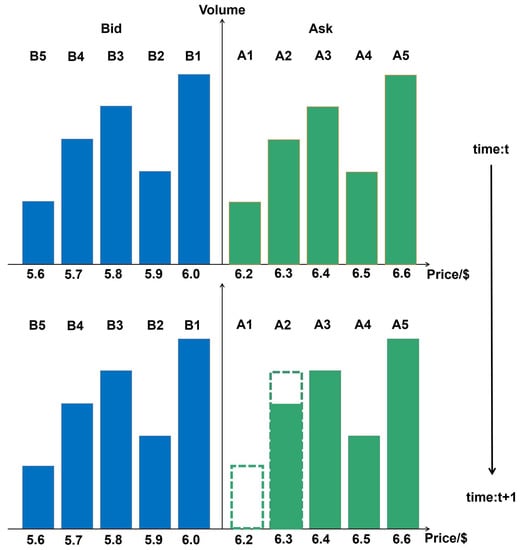
Figure 5.
Snapshot of limit order book at time step t and . The above plot shows the best five prices of bid and ask and their corresponding volumes. Between time t and , the volumes on price 6.2 are traded or canceled, and some extra ask volumes are ordered on price 6.3.
4.1.2. CSI-300
We choose 100 stocks from CSI-300 as our dataset. Our dataset includes 21 trading days in April, 2021. There are 3 h and 57 min active trading hours in each trading day. We update the LOB every 3 s. Hence, there are 4740 time steps of LOB records each day.
In addition, we employ the data normalization to transform the raw data into an appropriate range for deep learning algorithms. The data normalization maps the data into interval according to the following formula:
where the P is the price before normalization, and are the maximum and minimum price before normalization. is the price after the normalization.
4.2. Evaluation Criterion
For stock s, let denote the true rates of return and the predicted values obtained by a method, then
is the r square and
is the r square for the method. In general, a method with an r square higher than 0.01 will be regarded as a valid method.
4.3. Implementation Details
4.3.1. FDG-Trans
In this experiment, one specific FDG-Trans is trained for each stock. The dataset consists of 100 stocks in total for one month period from China Securities Index (CSI 300) market. For each stock, the first 19 trading days are used as training data and the rest 3 days test data. For the input of FDG-Trans, recall that we have 4740 time steps for each stock every trading day. LOB information in every continuous 130 time steps will be used as a single input, and the rate of return after 5 min is the corresponding output. The number of 130 is chosen by the cross validation. For test data, all the possible 130 continuous time step information will be used. In other words, , . Thus, we have around 4610 pieces of input data every trading day. For training data, every 1 in 10 possible 130 continuous time step information will be used, which means, , . Thus, we have around 461 pieces of data every trading data. The reason to skip the other 9 is to reduce the auto correlation of our inputs, which would possibly lead to the problem of over fitting.
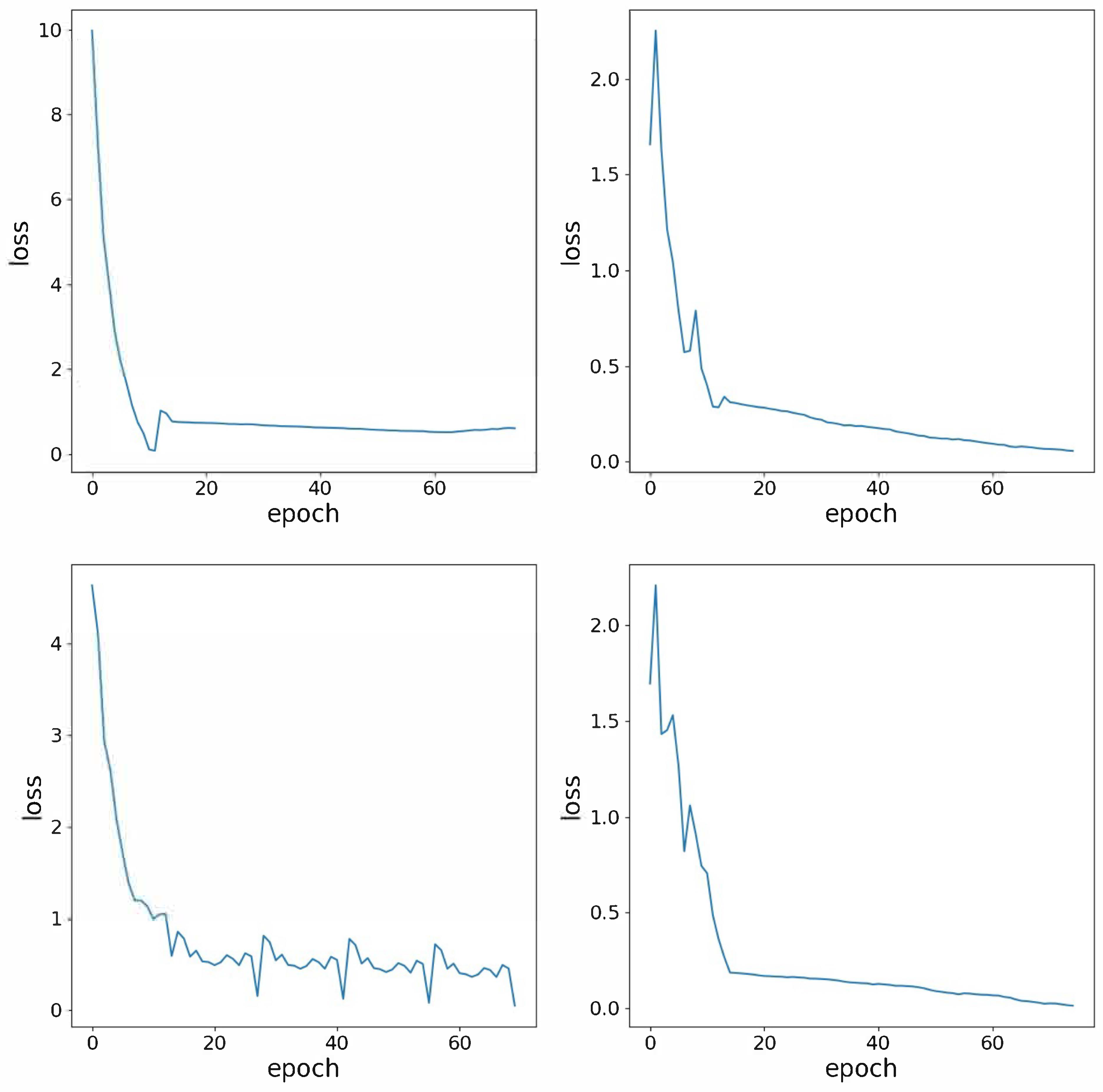
In the training of FDG-Trans, Adam is used as the optimizer. The initial learning parameter is set to be 0.001, with an exponential linear decay by 0.9 after every epoch. The training dataset is trained for 75 epochs. The detailed hyper-parameters are summarized in Table 1. The demonstrate the success of training process, the training losses on four sub-datasets are shown in Figure 6.

Table 1.
Experiment Hyper-parameter Details.
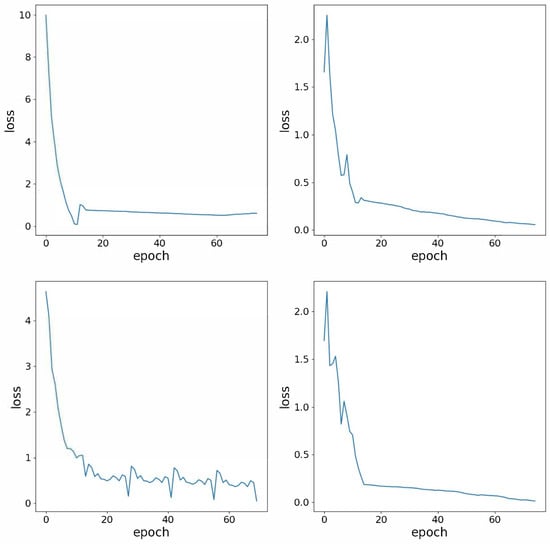
Figure 6.
Training losses of FDG-Trans.
4.3.2. Baseline Method
In previous price stock papers, the hybrid models always outperform traditional models such as linear model, SVM, LSTM, GRU or CNN. Hence, in this paper all the baseline methods will not include traditional models. Instead, 3 strong hybrid models are chosen as baseline models for comparison.
In [28] the model (DeepLOB) consists of 6 CNN layers, 3 parallel inception layers and 1 LSTM layer. In [29], the model (MHF) combines the aforementioned DeepLOB with an encoder-decoder structure to do the prediction. The encoder part is a DeepLOB model, through which the stock data is transformed into a vector, followed by a decoder to get the final predictions. In [54], the model contains 5 sequential CNN layers, batch normalized after each of the layers, followed by 1 LSTM layer.
In addition, wavelet transform and Fourier transform will be tried on the frequency decomposition part for the comparison with CEEMD.
4.4. Experiment Results
4.4.1. Comparison with the State-of-the-Art Method
In this part, we investigate the advantages of the proposed FDG-Trans method. We have compared the proposed FDG-Trans method over 3 other hybrid methods. The results are reported in Table 2. The results of 4 methods are all trained and calculated based on exactly the same training and validation datasets. Note that the average of means the mean of s of different stocks. Hence, values in the table with symbol ± does not indicate the confidence interval but the range of of different stocks. It is shown that FDG-Trans method has higher and less errors. For example, our method achieves 2.88 , surpassing DeepLOB [28], DeepAtt [54] and MHF [29] with 0.52, 1.13 and 1.59. This result validate the stronger regression capacity of our proposed method.

Table 2.
Performances of FDG-Trans and 3 other hybrid models.
4.4.2. Comparison with Baseline Frequency Decomposition
The experiments with different frequency decomposition techniques have been done for comparison purpose. CEEMD, together with wavelet transform [55], Fourier transform [56], and no decomposition have been studied respectively for each experiment. The result is showed in Table 3. It is indicated that CEEMD is the optimal choice. Wavelet is also a strong frequency decomposition technique, which can remove high frequency noise from the original time series. However, in this case, it is tricky to decide the threshold for the noise, as it might lose some information compared with CEEMD, while the latter keeps all the information of the price series. As the reason for Fourier transform, it is because that the transform has the assumption that the original series can be divided into several periodical series, but this is not reasonable for stock price series, otherwise everyone can make profits according to the fixed price movement.

Table 3.
Performances of FDG-Trans with different frequency decomposition methods. The results are trained based on MSE loss function.
4.4.3. Ablation Study
We have also conducted the ablation experiments to verify that each part is necessary. The CEEMD, LSTM, GRU, Transformer and concatenation part have been removed respectively under each trail. The result is showed in Table 4. The decreases more or less under each removal, which indicates that each part has an impact on the performance of the system, consistent with our expectations.

Table 4.
Performances of FDG-Trans with ablation experiments.
Meanwhile, we compared the proposed FDG-Trans method with other settings from the perspective of different loss functions. Table 5 shows the performances of the FDG-Trans method with different losses. The results of MAE, RMSE and Huber loss functions show that in this case MSE is the most suitable loss function. MSE can lead to an unbiased estimate and is sensitive to large errors, which is the kind of samples with the most potential profits. Note that MAE resulted in a low but comparatively best MAE loss, it is because that MAE is biased and tends to get the median value instead of the mean. When given a specific input, the rate of return distribution is with long tail in one side, can be much larger than , where Y is the random variable of the rate of return given the predictor matrix X.

Table 5.
Performances of FDG-Trans with different losses. The results are trained based on MSE loss function.
4.4.4. Visualization of Mode Decomposition
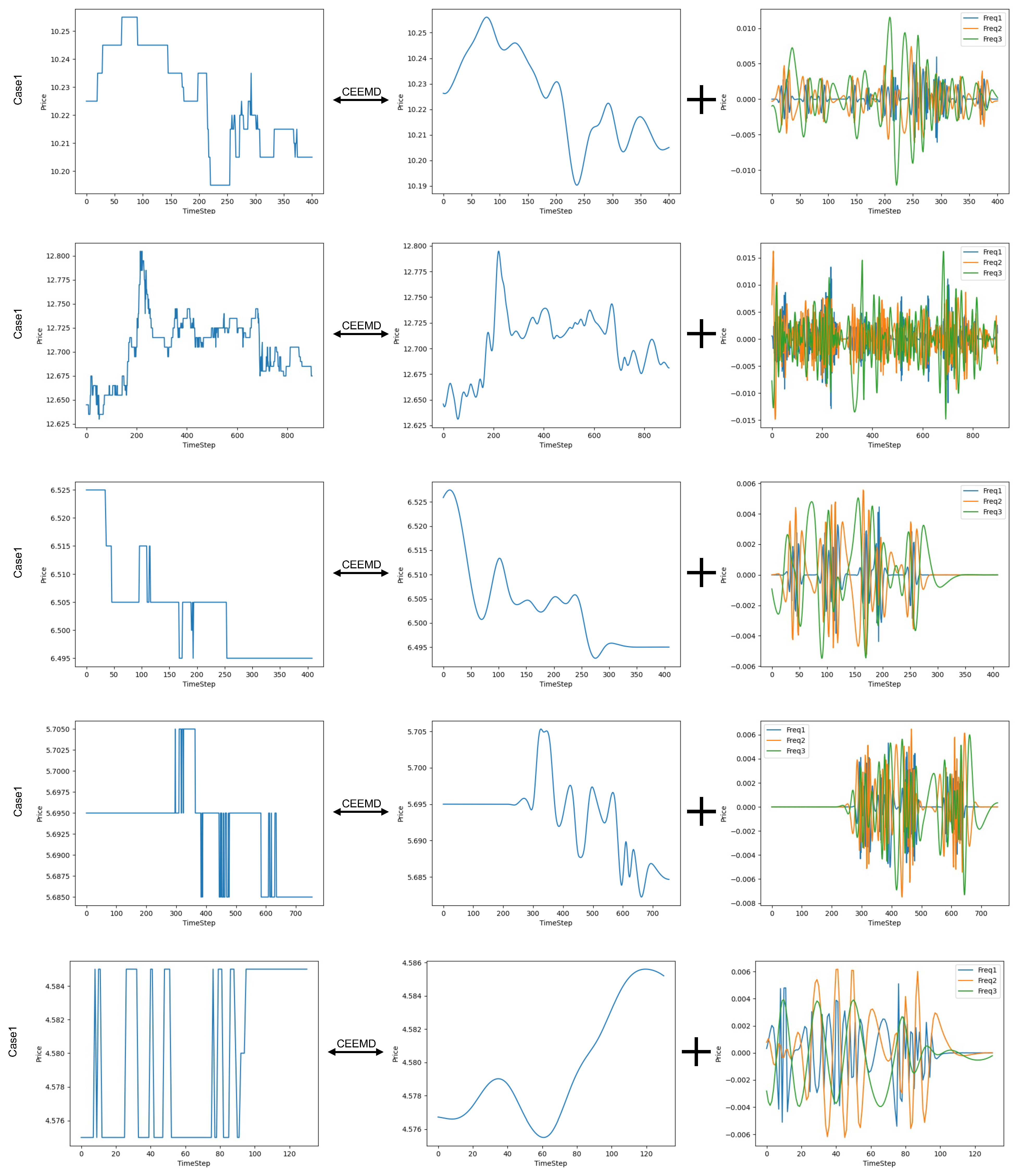
To validate the effectiveness of the complete ensemble empirical mode decomposition (CEEMD), we visualize several decomposition results and provide analysis for signal decomposition. The results are shown in Figure 7. Series 1 contains 400 time steps and have moderate fluctuations along the time axis. After the decomposition, the price trend is captured by the residual with a smooth curve and the IMFs are a little dense. Series 2 contains 1000 time steps and the price goes up and down frequently. The trend is not ideally smooth, the IMFs are dense. Even in this case, where more IMFs are needed, the series after decomposition is more accessible to a sequential model because of more structured pattern. Series 3 contains 400 time steps with a decrease trend. It is nicely captured by the residual. Series 4 is comparatively stable, but with sudden changes in a short period, which could be recognized as an oscillatory signal by a sequential model. After the decomposition, the problems are alleviated. Series 5 contains 130 time steps, which is exactly the same as our input data. It is originally bounced frequently. After the decomposition, the series are stable and smooth.
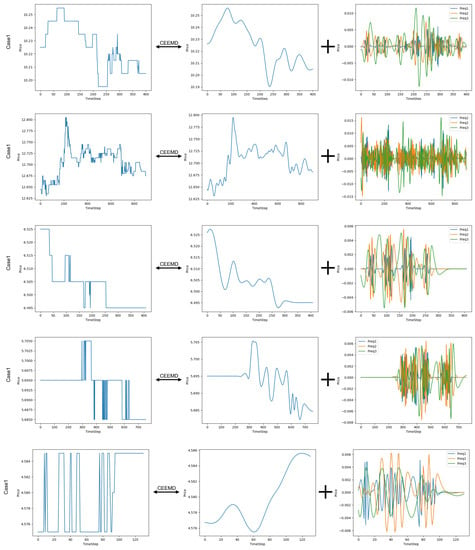
Figure 7.
Visualizations of price series after decomposition by CEEMD. From the plot we can see that, series with low or high variance, long or short time steps, it can be decomposed to several more smooth series.
These cases show that the CEEMD can decompose stock price series into a main trend component and several mode component revealing explicit fluctuation, e.g., oscillatory and stability.
5. Discussion
It is showed in the experiment that our model outperform 3 other strong hybrid neural networks in the model. We design FDG-Trans based on previous widely-used models, the data characteristic and how to better combine the model with the stock data. In the future, we plan to incorporate prior knowledge into the neural networks. As the hybrid neural network usually contains millions of parameters, it is helpful if we can make use of prior knowledge by artificially tailored structure to relief the training burden. Further more, the experimental results are based on Chinese stock data, we will utilize FDG-Trans to other datasets for further verification. In addition, because the latency in real market trade is super important, we aim to store the latent layer information obtained by RNN networks at time step t for further use at time step to save the computational time at the expense of little decrease of accuracy.
6. Conclusions
In this paper, we have proposed an effective hybrid deep learning neural network, FDG-Trans, consisting of CEEMD, transformer, LSTM, GRU and high frequency data adaptive structure. The CEEMD makes the input extreme low signal-to-noise ratio stock data more stable and stationary. The transformer captures fine-grained level interactions and the LSTM and GRU analyze further sequential information. The design of data concatenation after GRU makes the network more intelligent and particularly suitable for large and diverse datasets including the stock data. We have conducted experiments on real financial market and compared FDG-Trans with several baseline methods. The experiments demonstrate that FDG-Trans is effective and captures the signals efficiently to forecast the price movements.
Author Contributions
Conceptualization, C.L. and G.Q.; methodology, C.L.; software, C.L.; validation, G.Q.; formal analysis, C.L.; investigation, C.L. and G.Q.; writing—original draft preparation, C.L.; writing—review and editing, G.Q.; visualization, C.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We thank the two anonymous reviewers for valuable comments which has helped us to improve quality of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Thakkar, A.; Chaudhari, K. Fusion in stock market prediction: A decade survey on the necessity, recent developments, and potential future directions. Inf. Fusion 2021, 65, 95–107. [Google Scholar] [CrossRef]
- Idrees, S.M.; Alam, M.A.; Agarwal, P. A Prediction Approach for Stock Market Volatility Based on Time Series Data. IEEE Access 2019, 7, 17287–17298. [Google Scholar] [CrossRef]
- Rasekhschaffe, K.C.; Jones, R.C. Machine learning for stock selection. Financ. Anal. J. 2019, 75, 70–88. [Google Scholar] [CrossRef]
- Wong, C.S.; Li, W.K. On a mixture autoregressive model. J. R. Stat. Soc. Ser. B 2000, 62, 95–115. [Google Scholar] [CrossRef]
- Hassan, M.R.; Nath, B. Stock market forecasting using hidden Markov model: A new approach. In Proceedings of the 5th International Conference on Intelligent Systems Design and Applications (ISDA’05), Wroclaw, Poland, 8–10 September 2005; pp. 192–196. [Google Scholar]
- Ampomah, E.K.; Qin, Z.; Nyame, G. Evaluation of tree-based ensemble machine learning models in predicting stock price direction of movement. Information 2020, 11, 332. [Google Scholar] [CrossRef]
- Yu, X.; Li, D. Important trading point prediction using a hybrid convolutional recurrent neural network. Appl. Sci. 2021, 11, 3984. [Google Scholar] [CrossRef]
- Picon Ruiz, A.; Alvarez Gila, A.; Irusta, U.; Echazarra Huguet, J. Why deep learning performs better than classical machine learning? Dyna Ing. Ind. 2020. [Google Scholar] [CrossRef]
- Liu, J.; Guo, X.; Li, B.; Yuan, Y. COINet: Adaptive Segmentation with Co-Interactive Network for Autonomous Driving. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 4800–4806. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Masegosa, A. Learning under model misspecification: Applications to variational and ensemble methods. Adv. Neural Inf. Process. Syst. 2020, 33, 5479–5491. [Google Scholar]
- Diligenti, M.; Roychowdhury, S.; Gori, M. Integrating prior knowledge into deep learning. In Proceedings of the 2017 16th IEEE International Conference on Machine Learning and Applications (ICMLA), Cancun, Mexico, 18–21 December 2017; pp. 920–923. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Muralidhar, N.; Islam, M.R.; Marwah, M.; Karpatne, A.; Ramakrishnan, N. Incorporating prior domain knowledge into deep neural networks. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; pp. 36–45. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Internal Representations by Error Propagation; Technical Report; California Univ San Diego La Jolla Inst for Cognitive Science: San Diego, CA, USA, 1985. [Google Scholar]
- Nuruzzaman, M.; Hussain, O.K. A survey on chatbot implementation in customer service industry through deep neural networks. In Proceedings of the 2018 IEEE 15th International Conference on e-Business Engineering (ICEBE), Xi’an, China, 12–14 October 2018; pp. 54–61. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Graves, A.; Jaitly, N.; Mohamed, A.r. Hybrid speech recognition with deep bidirectional LSTM. In Proceedings of the 2013 IEEE Workshop on Automatic Speech Recognition and Understanding, Olomouc, Czech Republic, 8–12 December 2013; pp. 273–278. [Google Scholar]
- Gao, Y.; Wang, R.; Zhou, E. Stock Prediction Based on Optimized LSTM and GRU Models. Sci. Program. 2021, 2021, 1–8. [Google Scholar] [CrossRef]
- Sethia, A.; Raut, P. Application of LSTM, GRU and ICA for stock price prediction. In Information and Communication Technology for Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2019; pp. 479–487. [Google Scholar]
- Shahi, T.B.; Shrestha, A.; Neupane, A.; Guo, W. Stock price forecasting with deep learning: A comparative study. Mathematics 2020, 8, 1441. [Google Scholar] [CrossRef]
- Kubáň, P.; Hauser, P.C. Fundamental aspects of contactless conductivity detection for capillary electrophoresis. Part II: Signal-to-noise ratio and stray capacitance. Electrophoresis 2004, 25, 3398–3405. [Google Scholar] [CrossRef] [PubMed]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Wen, Q.; Zhou, T.; Zhang, C.; Chen, W.; Ma, Z.; Yan, J.; Sun, L. Transformers in time series: A survey. arXiv 2022, arXiv:2202.07125. [Google Scholar]
- Yang, L.; Ng, T.L.J.; Smyth, B.; Dong, R. Html: Hierarchical transformer-based multi-task learning for volatility prediction. In Proceedings of the Web Conference 2020, Taipei, Taiwan, 20–24 April 2020; pp. 441–451. [Google Scholar]
- Zhang, Z.; Zohren, S.; Roberts, S. Deeplob: Deep convolutional neural networks for limit order books. IEEE Trans. Signal Process. 2019, 67, 3001–3012. [Google Scholar] [CrossRef]
- Zhang, Z.; Zohren, S. Multi-horizon forecasting for limit order books: Novel deep learning approaches and hardware acceleration using intelligent processing units. arXiv 2021, arXiv:2105.10430. [Google Scholar]
- Arévalo, A.; Niño, J.; Hernández, G.; Sandoval, J. High-frequency trading strategy based on deep neural networks. In Proceedings of the International Conference on Intelligent Computing; Springer: Berlin/Heidelberg, Germany, 2016; pp. 424–436. [Google Scholar]
- Zhuge, Q.; Xu, L.; Zhang, G. LSTM Neural Network with Emotional Analysis for prediction of stock price. Eng. Lett. 2017, 25, 167–175. [Google Scholar]
- Srijiranon, K.; Lertratanakham, Y.; Tanantong, T. A Hybrid Framework Using PCA, EMD and LSTM Methods for Stock Market Price Prediction with Sentiment Analysis. Appl. Sci. 2022, 12, 10823. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Yoon, S. A Novel Approach to Short-Term Stock Price Movement Prediction using Transfer Learning. Appl. Sci. 2019, 9, 4745. [Google Scholar] [CrossRef]
- Araci, D. Finbert: Financial sentiment analysis with pre-trained language models. arXiv 2019, arXiv:1908.10063. [Google Scholar]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]
- Selvin, S.; Vinayakumar, R.; Gopalakrishnan, E.; Menon, V.K.; Soman, K. Stock price prediction using LSTM, RNN and CNN-sliding window model. In Proceedings of the 2017 International Conference on Advances in Computing, Communications and Informatics (icacci), Manipal, Karnataka, India, 13–16 September 2017; pp. 1643–1647. [Google Scholar]
- Kim, H.Y.; Won, C.H. Forecasting the volatility of stock price index: A hybrid model integrating LSTM with multiple GARCH-type models. Expert Syst. Appl. 2018, 103, 25–37. [Google Scholar] [CrossRef]
- Sunny, M.A.I.; Maswood, M.M.S.; Alharbi, A.G. Deep learning-based stock price prediction using LSTM and bi-directional LSTM model. In Proceedings of the 2020 2nd Novel Intelligent and Leading Emerging Sciences Conference (NILES), Giza, Egypt, 24–26 October 2020; pp. 87–92. [Google Scholar]
- Hossain, M.A.; Karim, R.; Thulasiram, R.; Bruce, N.D.; Wang, Y. Hybrid deep learning model for stock price prediction. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (ssci), Bengaluru, India, 18–21 November 2018; pp. 1837–1844. [Google Scholar]
- Wu, W.; Wang, Y.; Fu, J.; Yan, J.; Wang, Z.; Liu, J.; Wang, W.; Wang, X. Preliminary study on interpreting stock price forecasting based on tree regularization of GRU. In Proceedings of the International Conference of Pioneering Computer Scientists, Engineers and Educators, Guilin, China, 20–23 September 2019; pp. 476–487. [Google Scholar]
- Liu, Y.; Wang, Z.; Zheng, B. Application of regularized GRU-LSTM model in stock price prediction. In Proceedings of the 2019 IEEE 5th International Conference on Computer and Communications (ICCC), China, Chengdu, 6–9 December 2019; pp. 1886–1890. [Google Scholar]
- Li, H.; Shen, Y.; Zhu, Y. Stock price prediction using attention-based multi-input LSTM. In Proceedings of the Asian Conference on Machine Learning PMLR, Beijing, China, 14–16 November 2018; pp. 454–469. [Google Scholar]
- Muhammad, T.; Aftab, A.B.; Ahsan, M.; Muhu, M.M.; Ibrahim, M.; Khan, S.I.; Alam, M.S. Transformer-Based Deep Learning Model for Stock Price Prediction: A Case Study on Bangladesh Stock Market. arXiv 2022, arXiv:2208.08300. [Google Scholar]
- Liu, J.; Lin, H.; Liu, X.; Xu, B.; Ren, Y.; Diao, Y.; Yang, L. Transformer-based capsule network for stock movement prediction. In Proceedings of the First Workshop on Financial Technology and Natural Language Processing, Macao, China, 12 August 2019; pp. 66–73. [Google Scholar]
- Sridhar, S.; Sanagavarapu, S. Multi-head self-attention transformer for dogecoin price prediction. In Proceedings of the 2021 14th International Conference on Human System Interaction (HSI), Gdansk, Poland, 8–10 July 2021; pp. 1–6. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Dave, V.; Singh, S.; Vakharia, V. Diagnosis of bearing faults using multi fusion signal processing techniques and mutual information. Indian J. Eng. Mater. Sci. (IJEMS) 2021, 27, 878–888. [Google Scholar]
- Lipton, Z.C.; Berkowitz, J.; Elkan, C. A critical review of recurrent neural networks for sequence learning. arXiv 2015, arXiv:1506.00019. [Google Scholar]
- Yang, S.; Yu, X.; Zhou, Y. Lstm and gru neural network performance comparison study: Taking yelp review dataset as an example. In Proceedings of the 2020 International Workshop on Electronic Communication and Artificial Intelligence (IWECAI), Shanghai, China, 12–14 June 2020; pp. 98–101. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Gillioz, A.; Casas, J.; Mugellini, E.; Abou Khaled, O. Overview of the Transformer-based Models for NLP Tasks. In Proceedings of the 2020 15th Conference on Computer Science and Information Systems (FedCSIS), Sofia, Bulgaria, 6–9 September 2020; pp. 179–183. [Google Scholar]
- Huber, P.J. Robust estimation of a location parameter. In Breakthroughs in Statistics; Springer: Berlin/Heidelberg, Germany, 1992; pp. 492–518. [Google Scholar]
- Arévalo Murillo, A.R. High-Frequency trading strategy based on deep neural networks. Ing. Sist. 2019. [Google Scholar]
- Shensa, M.J. The discrete wavelet transform: Wedding the a trous and Mallat algorithms. IEEE Trans. Signal Process. 1992, 40, 2464–2482. [Google Scholar] [CrossRef]
- Bracewell, R.N. The Fourier Transform and Its Applications; McGraw-Hill: New York, NY, USA, 1986; Volume 31999. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).