The Approximate Solution of the Nonlinear Exact Equation of Deflection of an Elastic Beam with the Galerkin Method
Abstract
:1. Introduction
2. Exact Differential Equation of the Deflection of an Elastic Beam
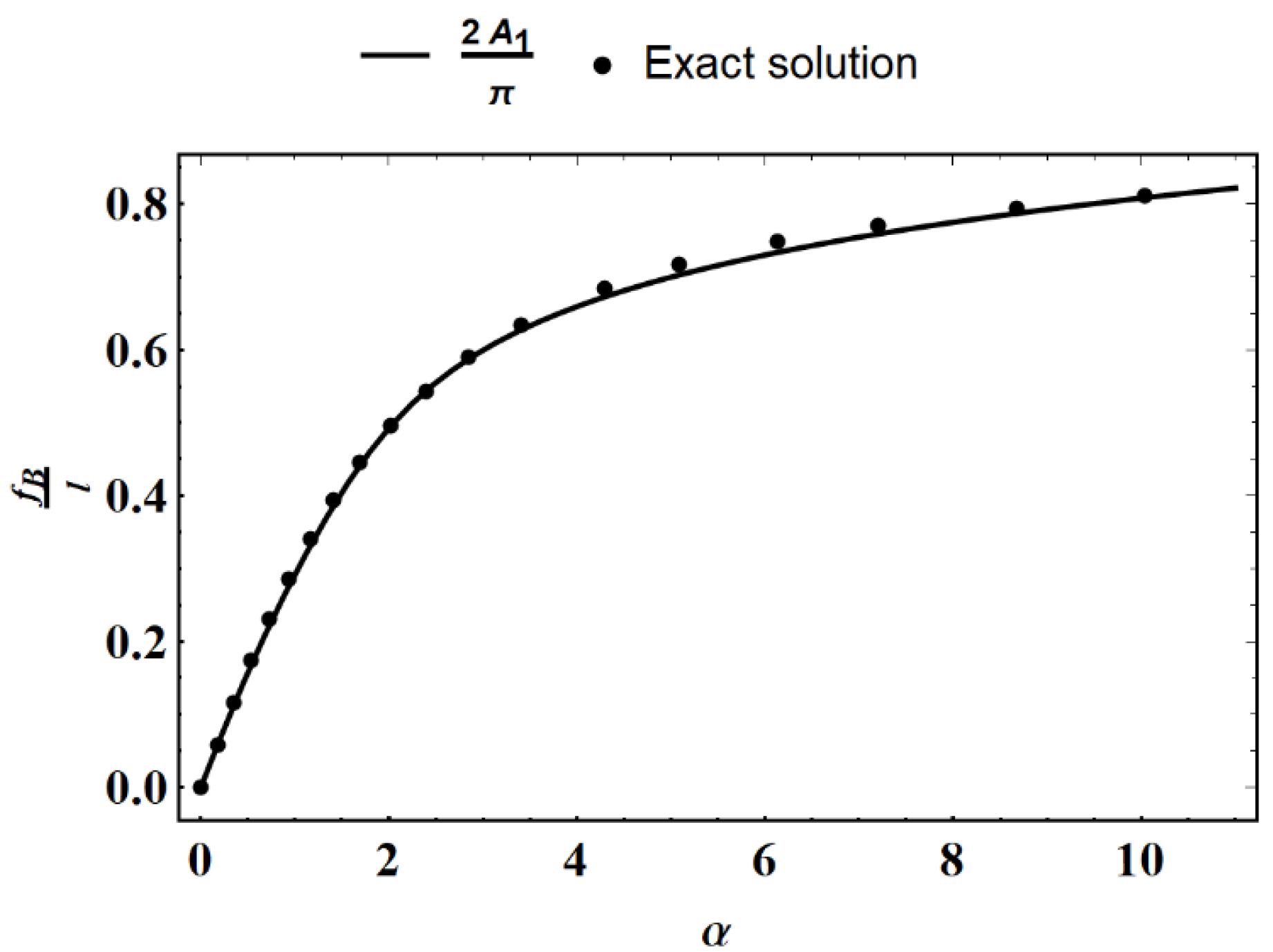
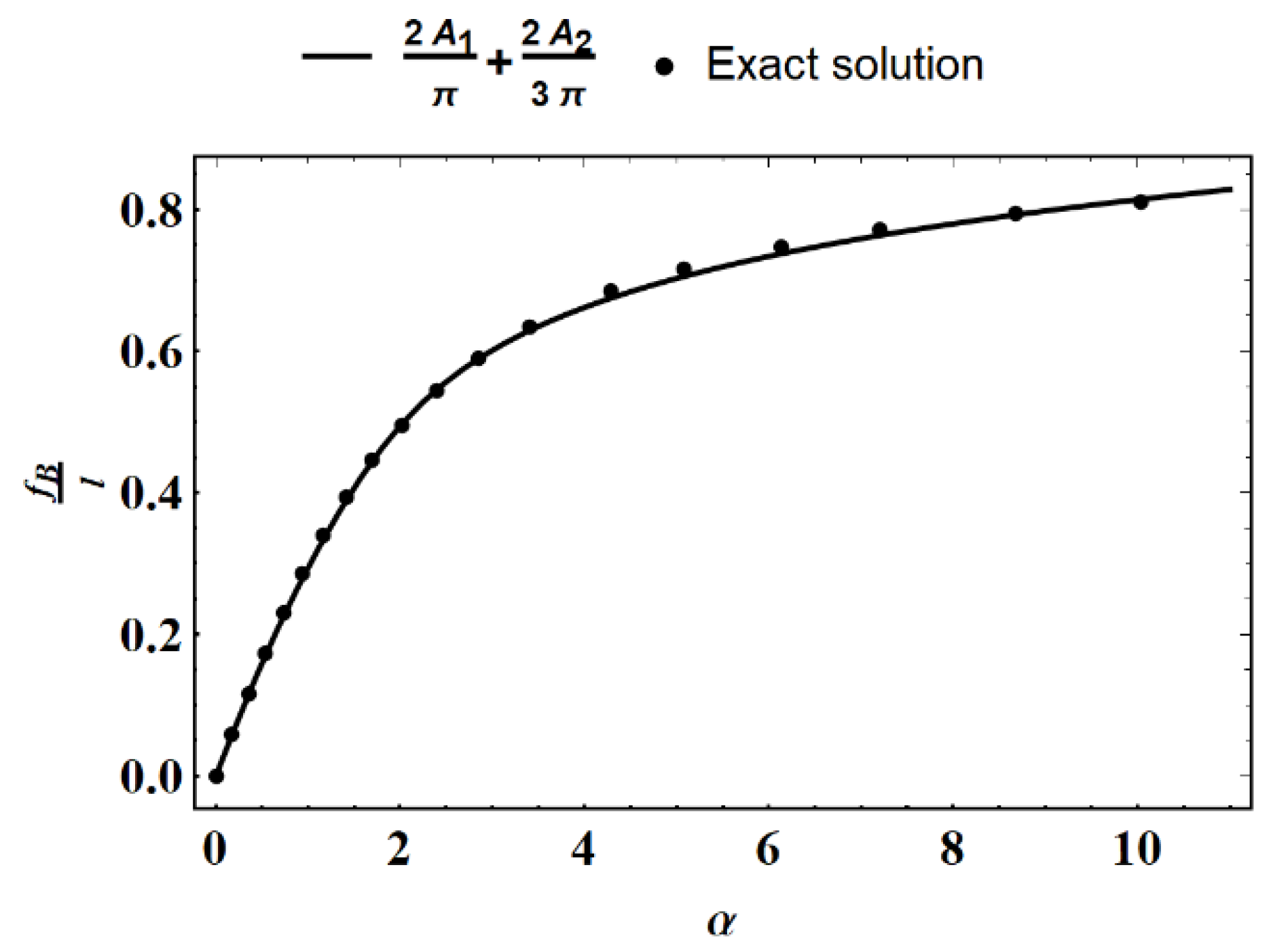
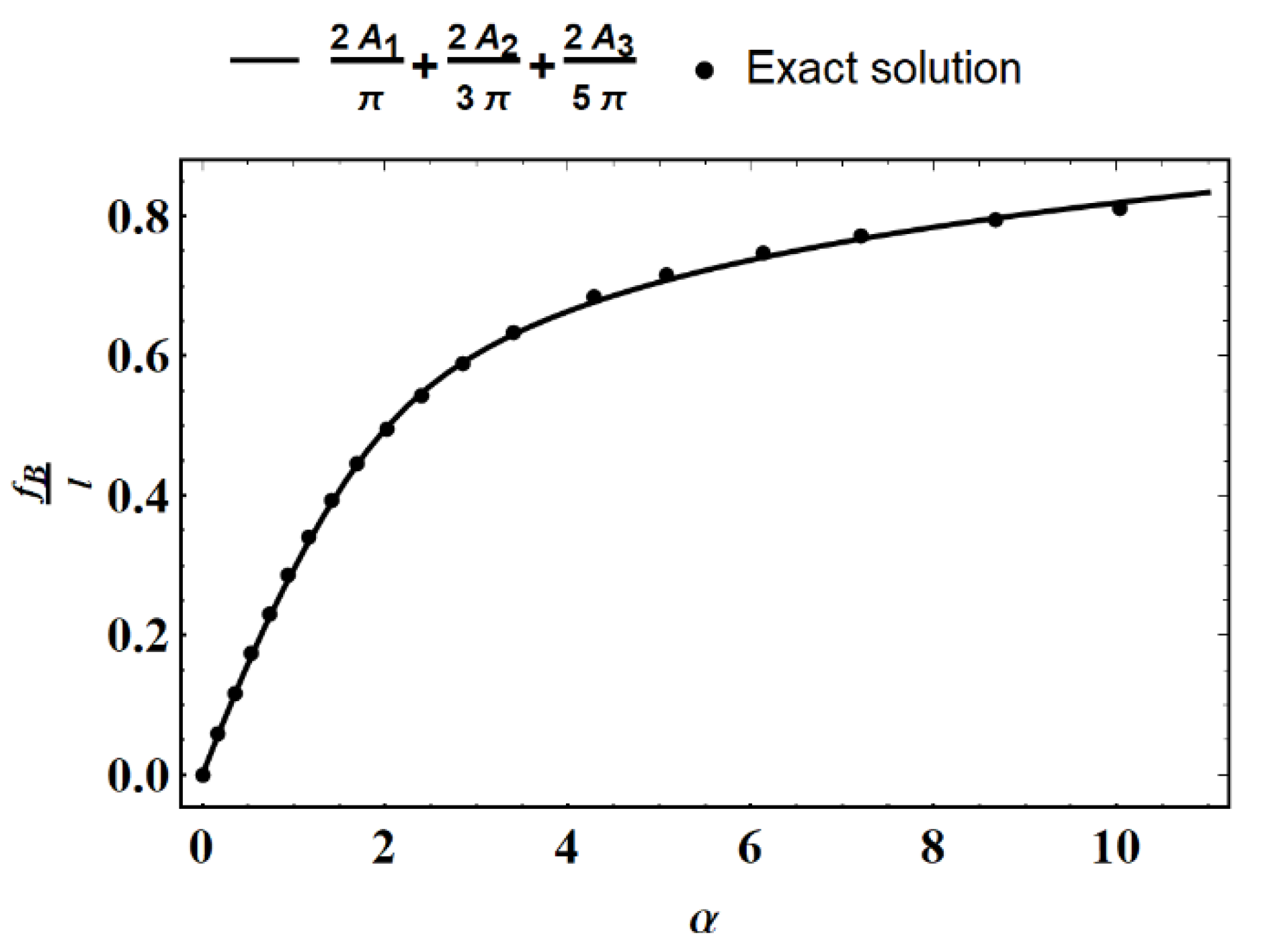
3. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Timoshenko, S. History of the Strength of Materials: With a Brief Account of the History of the Theory of Elasticity and Theory of Structures; Courier Corporation: Chelmsford, MA, USA, 1983. [Google Scholar]
- Vlase, S.; Marin, M.; Öchsner, A. Considerations of the transverse vibration of a mechanical system with two identical bars. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2019, 233, 1318–1323. [Google Scholar] [CrossRef]
- Montava, I.; Irles, R.; Estevan, L.; Vives, I. Equivalent Frame Model with a Decaying Nonlinear Moment-Curvature of Steel-Reinforced Concrete Joints. Appl. Sci. 2019, 9, 5533. [Google Scholar] [CrossRef] [Green Version]
- Timoshenko, S.; Goodier, J.N. Theory of Elasticity; Timoshenko, S., Goodier, J.N., Eds.; McGraw-Hill: New York, NY, USA, 1951. [Google Scholar]
- Soutas-Little, R.W. Elasticity; Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]
- Pearson, C.E. Theoretical elasticity. In Theoretical Elasticity; Harvard University Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Gould, P.L.; Feng, Y. Introduction to Linear Elasticity; Springer: New York, NY, USA, 1994. [Google Scholar]
- Marsden, J.E.; Hughes, T.J. Mathematical Foundations of Elasticity; Courier Corporation: Chelmsford, MA, USA, 1994. [Google Scholar]
- Barber, J.R. Elasticity; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability; Courier Corporation: Chelmsford, MA, USA, 2009. [Google Scholar]
- Goss, V.G.A. The history of the planar elastica: Insights into mechanics and scientific method. Sci. Educ. 2009, 18, 1057–1082. [Google Scholar] [CrossRef]
- Euler, L. Method of Finding Maximum Curve Lines with a Minimum Property of Joy or Isoperimetric Problem Solutions Acceptable; Springer Science & Business Media: Berlin, Germany, 1952; Volume 1. [Google Scholar]
- Bernoulli, D. The 26th letter to Euler. Math. Phys. Corresp. 1843, 2, 499. [Google Scholar]
- Levien, R. The Elastica: A Mathematical History; EECS Department, University of California: Los Angeles, CA, USA, 2008. [Google Scholar]
- Bisshopp, K.E.; Drucker, D.C. Large deflection of cantilever beams. Q. Appl. Math. 1945, 3, 272–275. [Google Scholar] [CrossRef] [Green Version]
- Saxena, A.; Kramer, S.N. A Simple and Accurate Method for Determining Large Deflections in Compliant Mechanisms Subjected to End Forces and Moments. ASME. J. Mech. Des. 1998, 120, 392–400. [Google Scholar] [CrossRef]
- Howell, L.L.; Midha, A. Parametric Deflection Approximations for End-Loaded, Large-Deflection Beams in Compliant Mechanisms. ASME J. Mech. Des. 1995, 117, 156–165. [Google Scholar] [CrossRef]
- Wang, J.; Chen, J.K.; Liao, S. An explicit solution of the large deformation of a cantilever beam under point load at the free tip. J. Comput. Appl. Math. 2008, 212, 320–330. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Li, X.; Huo, S.; Xie, C. Explicit Solutions to Large Deformation of Cantilever Beams by Improved Homotopy Analysis Method I: Rotation Angle. Appl. Sci. 2008, 12, 6400. [Google Scholar] [CrossRef]
- Li, Y.; Li, X.; Xie, C.; Huo, S. Explicit Solution to Large Deformation of Cantilever Beam by Improved Homotopy Analysis Method II: Vertical and Horizontal Displacements. Appl. Sci. 2022, 12, 2513. [Google Scholar] [CrossRef]
- Ghaffarzadeh, H.; Nikkar, A. Explicit solution to the large deformation of a cantilever beam under point load at the free tip using the variational iteration method-II. J. Mech. Sci. Technol. 2013, 27, 3433–3438. [Google Scholar] [CrossRef]
- Liao, S.; Tan, Y. A general approach to obtain series solutions of nonlinear differential equations. Stud. Appl. Math. 2007, 119, 297–354. [Google Scholar] [CrossRef]
- Beléndez, T.; Pérez-Polo, M.; Neipp, C.; Beléndez, A. Numerical and experimental analysis of large deflections of cantilever 373 beams under a combined load. Phys. Scr. 2005, 2005, 61. [Google Scholar] [CrossRef] [Green Version]
- Liao, S. Homotopy Analysis Method in Nonlinear Differential Equations; Higher Education Press: Beijing, China, 2012. [Google Scholar]
- Singhal, D.; Narayanamurthy, V. Large and small deflection analysis of a cantilever beam. J. Inst. Eng. India Ser. A 2019, 100, 83–96. [Google Scholar] [CrossRef]
- Sedighi, H.M.; Shirazi, K.H.; Noghrehabadi, A. Application of recent powerful analytical approaches on the nonlinear vibration of cantilever beams. Int. J. Nonlinear Sci. Numer. Simul. 2012, 13, 487–494. [Google Scholar] [CrossRef]
- Liao, S. Homotopy analysis method: A new analytic method for nonlinear problems. Appl. Math. Mech. 1998, 19, 957–962. [Google Scholar]
- Liao, S. Beyond Perturbation: Introduction to the Homotopy Analysis Method; Chapman and Hall/CRC: London, UK, 2003. [Google Scholar]
- Liao, S. On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 2004, 147, 499–513. [Google Scholar] [CrossRef]
- Liao, S. Notes on the homotopy analysis method: Some definitions and theorems. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 983–997. [Google Scholar] [CrossRef]
- Odibat, Z.M. A study on the convergence of homotopy analysis method. Appl. Math. Comput. 2010, 217, 782–789. [Google Scholar] [CrossRef]
- Abbasbandy, S. The application of homotopy analysis method to nonlinear equations arising in heat transfer. Phys. Lett. A 2006, 360, 109–111. [Google Scholar] [CrossRef]
- Behzadi, S.S.; Abbasbandy, S.; Allahviranloo, T.; Yildirim, A. Application of homotopy analysis method for solving a class of nonlinear Volterra-Fredholm integro-differential equations. J. Appl. Anal. Comput. 2012, 2, 127–136. [Google Scholar]
- Rashidi, M.M.; Domairry, G.; Doosthosseini, A.; Dinarvand, S. Explicit approximate solution of the coupled KdV equations by using the homotopy analysis method. Int. J. Math. Anal. 2008, 2, 581–589. [Google Scholar]
- Wang, J.; Wu, R. The extended Galerkin method for approximate solutions of nonlinear vibration equations. Appl. Sci. 2022, 12, 2979. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, R.; Wang, J.; Ma, T.; Wang, L. The Approximate Solution of Nonlinear Flexure of a Cantilever Beam with the Galerkin Method. Appl. Sci. 2022, 12, 6720. [Google Scholar] [CrossRef]
- Momeni, M.; Riahi Beni, M.; Bedon, C.; Najafgholipour, M.A.; Dehghan, S.M.; JavidSharifi, B.; Hadianfard, M.A. Dynamic Response Analysis of Structures Using Legendre–Galerkin Matrix Method. Appl. Sci. 2021, 11, 9307. [Google Scholar] [CrossRef]
- Shi, B.; Yang, J.; Wang, J. Forced vibration analysis of multi-degree-of-freedom nonlinear systems with the extended Galerkin method. Mech. Adv. Mater. Struct. 2022, 29, 1–9. [Google Scholar] [CrossRef]
- Wang, J. The extended Rayleigh-Ritz method for an analysis of nonlinear vibrations. Mech. Adv. Mater. Struct. 2022, 29, 3281–3284. [Google Scholar] [CrossRef]
- Akgöz, B.; Civalek, Ö. Buckling Analysis of Functionally Graded Tapered Microbeams via Rayleigh–Ritz Method. Mathematics 2022, 10, 4429. [Google Scholar] [CrossRef]
- Gere, J.M.; Goodno, B.J. Mechanics of Materials; Cengage Learning: Stanford City, CA, USA, 2012. [Google Scholar]
- Hearn, E.J. Mechanics of Materials 2: The Mechanics of Elastic and Plastic Deformation of Solids and Structural Materials; Elsevier: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Craig, R.R.; Taleff, E.M. Mechanics of Materials; Wiley: New York, NY, USA, 1996; Volume 2. [Google Scholar]
- Chouery, F.A. Exact and Numerical Solutions for Large Deflection of Elastic Non-Prismatic Beams; FAC Systems INC: Seattle, WA, USA, 2006. [Google Scholar]
- Bender, C.M.; Orszag, S.; Orszag, S.A. Advanced Mathematical Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory; Springer Science & Business Media: Berlin, Germany, 1999; Volume 1. [Google Scholar]
- Liu, H. Advanced Material Mechanics; Higher Education Development Association: Beijing, China, 1985. (In Chinese) [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lian, C.; Wang, J.; Meng, B.; Wang, L. The Approximate Solution of the Nonlinear Exact Equation of Deflection of an Elastic Beam with the Galerkin Method. Appl. Sci. 2023, 13, 345. https://doi.org/10.3390/app13010345
Lian C, Wang J, Meng B, Wang L. The Approximate Solution of the Nonlinear Exact Equation of Deflection of an Elastic Beam with the Galerkin Method. Applied Sciences. 2023; 13(1):345. https://doi.org/10.3390/app13010345
Chicago/Turabian StyleLian, Chencheng, Ji Wang, Baochen Meng, and Lihong Wang. 2023. "The Approximate Solution of the Nonlinear Exact Equation of Deflection of an Elastic Beam with the Galerkin Method" Applied Sciences 13, no. 1: 345. https://doi.org/10.3390/app13010345






