From Simulations to Accelerated Testing: Design of Experiments for Accelerated Load Testing of a Wind Turbine Drivetrain Based on Aeroelastic Multibody Simulation Data
Abstract
:Featured Application
Abstract
1. Introduction
It is a logical consequence of this reliance on the awareness of the experimenters that experiments, from Bacon’s point of view, can to a large extent be individual to the experimenter. Indeed, Schwarz explains Bacon’s belief “that it is possible to find the ultimate explanations if we only succeed to weed out those factors that are not necessary for the production of an effect” [19] (p. 80). This belief in the ability of scientists to identify and eliminate unimportant factors despite the “uneven mirror” is criticized by Fisher as a contradiction [17]:“The Baconian inductive method does not account for planing or glazing the ‘uneven mirror’. Instead it is very useful to be aware of the scratches and blind spots in it and mainly to appreciate them as they are calling for a permanent improvement of ourselves and the affairs with our environment.” [19] (p. 80)
“We are usually ignorant which, out of innumerable possible factors, may prove ultimately to be the most important, though we may have strong presuppositions that some few of them are particularly worthy of study. We have usually no knowledge that any one factor will exert its effects independently of all others that can be varied, or that its effects are particularly simply related to variations in these other factors.” [16] (p. 97)
“If the investigator, in these circumstances, confines his attention to any single factor we may infer either that he is the unfortunate victim of a doctrinaire theory as to how experimentation should proceed, or that the time, material or equipment at his disposal is too limited to allow him to give attention to more than one aspect of his problem.” [16] (p. 97)
2. Methods
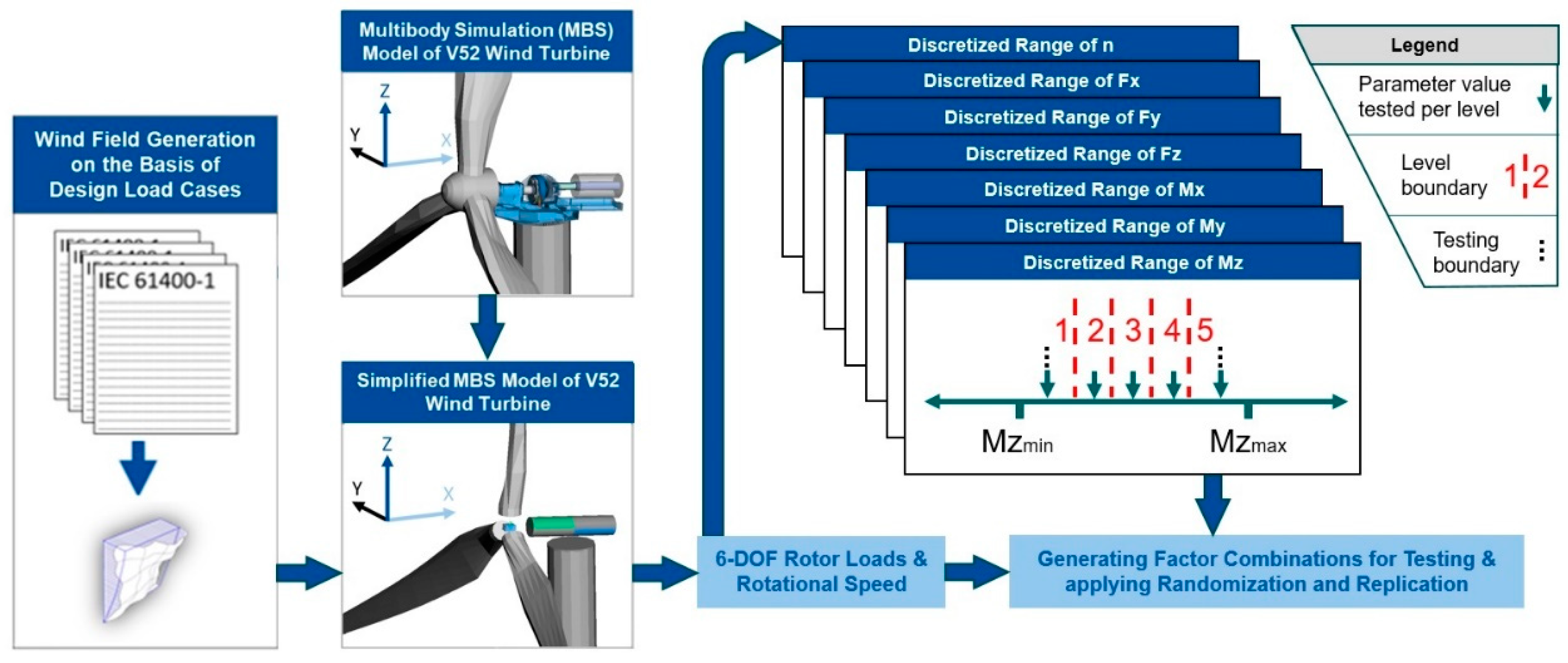
2.1. Simulation Approach
2.2. Data Description
2.3. Data Analysis
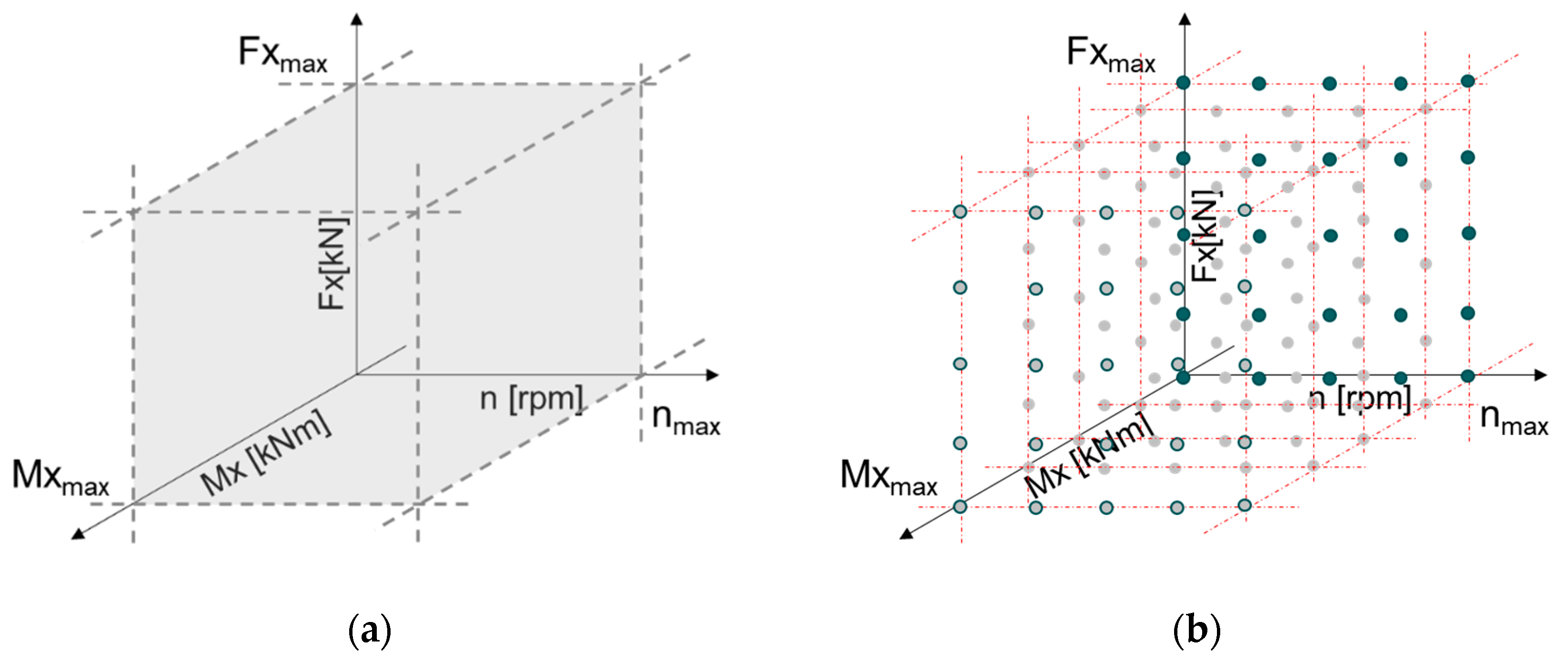
2.3.1. Definition of Design Space
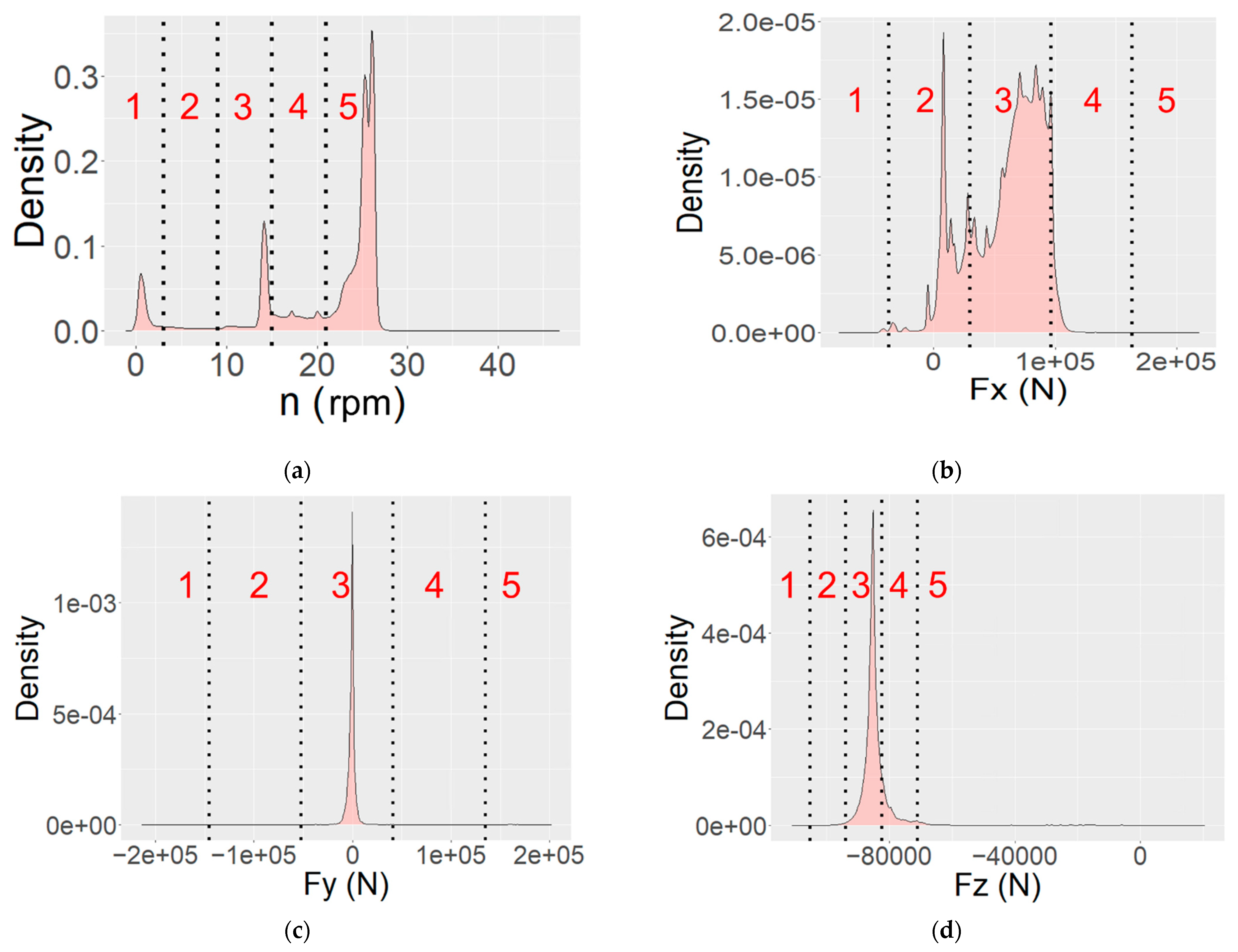
2.3.2. Discretization of Design Space and Factor Levels Definition
| Algorithm 1. Algorithm for binning a given factor into desired number of factor levels in available data set according to desired testing boundaries. |
| min_test = INPUT(“Define minimum testing boundary”) max_test = INPUT(“Define maximum testing boundary”) no_lvl = INPUT(“Define required number of levels”) lvl_width = (max_test − min_test) / no_lvl FOR each simulated data point DO IF factor < min_test + lvl_width THEN factor = 1 ELSE IF min_test + lvl_width < = factor < min_test + 2 * lvl_width THEN factor = 2 ELSE IF min_test + 2 * lvl_width < = factor < min_test + 3 * lvl_width THEN factor = 3 ⁞ ELSE IF min_test + (no_lvl − 1) * lvl_width < = factor THEN factor = no_lvl END IF END FOR |
| Algorithm 2. Alternative algorithm for binning a given factor into desired number of factor levels in available data set according to desired testing boundaries. |
| min_test = INPUT(“Define minimum testing boundary”) max_test = INPUT(“Define maximum testing boundary”) no_lvl = INPUT(“Define required number of levels”) no_increment = 2 * no_lvl − 2 lvl_increment = (max_test − min_test) / no_increment FOR each simulated data point DO IF factor < min_test + 1 * lvl_increment THEN factor = 1 ELSE IF min_test + 1 * lvl_increment < = factor < min_test + 3 * lvl_increment THEN factor = 2 ELSE IF min_test + 3 * lvl_increment < = factor < min_test + 5 * lvl_increment THEN factor = 3 ⁞ ELSE IF min_test + (no_increment − 1) * lvl_increment < = factor THEN factor = no_lvl END IF END FOR |
| Algorithm 3. Algorithm for defining the parameter value used for testing for each factor level. |
| min_test = INPUT(“Define minimum testing boundary”) max_test = INPUT(“Define maximum testing boundary”) no_lvl = INPUT(“Define required number of levels”) no_increment = 2 * no_lvl − 2 lvl_increment = (max_test − min_test) / no_increment FOR each unique factor level combination DO IF factor == 1 THEN factor = min_test + 0 * lvl_increment ELSE IF factor == 2 THEN factor = min_test + 2 * lvl_increment ELSE IF factor == 3 THEN factor = min_test + 4 * lvl_increment ⁞ ELSE IF factor == no_lvl THEN factor = min_test + no_increment * lvl_increment END IF END FOR |
2.3.3. Procedure for Factor Level Combinations of High Interest
2.3.4. Repetition and Randomization
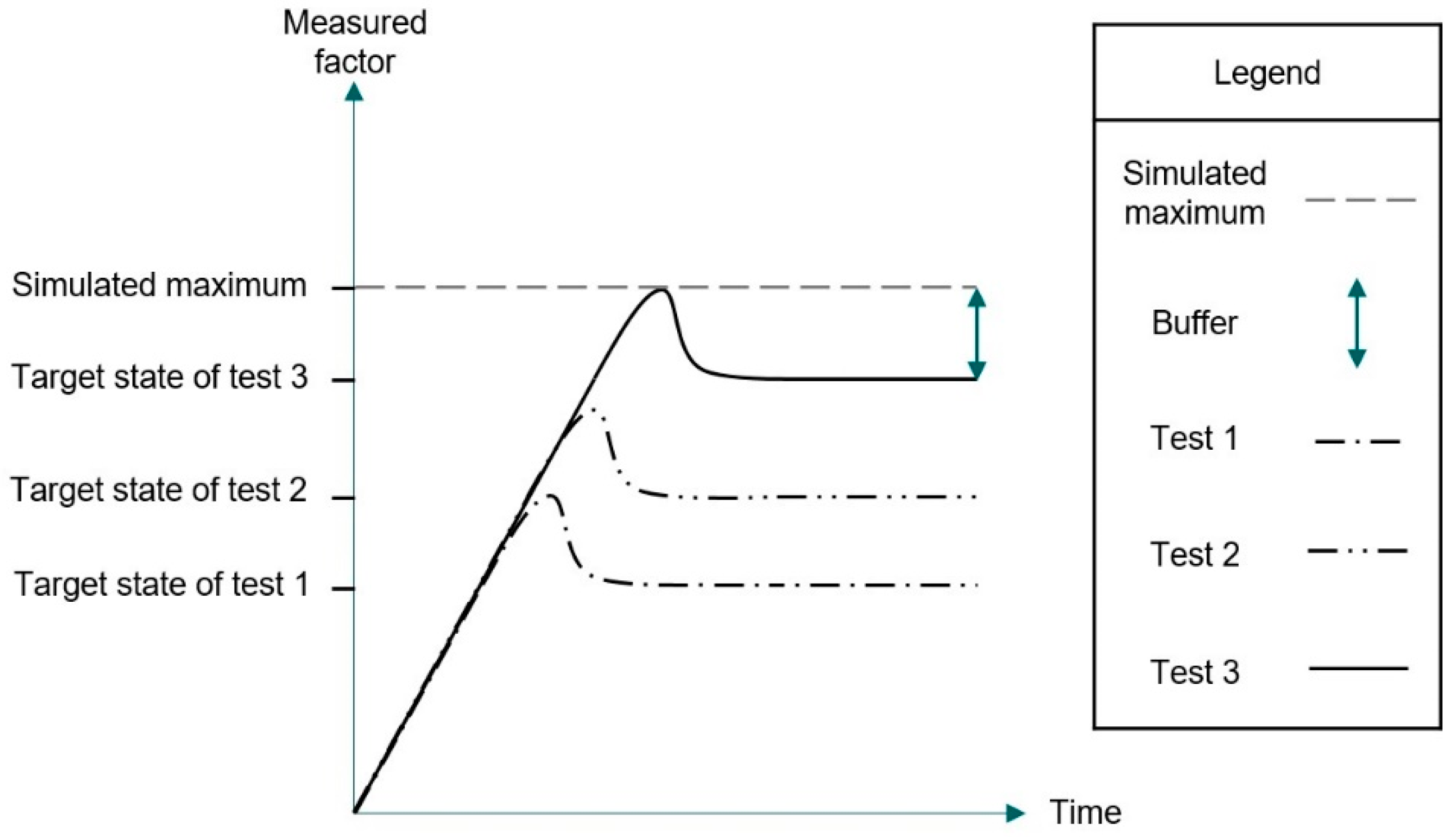
2.4. Considerations and Challenges in Practical Implementation
3. Results
4. Discussion
5. Conclusions
- Targeted aeroelastic multibody simulations covering different wind conditions based on the DLCs provided within the IEC 61400-1 standard can be implemented using the developed method to generate simulated time-series data of the 6-DOF rotor loads and rotational speeds that a WT is likely to experience during its lifetime;
- Simulated data can be analyzed using the developed method to define the design space of the factors under study as well as to reach realistic factor level combinations within the design space to lower the risk of premature drivetrain failure during testing;
- The proposed method can significantly limit the number of designed experiments as compared to a full factorial design, while targeting highly frequent load combinations at a greater resolution;
- Due to the promising results achieved using the presented methodology, the authors aim to utilize it in upcoming tests on the drivetrain a Vestas V52 using a WT system test bench capable of applying the generated factor combinations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Averous, N.; Stieneker, M.; Kock, S.; Andrei, C.; Helmedag, A.; de Doncker, R.W.; Hameyer, K.; Jacobs, G.; Monti, A. Development of a 4 MW Full-Size Wind-Turbine Test Bench. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 600–609. [Google Scholar] [CrossRef] [Green Version]
- Kaven, L.; Frehn, A.; Basler, M.; Jassmann, U.; Röttgers, H.; Konrad, T.; Abel, D.; Monti, A. Impact of Multi-Physics HiL Test Benches on Wind Turbine Certification. Energies 2022, 15, 1336. [Google Scholar] [CrossRef]
- Schkoda, R.; Fox, C. Integration of mechanical and electrical hardware for testing full scale wind turbine nacelles. In Proceedings of the 2014 Clemson University Power Systems Conference, Clemson, SC, USA, 11–14 March 2014. [Google Scholar]
- Lorentzen, T.; Rasmussen, L. Realistic full scale indoor testing of wind turbine nacelles. In Proceedings of the EWEA Offshore 2015, Copenhagen, Denmark, 10–12 March 2015. [Google Scholar]
- Gevorgian, V.; Link, H.; McDade, M.; Mander, A.; Fox, J.; Rigas, N. First International Workshop on Grid Simulator Testing of Wind Turbine Drivetrains: Workshop Proceedings; NREL: Boulder, CO, USA, 2013. [Google Scholar]
- Stetco, A.; Dinmohammadi, F.; Zhao, X.; Robu, V.; Flynn, D.; Barnes, M.; Keane, J.; Nenadic, G. Machine learning methods for wind turbine condition monitoring: A review. Renew. Energy 2019, 133, 620–635. [Google Scholar] [CrossRef]
- Black, I.; Richmond, M.; Kolios, A. Condition monitoring systems: A systematic literature review on machine-learning methods improving offshore-wind turbine operational management. Int. J. Sustain. Energy 2021, 40, 923–946. [Google Scholar] [CrossRef]
- Heinold, K.; Panyam, M.; Bibo, A. Considerations for testing full-scale wind turbine nacelles with hardware-in-the-loop. Forsch Ing. 2021, 85, 601–617. [Google Scholar] [CrossRef]
- Jassmann, U.; Reiter, M.; Abel, D. An Innovative Method for Rotor Inertia Emulation at Wind Turbine Test Benches. IFAC-PapersOnLine 2014, 47, 10107–10112. [Google Scholar] [CrossRef] [Green Version]
- Reisch, S.; Jacobs, G.; Bosse, D.; Matzke, D. Challenges and opportunities of full size nacelle testing of wind turbine generators. In Proceedings of the JSME International Conference on Motion and Power Transmissions, Kyoto, Japan, 28 February–3 March 2017. [Google Scholar]
- Riccobono, A.; Helmedag, A.; Berthold, A.; Averous, N.; De Doncker, R.; Monti, A. Stability and Accuracy Considerations of Power Hardware- in-the-Loop Test Benches for Wind Turbines. IFAC-Pap. 2017, 50, 10977–10984. [Google Scholar] [CrossRef]
- Azzam, B.; Schelenz, R.; Roscher, B.; Baseer, A.; Jacobs, G. Development of a wind turbine gearbox virtual load sensor using multibody simulation and artificial neural networks. Forsch Ing. 2021, 85, 241–250. [Google Scholar] [CrossRef]
- Liu, X.; Azzam, B.; Harzendorf, F.; Kolb, J.; Schelenz, R.; Hameyer, R.; Jacobs, G. Early stage white etching crack identification using artificial neural networks. Forsch Ing. 2021, 85, 153–163. [Google Scholar] [CrossRef]
- Azzam, B.; Schelenz, R.; Jacobs, G. Sensor Screening Methodology for Virtually Sensing Transmission Input Loads of a Wind Turbine Using Machine Learning Techniques and Drivetrain Simulations. Sensors 2022, 22, 3659. [Google Scholar] [CrossRef]
- Fisher, R. Statistical Methods for Research Workers; Oliver and Boyd: Edinburgh, UK, 1925. [Google Scholar]
- Fisher, R. The Design of Experiments; Oliver and Boyd: Edinburgh, UK, 1935. [Google Scholar]
- Niedz, R.; Evens, T. Design of experiments (DOE)—History, concepts, and relevance to in vitro culture. Vitr. Cell. Dev. Biol.-Plant 2016, 52, 547–562. [Google Scholar] [CrossRef]
- Bacon, F. The Novum Organum of Sir Francis Bacon, Baron of Verulam, Viscount St. Albans Epitomiz’d, for a Clearer Understanding of his Natural History; Thomas Lee: London, UK, 1676. [Google Scholar]
- Schwarz, A. The becoming of the experimental mode. Sci. Stud. 2012, 10, 65–83. [Google Scholar] [CrossRef] [Green Version]
- Bacon, F. Instauratio Magna (Novum Organum); Apud J. Billium: London, UK, 1620. [Google Scholar]
- Jardine, L.; Silverthorne, M. Francis Bacon: The New Organon; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Salsburg, D. The Lady Tasting Tea; W. H. Freeman and Co.: New York, NY, USA, 2001. [Google Scholar]
- Fisher, R. Development of the theory of experimental design. In Proceedings of the International Statistical Conferences, Washington, DC, USA, 6–18 September 1947. [Google Scholar]
- Deloach, R. Analysis of variance in the modern design of experiments. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010. [Google Scholar]
- Montgomery, D. Design and Analysis of Experiments, 8th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Cox, D. Planning of Experiments; Wiley: New York, NY, USA, 1958. [Google Scholar]
- Steel, R.; Torrie, J. Principles and Procedures of Statistics: A Biometrical Approach, 2nd ed.; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Mead, R. The Design of Experiments; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Hinkelmann, K.; Kempthorne, O. Design and Analysis of Experiments, Vol. I: Introduction to Experimental Design, 3rd ed.; Wiley-Interscience: New York, NY, USA, 2008. [Google Scholar]
- Hurlbert, S. Pseudofactorialism, response structures and collective responsibility. Austral Ecol. 2013, 38, 646–663. [Google Scholar] [CrossRef] [Green Version]
- Brown, S.; Staff, M.; Lee, R.; Love, J.; Parker, D.; Aves, S.; Howard, T. Design of Experiments Methodology to Build a Multifactorial Statistical Model Describing the Metabolic Interactions of Alcohol Dehydrogenase Isozymes in the Ethanol Biosynthetic Pathway of the Yeast Saccharomyces cerevisiae. ACS Synth. Biol. 2018, 7, 1676–1684. [Google Scholar] [CrossRef] [PubMed]
- Kasemiire, A.; Avohou, H.; De Bleye, C.; Sacre, P.-Y.; Dumont, E.; Hubert, P.; Ziemons, E. Design of experiments and design space approaches in the pharmaceutical bioprocess optimization. Eur. J. Pharm. Biopharm. 2021, 166, 144–154. [Google Scholar] [CrossRef] [PubMed]
- Nelson, W. An updated bibliography of accelerated test plans. In Proceedings of the 2015 Annual Reliability and Maintainability Symposium (RAMS), Palm Harbor, FL, USA, 26–29 January 2015. [Google Scholar]
- Fisher, R. The arrangement of field experiments. J. Minist. Agric. 1926, 33, 503–513. [Google Scholar]
- Yang, G. Life Cycle Reliability Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Chang, M.-S.; Park, T.-K.; Sung, B.-J.; Choi, B.-O. Life prediction of brazed plate heat exchanger based on several accelerated life test data. J. Mech. Sci. Technol. 2015, 29, 2341–2348. [Google Scholar] [CrossRef]
- Elsayed, E. Reliability Engineering; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Meeker, W.; Escobar, L.; Pascual, F. Statistical Methods for Reliability Data, 2nd ed.; Wiley: New York, NY, USA, 2021. [Google Scholar]
- Farooq, M.; Nóvoa, H.; Araújo, A.; Tavares, S. An innovative approach for planning and execution of pre-experimental runs for Design of Experiments. Eur. Res. Manag. Bus. Econ. 2016, 22, 155–161. [Google Scholar] [CrossRef] [Green Version]
- Gilman, J.; Walls, L.; Bandiera, L.; Menolascina, F. Statistical Design of Experiments for Synthetic Biology. ACS Synth. Biol. 2021, 10, 1–18. [Google Scholar] [CrossRef]
- Box, G.; Hunter, J.; Hunter, W. Statistics for Experimenters: Design, Innovation, and Discovery, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2005. [Google Scholar]
- Young, J. Blocking, replication, and randomization—The key to effective experimentation: A case study. Qual. Eng. 1996, 9, 269–277. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. IEC 61400-1. Wind Turbines—Part 1: Design Requirements; International Electrotechnical Commission: Geneva, Switzerland, 2019. [Google Scholar]
- Roach, S.; Park, S.; Gaertner, E.; Manwell, J.; Lackner, M. Application of the New IEC International Design Standard for Offshore Wind Turbines to a Reference Site in the Massachusetts Offshore Wind Energy Area. J. Phys. Conf. Ser. 2020, 1452, 012038. [Google Scholar] [CrossRef]
- Rexroth Bosch Group. Operating Instructions—GPV 306 S2 PG 50HZ 61,9 ONSHORE; Rexroth Bosch Group: Lohr am Main, Germany, 2006. [Google Scholar]
- Vestas. General Specification Vestas V52 850 kW 50/60 Hz OptiSpeed®- Wind Turbine; Vestas: Randers, Denmark, 2006. [Google Scholar]
- Berroth, J. Einfluss der Stelldynamik der Rotorblätter auf die Lasten der Blattverstellsysteme von Windenergieanlagen; Verlagsgruppe Mainz GmbH: Aachen, Germany, 2017. [Google Scholar]
- Craig, R.; Bampton, M. Coupling of Substructures for Dynamic Analysis. AIAA J. 1968, 6, 1313–1319. [Google Scholar] [CrossRef] [Green Version]
- Jonkman, B. Turbsim User’s Guide: Version 1.50; Technical Report No. NREL/EL-500-38230; National Renewable Energy Laboratory: Golden, CO, USA, 2009. [Google Scholar]
- Bi, L.; Schelenz, R.; Jacobs, G. Dynamic simulation of full-scale nacelle test rig with focus on drivetrain response under emulated loads. In Proceedings of the Conference for Wind Power Drives, Aachen, Germany, 3–4 March 2015. [Google Scholar]
- Laino, D. IECWind: A Program to Create IEC Wind Data Files, NWTC Design Codes; National Renewable Energy Laboratory: Golden, CO, USA, 2005. [Google Scholar]
- Cardaun, M.; Roscher, B.; Schelenz, R.; Jacobs, G. Analysis of Wind-Turbine Main Bearing Loads Due to Constant Yaw Misalignments over a 20 Years Timespan. Energies 2019, 12, 1768. [Google Scholar] [CrossRef] [Green Version]
- Renewable Energy Act of 21 July 2014 (BGBl. I S. 1066), Last Amended by Article 1 of the Act of 17 July 2017 (BGBl. I S. 2532). Available online: http://www.gesetze-im-internet.de/eeg_2014/EEG_2017.pdf (accessed on 21 January 2021).
- Sargent, R. Verification and validation of simulation models. In Proceedings of the 2010 Winter Simulation Conference, Baltimore, MD, USA, 5–8 December 2010. [Google Scholar]
- Babuska, I.; Oden, T. Verification and validation in computational engineering and science: Basic concepts. Comput. Methods Appl. Mech. Engrg. 2004, 193, 4057–4066. [Google Scholar] [CrossRef]
- Law, A. Simulation Modeling and Analysis; McGraw-Hill: New York, NY, USA, 2007. [Google Scholar]
- Logan, R.; Nitta, C. Verification & Validation: Process and Levels Leading to Qualitative or Quantitative Validation Statements. SAE Trans. 2004, 113, 804–816. [Google Scholar]
- Kutluay, K.; Winner, H. Validation of vehicle dynamics simulation models—A review. Veh. Syst. Dyn. 2014, 52, 186–200. [Google Scholar] [CrossRef]


| ID | Subject(s) | Measurement | Axis of Measurement |
|---|---|---|---|
| Mx | Rotor input load | Moment | x |
| My | y | ||
| Mz | z | ||
| Fx | Rotor input load | Force | x |
| Fy | y | ||
| Fz | z | ||
| n | Rotor | Rotational speed | x |
| Parameter | Values |
|---|---|
| Rated power | 850 kW |
| Wind class | Ia |
| Rotor diameter | 52 m |
| Rotor maximum speed | 31.4 rpm |
| Hub height | 55 m |
| Gearbox, type | Planetary and spur |
| Gearbox, number of stages | 3 |
| Gearbox ratio | i = 61.92 |
| Design Condition | DLC | Ambient Wind Condition | Wind Speed(s) 1 |
|---|---|---|---|
| 1. Production | 1.1 | Normal Turbulence Model | Vin < Vhub < Vout |
| 1.2 | |||
| 1.3 | Extreme Turbulence Model | ||
| 1.4 | Extreme Coherent gust with change of Direction | Vhub = Vr and Vr ± 2 m/s | |
| 1.5 | Extreme Wind Shear | Vin < Vhub < Vout | |
| 3. Startup | 3.1 | Normal Wind Profile | Vin < Vhub < Vout |
| 3.2 | Extreme Operating Gust | Vhub = Vin, Vr ± 2 m/s, and Vout | |
| 3.3 | Extreme wind Direction Change | ||
| 4. Normal shutdown | 4.1 | Normal Wind Profile | Vin < Vhub < Vout |
| 4.2 | Extreme Operating Gust | Vhub = Vout and Vr ± 2 m/s | |
| 5. Emergency stop | 5.1 | Normal Turbulence Model | Vhub = Vout and Vr ± 2 m/s |
| 6. Parked (idling) | 6.1 | Extreme Wind speed Model | 50-year return period |
| 6.2 | |||
| 6.3 | 1-year return period | ||
| 6.4 | Normal Turbulence Model | Vhub > 0.7*Vref |
| ID | Explanation | Value/Source |
|---|---|---|
| Vhub | Speed at hub of WT | Depends on DLC |
| Vin | Cut-in wind speed | 4 m/s |
| Vout | Cut-out wind speed | 25 m/s |
| Vr | Rated wind speed | 14 m/s |
| Vref | Reference wind speed | 50 m/s |
| - | 50-year return period | For formula, see [43] |
| - | 1-year return period | For formula, see [43] |
| Factors | Time (s) | Minimum/ Maximum | Simulated Wind Conditions [43] | ||
|---|---|---|---|---|---|
| DLC | Wind speed (m/s) | Yaw (deg) | |||
| n | 225 | −1.09 | 1.4 | 12 | 0 |
| 196 | 46.73 | 4.2 | 25 | +4 | |
| Fx | 200 | −78.05 | 4.2 | 25 | −4 |
| 200 | 217.97 | 4.2 | 25 | −12 | |
| Fy | 100 | −213.93 | 6.1 | 50-year | +15 |
| 161 | 201.37 | 6.1 | 50-year | −15 | |
| Fz | 692 | −111.04 | 1.3 | 25 | 0 |
| 297 | 20.28 | 6.1 | 50-year | 0 | |
| Mx | 161 | −123.52 | 1.4 | 12 | 0 |
| 198 | 602.72 | 4.2 | 25 | +4 | |
| My | 209 | −737.18 | 1.4 | 16 | 0 |
| 209 | 628.05 | 1.4 | 16 | 0 | |
| Mz | 158 | −595.65 | 1.4 | 12 | 0 |
| 337 | 445.88 | 1.3 | 25 | 0 | |
| Factors | Factor Value at Level Boundary (rpm, kN, kNm) | |||
|---|---|---|---|---|
| 1–2 | 2–3 | 3–4 | 4–5 | |
| n | 3 | 9 | 15 | 21 |
| Fx | −36.94 | 29.66 | 96.27 | 162.87 |
| Fy | −145.81 | −52.37 | 41.07 | 134.51 |
| Fz | −105.33 | −93.92 | −82.50 | −71.08 |
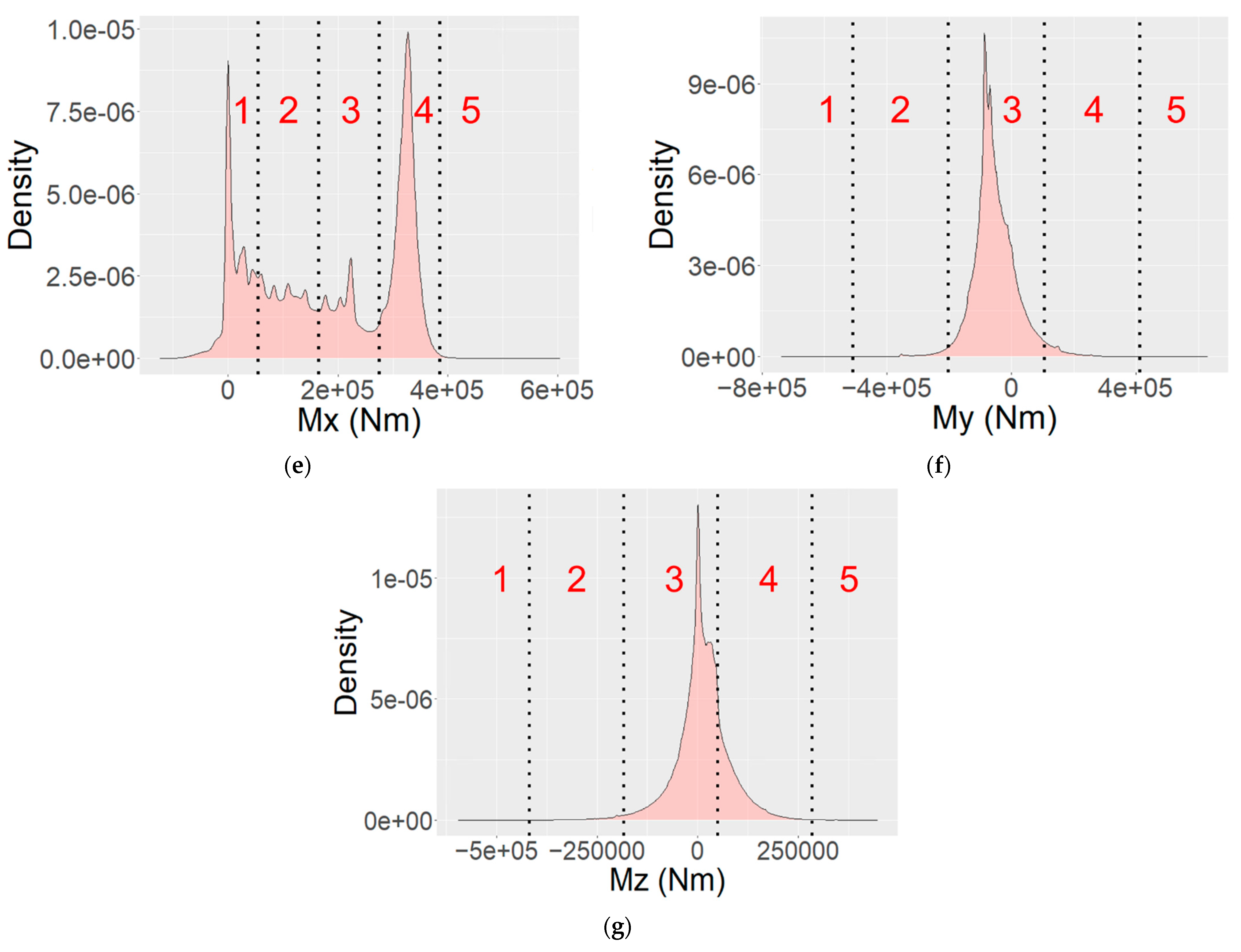
| Mx | 55 | 165 | 275 | 385 |
| My | −509.87 | −202.69 | 104.48 | 411.66 |
| Mz | −418.91 | −184.57 | 49.78 | 284.12 |
| Factors | Parameter Values Tested at each Factor Level (rpm, kN, kNm) | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| n | 0 | 6 | 12 | 18 | 24 |
| Fx | −70.25 | −3.64 | 62.97 | 129.57 | 196.18 |
| Fy | −192.53 | −99.09 | −5.65 | 87.79 | 181.23 |
| Fz | −111.04 | −99.63 | −88.21 | −76.79 | −65.37 |
| Mx | 0 | 110 | 220 | 330 | 440 |
| My | −663.46 | −356.28 | −49.11 | 258.07 | 565.25 |
| Mz | −536.08 | −301.74 | −67.39 | 166.95 | 401.29 |
| Combination ID | Factor Levels | ||||||
|---|---|---|---|---|---|---|---|
| n | Fx | Fy | Fz | Mx | My | Mz | |
| 1 | 5 | 3 | 3 | 3 | 4 | 3 | 3 |
| 2 | 3 | 2 | 3 | 3 | 1 | 3 | 3 |
| 3 | 5 | 3 | 3 | 3 | 4 | 3 | 4 |
| 4 | 5 | 3 | 3 | 3 | 2 | 3 | 3 |
| 5 | 5 | 3 | 3 | 3 | 3 | 3 | 3 |
| 6 | 4 | 3 | 3 | 3 | 2 | 3 | 3 |
| 7 | 1 | 2 | 3 | 4 | 1 | 3 | 3 |
| 8 | 5 | 3 | 3 | 4 | 4 | 3 | 3 |
| 9 | 5 | 3 | 3 | 3 | 2 | 3 | 4 |
| 10 | 5 | 3 | 3 | 3 | 3 | 3 | 4 |
| 11 | 3 | 3 | 3 | 3 | 1 | 3 | 3 |
| 12 | 5 | 4 | 3 | 3 | 3 | 3 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azzam, B.; Schelenz, R.; Cardaun, M.; Jacobs, G. From Simulations to Accelerated Testing: Design of Experiments for Accelerated Load Testing of a Wind Turbine Drivetrain Based on Aeroelastic Multibody Simulation Data. Appl. Sci. 2023, 13, 356. https://doi.org/10.3390/app13010356
Azzam B, Schelenz R, Cardaun M, Jacobs G. From Simulations to Accelerated Testing: Design of Experiments for Accelerated Load Testing of a Wind Turbine Drivetrain Based on Aeroelastic Multibody Simulation Data. Applied Sciences. 2023; 13(1):356. https://doi.org/10.3390/app13010356
Chicago/Turabian StyleAzzam, Baher, Ralf Schelenz, Martin Cardaun, and Georg Jacobs. 2023. "From Simulations to Accelerated Testing: Design of Experiments for Accelerated Load Testing of a Wind Turbine Drivetrain Based on Aeroelastic Multibody Simulation Data" Applied Sciences 13, no. 1: 356. https://doi.org/10.3390/app13010356
APA StyleAzzam, B., Schelenz, R., Cardaun, M., & Jacobs, G. (2023). From Simulations to Accelerated Testing: Design of Experiments for Accelerated Load Testing of a Wind Turbine Drivetrain Based on Aeroelastic Multibody Simulation Data. Applied Sciences, 13(1), 356. https://doi.org/10.3390/app13010356






