Environment-Aware Energy Efficient and Reliable Routing in Real-Time Multi-Sink Wireless Sensor Networks for Smart Cities Applications
Abstract
:Featured Application
Abstract
1. Introduction
- (1)
- Proposing an energy-efficient, reliably environmentally aware for a real-time routing for multi-sink WSNs considering the environmental data, link quality, delay, energy, and load balancing.
- (2)
- Describing the routing problem in large-scale multi-sink WSN in the form of 0/1 integer programming.
- (3)
- The routing problem is formulated in the form of 0/1 integer programming for other researchers to understand and reuse.
- (4)
- Swarm intelligence is introduced as a heuristic solution.
2. Related Work
3. Problem Modelling
- (1)
- Provides the shortest transmission distance to minimize energy consumption.
- (2)
- Provides the minimum value for the proposed load metric to achieve balanced energy consumption.
- (3)
- Away from the danger zones to keep the path of the data transmission safe as much as possible.
- (4)
- Provides the lowest end-to-end latency for real-time data transmission and eliminates sensor node buffer overflow due to limited buffer capacity.
- (1)
- Minimum communication distance.
- (2)
- Less likely to be cut off as a result of environmental reasons.
- (3)
- Maximum reliability.
- (4)
- Minimum end-to-end delay.
- (5)
- In order to establish a better energy balance, the nodes participating in the path have the highest value resulting from the new proposed energy load function.
4. Formulation for Optimal Solution
5. Swarm-Based Solution
5.1. Optimal Sink Selection Problem
- -
- represents the pheromone value at time t, between sink node si and source node s.
- -
- , , and are the weight factors that control the pheromone value and the heuristic information parameters, respectively, and and are the heuristic information.
5.1.1. Pheromone Calculation
5.1.2. Calculation of the Heuristic Information
5.2. Routing Problem
5.2.1. Pheromone Calculation
5.2.2. Heuristic Information Computation
6. Performance Evaluations
6.1. Performance Evaluation Criteria
- -
- Network Lifetime [8] is the amount of time that has passed since the network’s first node failed because of a dead battery.
- -
- Packet Delivery Ratio (PDR) [8]. The ratio of the number of messages successfully received by the sink node to the total number of messages sent by all source nodes.
- -
- Deadline miss ratio [8]. This is the number of packets whose deadlines were missed because they never reached the sink node.
- -
- Average end-to-end delay [8]. This is the meantime for a data packet to transit from its source nodes to the sink.
- -
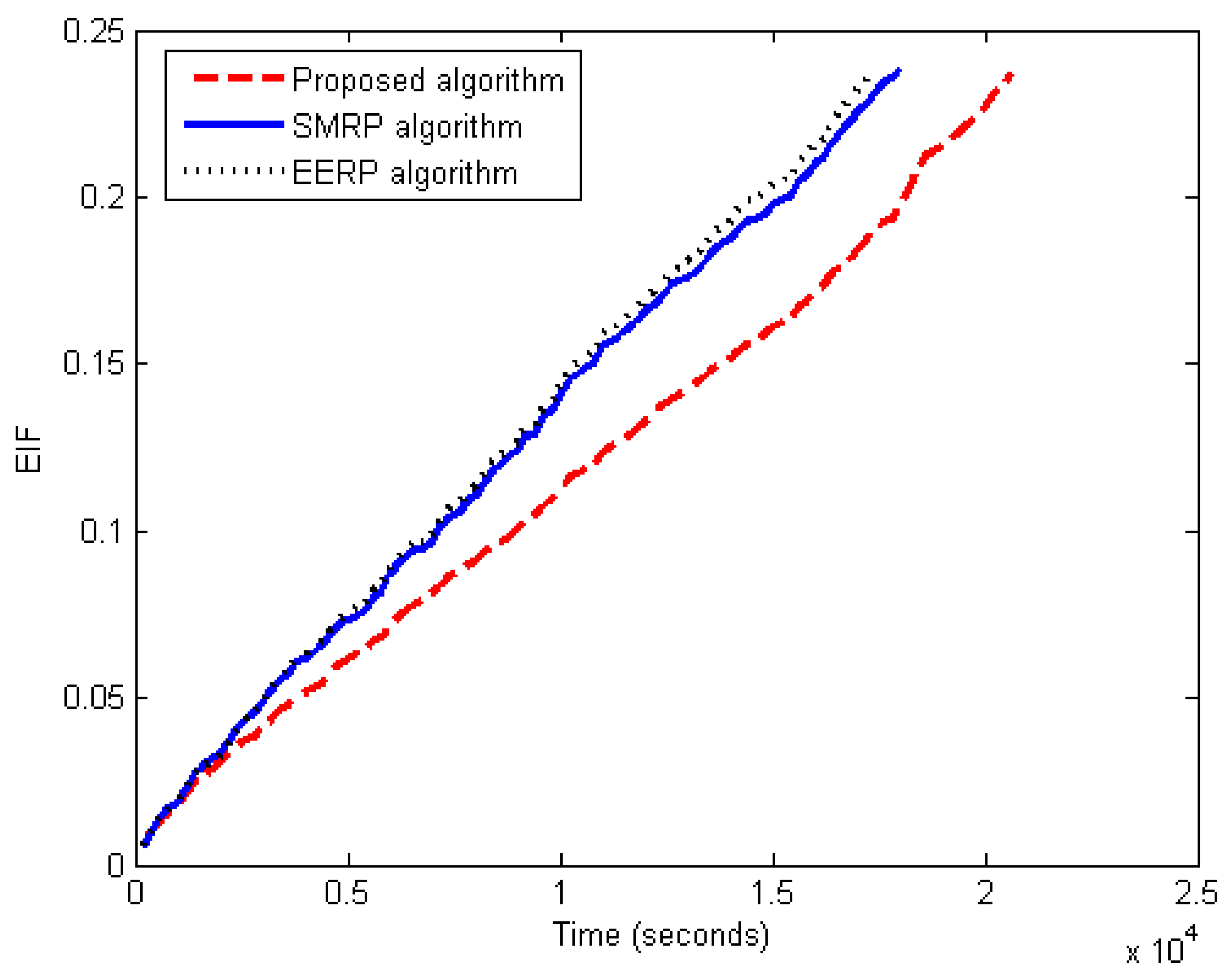
- Energy Imbalance Factor (EIF) [15]. This is the standard deviation of the network’s residual energy. It is a measure of the routing protocol’s efficacy in terms of energy-saving balance.
6.2. Simulation Model
6.3. Simulation Results
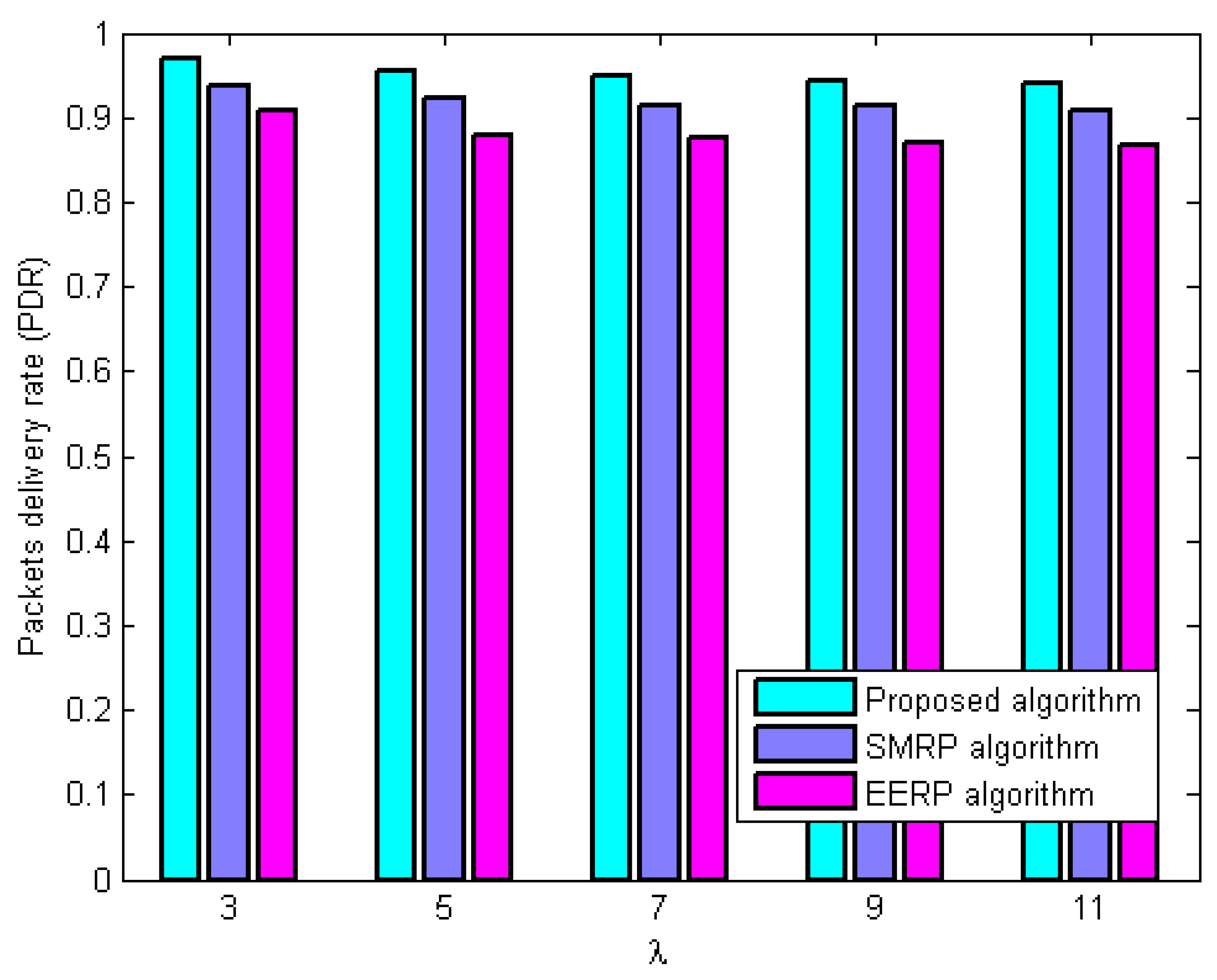
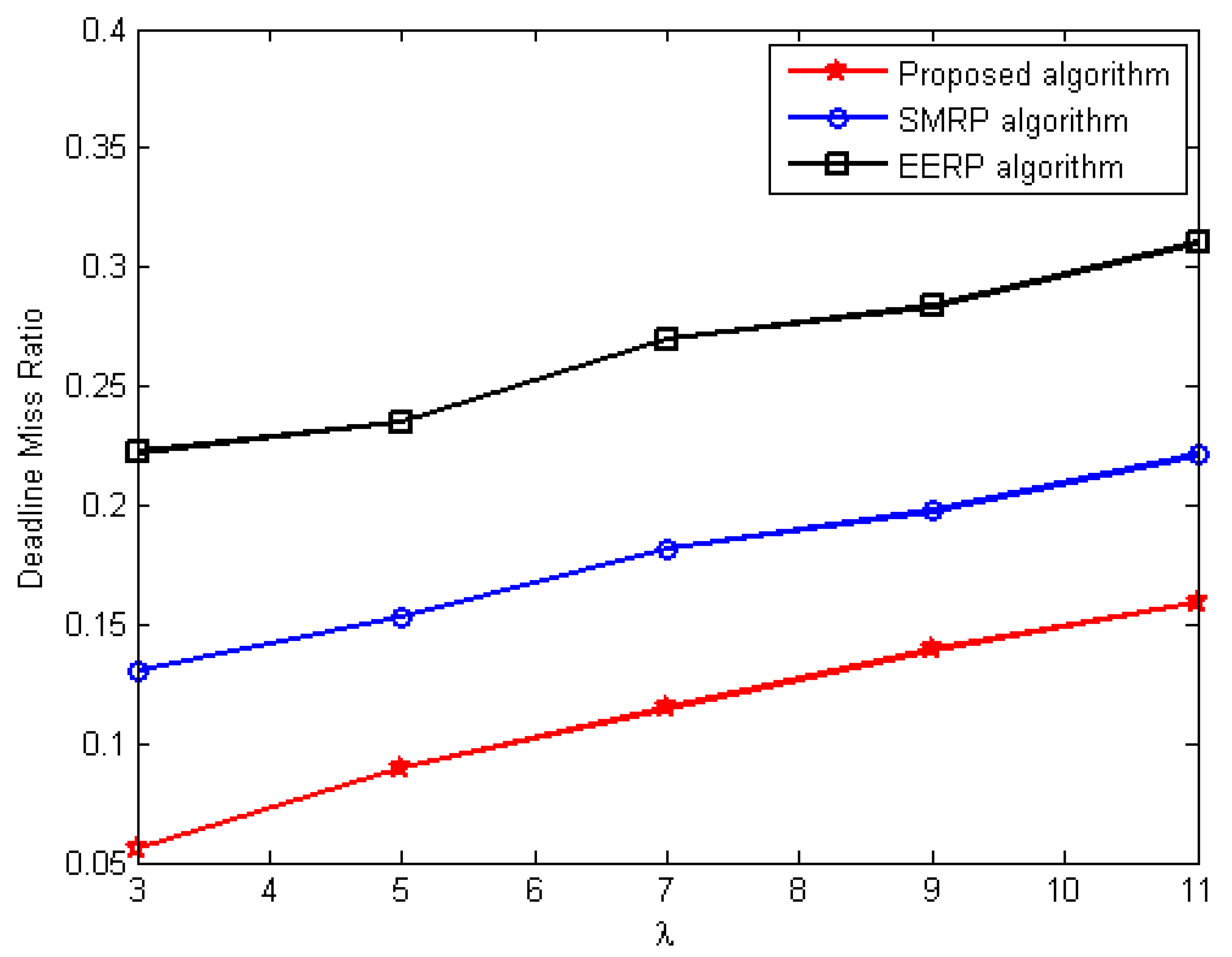
- First scenario: This is considered with regard to the environmental statistics that are within the normal range; therefore, environmental influences do not affect network performance. This demonstrates the performance of the approaches under normal environmental conditions.
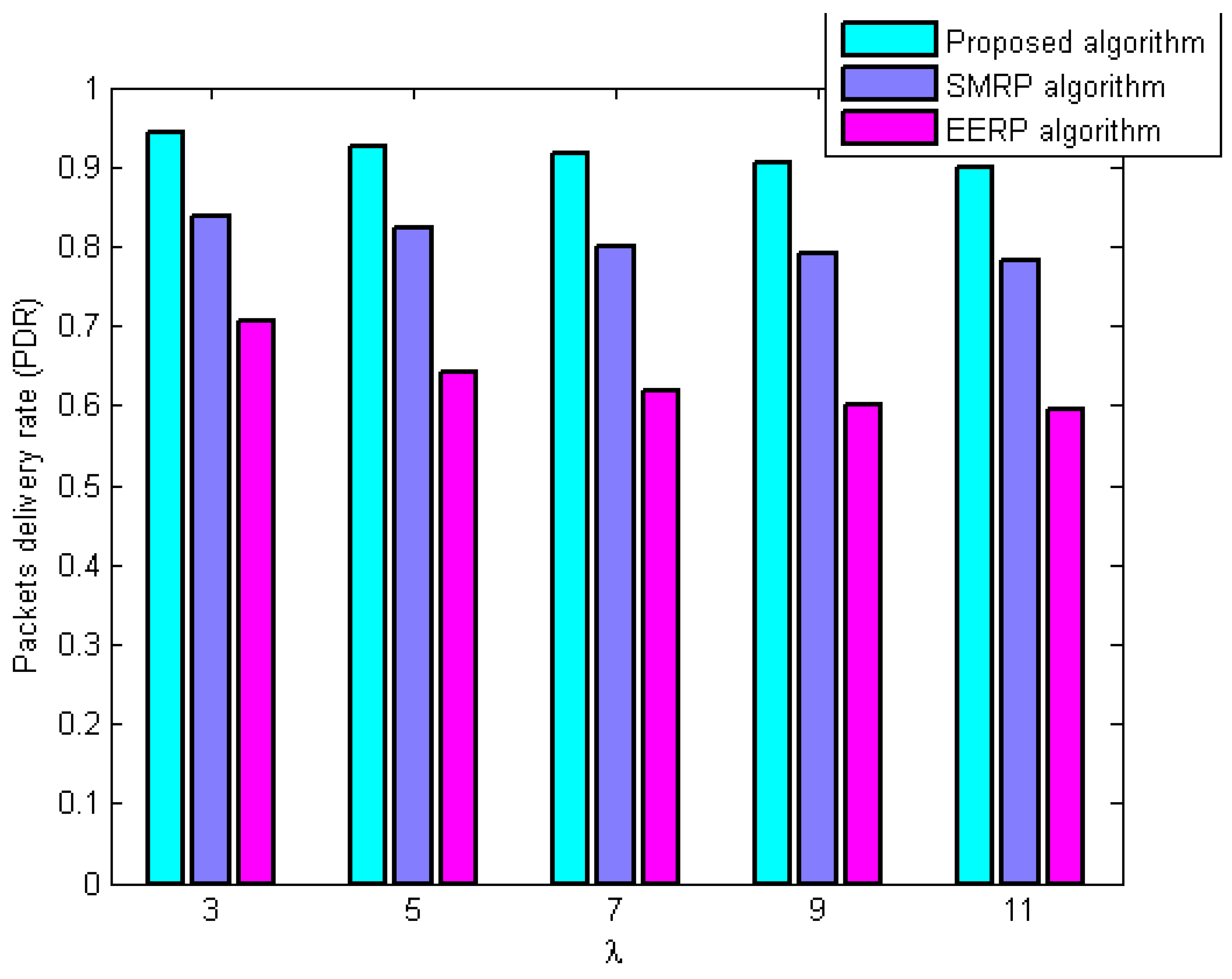
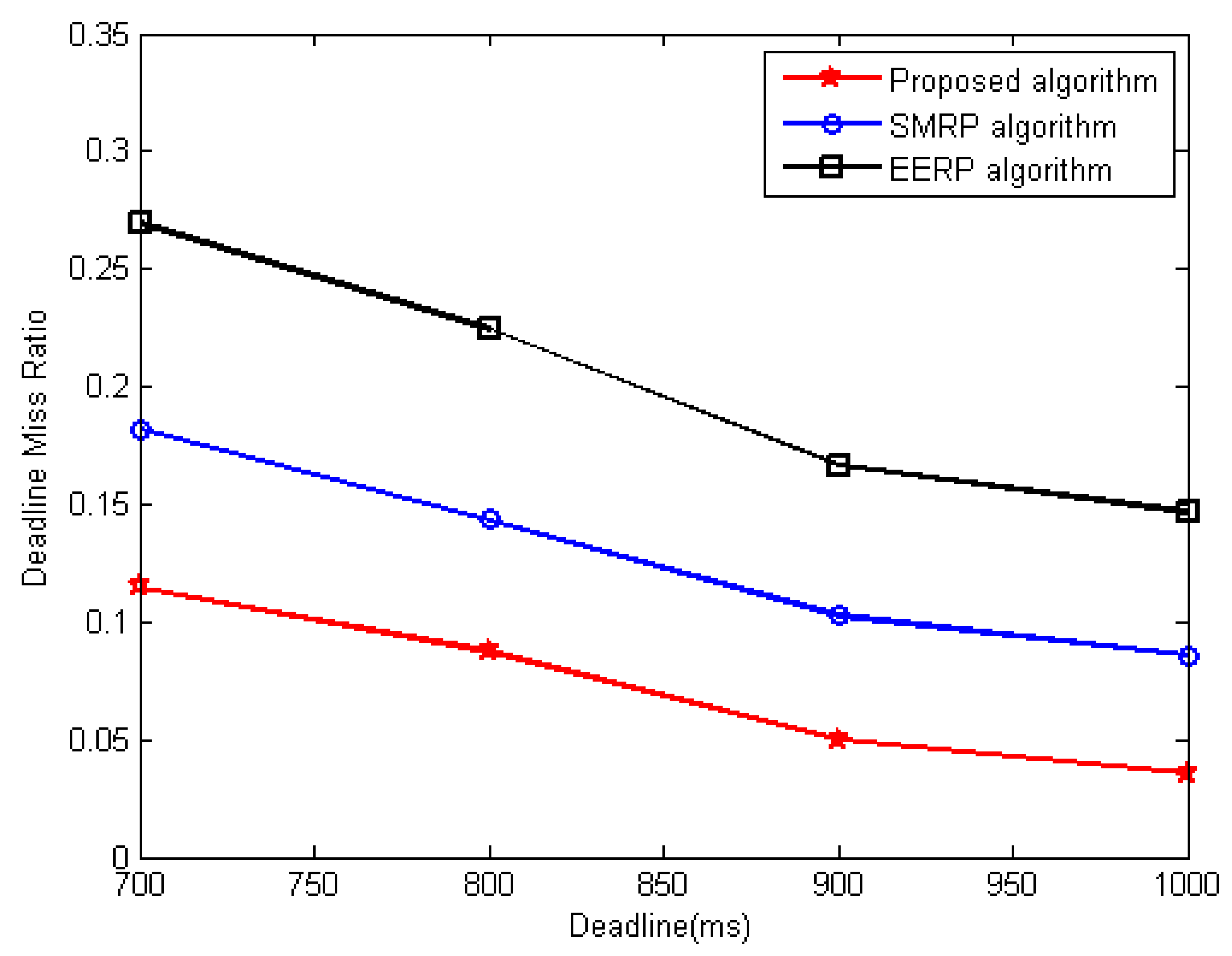
- Second scenario: It is assumed that the environmental data are outside the normal range. It demonstrates the performance of the approaches under environmental conditions outside the normal range. In the second scenario, all following studies assume the network is impacted by wildfire. Environmental events are considered to occur 400 s after network start-up.
6.3.1. Evaluation of Packets Delivery Ratio (PDR)
- 1.
- PDR evaluation under the first scenario
- 2.
- PDR evaluation under the second scenario
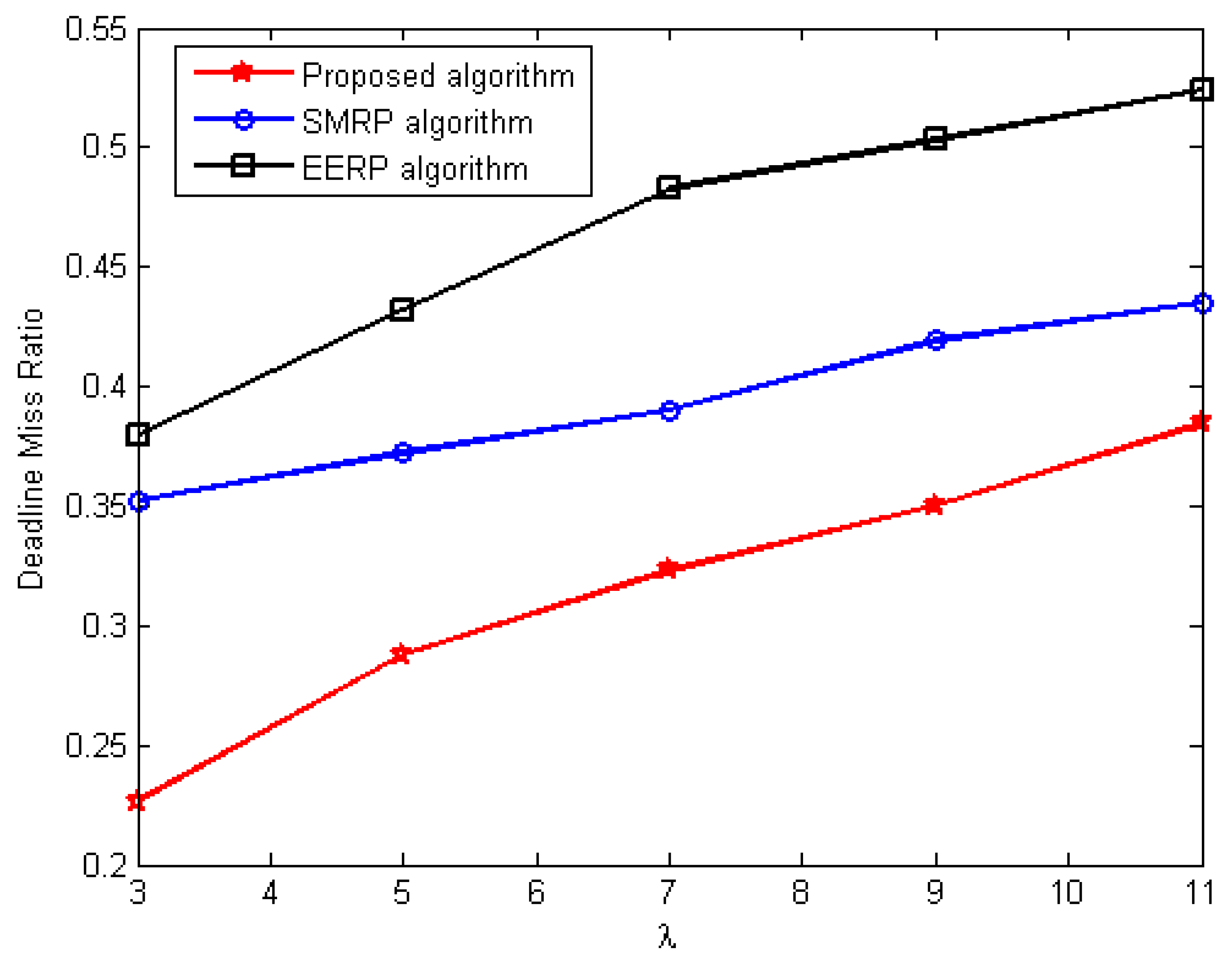
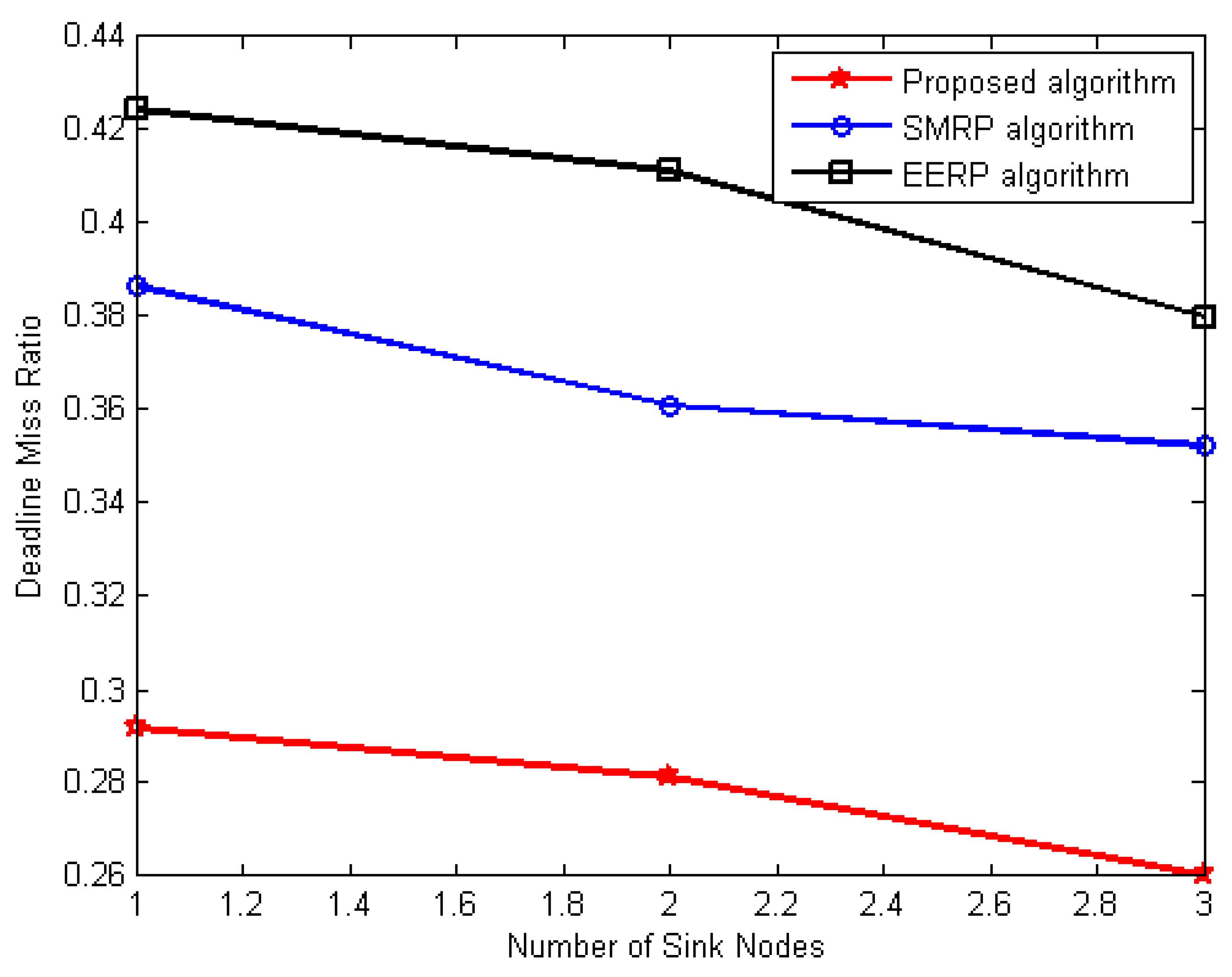
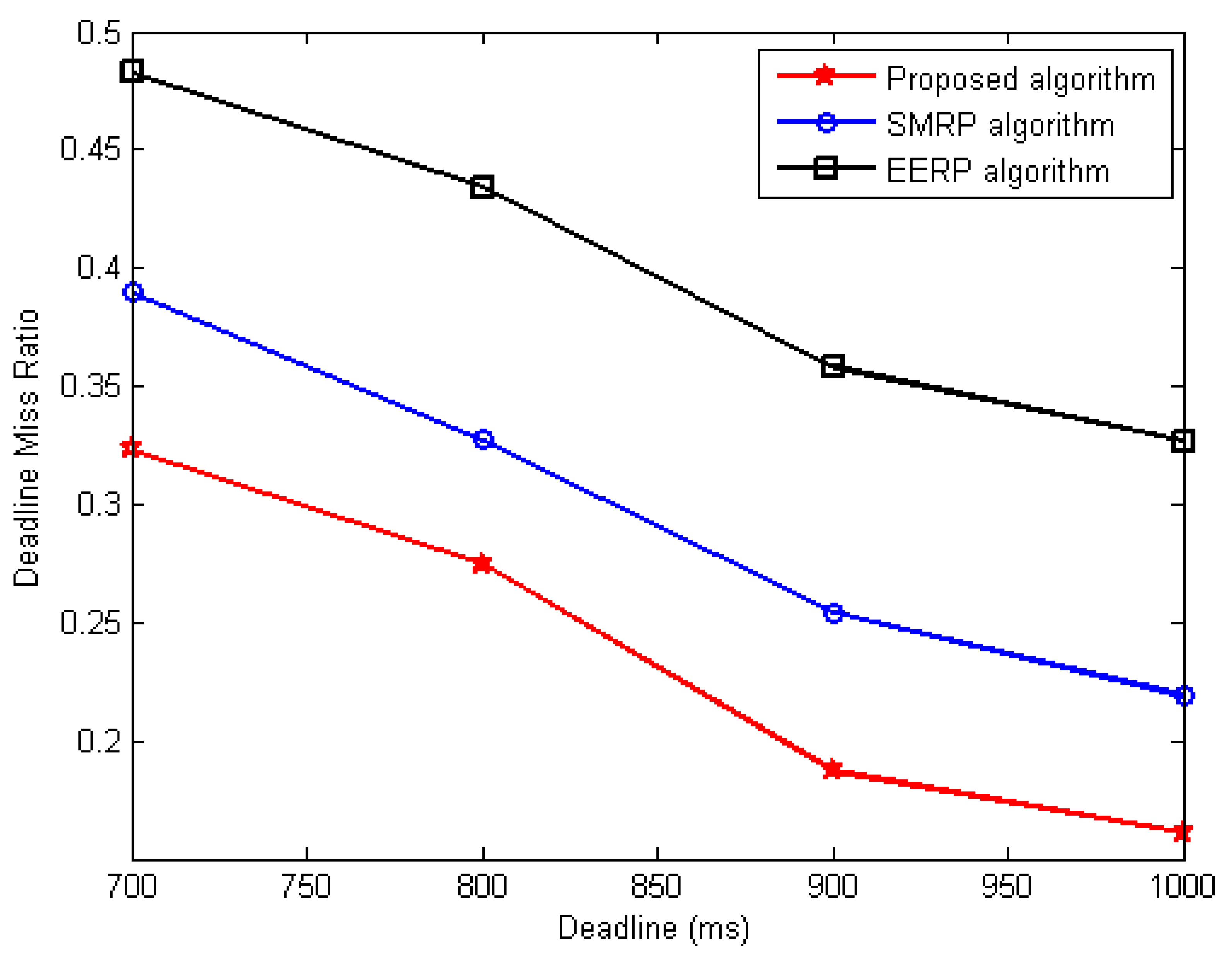
6.3.2. Miss Ratio Deadline Evaluation
- 1.
- Deadline miss ratio evaluation under the first scenario
- 2.
- Deadline miss ratio evaluation under the second scenario
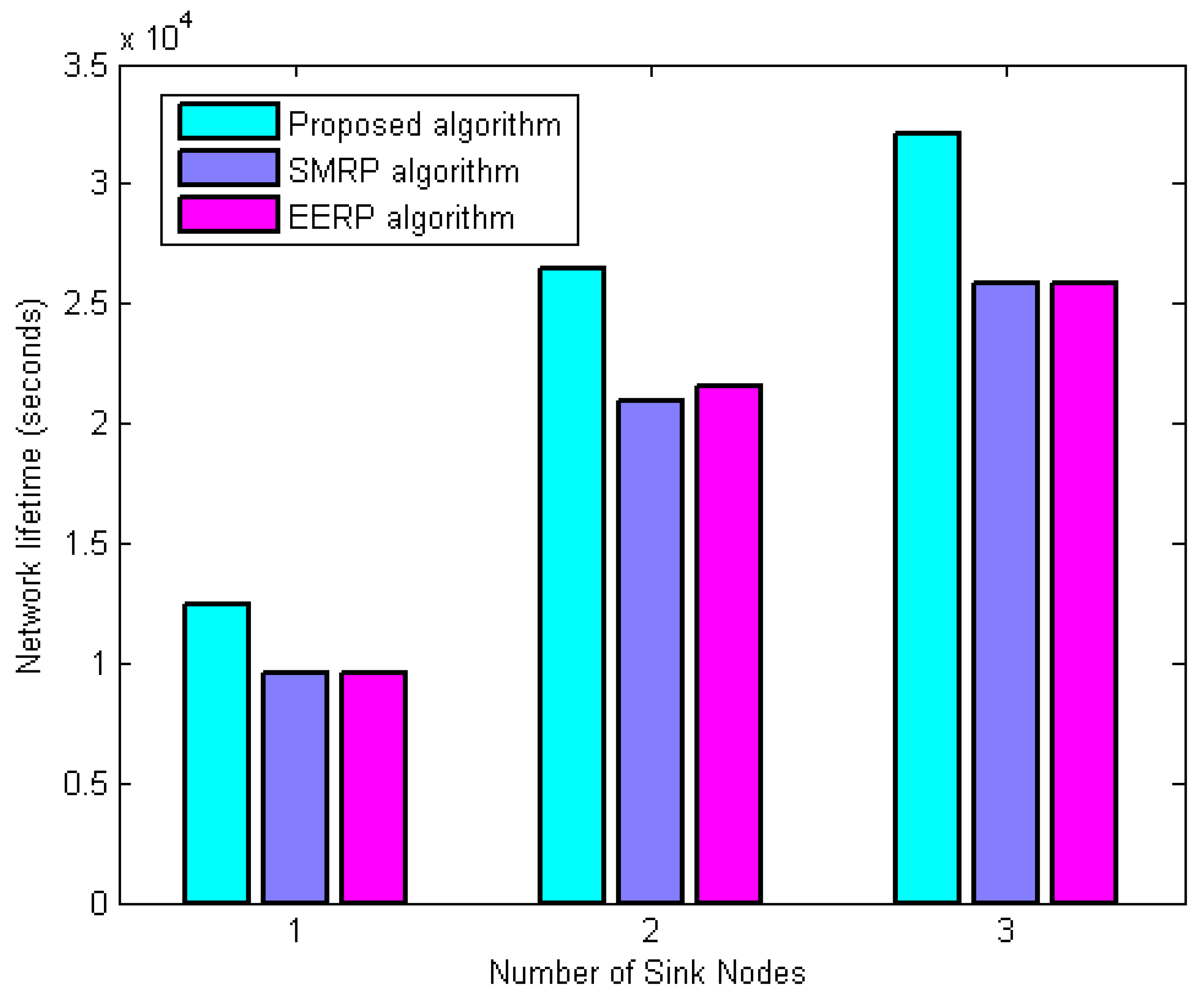
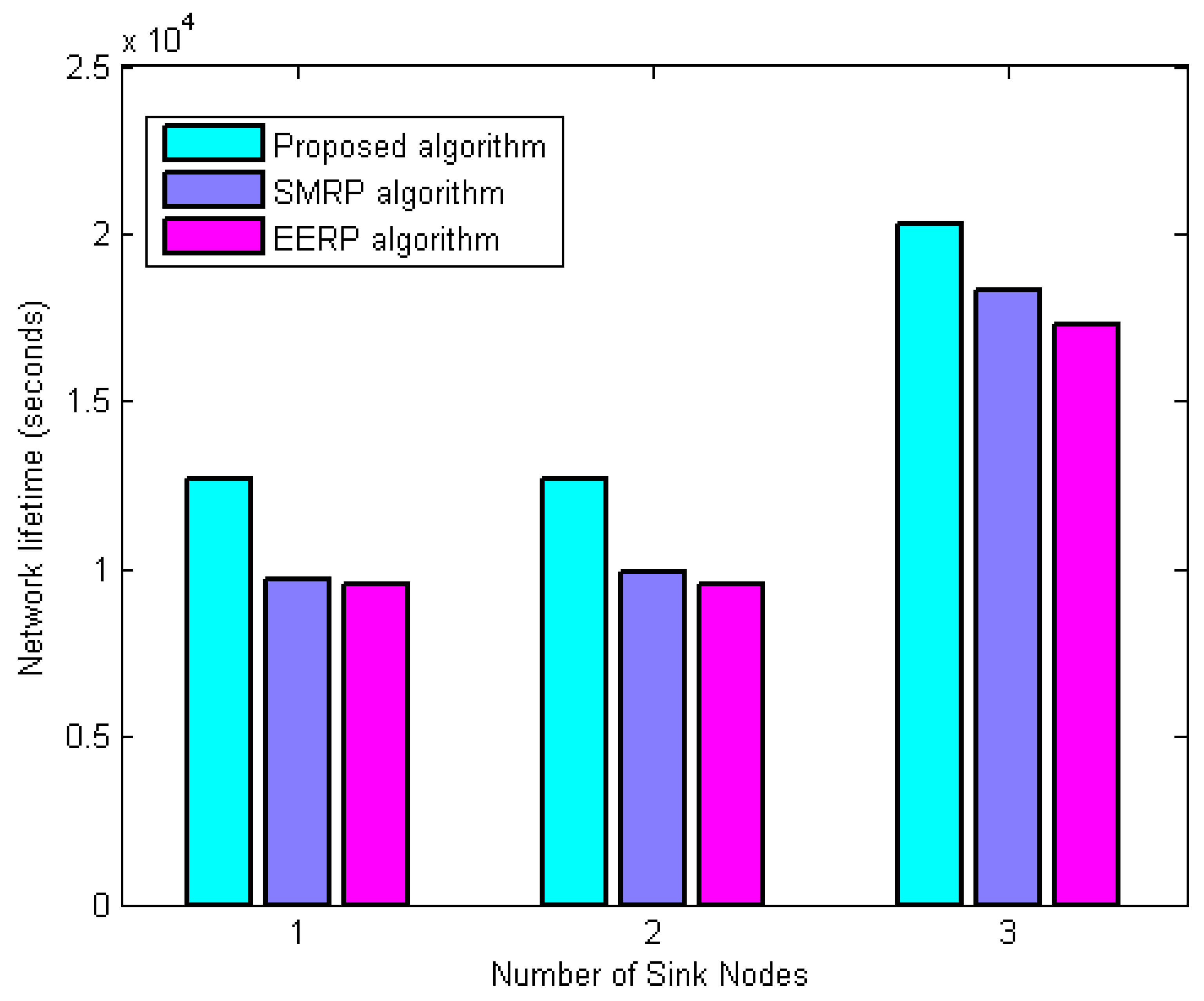
6.3.3. Network Lifetime Evaluation
- 1.
- Network lifetime evaluation under the first scenario
- 2.
- Network lifetime evaluation under the second scenario
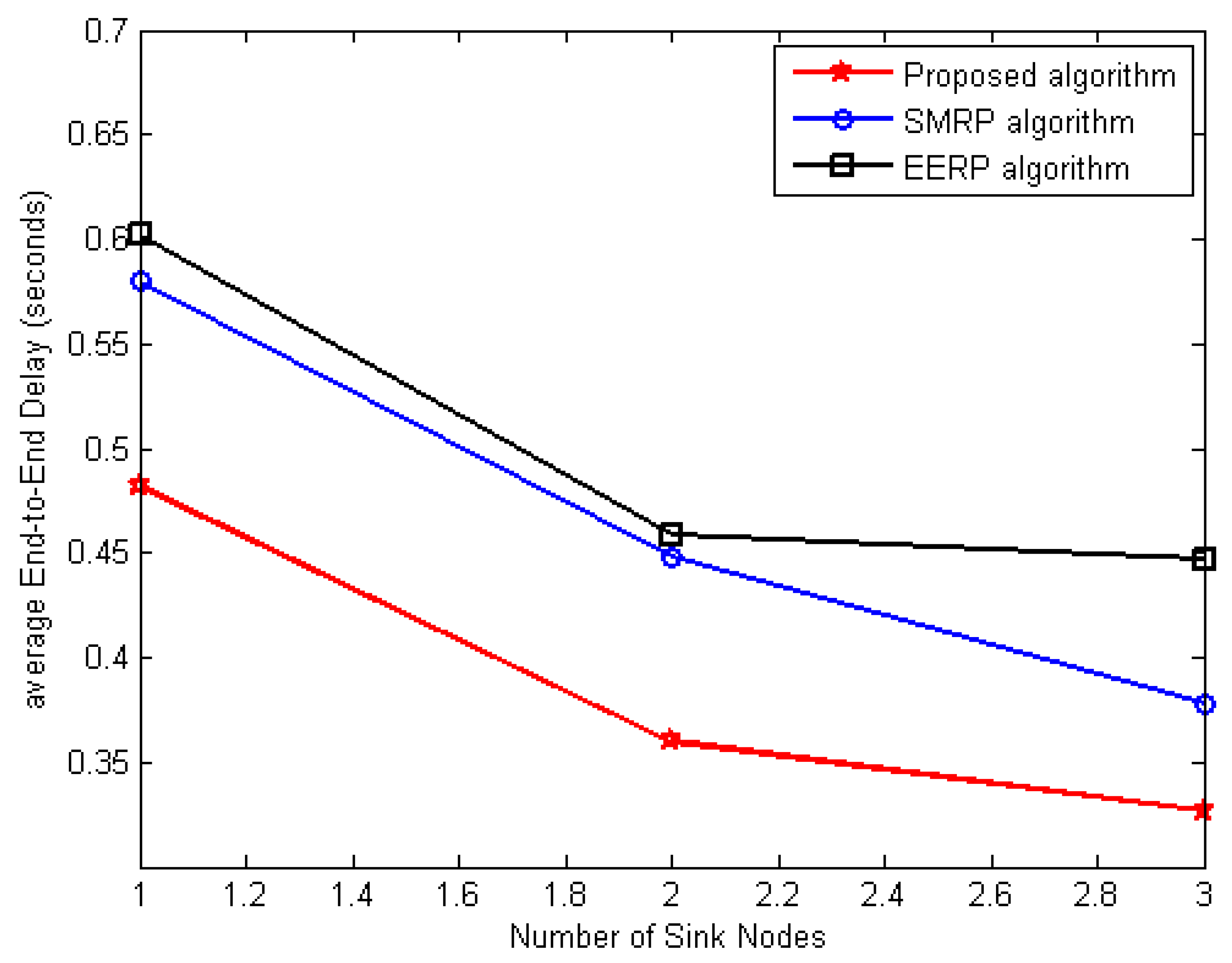
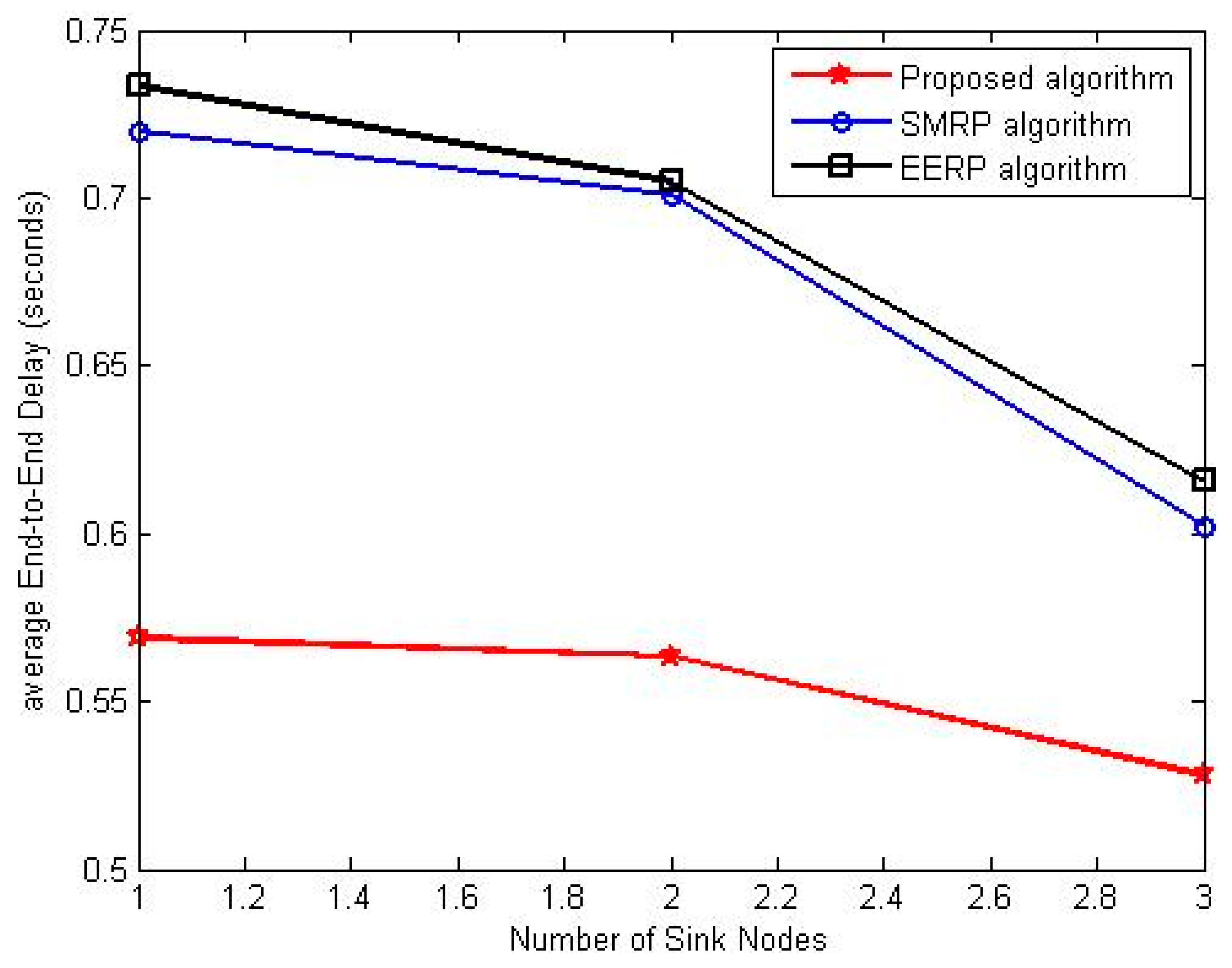
6.3.4. Average End-to-End Delay Evaluation
- 1.
- Average end-to-end delay evaluation under the first scenario
- 2.
- Average end-to-end delay evaluation under the second scenario
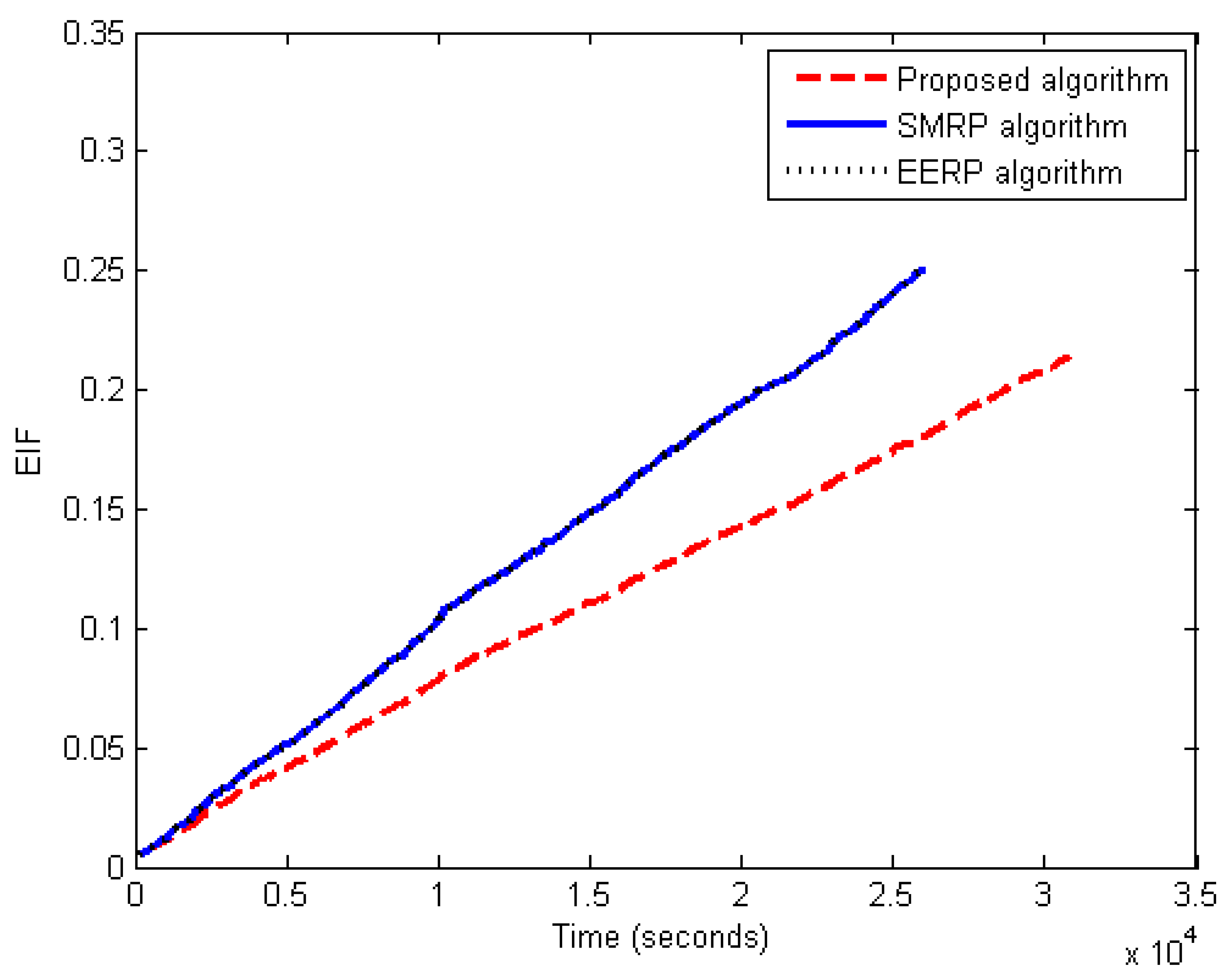
6.3.5. Energy Balance Evaluation
- 1.
- Energy balance evaluation under the first scenario
- 2.
- Energy balance evaluation under the second scenario
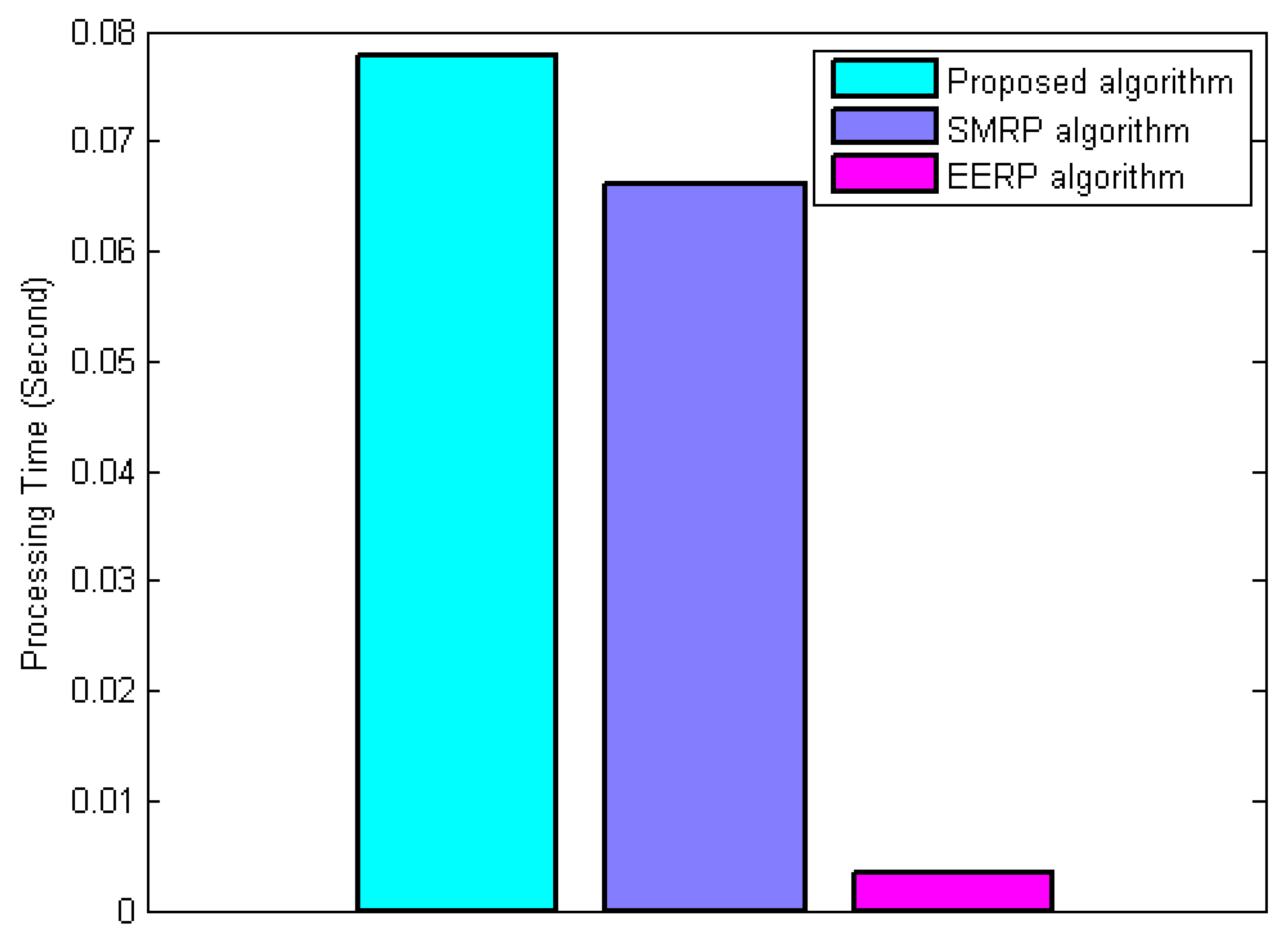
6.3.6. Complexity Evaluation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ilyas, M.; Mahgoub, I. Handbook of Sensor Networks; CRC Press: London, UK, 2005; pp. 117–140. [Google Scholar]
- Krishnan, M.; Jung, Y.M.; Yun, S. An Improved Clustering with Particle meta Optimization-Based Mobile Sink for Wireless Sensor Networks. In Proceedings of the 2nd International Conference on Trends in Electronics and Informatics, Tirunelveli, India, 11–12 May 2018. [Google Scholar]
- Pottie, G.; Kaiser, W. Wireless Integrated Network Sensors. Commun. ACM 2000, 43, 51–58. [Google Scholar] [CrossRef]
- Ghaffari, A. An Energy Efficient Routing Protocol for Wireless Sensor Networks using A-star Algorithm. J. Appl. Res. Technol. 2014, 12, 815–822. [Google Scholar] [CrossRef] [Green Version]
- Mukherjee, S.; Amin, R.; Biswas, G.P. Design of Routing Protocol for Multi-Sink Based Wireless Sensor Networks. J. Wirel. Netw. 2019, 25, 4331–4347. [Google Scholar] [CrossRef]
- Singh, A.; Nagaraju, A. Low Latency and Energy Efficient Routing-Aware Network Coding-Based Data Transmission in Multi-Hop and Multi-Sink WSN. Ad Hoc Netw. J. 2020, 107, 1–19. [Google Scholar] [CrossRef]
- El-Fouly, F.H.; Ramadan, R.A. E3AF: Energy Efficient Environment-Aware Fusion Based Reliable Routing in Wireless Sensor Networks. IEEE Access 2020, 8, 112145–112159. [Google Scholar] [CrossRef]
- El-Fouly, F.H.; Ramadan, R.A. Real-Time Energy-Efficient Reliable Traffic Aware Routing for Industrial Wireless Sensor Networks. IEEE Access 2020, 8, 58130–58145. [Google Scholar] [CrossRef]
- Habib, M. Energy-Efficient algorithm for reliable routing of wireless sensor networks. IEEE Trans. Ind. Electron. 2019, 66, 5567–5575. [Google Scholar]
- Zhang, W.; Liu, Y.; Han, G.; Feng, Y.; Zhao, Y. An Energy Efficient and QoS Aware Routing Algorithm Based on Data Classification for Industrial Wireless Sensor Networks. IEEE Access 2018, 6, 46495–46504. [Google Scholar] [CrossRef]
- Tavallaie, O.; Naji, H.R.; Sabaei, M.; Arastouie, N. RTEA: Real-Time and Energy Aware Routing for Industrial Wireless Sensor Networks. Wireless Pers. Commun. 2017, 95, 4601–4621. [Google Scholar] [CrossRef]
- Xu, C.; Cao, L.; Zhang, G.A.; Gu, J.Y. Overview of multiple sink routing protocols in wireless sensor networks. Appl. Res. Comput. 2010, 27, 816–823. [Google Scholar]
- Chen, S.; Huang, Q.; Zhang, Y.; Li, X. Double Sink Energy Hole Avoidance Strategy for Wireless Sensor Network. EURASIP J. Wirel. Commun. Netw. 2020, 226, 226. [Google Scholar] [CrossRef]
- Onwuegbuzie, I.U.; Razak, S.A.; Al-Dhaqm, A. Multi-Sink Load-Balancing Mechanism for Wireless Sensor Networks. In Proceedings of the IEEE International Conference on Computing (ICOC), Online, 10 May 2021; pp. 140–145. [Google Scholar]
- Fu, X.; Yang, Y.; Postolache, O. Sustainable Multipath Routing Protocol for Multi-Sink Wireless Sensor Networks in Harsh Environments. IEEE Trans. Sustain. Comput. 2021, 6, 168–181. [Google Scholar] [CrossRef]
- Awang, A. Multi-sink Routing using Path loss in Multihop Wireless Sensor Networks. In Proceedings of the Asia-Pacific Conference on Communications (APCC 2011), Kota Kinabalu, Malaysia, 2–5 October 2011. [Google Scholar]
- Wang, J.; Yin, Y.; Zhang, J.; Lee, S.; Sherratt, R.S. Mobility based energy efficient and multi-sink algorithms for consumer home networks. IEEE Trans. Consum. Electron. 2013, 59, 77–84. [Google Scholar] [CrossRef]
- Fu, X.; Fortino, G.; Pace, P.; Aloi, G.; Li, W. Environment-fusion multipath routing protocol for wireless sensor networks. Inf. Fusion 2020, 53, 4–19. [Google Scholar] [CrossRef]
- McCune, R.; Madey, G. Control of Artifial Swarms with DDDAS. Procedia Comput. Sci. 2014, 29, 1171–1181. [Google Scholar] [CrossRef] [Green Version]
- Nayyar, A.; Singh, R. Ant Colony Optimization (ACO) based Routing Protocols for Wireless Sensor Networks: A survey. Int. J. Adv. Comput. Sci. Appl. 2017, 8, 148–155. [Google Scholar]
- Liu, Z.; Xu, J.; Wang, W.; Zhang, Y.; Li, X. Probabilistic Routing Algorithm Based on Naive Bayesian Classification Model in Multi-sink Sensor Networks. J. Comput. Inf. Syst. 2013, 9, 9943–9951. [Google Scholar]
- Cao, L.; Xu, C.; Shao, W. Multiple Sink Dynamic estimation Geographic Routing in Wireless Sensor Networks. In Proceedings of the International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery (CyberC), Huangshan, China, 10–12 October 2010. [Google Scholar]
- Rajanna, M.; Murthy, G.S.; Varaprasad, G. Energy efficient routing protocol for multisink wireless sensor networks. In Applied Computational Technologies. ICCET 2022. Smart Innovation, Systems and Technologies; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Jiang, H.; Sun, R. Energy optimized routing algorithm in multi-sink wireless sensor networks. Appl. Math. Inf. Sci. 2014, 8, 349–354. [Google Scholar] [CrossRef]
- Mottola, L.; Picco, G.P. Muster: Adaptive energy-aware multisink routing in wireless sensor networks. IEEE Trans. Mob. Comput. 2010, 10, 1694–1709. [Google Scholar] [CrossRef] [Green Version]
- Tan, D.D.; Kim, D.S. Dynamic traffic-aware routing algorithm for multi-sink wireless sensor networks. Wirel. Netw. 2013, 20, 1239–1250. [Google Scholar] [CrossRef]
- Le, L.; Felea, V. Latency and network lifetime trade-off in geographic multicast routing for multi-sink wireless sensor networks. In Proceedings of the International Conference on Mobile, Secure, and Programmable Networking, Paris, France, 18–20 June 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 294–310. [Google Scholar]
- Safa, H.; Moussa, M.; Artail, H. An energy efficient genetic algorithm based approach for sensor-to-sink binding in multi-sink wireless sensor networks. Wirel. Netw. 2014, 20, 177–196. [Google Scholar] [CrossRef]
- El-Fouly, F.H.; Ramadan, R.A.; Mahmoud, M.I.; Dessouky, M.I. Abd El-Sami “REBTAM: Reliable Traffic Aware Energy Balance Data Reporting Algorithm for Object Tracking in Multi-Sink Wireless Sensor Networks. Int. J. Wirel. Netw. 2018, 24, 735–753. [Google Scholar] [CrossRef]
- Daas, M.S.; Chikhi, S.; Bourennane, E.-B. A dynamic Multi-Sink Routing Protocol for Static and Mobile Self-Organizing Wireless Networks: A Routing Protocol for Internet of Things. Ad Hoc Netw. 2021, 117, 102495. [Google Scholar] [CrossRef]
- Cheng, L.; Niu, J.; Cao, J.; Das, S.K.; Gu, Y. QoS aware geographic opportunistic routing in wireless sensor networks. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 1864–1875. [Google Scholar] [CrossRef]
- He, T.; Stankovic, J.A.; Lu, C.; Abdelzaher, T. SPEED: A stateless protocol for real-time communication in sensor networks. In Proceedings of the International Conference on Distributed Computing Systems, Providence, RI, USA, 19–22 May 2003; pp. 46–55. [Google Scholar]
- Liu, A.; Ren, J.; Li, X.; Chen, Z.; Shen, X.S. Design principles and improvement of cost function based energy aware routing algorithms for wireless sensor networks. Comput. Netw. 2012, 5, 1951–1967. [Google Scholar] [CrossRef]
- Li, Y.; Chen, C.S.; Song, Y.Q.; Wang, Z.; Sun, Y. Enhancing real-time delivery in wireless sensor networks with two-hop information. IEEE Trans. Ind. Inform. 2009, 5, 113–122. [Google Scholar] [CrossRef]








| Given Parameters | |
|---|---|
| Notation | Description |
| V | The monitored field’s sensor nodes. |
| Is the set of source nodes at time t, . | |
| T | The time horizon. |
| Z | All zones |
| Is the set of sink nodes deployed in the monitored field at time t, . | |
| Final set of sink nodes that have an environmental impact metric larger than a threshold Value in the monitored field at time t, . | |
| Set of all messages collected from the source node s at time t, ∀s ∈ S | |
| Zone i’s environmental data for factor f. | |
| Zone i’s single environmental factor f impact metric. | |
| Zone i’s multiple environmental impact metric. | |
| Zone i’s neighboring environmental impact metric | |
| Zone i’s final environmental impact metric. | |
| The sink/sensor node x final environmental impact metric in zone i at time t, i≠j. | |
| The environmental impact threshold. | |
| The coefficient of attenuation between zones i and j. | |
| Euclidean Distance (ED) between the center of zone i and j, i≠j. | |
| The Euclidean distance (ED) between the sensor node x and sink node si at time t, i≠j. | |
| IDL | The initial deadline defined by the application at each source node. |
| deadline | Each hop’s packet deadline. |
| The set of all candidate paths between any pair (y, si), ∀s ∈ S | |
| The desired message delivery speed from source s to sink si. | |
| Link’s (x,y), packet reception ratio, i, j ∈ L, and i ≠ j. | |
| The packet loss ratio for the link (x,y), i, j ∈ L, and i ≠ j. | |
| Link (x,y) delay. i, j ∈ L, and i ≠ j. | |
| Node x’s residual energy at time t, i ∈ S ∪ R. i∈ S ∪ R. | |
| Sensor node x, initial energy, i ∈ S ∪ R. i ∈ S ∪ R. | |
| Transmission energy from x to y in a single hop, | |
| Energy load function for each sensor node y at time t, | |
| Each sensor node x load at time t, | |
| Sensor node y, total number of messages, , | |
| The sink load metric of each sink node si, | |
| The distance hop metric between sink node si and each source node s, ∀s∈S | |
| The minimum hop count from any sensor node x to each sink node si, . i, NEBi ∈ S∪ R | |
| sink node si, neighbor set, . i, NEBi ∈ S∪ R | |
| sensor node x, neighbor set, | |
| The final neighbor set of sensor node x, | |
| Indicator Parameter | |
| 1 if sensor node y is on path p to the chosen sink node si and 0 otherwise, | |
| Decision Variables | |
| 1 if sensor node x utilizes the neighbor node y to relay message m of the source node s and 0 otherwise, | |
| 1 if the sensor node x utilizes neighbor node y to relay message m of the source node s and 0, otherwise, | |
| 1 if the sink node si has a final environmental metric greater than the threshold value and 0, otherwise, | |
| 1 if the difference between the environmental metric value of sink node si in zone i and sink node n in zone j is less than zero and 0, otherwise, | |
| 1 if the sink node si has the maximum environmental metric value compared to that of other sink nodes and 0, otherwise, . | |
| 1 if the computed difference between the sink load value of sink node si and sink node f is less than zero and 0, otherwise, | |
| 1 if the sink node si has the minimum sink load metric value compared to that of other sink nodes and 0, otherwise, | |
| 1 if the source node s selects the sink node si as an optimal sink and 0, otherwise, | |
| If the distance hop metric difference between sink nodes si and node k is less than zero, return the value will be 1; 0 otherwise. | |
| 1 if the sink node si has the minimum v distance hop metric value compared to that of other sink nodes and 0, otherwise, | |
| 1 if the neighbor node y has relaying delay less than or equal to the desired delay and 0, otherwise, | |
| 1 the sink node can be reached by neighbor node y and 0, otherwise, | |
| 1 if the neighbor node y has the minimum relaying delay value compared to that of other neighbor nodes and 0, otherwise, | |
| 1 if the difference between the relaying delay value of neighbor nodes l and y is less than zero and 0, otherwise, | |
| 1 if neighbour node y has maximum energy load function value compared to that of other neighbor nodes, 0 otherwise., | |
| 1 if the difference between nodes y and v’s energy load function values is less than zero, 0 otherwise, | |
| 1 if the difference between neighbour nodes y and n’s environmental metric values is smaller than zero; 0 otherwise, | |
| 1 if the neighbor node y has the maximum environmental metric value compared to that of other neighbor nodes and 0, otherwise, | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Fouly, F.H.; Kachout, M.; Alharbi, Y.; Alshudukhi, J.S.; Alanazi, A.; Ramadan, R.A. Environment-Aware Energy Efficient and Reliable Routing in Real-Time Multi-Sink Wireless Sensor Networks for Smart Cities Applications. Appl. Sci. 2023, 13, 605. https://doi.org/10.3390/app13010605
El-Fouly FH, Kachout M, Alharbi Y, Alshudukhi JS, Alanazi A, Ramadan RA. Environment-Aware Energy Efficient and Reliable Routing in Real-Time Multi-Sink Wireless Sensor Networks for Smart Cities Applications. Applied Sciences. 2023; 13(1):605. https://doi.org/10.3390/app13010605
Chicago/Turabian StyleEl-Fouly, Fatma H., Mnaouer Kachout, Yasser Alharbi, Jalawi Sulaiman Alshudukhi, Abed Alanazi, and Rabie A. Ramadan. 2023. "Environment-Aware Energy Efficient and Reliable Routing in Real-Time Multi-Sink Wireless Sensor Networks for Smart Cities Applications" Applied Sciences 13, no. 1: 605. https://doi.org/10.3390/app13010605
APA StyleEl-Fouly, F. H., Kachout, M., Alharbi, Y., Alshudukhi, J. S., Alanazi, A., & Ramadan, R. A. (2023). Environment-Aware Energy Efficient and Reliable Routing in Real-Time Multi-Sink Wireless Sensor Networks for Smart Cities Applications. Applied Sciences, 13(1), 605. https://doi.org/10.3390/app13010605









