Topology Optimization for Minimum Compliance with Material Volume and Buckling Constraints under Design-Dependent Loads
Abstract
1. Introduction
2. The Topology Optimization Problem
2.1. Problem Formulation
2.2. Material Model
2.3. Linear Buckling Analysis
3. Sensitivity Analysis
3.1. Sensitivity of Compliance
3.2. Sensitivity of Buckling Constraint Functions
3.3. Sensitivity of Total Material Volume
4. Design-Dependent Loads
- (1)
- Transfer the density matrix x to an 8-bit grayscale image.
- (2)
- Identify the boundary using the DRLSE method.
- (3)
- Extract boundary information and compute F.
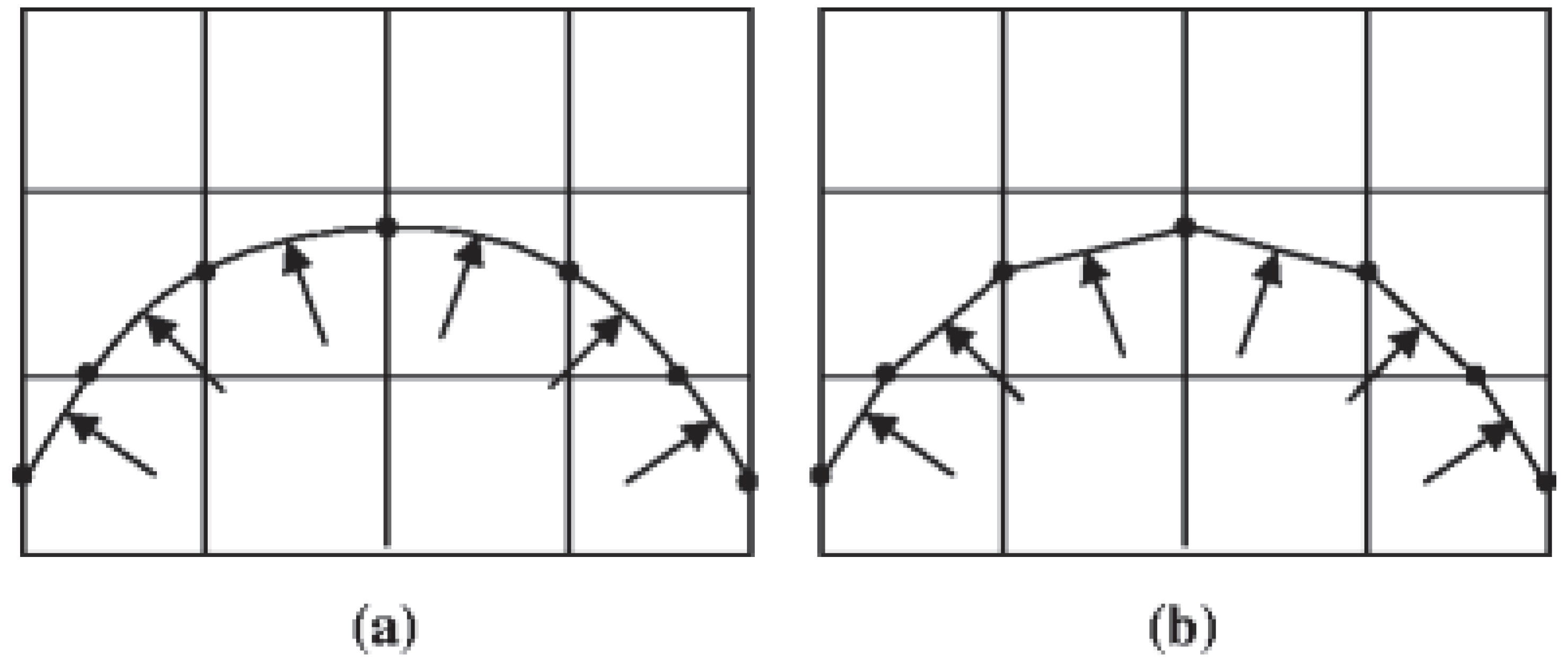
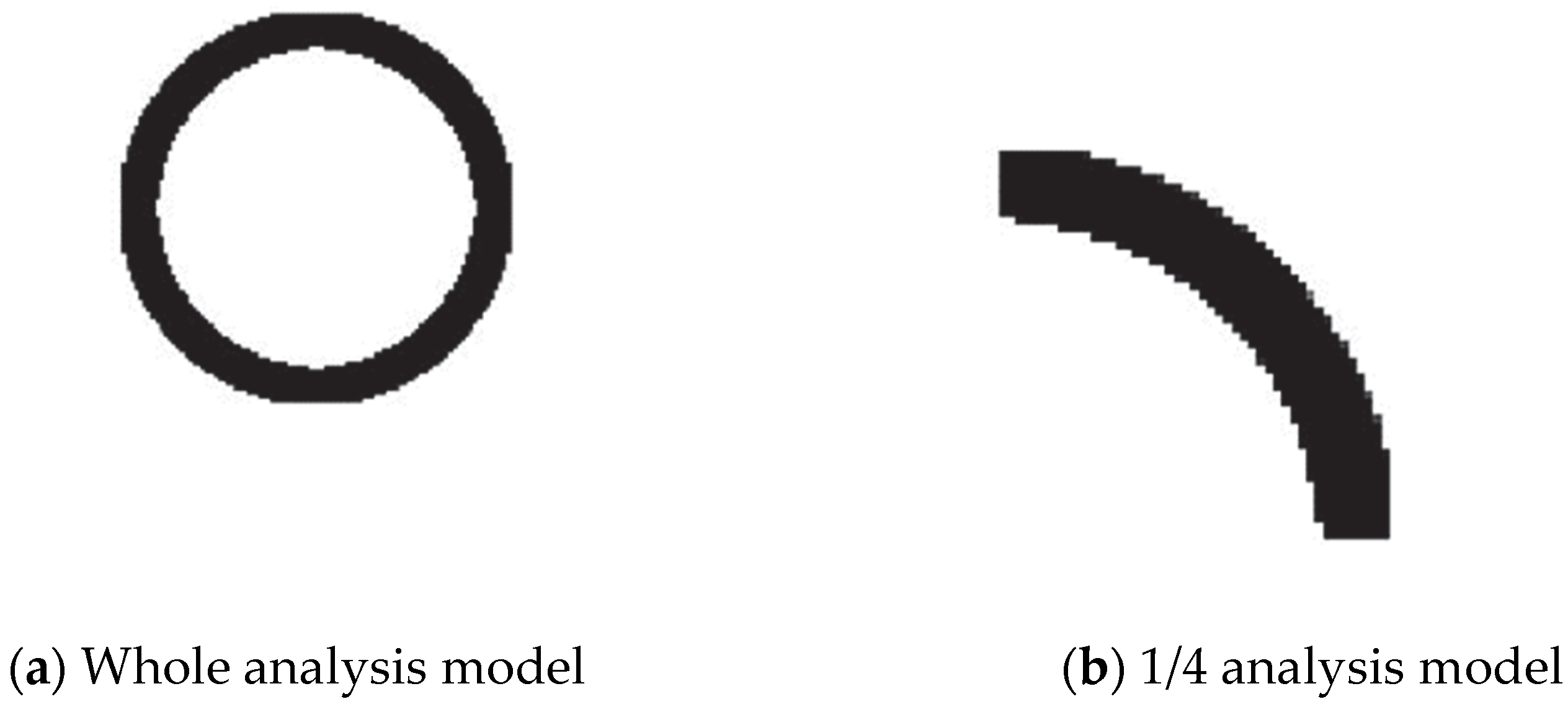
4.1. Identify the Boundary Using the DRLSE Method
4.2. Design-Dependent Load Computing
5. Optimization Algorithm
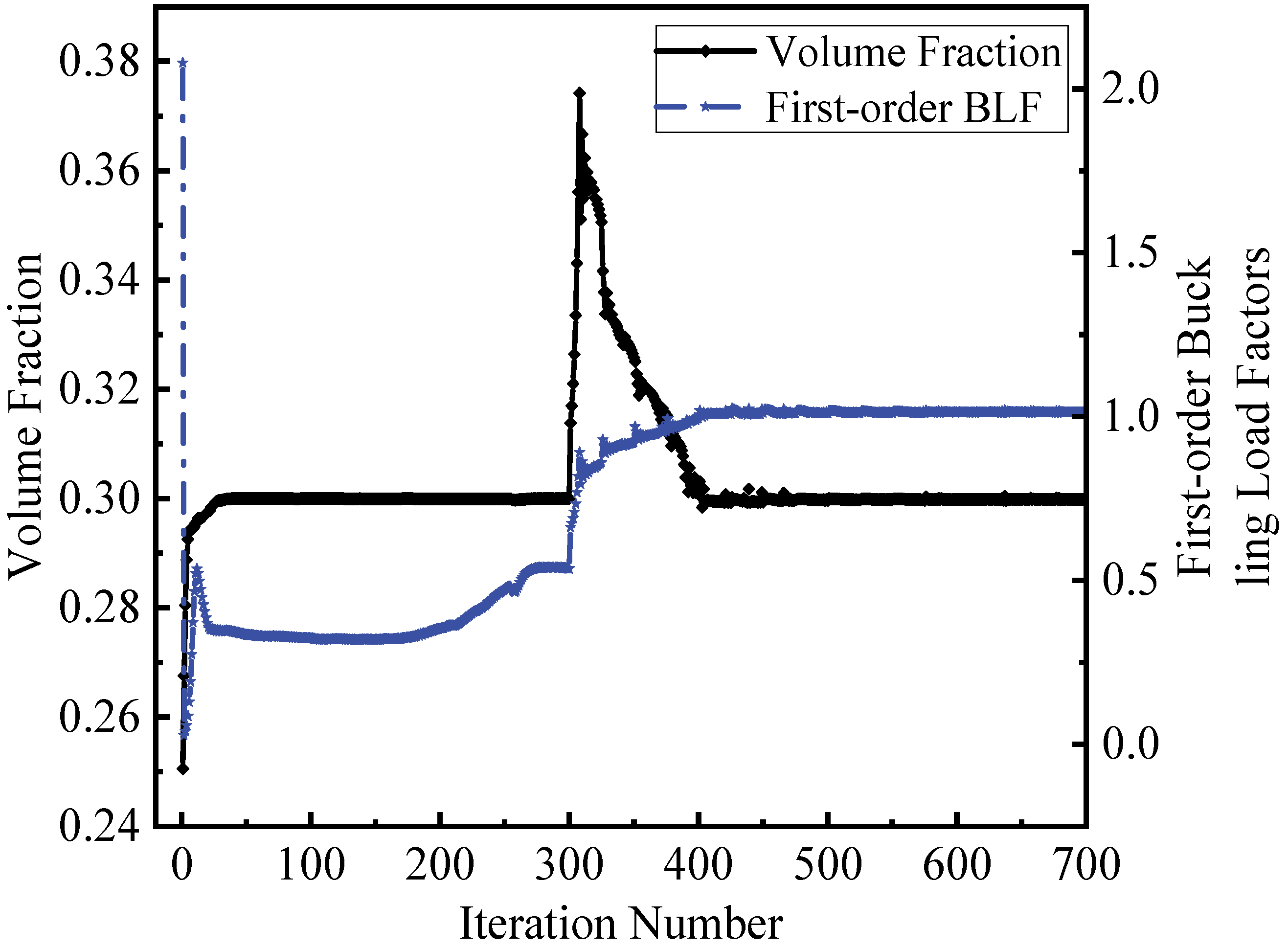
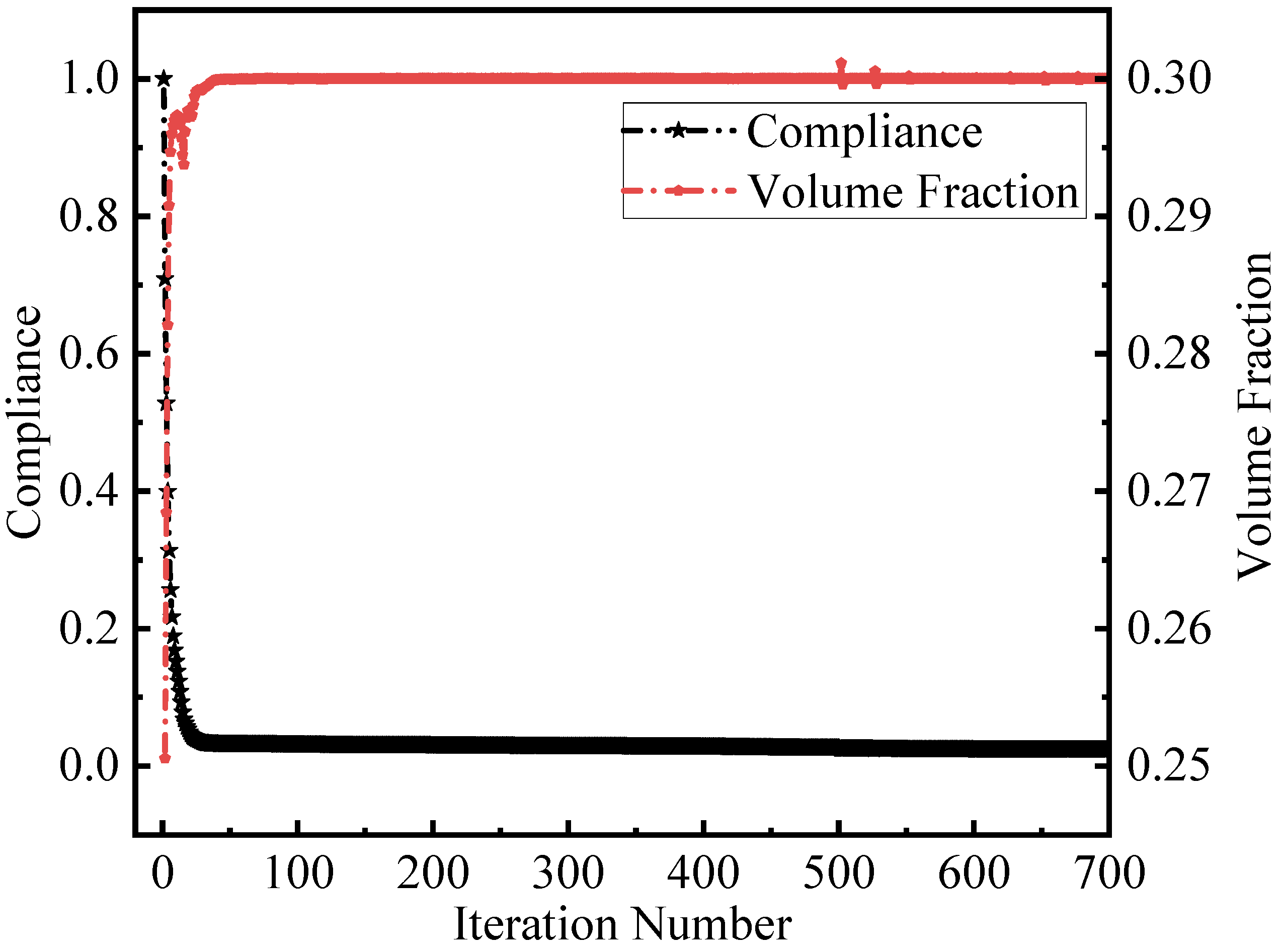
6. Numerical Examples
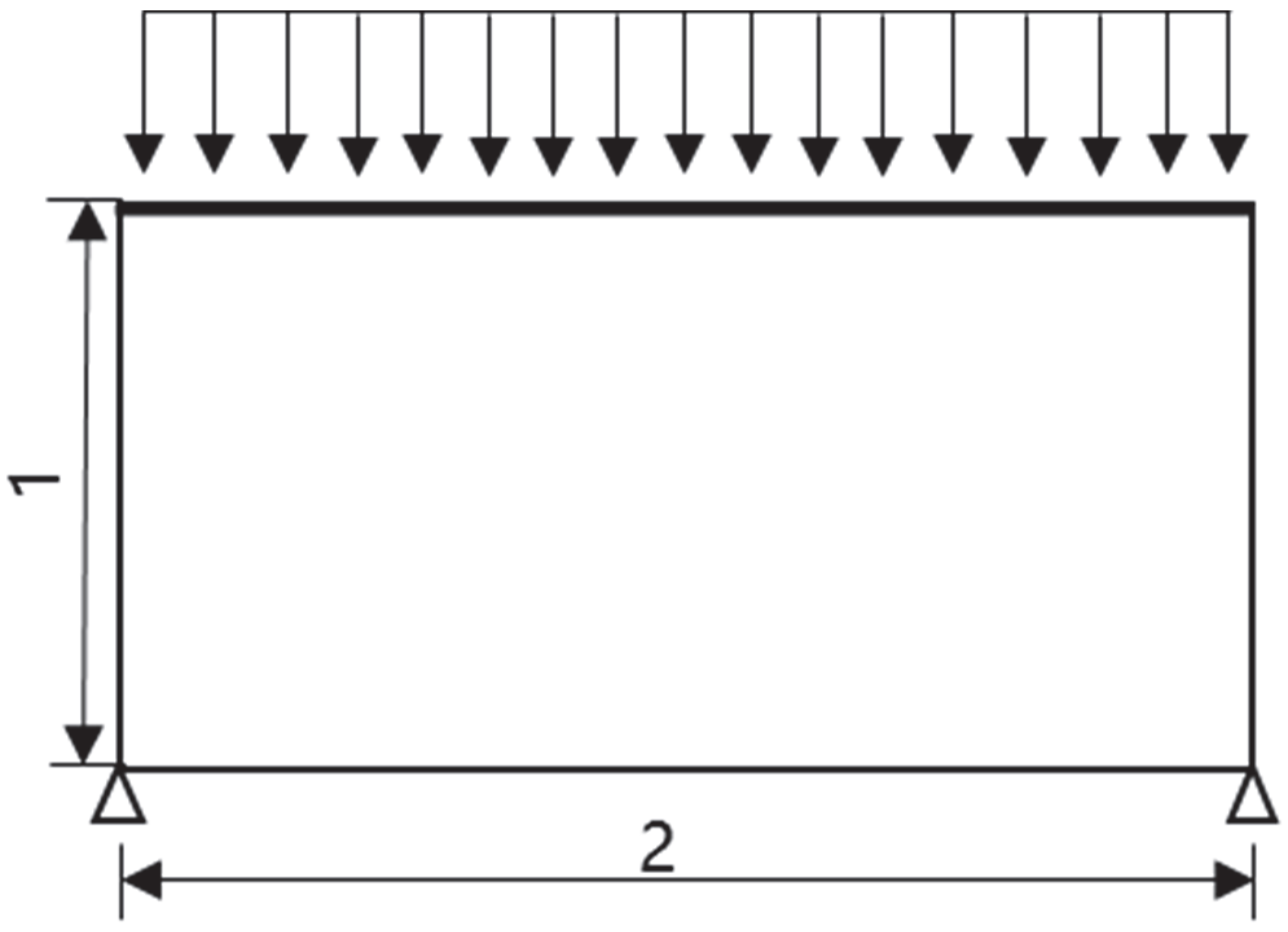
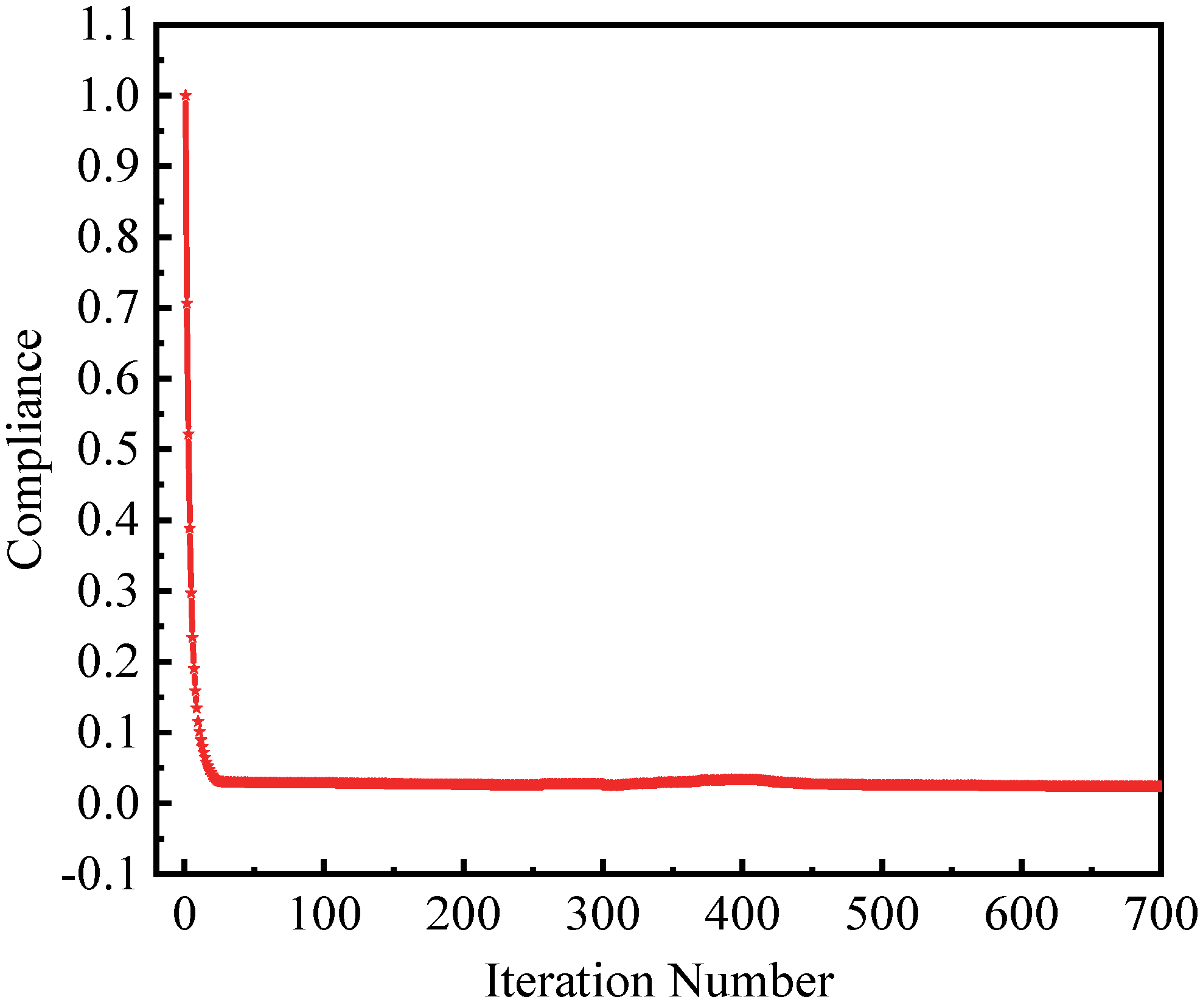
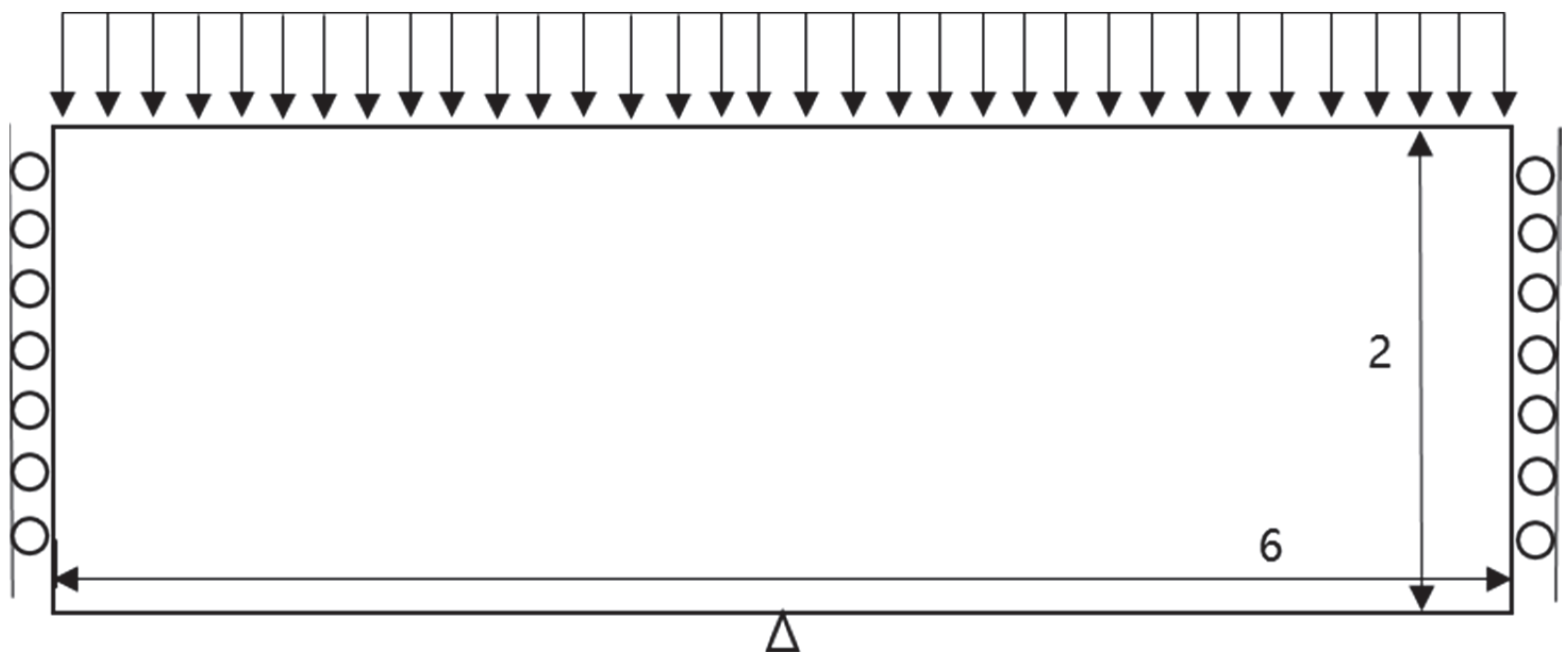
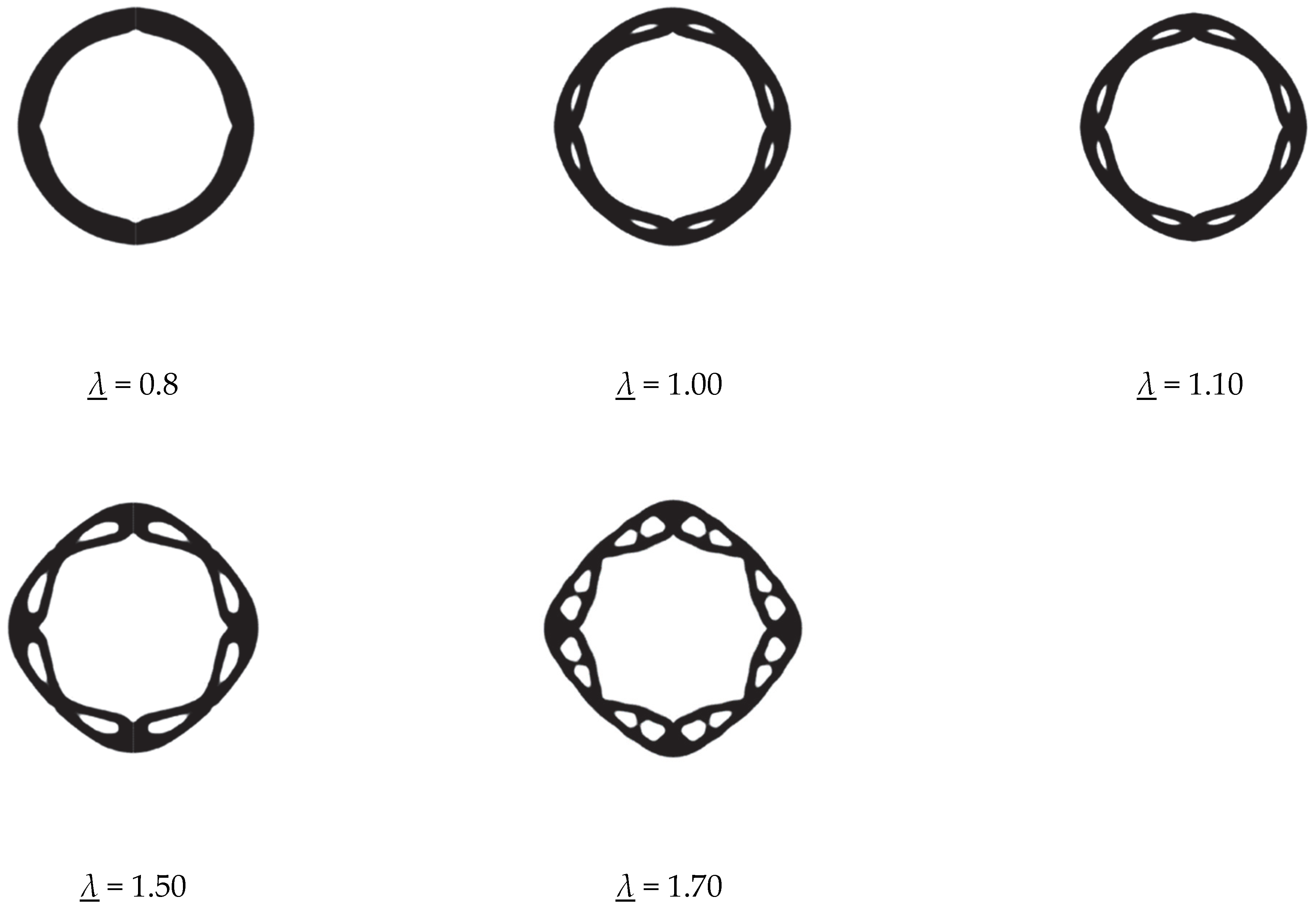
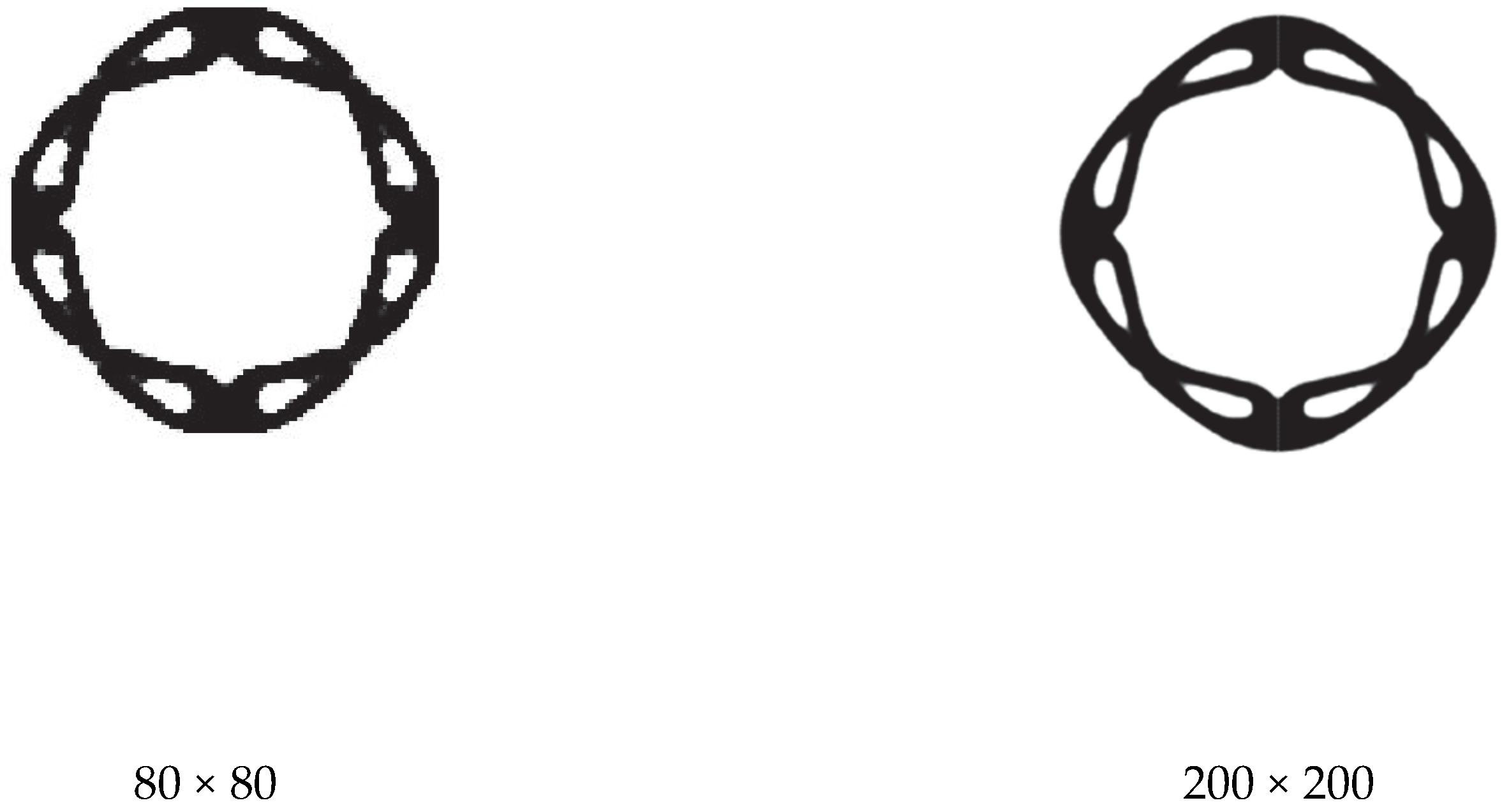
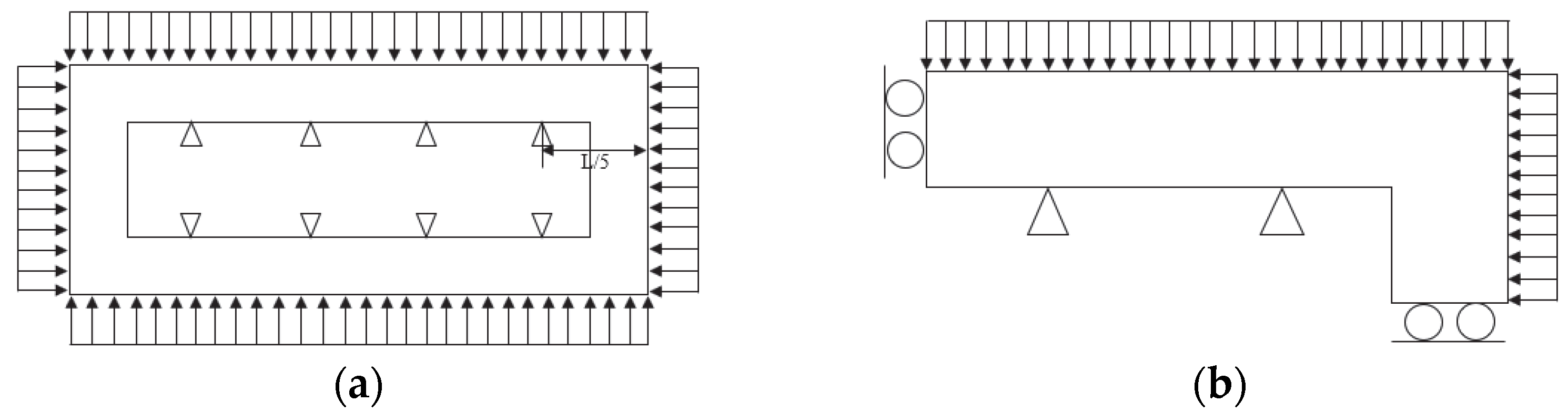
6.1. Arch Structure Subjected to External Pressure
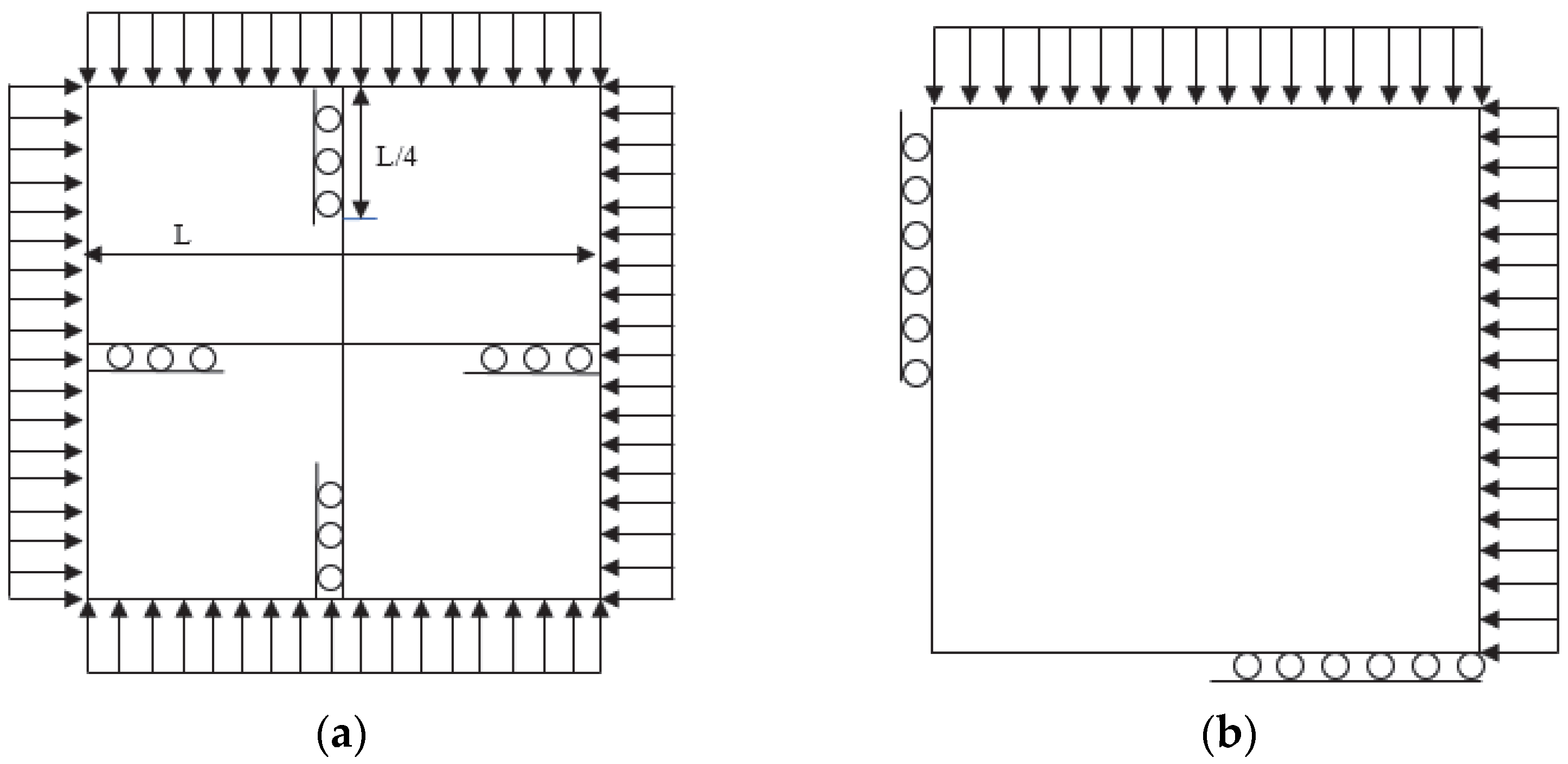
6.2. Piston Design Subjected to Hydrostatic Pressure
6.3. Structure Design Subjected to Hydrostatic Pressure
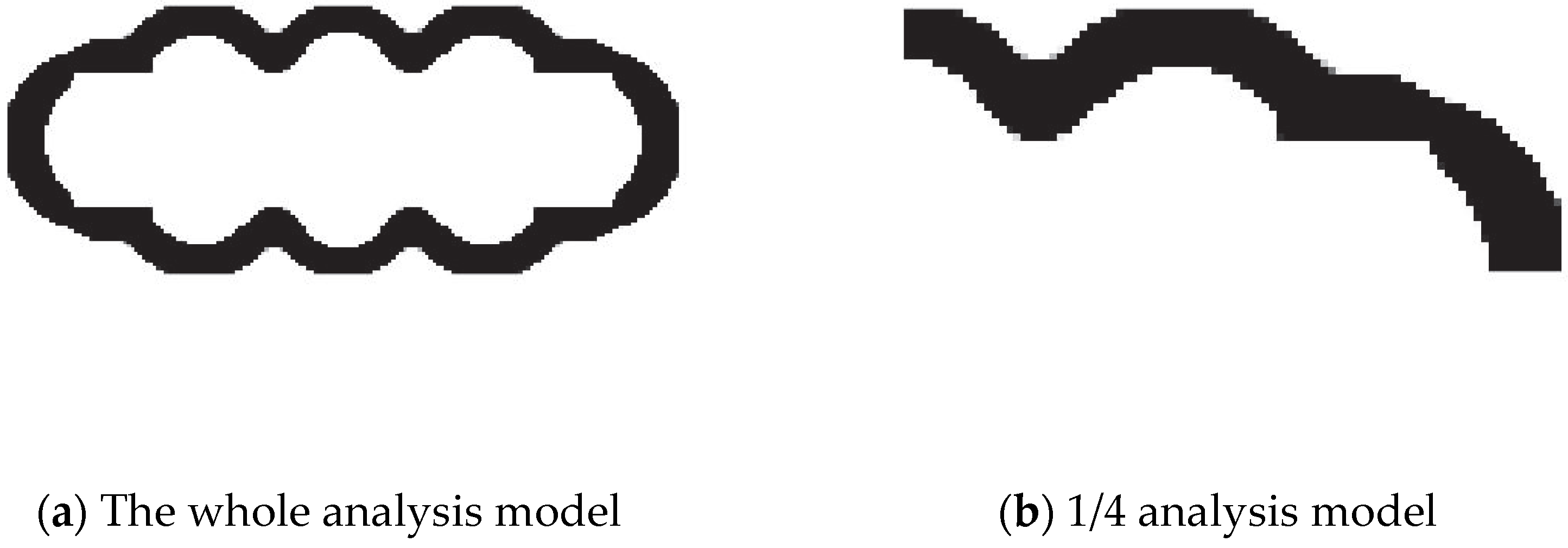
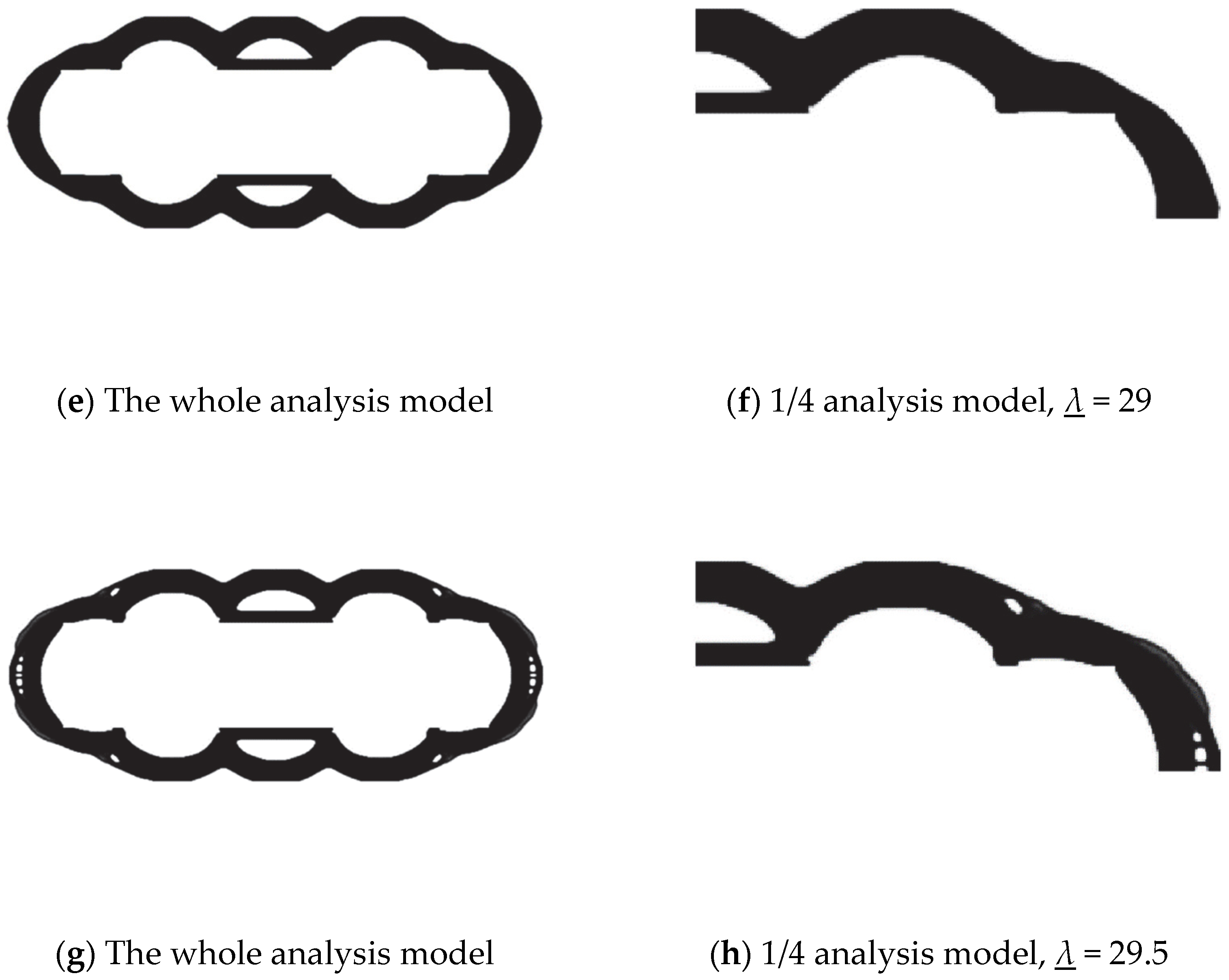
6.4. Multiple Intersecting Spherical Pressure Hulls
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hoang, V.N.; Wang, X.; Xuan, H.N. A three-dimensional multiscale approach to optimal design of porous structures using adaptive geometric components. Compos. Struct. 2021, 273, 114296. [Google Scholar] [CrossRef]
- Hoang, V.N.; Nguyen, H.B.; Xuan, H.N. Explicit topology optimization of nearly incompressible materials using polytopal composite elements. Adv. Eng. Softw. 2020, 149, 102903. [Google Scholar] [CrossRef]
- Hoang, V.N.; Nguyen, N.L.; Tran, D.Q.; Vu, Q.V.; Xuan, H.N. Data-driven geometry-based topology optimization. Struct. Multidiscip. Optim. 2022, 65, 69. [Google Scholar] [CrossRef]
- Neves, M.M.; Rodrigues, H.; Guedes, J.M. Generalized topology design of structures with a buckling load criterion. Struct. Optim. 1995, 10, 71–78. [Google Scholar] [CrossRef]
- Neves, M.M.; Sigmund, O.; Bendsøe, M.P. Topology optimization of periodic microstructures with a penalization of highly localized buckling modes. Int. J. Numer. Methods Eng. 2002, 54, 809–834. [Google Scholar] [CrossRef]
- Zhou, M. Topology optimization for shell structures with linear buckling responses. In Proceedings of the WCCM VI in conjunction with APCOM’04, Beijing, China, 5–10 September 2004; pp. 795–800. [Google Scholar]
- Wang, W.; Ye, H.; Sui, Y. Lightweight Topology Optimization with Buckling and Frequency Constraints Using the Independent Continuous Mapping Method. Acta Mech. Solida Sin. 2019, 32, 310–325. [Google Scholar] [CrossRef]
- Gao, X.J.; Ma, H.T. Topology optimization of continuum structures under buckling constraints. Comput. Struct. 2015, 157, 142–152. [Google Scholar] [CrossRef]
- Gao, X.J.; Ma, H.T.; Chen, G.F. Improving the overall performance of continuum structures: A topology optimization model considering stiffness, strength and stability. Comput. Methods Appl. Mech. Engrg. 2020, 359, 112660. [Google Scholar] [CrossRef]
- Clausen, A.; Aage, N.; Sigmund, O. Exploiting additive manufacturing infill in topology optimization for improved buckling load. Engineering 2016, 2, 250–257. [Google Scholar] [CrossRef]
- Ferrari, F.; Sigmund, O. Revisiting topology optimization with buckling constraints. Struct. Multidiscip. Optim. 2019, 59, 1401–1415. [Google Scholar] [CrossRef]
- Ferrari, F.; Sigmund, O. Towards solving large-scale topology optimization problems with buckling constraints at the cost of linear analyses. Comput. Methods Appl. Mech. Engrg. 2020, 363, 112911. [Google Scholar] [CrossRef]
- Ferrari, F.; Sigmund, O.; Guest, J.K. Topology optimization with linearized buckling criteria in 250 lines of MATLAB. Struct. Multidiscip. Optim. 2021, 63, 3045–3066. [Google Scholar] [CrossRef]
- Zhang, W.; Jiu, L.; Meng, L. Buckling-constrained topology optimization using feature-driven optimization method. Struct. Multidiscip. Optim. 2022, 65, 37. [Google Scholar] [CrossRef]
- Mendes, E.; Sivapuram, R.; Rodriguez, R.; Sampaio, M.; Picelli, R. Topology optimization for stability problems of submerged structures using the TOBS method. Comput. Struct. 2022, 259, 106685. [Google Scholar] [CrossRef]
- Hammer, V.B.; Olhoff, N. Topology optimization of continuum structures subjected to pressure loading. Struct. Multidiscip. Optim. 2000, 19, 85–92. [Google Scholar] [CrossRef]
- Du, J.; Olhoff, N. Topological optimization of continuum structures with design-dependent surface loading—Part II: Algorithm and examples for 3D problems. Struct. Multidiscip. Optim. 2004, 27, 166–177. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X.; Liu, S.T. A new boundary search scheme for topology optimization of continuum structures with design-dependent loads. Struct. Multidiscip. Optim. 2008, 37, 121–129. [Google Scholar] [CrossRef]
- Lee, E.; Martins, J.R.R.A. Structural topology optimization with design-dependent pressure loads. Comput. Methods Appl. Mech. Engrg. 2012, 233, 40–48. [Google Scholar] [CrossRef]
- Acar, O.; Saglam, H.; Saka, Z. Measuring curvature of trajectory traced by coupler of an optimal four-link spherical mechanism. Measurement 2021, 176, 109189. [Google Scholar] [CrossRef]
- Kuntoglu, M.; Acar, O.; Gupta, M.K.; Saglam, H.; Sarikaya, M.; Giasin, K.; Pimenov, D.Y. Parametric optimization for cutting forces and material removal rate in the turning of AISI 5140. Machines 2021, 9, 90. [Google Scholar] [CrossRef]
- Wang, C.F.; Zhao, M.; Ge, T. Structural topology optimization with design-dependent pressure loads. Struct. Multidiscip. Optim. 2016, 53, 1005–1018. [Google Scholar] [CrossRef]
- Li, C.; Xu, C.; Gui, C.; Fox, M.D. Distance Regularized Level Set Evolution and Its Application to Image Segmentation. IEEE Trans. Image Process. 2010, 19, 3243–3254. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.-M.; Yu, J.; Yu, Y.; Xu, L. Topology optimization of pressure structures based on regional contour tracking technology. Struct. Multidiscip. Optim. 2018, 58, 687–700. [Google Scholar] [CrossRef]
- Chen, B.C.; Kikuchi, N. Topology optimization with design-dependent loads. Finite Elem. Anal. Des. 2001, 37, 57–70. [Google Scholar] [CrossRef]
- Bourdin, B.; Chambolle, A. Design-dependent loads in topology optimization. ESAIM-Control. Optim. Calc. Var. 2003, 9, 19–48. [Google Scholar] [CrossRef]
- Sigmund, O.; Clausen, P.M. Topology optimization using a mixed formulation: An alternative way to solve pressure load problems. Comput. Methods Appl. Mech. Engrg. 2007, 196, 1874–1889. [Google Scholar] [CrossRef]
- Picelli, R.; Vicente, W.M.; Pavanello, R. Bi-directional evolutionary structural optimization for design-dependent fluid pressure loading problems. Engrg. Optim. 2014, 47, 1–19. [Google Scholar] [CrossRef]
- Picelli, R.; Vicente, W.M.; Pavanello, R. Evolutionary topology optimization for structural compliance minimization considering design-dependent FSI loads. Finite Elem. Anal. Des. 2017, 135, 44–55. [Google Scholar] [CrossRef]
- Sivapuram, R.; Picelli, R. Topology optimization of binary structures using integer linear programming. Finite Elem. Anal. Des. 2018, 139, 49–61. [Google Scholar] [CrossRef]
- Guo, X.; Zhao, K.; Gu, Y.X. Topology optimization with design-dependent loads by level set approach. In Proceedings of the 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Albany, NY, USA, 30 August–1 September 2004. [Google Scholar]
- Jiang, Y.T.; Zhao, M. Topology optimization under design-dependent loads with the parameterized level-set method based on radial-basis functions. Comput. Methods Appl. Mech. Engrg. 2020, 369, 113255. [Google Scholar] [CrossRef]
- Xia, Q.; Wang, M.Y.; Shi, T.L. Topology optimization with pressure load through a level set method. Comput. Methods Appl. Mech. Engrg. 2015, 283, 177–195. [Google Scholar] [CrossRef]
- Emmendoerfer, H.; Fancello, E.A.; Silva, E.C.N. Level set topology optimization for design-dependent pressure load problems. Int. J. Numer. Methods Eng. 2018, 115, 825–848. [Google Scholar] [CrossRef]
- Picelli, R.; Neofytou, A.; Kim, H.A. Topology optimization for design-dependent hydrostatic pressure loading via the level-set method. Struct. Multidiscip. Optim. 2019, 60, 1313–1326. [Google Scholar] [CrossRef]
- Kumar, P.; Frouws, J.S.; Langelaar, M. Topology optimization of fluidic pressure-loaded structures and compliant mechanisms using the Darcy method. Struct. Multidiscip. Optim. 2020, 61, 1637–1655. [Google Scholar] [CrossRef]
- Ibhadode, O.; Zhang, Z.; Rahnama, P.; Bonakdar, A.; Toyserkani, E. Topology optimization of structures under design-dependent pressure loads by a boundary identification-load evolution (BILE) model. Struct. Multidiscip. Optim. 2020, 62, 1865–1883. [Google Scholar] [CrossRef]
- Wang, C.F.; Qian, X.P. A density gradient approach to topology optimization under design-dependent boundary loading. J. Comput. Phys. 2020, 411, 109398. [Google Scholar] [CrossRef]
- Bourdin, B. Filters in topology optimization. Int. J. Numer. Methods Eng. 2001, 50, 2143–2158. [Google Scholar] [CrossRef]
- Wang, F.W.; Lazarov, B.S.; Sigmund, O. On projection methods, convergence and robust formulations in topology optimization. Struct. Multidiscip. Optim. 2010, 43, 767–784. [Google Scholar] [CrossRef]
- Rodrigues, H.C.; Guedes, J.M.; Bendsøe, M.P. Necessary conditions for optimal design of structures with a non-smooth eigenvalue based criterion. Struct. Optim. 1995, 9, 52–56. [Google Scholar] [CrossRef]
- Wang, C.F.; Zhao, M.; Ge, T. Study on the topology optimization design of underwater pressure structure. Engrg. Mech. 2015, 32, 247–256. [Google Scholar]




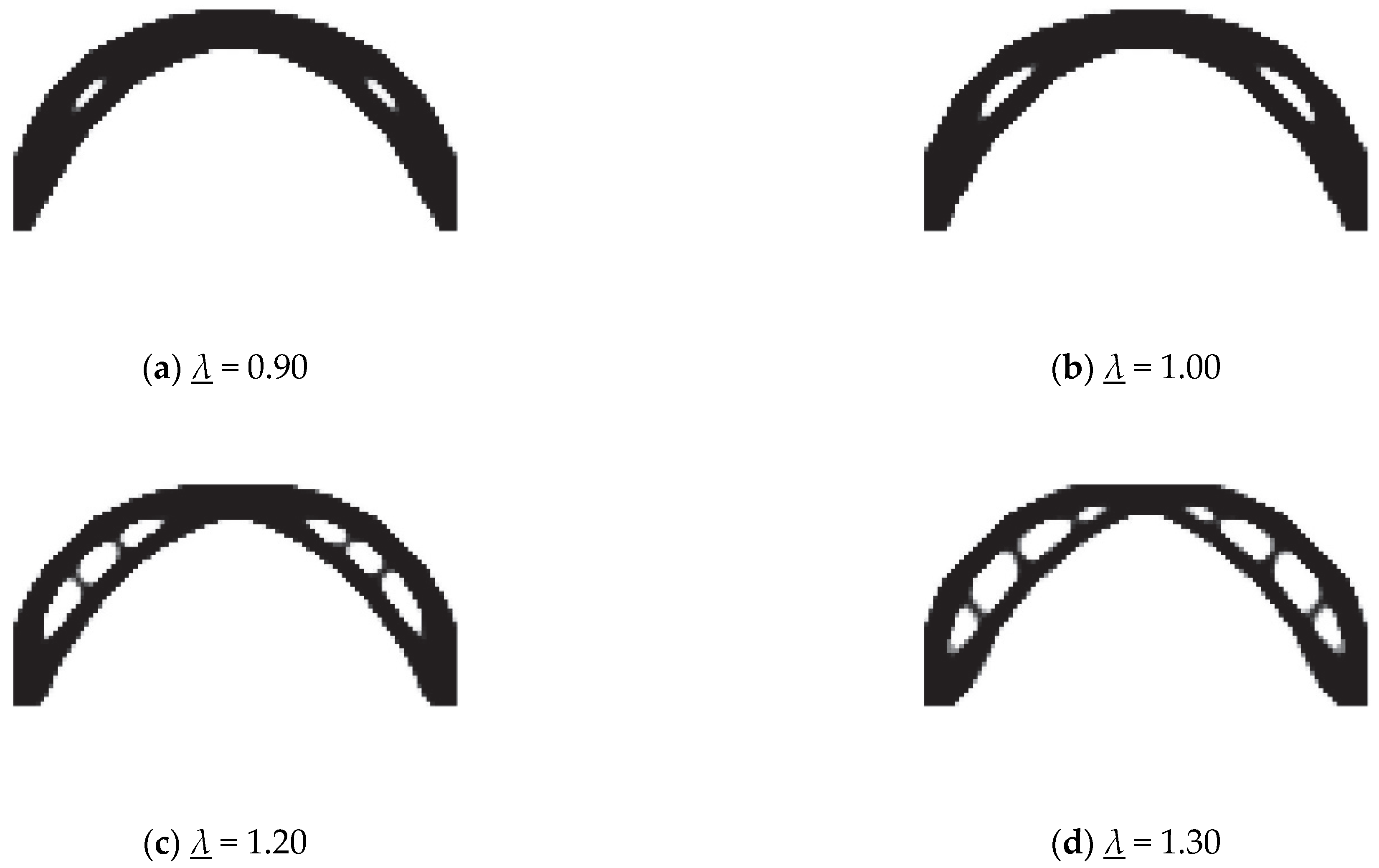






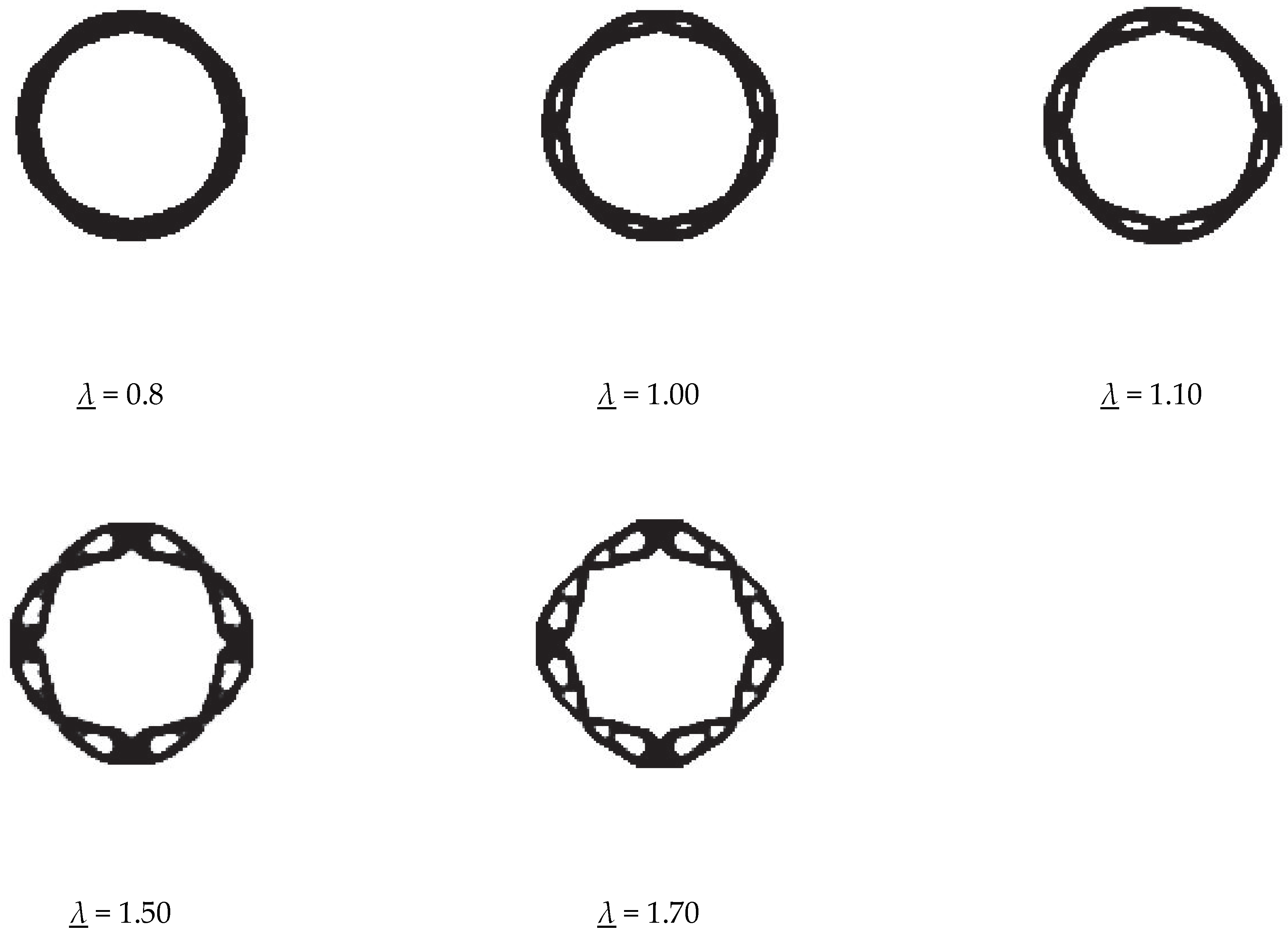




| The Value of the Buckling Restraint | The First Order Buckling Factor of the Optimization Result | The Compliance of the Optimization Result |
|---|---|---|
| 0.90 | 0.91 | 2.30 × 10−2 |
| 1.00 | 1.01 | 2.35 × 10−2 |
| 1.20 | 1.21 | 2.58 × 10−2 |
| 1.30 | 1.30 | 2.83 × 10−2 |
| The Value of Buckling Restraint | The First Order Buckling Factor of Optimization Result | The Compliance of Optimization Result |
|---|---|---|
| 1.20 | 1.23 | 2.41 × 10−2 |
| 1.40 | 1.42 | 2.46 × 10−2 |
| 1.60 | 1.62 | 2.47 × 10−2 |
| 1.80 | 1.82 | 2.53 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Zhan, K.; Xia, J.; Zhao, M. Topology Optimization for Minimum Compliance with Material Volume and Buckling Constraints under Design-Dependent Loads. Appl. Sci. 2023, 13, 646. https://doi.org/10.3390/app13010646
Jiang Y, Zhan K, Xia J, Zhao M. Topology Optimization for Minimum Compliance with Material Volume and Buckling Constraints under Design-Dependent Loads. Applied Sciences. 2023; 13(1):646. https://doi.org/10.3390/app13010646
Chicago/Turabian StyleJiang, Yuanteng, Ke Zhan, Jie Xia, and Min Zhao. 2023. "Topology Optimization for Minimum Compliance with Material Volume and Buckling Constraints under Design-Dependent Loads" Applied Sciences 13, no. 1: 646. https://doi.org/10.3390/app13010646
APA StyleJiang, Y., Zhan, K., Xia, J., & Zhao, M. (2023). Topology Optimization for Minimum Compliance with Material Volume and Buckling Constraints under Design-Dependent Loads. Applied Sciences, 13(1), 646. https://doi.org/10.3390/app13010646






