AC Electric Powertrain without Power Electronics for Future Hybrid Electric Aircrafts: Architecture, Design and Stability Analysis
Abstract
:1. Introduction
- -
- In hybrid-electric aircraft, this power–thrust dissociation enables the optimization of the design of the generation of power, in particular if an auxiliary power source hybridizing the main thermal source is used, thus offering precious degrees of freedom to optimize the thermal generator;
- -
- Literature Review
- -
- A high specific power;
- -
- A good efficiency and an excellent heat dissipation;
- -
- Low maintenance requirement in the absence of brushes.
- Main contribution
- -
- A transient modelling of an AC electric propulsion architecture composed of one surface mounted permanent magnet synchronous generator (PMSG) and one permanent magnet synchronous motor (PMSM).
- -
- An implementation of an analytical nonlinear then linearized state model in order to study the stability of the system based on the linearized model previously established.
- -
- A comparison of this analysis by means of a reduced power scale experimentation, in order to compare and validate the theoretical analysis results.
- -
- A characterization of the stability issues of the AC coupled powertrain and an assessment of the stability’s sensitivity to parametric variations.
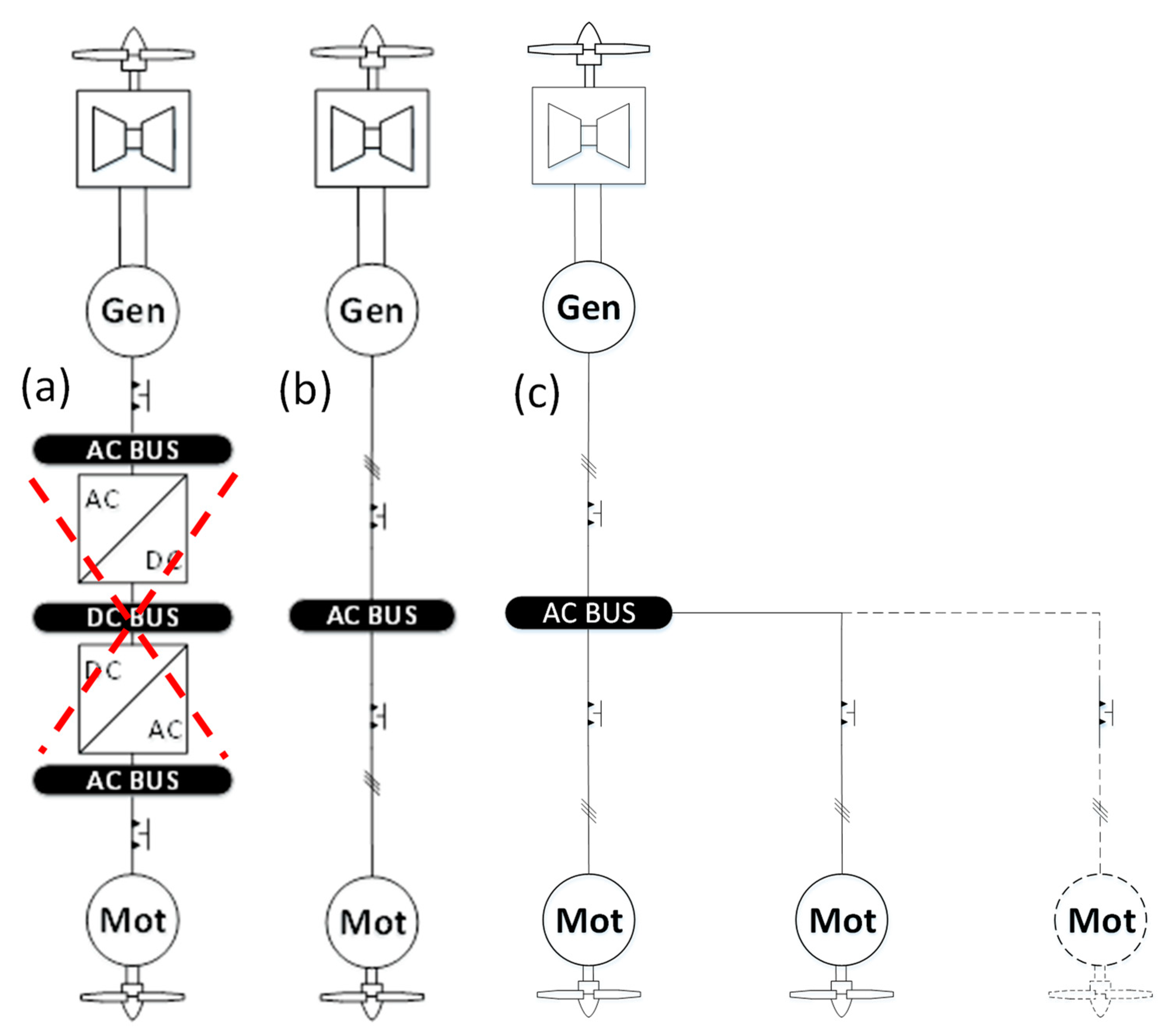
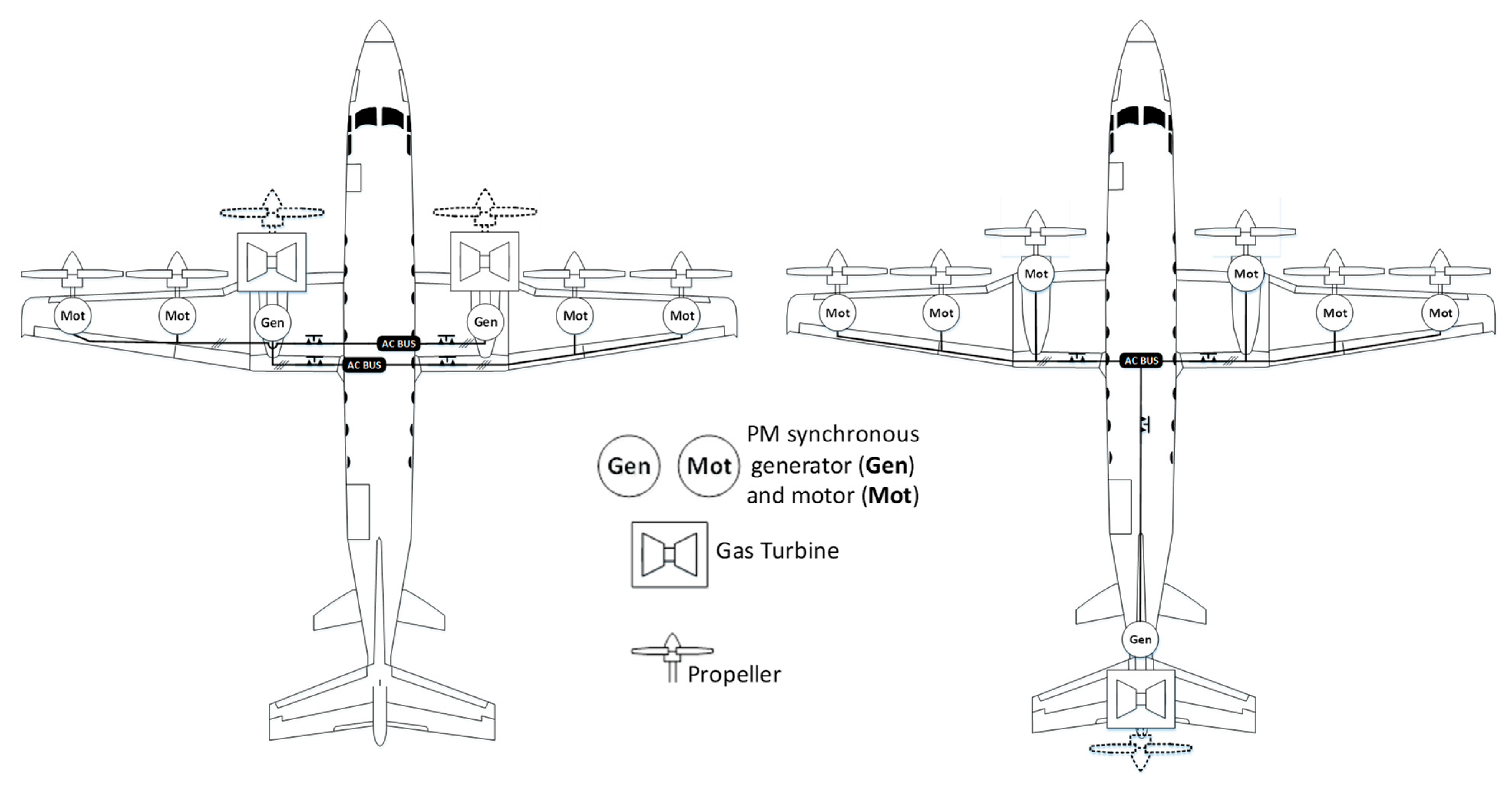
2. Context and Case Study of a “Power Electronic-Less” Powertrain for Aircraft Propulsion
3. Modelling, Analysis Tools and Experimental Support for Stability Analysis
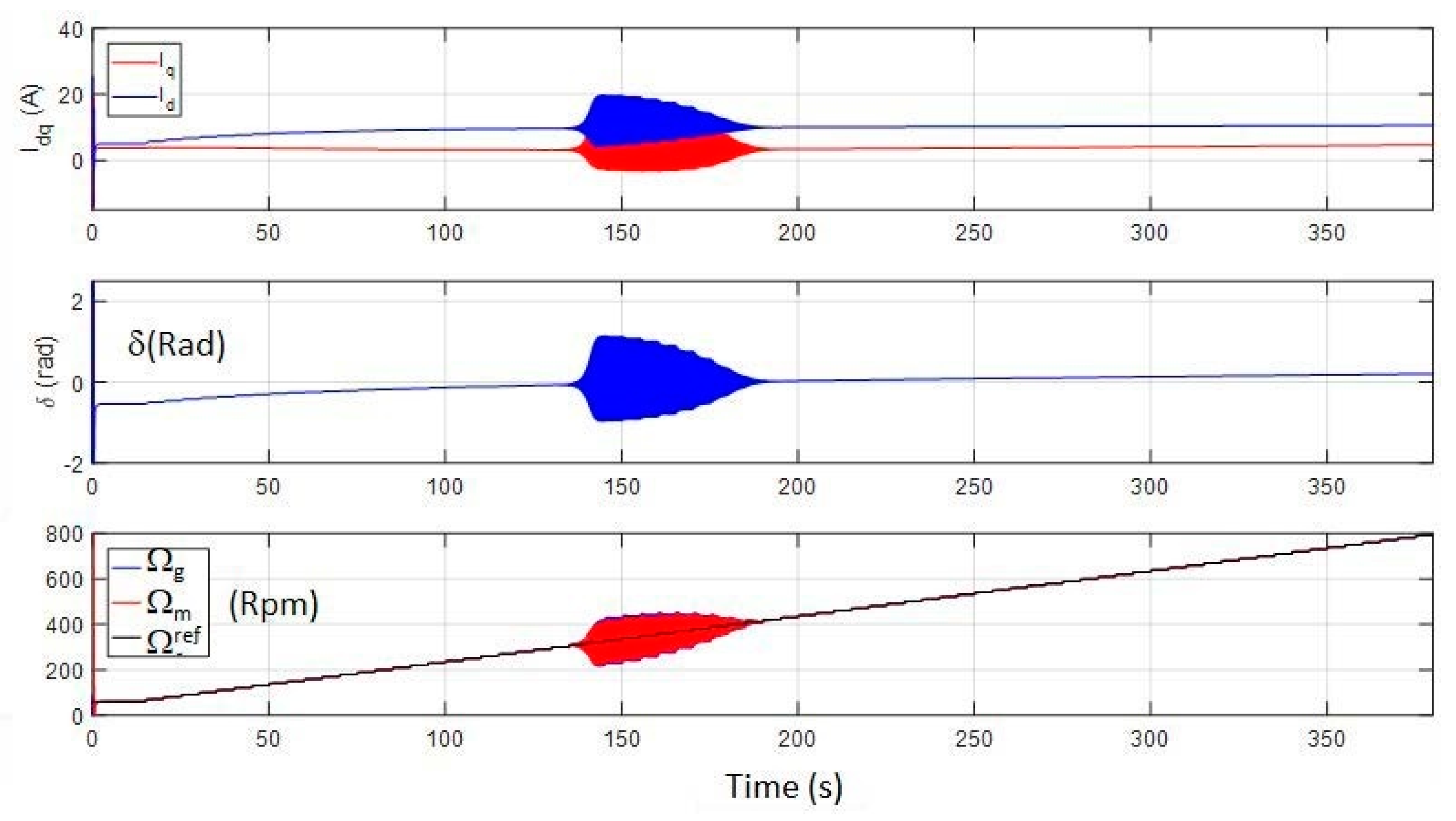
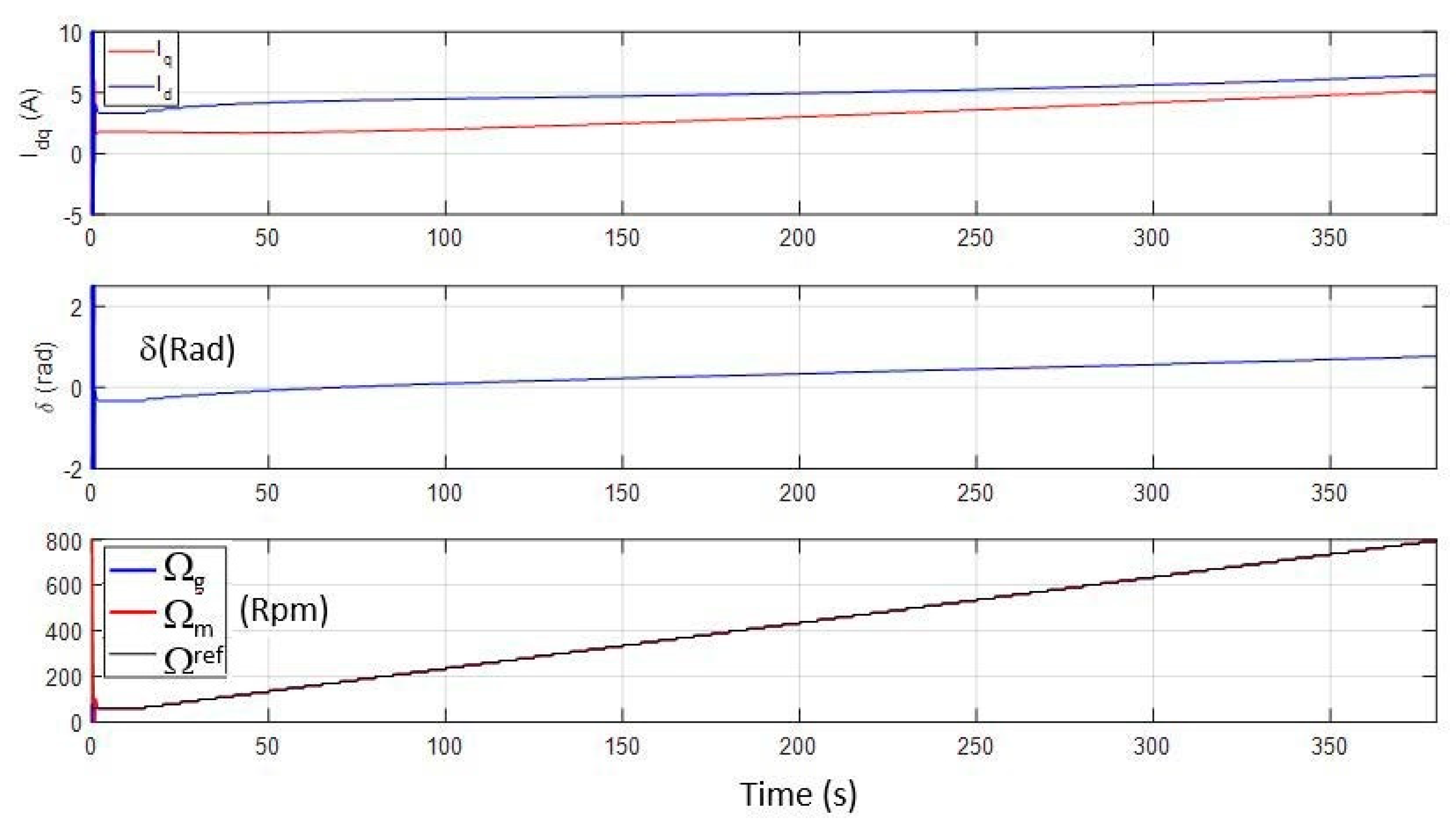
- First, a nonlinear state model is built, representing the transient behavior of the system. This analytic state model can be simulated in the time domain on Matlab Simulink and is compared for validation with another time simulation based on the Saber circuit solver [32].
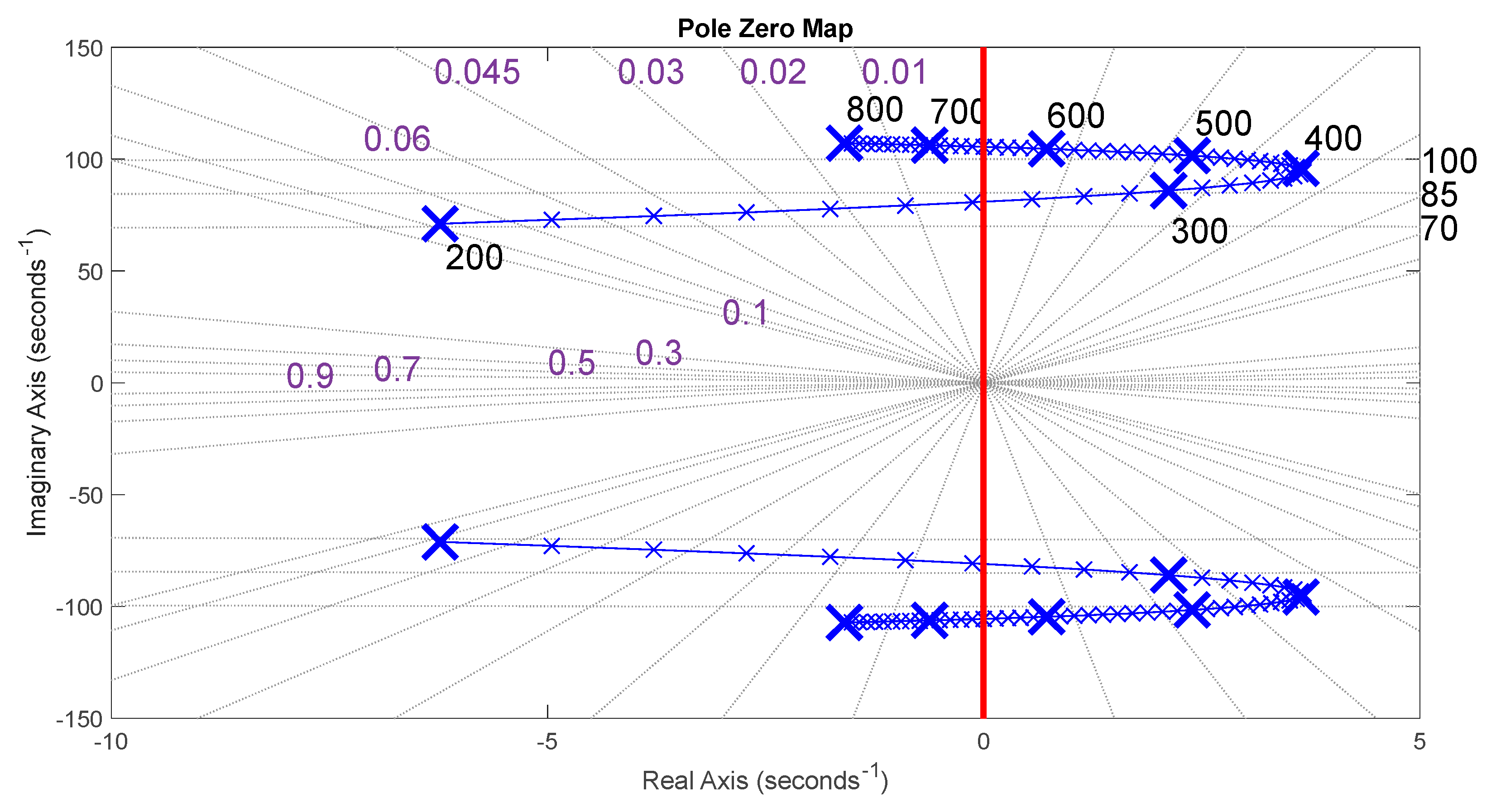
- Second, the previous analytic nonlinear state model can be small-signal linearized to set the root locus of the powertrain, in order to characterize the stability domain.
- Finally, a reduced power scale test bench was developed in order to validate theoretical analysis set from both previous approaches.
3.1. Nonlinear Analytic State Model
3.1.1. State Model Derivation
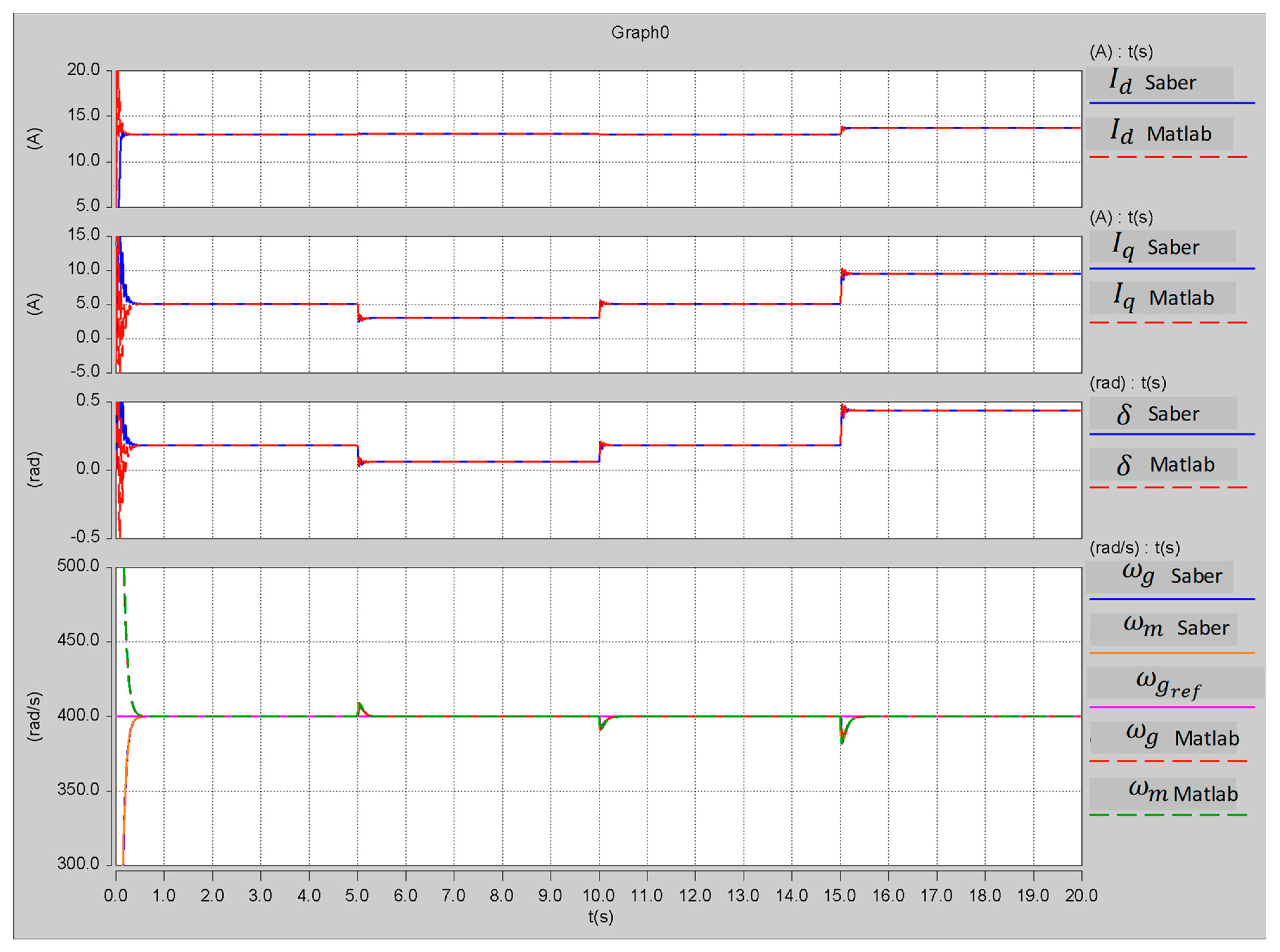
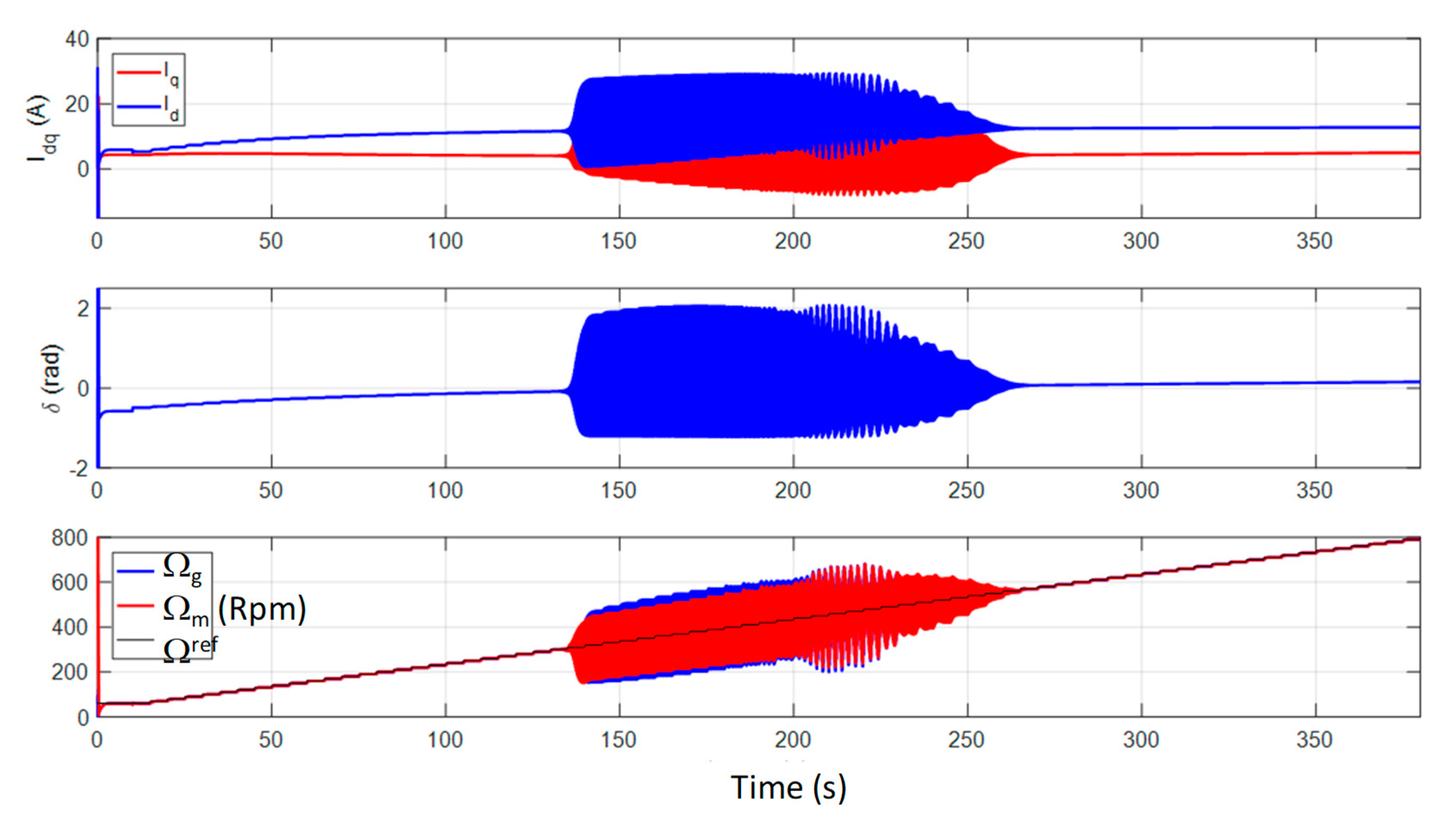
3.1.2. State Model Validation
3.2. Small-Signal Linearization of the Analytic Model
3.2.1. Steady-State Model Derivation
3.2.2. Linearized State Model Derivation
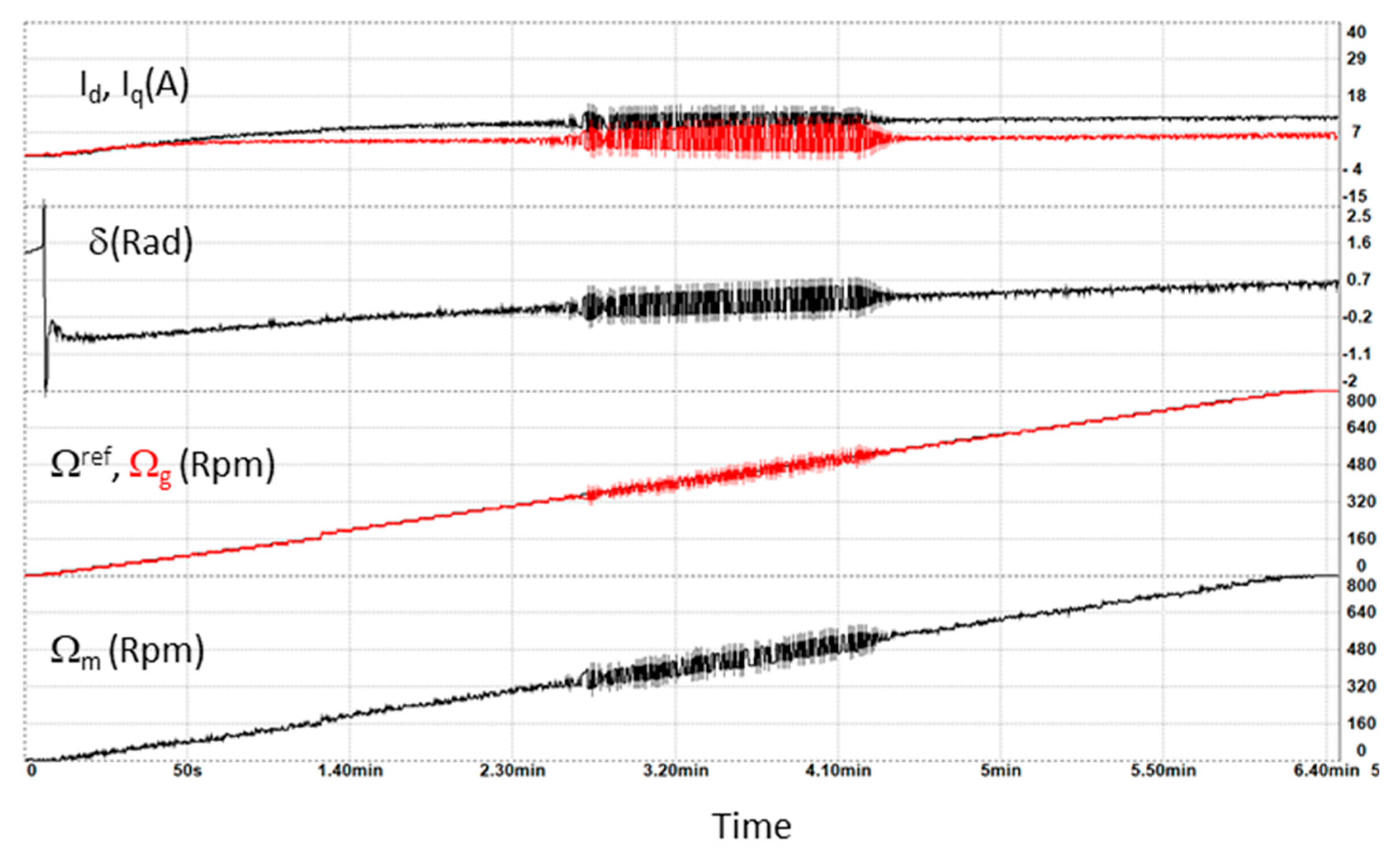
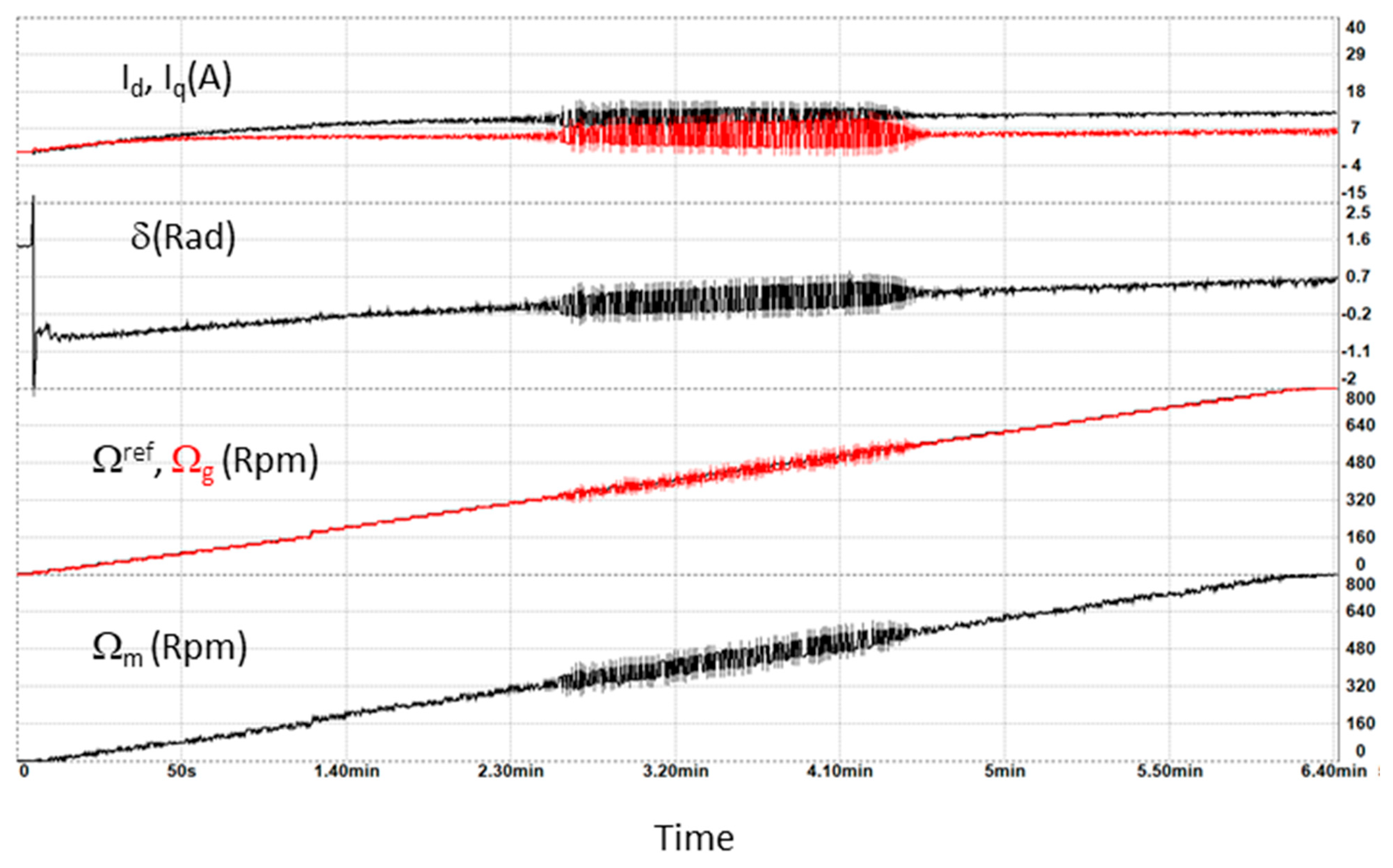
3.3. Reduced Power Scale Experimental Test Bench
4. Stability Analysis of the Powertrain
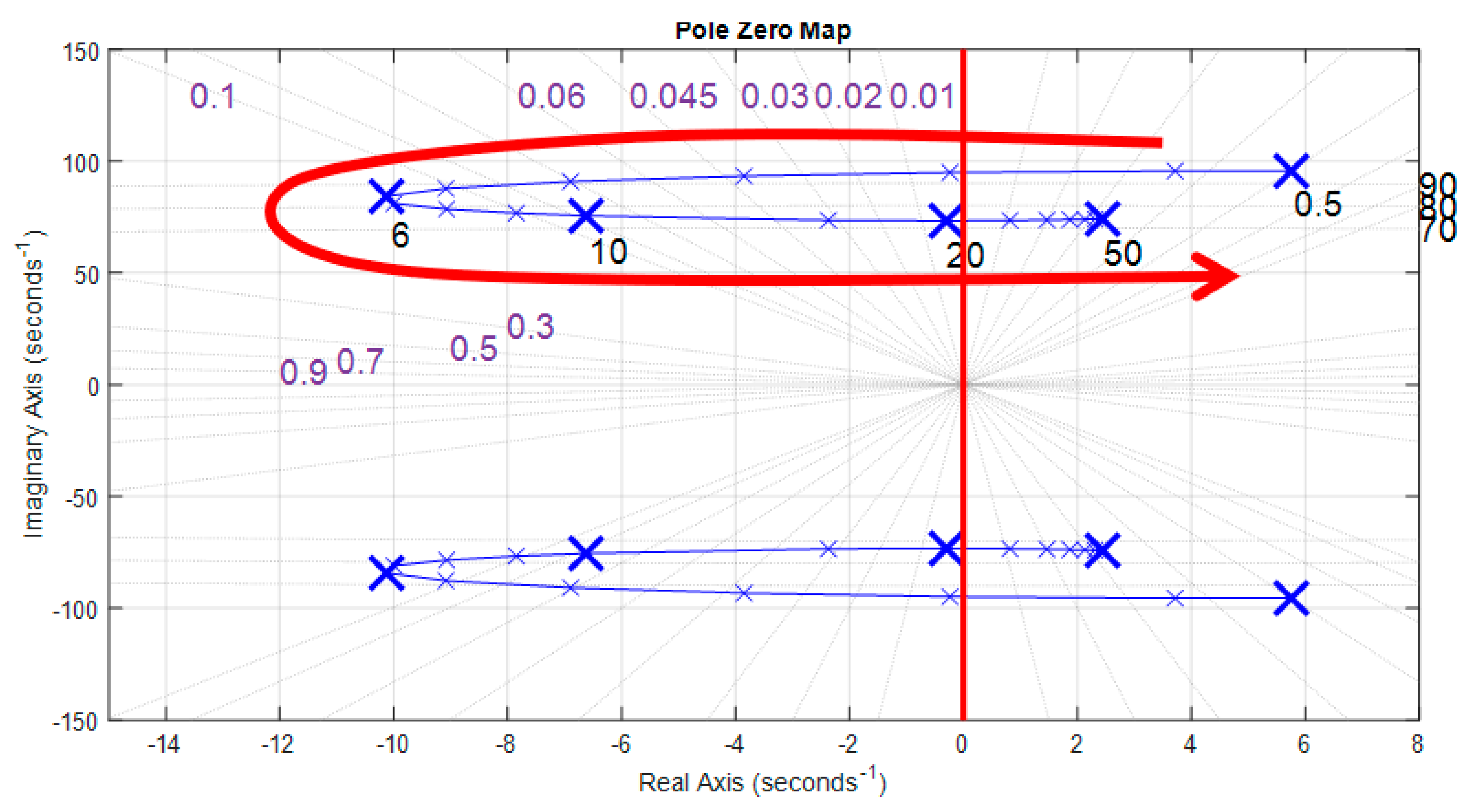
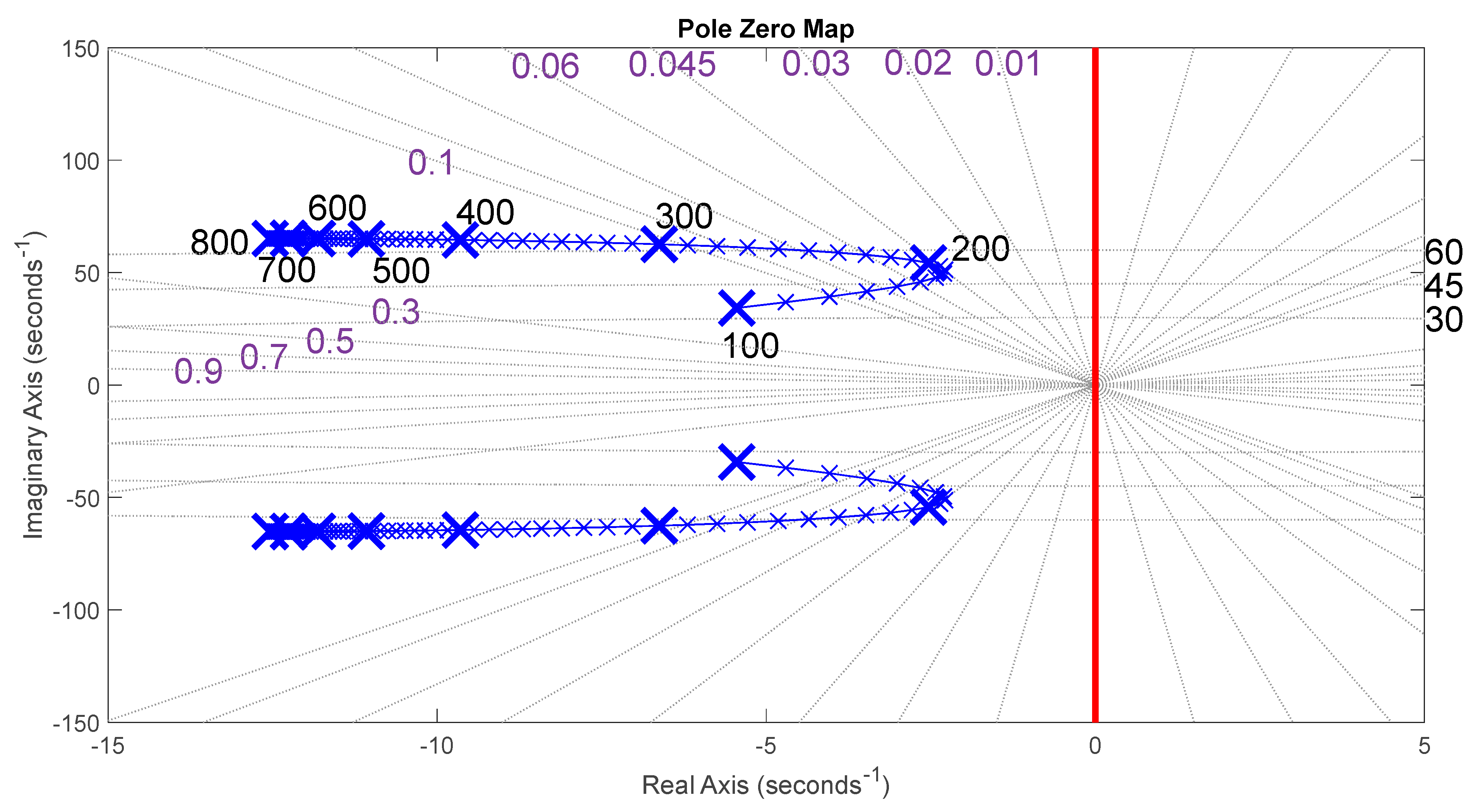
4.1. Stability Analysis with Respect to the Generator Speed
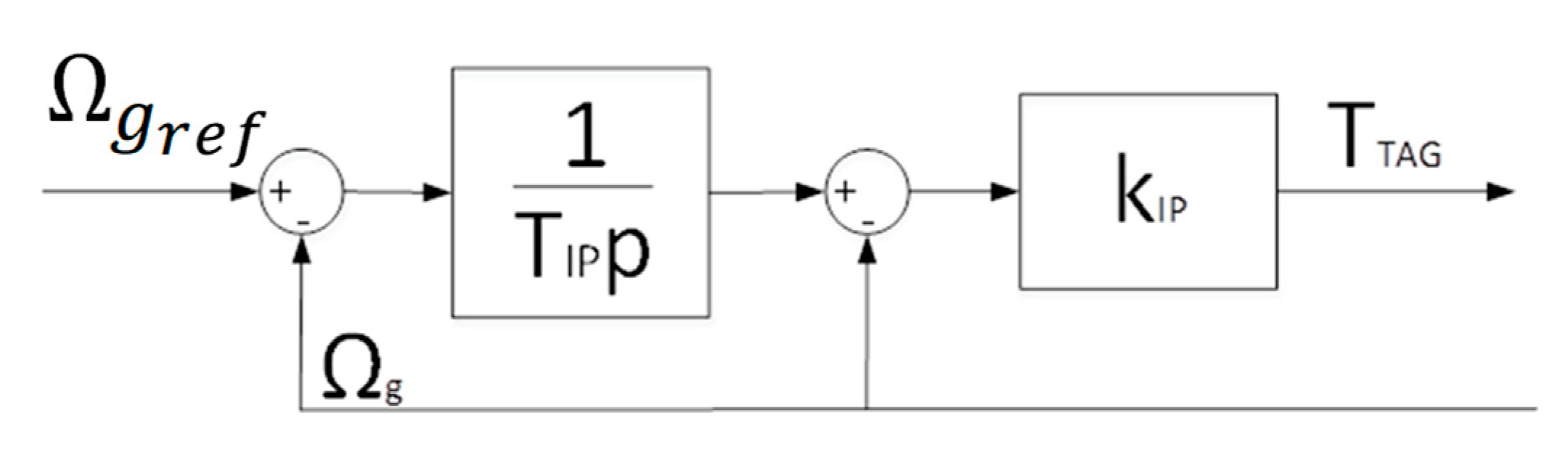
4.2. Influence of the Gas Turbine Control Dynamic on the Stability of the Powertrain
4.3. Influence of the Machine Inductances on the Stability of the Powertrain
- -
- Moving the unstable (oscillation) domain towards lower speeds;
- -
- A decrease in the speed range (Δ) inside which the AC powertrain is unstable or oscillates (on the left column, the unstable speed interval (Δ) is reduced by more than 30%.
4.4. Coupled Influence of System Parameters on the Stability of the Powertrain
- -
- Inductances;
- -
- Magnetic flux of the magnets;
- -
- Inertia of the generator set (gas turbine—permanent magnet synchronous generator);
- -
- Inertia of the motor set (propeller—permanent magnet synchronous motor).
- -
- Important inductances values;
- -
- Low electromotive forces (image of the magnetic fluxes);
- -
- Important inertia of the motor set.
- -
- In order to analyze the coupling effects between parameters and to verify potential antagonistic couplings, the following variations are simultaneously applied to the system:
- -
- 10% increase in the generator and the motor inductances;
- -
- 10% decrease in the generator and the motor magnetic flux of the magnets;
- -
- 10% decrease in the inertia of the generator set;
- -
- 10% increase in the inertia of the motor set.
- -
- 100% increase in the generator and the motor inductances;
- -
- 25% decrease in the generator and the motor magnetic flux;
- -
- 50% decrease in the inertia of the generator set;
- -
- 25% increase in the inertia of the motor set.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Roland Berger, Think: Act, Navigating Complexity. Aircraft electrical Propulsion—Onwards and Upwards. 2018. Available online: https://www.rolandberger.com/publications/publication_pdf/roland_berger_aircraft_electrical_propulsion_2.pdf (accessed on 1 September 2022).
- IATA. Aircraft Technology Roadmap to 2050. 2019. Available online: https://www.iata.org/contentassets/8d19e716636a47c184e7221c77563c93/Technology-roadmap-2050.pdf (accessed on 1 September 2022).
- Sarlioglu, B.; Morris, C.T. More Electric Aircraft: Review, Challenges, and Opportunities for Commercial Transport Aircraft. IEEE Trans. Transp. Electrif. 2015, 1, 54–64. [Google Scholar] [CrossRef]
- Roland Berger. Electric Propulsion Is Finally on the Map. Available online: https://www.rolandberger.com/en/Insights/Publications/Electric-propulsion-is-finally-on-the-map.html (accessed on 1 September 2022).
- Epstein, A.H.; O’Flarity, S.M. Considerations for Reducing Aviation’s CO2 with Aircraft Electric Propulsion. J. Propuls. Power 2019, 35, 572–582. [Google Scholar] [CrossRef]
- Pornet, C.; Isikveren, A. Conceptual design of hybrid-electric transport aircraft. Prog. Aerosp. Sci. 2015, 79, 114–135. [Google Scholar] [CrossRef]
- Ansell, P.J.; Haran, K.S. Electrified Airplanes: A Path to Zero-Emission Air Travel. IEEE Electrif. Mag. 2020, 8, 18–26. [Google Scholar] [CrossRef]
- Madonna, V.; Giangrande, P.; Galea, M. Electrical Power Generation in Aircraft: Review, Challenges, and Opportunities. IEEE Trans. Transp. Electrif. 2018, 4, 646–659. [Google Scholar] [CrossRef]
- Thauvin, J. Exploring the Design Space for a Hybrid-Electric Regional Aircraft with Multidisciplinary Design Optimisation Methods. Ph.D. Thesis, Institut National Polytechnique de Toulouse (Toulouse INP), Toulouse, France, 2018. Available online: https://oatao.univ-toulouse.fr/23607/1/Thauvin_jerome.pdf (accessed on 1 September 2022).
- Clarke, S.; Redifer, M.; Papathakis, K.; Samuel, A.; Foster, T. X-57 power and command system design. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo (ITEC), Chicago, IL, USA, 22–24 June 2017; pp. 393–400. [Google Scholar] [CrossRef] [Green Version]
- Dillinger, E.; Döll, C.; Liaboeuf, R.; Toussaint, C.; Hermetz, J.; Verbeke, C.; Ridel, M. Handling qualities of ONERA’s small business concept plane with distributed electric propulsion. In Proceedings of the 31st Congress of International Council of Aeronautical Sciences (ICAS), Belo Horizonte, Brazil, 9–14 September 2018; pp. 1–10. [Google Scholar]
- Bidart, D.; Pietrzak-David, M.; Maussion, P.; Fadel, M. Mono inverter multi-parallel permanent magnet synchronous motor: Structure and control strategy. IET Electr. Power Appl. J. 2011, 5, 288–294. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, S.; Zhao, X.; Kyprianidis, K. A Review of Concepts, Benefits, and Challenges for Future Electrical Propulsion-Based Aircraft. Aerospace 2020, 7, 44. [Google Scholar] [CrossRef] [Green Version]
- Mouty, S. Conception de Machines à Aimants Permanents à Haute Densité de Couple Pour les éoliennes de Forte Puissance. Ph.D. Thesis, Université de Franche-Comté, Besancon, France, 2013. [Google Scholar]
- Courtecuisse, V. Supervision d’une Centrale Multisources à Mase d’éoliennes et de Stockage d’énergie Connectée au Réseau électrique. Ph.D. Thesis, Ecole Nationale Supérieure d’Arts et Métiers, Paris, France, 2008. [Google Scholar]
- Merwerth, J. The Hybrid-Synchronous Machine of the New BMW i3 & i8. 2014. Available online: https://www.speakev.com/attachments/20140404_bmw-pdf.80577/ (accessed on 1 September 2022).
- Alstom. AGV-Le 21ème Siècle à Très Grande Vitesse. 2009. Available online: https://docplayer.fr/205073-Agv-le-21-eme-siecle-a-tres-grande-vitesse.html (accessed on 1 September 2022).
- Pinheiro, M.D.L.; Suemitsu, W.I. Permanent magnet synchronous motor drive in vessels with electric propulsion system. In Proceedings of the 2013 Brazilian Power Electronics Conference, Gramado, Brazil, 27–31 October 2013. [Google Scholar] [CrossRef]
- Bordianu, A.; Samoilescu, G. Electric and Hybrid Propulsion in the Naval Industry. In Proceedings of the 2019 11th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 28–30 March 2019. [Google Scholar] [CrossRef]
- Thongam, J.S.; Tarbouchi, M.; Okou, A.F.; Bouchard, D.; Beguenane, R. Trends in naval ship propulsion drive motor technology. In Proceedings of the 2013 IEEE Electrical Power & Energy Conference, Halifax, NS, Canada, 21–23 August 2013. [Google Scholar] [CrossRef]
- Pettes-Duler, M. Integrated Optimal Design of a Hybrid-Electric Aircraft Powertrain. Ph.D. Thesis, Institut National Polytechnique de Toulouse (INPT), Toulouse, France, 2021. [Google Scholar]
- Pettes-Duler, M.; Roboam, X.; Sareni, B. Integrated Optimal Design for Hybrid Electric Powertrain of Future Aircrafts. Energies 2022, 15, 6719. [Google Scholar] [CrossRef]
- Blackwelder, M.J.; Rancuret, P.M. Multiple Generator Synchronous Electrical Power Distribution System. U.S. Patent EP3197043A1, 26 July 2017. [Google Scholar]
- Armstrong, M.; Blackwelder, M. Combined AC and DC Turboelectric Distributed Propulsion System. U.S. Patent EP3318492A1, 9 May 2018. [Google Scholar]
- Armstrong, M.; Blackwelder, M.J.; Bollman, A.M. Synchronizing Motors for an Electric Propulsion System. U.S. Patent US20160365810A1, 15 December 2016. [Google Scholar]
- Bachmann, C.; Bergmann, D.; Bachmaier, G.; Gerlich, M.; Pais, G.; Vittorias, I. Propellerantrieb und Fahrzeug, Insbesondere Flugzeug. Germany Patent DE102015213580A1, 26 January 2017. [Google Scholar]
- Himmelmann, R.A. Variable Speed AC Bus Powered Tail Cone Boundary Layer Ingestion Thruster. U.S. Patent US20180265206A1, 20 September 2018. [Google Scholar]
- Rougier, F.; Viguier, C. Système Electrique Pour Canal Propulsif Synchrone. France Patent FR3092948A1, 21 August 2020. [Google Scholar]
- Sadey, D.J.; Taylor, L.M.; Beach, R.F. Proposal and Development of a High voltage Variable Frequency alternating Current Power System for Hybrid Electric Aircraft. In Proceedings of the 14th International Energy Conversion Engineering Conference, Salt Lake City, UT, USA, 25–27 July 2016. [Google Scholar] [CrossRef] [Green Version]
- Sadey, D.J.; Bodson, M.; Csank, J.T.; Hunker, K.R.; Theman, C.J.; Taylor, L.M. Control Demonstration of Multiple Doubly-Fed Induction Motors for Hybrid Electric Propulsion. In Proceedings of the 53rd AIAA/SAE/ASEE Joint Propulsion Conference, Atlanta, GA, USA, 10–12 July 2017. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; Power System Engineering Series; Electric Power Research Institute: Palo Alto, CA, USA, 1993. [Google Scholar]
- Saber Simulation Solver. Available online: https://www.synopsys.com/verification/virtual-prototyping/saber.html (accessed on 1 November 2022).





| Parameters | Generator | Motor |
|---|---|---|
| Cyclic inductance () | 6.5 | 2.7 |
| Magnetic flux of the magnets () | 286.5 | 162.1 |
| Inertia () | 0.0097 | 0.0062 |
| Inertia of the associated asynchronous machines acting as a gas turbine (generator) or propeller (motor) () | 0.0113 | 0.024 |
| Gas Turbine Dynamic (Hz) | Unstable Speed Range (rpm) from Root Locus | Unstable Speed Range (rpm) from Time Simulation | Unstable Speed Range (rpm) from Experiments |
|---|---|---|---|
| 0.9 | 260 → 660 (Δ = 400) | 280 → 610 | 270 → 620 |
| 1 | 260 → 620 (Δ = 360) | 290 → 580 | 300 → 560 |
| 1.25 | 270 → 540 (Δ = 270) | 310 → 510 | 310 → 530 |
| 1.5 | 280 → 480 (Δ = 200) | 340 → 440 | 320 → 520 |
| 1.75 | 310 → 420 (Δ = 110) | No oscillation | 320 → 380 |
| 2 | No oscillation | No oscillation | No oscillation |
| Addition of Inductances (mH) | Unstable Speed Range (rpm) from Root Locus | Unstable Speed Range (rpm) from Time Simulation | Unstable Speed Range (rpm) from Experiments |
|---|---|---|---|
| 0 (base setting) | 260 → 620 (Δ = 360) | 290 → 580 | 300 → 560 |
| 1 | 240 → 560 (Δ = 320) | 270 → 530 | 270 → 530 |
| 2 | 230 → 520 (Δ = 290) | 250 → 490 | 250 → 500 |
| 3 | 210 → 480 (Δ = 270) | 240 → 450 | 270 → 490 |
| 4 | 200 → 440 (Δ = 240) | 230 → 420 | 250 → 470 |
| 5 | 190 → 420 (Δ = 230) | 220 → 390 | 240 → 450 |
| Parameters Modification | Unstable Speed Range (rpm) from Root Locus |
|---|---|
| No modification—Base setting | 260 → 620 (Δ = 360) |
| 10% increase in the generator and the motor inductances | 240 → 570 (Δ = 330)↘ |
| 10% decrease in the generator and the motor inductances | 280 → 680 (Δ = 400)↗ |
| 10% increase in the generator and the motor magnetic flux of the magnets | 270 → 690 (Δ = 420)↗ |
| 10% decrease in the generator and the motor magnetic flux of the magnets | 250 → 540 (Δ = 290)↘↘ |
| 10% increase in the inertia of the generator set | 260 → 620 (Δ = 360) |
| 10% decrease in the inertia of the generator set | 260 → 610 (Δ = 350)↘ |
| 10% increase in the inertia of the motor set | 260 → 580(Δ = 320)↘ |
| 10% decrease in the inertia of the motor set | 260 → 660 (Δ = 400)↗ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Richard, A.; Roboam, X.; Rougier, F.; Roux, N.; Piquet, H. AC Electric Powertrain without Power Electronics for Future Hybrid Electric Aircrafts: Architecture, Design and Stability Analysis. Appl. Sci. 2023, 13, 672. https://doi.org/10.3390/app13010672
Richard A, Roboam X, Rougier F, Roux N, Piquet H. AC Electric Powertrain without Power Electronics for Future Hybrid Electric Aircrafts: Architecture, Design and Stability Analysis. Applied Sciences. 2023; 13(1):672. https://doi.org/10.3390/app13010672
Chicago/Turabian StyleRichard, Alexandre, Xavier Roboam, Florent Rougier, Nicolas Roux, and Hubert Piquet. 2023. "AC Electric Powertrain without Power Electronics for Future Hybrid Electric Aircrafts: Architecture, Design and Stability Analysis" Applied Sciences 13, no. 1: 672. https://doi.org/10.3390/app13010672
APA StyleRichard, A., Roboam, X., Rougier, F., Roux, N., & Piquet, H. (2023). AC Electric Powertrain without Power Electronics for Future Hybrid Electric Aircrafts: Architecture, Design and Stability Analysis. Applied Sciences, 13(1), 672. https://doi.org/10.3390/app13010672







