Signature Split Method for a PQC-DSA Compliant with V2V Communication Standards

Abstract

The development of quantum computing systems poses a great threat to the security of existing public key-based systems. As a result, the National Institute of Standards and Technology (NIST) started a Post-Quantum Cryptography (PQC) standardization project in 2015, and currently active research is being conducted to apply PQC to various cryptographic protocols. Unlike elliptic curve cryptography (ECC)-based schemes, PQC requires a large memory footprint and key/signature size. Therefore, when migrating PQC to a protocol, depending on the PQC and protocol specifications, it can be hard to migrate PQC. In the case of the WAVE protocol, it is difficult to satisfy the accuracy of a specific PQC algorithm because segmentation of the signature occurs during transmission due to the limitation of the maximum packet size. Therefore, in this paper, we present two methodologies that can apply PQC while complying with IEEE 1609.2 standards to the WAVE protocol in the V2V environment. Whereas previous migration studies have focused on designing a hybrid mode of protocols, this paper explores solutions more intuitively at the application layer of protocols. We analyzed two postquantum digital signature algorithms (Crystals-Dilithium and Falcon) and the structure of basic-safety messages (BSMs) of the V2V protocol on the size side. Through this, we propose methods that can perform an independent signature verification process without waiting for all divided signatures in the WAVE protocol. Our methodology overcomes the limitation that schemes with large signature sizes cannot be mounted into the WAVE protocol. We also note that the architecture used as an on-board unit (OBU) in an autonomous driving environment is mainly a microprocessor. We investigated an optimized PQC implementation in the OBU environment and simulated our methodology with the V2Verifier. Finally, we measured the accurate latency through simulation in Jetson Xavier, which is mainly used as an OBU in the V2V communication network.

1. Introduction

Advances in quantum computing may invalidate the discrete logarithm and elliptic curve-based public key cryptography schemes used in current protocols [1]. In various protocols, public key-based schemes such as key exchange algorithms for mutual communication and digital signature algorithms (DSAs) for authentication should be replaced with algorithms that can achieve quantum security in the future. As a result, the National Institute of Standards and Technology (NIST) conducted the Post-Quantum Cryptography (PQC) standardization project. and the selected algorithms to be standardized were recently announced [2]. Efforts to achieve quantum security for protocols are moving in two major directions. The first is a designing hybrid mode, which has the advantage of being more compatible with existing protocols and conforming to standards. The purpose of the hybrid mode is to achieve universal quantum security for common commercial devices. Therefore, hybrid awareness of client and server is important [3]. PQC can be used in environments that are hybrid-aware of each other and able to work with PQC but cannot be used in existing public-key-based crypto-systems if neither is hybrid-awareHowever, because PQC is based on a variety of mathematical challenges, and algorithm-specific parameters are all different, certain PQC algorithms have difficulty meeting protocol requirements, such as packet size and latency. For example, In the TLS 1.3 protocol, there is a report that failed to mount Classic McEliece, a 3-round candidate for PQC [2]. The second way is to be aware of potential problems in the hybrid mode and revise the instantiation method. This means redesigning existing protocols to more efficiently apply PQC. However, this method has the disadvantage in being difficult to apply unless it is enacted as a standard.

Broadcast-based V2V communication has the ultimate goal of secure communication in autonomous driving environments. Autonomous vehicles can receive real-time information from other vehicles, know each vehicle’s location, and precalculate their travel paths. In V2V communication. basic-safety messages (BSM)s conforming the IEEE 1609.2 standard allow for the protocol to send and receive the current vehicle state, such as vehicle position and speed [4]. Without a cryptographic algorithm between autonomous driving communications, real-time relocation, rerouting, etc. by attackers could lead to security incidents or even death, so BSM achieves authentication and nonrepudiation through DSA [5]. Since the V2V communication protocol also needs to achieve quantum security in the future, it is a necessary to apply PQC-DSA to the V2V protocol.

We consider three research direction perspectives based on V2V communication. The first is to suggest a method for applying the PQC algorithm to the V2V protocol in the application layer. For example, research suggests that Crystals-Dilithium is difficult to use in V2V communication due to its large signature size. Not all protocols used for V2V communication can equipped with Crystals-Dilithium. Dedicated short range communication (DSRC) and WAVE protocols have a BSM packet size of fewer than 2000 bytes [6]; therefore, Crystals-Dilithium with a minimum-security level (2) of 2000 bytes or more signature size cannot be installed. Ultimately, we aimed to apply PQC-DSA with Crystals-Dilithium to all V2V protocols. Therefore, before designing the hybrid protocol, we explored an efficient way to mount Crystals-Dilithium onto V2V communication. The second perspective is the need for simulation in the V2V communication protocol. In the V2V protocol, remote cars broadcasts BSM messages at 100 m/s. Therefore, the local car should verify received BSMs from remote cars. In the V2V protocol, the local car generally verifies in real time the BSMs sent by the surrounding remote cars in standby mode. The count of BSMs received may vary depending on the location of the local car. Therefore, simulations are needed to measure latency. In the previous research [7], simulation was performed with V2Verifier, but as mentioned above, Crystals-Dilithium cannot satisfy the correctness in the WAVE protocol. Therefore, in this paper, we propose a methodology to overcome these limitations and simulate our methodology. Finally, we focused on the on-board unit (OBU), which is the terminal platform in the autonomous driving environment. Most of the simulation research conducted thus far has examined CPU architectures. Currently, one mainly uses embedded-based OBUs as terminal platforms for V2V environments; therefore, simulation in that environment is essential. Since the embedded environment is mainly limited by performance and memory size, it is effective to use the optimization code for each OBU architecture.

1.1. Related Work

PQC migration research in the V2V communication environment has been recently conducted [5]. Research on the hybrid mode design with PQC based on IEEE 1609.2 was conducted in [5], and benchmark research on protocol-specific PQC was conducted in [7] using the simulation tool V2Verifier. Here, we concentrate on applying PQC to the V2V communication mentioned in existing research, considering that specific PQC algorithms with large signature and key sizes are difficult to mount in protocols. For example [5,7], it was reported that the signature size of Crystals-Dilithium [8] for PQC-DSA is generally too large, making it difficult to apply to V2V communication. In [5], a new hybrid protocol was designed that satisfies the IEEE 1609.2 standard and quantum security, even if PQC-DSA with a larger signature size was later proposed to solve this. The benchmark study [7] suggests that research is needed to apply PQC to V2V protocols with small BSM packet sizes, such as the WAVE protocol.

1.2. Contribution

In this paper, through a detailed analysis of the BSM structure and NIST PQC-DSA, we present two methodologies that enable accurate verification even for large signature sizes (especially Crystals-Dilithium) in V2V communications. First, we propose a “simple split way” that uses order-bit to guarantee the correctness of PQC-DSA during transmission and reception. The second method, “split way for Crystals-Dilithium” split packets based on the characteristics of the Crystals-Dilithium signature structure without the need to receive and sort all the signature blocks received. Our method allows the signature verification process to proceed immediately upon receipt of the split signature block. In the autonomous driving environment, one local car needs to be accutely aware of the location information of all remote cars around it. In other words, the local car effectively needs to proceed through the several signature verification processes in parallel. Our “split way for Crystals-Dilithium” has the advantage of being able to set the verification logic for each signature packet from the perspective of parallelism. Additionally, the signature verification process can be started on any packet received, reducing the latency incurred during the verification. We performed simulations with V2Verifier. We proceeded to experiment with an ARMv8-based OBU actually used in an autonomous-driving environment. We also simulated signature generation and verification using the latest optimization work of PQC-DSA proposed for the ARMv8 platform and analyzed the simulation results in detail.

The remainder of this paper is structured as follows: Section 2 introduces PQC-DSA and V2Verifier. Section 3 describes our simulation environment, the code we used, and the proposed methodology for applying PQC-DSA to V2Verifier. Results and discussion of our simulation are presented in Section 4 and Section 5 before we conclude the article in Section 6.

2. Preliminaries

2.1. Post-Quantum Cryptography

Postquantum cryptography is a next-generation public-key cryptographic system, an alternative to existing public-key cryptography, whose hardness is threatened by the quantum-circuit algorithm presented by Shor in 1994. The NIST is holding competitions in two fields, public key encryption/key encapsulation mechanism (PKE/KEM) and digital signature algorithm (DSA), to standardize secure PQC in the quantum computing environment, and the algorithms targeted for final standardization have now been announced. The cryptographic scheme used in V2Verifier, the target of this paper, is a DSA, and the final standardized algorithms are Crystals-Dilithium [8] and Falcon [9], both of which are lattice-based algorithms.

Table 1. Parameters of Crystals-Dilithium and Falcon, size of the public key, secret key, and signature measured in bytes.

	Crystals-Dilithium			Falcon
Problem	Module-LWE			NTRU
NIST Security Level	Public Key [B]	Secret Key [B]	Signature [B]	Public Key [B]	Secret Key [B]	Signature [B]
1 (AES-128)	-	-	-	897	1281	690
2 (SHA256)	1312	2528	2420	-	-	-
3 (AES-192)	1952	4000	3293	-	-	-
5 (AES-256)	2592	4864	4595	1793	2305	1330

shows the parameters of the two algorithms.

The shortest vector problem (SVP) problem is known as the NP-hard problem, and in the case of the problem in the NTRU lattice used by Falcon, it can be thought of as an instance of finding a nonzero short vector in the NTRU lattice, assuming that the NTRU lattice contains short vectors. The learning with errors (LWE) difficulty has security based on reduction to SVP. That is, it belongs to lattice-based encryption at a higher level. The LWE problem can be viewed as solving a linear system of $Z_q$ to which a secret (noise) vector is added. When there is no noise in $Z_q$, it can generally be easily solved using Gaussian elimination, but when there is a noise, the difficulty increases. In general, the LWE problem constructs the linear system as a matrix and the elements of the matrix as polynomials (module LWE). This structure leads to the advantage that the internal operation is the same regardless of the security level. Therefore, for the public matrix $\mathbf{A}$, the secret vector $\mathbf{s}$, and the noise $\mathbf{e}$, ($\mathbf{A}$, $\mathbf{b}$ = $\mathbf{A}$$\mathbf{s}$ + $\mathbf{e}$) and uniform random numbers (${\mathbf{A}}^{\prime }$, ${\mathbf{b}}^{\prime }$) are computationally indistinguishable. Security proofs of Crystals-Dilithium lean on the learning with errors (LWE) scheme. Falcon [9] is a PQC-DSA with a small key size and signature size based on the NTRU lattice, and the security proofs of Falcon lean on the short vectors problem (SVP).

2.2. Crystals-Dilithium

Crystals-Dilithium [8] employs Fiat–Shamir with an abort method and borrows from nodule-LWE; as a result, it provides a higher level of security than do other ring-LWE-based ciphers. Furthermore, for all security levels, Crystals-Dilithium employs the same ring and modulus. This has an advantage in terms of implementation over other competitors. The polynomial ring used by Dilithium is ${\mathbb{Z}}_q\left[X\right]/(X^{256}+1$, where q is $2^{23}-2^{13}+1$, and the parameters are maintained by simply changing the dimension of the public matrix $\mathbf{A}$ according to the security level. Therefore, the core process of Crystals-Dilithium is the operation to generate the open matrix $\mathbf{A}$ and polynomial multiplication to generate the LWE-based problem. Similar to the general digital-signature algorithm, the structure of Crystals-Dilithium consists of keygen, sign, and verify processes. Keygen process computes $\mathbf{b}=\mathbf{As}+\mathbf{e}$ via the public matrix $\mathbf{A}$, secret vector $\mathbf{s}$, and noise $\mathbf{e}$, where $\mathbf{b}$ and $\mathbf{A}$ are public information and $\mathbf{s}$ and $\mathbf{e}$ are secret information. Sign process (Algorithm 1) produces $\mathbf{w}=\mathbf{Ay}$ via the masking vector $\mathbf{y}$ and produces $\mathbf{z}=\mathbf{y}+c{\mathbf{s}}_{\mathbf{1}}$ via the digest c hashed w and the message M. A masking vector for polynomial $\mathbf{y}$ is generated during the signing process, and $\mathbf{Ay}$ is calculated. In this case, a challenge is generated by hashing the message with ${\mathbf{w}}_{\mathbf{1}}$, which is the $\mathbf{Ay}$’s high-order bit. In the verify process, ${\mathtt{MakeHint}}_q$ and ${\mathtt{UseHint}}_q$ are in charge of reconstructing the bits. The public key can be reduced by about 2.5 times using this method at the cost of a slight increase in signature size. Please note that the size of the signature of Crystals-Dilithium is very large because, the elements of the public matrix $\mathbf{A}$ are polynomials of degree 256 and the size of the public matrix is the lowest case (4, 4). Signature sig of Crystals-Dilithium consists of $\mathbf{z}$, h, and c. The size of $\mathbf{z}$ depends on the security level (the size of the public matrix). Packing a polynomial of Crystals-Dilithium has 640 bytes; therefore, the size of $\mathbf{z}$ is 4 × 640, 5 × 640, and 7 × 640 depending on the security level, respectively, where security level 2, 3, and, 5. c is the challenge, and its size is 32 bytes as the result of the hash function. h is hint information, which is a value for identifying the carry generation part by dividing the upper/lower bits of each polynomial coefficient and using only the high-order bits. Hint h requires 80, 55, and 75 bytes, respectively, depending on security level. Algorithm 2 depicts the Crystals-Dilithium’s $\mathtt{Verify}$ process. The signature verifier determines whether ${\mathbf{w}}_{\mathbf{1}}^{\prime }$ is accepted and whether the signature $\mathbf{z}$ is within the acceptable range.

Algorithm 1 Ditlihium.$\mathtt{Sign}$($sk,M$)

1:  $\mathbf{A}\in R_q^{k\times \ell }$ := $\mathtt{ExpandA}\left(\rho \right)$   2:  $\mu \in {\{0,1\}}^{384}$ := $\mathtt{CRH}(tr\Vert M)$   3:  $\kappa$ := 0, $(\mathbf{z},\mathbf{h})$ := ⊥   4:  while $(\mathbf{z},\mathbf{h})$ := ⊥ do   5:        $y\in S_{{\gamma }_1-1}^{\ell }$ := $\mathtt{ExpandMask}(K\Vert \mu \Vert \kappa )$   6:        $\mathbf{w}:=\mathbf{Ay}$   7:        ${\mathbf{w}}_{\mathbf{1}}:={\mathtt{HighBits}}_q(\mathbf{w},2{\gamma }_2)$   8:        $c\in B_{60}$ := $\mathtt{H}(\mu \Vert {\mathbf{w}}_{\mathbf{1}})$   9:        $\mathbf{z}$ := $\mathbf{y}+c{\mathbf{s}}_{\mathbf{1}}$ 10:        $({\mathbf{r}}_{\mathbf{0}},{\mathbf{r}}_{\mathbf{1}})$ := ${\mathtt{Decompose}}_q(\mathbf{w}-c{\mathbf{s}}_{\mathbf{2}},2{\gamma }_2)$ 11:        if ${∥\mathbf{z}∥}_{\infty }\ge {\gamma }_1-\beta$ or ${∥{\mathbf{r}}_0∥}_{\infty }\ge {\gamma }_2-\beta$ or ${\mathbf{r}}_1\ne {\mathbf{w}}_1$ 12:  then $(\mathbf{z},\mathbf{h})$ := ⊥ 13:        else 14:             $\mathbf{h}$ := ${\mathtt{MakeHint}}_q(-c{\mathbf{t}}_0,\mathbf{w}-c{\mathbf{s}}_2-c{\mathbf{t}}_0,2{\gamma }_2)$ 15:             if $∥c{\mathbf{t}}_0∥\ge {\gamma }_2$ or the # of 1’s in $\mathbf{h}$ is greater than w then $(\mathbf{z},\mathbf{h})$ := ⊥ 16:        $\kappa =\kappa +1$ 17:  return $\sigma =(\mathbf{z},\mathbf{h},c)$

Algorithm 2 Ditlihium.$\mathtt{Verify}(pk,M,\sigma =(\mathbf{z},\mathbf{h},c\left)\right)$

1:  $\mathbf{A}\in R_q^{k\times \ell }$ := $\mathtt{ExpandA}\left(\rho \right)$   2:  $\mu \in {\{0,1\}}^{384}$ := $\mathtt{CRH}(\mathtt{CRH}(\rho \Vert {\mathbf{t}}_1)\Vert M)$   3:  ${\mathbf{w}}_1^{\prime }$ := ${\mathtt{UseHint}}_q(\mathbf{h},\mathbf{Az}-c{\mathbf{t}}_1·2^d,2{\gamma }_2)$   4:  return ${∥\mathbf{z}∥}_{\infty }<{\gamma }_1-\beta$ and c := $\mathtt{H}\left(\mu \right|\left|{\mathbf{w}}_1\right)$ and # of 1’s in $\mathbf{h}$ is $\le w$

2.3. Falcon

The keygen process of Falcon roughly consists of the process of generating the NTRU lattice, solving the NTRU equation, and generating a Falcon tree for trapdoor sampler operations. To generate the NTRU lattice, first, Falcon generates the polynomials f and $\mathbf{g}$ with Gaussian distributions and then check that $f^{(-1)}$ exists in modulus q (12,289). After this, the keygen process computes the polynomials F and G that satisfy the NTRU equation. Falcon performs the process of moving from the lower field to the upper field using the field norm map. The process of generating a Falcon tree consists of preprocessing a polynomial f, g, F, and G into a suitable private key form. The sign process generates a signature over a message, and secret key id generated by keygen. First, the process computes a hash value c, where c in ${\mathbb{Z}}_q\left[X\right]/(X^n+1)$ using the message M and random value r where n is 256 and 512 for security level 1 and 5, respectively. Then, it computes the short vector that satisfies ${\mathbf{s}}_{\mathbf{1}}+{\mathbf{s}}_{\mathbf{2}}h\equiv c$ mod q using the private key $sk=f$, g, F, and G. To prevent secret information leakage, Falcon uses a trapdoor sampler (fast Fourier sampling, ffSampling) to generate ${\mathbf{s}}_{\mathbf{1}}$ and ${\mathbf{s}}_{\mathbf{2}}$ without revealing the secret key. The verify process ensures that the SVP challenge is met. This is simple to configure compared to other algorithms.

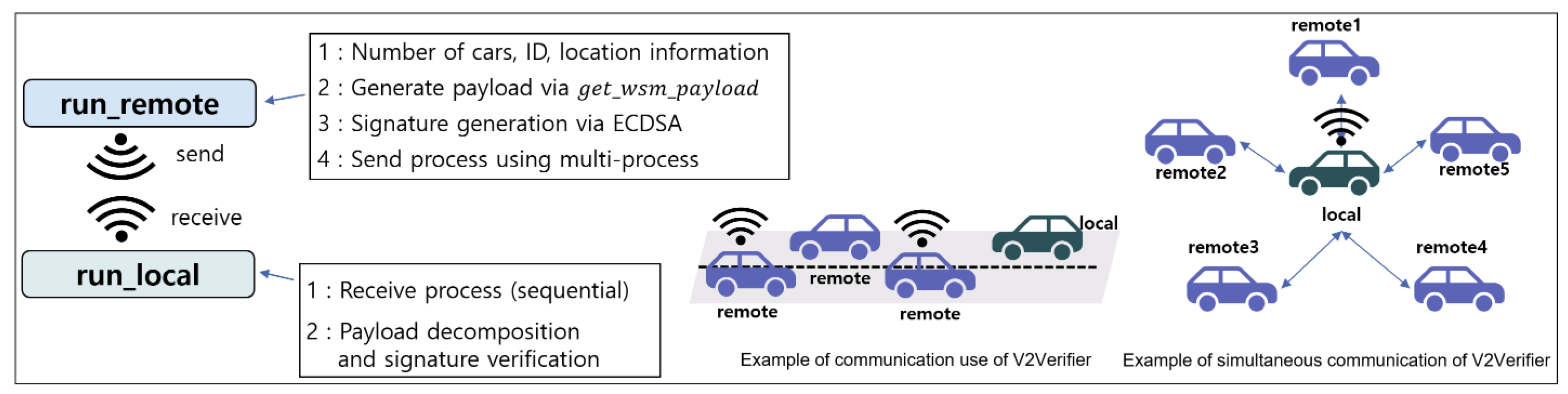
2.4. V2Verifier

V2Verifier is an open-source project dedicated to wireless experimentation focused on the security of V2V communications. The V2Verifier project features the first open-source implementation of the IEEE 1609.2 standard for V2V security [10]. V2Verifier uses a combination of software-defined radio such as Universal Software Radio Peripheral (USRP) and commercial V2V equipment to support extensive experimentation with V2V technology and security protocols.

Table 2. Attribute parameters required for V2X communication.

Type	WAVE (IEEE 802.11p)	C-V2X (3GPP Rel.14)	eC-V2X (3GPP Rel.15)	5G-V2X
Processing rate (Mbps)	3∼27	10∼100 (Maximum 1000)		Maximum 2000
BSM packet size	2000	400 (advanced: 12,000 )		Platooning: 6000 Advanced: 12,000 Autonomous: 41,700
Maximum communication radius	1 km	320 m	1 km	Platooning : 350 m Advanced : 700 m Autonomous : 1 km
End-to-end latency (ms)	100	100	100 (platooning: 10)	Platooning: 25 Advanced: 100 Autonomous: 5
Vehicle maximum relative speed (km/h)	200	280		500
Correctness		80∼95%	90∼100%	90∼100%

shows the attributes required for V2V communication, with the following being supported:

• Security features from the IEEE 1609.2 standard for V2V security, including message signing and verification and V2V certificates.
• Dedicated short-range communication (DSRC)—adapted from the WiME Project’s IEEE 802.11p transceiver
• Cellular vehicle-to-everything (C-V2X)—based on the srsRAN project (formerly srsLTE) (temporarily not supported).

V2Verifier is designed to run on software-defined radio (SDR). V2Verifier consists of communication between multiple wireless (hereafter: remote) vehicles and one receiving (hereafter: local) vehicle. To run the actual V2Verifier, one PC is responsible for transmitting multiple remote vehicles, and another PC is responsible for receiving local vehicles. Recently, researchers at the University of Waterloo, Canada, applied the NIST PQC signature round 3 candidates (Crystals-Dilithium, Falcon, Rainbow) to V2Verifier at the 2021 NIST PQC conference [7]. They presented an experiment to verify the feasibility of the PQC-DSA algorithm in a secure V2V communication (IEEE 1609.2) environment as a replacement for ECDSA, an existing elliptic curve-based digital signature. In terms of packet size and delay time, the applicability of the PQC-DSA electronic signature algorithm to an autonomous driving environment was analyzed. In addition, the test was designed considering various environments, such as the general autonomous driving environment and the platooning driving stage. According to the result of [7], the minimum signature size of Crystals-Dilithium is about 2500 bytes based on security level 2, which exceeds WAVE’s packet size of 2000 bytes; therefore, verification fails during actual communication. Falcon has a maximum signature size of about 1330 bytes, so it meets WAVE’s requirements. For signature generation, Crystals-Dilithium achieved a better performance than did ECDSA, while Falcon achieved a worse performance than did ECDSA. Both Crystals-Dilithium and Falcon outperformed ECDSA in signature verification.

In V2Verifier, one local car communicates with multiple remote cars. Figure 1 shows an example of the work structure for V2Verifier. The local car receives a payload containing the current position of the remote cars. For handling remote cars, V2Verifier generates multiple processes for the number of remote cars and broadcasts basic safety messages (BSMs) to the local car. The top-level API of V2Verifier for handling cars are “run_remote” for remote cars and “run_local” for local cars. V2Verifier uses the Python “yml” module to manage remote car algebra and location information. One can adjust the number of remote cars in action via the “NumberOfVehicles” variable in the “yml” dataset. This allows remote cars to generate a location-only payload and send it in broadcast format to the local car. At this time, broadcasts occur at 0.1 s intervals and can be controlled by the user. Figure 2 shows an overall structure of the “run_remote” (“run_local”) API and components of the payload of V2Verifier.

The detailed structure of “run_remote” and “run_local” API is as follows:

• run_remote
  “run_remote” API simultaneously generates as many payloads as the number of remote cars using a multiple processes and broadcasts the payloads to local car. Using “yml” module, 300 pieces of location information are sent in a text file unique to each remote car to the local car at 0.1 s intervals. Additionally, based on the time function of the “time” module, the payload generation time for 300 pieces of location information is measured. In this process, each specific payload of remote cars is generated by calling the internal “Get_wsm_payload” API. The payload has three components, Bytestring (communication flag), Wsm header (Wsm header), and IEEE 1609.data (IEEE standard protocol), and consists of a total of 16 pieces of information. It requires about 500 bytes, excluding signature length information and signature. Therefore, if the sum of the signature length information and the signature of PQC-DSA is less than 1500 bytes, then the WAVE protocol requirement of less than 2000 bytes is satisfied, and it is applicable to the WAVE protocol. This process maintains the IDs and locations of n cars in context. The payload generation process includes a signature to the current location. Moreover, when the payload is generated, it uses multiprocessing to send the payload to “run_local” API. The initial communication of between remote cars and local car involves the process of generating a key used for signing.
• run_local
  Local car receives a payload containing the current position of remote cars. “run_local” API is always active in receive standby mode. It then goes through a signature verification process and deconstructs the payload when the verification is successful. If the signature verification succeeds, API disassembles payload, and the local car obtains the location information. If the signature verification fails, one waits for the next payload reception.

3. Proposed Simulation

3.1. Selection of Crypto Codes

The purpose of this study is to apply PQC-DSA to V2Verifier and, at the same time, satisfy the correctness of the WAVE protocol, which was not achieved by Crystals-Dilithium in a previous study [7]. The target PQC-DSAs in this study were initially Crystals-Dilithium, Falcon, and SPHINCS+, as these are the target algorithms chosen by the NIST for standardization after [5] was published. However, the signature size of SPHINCS+ [11] is in the order of tens of kilobytes, which is not suitable for simulation considering the latency of the specification of V2V protocol and the capacity of SRAM in embedded devices used as the OBU. Therefore, we chose the Crystals-Dilithium and Falcon as the target algorithms. We investigated state-of-the-art optimization implementations in OBUs, which are widely used in autonomous driving environments. Among various optimization studies, we selected Crystals-Dilithium [2] and Falcon [12] implementations performed on the ARMv8-based OBU.

3.2. Proposed Split Signature Transmission

In this section, we discuss a methodology to apply PQC-DSA that has large signature sizes such as that of Crystals-Dilithium in V2V protocols. After this, we apply our methodology with V2Verifier, which can simulate the WAVE protocol. We do not consider changing any component of the payload, as the payload must maintain the IEEE 1609 standard. In the case of Crystals-Dilithium, which requires the signature to be split and transmitted in WAVE protocol, it is necessary that the signature split with up to 4 payloads for transmitting. The headers of the second and lower payload are the same as those of the first payload except the signature; therefore, our goal is to allow the local car to correctly recover the split signature from the payloads and perform signature verification. The two methods proposed in this paper are as follows:

• Naive split way
  The first method involves a very simple means for dividing the signature, which is to keep the size of the signature less than 1400 bytes, excluding the header information or payload (approximately 500 bytes). Please note that maximum packet size of the WAVE protocol is 2000 bytes. For example, depending on the level of security of the Crystals-Dilithium, signatures can be split into 2, 3, and 4 blocks (the signature sizes of Crystals-Dilithium are 2420, 3293, and 4595 bytes for security level 2, 3, and 5, respectively). We add an an 8-bit order-bit to the MSB of the partitioned block. Signature verification of Crystals-Dilithium adds a block alignment process, but this is not expensive because in the sorting process, only 4 blocks are searched based on security level 5. “Simple split way” is very simple, but not very good in terms of efficiency. As the length of the signature increases, the number of order-bits required for sorting increases; therefore, if an algorithm with a very large signature size is proposed in the future, such as SPHINCS+, the amount of signature that can actually be transmitted will decrease, which is an inefficient method.
• Split way for Crystals-Dilithium
  We aim to analyze the structure of signature of Crystals-Dilithium and observe the signature length for each security level. Algorithm 1 shows the pseudocode of the overall structure of “Split way for Crystals-Dilithium”. As analyzed in Section 2.1, the signature consists of $\mathbf{z}$, h, and c. Since the combined sizes of c and h are less than 120 bytes, they can be composed of one block. In addition, since 2 × 640 bytes can be additionally assigned to its block, the first block can be composed of c, h, and two packed polynomials of $\mathbf{z}$. From the second block, we continue to construct two packed polynomials of $\mathbf{z}$. Based on security level 5, if we assign 1 bit to determine the first block and 2 bits to determine the order of each block, the order-bit, which is in the MSB of the block, can be composed of a total of 3 bits. Compared to the above “Simple split way” method, the number of blocks is not changed. However, this method has advantages in the long run. In V2Verifier, the local car receives multiple signature blocks in random order. At this time, the local car checks for the existence of the first block through MSB 1-bit, and if the first block c and h are divided, hint information is collected using h data. After this, the unpacking process is performed on the two packed polynomials of $\mathbf{z}$ in the first block. If the received signature block is not the first block, the unpacking process can be started immediately because there are only two polynomials in the second and lower block. In the “Simple split way” approach, one can wait for the receipt of all signature blocks and start the verification process of Crystals-Dilithium after sorting the blocks. However, our method can start the signature verification process before all the blocks arrive. Since the process of checking the order-bit is the same as that in “Simple split way”, additional costs are not incurred and performance can be expected to increase. Therefore, our method is effective when a parallel process is introduced in the local car API or when the length of the signature is increased in the future with the rise of the security level.

3.3. Application Plan for V2Verifier

The structure of V2Verifier simulates a situation where one local car sends and receives communication with n remote cars. In this study, we proceeded with the simulation using the same structure. Unfortunately, there were equipment limitations, and we were not able to use the original V2Verifier test equipment, the HW USRP (Universal Software Radio Peripheral). Therefore, we modified the code to simulate on one PC and configured remote cars through multiprocessing. V2Verifier is a Python-based code, and the codes suggested in [12,13] are C code mixed with hand-written assembly. To apply this to Python language, we recompiled the code to gcc and built it in the form of a dynamic library. First, we generated a payload using the coordinate information used in the V2Verifier source code (choosing the number of coordinates variably). We considered and generated packets according to the signature size and WAVE protocol requirements. For example, the minimum signature size for Crystals-Dilithium is approximately 2500 bytes (security level 2), which exceeds the WAVE protocol requirement of 2000 bytes. Therefore, it is difficult to satisfy correctness when using Crystals-Dilithium in WAVE. To solve this, we used our “Split way for Crystals-Dilithium”. For Falcon, the maximum signature size is about 1330 bytes (Falcon-1024), and the total payload length (1330 + 500) meets WAVE’s requirements.

The generating payload, generating key pair, and signing payload processes are performed with the “run_remote” API, and the verifying signature and decomposing payload processes are performed with the “run_local” API. The steps for simulation are as follows:

• Generating the payload
  V2Verifier generates the payload in V2Verifier using “Get_wsm_payload” API. The payload consists of three components (Bytestring, Wsm-header, and IEE 1609.data) and a total of 16 pieces of information. The payload requires approximately 500 bytes, excluding signature length information and the signature.
• Generating key pair and signing the payload
  Generating the key pair process for generating the public and private keys for PQC-DSA is completed in the first session for local and remote cars. It does not work on session reconnect. Signing payload process generates a signature for the current location of the remote car. For satisfying the correctness of the verification of Crystals-Dilithium on V2Verifier, we used the “Split way for Crystals-Dilithium” for this process.
• Verifying the signature and decomposing the payload
  In the verifying signature process, only the signature block is extracted from the received payloads to verify the signature. In the case of Crystals-Dilithium, the process of checking or sorting the order of blocks is added. The decomposing payload process splits the payload, where the signature is validated in the verifying signature process. In “Split way for Crystals-Dilithium”, only the first received payload is split.

The simulation proceeds without using the USRP, as mentioned in the previous paragraph. Therefore, protocol simulations are all the same except for the transport layer. Remote cars send payloads to the local car in parallel. The local car performs signature verification on the received payload. The transmission/reception part of remotes car and local car advances the simulation with file input/output. The C-V2X protocol and the WAVE protocol payload are set in the same way, and payloads exceeding 2000 bytes are divided in order with the WAVE protocol. However, when the local car receives the split payload, it changes the simulation to randomly receive it. When the “Split way for Crystals-Dilithium” is applied, additional work proposed by Algorithm 3 is performed before payload transmission. Figure 3 shows the process in which the local car receives the signed bsm in parallel and performs dilithium verification.

Algorithm 3 Split Way for Crystals-Dilithium

Input: Param:       - Basic-Safety Message: bsm,       - public key: pk,       - secret key: sk,       - signature: $z\left[k\right]$, h, and c (k has a value of 4, 6, or 8 depending on the security level, respectively.),       - payload: payload[k/2], - verification flag: flag,        Func:       - unpack API of Dilithium: Dilithium.Verify.unpack_sig,       - align split signature: Align_sig   1:  [run_remote] API   2:  … (Generate bsm)   3:  $\mathbf{z}$, h, and $c\leftarrow$Dilithium.Sign($pk$, $bsm$)   4:  for $i=0$ to $k/2$ do   5:      if i = 0 then   6:          $payload\left[0\right]\leftarrow \left(bsm\right|\left|0b100\right|\left|c\right|\left|h\right|\left|\mathbf{z}\right[0\left]\right|\left|\mathbf{z}\right[1\left]\right)$   7:      else   8:          $payload\left[i\right]\leftarrow \left(bsm\right|\left|i\right|\left|\mathbf{z}\right[2i\left]\right|\left|\mathbf{z}\right[2i+1\left]\right)$   9:      end if 10:      Sending $payload\left[i\right]$ to "local car" 11:  end for 12:  … 13:  [run_local] API 14:  for $j=0$ to $k/2$ do 15:      if there is no received payload then 16:         return                                             // waiting payload of next remote car 17:      end if 18:      Receiving payload[j] from "remote car"                              // random order 19:      $\left(bsm\right|\left|order\right|\left|sig\right[j\left]\right)\leftarrow payload\left[j\right]$ 20:      if order < 4 then 21:          $unpacked\_sig\left[j\right]\leftarrow$ Dilithium.Verify.unpack_sig_for_z(sig[j]) 22:      else 23:          $unpacked\_sig\left[j\right]\leftarrow$ Dilithium.Verify.unpack_sig_for_zch(sig[j]) 24:      end if 25:  end for 26:  $merged\_unpack\_sig$$\leftarrow Align\_sig(unpacked\_sig)$ 27:  $flag\leftarrow$Dilithium.Verify($merged\_unpack\_sig$)          // Verify API without unpack process 28:  if $flag$ == SUCCESS then 29:      Decomposing $bsm$ 30:  else 31:      return                             // waiting payload of next remote car 32:  end if 33:  …

4. Experiments

We used an NVIDIA Jetson AGX Xavier as our target OBU which contains a 64-bit ARM A5x processor with 32 GB of RAM, 32 GB of storage, and a 512-Core Volta GPU with 64 Tensor Cores (8 SM, 64 kB register, 128 kB shared memory). All PQC-DSA code for our simulation wa compiled with gcc with -shared, -O3 options and integrated into V2Verifier in the form of a dynamic library. The benchmark used exactly the method described in the simulation process and performed two tests. The first was when the remote and local cars made up the first session, and the second simulation was when the remote and local cars communicated in successive sessions. Each API was calculated with 300 average values. Dummy operations were inserted in between to avoid using cache memory, and this process was excluded when performance was measured. The “run_remote” APIs were configured in multiprocessing. The operating environment was the 4.4.0-59-generic kernel version Linux. In the advanced mode of the C-V2X protocol, we did not consider our method of splitting and merging packets because splitting does not occur during the transmission of packets. For the simulation of the WAVE protocol, we experimented with “Simple split way” and “Split way for Crystals-Dilithium”, respectively. However, as a result of the actual experiment, the execution time of the two methodologies was almost the same, so we mainly report the results of “Split way for Crystals-Dilithium”.

Table 3. Measurement including [generating key pair +“run_remote”+“run_local”] for 300 payloads (ms/300) on C-V2X (advanced) protocol.

Algorithm	Security	Ref	Correctness	This Work	Correctness
ECDSA (P-256)	1	3.9	✓	-	-
Crystals-Dilithium	2	2.2	✓	1.9	✓
	3	4.1	✓	2.4	✓
	5	4.7	✓	3.0	✓
Falcon	1	14.3	✓	12.7	✓
	5	38.9	✓	33.3	✓

and

Table 4. Measurements including [generating key pair +“run_remote”+“run_local”] for 300 payloads (ms/300) on the WAVE protocol.

Algorithm	Security	Ref	Correctness	This Work	Correctness
ECDSA (P-256)	1	3.9	✓	-	-
Crystals-Dilithium	2	2.8	✗	2.4	✓
	3	5.2	✗	3.6	✓
	5	6.1	✗	4.5	✓
Falcon	1	14.3	✓	12.7	✓
	5	38.9	✓	33.3	✓

show the measurements including [generating payload + generating key pair + generating Signature + verifying signature] for an average of 300 payloads on the WAVE and C-V2X protocols, respectively. In this scenario, when the remote and local cars first configure a session, “run_remote” API runs the key generation process of PQC-DSA. Unfortunately, there is no open-source code for [7], as far as we know. Therefore, we reconstructed the simulation proposed in [7].

Table 3 is a simulation assuming communication in the advanced mode of the C-V2X protocol. In C-V2X, the maximum BSM packet size is 12,000 bytes, making it easy to load the signatures of each PQC-DSA. Therefore, correctness can be satisfied in any case. Since we use an optimized PQC-DSA implementation, there is a performance improvement compared to the reference-based simulation.

Table 4 is a simulation assuming communication with the WAVE protocol. The signature of Crystals-Dilithium is split and transmitted due to the limitation of packet size. The splitting and combining packets processes occur in “run_remote” and “run_local” API, respectively. Therefore, even though we ran the same signature generation and verification process, a small amount of latency compared to the results of C-V2X simulation occurred. As in previous research, the reference-based results of Crystals-Dilithium did not achieve correctness in the WAVE protocol. However, in our simulation results with the “Split way for Crystals-Dilithium”, correctness was satisfied.

Table 5. Measurements result of the maximum termination delay time in “run_remote” and “run_local” marked by $\frac{run\_remote}{run\_local}$ (ms/300) on the WAVE protocol.

Algorithm	Security	Ref	This Work
ECDSA (P-256)	1	$\frac{1.9}{1.6}$	-
Crystals-Dilithium	2	$\frac{1.9}{0.5}$	$\frac{1.6}{0.4}$
	3	$\frac{3.6}{1.1}$	$\frac{2.5}{0.8}$
	5	$\frac{4.0}{1.4}$	$\frac{2.9}{1.0}$
Falcon	1	$\frac{1.2}{0.1}$	$\frac{1.1}{0.1}$
	5	$\frac{2.2}{0.2}$	$\frac{2.0}{0.1}$

shows the measurement result of maximum termination delay time in “run_remote” and “run_local” marked by ($\frac{run\_remote}{run\_local}$). This scenario assumes continuous communication between the remote car and the local car. The remote car already has the private key, and the local car knows the public key of the remote car. Similar to the result ub Table 4, our simulation achieves correctness for all PQC-DSAs. In addition, there is a performance improvement compared to the previous work due to the application of an optimized PQC-DSA.

5. Discussion

There are several main points of discussion in this section. The first is the need to apply an optimized PQC-DSA compared to the reference implementation. Based on a single packet, as shown in Table 3, the reference implementation already meets the run 5G-V2X requirement of less than 5 m/s latency. However, remote vehicles need to continuously transmit their location to nearby remote vehicles. Therefore, research should be advanced not only on the performance of a single “run_remote” but also on generating signatures concurrently using parallel implementations later. Simultaneous verification of signatures should also be considered for local vehicles. Therefore, parallel optimization implementation methodology for PQC should be considered in the future.

The second case concerns when the signature size exceeds the limitation of the maximum packet size, such as the case with Crystals-Dilithium in the WAVE protocol. If the actual transmission layer does not guarantee packet ordering reliability, such as TCP, then it may not arrive in the correct order at the receiver. Especially in the case of Crystals-Dilithium, the signature size is basically 2000 bytes or more, so it is always divided and sent to the WAVE environment. We applied “Split way for Crystals-Dilithium” which ensures correctness while meeting IEEE standards. Of course, since this is a temporary solution, agreement for signature generation and verification between sender and receiver is essential. In our study, for the WAVE protocol, regardless of the Crystals-Dilithium security level, 3 bits could represent the order of a signature block, but protocols more restrictive than WAVE protocol may require more order-bits to align the signature.

The final point of discussion is the choice of PQC-DSA in a V2V communication environment. The selected PQC-DSAs for standardization are Crystals-Dilithium, Falcon, and SPHINCS+. Among these, SPHINCS+ has an advantage derived from short key length, but as mentioned earlier, the signature size with a kilobyte unit is unfortunately not suitable for V2V environments where broadcasting-based communication is the primary focus. Therefore, for PQC migration on a V2V communication environment, Crystals-Dilithium and Falcon are more suitable. In this paper, we report simulation results for Crystals-Dilithium and Falcon via V2Verifier. Based on the results shown in Table 4 and Table 5, we believe that the most important consideration for PQC migration on V2V communication is communication continuity for each remote car. In the results of Table 4, Falcon looks very inefficient compared to Crystals-Dilithium because of the high latency. On the other hand, Table 5 shows the opposite result. Falcon has a high computational load for generating NTRU lattices and deriving a lattice-based problem; therefore, the reason for the performance decrease is mainly related to the key generation process. In other words, in an environment where the subject of communication frequently changes, Crystals-Dilithium, which has a performance balance for key generation, signature generation, and signature verification, appears efficient, and in a situation where communication is maintained for a long time, the initial key generation cost is high, but Falcon, with fast signature generation and verification, looks efficient. The V2V communication environment is ultimately aimed at an environment where autonomous vehicles communicate. In an autonomous environment, the local car moves in real time, so information about the surrounding remote cars can be updated every moment. This means that the number of messages the local car receives from the BSM from one remote car is variable, which can be low or high. In a high of a high number, the local and remote cars have the same destination. Although the initial key generation cost is high, it is most desirable to use Falcon, which is most efficient for continuous broadcast situations. Of course, statistically, an investigation of the average of session hold time between one local car and a remote car should be preceded. For the simulation of Crystals-Dilithium in the reference code-based previous research, it was difficult to achieve the recommended latency limit of 5 m/s in an autonomous driving environment. In this study, we used the optimized PQC-DSA code to achieve a latency below 5 m/s at all security levels of Crystals-Dilithium and to further satisfy correctness for the WAVE protocol. Therefore, we believe that Crystals-Dilithium can also be used efficiently in a V2V communication environment.

6. Conclusions

In this study, we used V2verifier to simulate PQC migration for a V2V communication environment in the on-board unit. We analyzed the simulation method for testing with V2verifier and carefully examined the performance of V2verifier using an optimized PQC-DSA. In this work, the optimized PQC-DSA achieved 5 m/s, which is recommended in an autonomous driving environment. Finally, we proposed a “Split way for Crystals-Dilithium” to achieve correctness of the WAVE protocol with a limitation of maximum packet size. In addition, we summarized the discussions on the proposed method and analyzed the application level of the V2V communication environment.