Research on Magnetohydrodynamic Angular Rate Sensor Denoising for a Space Laser Stabilization Control System
Abstract
1. Introduction
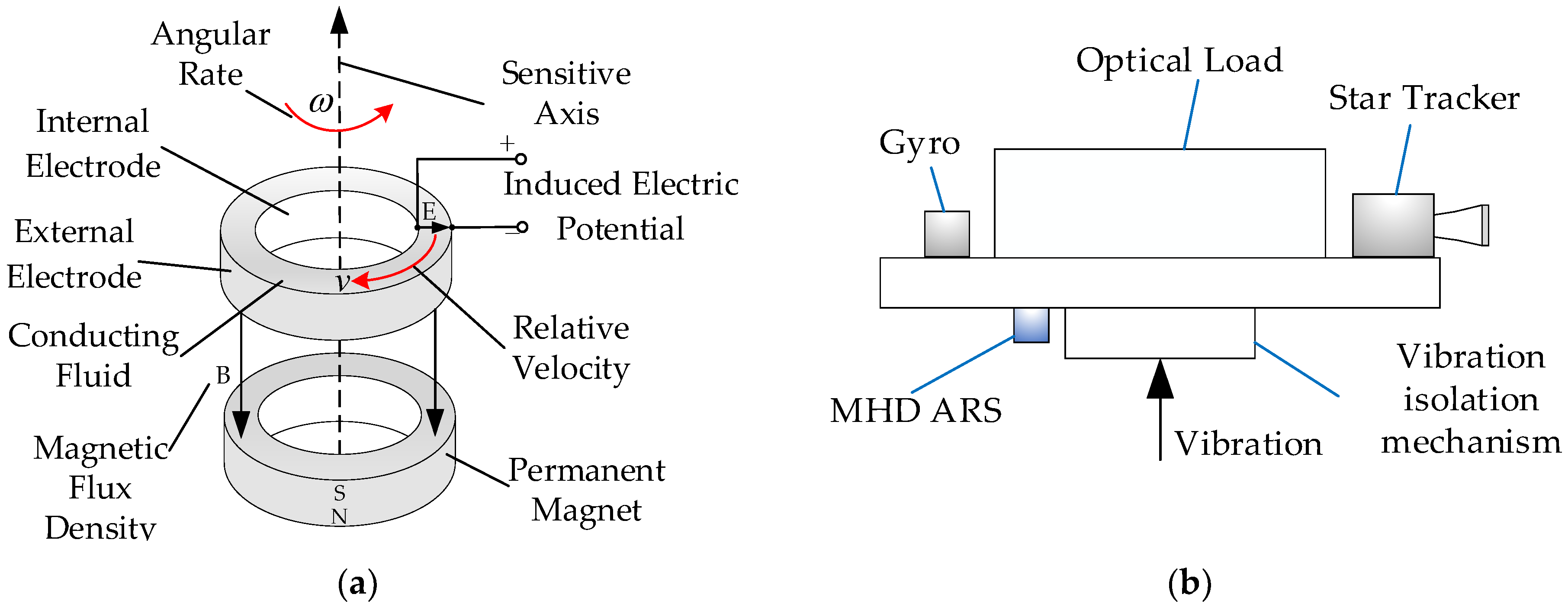
2. Measurement Principle of MHD ARS
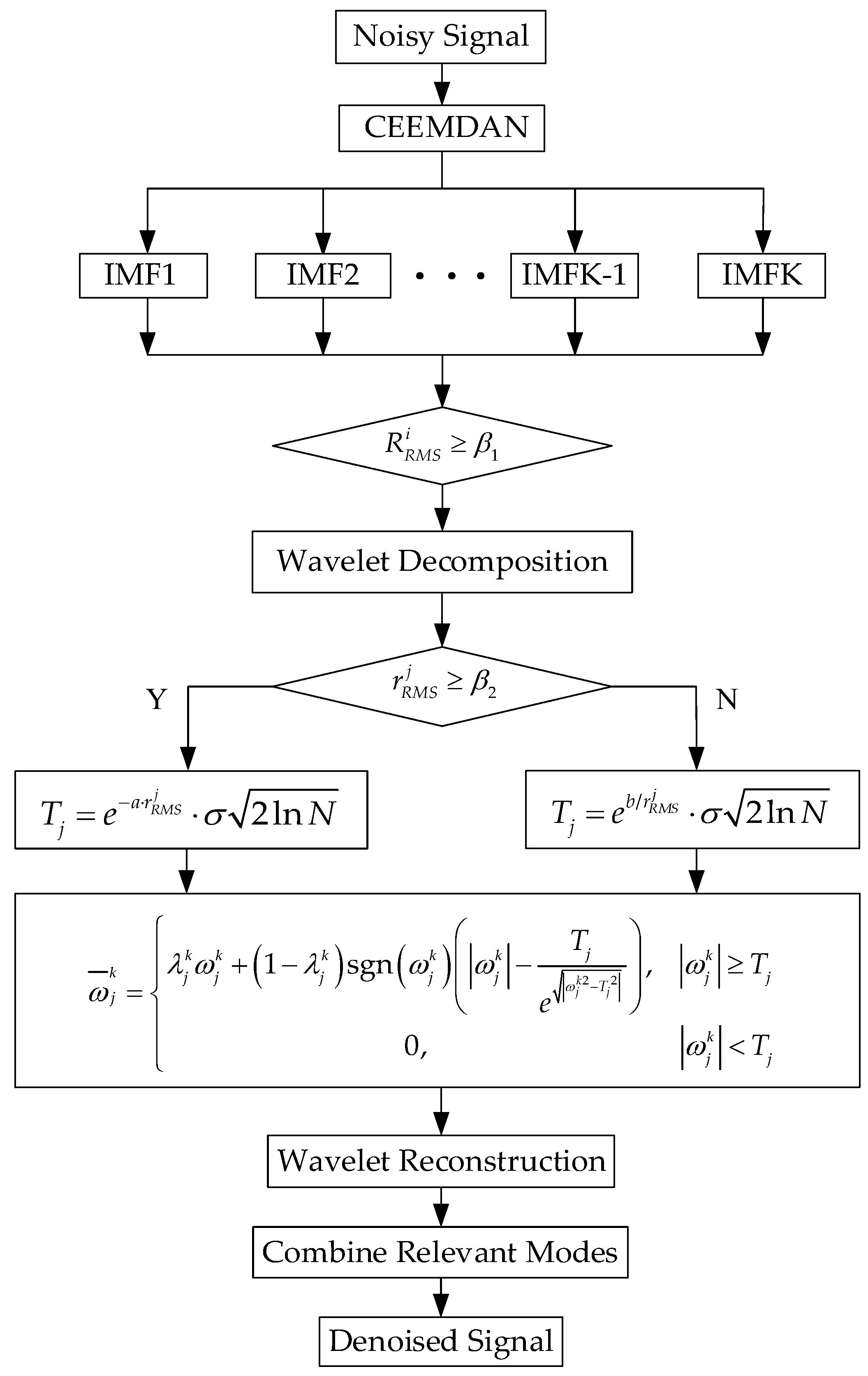
3. Improved Algorithm
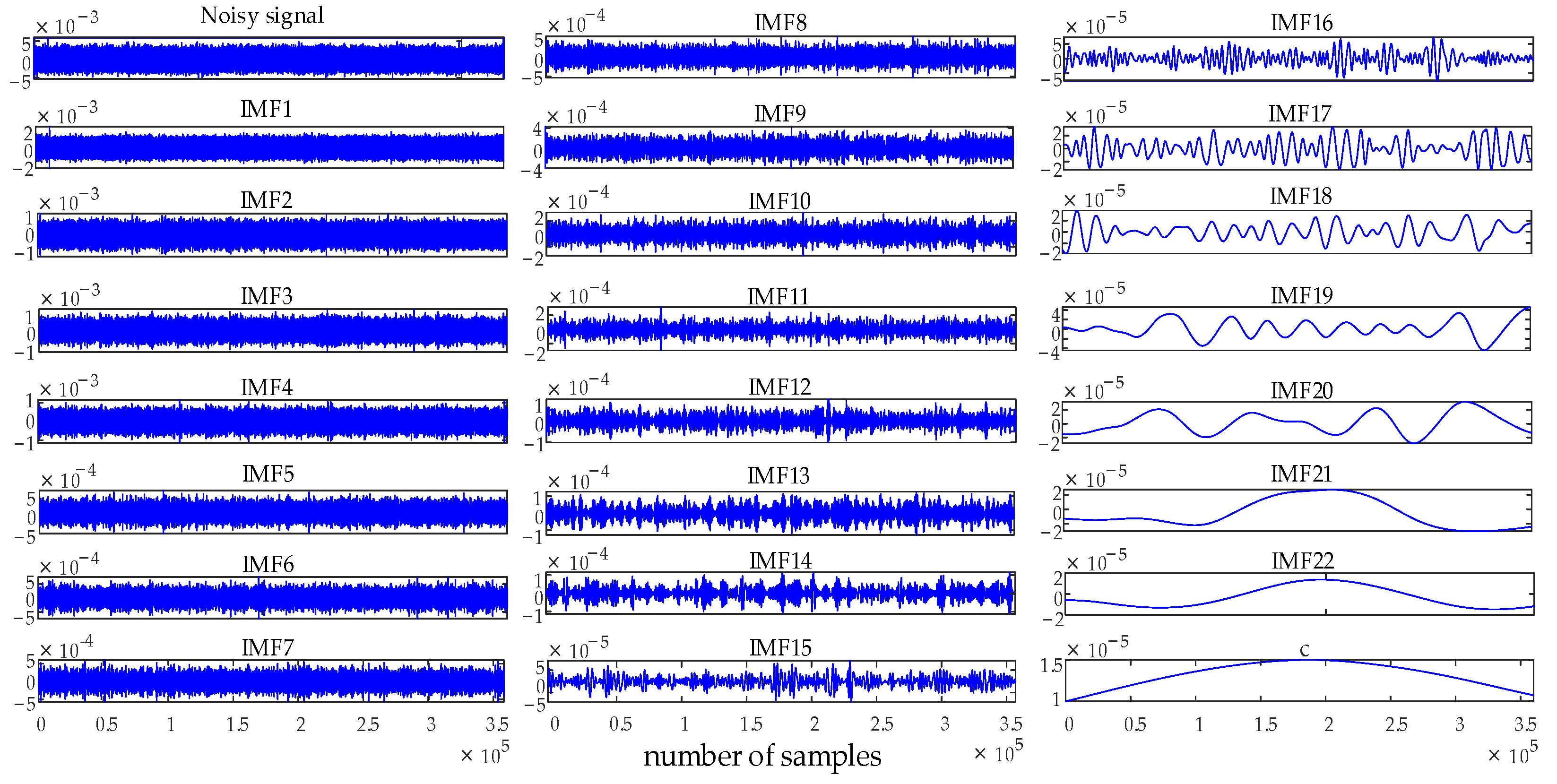
3.1. Determining Relevant Modes Based on Autocorrelation
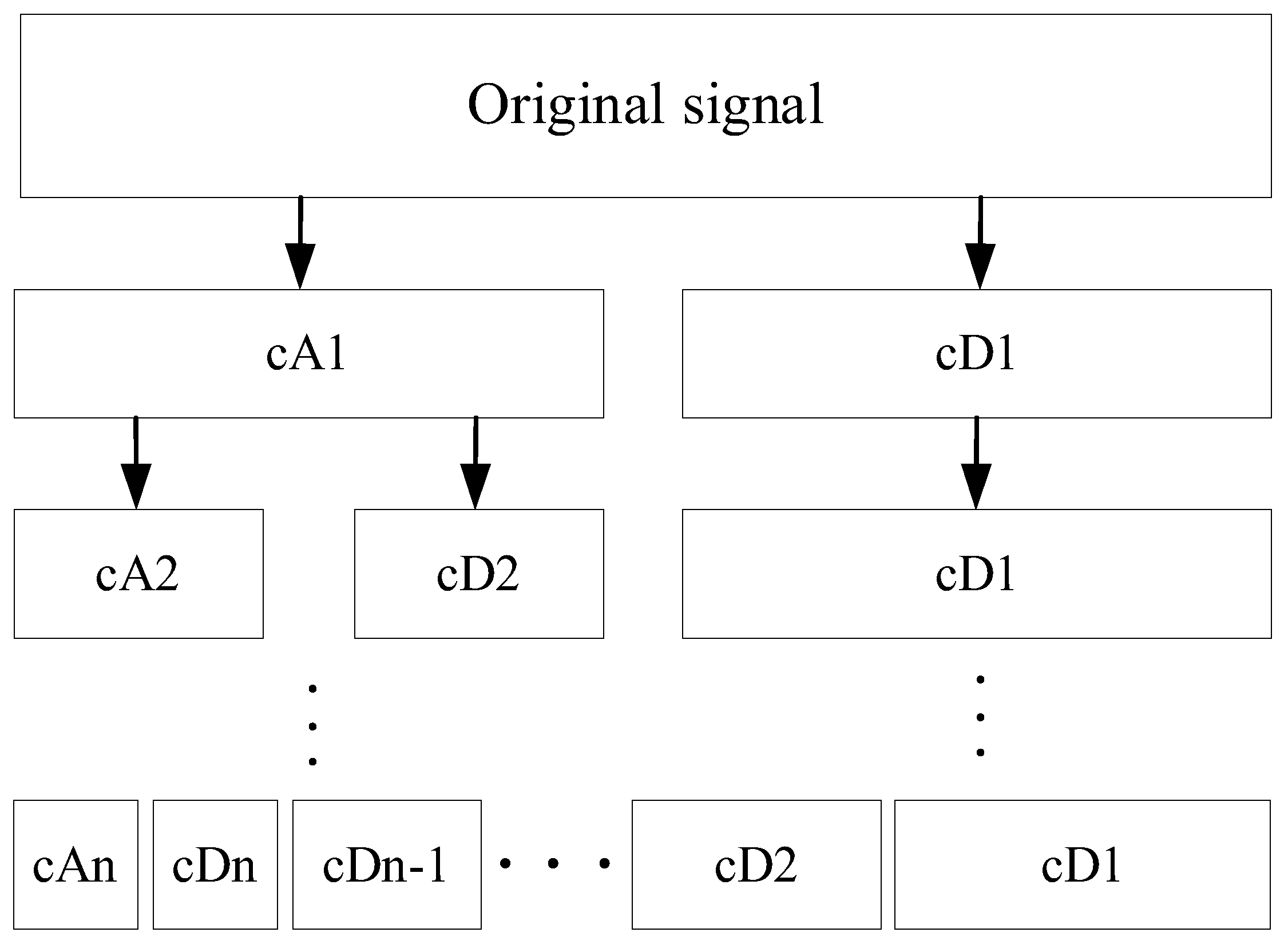
3.2. Improved Wavelet Threshold Based on Autocorrelation
3.3. Improved Thresholding Function
3.3.1. Continuity Analysis
3.3.2. Deviation Analysis
4. Experimental Platform and Result Analysis
4.1. Static Test Analysis
4.2. Dynamic Test Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Roumelas, G.D.; Nistazakis, H.E.; Leitgeb, E.; Stassinakis, A.N.; Tombras, G.S. On the performance of optical wireless communication links impaired by time jitter, M-turbulence and pointing errors. Opt. Commun. 2020, 472, 126033. [Google Scholar] [CrossRef]
- Danzmann, K.; Rüdiger, A. LISA technology—Concept, status, prospects. Class. Quantum Gravity 2003, 20, S1–S9. [Google Scholar] [CrossRef]
- Wang, X.; Su, X.Q.; Liu, G.Z.; Hang, J.F.; Wang, R. Investigation of high-precision algorithm for the spot position detection for four-quadrant detector. Optik 2020, 203, 163941. [Google Scholar]
- Jennrich, O. LISA technology and instrumentation. Class. Quantum Gravity 2009, 26, 15. [Google Scholar] [CrossRef]
- Xue, Y.Z.; Bo, Q.; Ge, R. Vibration-induced jitter control in satellite optical communication. In Proceedings of the International Symposium on Photoelectronic Detection and Imaging 2013: Laser Communication Technologies and Systems, Beijing, China, 21 August 2013. [Google Scholar]
- Skormin, V.A.; Tascillo, M.A.; Busch, T.E. Demonstration of a Jitter Rejection Technique for Free-Space Laser Communication. IEEE Trans. Aerosp. Electron. Syst. 1994, 2123, 568–576. [Google Scholar]
- Glaese, R.M.; Anderson, E.H.; Janzen, P.C. Active Suppression of Acoustically Induced Jitter for the Airborne Laser. In Proceedings of the Laser Weapons Technology, Orlando, FL, USA, 21 July 2000. [Google Scholar]
- Scozzafava, J.J.; Boroson, D.M.; Burnside, J.W.; Glynn, M.L.; DeVoe, C.E.; DeFranzo, C.M.; Doyle, K.B. Design of a very small inertially stabilized optical space terminal. In Proceedings of the Free-Space Laser Communications VII, San Diego, CA, USA, 27 September 2007. [Google Scholar]
- Ji, Y.; Li, X.F.; Wu, T.F.; Chen, C. Theoretical and experimental study of radial velocity generation for extending bandwidth of magnetohydrodynamic angular rate sensor at low frequency. Sensors 2015, 15, 31606–31619. [Google Scholar] [CrossRef]
- Anspach, J.E.; Sydney, P.F.; Hendry, G. Effects of Base Motion on Space-Based Precision Laser Tracking in the Relay Mirror Experiment. In Proceedings of the International Society for Optics and Photonics, Orlando, FL, USA, 1 August 1991. [Google Scholar]
- Iwata, T.; Hoshino, H.; Yoshizawa, T.; Kawahara, T. Precision attitude determination for the advanced land observing satellite (ALOS): Design, verification, and on-orbit calibration. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Hilton Head, SC, USA, 20 August 2007. [Google Scholar]
- Boroson, D.M.; Biswas, A.; Edwards, B.L. MLCD: Overview of NASA’s Mars laser communications demonstration system. In Proceedings of the Free-Space Laser Communication Technologies XVI, San Jose, CA, USA, 16 June 2004. [Google Scholar]
- Pinney, C.; Hawes, M.A.; Blackburn, J. A cost-effective inertial motion sensor for short-duration autonomous navigation. In Proceedings of the 2003 IEEE International Conference on Intelligent Transportation Systems, Las Vegas, NV, USA, 11–15 April 1994. [Google Scholar]
- Iwata, T.; Kawahara, T.; Muranaka, N.; Laughlin, D.R. High-bandwidth attitude determination using jitter measurements and optimal filtering. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009. [Google Scholar]
- Ji, Y.; Du, Y.; Yan, G.; Li, X.; Wu, J.; Tuo, W.; Li, J. Adaptive Kalman filter enhanced with spectrum analysis for wide-bandwidth angular velocity estimation fusion. IEEE Sens. J. 2020, 20, 11527–11536. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, M.L.; Qu, W.D.; Long, S.R.; Shen, S.S.P. Applications of Hilbert–Huang transform to non-stationary financial time series analysis. Appl. Stoch. Models Bus. Ind. 2003, 19, 245–268. [Google Scholar] [CrossRef]
- Gan, Y.; Sui, L.; Wu, J.; Wang, B.; Zhang, Q.; Xiao, G. An EMD threshold denoising method for inertial sensors. Measurement 2014, 49, 34–41. [Google Scholar] [CrossRef]
- Shen, C.; Li, J.; Zhang, X.; Shi, Y.; Tang, J.; Cao, H.; Liu, J. A noise reduction method for dual-mass micro-electro mechanical gyroscopes based on sample entropy empirical mode decomposition and time-frequency peak filtering. Sensors 2016, 16, 796. [Google Scholar] [CrossRef]
- Abdelkader, R.; Kaddour, A.; Bendiabdellah, A.; Derouiche, Z. Rolling bearing fault diagnosis based on an improved denoising method using the complete ensemble empirical mode decomposition and the optimized thresholding operation. IEEE Sens. J. 2018, 18, 7166–7172. [Google Scholar] [CrossRef]
- Omitaomu, O.A.; Protopopescu, V.A.; Ganguly, A.R. Empirical mode decomposition technique with conditional mutual information for denoising operational sensor data. IEEE Sens. J. 2011, 11, 2565–2575. [Google Scholar] [CrossRef]
- Tian, Z.W.; Jia, Y.F. A method for portable PPG signal dynamic acquisition and denoise based on CEEMDAN and wavelet transform. J. Instrum. 2023, 18, 01023. [Google Scholar] [CrossRef]
- Fang, J.W.; Ren, L.Y.; Tian, J.Y.; Li, G.S. CEEMDAN-Wavelet Threshold Denoising Method on sEMG. In Proceedings of the 2022 11th International Conference on Bioinformatics and Biomedical Science, Nanning, China, 28–30 October 2022. [Google Scholar]
- Onyejekwe, S.; Kang, X.; Ge, L. Evaluation of the scale of fluctuation of geotechnical parameters by autocorrelation function and semi-variogram function. Eng. Geol. 2016, 214, 43–49. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing, Prague, Czech Republic, 22–27 May 2011. [Google Scholar]
- Seyrek, P.; Şener, B.; Özbayoğlu, A.M.; Ünver, H.Ö. An evaluation study of EMD, EEMD, and VMD for chatter detection in milling. Procedia Comput. Sci. 2022, 200, 160–174. [Google Scholar] [CrossRef]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Jiang, J.; Guo, J.; Fan, W.H.; Chen, Q.W. An improved adaptive wavelet denoising method based on neighboring coefficients. In Proceedings of the 2010 8th World Congress on Intelligent Control and Automation, Jinan, China, 7–9 July 2010. [Google Scholar]
- Cai, Y.; Yu, C.M.; Ren, Y.; Wang, W.J.; Yin, Z.Y.; Xia, C.F. High precision attitude-rate measurement of magnetically suspended control and sensing gyroscope using variational mode decomposition and wavelet transform. IEEE Sens. J. 2022, 22, 1188–1198. [Google Scholar] [CrossRef]
- Donoho, D. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Jang, Y.I.; Sim, J.Y.; Yang, J.R.; Kwon, N.K. The optimal selection of mother wavelet function and decomposition level for denoising of DCG signal. Sensors 2021, 21, 1851. [Google Scholar] [CrossRef]
- Shi, Y.B.; Zhang, J.J.; Jiao, J.J.; Zhao, R.; Cao, H.L. Calibration analysis of high-G MEMS accelerometer sensor based on wavelet and wavelet packet denoising. Sensors 2021, 21, 1231. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.W.; Liang, Y.; He, P.; Yang, J.L. Adaptive motion artifact reduction based on empirical wavelet transform and wavelet thresholding for the non-contact ECG monitoring systems. Sensors 2019, 19, 2916. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.L.; Zhang, Z.; Zheng, Y.; Guo, H.; Zhao, R.; Shi, Y.; Chou, X. A new joint denoising algorithm for high-G calibration of MEMS accelerometer based on VMD-PE-wavelet threshold. Shock Vib. 2021, 2021, 1–16. [Google Scholar] [CrossRef]
- Yang, G.L.; Liu, Y.Y.; Li, M.; Song, S.G. AMA-and RWE-based adaptive Kalman filter for denoising fiber optic gyroscope drift signal. Sensors 2015, 15, 26940–26960. [Google Scholar] [CrossRef] [PubMed]
- Narasimhappa, M.; Sabat, S.L.; Nayak, J. Adaptive sampling strong tracking scaled unscented Kalman filter for denoising the fiber optic gyroscope drift signal. IET Sci. Meas. Technol. 2015, 9, 241–249. [Google Scholar] [CrossRef]
- Wittig, M.E.; Holtz, L.V.; Tunbridge, D.E.L.; Vermeulen, H.C. In-Orbit Measurements of Microaccelerations of ESA’s Communication Satellite OLYMPUS. In Proceedings of the Free-Space Laser Communication Technologies, Los Angeles, CA, USA, 1 July 1990. [Google Scholar]
- Sudey, J.J.; Schulman, J.R. In-orbit measurements of Landsat-4 thematic mapper dynamic disturbances. Acta Astronaut. 1985, 12, 485–503. [Google Scholar] [CrossRef]



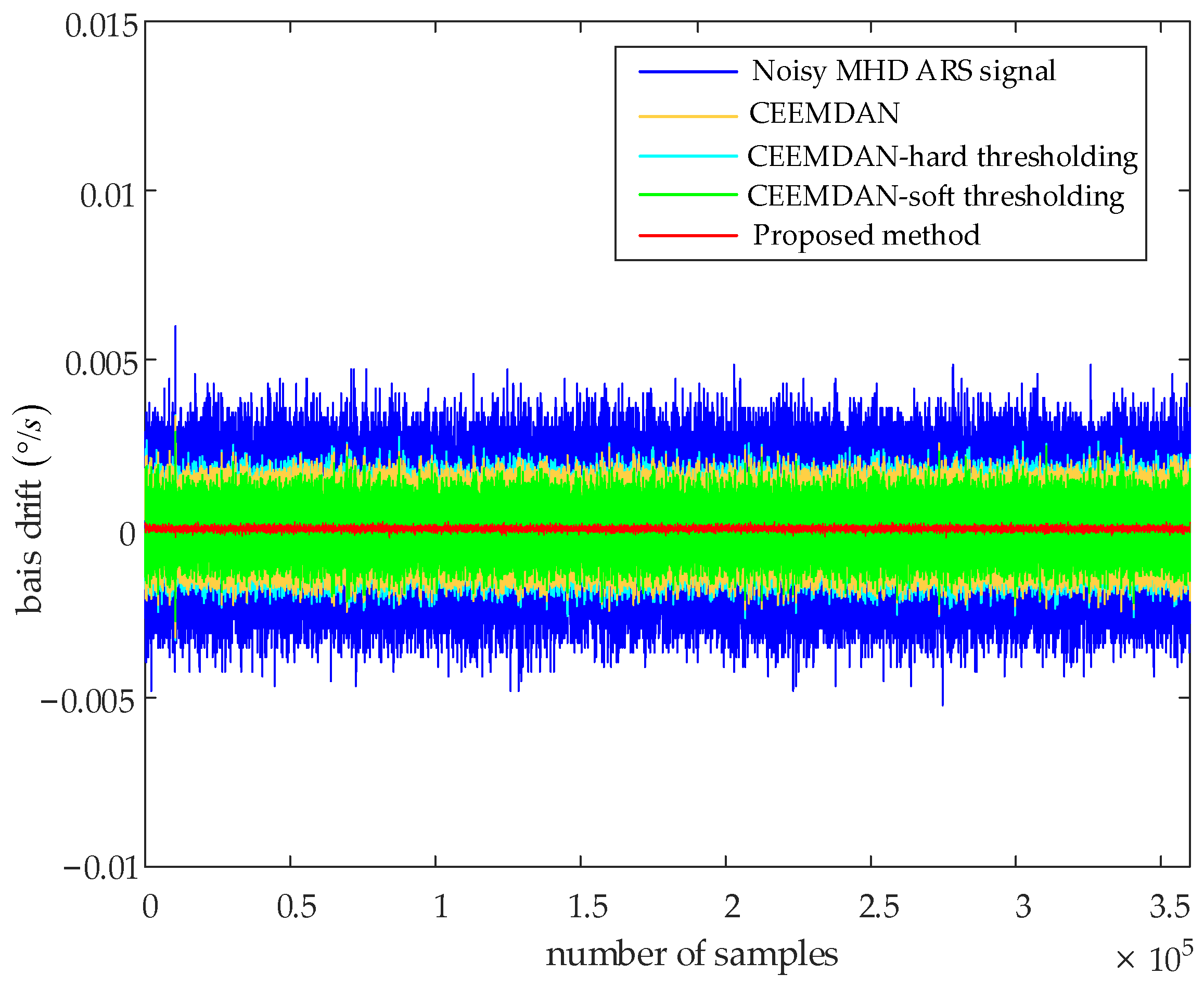
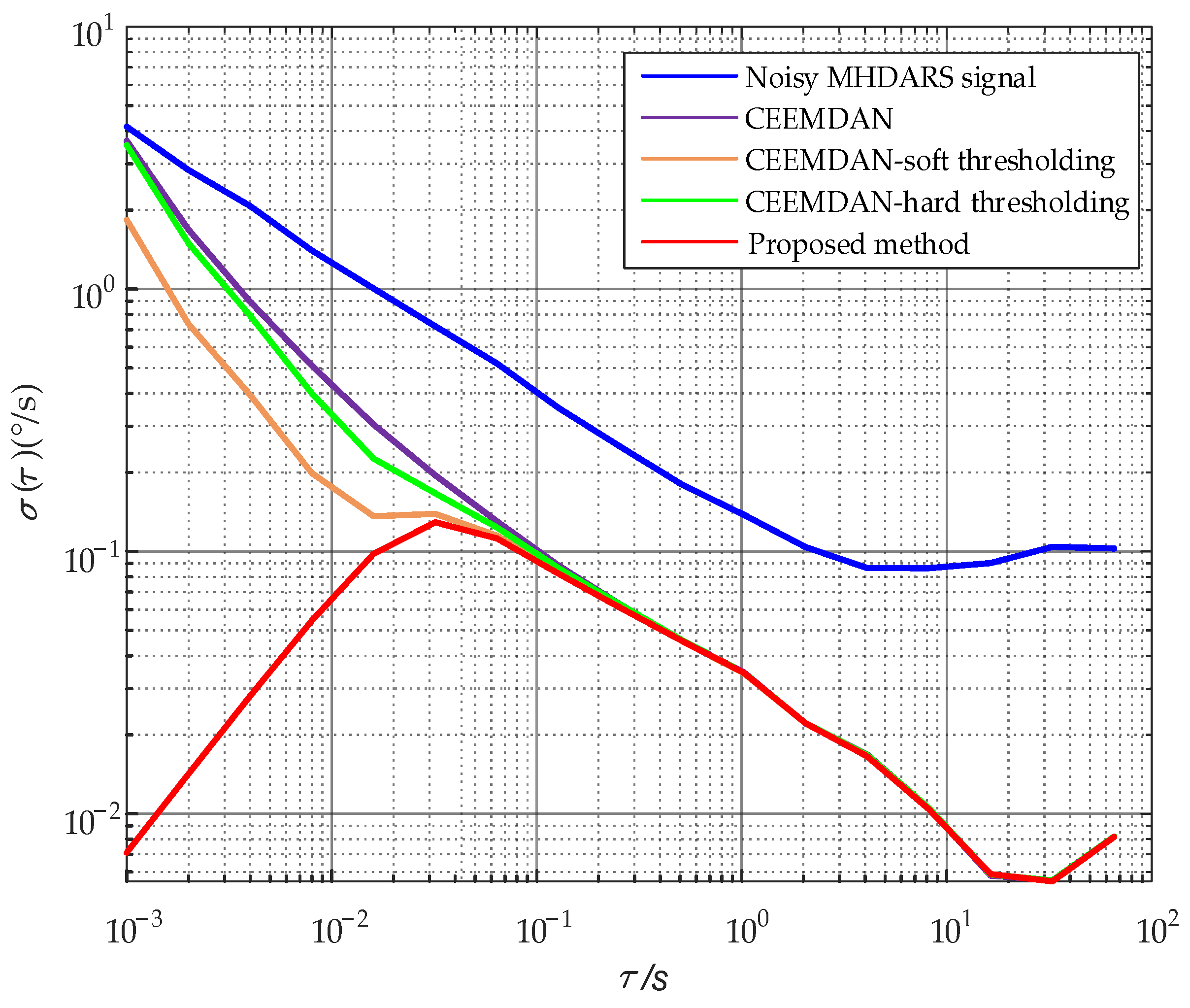
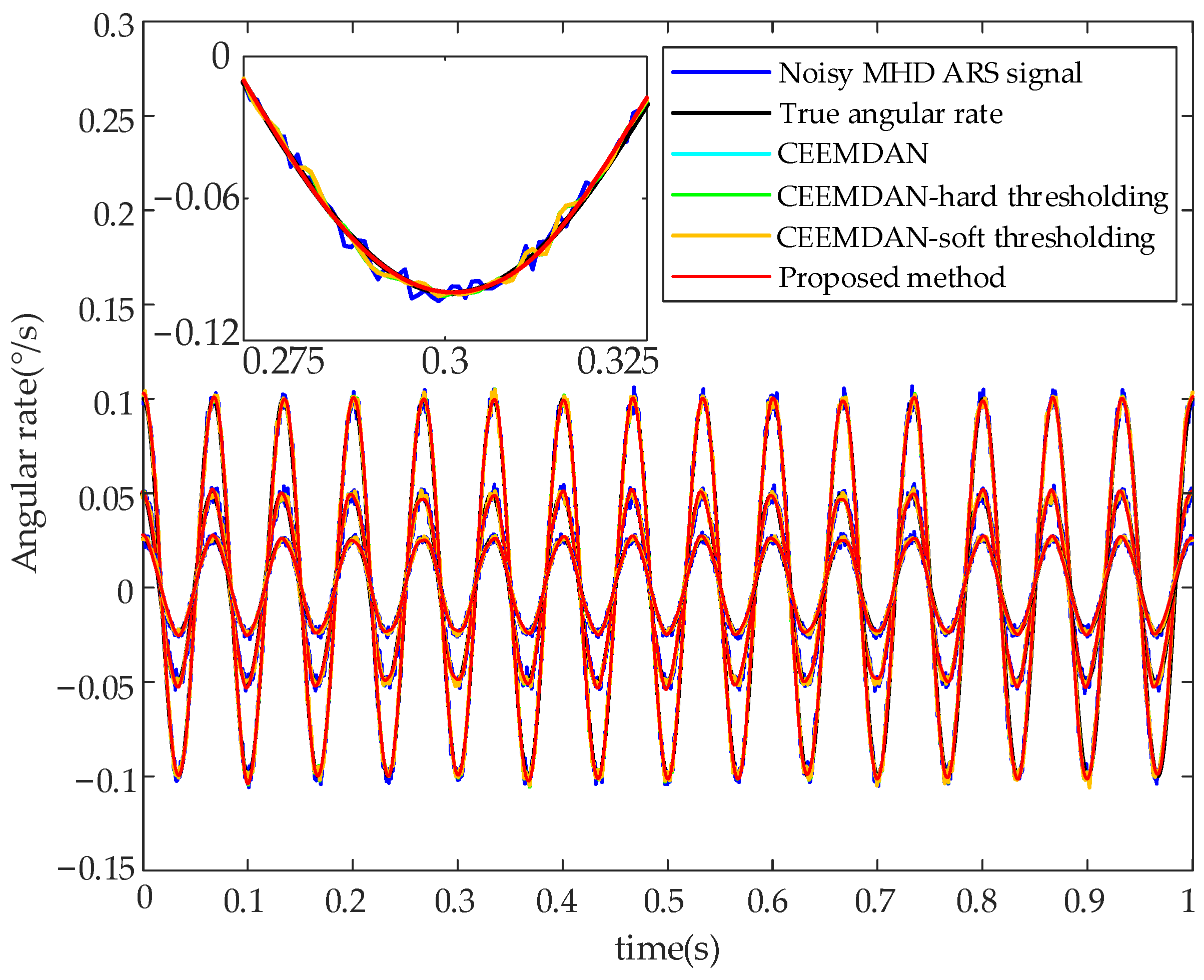
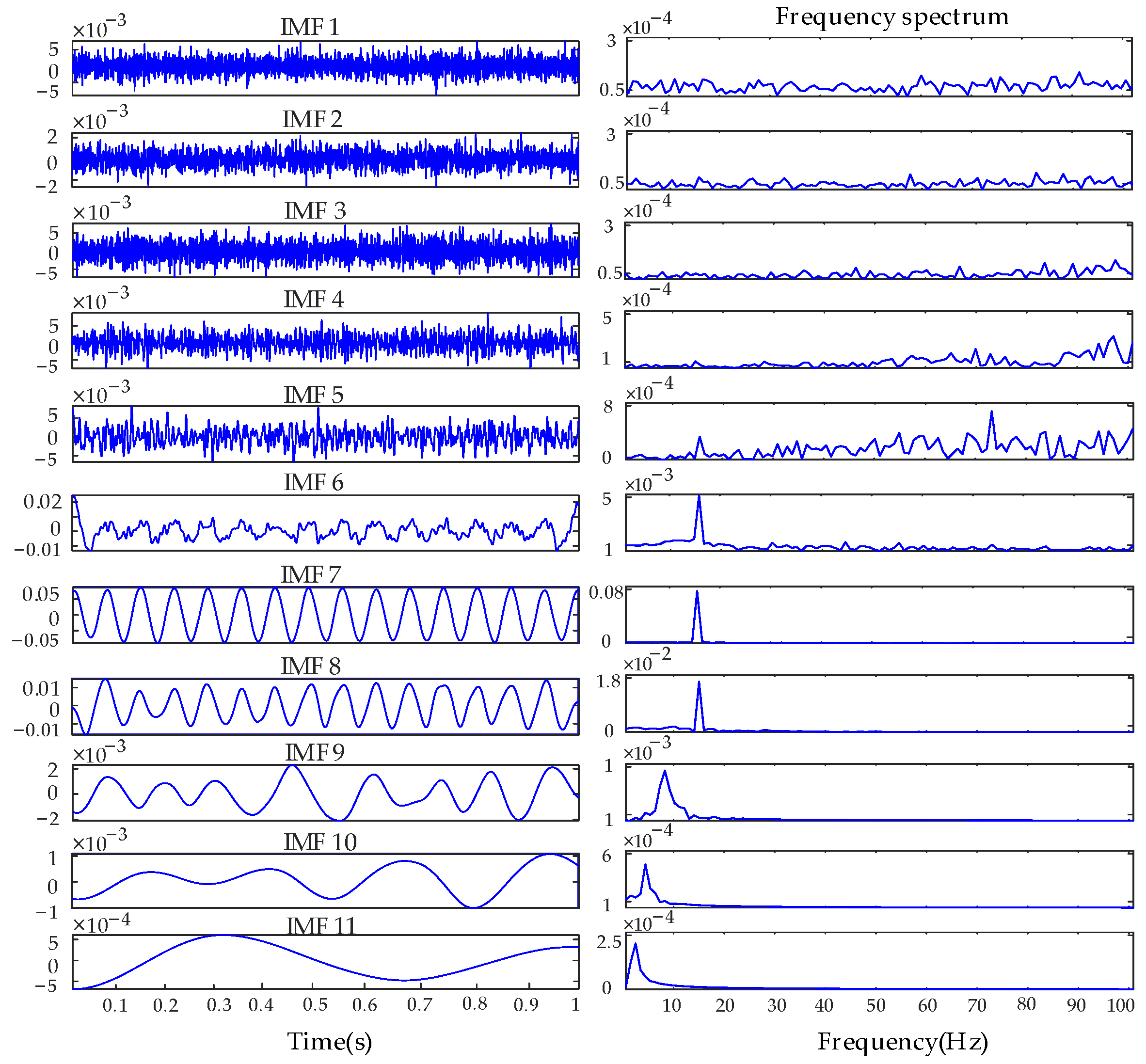
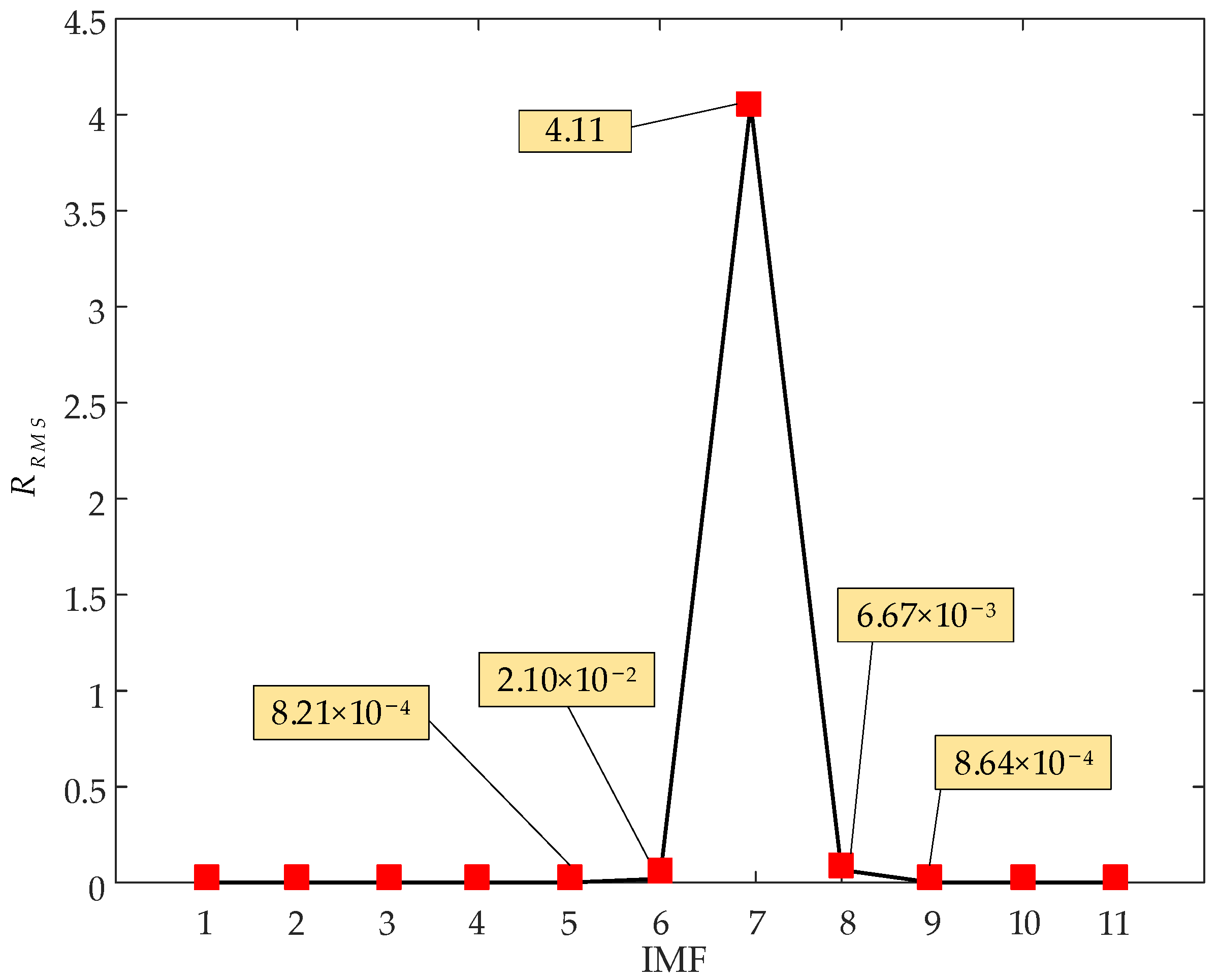

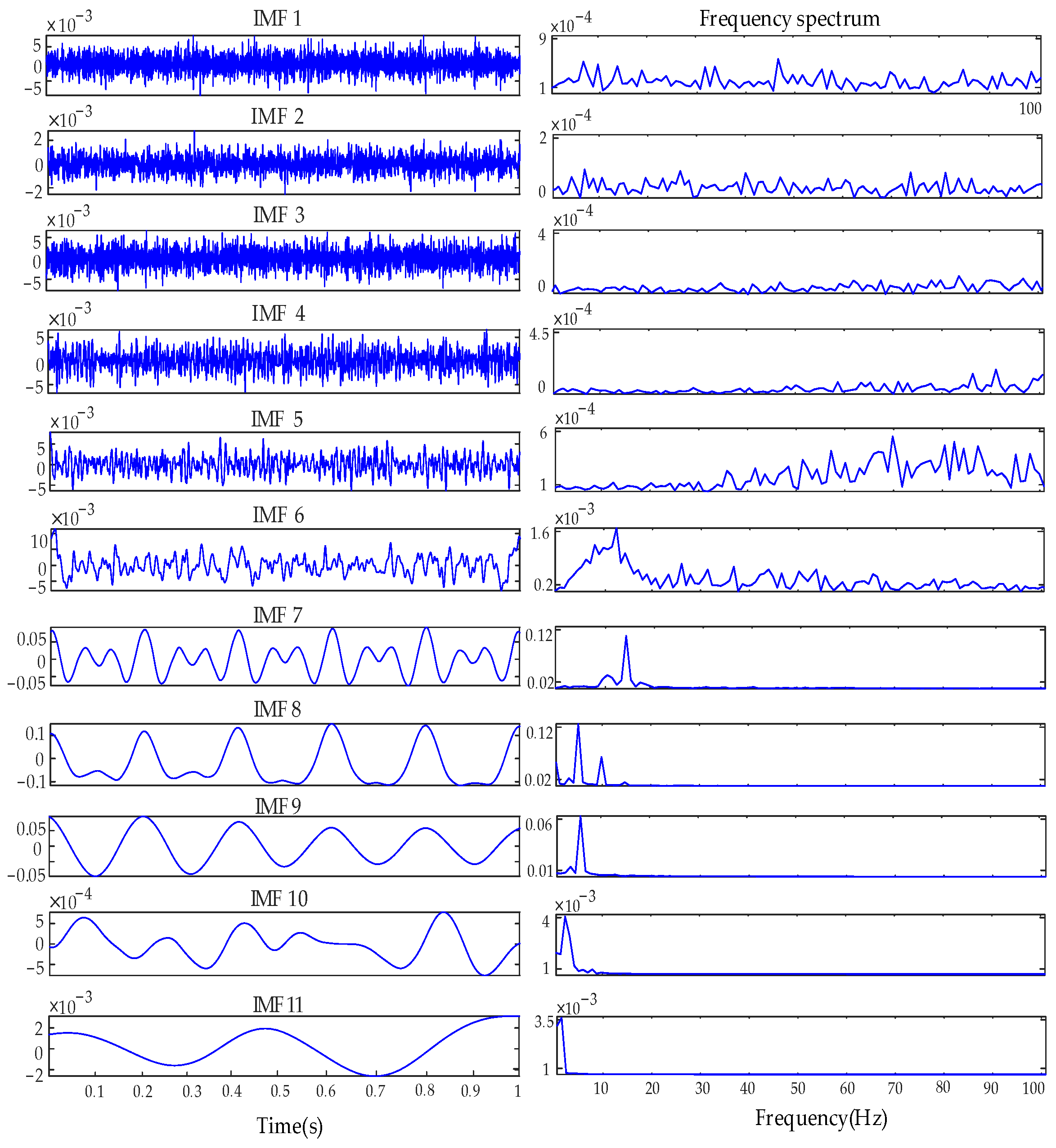
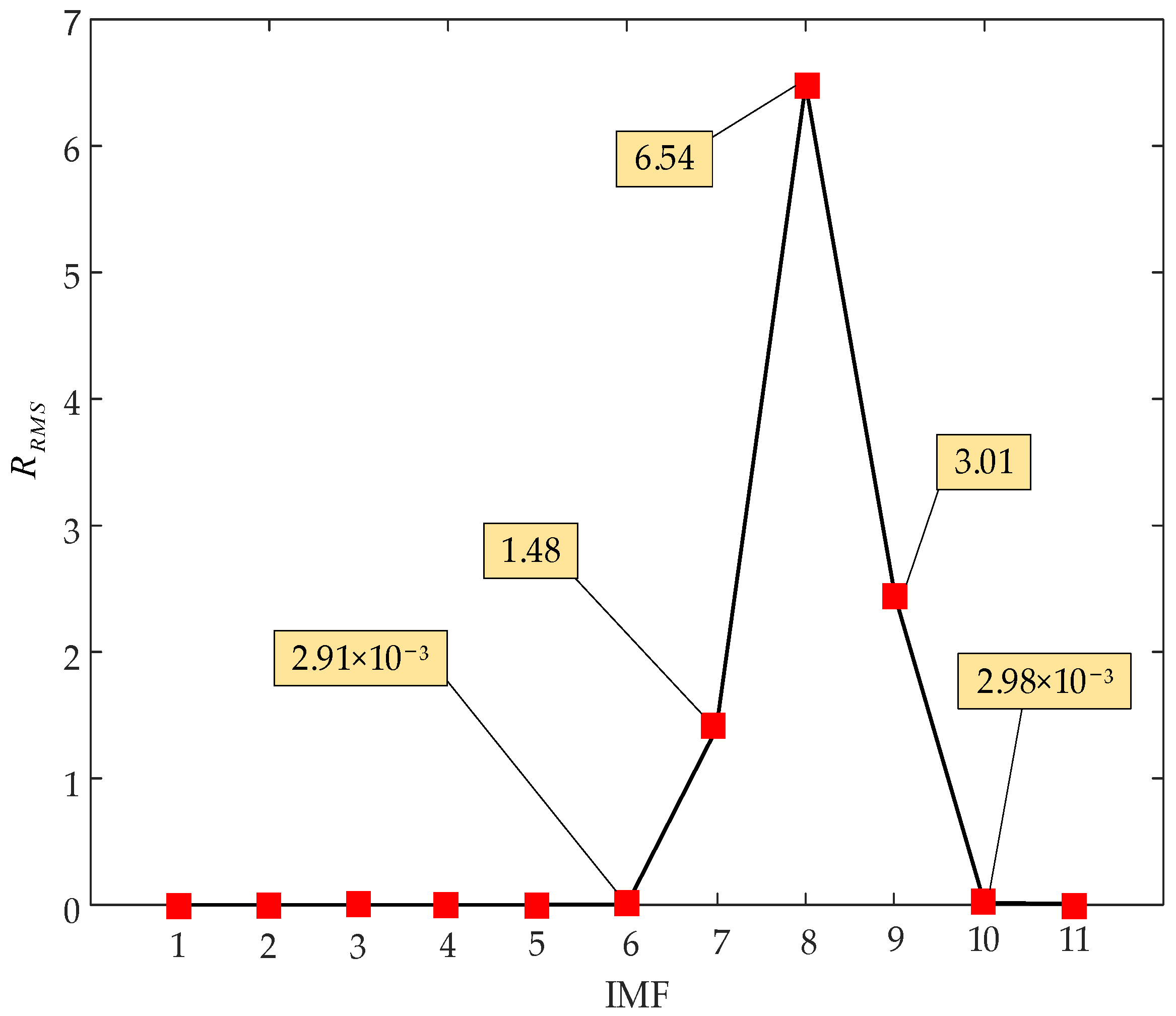
| Methods | Q (°) | B (°/h) | K (°/h3/2) | R (°/h2) | |
|---|---|---|---|---|---|
| Noisy MHD ARS signal | 7.171 × 10−4 | 2.088 × 10−3 | 0.205 | 3.151 | 18.056 |
| CEEMDAN | 2.225 × 10−3 | 6.289 × 10−4 | 0.337 | 6.539 | 36.058 |
| CEEMDAN-Soft Thresholding | 1.185 × 10−3 | 4.941 × 10−4 | 0.242 | 4.687 | 25.829 |
| CEEMDAN-Hard Thresholding | 2.230 × 10−3 | 8.403 × 10−4 | 0.386 | 7.474 | 41.206 |
| Proposed Method | 5.400 × 10−5 | 6.466 × 10−5 | 0.117 | 2.249 | 12.370 |
| Methods | Angular Rate (°/s) | RMSE | SNR (dB) | SNR Gain (%) |
|---|---|---|---|---|
| Noisy MHD ARS signal | 0.300 | 2.564 × 10−3 | 31.3682 | - |
| 0.200 | 2.424 × 10−3 | 28.3353 | - | |
| 0.100 | 1.452 × 10−3 | 26.8497 | - | |
| CEEMDAN | 0.300 | 2.454 × 10−3 | 31.7504 | 1.22 |
| 0.200 | 1.613 × 10−3 | 31.8698 | 12.47 | |
| 0.100 | 1.217 × 10−3 | 28.3814 | 5.70 | |
| CEEMDAN-Soft Thresholding | 0.300 | 2.453 × 10−3 | 31.7515 | 1.22 |
| 0.200 | 1.613 × 10−3 | 31.8705 | 12.48 | |
| 0.100 | 1.217 × 10−3 | 28.3872 | 5.72 | |
| CEEMDAN-Hard Thresholding | 0.300 | 2.382 × 10−3 | 32.0061 | 2.03 |
| 0.200 | 1.613 × 10−3 | 31.8703 | 12.48 | |
| 0.100 | 1.120 × 10−3 | 28.5281 | 6.25 | |
| Proposed Method | 0.300 | 2.005 × 10−3 | 33.5042 | 6.81 |
| 0.200 | 1.333 × 10−3 | 33.5232 | 18.31 | |
| 0.100 | 7.462 × 10−4 | 32.6329 | 21.54 |
| Methods | Angular Rate (°/s) | RMSE | SNR (dB) | SNR Gain (%) |
|---|---|---|---|---|
| Noisy MHD ARS signal | 0.150 | 1.638 × 10−3 | 29.2376 | - |
| 0.100 | 1.306 × 10−3 | 27.6868 | - | |
| 0.050 | 1.309 × 10−3 | 21.6461 | - | |
| CEEMDAN | 0.150 | 1.165 × 10−3 | 32.2010 | 10.14 |
| 0.100 | 9.543 × 10−4 | 30.2935 | 9.41 | |
| 0.050 | 9.012 × 10−4 | 24.8867 | 14.97 | |
| CEEMDAN-Soft Thresholding | 0.150 | 8.007 × 10−4 | 35.4563 | 21.27 |
| 0.100 | 7.434 × 10−4 | 30.3009 | 9.44 | |
| 0.050 | 7.697 × 10−4 | 26.2572 | 21.30 | |
| CEEMDAN-Hard Thresholding | 0.150 | 1.114 × 10−3 | 32.5879 | 11.46 |
| 0.100 | 9.264 × 10−4 | 30.6676 | 10.77 | |
| 0.050 | 8.911 × 10−4 | 24.9846 | 13.55 | |
| Proposed Method | 0.150 | 5.513 × 10−4 | 38.6975 | 23.36 |
| 0.100 | 5.820 × 10−4 | 34.7052 | 25.34 | |
| 0.050 | 5.992 × 10−4 | 28.4324 | 31.35 |
| Methods | Angular Rate (°/s) | RMSE | SNR (dB) | SNR Gain (%) |
|---|---|---|---|---|
| Noisy MHD ARS signal | 0.100 | 1.615 × 10−3 | 25.8416 | - |
| 0.050 | 1.717 × 10−3 | 19.2888 | - | |
| 0.025 | 1.165 × 10−3 | 16.6340 | - | |
| CEEMDAN | 0.100 | 1.419 × 10−3 | 26.9644 | 4.34 |
| 0.050 | 1.140 × 10−3 | 22.8417 | 18.42 | |
| 0.025 | 8.549 × 10−4 | 19.3249 | 15.64 | |
| CEEMDAN-Soft Thresholding | 0.100 | 1.294 × 10−3 | 27.7629 | 7.43 |
| 0.050 | 1.140 × 10−3 | 22.8421 | 18.42 | |
| 0.025 | 8.548 × 10−4 | 19.3252 | 16.18 | |
| CEEMDAN-Hard Thresholding | 0.100 | 1.405 × 10−3 | 27.0507 | 4.68 |
| 0.050 | 1.131 × 10−3 | 22.9154 | 18.80 | |
| 0.025 | 8.507 × 10−4 | 19.3676 | 16.43 | |
| Proposed Method | 0.100 | 1.198 × 10−3 | 28.4383 | 10.05 |
| 0.050 | 8.862 × 10−4 | 25.0325 | 29.78 | |
| 0.025 | 6.224 × 10−4 | 22.0809 | 32.75 |
| Methods | Angular Rate (°/s) | RMSE | SNR (dB) | SNR Gain (%) |
|---|---|---|---|---|
| Noisy MHD ARS signal | 0.180, 0.090, 0.054 | 1.912 × 10−3 | 30.7586 | - |
| 0.135, 0.072, 0.046 | 1.718 × 10−3 | 29.3816 | - | |
| 0.090, 0.054, 0.027 | 1.306 × 10−3 | 28.3960 | - | |
| CEEMDAN | 0.180, 0.090, 0.054 | 1.740 × 10−3 | 31.5782 | 2.66 |
| 0.135, 0.072, 0.046 | 1.457 × 10−3 | 30.8117 | 4.87 | |
| 0.090, 0.054, 0.027 | 1.009 × 10−3 | 30.6355 | 7.89 | |
| CEEMDAN-Soft Thresholding | 0.180, 0.090, 0.054 | 1.435 × 10−3 | 33.2485 | 8.09 |
| 0.135, 0.072, 0.046 | 1.211 × 10−3 | 32.4143 | 10.32 | |
| 0.090, 0.054, 0.027 | 8.126 × 10−4 | 32.5149 | 14.51 | |
| CEEMDAN-Hard Thresholding | 0.180, 0.090, 0.054 | 1.683 × 10−3 | 31.8686 | 3.61 |
| 0.135, 0.072, 0.046 | 1.418 × 10−3 | 31.0493 | 5.68 | |
| 0.090, 0.054, 0.027 | 9.795 × 10−4 | 30.8916 | 8.79 | |
| Proposed Method | 0.180, 0.090, 0.054 | 1.329 × 10−3 | 33.9170 | 10.27 |
| 0.135, 0.072, 0.046 | 1.091 × 10−3 | 33.3205 | 13.41 | |
| 0.090, 0.054, 0.027 | 7.618 × 10−4 | 33.0754 | 16.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.; Ma, C.; Han, J.; Wang, X.; Wang, Y.; Ji, Z. Research on Magnetohydrodynamic Angular Rate Sensor Denoising for a Space Laser Stabilization Control System. Appl. Sci. 2023, 13, 5895. https://doi.org/10.3390/app13105895
Su Y, Ma C, Han J, Wang X, Wang Y, Ji Z. Research on Magnetohydrodynamic Angular Rate Sensor Denoising for a Space Laser Stabilization Control System. Applied Sciences. 2023; 13(10):5895. https://doi.org/10.3390/app13105895
Chicago/Turabian StyleSu, Yunhao, Caiwen Ma, Junfeng Han, Xuan Wang, Yuanyuan Wang, and Zhou Ji. 2023. "Research on Magnetohydrodynamic Angular Rate Sensor Denoising for a Space Laser Stabilization Control System" Applied Sciences 13, no. 10: 5895. https://doi.org/10.3390/app13105895
APA StyleSu, Y., Ma, C., Han, J., Wang, X., Wang, Y., & Ji, Z. (2023). Research on Magnetohydrodynamic Angular Rate Sensor Denoising for a Space Laser Stabilization Control System. Applied Sciences, 13(10), 5895. https://doi.org/10.3390/app13105895






