Analysis of Numerical Micromodulus Coupled with Influence Function for Brittle Materials via Bond-Based Peridynamics
Abstract
:1. Introduction
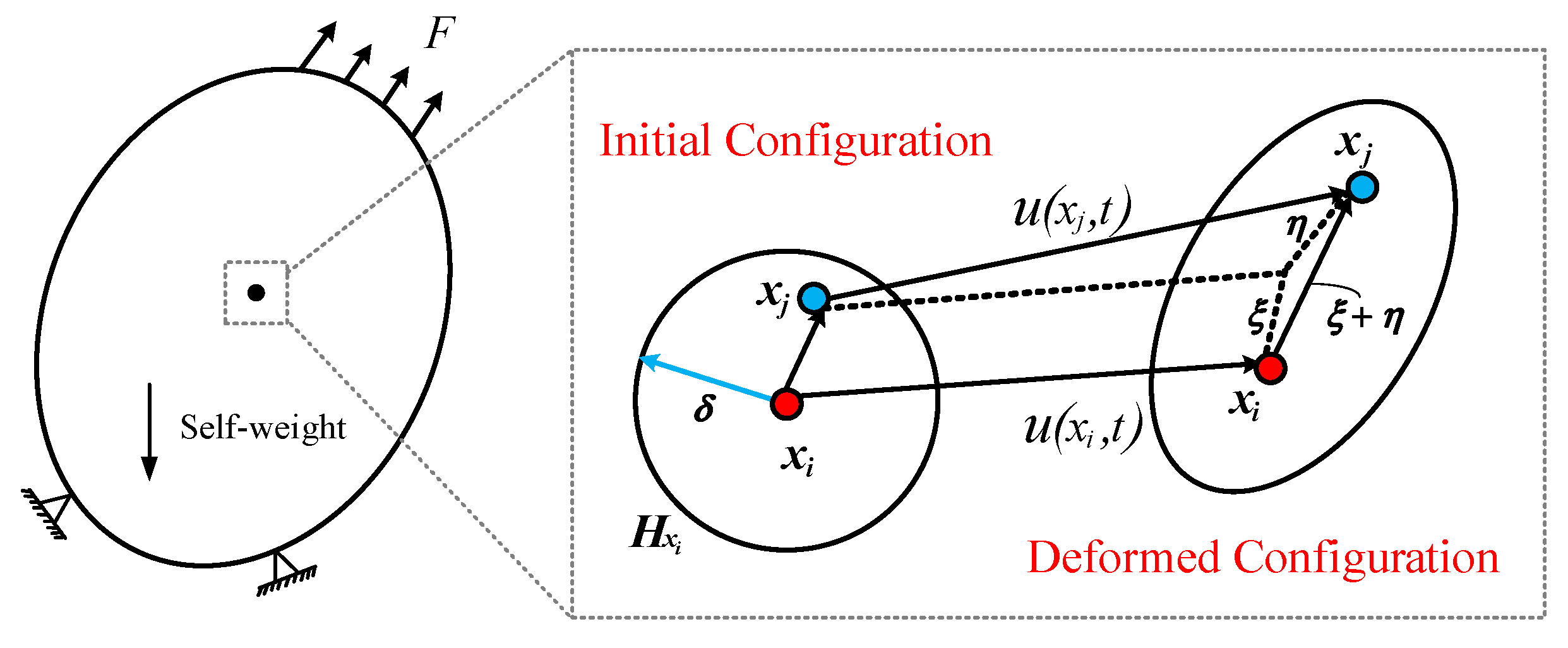
2. Theoretical Foundation
3. Numerical Micromodulus
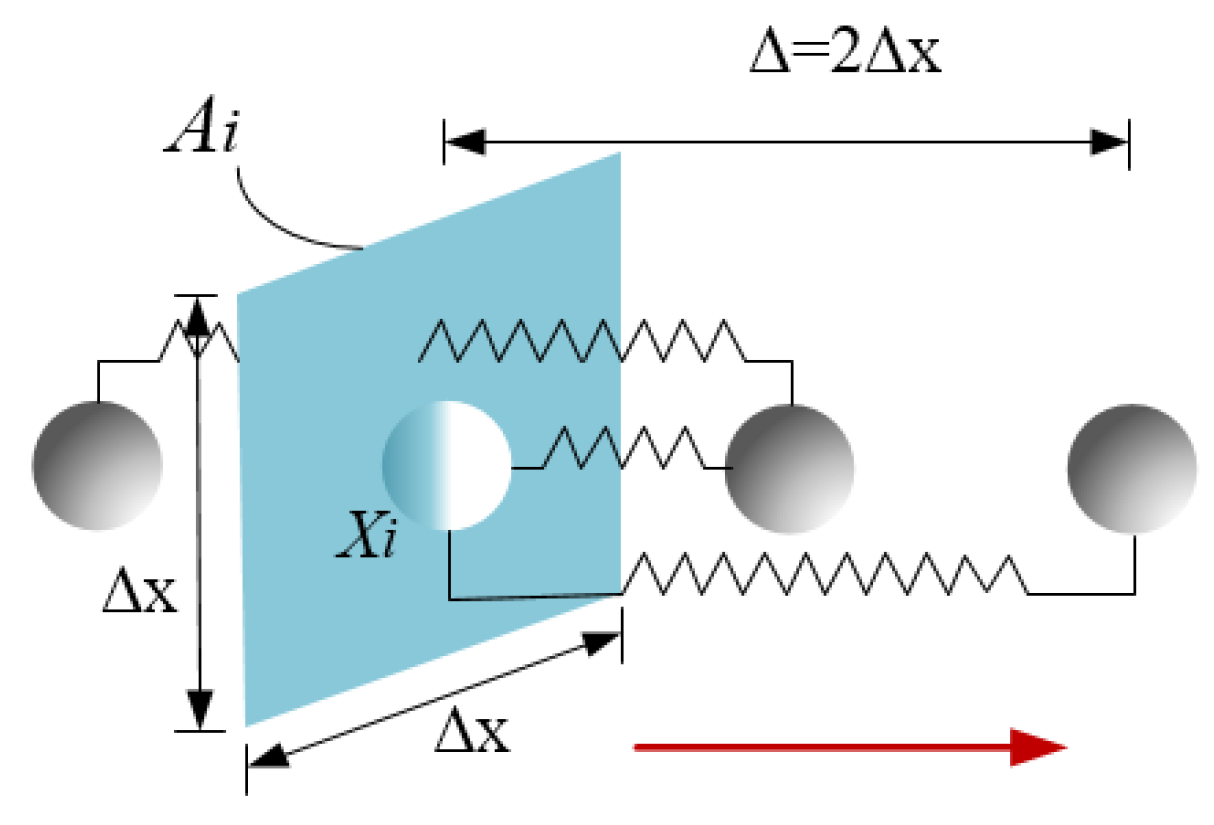
3.1. One-Dimensional Numerical Micromodulus
3.2. Two-Dimensional Numerical Micromodulus
3.3. Influence Function
4. Numerical Implementation
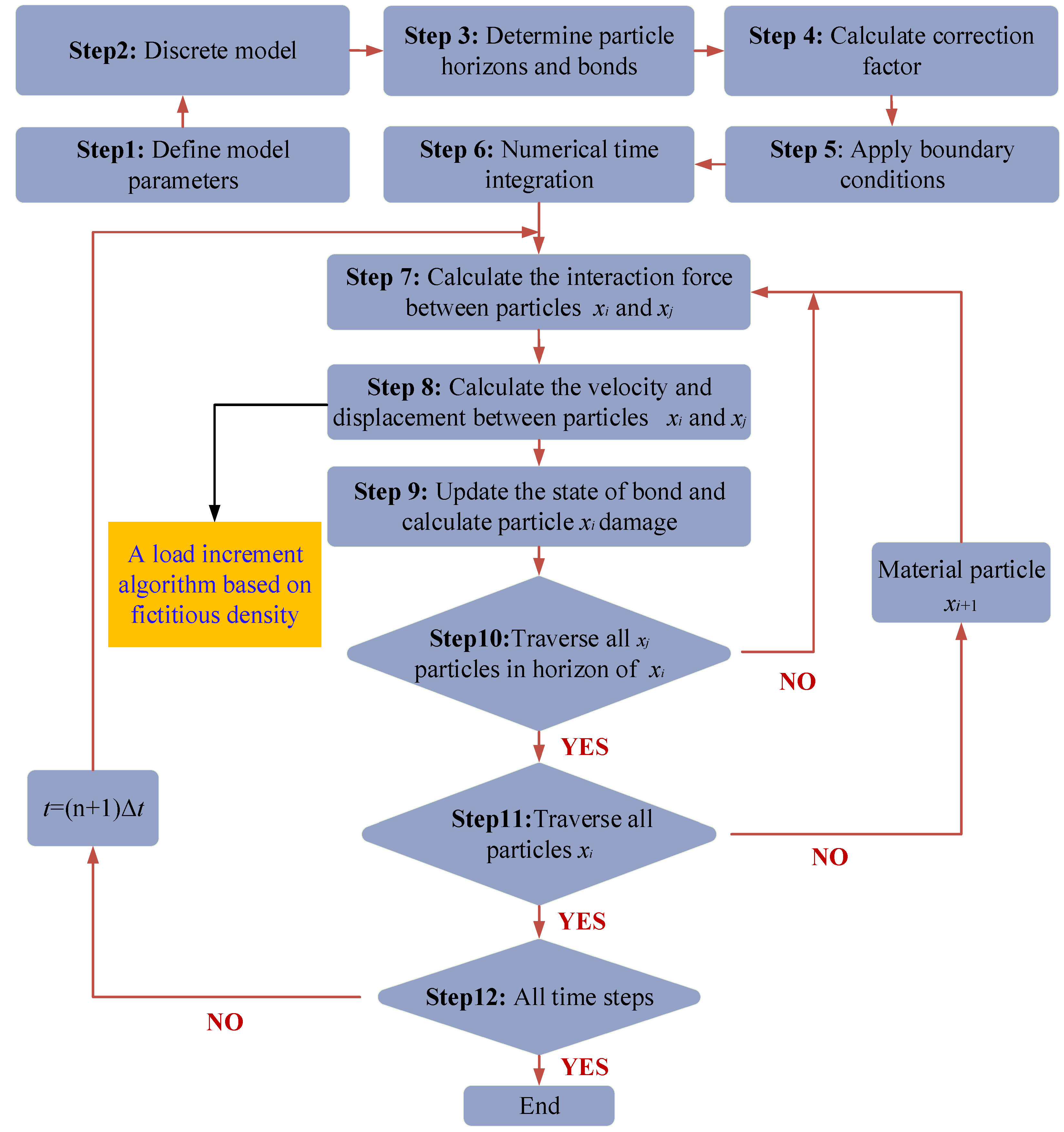
4.1. Discretization and Computation Processes
4.2. A Load Increment Algorithm Based on Fictitious Density
- (i)
- The external load is gradually applied to the object in increments. The load increment is calculated in Equation (22).
- (ii)
- The time step integral describes how points move in space and interact with their horizon points. The velocity and displacement of points are obtained by employing the central difference formula combined with the damping relaxation method, seen in Equation (23).
- (iii)
- After numerical iteration, the model would come to equilibrium when the convergence criterion is reached, which indicates that the next time step and load increment can be practiced in simulation. The convergence criterion iswhere N stands for total number of material points. represents relative error of displacement between the current iteration and the last iteration. is a given convergence index.
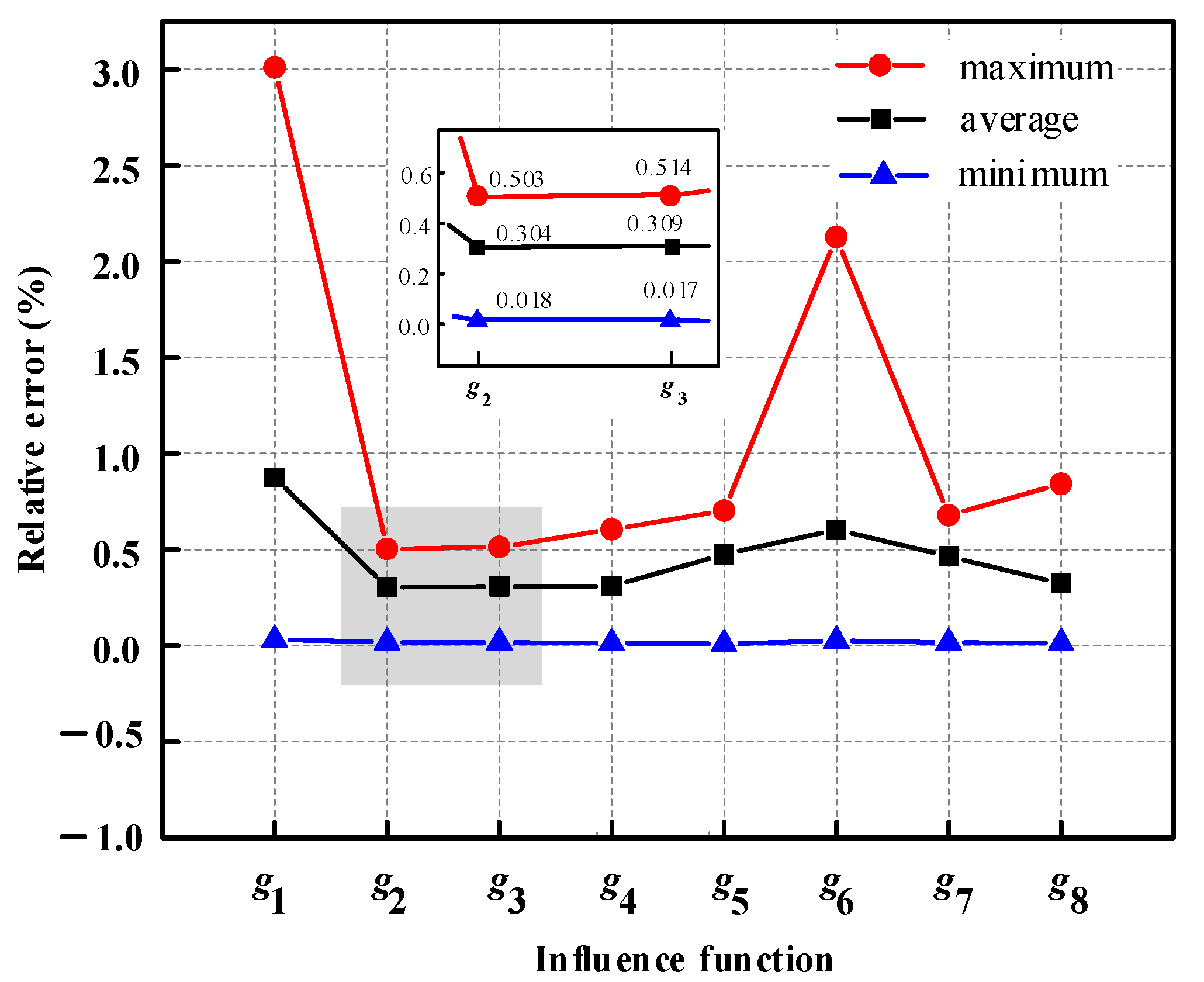
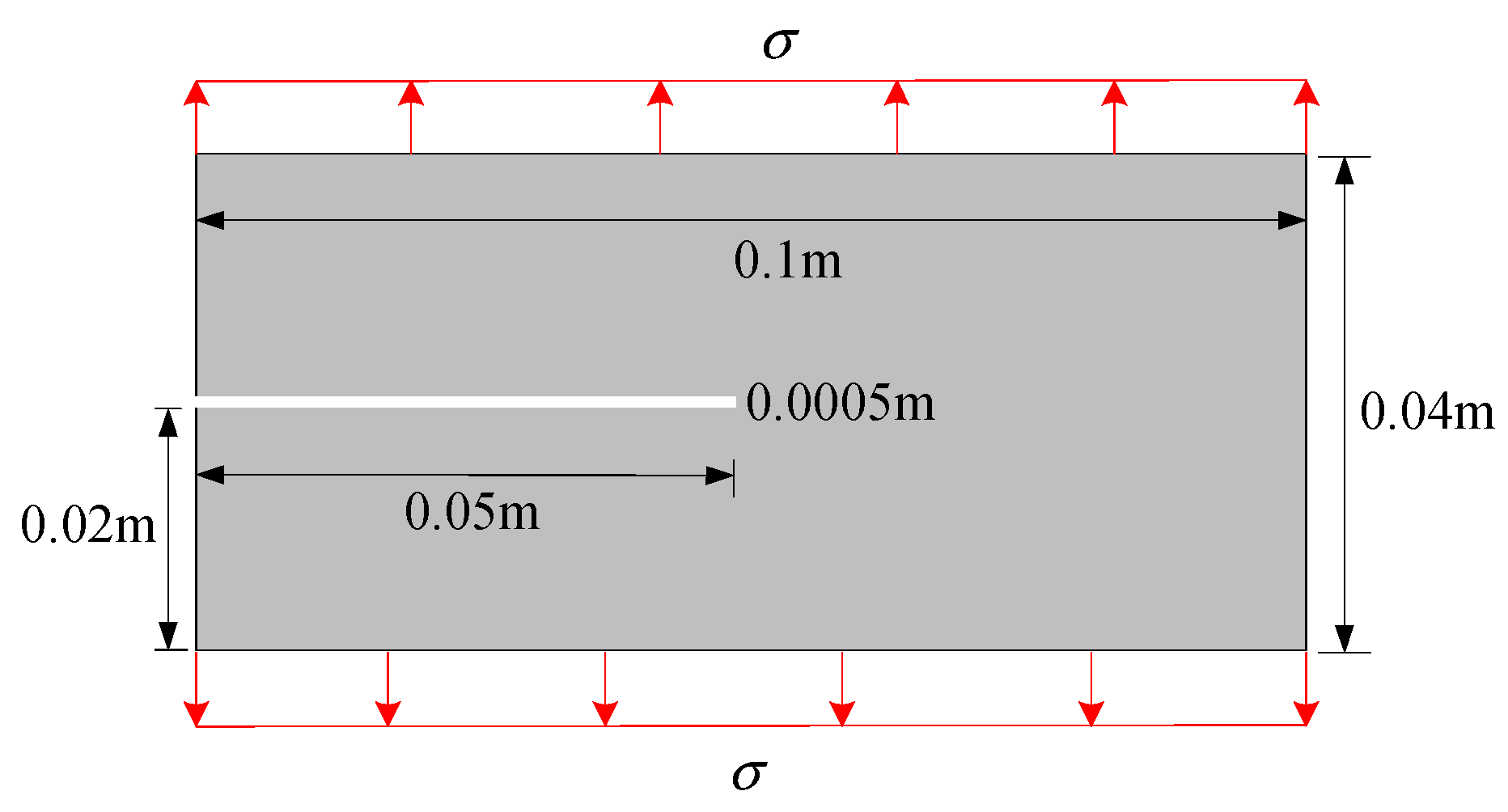
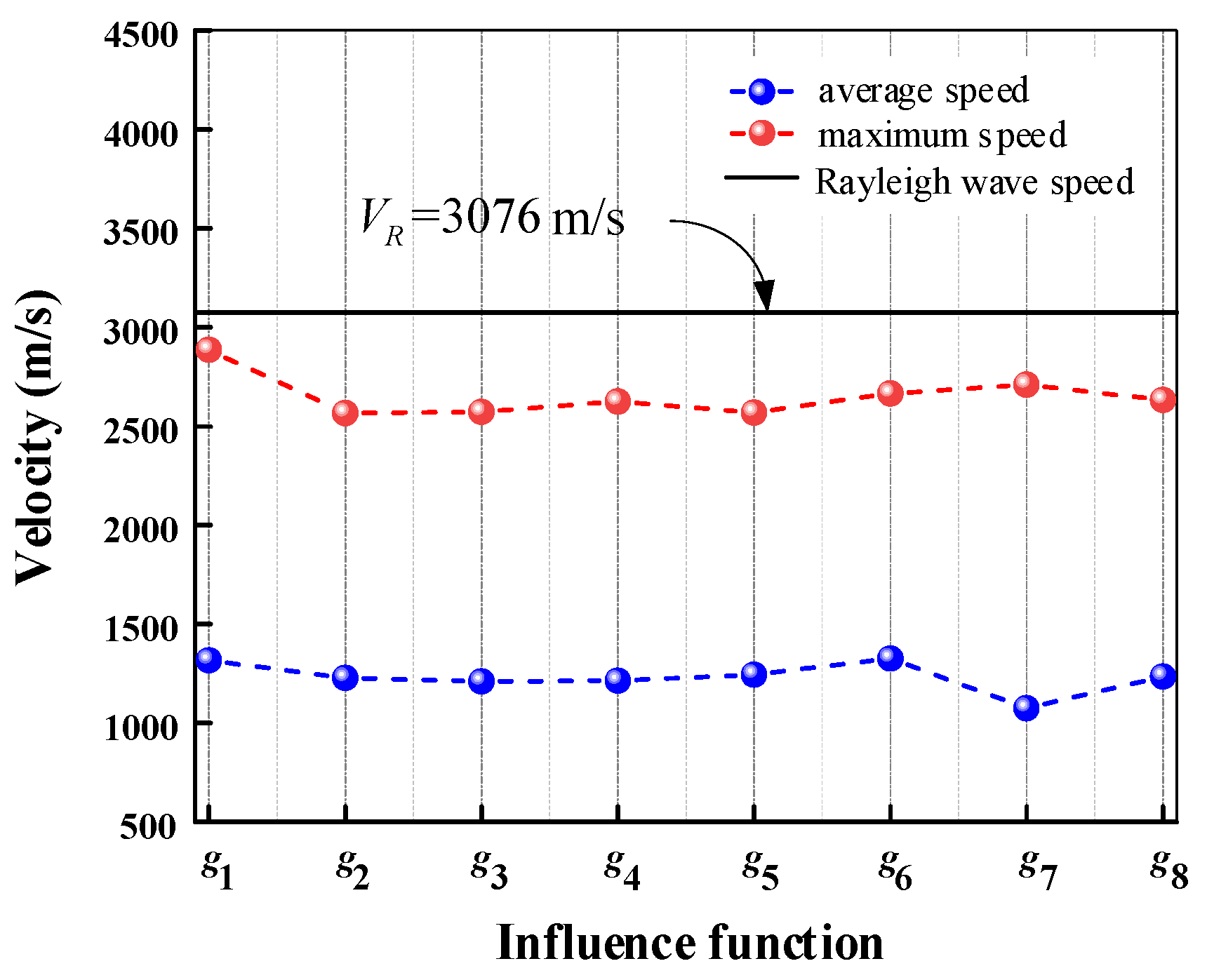
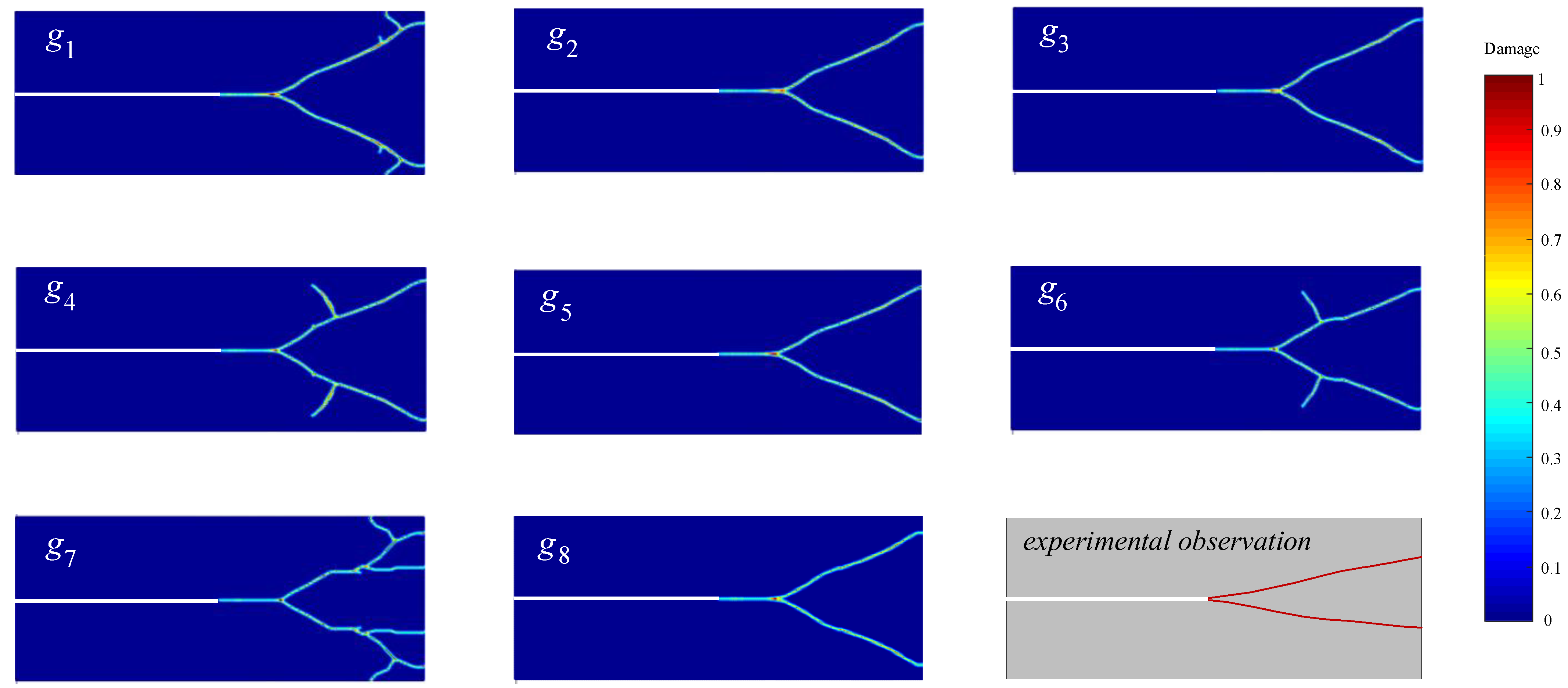
5. Numerical Applications and Discussion
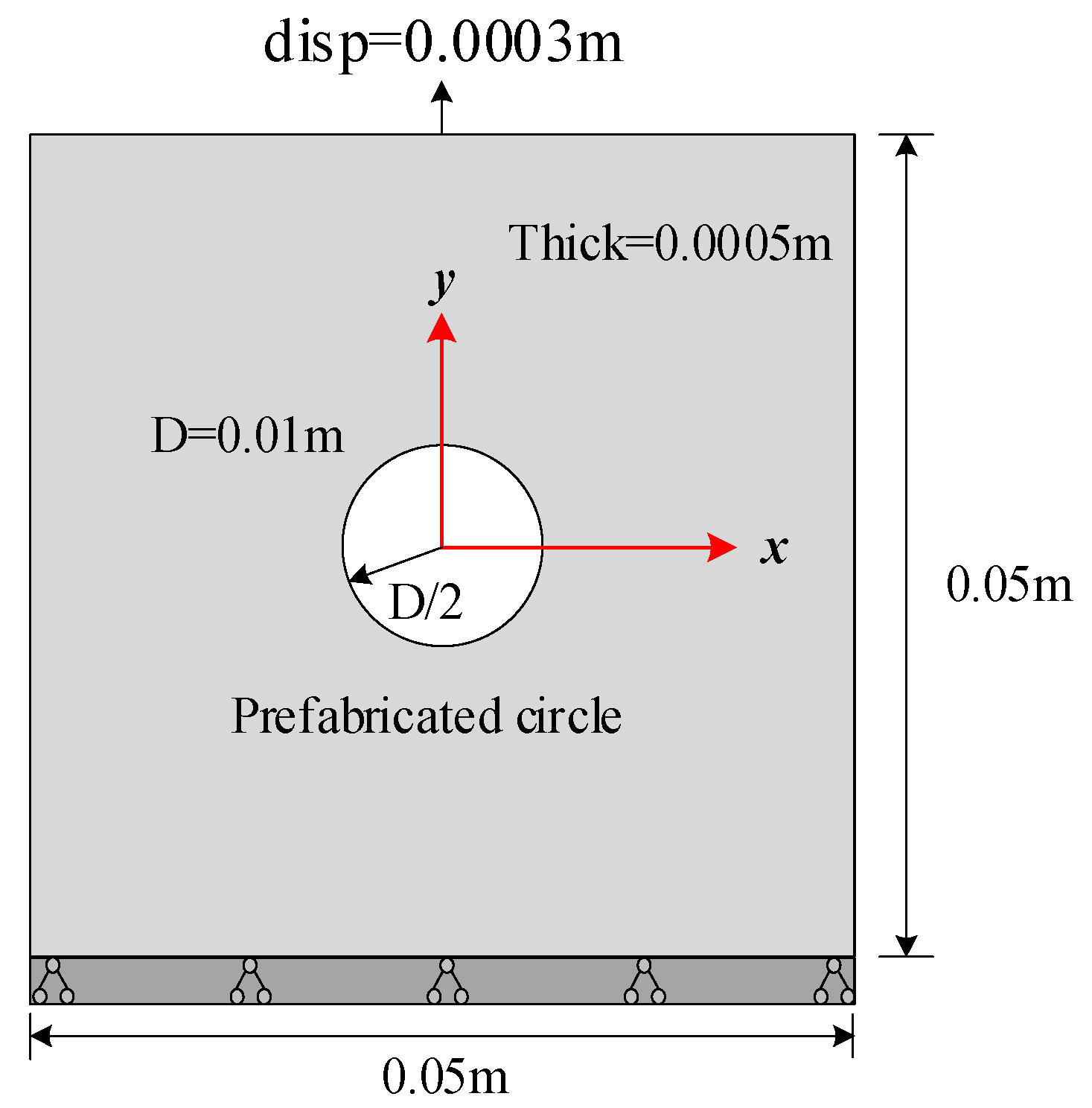
5.1. Benchmark
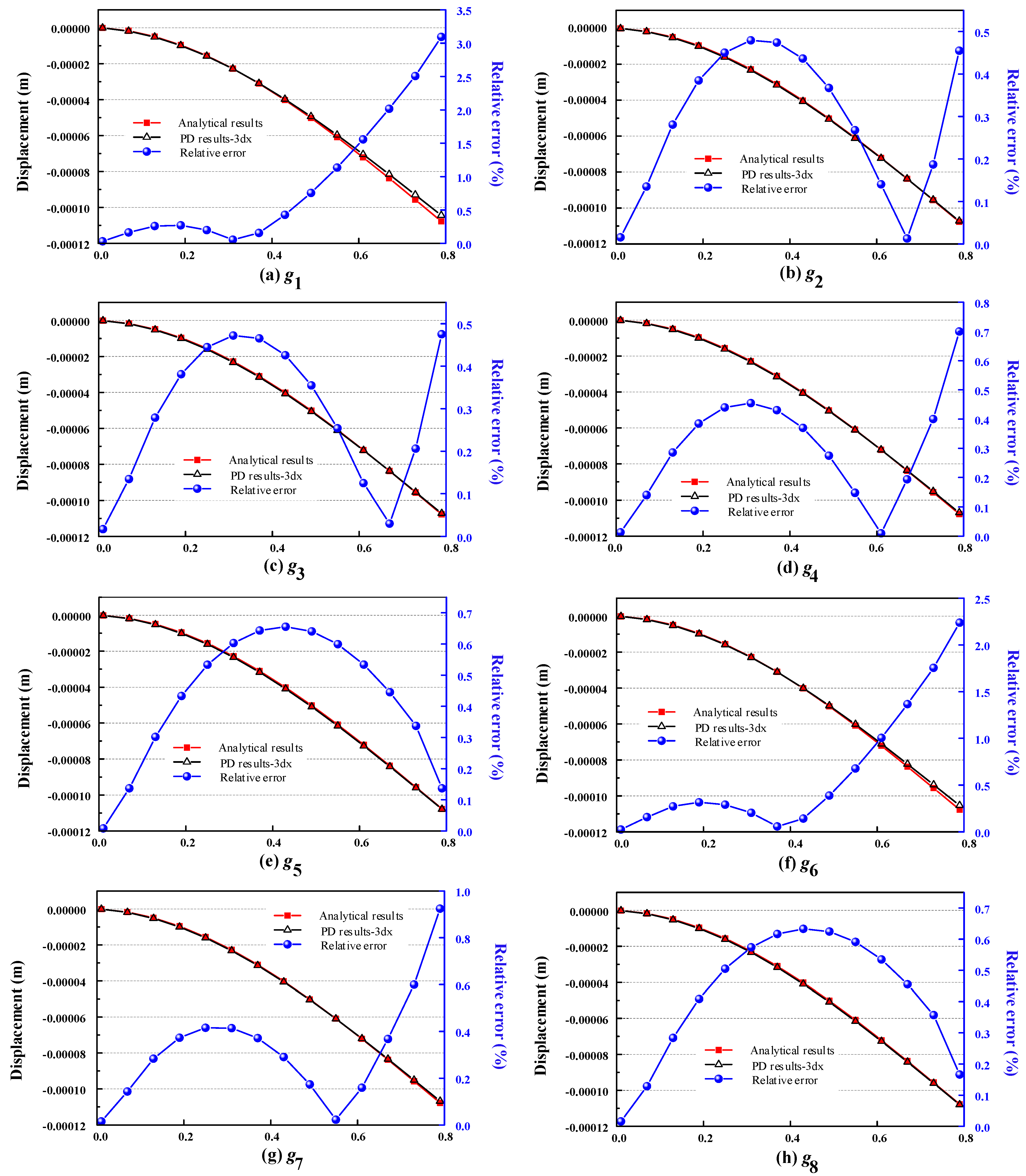
5.2. Analysis of Quantitative Accuracy
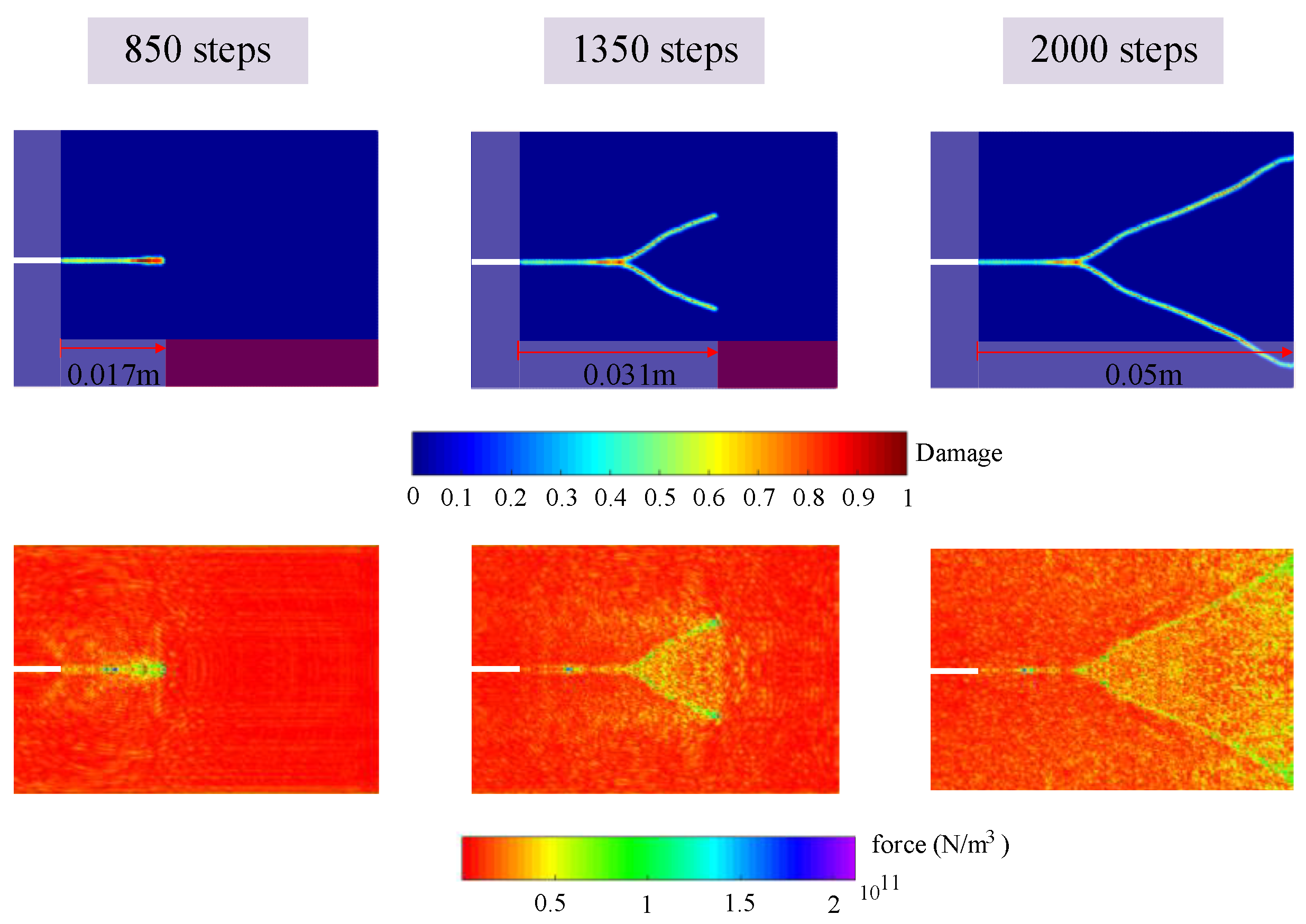
5.3. Qualitative Failure Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| PD = peridynamics; | BBPD = Bond-based peridynamics; |
| CCM = Conventional continuum mechanics; | 1D = One-dimensional; |
| 2D = Two-dimensional; | SBPD = State-based peridynamics; |
| PMB = Prototype microelastic brittle; | = Relative position; |
| FEM = finite element method; | f = Bond force function; |
| s = Bond elongation; | = Relative displacement; |
| E = Elastic modulus; | c = Micromodulus (Bond stiffness); |
| δ = Horizon radius; | v = Poisson’s ratio; |
| = Damage function of a bond | ; |
| ; | = Critical elongation; |
| = One-dimension numerical micromodulus; | Δx = Material point spacing; |
| = Two-dimension numerical micromodulus; | M = Fictitious density; |
| = Influence function type; = Load increment; | C = Artificial damping coefficient; |
| ADR = Adaptive dynamic relaxation |
References
- Silling, S.A. Reformulation of Elasticity Theory for Discontinuities and Long-Range Forces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef]
- Chen, Z.; Chu, X.; Duan, Q. A Micromorphic Peridynamic Model and the Fracture Simulations of Quasi-Brittle Material. Eng. Fract. Mech. 2022, 271, 108631. [Google Scholar] [CrossRef]
- Silling, S.A.; Weckner, O.; Askari, E.; Bobaru, F. Crack Nucleation in a Peridynamic Solid. Int. J. Fract. 2010, 162, 219–227. [Google Scholar] [CrossRef]
- Basoglu, M.F.; Zerin, Z.; Kefal, A.; Oterkus, E. A Computational Model of Peridynamic Theory for Deflecting Behavior of Crack Propagation with Micro-Cracks. Comput. Mater. Sci. 2019, 162, 33–46. [Google Scholar] [CrossRef]
- Deng, X.; Wang, B. Peridynamic Modeling of Dynamic Damage of Polymer Bonded Explosive. Comput. Mater. Sci. 2020, 173, 109405. [Google Scholar] [CrossRef]
- Breitenfeld, M.S.; Geubelle, P.H.; Weckner, O.; Silling, S.A. Non-Ordinary State-Based Peridynamic Analysis of Stationary Crack Problems. Comput. Methods Appl. Mech. Eng. 2014, 272, 233–250. [Google Scholar] [CrossRef]
- Silling, S.A. Dynamic Fracture Modeling with a Meshfree Peridynamic Code. In Computational Fluid and Solid Mechanics 2003, Proceedings of the Second MIT Conference on Compurational Fluid and Solid Mechanics, Cambridge, MA, USA, 17–20 June 2003; Bathe, K.J., Ed.; Elsevier Science Ltd.: Oxford, UK, 2003; pp. 641–644. ISBN 978-0-08-044046-0. [Google Scholar]
- Weckner, O.; Abeyaratne, R. The Effect of Long-Range Forces on the Dynamics of a Bar. J. Mech. Phys. Solids 2005, 53, 705–728. [Google Scholar] [CrossRef]
- Zhang, Y.; Deng, H.; Deng, J.; Liu, C.; Yu, S. Peridynamic Simulation of Crack Propagation of Non-Homogeneous Brittle Rock-like Materials. Theor. Appl. Fract. Mech. 2020, 106, 102438. [Google Scholar] [CrossRef]
- Zhou, L.M.; Zhu, S.; Zhu, Z.D.; Xie, X.H. Simulations of Fractures of Heterogeneous Orthotropic Fiber-Reinforced Concrete with Pre-Existing Flaws Using an Improved Peridynamic Model. Materials 2022, 15, 3977. [Google Scholar] [CrossRef]
- Rivera, J.; Berjikian, J.; Ravinder, R.; Kodamana, H.; Das, S.; Bhatnagar, N.; Bauchy, M.; Krishnan, N.M.A. Glass Fracture Upon Ballistic Impact: New Insights from Peridynamics Simulations. Front. Mater. 2019, 6, 239. [Google Scholar] [CrossRef]
- Shi, Z.; Yue, J.; Xu, L.; Wang, X. Peridynamics for Fracture Analysis of Reflective Cracks in Semi-Rigid Base Asphalt Pavement. Appl. Sci. 2022, 12, 3486. [Google Scholar] [CrossRef]
- Han, J.; Chen, W. An Ordinary State-Based Peridynamic Model for Fatigue Cracking of Ferrite and Pearlite Wheel Material. Appl. Sci. 2020, 10, 4325. [Google Scholar] [CrossRef]
- Jiang, X.-W.; Guo, S.; Li, H.; Wang, H. Peridynamic Modeling of Mode-I Delamination Growth in Double Cantilever Composite Beam Test: A Two-Dimensional Modeling Using Revised Energy-Based Failure Criteria. Appl. Sci. 2019, 9, 656. [Google Scholar] [CrossRef]
- Guan, J.; Yan, X.; Guo, L. An Improved Bond-Based Peridynamic Model with Shear Bonds for Eliminating Rigid Body Rotation. Theor. Appl. Fract. Mech. 2022, 119, 103369. [Google Scholar] [CrossRef]
- Huang, D.; Lu, G.; Wang, C.; Qiao, P. An Extended Peridynamic Approach for Deformation and Fracture Analysis. Eng. Fract. Mech. 2015, 141, 196–211. [Google Scholar] [CrossRef]
- Ha, Y.D. An Extended Ghost Interlayer Model in Peridynamic Theory for High-Velocity Impact Fracture of Laminated Glass Structures. Comput. Math. Appl. 2020, 80, 744–761. [Google Scholar] [CrossRef]
- Silling, S.A.; Bobaru, F. Peridynamic Modeling of Membranes and Fibers. Int. J. Non. Linear. Mech. 2005, 40, 395–409. [Google Scholar] [CrossRef]
- Postek, E.; Sadowski, T.; Boniecki, M. Impact of Brittle Composites: Peridynamics Modelling. Mater. Today Proc. 2021, 45, 4268–4274. [Google Scholar] [CrossRef]
- Jenabidehkordi, A.; Abadi, R.; Rabczuk, T. Computational Modeling of Meso-Scale Fracture in Polymer Matrix Composites Employing Peridynamics. Compos. Struct. 2020, 253, 112740. [Google Scholar] [CrossRef]
- Shi, C.; Shi, Q.; Tong, Q.; Li, S. Peridynamics Modeling and Simulation of Meso-Scale Fracture in Recycled Coarse Aggregate (RCA) Concretes. Theor. Appl. Fract. Mech. 2021, 114, 102949. [Google Scholar] [CrossRef]
- Huang, D.; Lu, G.; Qiao, P. An Improved Peridynamic Approach for Quasi-Static Elastic Deformation and Brittle Fracture Analysis. Int. J. Mech. Sci. 2015, 94–95, 111–122. [Google Scholar] [CrossRef]
- Jo, G.; Ha, Y.D. Two-Grid Based Sequential Peridynamic Analysis Method for Quasi-Static Crack Propagation. Eng. Fract. Mech. 2022, 269, 108549. [Google Scholar] [CrossRef]
- Silling, S.A.; Askari, E. A Meshfree Method Based on the Peridynamic Model of Solid Mechanics. Comput. Struct. 2005, 83, 1526–1535. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, Q.; Huang, D.; Yv, Y. Wave Dispersion Analysis and Simulation Method for Concrete SHPB Test in Peridynamics. Eng. Fract. Mech. 2016, 160, 124–137. [Google Scholar] [CrossRef]
- Qin, H.-Y.; Huang, D.; Liu, Y.-M.; Zhang, Q. An Extended Peridynamic Approach for Analysis of Multiple Crack Growth. Gongcheng Lixue Eng. Mech. 2017, 34, 31–38. [Google Scholar] [CrossRef]
- Das, S.; Hoffarth, C.; Ren, B.; Spencer, B.; Sant, G.; Rajan, S.D.; Neithalath, N. Simulating the Fracture of Notched Mortar Beams through Extended Finite-Element Method and Peridynamics. J. Eng. Mech. 2019, 145, 04019049. [Google Scholar] [CrossRef]
- Torrence, C.E.; Trageser, J.E.; Jones, R.E.; Rimsza, J.M. Sensitivity of the Strength and Toughness of Concrete to the Properties of the Interfacial Transition Zone. Constr. Build. Mater. 2022, 336, 126875. [Google Scholar] [CrossRef]
- Li, W.; Guo, L. A Mechanical-Diffusive Peridynamics Coupling Model for Meso-Scale Simulation of Chloride Penetration in Concrete under Loadings. Constr. Build. Mater. 2020, 241, 118021. [Google Scholar] [CrossRef]
- Rao, F.; Zhang, Z.; Ye, G. Three-Dimensional Mesoscale Modeling of Foamed Cement Paste Using Peridynamics. Constr. Build. Mater. 2021, 310, 125230. [Google Scholar] [CrossRef]
- Hou, D.; Zhang, W.; Ge, Z.; Wang, P.; Wang, X.; Zhang, H. Experimentally Validated Peridynamic Fracture Modelling of Mortar at the Meso-Scale. Constr. Build. Mater. 2021, 267, 120939. [Google Scholar] [CrossRef]
- Liu, W.; Hong, J.-W. Discretized Peridynamics for Linear Elastic Solids. Comput. Mech. 2012, 50, 579–590. [Google Scholar] [CrossRef]
- Li, S.; Jin, Y.; Lu, H.; Sun, P.; Huang, X.; Chen, Z. Wave Dispersion and Quantitative Accuracy Analysis of Bond-Based Peridynamic Models with Different Attenuation Functions. Comput. Mater. Sci. 2021, 197, 110667. [Google Scholar] [CrossRef]
- Li, X.; Gu, X.; Xia, X.; Madenci, E.; Chen, X.; Zhang, Q. Effect of Water-Cement Ratio and Size on Tensile Damage in Hardened Cement Paste: Insight from Peridynamic Simulations. Constr. Build. Mater. 2022, 356, 129256. [Google Scholar] [CrossRef]
- Gerstle, W.; Sau, N.; Aguilera, E. Micropolar Peridynamic Modeling of Concrete Structures BT. In Proceedings of the 6th International Conference on Fracture Mechanics of Concrete and Concrete Structures, Catania, Italy, 17–22 June 2007; Taylor and Francis: Balkema, Slovakia, 2007; Volume 1. [Google Scholar]
- Gerstle, W.H.; Sau, N.; Sakhavand, N. On Peridynamic Computational Simulation of Concrete Structures BT. In Proceedings of the ACI Fall 2009 Convention, New Orleans, LA, USA, 8–12 November 2009; American Concrete Institute: Farmington Hills, MI, USA, 2009; pp. 245–264. [Google Scholar]
- Ha, Y.D.; Bobaru, F. Studies of Dynamic Crack Propagation and Crack Branching with Peridynamics. Int. J. Fract. 2010, 162, 229–244. [Google Scholar] [CrossRef]
- Chen, Z.; Woody Ju, J.; Su, G.; Huang, X.; Li, S.; Zhai, L. Influence of Micro-Modulus Functions on Peridynamics Simulation of Crack Propagation and Branching in Brittle Materials. Eng. Fract. Mech. 2019, 216, 106498. [Google Scholar] [CrossRef]
- Kilic, B.; Madenci, E. Structural Stability and Failure Analysis Using Peridynamic Theory. Int. J. Non. Linear. Mech. 2009, 44, 845–854. [Google Scholar] [CrossRef]
- Kilic, B.; Madenci, E. An Adaptive Dynamic Relaxation Method for Quasi-Static Simulations Using the Peridynamic Theory. Theor. Appl. Fract. Mech. 2010, 53, 194–204. [Google Scholar] [CrossRef]
- Ha, Y.D.; Bobaru, F. Characteristics of Dynamic Brittle Fracture Captured with Peridynamics. Eng. Fract. Mech. 2011, 78, 1156–1168. [Google Scholar] [CrossRef]
- Ramulu, M.; Kobayashi, A.S. Mechanics of Crack Curving and Branching—A Dynamic Fracture Analysis. Int. J. Fract. 1985, 27, 187–201. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, Y.; Qian, Q. Numerical Simulation of Crack Curving and Branching in Brittle Materials under Dynamic Loads Using the Extended Non-Ordinary State-Based Peridynamics. Eur. J. Mech. A Solids 2016, 60, 277–299. [Google Scholar] [CrossRef]


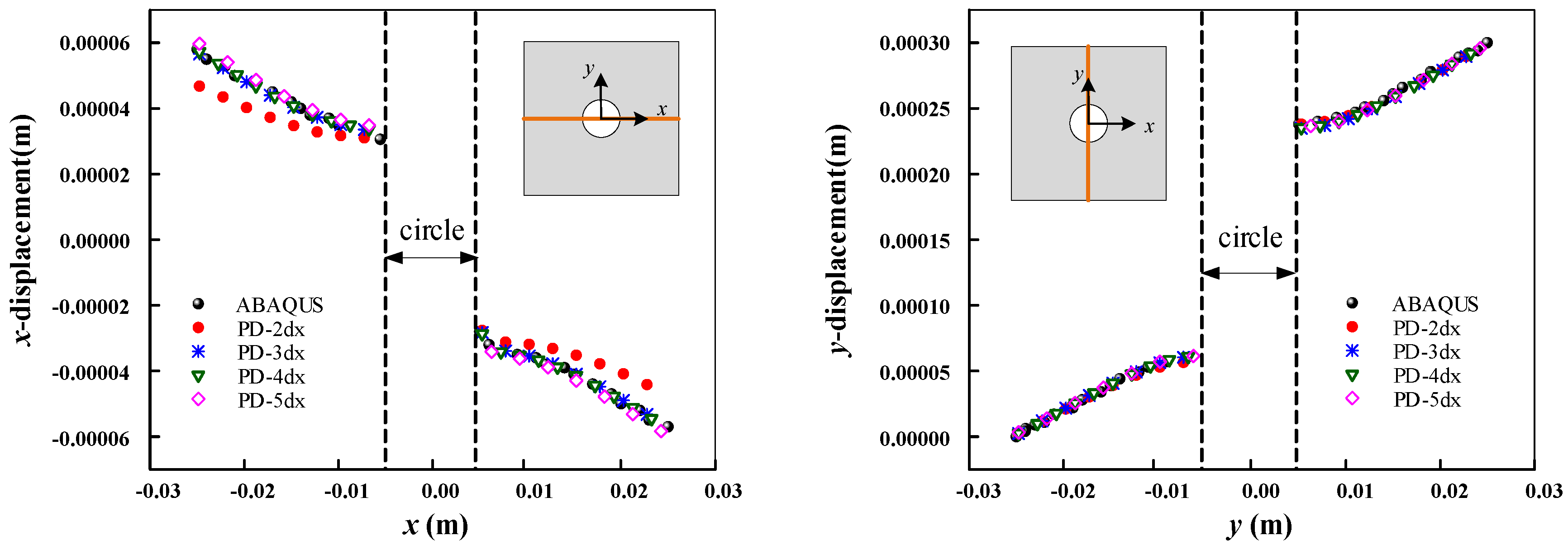
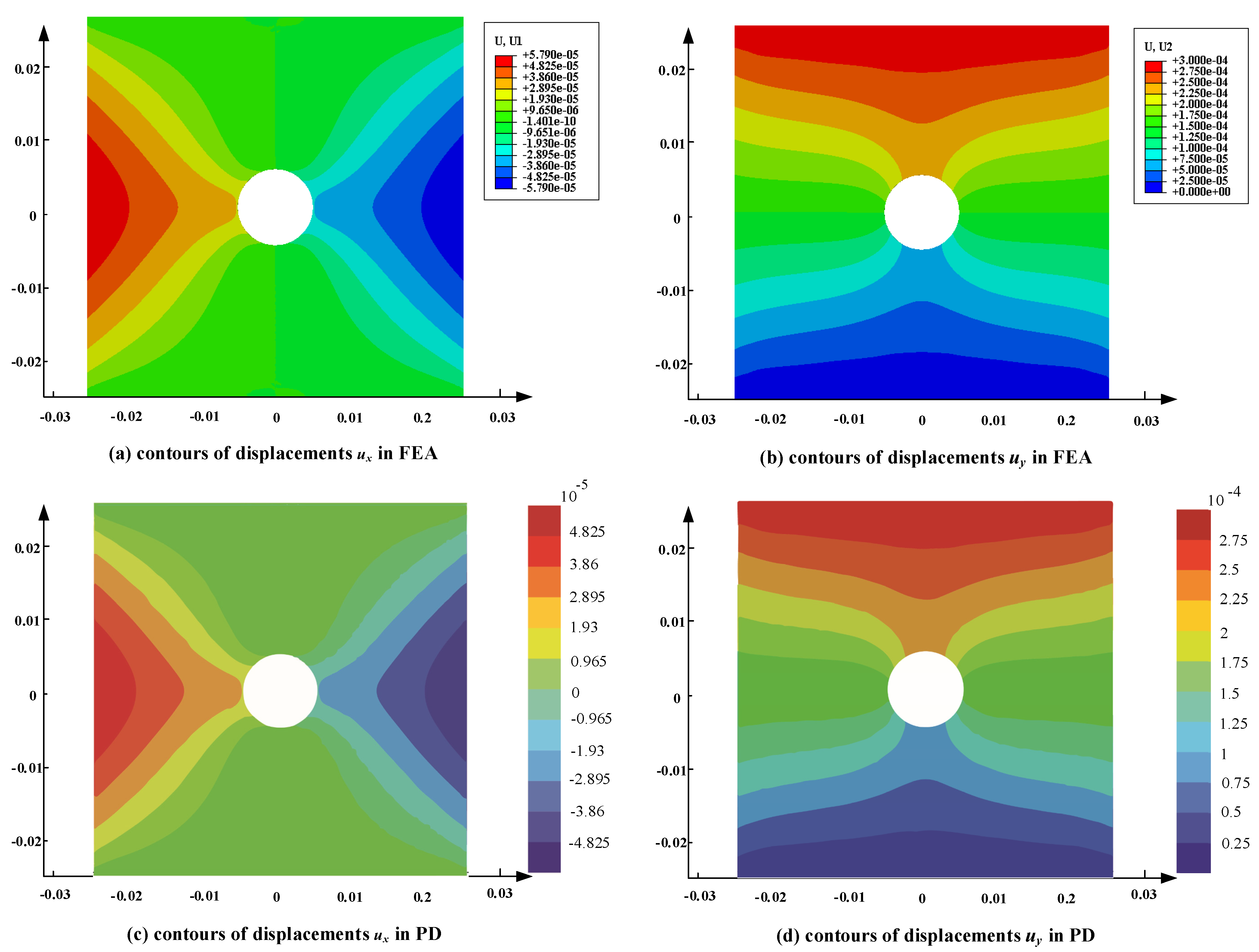

| 2Δx | |
| 3Δx | |
| 4Δx | |
| 5Δx |
| 2Δx | |
| 3Δx | |
| 4Δx | |
| 5Δx |
| Type | Symbol | |
|---|---|---|
| Constant [24,37] | 1 | |
| Exponential [38] | ||
| Gaussian [39] | ||
| Semi-elliptical [38] | ||
| Quartic polynomial [33] | ||
| Parabolic [16] | ||
| Sixth-order polynomial [26] | ||
| Cosine [26] |
| E(GPa) | v | (kg/m3) | (m) | (m) | Influence Function |
|---|---|---|---|---|---|
| 192 | 1/3 | 8000 | 0.0005 |
| E (GPa) | G (GPa) | v | (kg/m3) | (m) | Influence Function |
|---|---|---|---|---|---|
| 24.8 | 9.2 | 1/3 | 2400 | 0.02 |
| E (GPa) | v | (kg/m3) | (m) | (m) | (m) | Influence Function | |
|---|---|---|---|---|---|---|---|
| 65 | 1/3 | 2235 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, Y.; Jia, S. Analysis of Numerical Micromodulus Coupled with Influence Function for Brittle Materials via Bond-Based Peridynamics. Appl. Sci. 2023, 13, 5959. https://doi.org/10.3390/app13105959
You Y, Jia S. Analysis of Numerical Micromodulus Coupled with Influence Function for Brittle Materials via Bond-Based Peridynamics. Applied Sciences. 2023; 13(10):5959. https://doi.org/10.3390/app13105959
Chicago/Turabian StyleYou, Yachen, and Siyi Jia. 2023. "Analysis of Numerical Micromodulus Coupled with Influence Function for Brittle Materials via Bond-Based Peridynamics" Applied Sciences 13, no. 10: 5959. https://doi.org/10.3390/app13105959
APA StyleYou, Y., & Jia, S. (2023). Analysis of Numerical Micromodulus Coupled with Influence Function for Brittle Materials via Bond-Based Peridynamics. Applied Sciences, 13(10), 5959. https://doi.org/10.3390/app13105959





