A Fault Section Location Method for Distribution Networks Based on Divide-and-Conquer
Abstract
1. Introduction
- (1)
- Matrix algorithm-based fault location methods for distribution networks. The basic principle of this method is to construct a fault discrimination matrix based on the topology of the distribution network and the fault information reported by FTUs and locate the faulty equipment via comprehensive analysis of the fault discrimination matrix [12,13]. The matrix algorithm has the advantages of simple principles and fast calculation speed. However, in actual engineering, FTUs are usually installed outdoors and work in harsh environments, resulting in possible misreporting or omission of the reported information. When the fault information is distorted, the matrix constructed by the algorithm cannot correctly reflect the real fault situation, thereby causing the algorithm function to fail [14]. Reference [15] proposes using the adjacency of FTUs measurement points to correct the fault information. Reference [16] proposes introducing telemetry data to check the localization results. However, these methods are only valid for partial cases of fault information distortion [17], and the fault tolerance process of the algorithm additionally increases fault location time. With the expansion of the network scale, the number of FTU measurement points increases, and the probability of fault information distortion increases; thus, the method is difficult to apply to the fault location problem of large distribution networks.
- (2)
- Fault location methods based on the intelligent optimization algorithm. Reference [18] proposes applying logical operations to express the causal relationship between FTU fault information and faulty equipment and proposes a mathematical model of fault location based on the state approximation principle, which transforms fault location into a combinatorial optimization problem. Since then, scholars have successively used the genetic algorithm (GA) [19], binary particle swarm optimization algorithm (BPSO) [20], ant colony algorithm (AC) [21], harmony search algorithm (HS) [22], and other intelligent algorithms to implement the solution of this model. The intelligent optimization algorithm has a strong information fault tolerance capability. However, the method requires iterative search operations in a high-dimensional solution space, which affects the speed of fault location [23]. Moreover, its search process has a certain degree of randomness, which leads to a certain probability of local convergence. Therefore, this method has the inherent defect of insufficient convergence stability [24].
- (3)
- Fault location methods based on the linear integer programming model. The basic principle of this method is to transform the mathematical model of fault location into a linear integer programming model (LIP) using algebraic operation substitution [25], ascending dimension [26], etc. Then, classical LIP methods (such as the branch and bound method, cut plane method, and implicit enumeration method) are applied to solve the model to locate the fault. The “optimality checking” step in the LIP solution method enables it to gradually approximate and eventually converge to the global optimal solution through iterations and thus has good convergence stability. However, the solution of the LIP model involves the computation of its continuous relaxed linear programming model (LP) several times, resulting in high time complexity for the algorithm [27]. Tests have shown that the fault location time of small and medium-sized distribution networks is in the range of seconds [26], which does not meet the requirements of rapidity.
- (4)
- Fault location methods based on the hierarchical optimization model. Reference [28] proposes that the branch of the network is externally equivalent to a two-port based on the equivalence principle and constructs a hierarchical optimization model of fault location. The basic idea is to solve the mathematical model of fault location in a reduced dimension: first, locate the branch where the fault is located, then determine the faulty device from the faulty branch. Since then, scholars have successively used the multiverses optimization algorithm (MVO) [29], quantum computing and immune optimization algorithm(QIOA) [30], bald eagle search algorithm (BES) [31], and other intelligent algorithms to implement the solution of hierarchical optimization models. This method converts effectively reduces the size of solution space and improves the speed and accuracy of fault location. However, the method requires high soundness of FTU fault information at the branch port, which may produce misjudgment when the port information is distorted, and it cannot completely eradicate the defect of insufficient convergence stability of the intelligent algorithm.
- The application of road vectors to establish causal links between fault information and faulty equipment, the equivalent transformation of logical operations in the mathematical model of traditional fault location, and the construction of a numerical computational model of fault location.
- Defines “compatible sets” and “approximation gains” and validates its properties, and then proves that the mathematical model constructed in this paper conforms to the recursive structure of DAC.
- Proposes a fault location method based on DAC, which uses the recursive model of “Divide-Conquer-Combine” in each level of recursion. The linear time “approximation gain” computations and constant time divide and combine operations are included in each layer of recursion to improve the computational efficiency while ensuring the accuracy of fault location.
2. Numerical Computational Model for Distribution Grid Fault Location
2.1. Basic Principle of Distribution Network Fault Location
2.1.1. Fault Information Code
2.1.2. Switching Function
2.1.3. Objective Function
2.2. Construction of the Numerical Computation Model
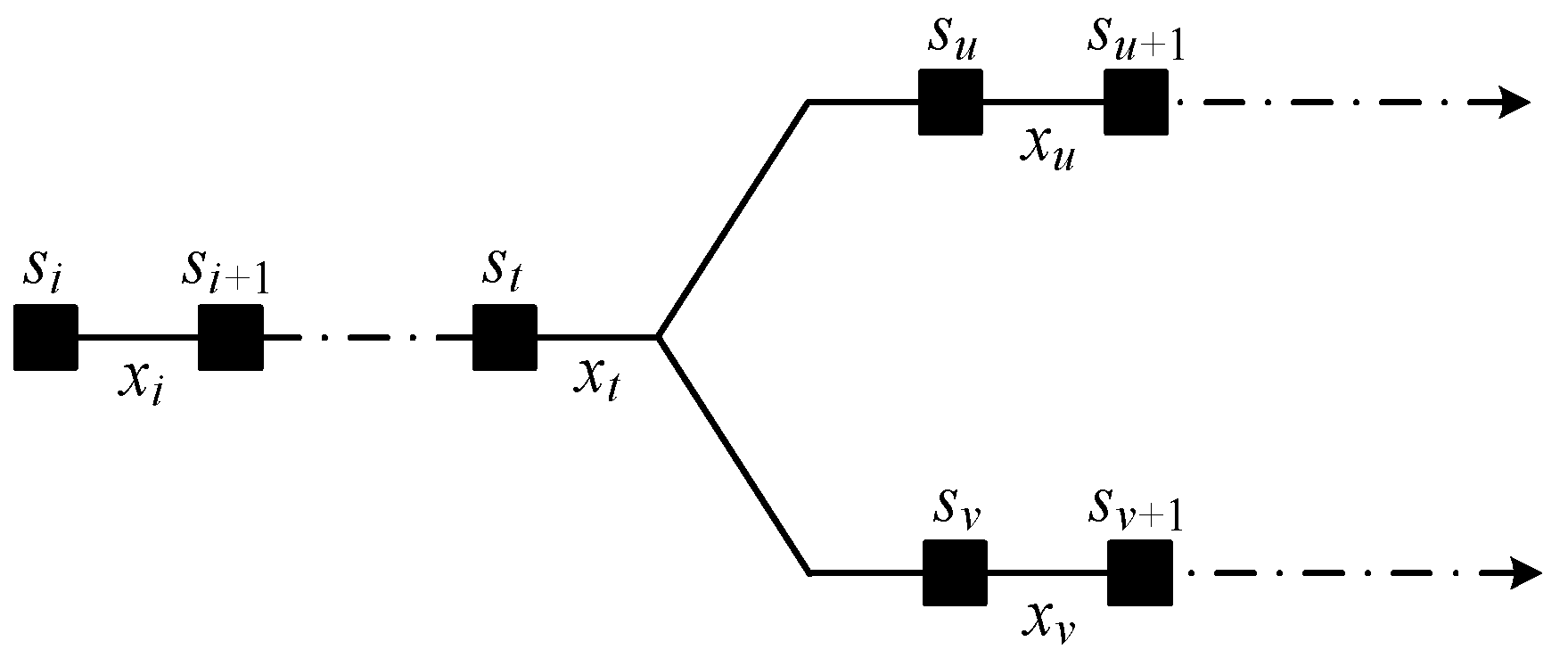
2.2.1. Road Vector
2.2.2. Properties of the Road Vector
- (1)
- ;
- (2)
- Section xi is on the road of section xj;
- (3)
- ;
2.2.3. Numerical Computational Expressions for the Switching Function
- (1)
- When u = 1, by Equation (10), . Obviously, .
- (2)
- Suppose that when u = p. When u = p + 1, we apply Equation (10) to expand :
2.2.4. Numerical Computational Expression for the Minimum Fault Set Constraint
- (1)
- Necessity. Suppose for the sake of contradiction that the set of fault sections satisfies the “minimum fault set” constraint but such that . Then: . Let , , according to Equation (19):is a proper subset of , contradicting the assumption that satisfies the “minimum fault set” constraint.
- (2)
- Sufficiency. Suppose for the sake of contradiction that , , but the set of fault section does not satisfy the “minimum fault set” constraint. Then, there exists a proper subset of such that . Let , and . Then: . According to Equations (14) and (19):
2.2.5. Numerical Computational Expression for the Objective Function
3. Recursive Structure of Fault Location for the Distribution Network
3.1. Theoretical Foundation
3.1.1. Compatible Sets
3.1.2. Approximation Gains
3.2. Recursive Structure
- The original problem and the subproblem should have the same descriptive form.
- When the “bottoms out” condition is satisfied, it enters the “base case” and can be solved directly.
- If the condition of “bottoms out” is not satisfied, it enters the “recursive case”, and the solution of the original problem can be created by combining the solutions of the subproblem.
3.2.1. Subproblem Description
3.2.2. Base Case
3.2.3. Recursive Case
4. Fault Section Location Method for Distribution Networks Based on Divide-and-Conquer
4.1. Algorithm Design
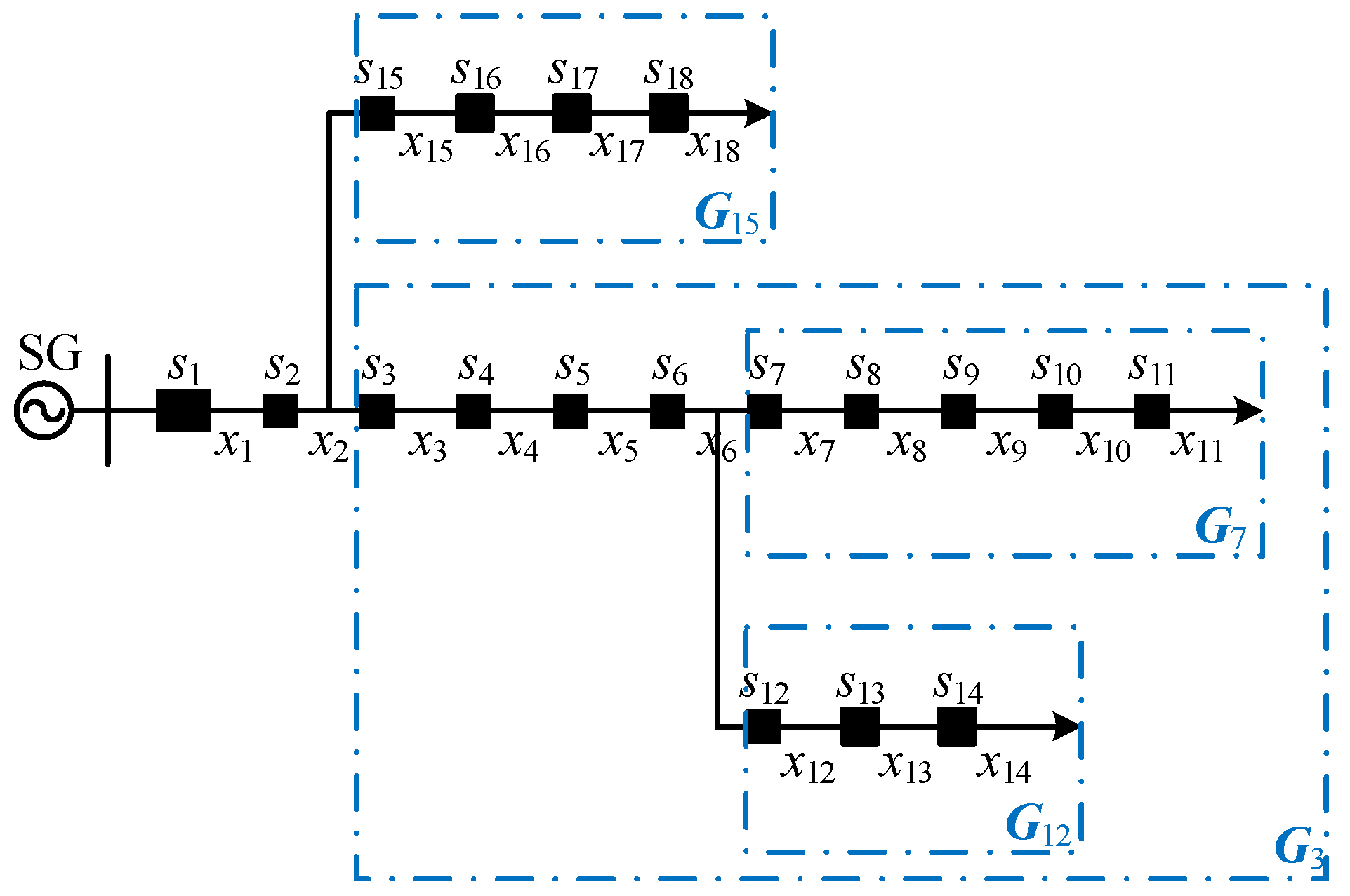
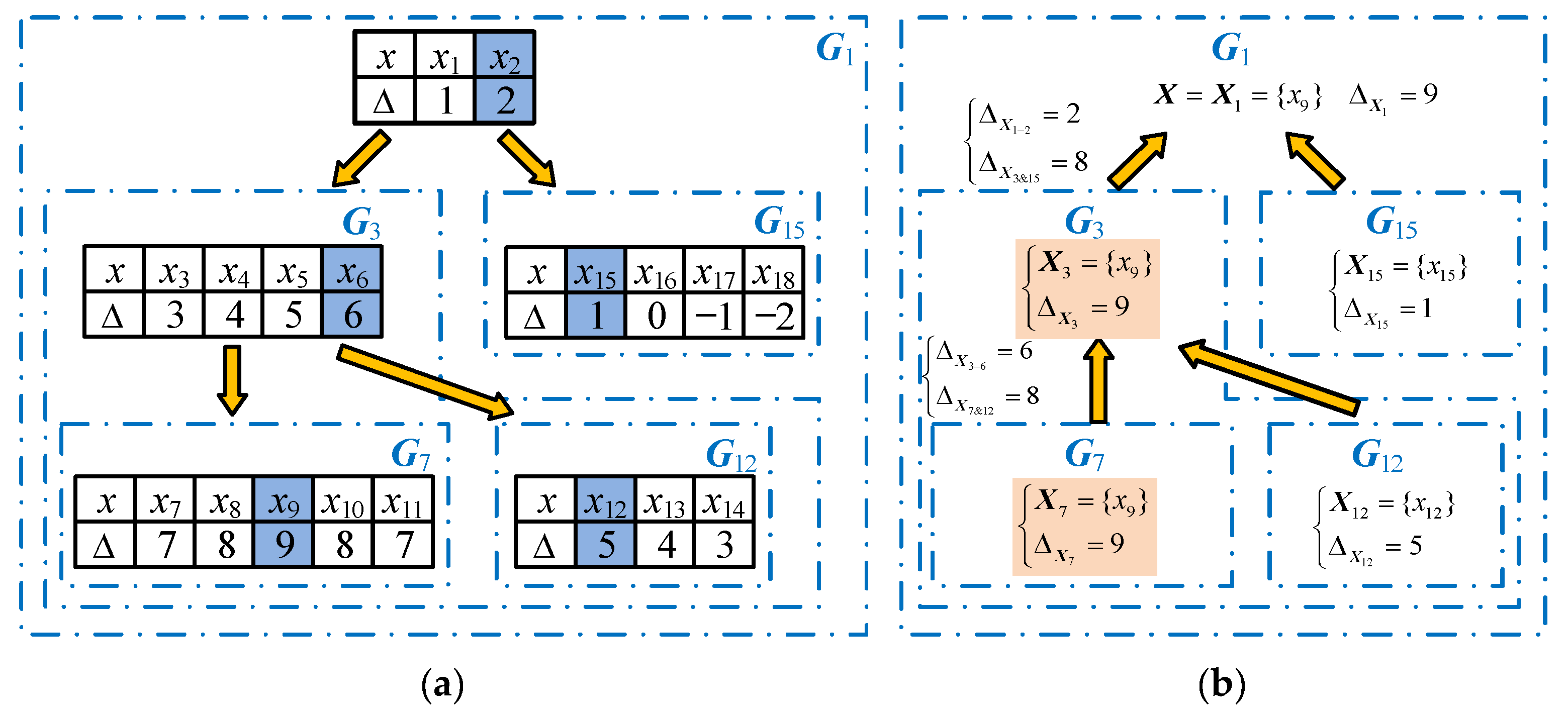
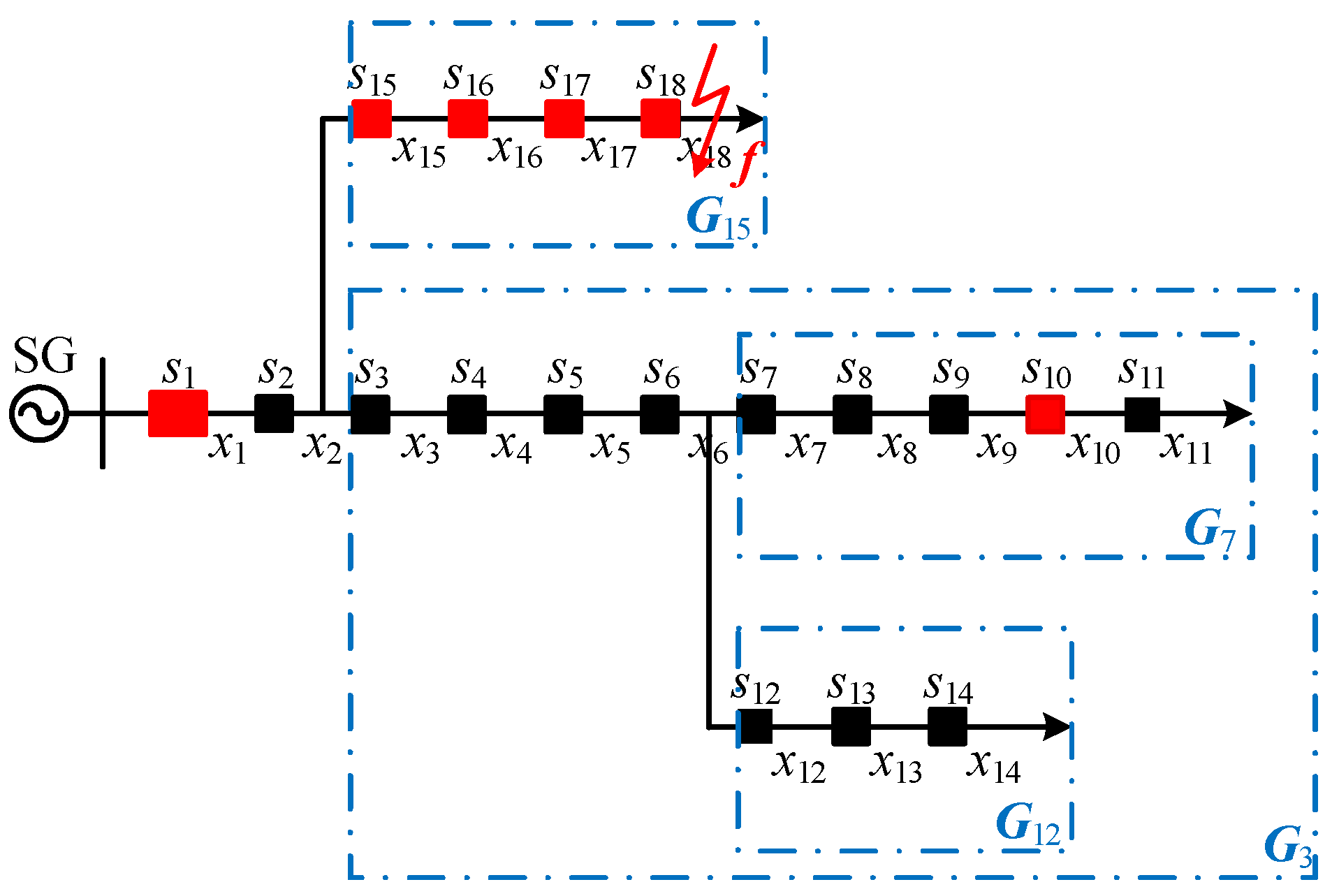
- Divide. Divide the distribution network into smaller subnetworks using the T-type section closest to the main power source as the boundary (the decomposition effect is shown in Figure 4).
- Conquer. Recursively invoke the algorithm to solve the fault candidate set of the subnetwork. If the subnetwork no longer contains a T-type section, the recursion is stopped, and the fault candidate set is constructed directly according to Theorem 8.
- Combine. Combine the fault candidate set of subnetworks to create the fault candidate set of the original network according to Theorem 9.
- Node number and section number. By applying the depth-first search algorithm, the section is traversed with the main power supply as the source node, and the sections are numbered in the order they are accessed so that the section numbers of any subnetwork in the network are consecutive and conform to the numbering rules in this paper.
- Section type vector T. Construct the section type vector T to determine the type of the section. When xk is a T-type section, let T(k) = 1; otherwise, T(k) = 0.
- Adjacency list(Adj). Construct the adjacency list of the section to record the downstream section of each section for a fast search of the adjacency section of the T-type section, which helps implement the “divide” step in the recursive case.
| Algorithm 1 DACFL (i, j, Gragh, I, D) |
| 1: |
| 2: |
| 3: while and do |
| 4: |
| 5: |
| 6: end while |
| 7: if then // base case |
| 8: return (FIND-MAX ()) |
| 9: end if |
| 10: // divide |
| 11: |
| 12: if then |
| 13: |
| 14: |
| 15: else then |
| 16: |
| 17: |
| 18: end if |
| 19: // conquer |
| 20: |
| 21: // combine |
| 22: |
| 23: |
| 24: if then |
| 25: return () |
| 26: elseif then |
| 27: return () |
| 28: elseif then |
| 29: return () |
| 30: else then |
| 31: return () |
| 32: end if |
4.2. Efficiency Analysis
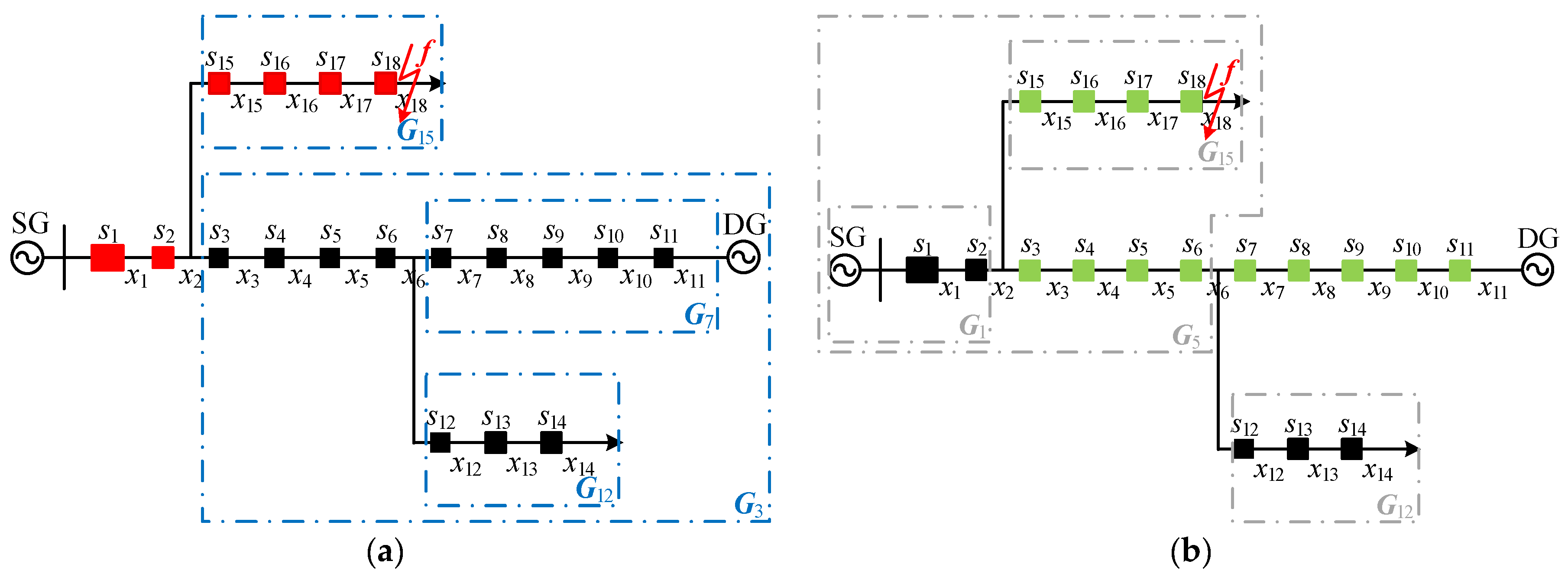
4.3. Active Distribution Network Application Note
- Step 1: Store the network topology information (including node section number, adjacency list, and section type vector T) of the distribution network with each power source as the main power source.
- Step 2: After the failure of the distribution network, take the grid-connected power supply as the main power supply, and the corresponding network topology information and node fault information vector determined by Equation (36) are taken as the input. The fault candidate sets X of each power supply as the main power supply are determined by the fetching algorithm.
- Step 3: The fault candidate sets X obtained from Step 2 is combined to obtain the final fault location result.
4.4. Fault Location Case
4.4.1. Test Case 1: Single Fault
4.4.2. Test Case 2: Multiple Faults
4.4.3. Test Case 3: Fault Information Distortion
4.4.4. Test Case 4: Active Distribution Network
5. Simulation Analysis
5.1. IEEE 33-Node Distribution Network
5.1.1. Accuracy
5.1.2. Fault Tolerance
5.1.3. Computational Efficiency
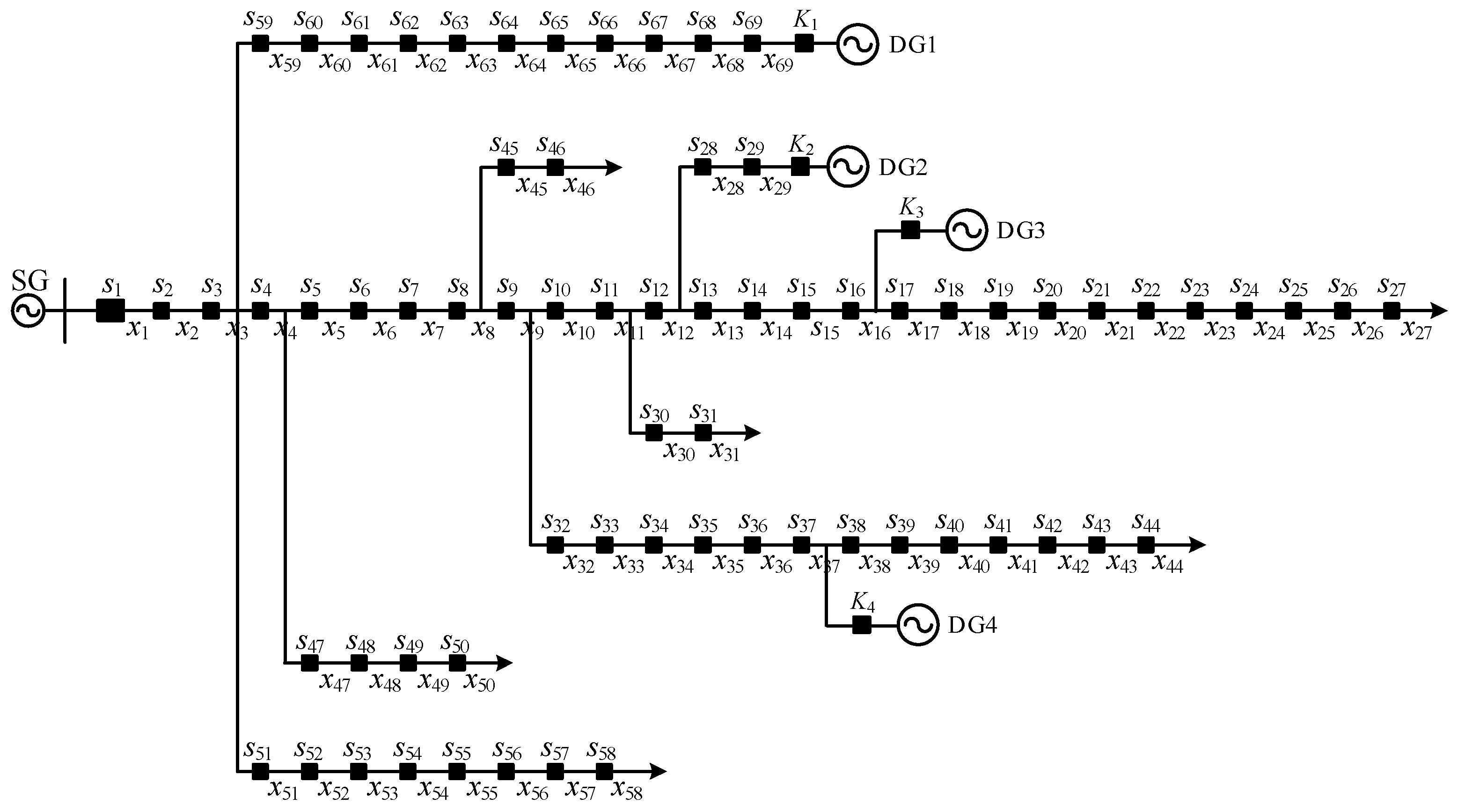
5.2. IEEE 69-Node Distribution Network
5.2.1. Accuracy
5.2.2. Computational Efficiency
5.3. Comparative Analysis of Performance
6. Conclusions
- DAC reduces the operational dimension of fault location to have a linear level of time complexity, which improves the computational efficiency of fault location more significantly. The test results show that for distribution networks with a scale of 33 and 69 nodes, the computational efficiency of the algorithm in this paper is below 20 ms and 50 ms, respectively, which is more than eight times faster than the traditional intelligent optimization algorithms.
- The algorithm in this paper does not contain random search operation; thus, it has strong numerical stability. The test results show that the accuracy of the algorithm in this paper is not affected by the size of the network, and it is more than 19.25% higher than the traditional intelligent optimization algorithm.
- The numerical calculation model of fault location proposed in this paper uses the redundancy of fault information in the whole network to tolerate the distorted information, which can accurately locate the fault with a small amount of distortion in the fault information.
Author Contributions
Funding
Conflicts of Interest
Appendix A. The Proofs of the Properties of Road Vectors


Appendix B. The Proofs of the Properties of Compatible Sets
- (1)
- Sufficiency. , there are obviously . Because satisfies the inequality constraint, , i.e., satisfies the inequality constraint. Similarly, satisfies the inequality constraint. Then, , , and there are . Because satisfies the inequality constraint, and . According to the compatibility set definition, . Because is any element of , .
- (2)
- Necessity. , and if or , due to satisfying the inequality constraint. If , , due to , according to the definition of the following compatible set, . In summary, , and we have . Thus, satisfies the inequality constraint. □
- (1)
- Suppose for the sake of contradiction that but . It is known that section is on the road of section , and according to Theorem 1, , substituting the assumption contradicts the assumption .
- (2)
- Suppose for the sake of contradiction that but . According to Theorem 2, or . If the former equation holds, then , substituting the assumptions , and contradicting the assumption . If the latter equation holds, then . Because is on the road of , , , contradicting the assumption . □
- (1)
- Suppose for the sake of contradiction that but . It is known that section is on the road of section , and according to Theorem 1: . Substitute the assumption , contradicting the assumption .
- (2)
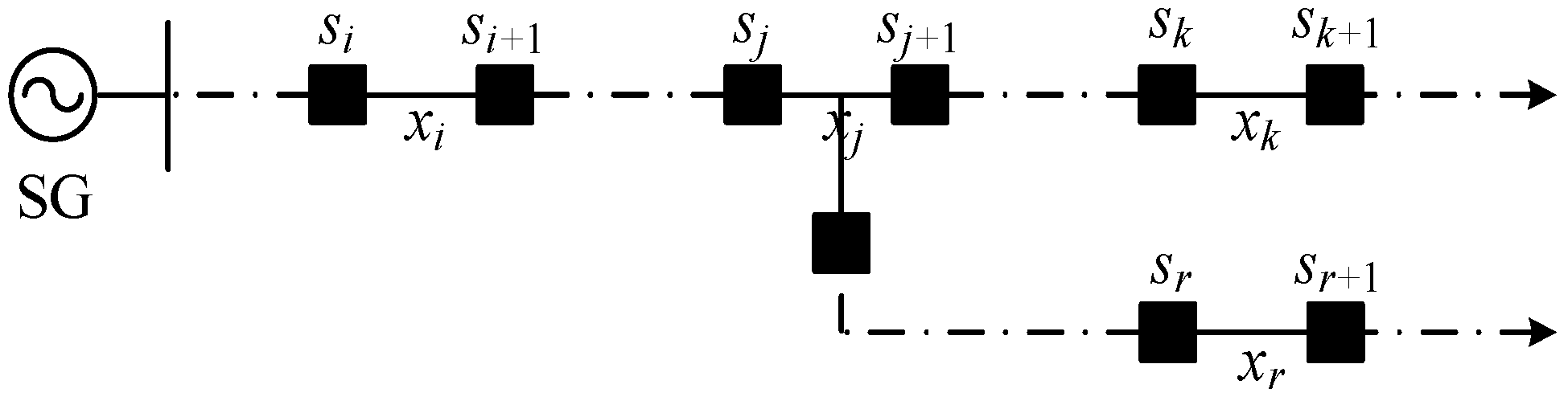
- Suppose for the sake of contradiction that but . According to Theorem 1, section is on the road of section . We claim that there is a path between section and section . Otherwise, under the premise that section is simultaneously on the road of and , the only possibility that there is no path between and , as shown in Figure A3. As can be seen in Figure A3, section is a T-type section, contradicting the condition that the path from to does not contain a T-type section; thus, there is a path between section and section . That is, is on the road of or is on the road of . According to Theorem 1, or , contradicting the assumption . □
Appendix C. The Proofs of the Properties of Approximation Gains
- (1)
- is on the road of . According to Theorem 1, . According to Theorem 2, or . The previous equation cannot hold; otherwise, , substituting , ; thus, , contradicting what is known. According to the latter equation, , substituting into .
- (2)
- is on the road of . According to Theorem 1, . According to Theorem 2, or . The previous equation cannot hold; otherwise, , substituting , , ; thus, . Because and , . The two conclusions contradict each other. According to the latter equation, , substitute into . □
Appendix D. The Proofs of Recursive Structure
- (1)
- Because contains only one element, and are fault candidate sets; thus, , , satisfy the inequality constraint. Then, , , we claim that . Otherwise, by :. Substitute for ; that is, . According to Figure 4, ; thus, , contradicting what is known, . Similarly, . Therefore, , . According to Theorem 4, satisfies the inequality constraint.
- (2)
- Let section xi be the starting section of . Then, , , according to Theorem 4, . We claim that and . If , then , contradicting what is known, . If , by , , then ; thus, , contradicting what is known, . Thus, and hold, i.e., , . Due to : , , , , according to Theorem 1, section xi is on the road of . According to Theorem 5, , , , . Combined with : , , , .
- (1)
- . Same procedure as the proof of Theorem 8: the satisfying the inequality constraint contains only one section, and let . Apply Equations (31) and (33) to rewrite : (the derivation process is similar to Equation (A8)). Similarly, . Because there is no T-type section on the path between and , according to Theorem 6, . , according to the conclusion of step 1, and according to Theorem 7, . Combined with : .
- (2)
- . Because , is the fault candidate set of , according to the definition of fault candidate sets, .
- (3)
- . Because , is the fault candidate set of , according to the definition of fault candidate sets, .
- (4)
- . Let the sets of sections , . Because , . can be equivalently expressed as . It is known that is a fault candidate set of , , , and therefore, . It is known that is a fault candidate set of , , ; therefore, . Combined with , : .
Appendix E. Explanation of the Fast Method for Calculating the Section Approximation Gain in Lines 2 and 5 of the Pseudocode DACFL Recursive Structure
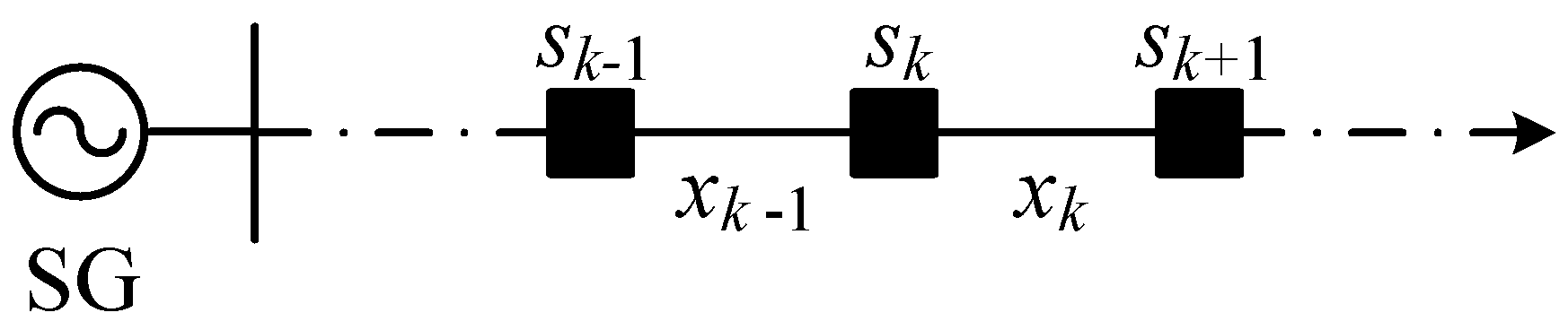
Appendix F. Explanation of the Fast Method for Calculating the Set Approximation Gain in Line 23 of the Pseudocode DACFL
References
- Li, G.; Chen, Q.; Zhang, J. Novel faulted section location method for distribution network based on status information of fault indicating equipment. Appl. Sci. 2020, 10, 5910. [Google Scholar] [CrossRef]
- He, W.; Wang, S.; Xu, T.; Shen, H.; Su, Y.; Liu, Z.; Xiong, Z.; Wang, X. A construction and development path of the urban resilient distribution network. Power Syst. Technol. 2022, 46, 680–690. [Google Scholar]
- Galvez, C.; Abur, A. Fault location in active distribution networks containing distributed energy resources (DERs). IEEE Trans. Power Deliv. 2021, 36, 3128–3139. [Google Scholar] [CrossRef]
- Zhao, F.; Meng, Z.; Li, Y.; Liu, C. Pilot protection scheme for active distribution network based on fault components. High Volt. Eng. 2019, 45, 3092–3100. [Google Scholar]
- Wang, S.; Liu, Q.; Zhao, Q.; Wang, H. Connotation Analysis and Prospect of Distribution Network Elasticity. Autom. Electr. Power Syst. 2021, 45, 1–9. [Google Scholar]
- Shen, G.; Zhang, Y.; Qiu, H.; Wang, C.; Wen, F.; Salam, M.; Weng, L.; Zhang, L.; Zhang, S. Fault diagnosis with false and/or missing alarms in distribution systems with distributed generators. Energies 2018, 11, 2579. [Google Scholar] [CrossRef]
- Wang, S.; Song, L.; Shu, X. Adaptive overcurrent protection of active distribution network with high penetration of distributed generations and multiple loads. High Volt. Eng. 2019, 45, 1783–1794. [Google Scholar]
- Zheng, T.; Ma, L.; Zhang, B. Fault tolerant fast fault section location method for active distribution network. J. N. China Electr. Power Univ. 2022, 49, 12–20. [Google Scholar]
- Zhao, Q. Research on Wide Area Protection of Smart Distribution Grid; North China Electric Power University: Beijing, China, 2017. [Google Scholar]
- Xu, B.; Yin, X.; Zhang, Z.; Pang, S.; Li, X. Fault location for distribution network based on matrix algorithm and optimization algorithm. Autom. Electr. Power Syst. 2019, 43, 152–158. [Google Scholar]
- Ji, X.; Zhang, S.; Zhang, Y.; Han, X.; Xiao, Y.; Zeng, R. Fault section location for distribution network based on improved electromagnetism-like mechanism algorithm. Autom. Electr. Power Syst. 2021, 45, 157–165. [Google Scholar]
- Teng, J.; Huang, W.; Luan, S. Automatic and fast faulted line-section location method for distribution systems based on fault indicators. IEEE Trans. Power Syst. 2014, 4, 1653–1662. [Google Scholar] [CrossRef]
- Ma, T.; Gao, L. Fault location algorithm for active distribution network with multi micro-grids. Power Syst. Prot. Control 2017, 45, 64–68. [Google Scholar]
- Wang, Q.; Jin, T.; Mohamed, A. A fast and robust fault section location method for power distribution systems considering multisource information. IEEE Syst. J. 2022, 16, 1954–1964. [Google Scholar] [CrossRef]
- Jiao, Y.; Du, S.; Wang, Q.; Chen, C. Information aberrance correction and fault-section location for distribution networks based on the information contradiction theory. Power Syst. Prot. Control 2014, 42, 43–48. [Google Scholar]
- Zheng, T.; Ma, L.; Li, B. Fault section location of active distribution network based on feeder terminal unit information distortion correction. Power Syst. Technol. 2021, 45, 3926–3934. [Google Scholar]
- Kong, B.; Liu, J.; Zhou, J.; Zhou, Y.; Song, Z. Fault-tolerant algorithm for fault location in distribution network based on integer linear programming. Power Syst. Prot. Control 2020, 48, 27–35. [Google Scholar]
- Wei, Z.; He, H.; Zheng, Y. A refined genetic algorithm for the fault sections location. Proc. CSEE 2002, 22, 127–130. [Google Scholar]
- Guo, Z.; Chen, B.; Liu, C.; Xu, K.; Li, J. Fault location of distribution network based on genetic algorithm. Power Syst. Technol. 2007, 31, 88–92. [Google Scholar]
- Zhao, Q.; Wang, Z.; Dong, W.; Bao, W. Research on fault location in a distribution network based on an immune binary particle swarm algorithm. Power Syst. Prot. Control 2020, 48, 83–89. [Google Scholar]
- Zhang, Y.; Zhou, R.; Zhong, K. Application of improved ant colony algorithm in fault-section location of complex distribution network. Power Syst. Technol. 2011, 35, 224–228. [Google Scholar]
- Liu, B.; Wang, F.; Chen, C.; Huang, H.; Dong, X. Harmony search algorithm for solving fault location in distribution networks with DG. Trans. China Electrotech. Soc. 2013, 28, 280–284. [Google Scholar]
- Wang, Q.; Jin, T.; Tan, H.; Zhu, S.; Liu, S. A complete analytic model of section location in distribution network based on multi-factor dimensionality deduction. Trans. China Electrotech. Soc. 2019, 34, 3012–3024. [Google Scholar]
- Guo, Z.; Xu, Q.; Hong, J.; Mao, X. Integer linear programming based fault section diagnosis method with high fault-tolerance and fast performance for distribution network. Proc. CSEE 2017, 37, 786–795. [Google Scholar]
- He, R.; Hu, Z.; Li, Y.; Wang, T. Fault section location method for DG-DNs based on integer linear programming. Power Syst. Technol. 2018, 42, 3684–3690. [Google Scholar]
- Li, Z.; Wang, Z.; Zhang, Y.; Qiao, X. Fault section location method for active distribution network based on linear programming with ascending dimension. Autom. Electr. Power Syst. 2021, 12, 122–131. [Google Scholar]
- Yin, Y.; Wang, D.; Yu, Y. Integer Programming, 1st ed.; Science Press: Beijing, China, 2022; pp. 56–66. [Google Scholar]
- Wang, Q.; Jin, T.; Tan, H.; Li, Z. The technology on fault location of distribution network based on hierarchical model and intelligent checking algorithm. Trans. China Electrotech. Soc. 2018, 33, 5327–5337. [Google Scholar]
- Zheng, C.; Zhou, H.; Zheng, D.; Lin, Z.; Zhang, X. An active distribution network fault location method based on improved multi-universe algorithm. Power Syst. Prot. Control 2023, 51, 169–179. [Google Scholar]
- Gao, F.Y.; Li, Z.J.; Yuan, C.; Qi, X.D.; Li, X.F.; Zhuang, S.X. Fault location for active distribution network based on quantum computing and immune optimization algorithm. High Volt. Eng. 2021, 47, 396–406. [Google Scholar]
- Yang, G.; Feng, J.; Liu, X.; Chen, R.; Pan, H.; Yang, Q. Fault location of a distribution network hierarchical model with a distribution generator based on IBES. Power Syst. Prot. Control 2022, 50, 1–9. [Google Scholar]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.; The MIT Press: London, UK, 2009; pp. 24–37. [Google Scholar]
- Li, Y.; Wang, Z.; Zhao, Q. Distributed fault section location for ADN based on bayesian complete analytic model and multi-factor dimension reduction. Power Syst. Technol. 2021, 45, 3917–3925. [Google Scholar]









| Method | Characteristics |
|---|---|
| Matrix algorithm | It has fast location speed but poor information fault tolerance. |
| Intelligent optimization algorithm | It has high fault information tolerance, but its computational efficiency and convergence stability are poor. |
| Linear integer programming algorithm | It has high fault information tolerance and strong convergence stability but poor computational efficiency. |
| Hierarchical fault location method | Its convergence reliability and computational efficiency are better than the intelligent optimization algorithm, but it requires higher information reliability in port nodes. |
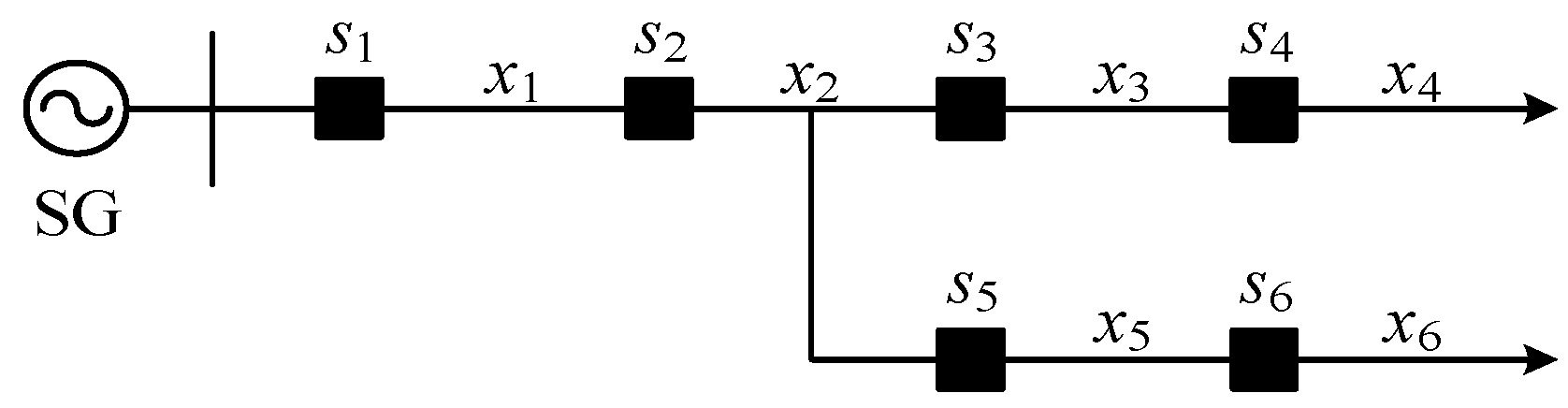
| Node | Causal Device (Section) | Status Information of the Causal Device | Total Number |
|---|---|---|---|
| s1 | x1~x6 | y1~y6 | 6 |
| s2 | x2~x6 | y2~y6 | 5 |
| s3 | x3, x4 | y3, y4 | 2 |
| s4 | x4 | y4 | 1 |
| s5 | x5, x6 | y5, y6 | 2 |
| s6 | x6 | y6 | 1 |
| Number | Fault Scenario | X | [J1(X)~J6(X)] | f(X) |
|---|---|---|---|---|
| 1 | x1 failure | {x1} | [1 0 0 0 0 0] | 3 + ω |
| 2 | x2 failure | {x2} | [1 1 0 0 0 0] | 2 + ω |
| 3 | x3 failure | {x3} | [1 1 1 0 0 0] | 1 + ω |
| 4 | x4 failure | {x4} | [1 1 1 1 0 0] | ω |
| 5 | x5 failure | {x5} | [1 1 0 0 1 0] | 3 + ω |
| 6 | x6 failure | {x6} | [1 1 0 0 1 1] | 4 + ω |
| 7 | x1 and x2 failure | {x1, x2} | [1 1 0 0 0 0] | 2 + 2ω |
| 8 | x1 and x3 failure | {x1, x3} | [1 1 1 0 0 0] | 1 + 2ω |
| … | … | … | … | … |
| 26 | x1~x6 failure | {x1, x2, x3, x4, x5, x6} | [1 1 1 1 1 1] | 2 + 6ω |
| Steps | Number of Executions | Operation Cost | f(X) |
|---|---|---|---|
| Lines 1~2 | l | Θ(1) | Θ(l) |
| Lines 3~5 | n | Θ(1) | Θ(n) |
| Line 6~7 | l | Θ(1) | Θ(l) |
| Lines 8, 21 | < l | Θ(j-i) or Θ(k-i) | Θ(n) |
| Line 9 | l | Θ(1) | Θ(l) |
| Lines 10~20 | < l | Θ(1) | O(l) |
| Lines 22~32 | < l | Θ(1) | O(l) |
| Algorithm Number | Algorithm Type | Fault Location Method |
|---|---|---|
| Algorithm 1 | Algorithm in this paper | Algorithm in this paper. Construct a numerical computational model for fault location with the help of road vector, and apply DAC to locate the fault. |
| Algorithm 2 | Intelligent optimization algorithm | Assuming all possible fault scenarios in the distribution network, construct a solution space and apply the binary particle swarm optimization algorithm to locate the fault section in the solution space. |
| Algorithm 3 | Hierarchical fault location algorithm | Partition the distribution network according to the branch structure, apply the bald eagle search algorithm to locate the fault branch first, and then determine the fault section by applying the exhaustive method in the fault branch. |
| Algorithm 4 | Linear integer programming algorithm | Construct a linear integer programming model for fault location using ascending dimension and apply the branch and bound method to locate the fault. |
| Equipment Number | Preset Fault Section | Accuracy (%) | |||
|---|---|---|---|---|---|
| Algorithm 1 | Algorithm 2 | Algorithm 3 | Algorithm 4 | ||
| 1 | x8 | 100 | 94 | 99 | 100 |
| 2 | x26 | 100 | 80 | 100 | 100 |
| 3 | x28 | 100 | 82 | 100 | 100 |
| 4 | x30 | 100 | 78 | 99 | 100 |
| 5 | x4, x29 | 100 | 96 | 100 | 100 |
| 6 | x11, x28 | 100 | 84 | 96 | 100 |
| 7 | x25, x30 | 100 | 81 | 100 | 100 |
| 8 | x6, x27 | 100 | 95 | 100 | 100 |
| Equipment Number | Preset Fault Section | Preset Information Distortion | Accuracy (%) | |||
|---|---|---|---|---|---|---|
| Algorithm 1 | Algorithm 2 | Algorithm 3 | Algorithm 4 | |||
| 1 | x3 | I16: 0 → 1 | 100 | 84 | 100 | 100 |
| 2 | x18 | I7: 1 → 0, I32: 0 → 1 | 100 | 80 | Misjudgment | 100 |
| 3 | x23 | I4: 1 → 0 | 100 | 88 | 100 | 100 |
| 4 | x33 | I11: 0 → 1, I20: 0 → 1 | 100 | 86 | 99 | 100 |
| 5 | x7, x22 | I14: 1 → 0 | 100 | 90 | 100 | 100 |
| 6 | x10, x33 | I6: 1 → 0, I30: 1 → 0 | 100 | 70 | 98 | 100 |
| 7 | x16, x27 | I7: 1 → 0, I22: 0 → 1, I32: 0 → 1 | 100 | 76 | Misjudgment | 100 |
| 8 | x14, x26 | I10: 1 → 0 | 100 | 72 | 100 | 100 |
| Equipment Number | Preset Fault Section | Preset Information Distortion | Computational Efficiency (ms) | |||
|---|---|---|---|---|---|---|
| Algorithm 1 | Algorithm 2 | Algorithm 3 | Algorithm 4 | |||
| 1 | x18 | 13.27 | 131.43 | 75.27 | 118.18 | |
| 2 | x24 | I9: 0 → 1, I20: 1 → 0 | 13.86 | 128.29 | 79.34 | 116.76 |
| 3 | x6 | I12: 0 → 1 | 15.16 | 128.45 | 77.98 | 126.72 |
| 4 | x33 | I2: 1 → 0 | 16.85 | 129.23 | 76.25 | 142.61 |
| 5 | x11, x20 | I8: 1 → 0, I29: 0 → 1 | 14.33 | 133.67 | 103.56 | 121.98 |
| 6 | x17, x33 | I22: 0 → 1 | 13.46 | 128.92 | 109.54 | 130.47 |
| 7 | x4, x29 | 15.32 | 133.96 | 108.48 | 152.42 | |
| 8 | x12, x23 | I5: 1 → 0, I8: 1 → 0, I15: 0 → 1 | 15.05 | 149.75 | 106.26 | 112.01 |
| Equipment Number | [K1, K2, K3, K4] | Preset Fault Section | Preset Information Distortion |
|---|---|---|---|
| 1 | [1, 1, 1, 1] | x52 | I8: −1 → 0 |
| 2 | [0, 1, 1, 1] | x15 | I49: 0 → 1 |
| 3 | [1, 1, 1, 1] | x57 | I20: 0 → −1, I51: 1 → 0 |
| 4 | [1, 0, 1, 1] | x16, x32 | I8: 1 → 0, I25: 0 → 1, I39: 0 → −1 |
| 5 | [0, 1, 1, 1] | x64 | |
| 6 | [1, 1, 0, 1] | x10, x36 | I15: 0 → −1 |
| 7 | [1, 1, 1, 0] | x12, x35 | I7: 1 → 0, I32: 1 → 0, I41: 0 → −1 |
| 8 | [1, 1, 1, 1] | x56, x67 | I35: −1 → 0, I63: 1 → −1 |
| 9 | [1, 1, 1, 1] | x14, x23 | I17: 1 → 0, I34: −1 → 1, I43: 0 → 1 |
| 10 | [1, 1, 1, 1] | x9, x59 | I24: 0 → 1, I63: −1 → 0 |
| 11 | [1, 0, 0, 1] | x27, x34 | |
| 12 | [1, 0, 1, 1] | x7 | I34: −1 → 1, I62: −1 → 0 |
| Algorithm Number | Algorithm Type | Accuracy | Computational Efficiency |
|---|---|---|---|
| Algorithm 1 | Algorithm in this paper | Highest | Highest |
| Algorithm 2 | Intelligent optimization algorithm | Low | Low |
| Algorithm 3 | Hierarchical fault location algorithm | Higher | Higher |
| Algorithm 4 | Linear integer programming algorithm | Highest | Lowest |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Q.; Wang, Z.; Li, G.; Liu, X.; Wang, Y. A Fault Section Location Method for Distribution Networks Based on Divide-and-Conquer. Appl. Sci. 2023, 13, 5974. https://doi.org/10.3390/app13105974
Zhao Q, Wang Z, Li G, Liu X, Wang Y. A Fault Section Location Method for Distribution Networks Based on Divide-and-Conquer. Applied Sciences. 2023; 13(10):5974. https://doi.org/10.3390/app13105974
Chicago/Turabian StyleZhao, Qiao, Zengping Wang, Guomin Li, Xuanjun Liu, and Yuxuan Wang. 2023. "A Fault Section Location Method for Distribution Networks Based on Divide-and-Conquer" Applied Sciences 13, no. 10: 5974. https://doi.org/10.3390/app13105974
APA StyleZhao, Q., Wang, Z., Li, G., Liu, X., & Wang, Y. (2023). A Fault Section Location Method for Distribution Networks Based on Divide-and-Conquer. Applied Sciences, 13(10), 5974. https://doi.org/10.3390/app13105974





