Adaptive PI + VPI Harmonic Current Compensation Strategy under Weak Grid Conditions
Abstract
:1. Introduction
2. Influence of Weak Grid Conditions on the APF System
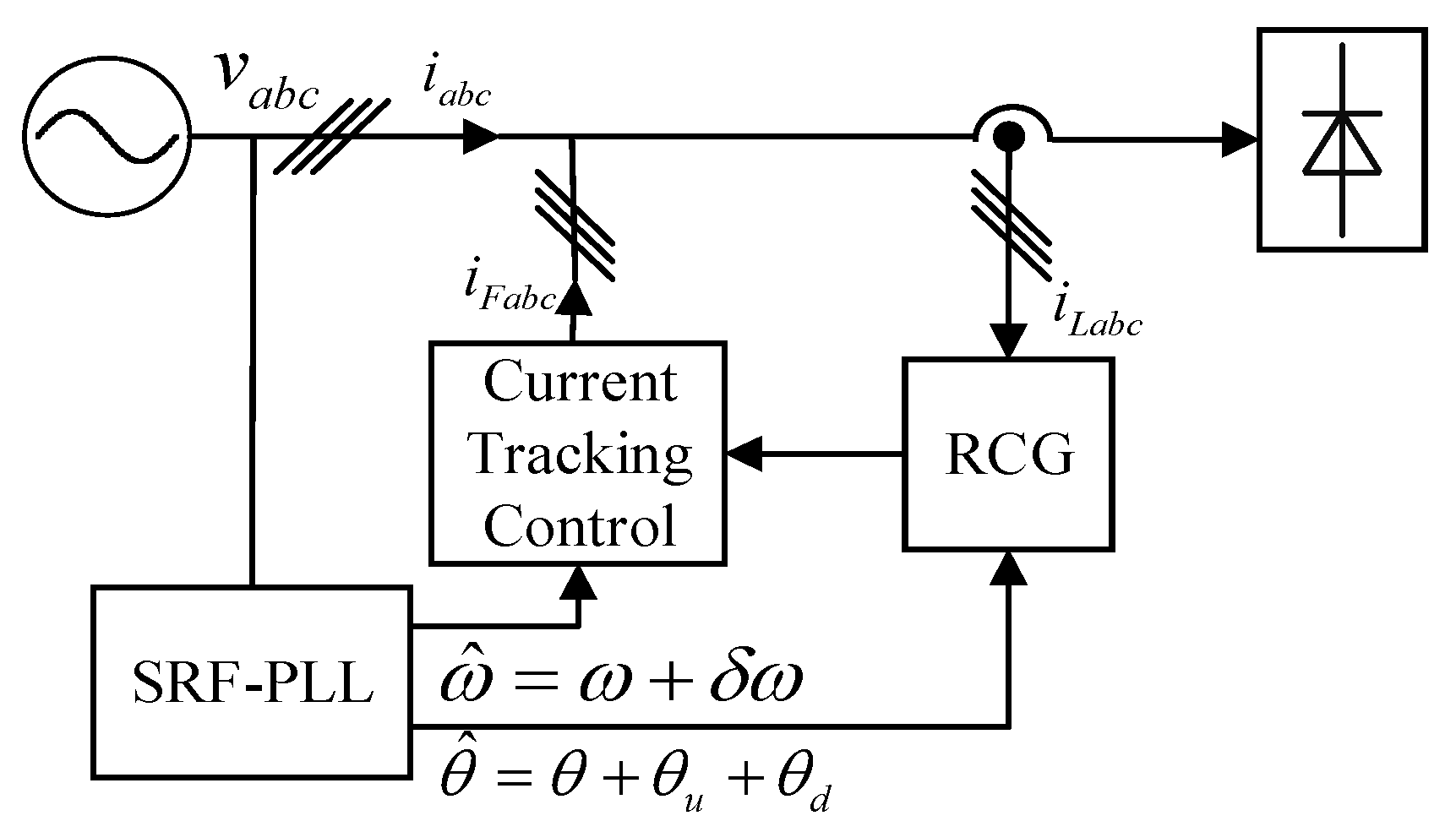
2.1. Three-Phase SRF-PLL and APF Control System
2.2. Structure and Modeling of the Synchronous Phase-Locked Loop
2.3. Influence of Grid Voltage Distortion and Unbalance
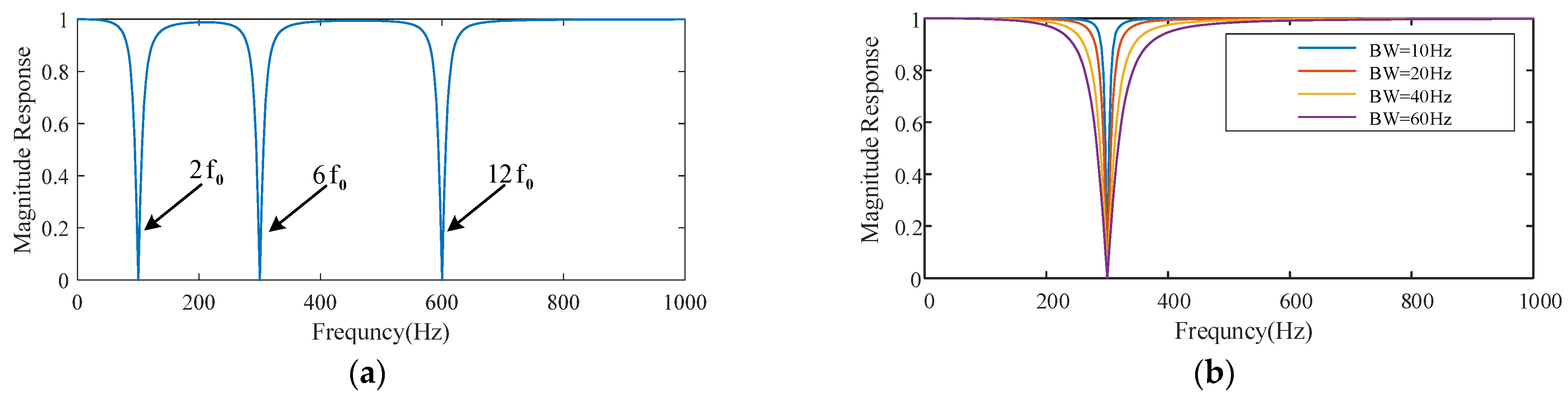
2.4. SRF-PLL Based on the Notch Filter
2.5. Influence of Grid-Side Voltage Frequency Deviation
3. Adaptive SRF-PLL Based on a Lattice Notch Filter
3.1. Lattice Notch Filter
3.2. Adaptive Lattice Notch Filter
3.3. SRF-PLL Based on Adaptive Notch Filter
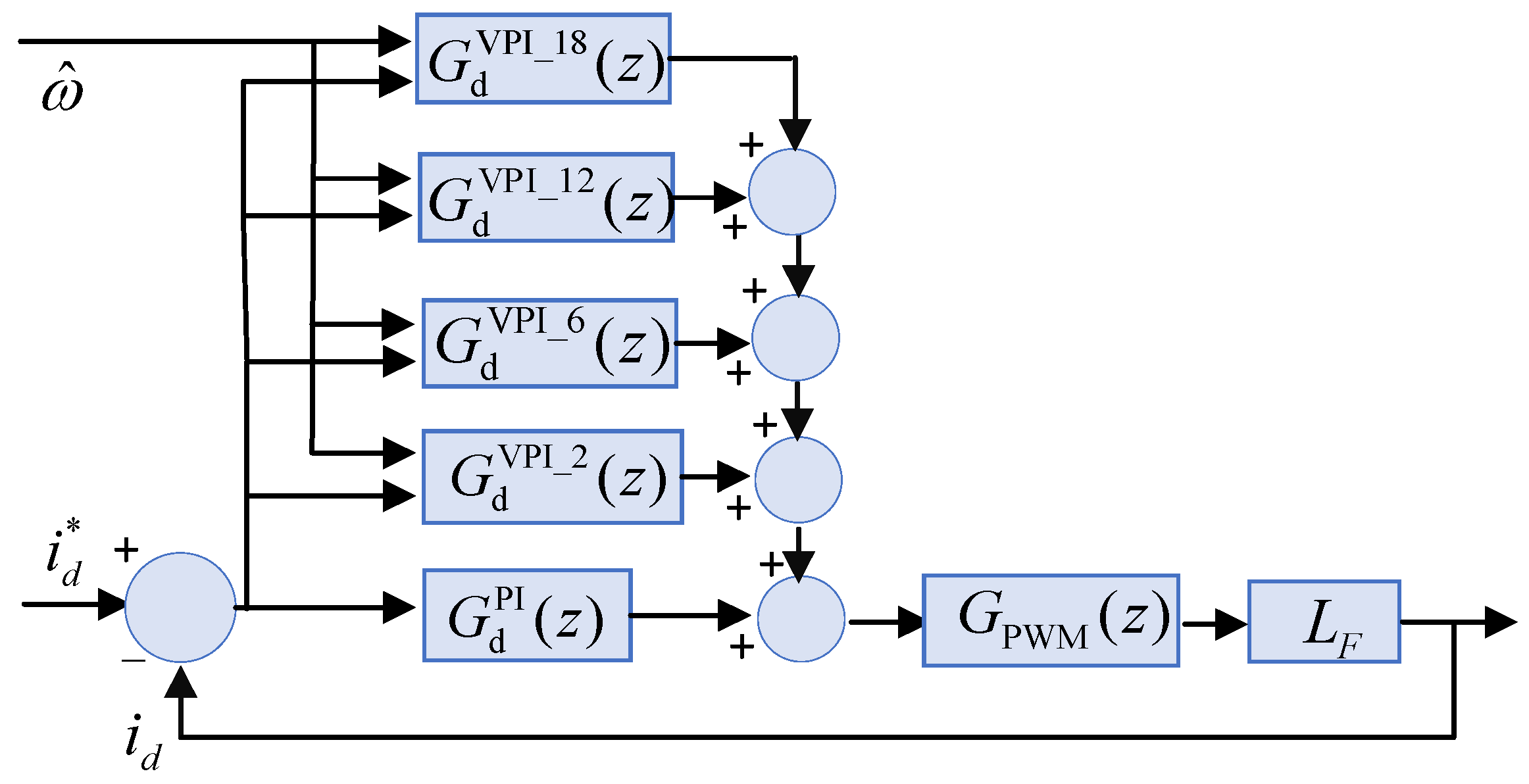
4. Adaptive VPI Current Tracking Control System
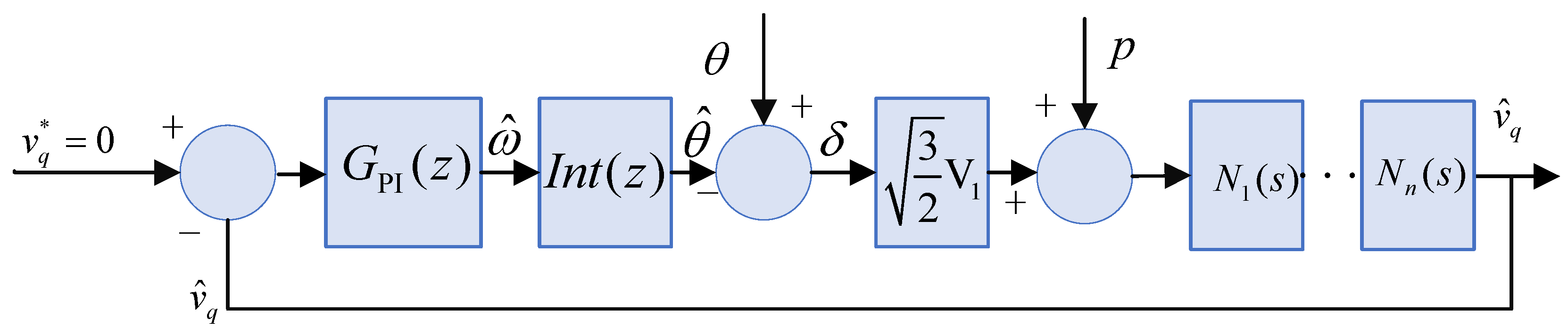
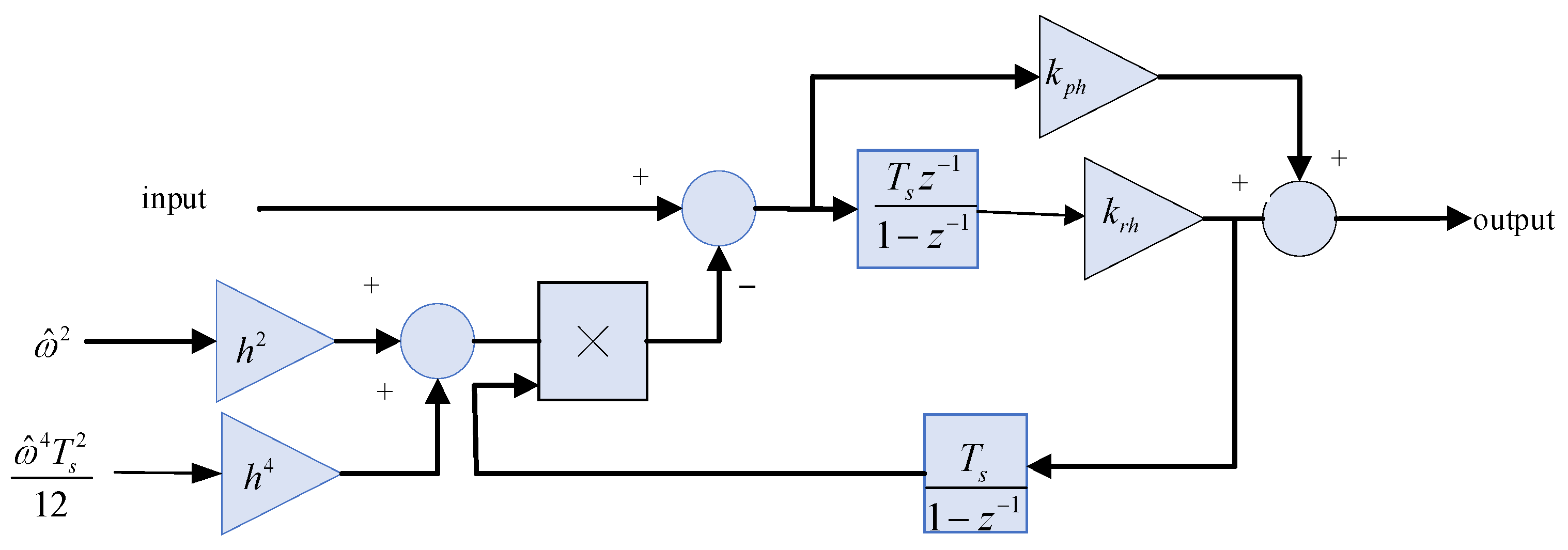
4.1. Mathematical Modeling of Digital Frequency Adaptive VPI Current Tracking Controller
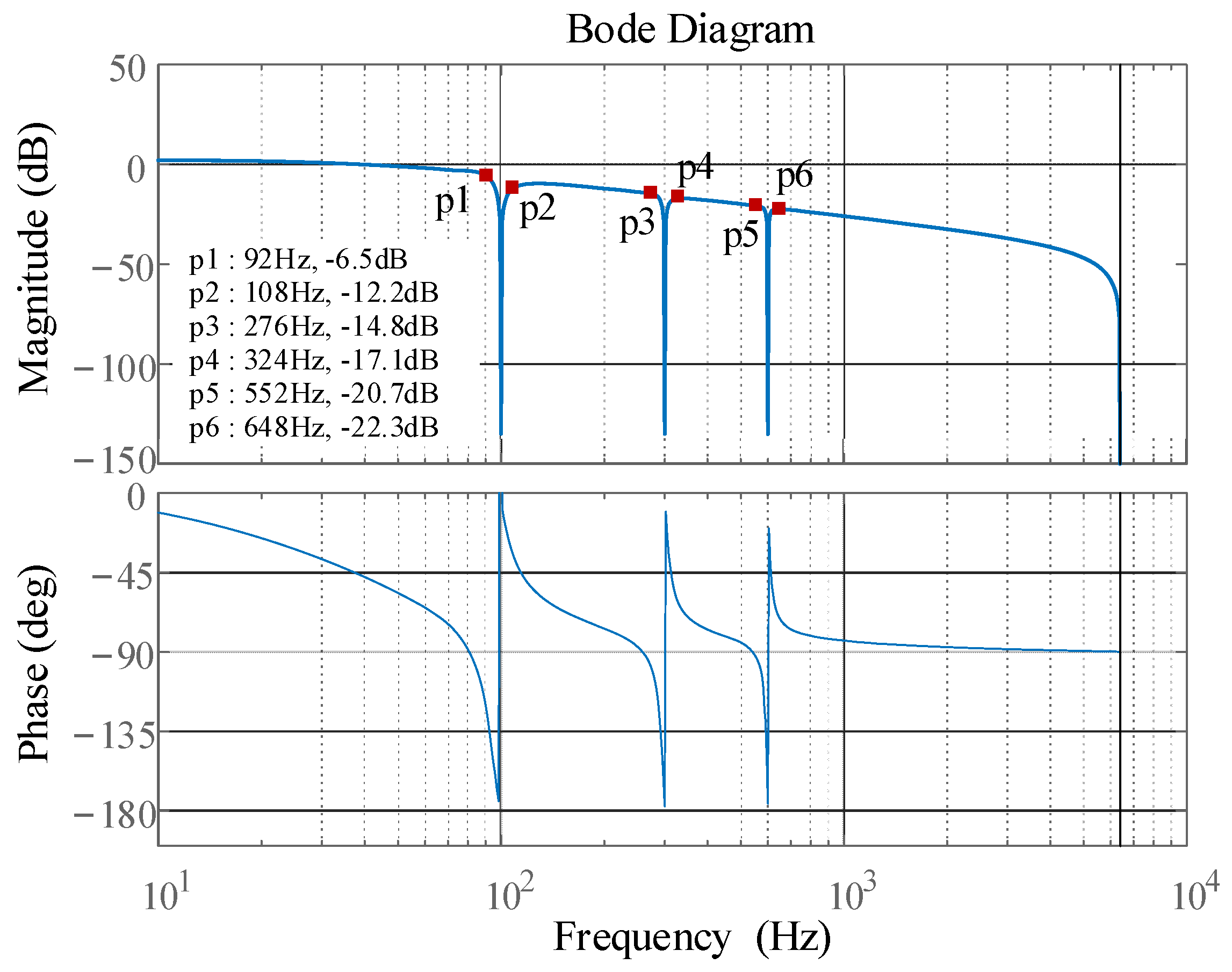
4.2. Analysis and Design of Controller
5. Simulation Analysis and Experiment
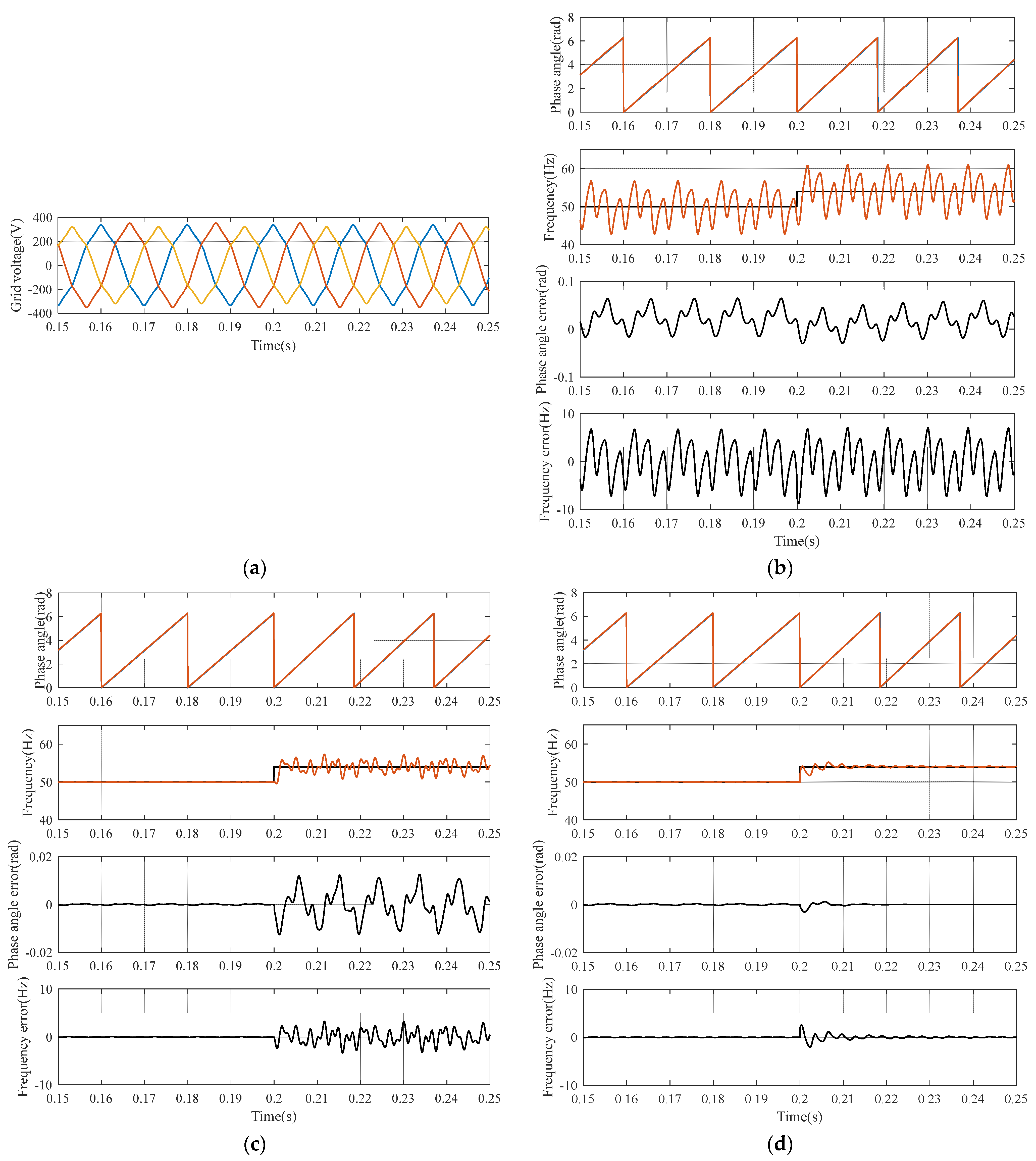
5.1. Phase-Locked Performance Verification under Various Grid Voltage Conditions
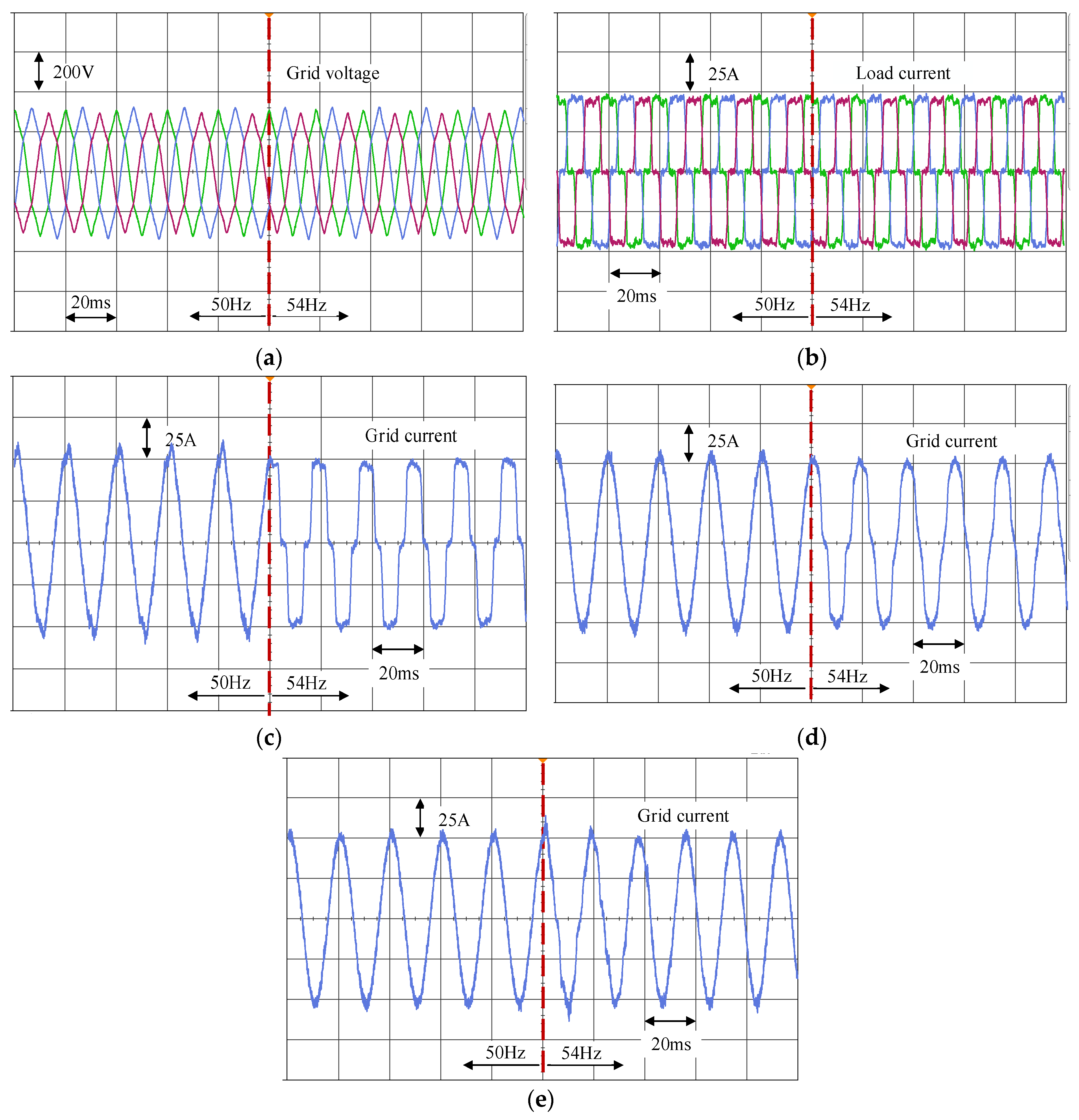
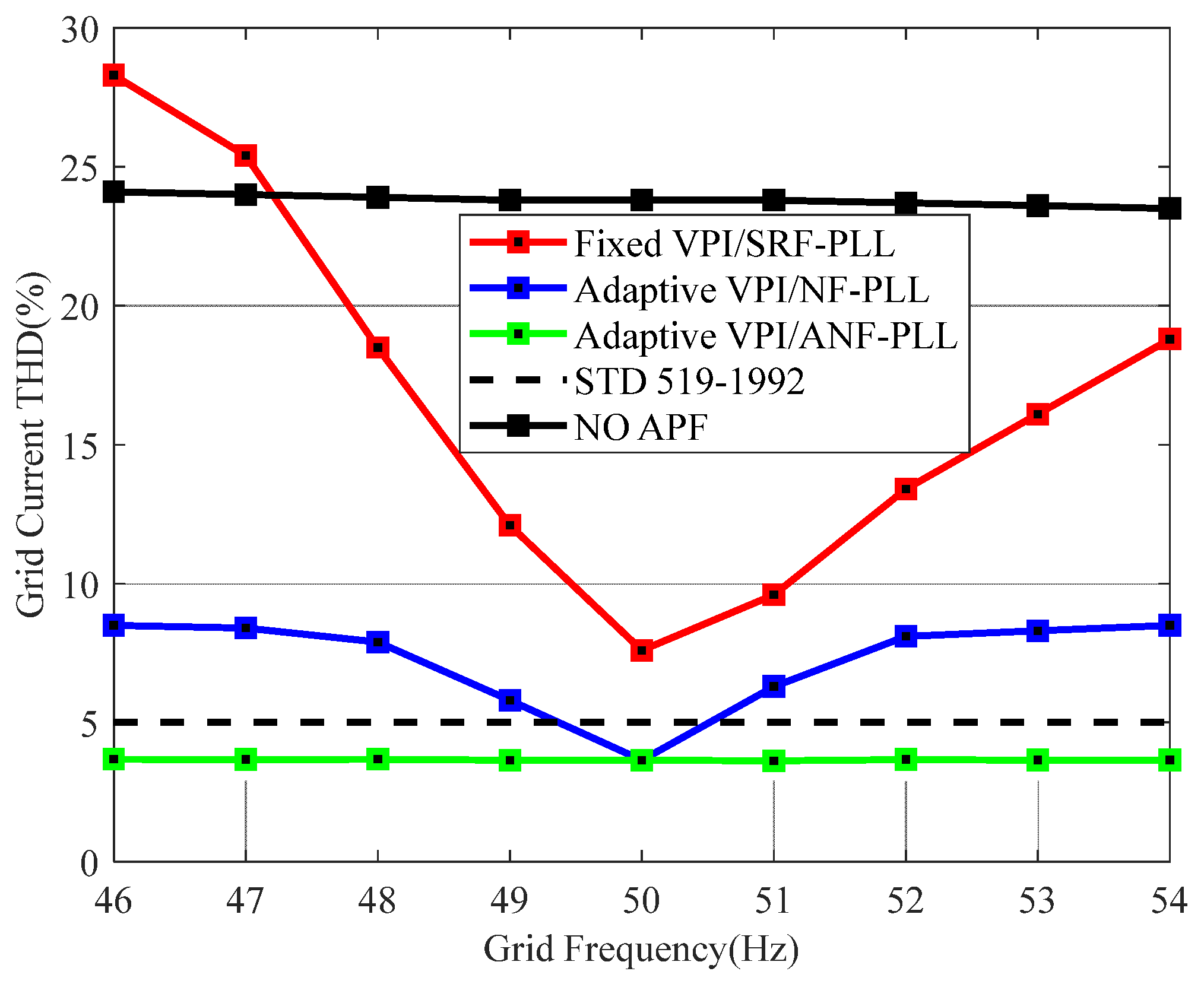
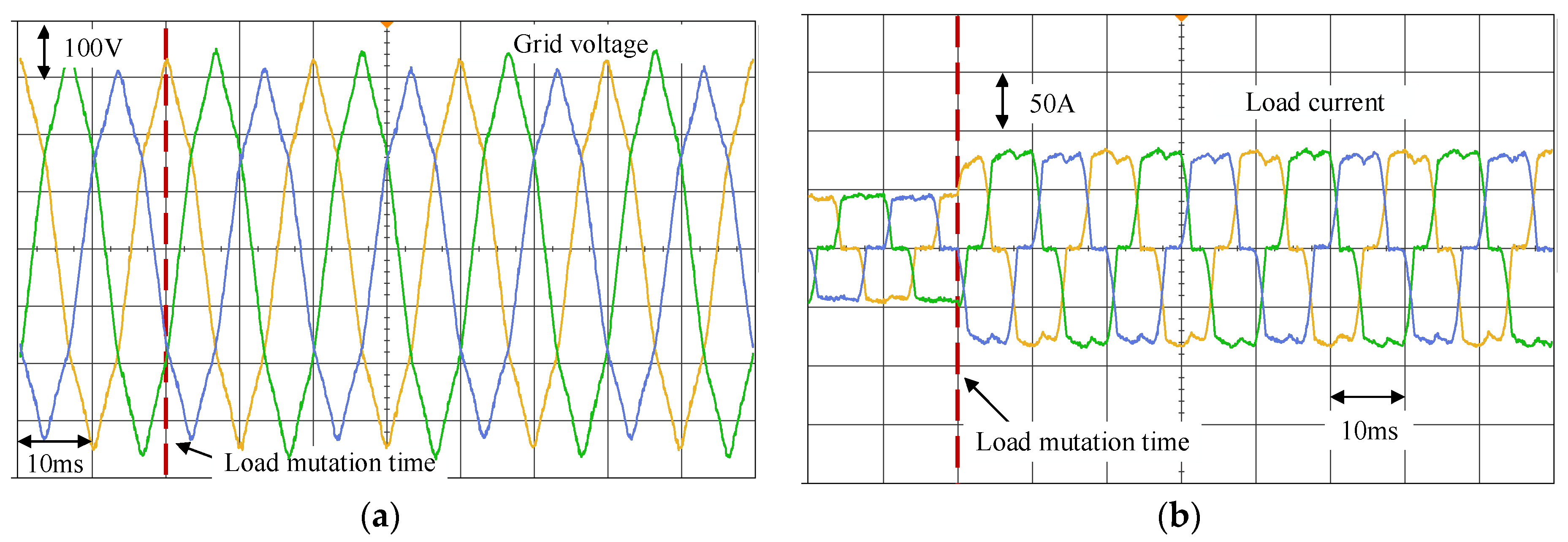
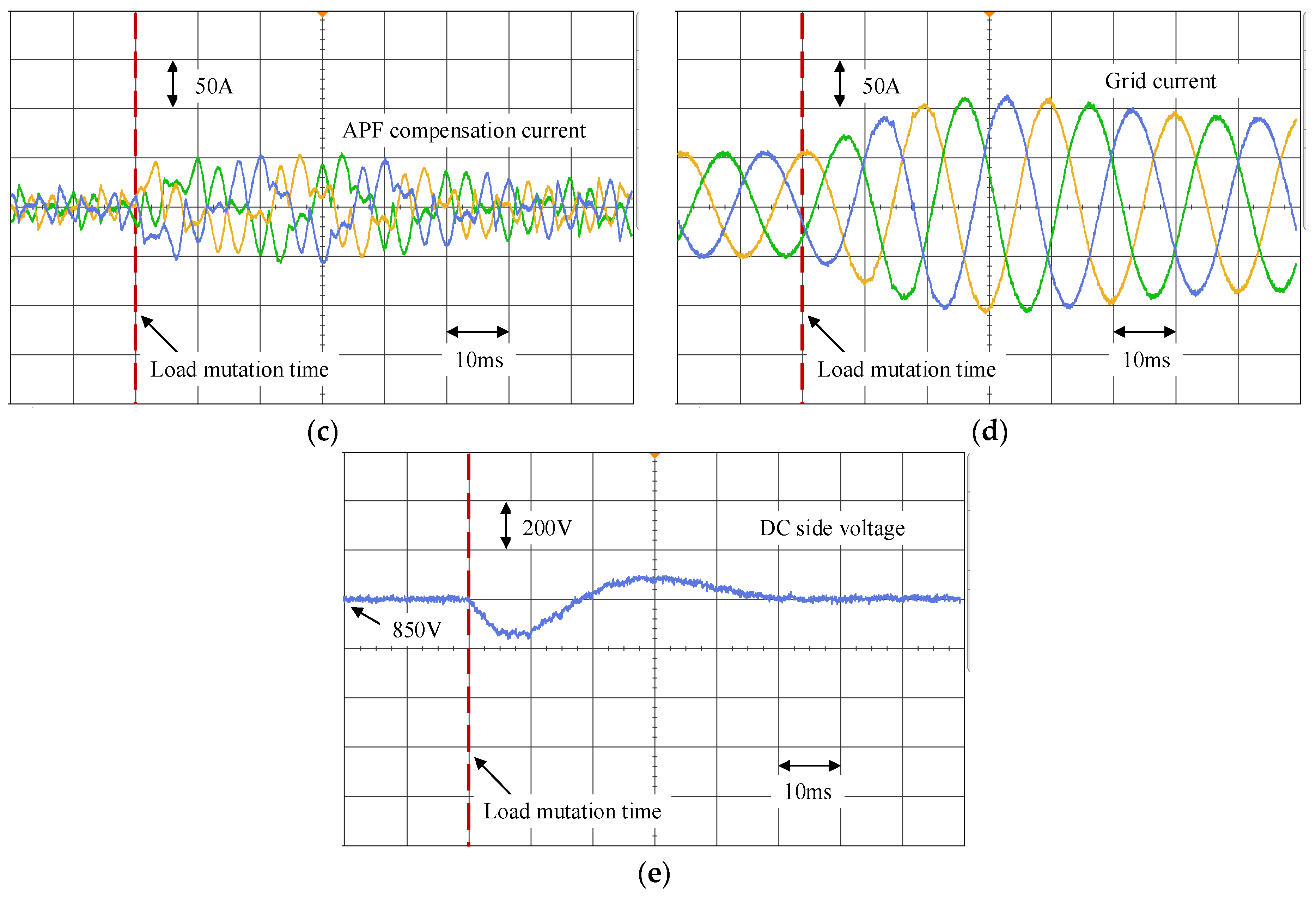
5.2. Verification of APF Compensation Performance under Weak Grid Conditions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. On the inertia of future more-electronics power systems. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 7, 2130–2146. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Y.; Wang, S.; Chen, J.; Gong, C. Impedance-phased dynamic control method for grid-connected inverters in a weak grid. IEEE Trans. Power Electron. 2016, 32, 274–283. [Google Scholar] [CrossRef]
- Yoon, S.J.; Tran, T.V.; Kim, K.H. Stability assessment of current controller with harmonic compensator for LCL-filtered grid-connected inverter under distorted weak grid. Appl. Sci. 2020, 11, 212. [Google Scholar] [CrossRef]
- Lin, P.; Shi, Y.; Sun, X.M. A Class of Nonlinear Active Disturbance Rejection Loop Filters for Phase-Locked Loop. IEEE Trans. Ind. Electron. 2021, 69, 1920–1928. [Google Scholar] [CrossRef]
- Pan, H.; Li, Z.; Wei, T. A Novel Phase-Locked Loop with Improved-Dual Adaptive Notch Filter and Multi-Variable Filter. IEEE Access 2019, 7, 176578–176586. [Google Scholar] [CrossRef]
- Mellouli, M.S.; Hamouda, M.; Slama, J.B.H.; Al-Haddad, K. A Third-order MAF Based QT1-PLL That is Robust against Harmonically Distorted Grid Voltage with Frequency Deviation. IEEE Trans. Energy Conver. 2021, 36, 1600–1613. [Google Scholar] [CrossRef]
- Asadi, Y.; Eskandari, M.; Mansouri, M.; Chaharmahali, S.; Moradi, M.H.; Tahriri, M.S. Adaptive Neural Network for a Stabilizing Shunt Active Power Filter in Distorted Weak Grids. Appl. Sci. 2022, 12, 8060. [Google Scholar] [CrossRef]
- Reza, M.S.; Hossain, M.M. Integrator-Less Method for Phase Angle Estimation of Fundamental Frequency Positive-Sequence Component under Adverse Condition. IEEE Trans. Instrum. Meas. 2021, 70, 9003010. [Google Scholar] [CrossRef]
- Hung, G.K.; Chang, C.C.; Chen, C.L. Automatic phase-shift method for islanding detection of grid-connected photovoltaic inverters. IEEE Power Eng. Rev. 2007, 22, 55. [Google Scholar] [CrossRef]
- Han, Y.; Young, P.M.; Jain, A.; Zimmerle, D. Robust Control for Microgrid Frequency Deviation Reduction with Attached Storage System. IEEE Trans. Smart Grid 2014, 6, 557–565. [Google Scholar] [CrossRef]
- Rodriguez, P.; Luna, A.; Candela, I.; Mujal, R.; Teodorescu, R.; Blaabjerg, F. Multiresonant Frequency-Locked Loop for Grid Synchronization of Power Converters under Distorted Grid Conditions. IEEE Trans. Ind. Electron. 2010, 58, 127–138. [Google Scholar] [CrossRef] [Green Version]
- Hadjidemetriou, L.; Kyriakides, E.; Blaabjerg, F. A Robust Synchronization to Enhance the Power Quality of Renewable Energy Systems. IEEE Trans. Ind. Electron. 2015, 62, 4858–4868. [Google Scholar] [CrossRef]
- Li, Y.; Wang, D.; Han, W.; Tan, S.; Guo, X. Performance improvement of quasi-type-1 PLL by using a complex notch filter. IEEE Access 2016, 4, 6272–6282. [Google Scholar] [CrossRef]
- Li, Y.; Wang, D.; Han, W.; Sun, Z.; Yuan, T. A Hybrid Filtering Stage Based Quasi-type-1 PLL under Distorted Grid Conditions. J. Power Electron. 2017, 17, 704–715. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.-J.; Lee, J.P.; Shin, D.; Yoo, D.W.; Kim, H.J. A Novel Grid Synchronization PLL Method Based on Adaptive Low-Pass Notch Filter for Grid-Connected PCS. IEEE Trans. Ind. Electron. 2013, 61, 292–301. [Google Scholar] [CrossRef]
- Lascu, C.; Asiminoaei, L.; Boldea, I.; Blaabjerg, F. High Performance Current Controller for Selective Harmonic Compensation in Active Power Filters. IEEE Trans. Power Electron. 2007, 22, 1826–1835. [Google Scholar] [CrossRef]
- Lascu, C.; Asiminoaei, L.; Boldea, I.; Blaabjerg, F. Frequency Response Analysis of Current Controllers for Selective Harmonic Compensation in Active Power Filters. IEEE Trans. Ind. Electron. 2008, 56, 337–347. [Google Scholar] [CrossRef]
- Chen, J.; Shao, H.; Liu, C. An Improved Deadbeat Control Strategy Based on Repetitive Prediction Against Grid Frequency Fluctuation for Active Power Filter. IEEE Access 2021, 9, 24646–24657. [Google Scholar] [CrossRef]
- Yang, S.; Wang, P.; Tang, Y.; Zhang, L. Explicit Phase Lead Filter Design in Repetitive Control for Voltage Harmonic Mitigation of VSI-Based Islanded Microgrids. IEEE Trans. Ind. Electron. 2016, 64, 817–826. [Google Scholar] [CrossRef]
- Cao, Y.; Xu, Y.; Li, Y.; Yu, J.; Yu, J. A Lyapunov Stability Theory-Based Control Strategy for Three-Level Shunt Active Power Filter. Energies 2017, 10, 112. [Google Scholar] [CrossRef] [Green Version]
- Geng, H.; Zheng, Z.; Zou, T.; Chu, B.; Chandra, A. Fast repetitive control with harmonic correction loops for shunt active power filter applied in weak grid. IEEE Trans. Ind. Appl. 2019, 61, 3198–3206. [Google Scholar] [CrossRef]
- Shen, Y.Y.; Tsai, M.J.; Liou, Y.F.; Cheng, P.T. Active Power Filtering with A Low Switching Frequency Converter. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 1457–1465. [Google Scholar] [CrossRef]
- Wang, Y.F.; Sun, X.P.; Wang, Y.P.; Liu, C.G. Application of VPI resonance controller in SAPF. J. Liaoning Tech. Univ. 2017, 36, 96–102. (In Chinese) [Google Scholar]
- Liu, D.D.; Zhou, L.; Sai, X.Y. Vector-proportional-integral control of inductor-capacitor-inductor active power filter under the alpha-beta stationary coordinate system. EJEE 2020, 22, 79–86. [Google Scholar] [CrossRef]
- Trinh, Q.N.; Peng, W.; Choo, F.H. An Improved Control Strategy of Three-Phase PWM Rectifiers under Input Voltage Distortions and DC-Offset Measurement Errors. IEEE J. Emerg. Sel. Topics Power Electron. 2017, 5, 1164–1176. [Google Scholar] [CrossRef]
- Gong, C.; Sou, W.K.; Lam, C.S. Design and analysis of vector proportional–integral current controller for LC-coupling hybrid active power filter with minimum dc-link voltage. IEEE Trans. Power Electron. 2021, 36, 9041–9056. [Google Scholar] [CrossRef]
- González-Espín, F. An Adaptive Control System for Three-Phase Photovoltaic Inverters Working in a Polluted and Variable Frequency Electric Grid. IEEE Trans. Power Electron. 2012, 27, 4248–4261. [Google Scholar] [CrossRef] [Green Version]
- Hogan, D.J.; Gonzalez-Espin, F.J.; Hayes, J.G.; Lightbody, G.; Foley, R. An adaptive digital-control scheme for improved active power filtering under distorted grid conditions. IEEE Trans. Ind. Electron. 2017, 65, 988–999. [Google Scholar] [CrossRef]
- Trinh, Q.N.; Lee, H.H. An advanced current control strategy for three-phase shunt active power filters. IEEE Trans. Ind. Electron. 2013, 60, 5400–5410. [Google Scholar] [CrossRef]
- Yepes, A.G.; Freijedo, F.D.; Lopez, O.; Doval-Gandoy, J. High performance digital resonant controllers implemented with two integrators. IEEE Trans. Power Electron. 2011, 26, 563–576. [Google Scholar] [CrossRef]
- Dannehl, J.; Fuchs, F.W.; Hansen, S.; Thøgersen, P.B. Investigation of active damping approaches for PI-based current control of grid-connected pulse width modulation converters with LCL filters. IEEE Trans. Ind. Appl. 2010, 46, 1509–1517. [Google Scholar] [CrossRef]
- Figueres, E.; Garcera, G.; Sandia, J.; Gonzalez-Espin, F.; Rubio, J.C. Sensitivity study of the dynamics of three-phase photovoltaic inverters with an LCL grid filter. IEEE Trans. Ind. Electron. 2009, 56, 706–717. [Google Scholar] [CrossRef] [Green Version]



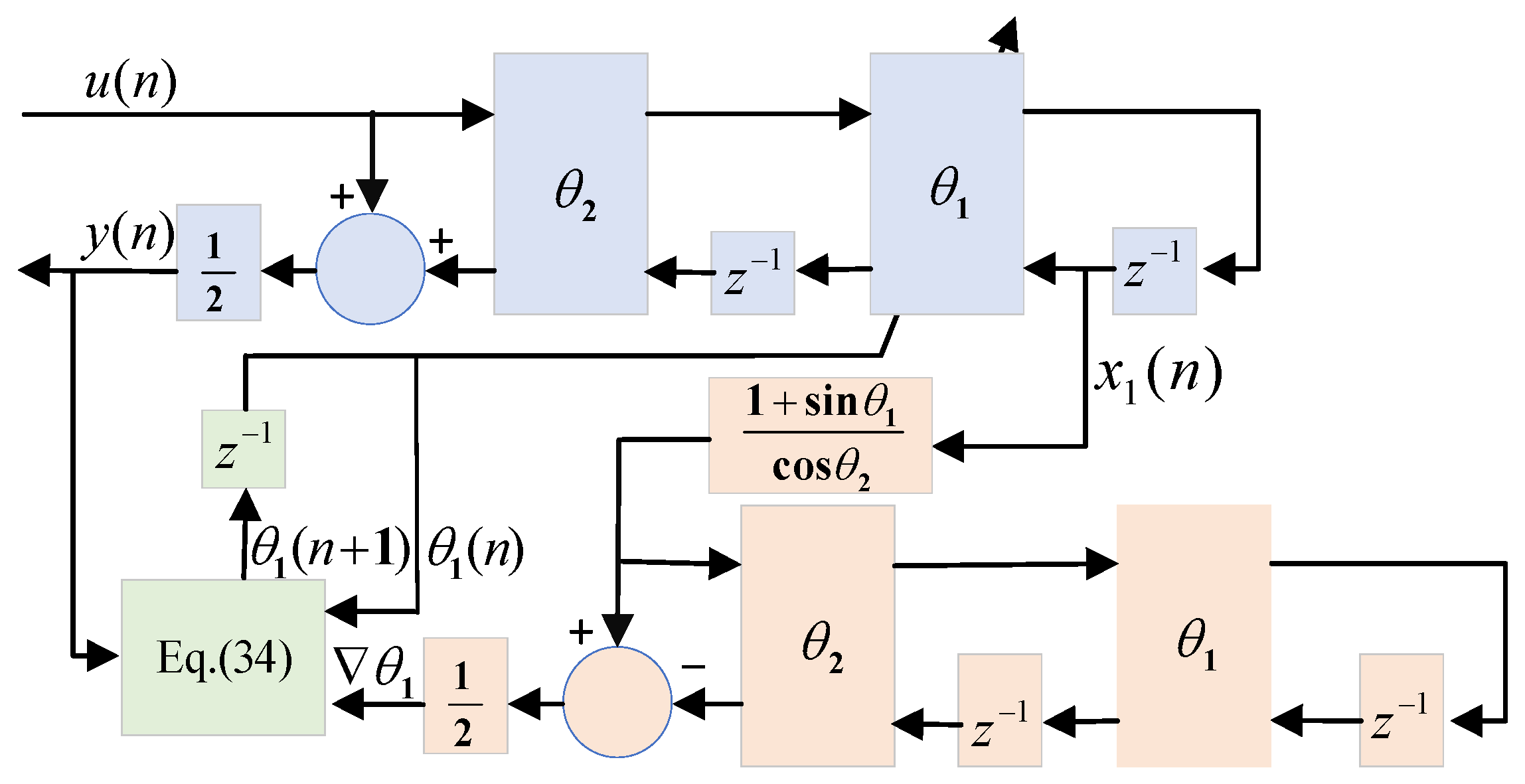

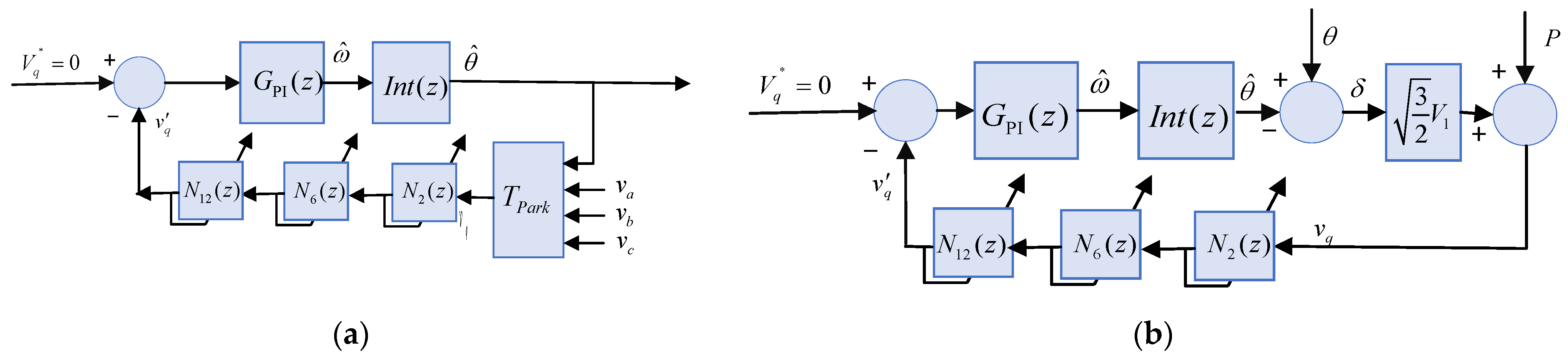
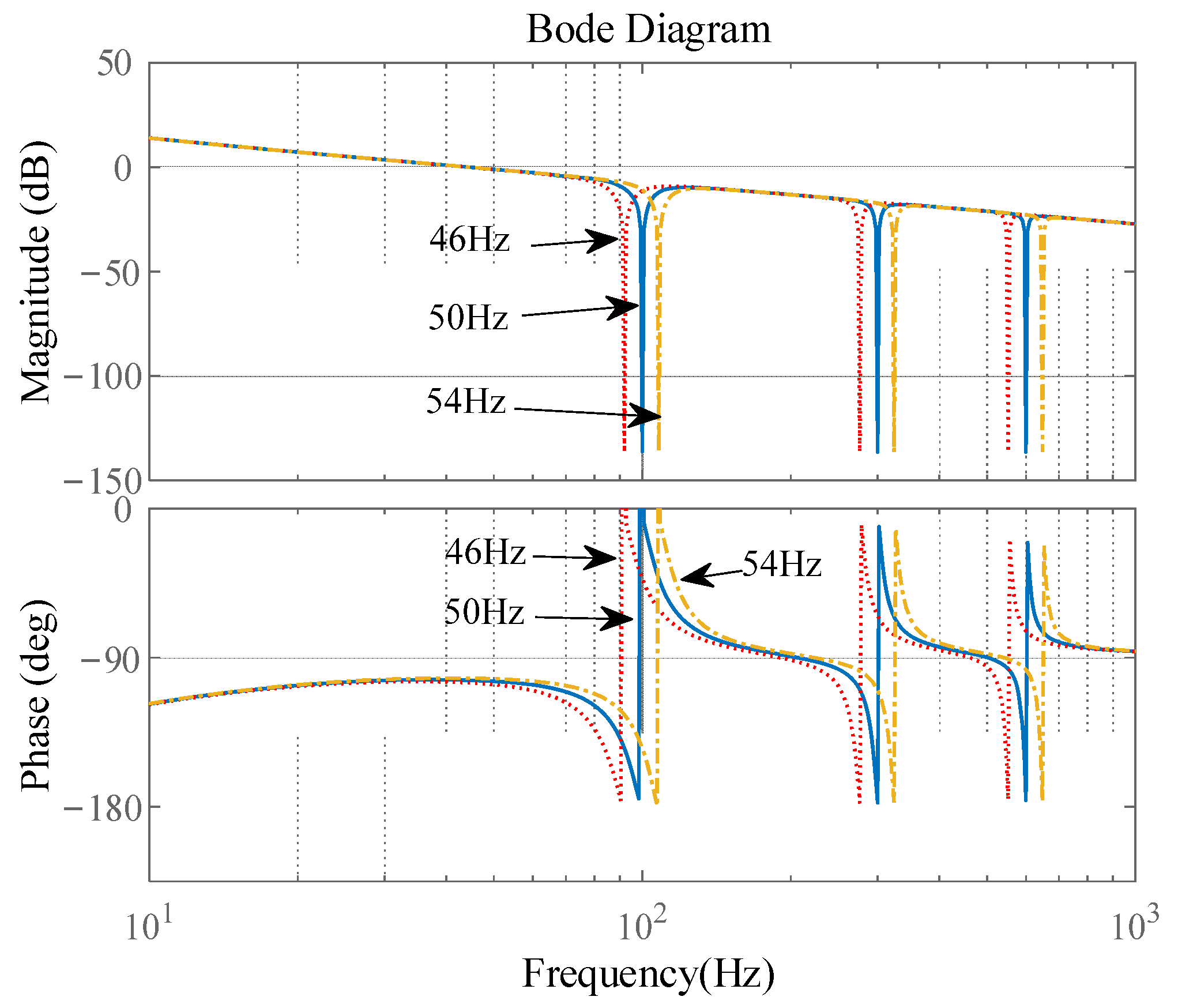
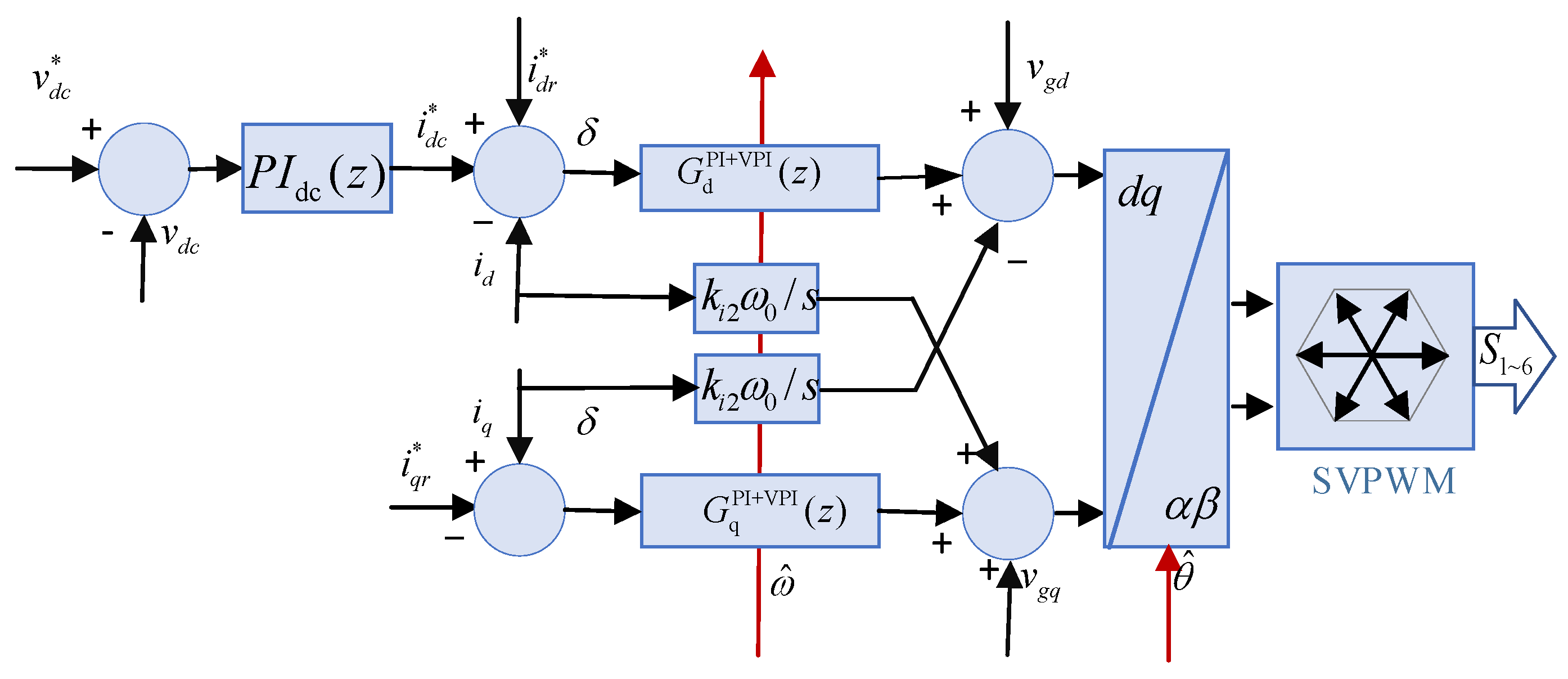

| Variables Known at Time n | Adaptive Calculation Formula |
|---|---|
| Notch filter frequency parameters | |
| Filter state parameters and | |
| Input signal |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Kp | 5.364 | −1.5217 | |
| Ki | 289.30 | −1.4235 | |
| V1 | 311 V | −1.2763 | |
| fS | 12,800 Hz | , , | 1.4309 |
| fc | Approximately 44 Hz | rad/s | |
| PM | Above 72° | rad/s | |
| 0.0001 | rad/s | ||
| 0.0001 | BW_2, BW_6, BW_12 | 20 Hz | |
| 0.001 |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| 311 V | 15.55 V | ||
| 0.05 | 6.22 V | ||
| −0.05 | 2.49 V | ||
| THD | 5.86% | 0.62 V |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Rated voltage/frequency | Three-phase 380 V/50 Hz | Sampling frequency (equal to switching frequency) | 12.8 kHz |
| Dc-link capacitor | Cdc = 2000 µF | DC side voltage PI regulator parameters | kpdc = 1.1, kidc = 105 |
| DC side voltage setting value | V*dc = 850 V | Current PI controller parameters | kpi = 0.75, kii = 123.8 |
| APF output filter inductance | LF = 1 mH | Current VPI controller parameters | kph = 0.82, krh = 0.82 |
| APF output equivalent resistance | R = 0.5 Ω | PLL algorithm parameters | Table 2 |
| Dead time | 2.5 µs | Grid-side voltage parameters | Table 3 |
| Resistive-inductive nonlinear load parameters | L = 5 mH R = 10 Ω |
| THD after Compensation for 3 Control Strategies under Various Working Conditions | under Ideal Condition (No Unbalance and Distortion of the Grid-Side Voltage, No Frequency Deviation) | under the Condition of Unbalanced and Distorted Grid-Side Voltage | under the Condition of Unbalanced, Distorted and +4 Hz Frequency Deviated Grid-Side Voltage |
|---|---|---|---|
| Fixed VPI/SRF-PLL | 3.6% | 7.6% | 18.8% |
| Adaptive VPI/NF-PLL | 3.6% | 3.65% | 8.5% |
| Adaptive VPI/ANF-PLL | 3.62% | 3.65% | 3.68% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Han, W.; Qi, J.; Zhou, Z. Adaptive PI + VPI Harmonic Current Compensation Strategy under Weak Grid Conditions. Appl. Sci. 2023, 13, 5983. https://doi.org/10.3390/app13105983
Zhou L, Han W, Qi J, Zhou Z. Adaptive PI + VPI Harmonic Current Compensation Strategy under Weak Grid Conditions. Applied Sciences. 2023; 13(10):5983. https://doi.org/10.3390/app13105983
Chicago/Turabian StyleZhou, Lili, Wei Han, Jia Qi, and Zhen Zhou. 2023. "Adaptive PI + VPI Harmonic Current Compensation Strategy under Weak Grid Conditions" Applied Sciences 13, no. 10: 5983. https://doi.org/10.3390/app13105983
APA StyleZhou, L., Han, W., Qi, J., & Zhou, Z. (2023). Adaptive PI + VPI Harmonic Current Compensation Strategy under Weak Grid Conditions. Applied Sciences, 13(10), 5983. https://doi.org/10.3390/app13105983





