Free Vibration Characteristics Analysis of Metal-Rubber Cylindrical Shells Based on Viscoelastic Theory
Abstract
1. Introduction
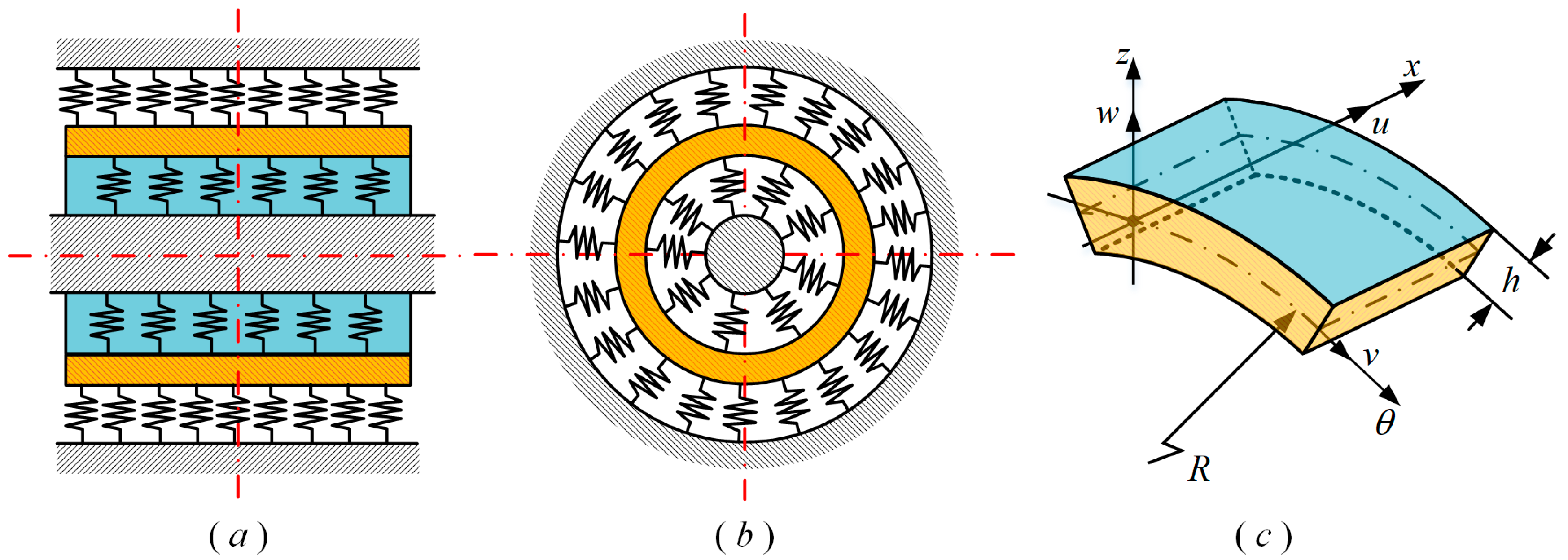
2. Shell Dynamics
2.1. Energy Equation of the Shell
2.2. The Motion Equation of the Shell
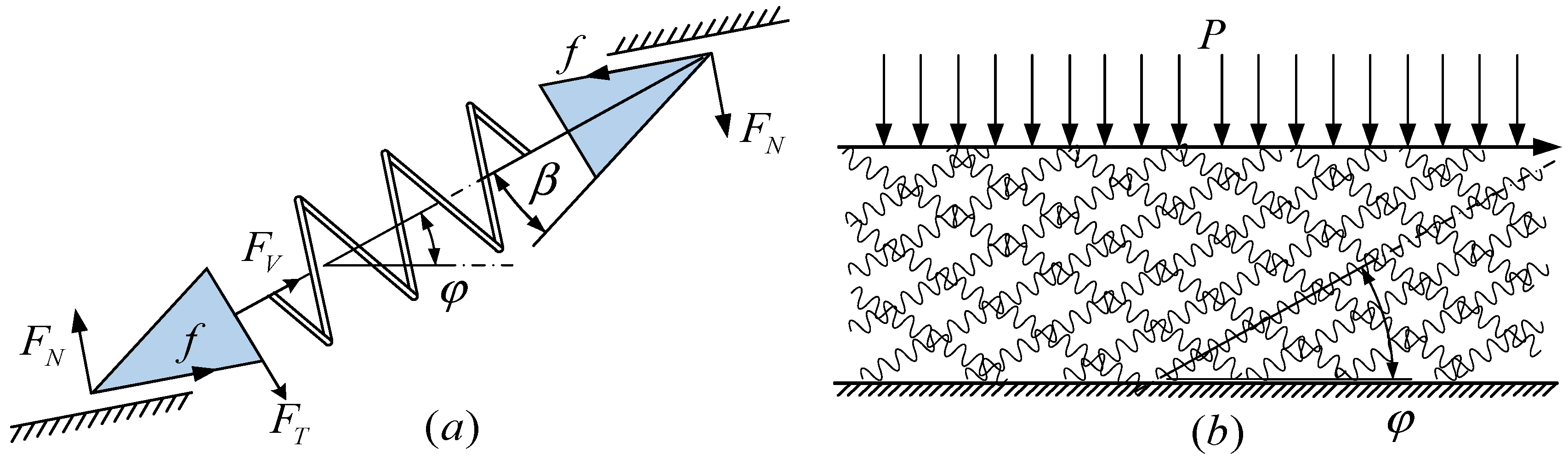
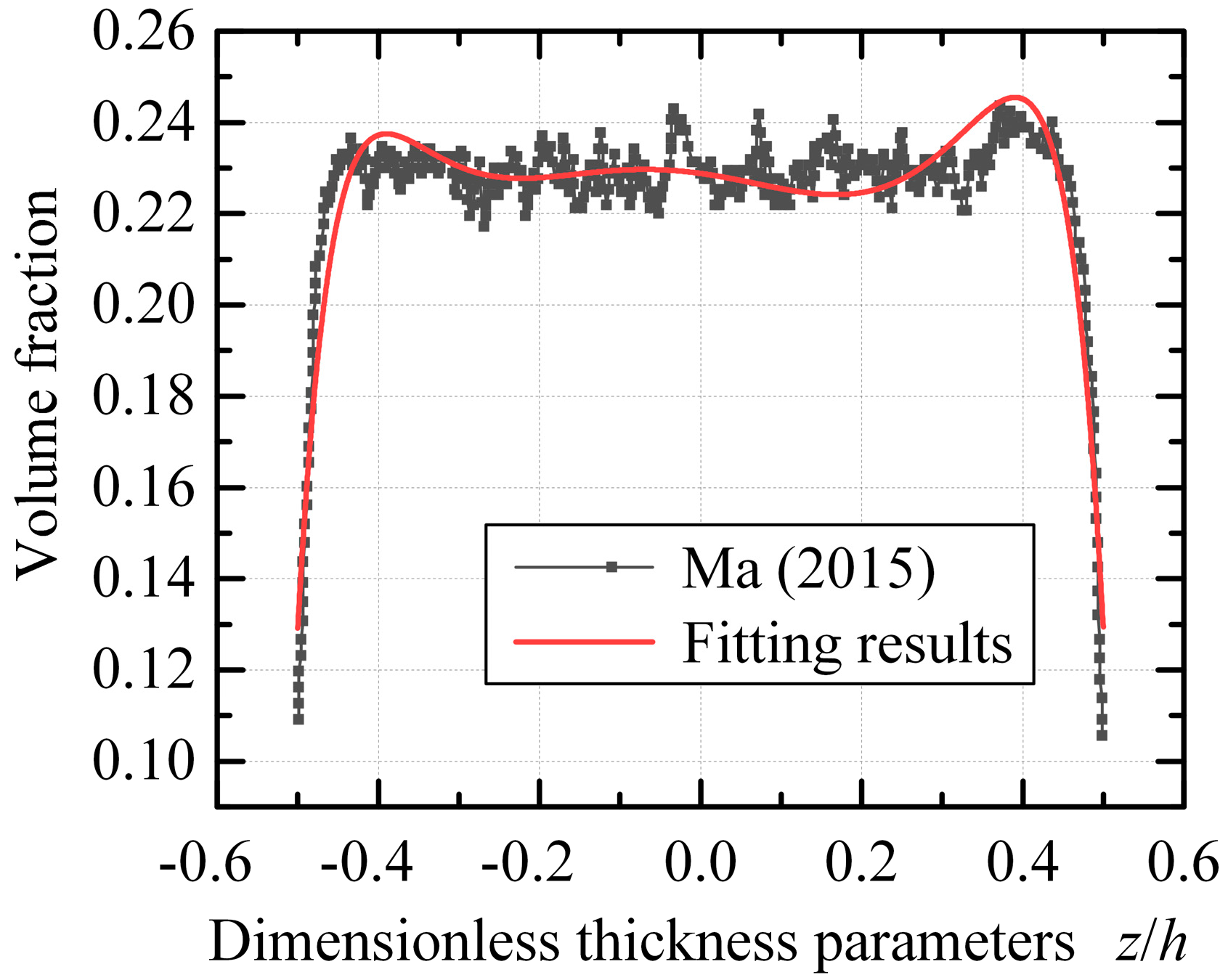
2.3. Estimation of the Characteristic Properties of MR
3. Numerical Calculation and Discussion of Results
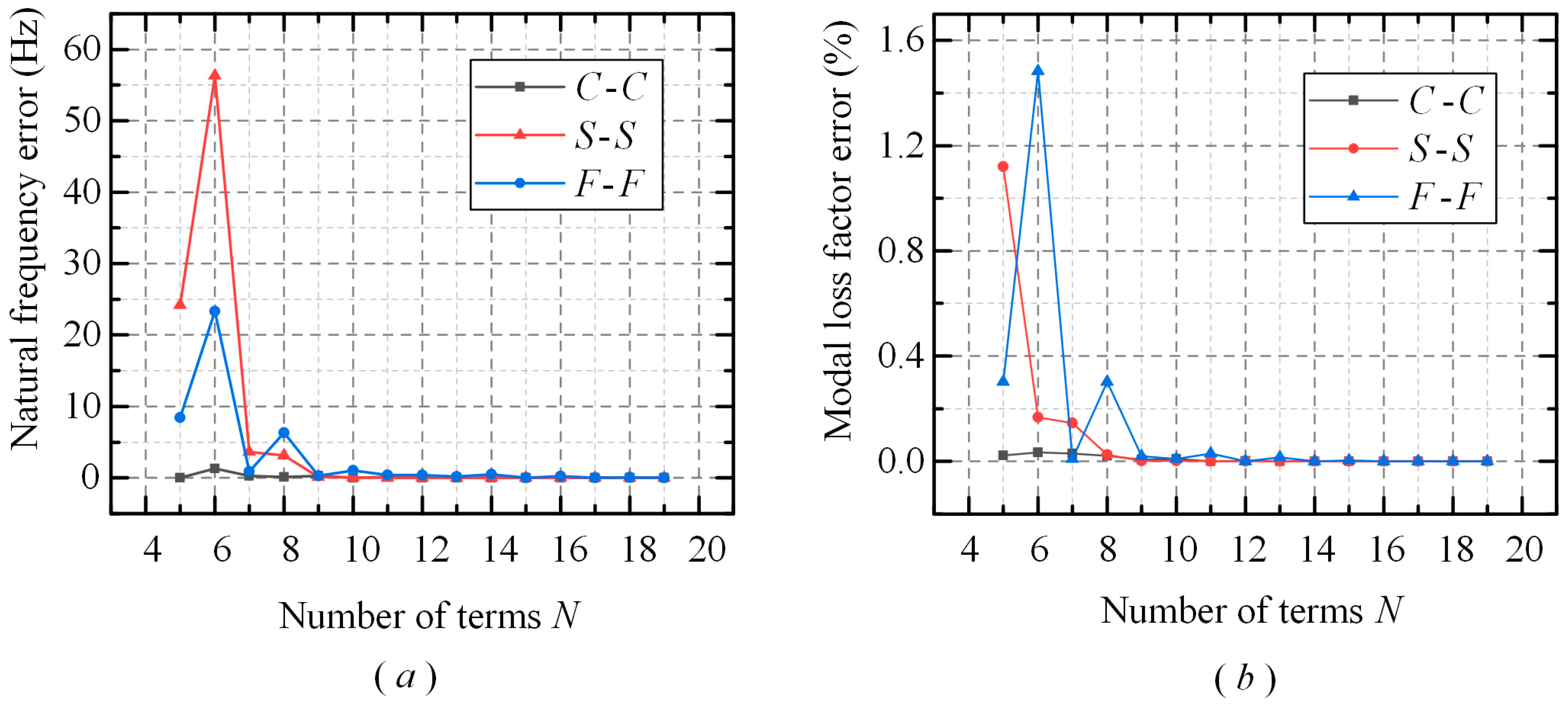
3.1. Analysis of the Convergence and Validity of the Model
3.2. Effect of the Preload State and Axial Boundary Conditions
3.3. Effect of the Pasternak Elastic Foundation
4. Validation and Discussion of the Results
5. Conclusions
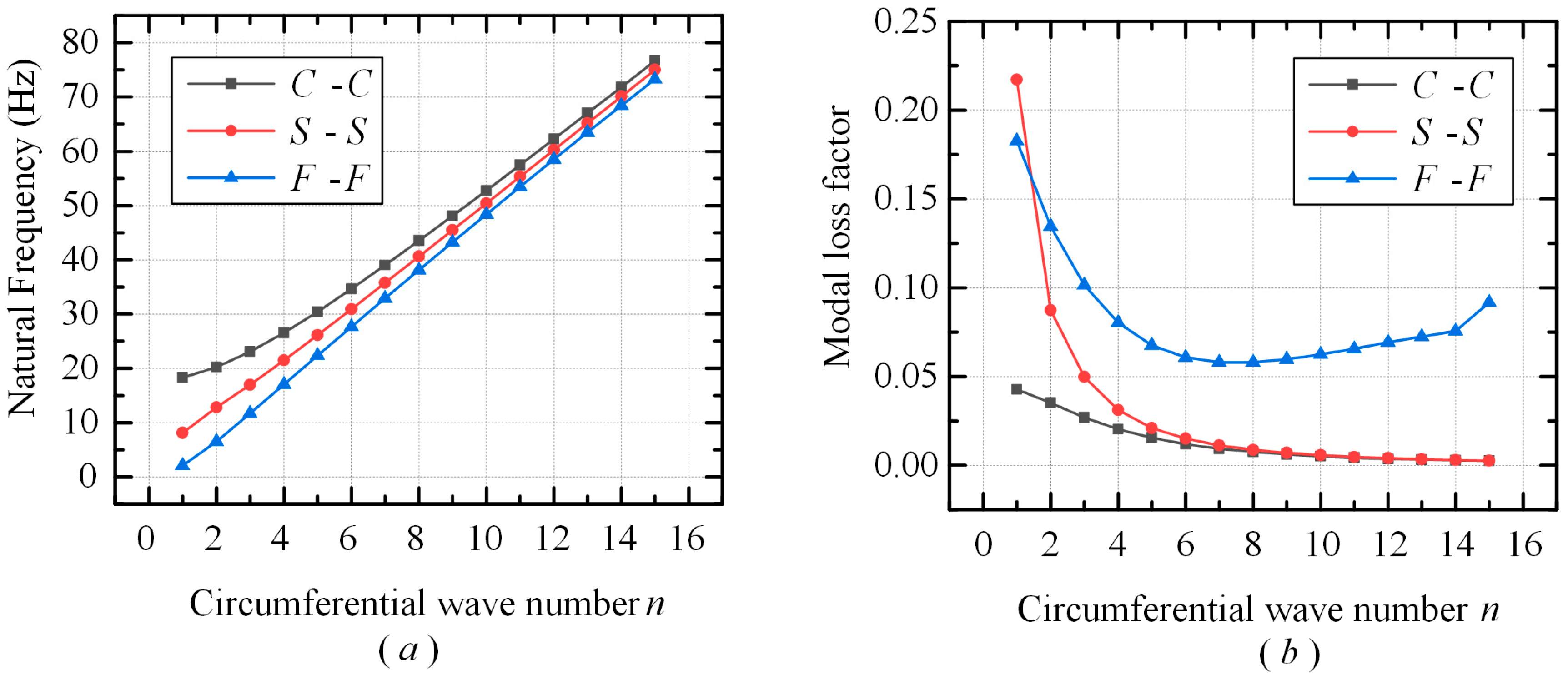
- The boundary conditions at both ends have a significant impact on the natural frequency and modal loss factor of the MRCS. The C-C boundary condition has the highest natural frequency and damping ratio, while the F-F boundary condition has the lowest.
- The Pasternak elastic foundation has a significant effect on the natural frequency and modal loss factor of the MRCS. In low-order modes, the natural frequency increases with increasing ki (i = 1, 2, 3, 4), and the modal loss factor decreases with increasing ki (i = 1, 2, 3, 4). In higher-order modes, the effect of ki (i = 1, 2, 3, 4) on the natural frequency and modal loss factor is the same as that of the artificial spring. Additionally, the radially applied position of the Pasternak elastic foundation does not affect the natural frequency and modal loss factor.
- The preload displacement has a significant effect on the natural frequency and modal loss factor of the MRCS. The natural frequency increases with an increasing preload displacement, and the modal loss factor decreases with an increasing displacement. Furthermore, the effects of internal and external preload on the natural frequency and modal loss factor are the same.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| h | The thickness of MRCS (m) | δ | Variable Score Symbols (-) |
| R | The radius of the middle surface of MRCS (m) | t, t1, t2 | Times, Starting moment, Ending moment (s) |
| L | Cylindrical shell length (m) | ω | Round Frequency(rad) |
| u, v, w | Displacement of the shell along x, θ, z direction (m) | n | Circumferential wave number (-) |
| ψx, ψθ | Rotation angles normal to the direction of the x and θ axis (rad) | m | axial half-wave number (-) |
| a1, a2 | Lamé coefficient in the x, θ direction in the middle surface (-) | δkl | Kronecker constant (-) |
| R1,R2 | The radius of curvature in the x, θ direction in the middle surface (m) | f | Natural frequency of MRCS (Hz) |
| A1, A2 | Lamé coefficient along x, θ direction in cylindrical shell (-) | η | The modal loss factor of MRCS |
| nm | Number of screws of equivalent spring unit (-) | β | Half cone angle of equivalent spring unit (rad) |
| EU/L | Equivalent modulus of elasticity (MPa) | η1, η2 | Normal strain loss factor and shear strain loss factor of MR |
| εx, εθ | Normal strain of shell along x, θ direction (-) | NA | Number of helix unit in the axial section of MRCS (-) |
| γxθ, γθz, γxz | Shear strain of the shell normal to the z-axis, x-axis and θ-axis (-) | NL | Number of helix unit in length L of MRCS (-) |
| A | Cylindrical shell shaft cross-sectional area (m2) | ρm | Relative density of Metal-Rubber samples (%) |
| κx, κθ | The slope of strain εx, εθ along the z-direction (-) | Relative density of Metal-Rubber blanks (%) | |
| E, Em | Young’s modulus of MRCS, metal wire (GPa) | a, b | Load correction factor (-) |
| μ | Poisson’s ratio (-) | α | Guidance angle (rad) |
| ρ | The density of MRCS (kg/m3) | d, D | Wire diameter, Coil diameter (mm) |
| Ns, Qs | Membrane stresses (Pa) | N | Order number of mode phase function (-) |
| Ms | Membrane moments (Pa·m) | C | Spring index of the helix unit (-) |
| Ks | Transverse shear correction factor (-) | φ, | Inclination angle of the helix unit and its mean value (rad) |
| Ue | Shell strain energy (N·m) | r | molding ratio of MR (-) |
| Te | Shell kinetic energy (N·m) | KT | Axial stiffness of the helix unit (N/m) |
| μm | Poisson’s ratio of MR | KV | Tangential stiffness of the helix unit (N/m) |
Appendix A
References
- Liu, P.; He, G.; Wu, L. Uniaxial tensile stress–strain behavior of entangled steel wire material. Mater. Sci. Eng. A 2009, 509, 69–75. [Google Scholar] [CrossRef]
- He, G.; Liu, P.; Tan, Q. Porous titanium materials with entangled wire structure for load-bearing biomedical applications. J. Mech. Behav. Biomed. 2012, 5, 16–31. [Google Scholar] [CrossRef] [PubMed]
- Zarzour, M.; Vance, J. Experimental evaluation of a metal mesh bearing damper. J. Eng. Gas Turbines Power 2000, 122, 326–329. [Google Scholar] [CrossRef]
- Li, S.; Mao, C.; Li, H.; Zhao, Y. Mechanical properties and theoretical modeling of self-centering shape memory alloy pseudo-rubber. Smart Mater. Struct. 2011, 20, 115008. [Google Scholar] [CrossRef]
- Huang, M.; Fu, Y.; Qiao, X.; Chen, P. Investigation into Friction and Wear Characteristics of 316L Stainless-Steel Wire at High Temperature. Materials 2023, 16, 213. [Google Scholar] [CrossRef]
- Li, H.; Ren, Z.; Huang, J.; Zhong, S. Fretting wear evolution model of the metal filaments inside metal rubber. Wear 2022, 506, 204438. [Google Scholar] [CrossRef]
- Ren, Z.; Wen, G.; Guo, Z. Biomimetic high-intensity superhydrophobic metal rubber with anti-corrosion property for industrial oil–water separation. New J. Chem. 2019, 43, 1894–1899. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Q.; Zhang, D.; Scarpa, F.; Liu, B.; Hong, J. Tuning the vibration of a rotor with shape memory alloy metal rubber supports. J. Sound Vib. 2015, 351, 1–16. [Google Scholar] [CrossRef]
- Yanhong, M.; Zhichao, L.; Hong, W.; Dayi, Z.; Jie, H. Theoretical and experimental steady-state rotordynamics of an adaptive air film damper with metal rubber. J. Sound Vib. 2013, 332, 5710–5726. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Xue, X.; Zhang, L. Experimental investigation on enhanced mechanical and damping performance of corrugated structure with metal rubber. Thin Wall. Struct. 2020, 154, 106816. [Google Scholar] [CrossRef]
- Chegodaev, D.E.; OP, M.; EV, K. Design of Metal Rubber Components; National Defense Industry Press: Beijing, China, 2000; p. 258. [Google Scholar]
- Ma, Y.; Zhang, Q.; Zhang, D.; Scarpa, F.; Liu, B.; Hong, J. The mechanics of shape memory alloy metal rubber. Acta Mater. 2015, 96, 89–100. [Google Scholar] [CrossRef]
- Xue, X.; Ruan, S.; Bai, H.; Chen, X.; Shao, Y.; Lu, C. An enhanced constitutive model for the nonlinear mechanical behavior of the elastic-porous metal rubber. Mech. Mater. 2020, 148, 103447. [Google Scholar] [CrossRef]
- Ren, Z.; Shen, L.; Bai, H.; Pan, L.; Zhong, S. Constitutive model of disordered grid interpenetrating structure of flexible microporous metal rubber. Mech. Syst. Signal Process. 2021, 154, 107567. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Q.; Wang, Y.; Hong, J.; Scarpa, F. Topology and mechanics of metal rubber via X-ray tomography. Mater. Design 2019, 181, 108067. [Google Scholar] [CrossRef]
- Zhang, D.; Scarpa, F.; Ma, Y.; Boba, K.; Hong, J.; Lu, H. Compression mechanics of nickel-based superalloy metal rubber. Mater. Sci. Eng. A 2013, 580, 305–312. [Google Scholar] [CrossRef]
- Do, V.T.; Pham, V.V.; Nguyen, H.N.; Tornabene, F. On the Development of Refined Plate Theory for Static Bending Behavior of Functionally Graded Plates. Math. Probl. Eng. 2020, 2020, 2836763. [Google Scholar] [CrossRef]
- Duc, D.H.; Thom, D.V.; Cong, P.H.; Minh, P.V.; Nguyen, N.X. Vibration and static buckling behavior of variable thickness flexoelectric nanoplates. Mech. Based Des. Struct. Mach. 2022, 1–29. [Google Scholar] [CrossRef]
- Duc, D.H.; Van Minh, P.; Tung, N.S. Finite element modelling for free vibration response of cracked stiffened FGM plates. Vietnam. J. Sci. Technol. 2020, 58, 119–129. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Ye, C.; Zu, J.W. Vibration analysis of circular cylindrical shells made of metal foams under various boundary conditions. Int. J. Mech. Mater. Des. 2019, 15, 333–344. [Google Scholar] [CrossRef]
- Miao, X.; Li, C.; Jiang, Y. Free vibration analysis of metal-ceramic matrix composite laminated cylindrical shell reinforced by CNTs. Compos. Struct. 2021, 260, 113262. [Google Scholar] [CrossRef]
- Chen, W.; Luo, W.M.; Chen, S.Y.; Peng, L.X. A FSDT meshfree method for free vibration analysis of arbitrary laminated composite shells and spatial structures. Compos. Struct. 2022, 279, 114763. [Google Scholar] [CrossRef]
- Li, Z.; Zhong, R.; Wang, Q.; Qin, B.; Yu, H. The thermal vibration characteristics of the functionally graded porous stepped cylindrical shell by using characteristic orthogonal polynomials. Int. J. Mech. Sci. 2020, 182, 105779. [Google Scholar] [CrossRef]
- Rachid, A.; Ouinas, D.; Lousdad, A.; Zaoui, F.Z.; Achour, B.; Gasmi, H.; Butt, T.A.; Tounsi, A. Mechanical behavior and free vibration analysis of FG doubly curved shells on elastic foundation via a new modified displacements field model of 2D and quasi-3D HSDTs. Thin Wall. Struct. 2022, 172, 108783. [Google Scholar] [CrossRef]
- Qin, B.; Wang, Q.; Zhong, R.; Zhao, X.; Shuai, C. A three-dimensional solution for free vibration of FGP-GPLRC cylindrical shells resting on elastic foundations: A comparative and parametric study. Int. J. Mech. Sci. 2020, 187, 105896. [Google Scholar] [CrossRef]
- Duc, N.D.; Tuan, N.D.; Tran, P.; Dao, N.T.; Dat, N.T. Nonlinear dynamic analysis of Sigmoid functionally graded circular cylindrical shells on elastic foundations using the third order shear deformation theory in thermal environments. Int. J. Mech. Sci. 2015, 101, 338–348. [Google Scholar] [CrossRef]
- Johnson, C.D.; Kienholz, D.A. Finite Element Prediction of Damping in Structures with Constrained Viscoelastic Layers. Aiaa J. 1982, 20, 1284–1290. [Google Scholar] [CrossRef]
- Ma, B.; He, J. A finite element analysis of viscoelastically damped sandwich plates. J. Sound Vib. 1992, 152, 107–123. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Kurosawa, Y.; Enomoto, H. Damped vibration analysis using finite element method with approximated modal damping for automotive double walls with a porous material. J. Sound Vib. 2009, 325, 436–450. [Google Scholar] [CrossRef]
- Qin, Z.; Chu, F.; Zu, J. Free vibrations of cylindrical shells with arbitrary boundary conditions: A comparison study. Int. J. Mech. Sci. 2017, 133, 91–99. [Google Scholar] [CrossRef]
- Qu, Y.; Hua, H.; Meng, G. A domain decomposition approach for vibration analysis of isotropic and composite cylindrical shells with arbitrary boundaries. Compos. Struct. 2013, 95, 307–321. [Google Scholar] [CrossRef]
- Xue, Y.; Jin, G.; Zhang, C.; Han, X.; Chen, J. Free vibration analysis of functionally graded porous cylindrical panels and shells with porosity distributions along the thickness and length directions. Thin Wall. Struct. 2023, 184, 110448. [Google Scholar] [CrossRef]
- Yang, S.W.; Hao, Y.X.; Zhang, W.; Yang, L.; Liu, L.T. Buckling and free vibration of eccentric rotating CFRP cylindrical shell base on FSDT. Appl. Math. Model. 2021, 95, 593–611. [Google Scholar] [CrossRef]
- CAO, F. Research on Effects of Loading Amplitude on Fatigue Life of Metal Rubber Material. China Mech. Eng. 2013, 24, 671. [Google Scholar]
- Ilanko, S.; Monterrubio, L.; Mochida, Y. The Rayleigh-Ritz Method for Structural Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2014; p. 254. [Google Scholar]
- Zhang, W.; Fang, Z.; Yang, X.D.; Liang, F. A series solution for free vibration of moderately thick cylindrical shell with general boundary conditions. Eng. Struct. 2018, 165, 422–440. [Google Scholar] [CrossRef]




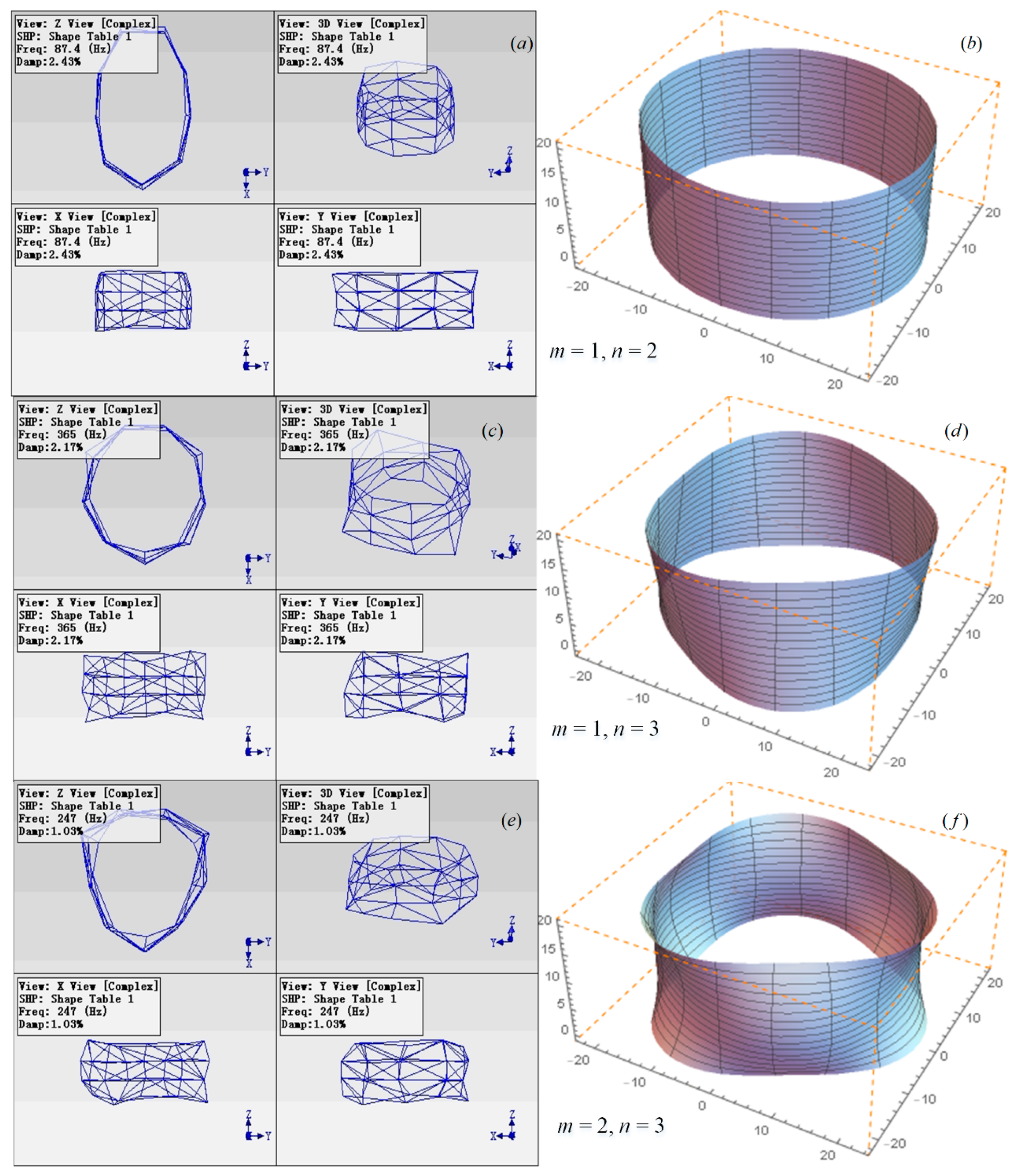
| Vibration | Present | Zhang [36] | FEM |
|---|---|---|---|
| Parameters | |||
| m = 1, n = 2 | 269.108 | 268.49 | 269.71 |
| m = 2, n = 2 | 270.855 | 272.58 | 276.95 |
| m = 1, n = 3 | 760.599 | 758.3 | 765.17 |
| m = 2, n = 3 | 774.53 | 770.67 | 762.721 |
| m = 1, n = 4 | 1456.99 | -- | 1473.5 |
| m = 2, n = 4 | 1459.04 | -- | 1483.3 |
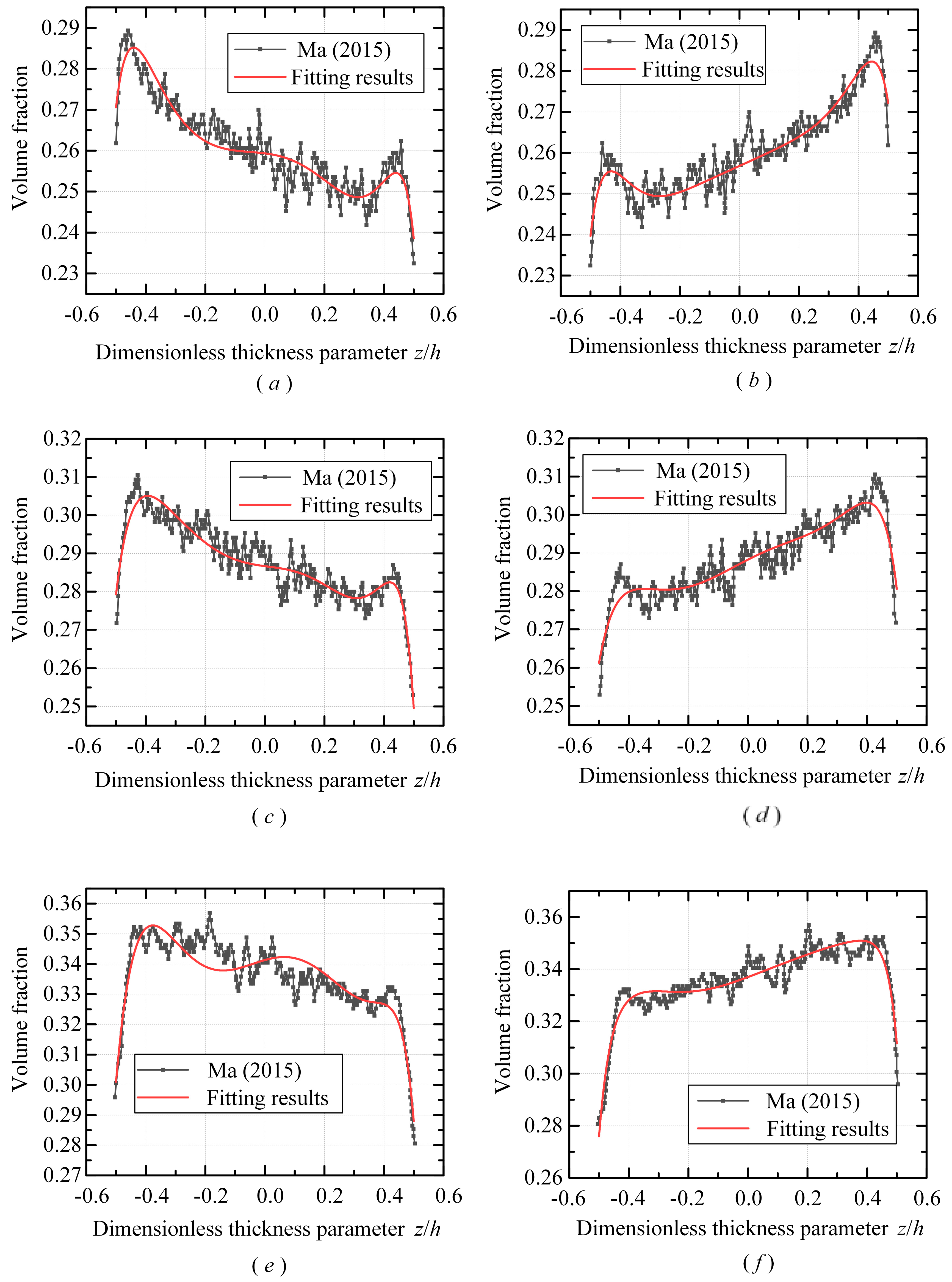
| Coefficient | Internal Preload | External Preload | ||||
|---|---|---|---|---|---|---|
| 0.8% | 1.6% | 2.5% | 0.8% | 1.6% | 2.5% | |
| a1 | 0.2593 | 0.2867 | 0.3413 | 0.2558 | 0.2883 | 0.3370 |
| a2 | −0.0092 | −0.0105 | 0.0275 | 0.0140 | 0.0394 | 0.0425 |
| a3 | −0.0675 | 0.0221 | −0.1313 | 0.1344 | −0.0369 | 0.0272 |
| a4 | −0.4254 | −0.5379 | −0.9656 | 0.2838 | −0.1799 | −0.1885 |
| a5 | 0.4385 | 2.7711 | 2.9038 | −1.4229 | 1.3868 | 0.3617 |
| a6 | 1.4708 | 5.3331 | −0.3238 | −0.8294 | −2.8985 | −3.6424 |
| a7 | 4.2736 | −0.3495 | 1.2461 | −2.6517 | 0.8550 | 0.4057 |
| a8 | 1.3357 | 0.9991 | 11.6435 | −2.1848 | −5.2641 | 1.5481 |
| a9 | −10.9707 | −0.4705 | −10.2659 | 58.3857 | 2.6007 | 5.7922 |
| a10 | 0.2158 | 2.4878 | −39.4096 | −9.5983 | 7.3398 | 1.4243 |
| a11 | 0.7160 | −87.9092 | −45.8087 | 33.6653 | −19.3324 | 3.4407 |
| a12 | −30.8714 | −85.8314 | 1.2025 | 95.1276 | 8.7059 | −0.3547 |
| a13 | −164.4423 | −5.9095 | −7.2920 | −5.0656 | −32.2820 | −32.8691 |
| a14 | −0.7037 | 2.1150 | −40.9135 | −88.8018 | −68.1837 | −17.7638 |
| a15 | 0.2467 | −3.4719 | −4.3433 | −2820.6377 | 0.9387 | 1.2630 |
| a16 | 2.1301 | 0.9619 | 1.4475 | 5.4057 | −1.7299 | −123.6476 |
| a17 | 10.3865 | 1.9055 | 3.2611 | 2.0014 | 15.4294 | −2396.1895 |
| Preload | n | Natural Frequency | Modal Loss Factor | ||||
|---|---|---|---|---|---|---|---|
| C-C | S-S | F-F | C-C | S-S | F-F | ||
| Internal preload | 1 | 37.342 | 18.182 | 4.502 | 0.052 | 0.208 | 0.163 |
| 2 | 45.455 | 32.393 | 12.896 | 0.140 | 0.262 | 0.153 | |
| 3 | 54.907 | 45.920 | 22.743 | 0.215 | 0.281 | 0.122 | |
| 4 | 60.380 | 53.575 | 32.947 | 0.188 | 0.265 | 0.098 | |
| 5 | 67.262 | 62.236 | 43.175 | 0.162 | 0.226 | 0.084 | |
| 6 | 75.153 | 71.428 | 53.338 | 0.138 | 0.186 | 0.076 | |
| 7 | 83.731 | 80.917 | 63.425 | 0.118 | 0.152 | 0.072 | |
| 8 | 92.774 | 90.595 | 73.447 | 0.100 | 0.125 | 0.072 | |
| 9 | 102.137 | 100.406 | 83.412 | 0.086 | 0.104 | 0.074 | |
| 10 | 111.725 | 110.319 | 93.322 | 0.074 | 0.087 | 0.077 | |
| External preload | 1 | 37.341 | 18.180 | 4.500 | 0.052 | 0.208 | 0.163 |
| 2 | 45.451 | 32.388 | 12.893 | 0.140 | 0.262 | 0.153 | |
| 3 | 54.904 | 45.916 | 22.738 | 0.215 | 0.281 | 0.122 | |
| 4 | 60.376 | 53.570 | 32.941 | 0.188 | 0.265 | 0.098 | |
| 5 | 67.256 | 62.229 | 43.167 | 0.162 | 0.226 | 0.084 | |
| 6 | 75.145 | 71.419 | 53.328 | 0.138 | 0.186 | 0.076 | |
| 7 | 83.721 | 80.906 | 63.414 | 0.118 | 0.152 | 0.072 | |
| 8 | 92.762 | 90.582 | 73.435 | 0.100 | 0.125 | 0.072 | |
| 9 | 102.123 | 100.392 | 83.398 | 0.086 | 0.104 | 0.074 | |
| 10 | 111.709 | 110.303 | 93.306 | 0.074 | 0.087 | 0.077 | |
| Grades | Yield Strength (N/mm2) | Young’s Modulus (Gpa) | Density (kg/m3) | Poisson’s Ratio |
|---|---|---|---|---|
| 06Cr19ni10 | 205 | 193 | 7930 | 0.285 |
| Characteristic Parameters | Numerical Value |
|---|---|
| Diameter of metal wire (mm) | 0.3 |
| Metal coil diameter (mm) | 3 |
| Density (kg/m3) | 3172 |
| Young’s modulus (GPa) | 5.2 × 106 |
| Loss factor (%) | 22.609 |
| Shell thickness (mm) | 1.5 × 10−2 |
| Cylindrical shell diameter (mm) | 6.85 × 10−2 |
| Cylindrical shell length (mm) | 6.20 × 10−2 |
| Vibration Type Parameters | Natural Frequency | Damping Ratio | ||||
|---|---|---|---|---|---|---|
| Theoretical Value (Hz) | Experimental Value (Hz) | Error (Hz) | Theoretical Value (%) | Experimental Value (%) | Error (%) | |
| m = 1, n = 2 | 88.3 | 85.512 | 2.79 | 0.738 | 1.08 | 0.342 |
| m = 3, n = 3 | 248 | 235.058 | 12.942 | 1.389 | 1.03 | 0.359 |
| m = 2, n = 4 | 449.779 | 452.344 | 2.565 | 2.32 | 1.72 | 0.6 |
| m = 4, n = 4 | 459.263 | 461 | 1.74 | 1.8 | 1.4 | 0.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Y.; Deng, P.; Fu, K.; Li, H. Free Vibration Characteristics Analysis of Metal-Rubber Cylindrical Shells Based on Viscoelastic Theory. Appl. Sci. 2023, 13, 6085. https://doi.org/10.3390/app13106085
Bai Y, Deng P, Fu K, Li H. Free Vibration Characteristics Analysis of Metal-Rubber Cylindrical Shells Based on Viscoelastic Theory. Applied Sciences. 2023; 13(10):6085. https://doi.org/10.3390/app13106085
Chicago/Turabian StyleBai, Yan, Pengfei Deng, Ke Fu, and He Li. 2023. "Free Vibration Characteristics Analysis of Metal-Rubber Cylindrical Shells Based on Viscoelastic Theory" Applied Sciences 13, no. 10: 6085. https://doi.org/10.3390/app13106085
APA StyleBai, Y., Deng, P., Fu, K., & Li, H. (2023). Free Vibration Characteristics Analysis of Metal-Rubber Cylindrical Shells Based on Viscoelastic Theory. Applied Sciences, 13(10), 6085. https://doi.org/10.3390/app13106085





