Internet of Medical Things with a Blockchain-Assisted Smart Healthcare System Using Metaheuristics with a Deep Learning Model

Abstract

The Internet of Medical Things (IoMT) is a network of healthcare devices such as wearables, diagnostic equipment, and implantable devices, which are linked to the internet and can communicate with one another. Blockchain (BC) technology can design a secure, decentralized system to store and share medical data in an IoMT-based intelligent healthcare system. Patient records were stored in a tamper-proof and decentralized way using BC, which provides high privacy and security for the patients. Furthermore, BC enables efficient and secure sharing of healthcare data between patients and health professionals, enhancing healthcare quality. Therefore, in this paper, we develop an IoMT with a blockchain-based smart healthcare system using encryption with an optimal deep learning (BSHS-EODL) model. The presented BSHS-EODL method allows BC-assisted secured image transmission and diagnoses models for the IoMT environment. The proposed method includes data classification, data collection, and image encryption. Initially, the IoMT devices enable data collection processes, and the gathered images are stored in BC for security. Then, image encryption is applied for data encryption, and its key generation method can be performed via the dingo optimization algorithm (DOA). Finally, the BSHS-EODL technique performs disease diagnosis comprising SqueezeNet, Bayesian optimization (BO) based parameter tuning, and voting extreme learning machine (VELM). A comprehensive set of simulation analyses on medical datasets highlights the betterment of the BSHS-EODL method over existing techniques with a maximum accuracy of 98.51%, whereas the existing methods such as DBN, YOLO-GC, ResNet, VGG-19, and CDNN models have lower accuracies of 94.15%, 94.24%, 96.19%, 91.19%, and 95.29% respectively.

1. Introduction

Smart healthcare is the advancement of conventional healthcare with advanced internet technologies. It incorporates various technologies to render real-time health-relevant data collected from patients utilizing smart wearable devices and detection of health problems in real time from the collected data [1]. The Internet of Medical Things (IoMT) plays a crucial role in the medical field to increase electronic devices’ throughput, precision, and consistency. Due to the outbreak of the coronavirus pandemic, visiting a doctor becomes a high risk for a person with small problems [2]. With the help of IoMT devices, it becomes easy to monitor health records daily, and preventive measures can be taken on our own. An IoMT-based smart healthcare system refers to a collection of several smart medical devices linked within the network over the internet [3]. Analysis can be done by making use of proper AI-based data transformation and interpretation methods after getting the medical dataset. However, easy access to healthcare applications and services has increased the risks and vulnerabilities that hinder smart healthcare systems’ performance. Also, many more heterogeneous devices collect data that differ in formats and size, making it a challenge to manage the data in the healthcare repositories and secure it from attackers who seek to profit from the data [4]. Therefore, smart healthcare schemes are prone to several security risks and threats, such as network attacks, software and hardware-based attacks, and system-level attacks, which put the lives of patients at risk.

Developing technologies, namely blockchain (BC), were utilized for providing cutting-edge solutions in several settings [5], one among them being the healthcare sector. BC technology is used in the medical field to guarantee the security of patient reports and rationalise data sharing amongst pharmaceutical companies, health care providers, and labs [6]. In the medical world, applications (apps) built on BC technology can detect significant and even hazardous errors [7]. Thus, it is capable of enhancing the openness, efficacy, and safety of the systems to exchange healthcare data in the medical field. Medical institutions are aided by BC technology to obtain insight and enhance medical record analysis. Then, the healthcare support system demands a new processing method with delay-sensitive monitoring which should be smart and managed stably [8].

Deep learning (DL) related medical diagnosis in the IoMT signifies the use of machine learning (ML) and artificial intelligence (AI) approaches to examine medical datasets collected from different devices connected to the internet, namely medical equipment and wearable devices [9]. It enhances the precision level of diagnostic decisions, helps identify trends and patterns in patient data, and enables efficient and more personalized healthcare delivery [10]. Simultaneously, hyperparameter tuning of the DL models becomes essential to improve the overall classification performance. Since trial-and-error hyperparameter selection is a challenging task, metaheuristic optimization techniques are used. In addition, image encryption schemes can be used to securely transmit healthcare data in the IoMT encryption. Furthermore, the key generation process is critical to the security of an encryption algorithm, as the strength of the key directly impacts the security of the encrypted data. Therefore, it is important to use strong and secure key generation methods and to properly manage and protect the keys.

This article develops an IoMT with a blockchain-based smart healthcare system using encryption with an optimal deep learning (BSHS-EODL) model. The presented BSHS-EODL technique comprises a few processes: data collection, image encryption, and data classification. Initially, the IoMT devices enable data collection processes, and the gathered images are stored in BC for security. Then, image encryption is employed to encrypt the data, and its key generation process is performed via the dingo optimization algorithm (DOA). Finally, the BSHS-EODL technique performs disease diagnosis comprising SqueezeNet, Bayesian optimization (BO) based parameter tuning, and voting extreme learning machine (VELM). A comprehensive set of simulation analyses is performed on medical datasets.

The rest of the paper is organized as follows: Section 2 discusses the related works, Section 3 demonstrates the proposed approach, performance validation is depicted in Section 4, and the conclusion is shown in Section 5.

2. Related Works

Almaiah et al. [11] present a DL framework based on BC that offers a dual level of security and privacy. Initially, a BC technique was modelled in which each participating entity was verified, validated, and registered by making use of a smart contract related enhanced proof-of-work to reach the target of privacy and security. Then, a DL approach including bidirectional long short-term memory (BLSTM) for a variational autoencoder (VAE) and intrusion detection systems for privacy were devised. Khan et al. [12] introduced BIoMT, a BC Hyperledger fabric-assisted consortium architecture which offers transparency, security, and integrity to health-oriented transactions and interchanges delicate medical data in serverless peer-to-peer (P2P) secured network settings. A consensus was devised and constituted to decrease rate of BC resource limitations on the IoMT.

In [13], suggesting a BC-based secured data management framework (BSDMF) for medical data related to the IoTs to exchange patients’ data securely and improve data accessibility and scalability. To assure data management and data transmission security among associated nodes, the IoMT-related security structure uses BC. In [14], this study evaluated offloading and scheduling issues for medical workflow in IoMT fog-cloud platforms. Thus, this study addressed the issue as an offloading and scheduling issue and developed deep reinforcement learning (DRL) as a Markov problem. This study designed an innovative DRL and BC-based system which contained multi-criteria offloading depending on DRL policies.

Lakhan et al. [15] developed an LSEOS method called lightweight secure efficient offloading scheduling. LSEOS has lightweight and secured offloading and scheduling methodologies whose offloading delay will be lesser compared to prevailing techniques. The end goal of LSEOS is to run the application over other nodes and diminish the delay and security threats in the mechanism. The metaheuristic LSEOS has the elements they are scheduling with neighbourhood search schemes, adaptive deadlines, and sorting. Kumar and Tripathi [16] offered an innovative contract-based consortium BC technique. The authors compiled interplanetary file systems (IPFS) and cluster nodes where smart contracts are deployable in the early phase. The IPFS cluster node assures the authentication and security of gadgets and even offers safe storage in IoMT based health care systems. Alqaralleh et al. [17] designed DL with BC-based secured image transmission and diagnosis system for the IoMT environment. The elliptic curve cryptography (ECC) was implemented in the initial stage, and then by combining grasshopper and fruit fly optimization (GO-FFO) system, ECC’s optimum key generation is taken. Finally, a method called a deep belief network (DBN) is applied to find the existence of disease. In [18], a novel secure authentication method utilizing ML was presented. To find the attack authentication and detection in an IoMT platform, this study applies ML and k-nearest neighbour (KNN) with smart contract (KNN-MLSC).

Uppal et al. [19] proposed an interplanetary file system (IPFS) enabled model for secure healthcare system. It enables the client to continuously upload the healthcare information gathered by IoT devices and to add to the BC transactions. The authors in [20] developed a BC based electronic medical records (EMR) management model for a smart healthcare system. The privacy of the healthcare data can be accomplished using BC technology. It offers off-chain storage for the records and assuring the authenticity and integrity of the health records. In [21], a new hybrid Elman Neural-based Blowfish BC approach has been introduced for the security of the healthcare data in the IoT environment. The Elman network offered continual monitoring to predict abnormal activities in the trained multimedia data. The authors in [22] developed a Lionized Golden Eagle based Homomorphic Elapid Security (LGE-HES) technique with blockchain in healthcare network. The blockchain provides the privacy of the medical images using hash operations.

Although several encryption techniques have been presented in the literature, security performance still needs to be improved. Since the images encompass a massive quantity of data, high redundancy rate, and increased correlation between neighboring pixels, classical encryption models cannot be used to resolve the requirements of the image encryption technique. Therefore, several approaches have been presented based on chaotic concepts, pixel swapping, etc. On the other hand, the continuous deepening of the DL model has resulted in the model overfitting issue. In addition, various hyperparameters have provided a substantial impact on the performance of the CNN model. In particular, the hyperparameters such as learning rate, batch size, and number of epochs are important to attain effectual outcome. As the trial-and-error technique for hyperparameter tuning is a challenging and erroneous procedure, a BO algorithm is used in this study.

3. The Proposed Model

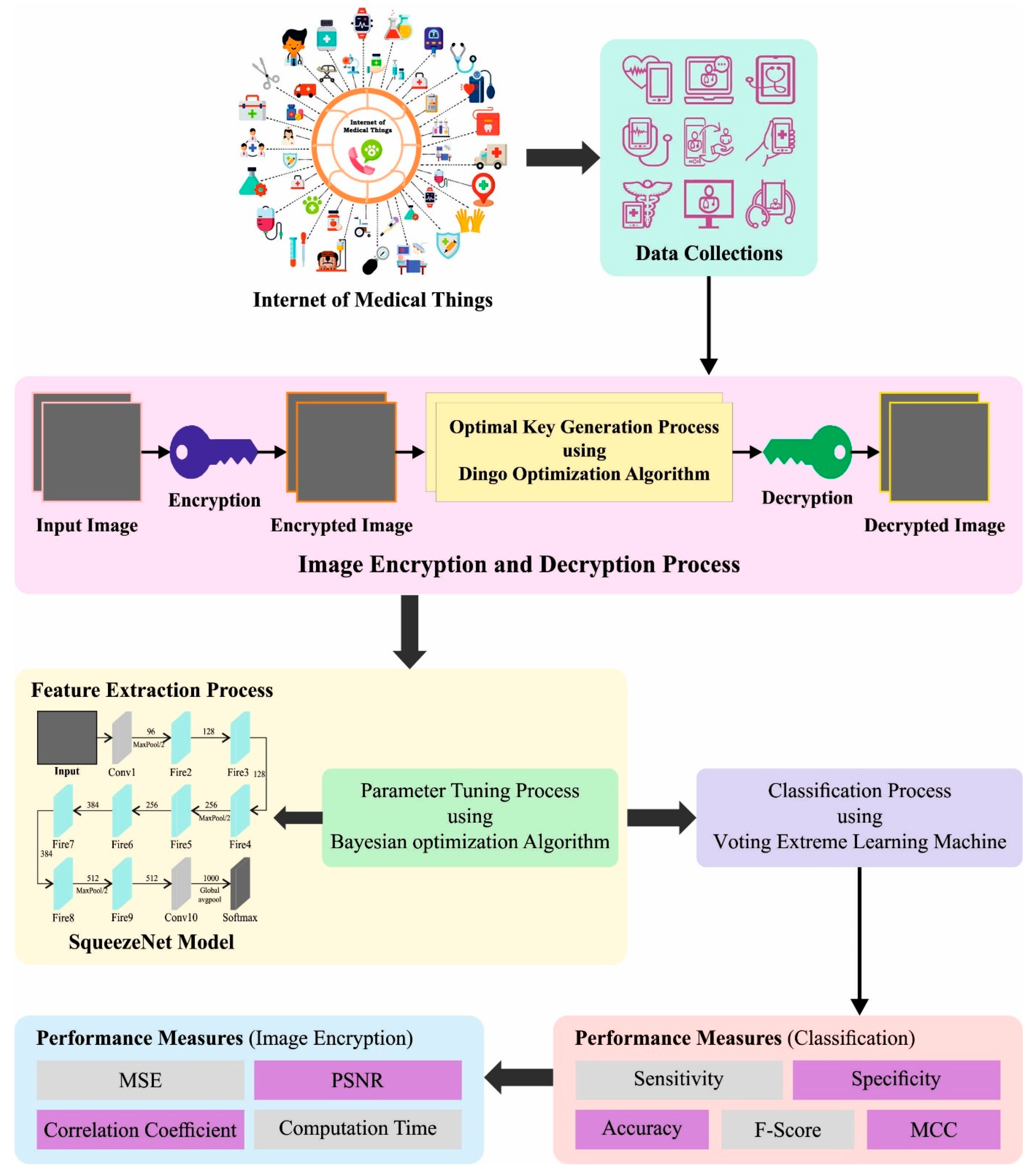
In this paper, we develop a new BSHS-EODL method for secured medical image transmission and analysis in the IoMT environment. The presented BSHS-EODL technique enables BC assisted secured image communication and detection models for the IoMT environment. The proposed method includes data classification, data collection, and image encryption. At the initial stage, the IoMT devices enable data collection processes, and the gathered images are stored in BC for security. Once the images are gathered, they are encrypted using effective image encryption technique with a DOA based key generation process. Next, the encrypted image was securely transferred using BC technology. At the receiver end, the image decryption was implemented, and the disease diagnosis process was later. Figure 1 demonstrates the working process of the BSHS-EODL method.

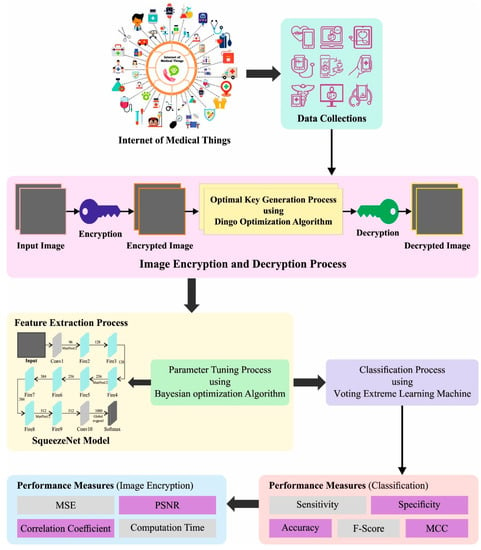
Figure 1. Working process of BSHS-EODL approach.

3.1. Image Encryption

In this work, image encryption method takes place to secure medical images. The image encryption procedure mostly comprises key selection, chaotic sequence pre-processing, diffusion, block scrambling, confusion, and expansion [23]. The chaotic sequence pre-processing makes the sequence more arbitrary. Block scrambling has been separated, as intra- and inter-block scrambling decrease the correlation and offer optimum protection against statistical attack. The expansion stage enhances arbitrary numbers to novel images towards all the encryption and thus gains a distinct ciphertext image that is optimally prepared to resist chosen plaintext attack. Diffusion and confusion complicate the connection amongst ciphertext and keys, which make it complex for adversaries to decrypt a ciphertext image and that improves the resistance of such scenarios.

• Key Selection

Optimizing values $x_0,$ $y_0,$ ${\mu }_1,$ ${\mu }_2,$ ${\lambda }_1$, and ${\lambda }_2$ created by the DOA technique can be utilized as the keys for 2-D logistic maps. For avoiding transient impact, the first 200 points can be discarded and generate 2 chaotic sequences $\left\{x_n\right\},$ $\left\{y_n\right\}$ that are of length $MN.$

• Chaotic Sequence Preprocessing

The 2 chaotic sequences $\left\{x_n\right\},$ $\left\{y\right\}$ can be pre-processed based on Equation (1).

$$\begin{gathered} x_1\left(i\right)={10}^q\cdot x_n\left(i\right)-round\left({10}^q\cdot x_n\left(i\right)\right)+0.5 \\ {y}_1\left(i\right)={10}^q\cdot y_n\left(i\right)-round\left({10}^q\cdot y_n\left(i\right)\right)+0.5 \end{gathered}$$

(1)

whereas $x_1\left(i\right)$ and $y_1\left(i\right)$ implies the chaotic sequences $\left\{x_n\right\},$ $\left\{y\right\}$ pre-processed sequence, whereas $q=8$.

• Image Scrambling

The 16 sub-blocks $B\left(i\right),i=1,2,\dots ,16$ of similar sizes can be separated by the new image $P_1$, and the remaining $16$ numbers of sequences $x\left(i\right)$ are acquired for composing a sequences $D\left(i\right)$. The acquired integer sequence $S\left(i\right)$ was sorted, and inter-block scrambling was attained based on Equation (2).

$$\begin{gathered} S\left(i\right)=floor\left(mod\left(D\left(i\right)\times {10}^{14},16\right)\right)+1 \\ \left[s,l\right]=sort\left(S\right) \\ B1=B\left(l\right) \end{gathered}$$

(2)

Sequences $t_1$ and $t_2$ refer to the collection of $8$ sequence values from the mid sequences $x\left(i\right)$ and $\left(i\right)$, correspondingly and a novel sequence $t$ was created based on Equation (3). All the sub-blocks were disordered $t_j$ times by intra-block scrambling established to process the novel disordered sixteen sub-blocks.

$$\left\{\begin{array}{l}t\left(2\left(i-1\right)+1\right)=floor\left(mod \left(t1\times {10}^{14},3\right)\right)+4\hfill \\ t\left(2i\right)=floor\left(mod \left(t2\times {10}^{14},3\right)\right)+4\hfill \end{array}\right.$$

(3)

Finally, the 16 sub-blocks can be combined with procedure image $P_2.$

• Image Expansion

The $R_0$ and $R_1$ are 2 random matrices created, whereas the sizes of $R_0$ and $R_1$ are 4 $\times \left(N+4\right)$ and $M\times 4$, correspondingly. Develop image $P_2$ based on the system for forming an expanded image $P_3.$

• Confusion and Diffusion

The chaotic scheme comprises two stages: diffusion and confusion. Confusion seeks to obscure and confound the relationships among key and the cipher images. Diffusion aims to obscure the relationships among the cipher and plain images by making it as convoluted. Principally, the swapping operation on the rows and the columns was performed for the realization of the confusion effects. Primarily, compute the novel row index $r\left(i\right)=ceil\left(x_1\left(i\right)\times \left(M+4\right)\right)$ utilizing $x_1\left(i\right)$, followed by related row $i$ with row indexes $r\left(i\right)$.

$$\begin{gathered} if r\left(i\right)<i, then \\ r\left(i\right)=i \end{gathered}$$

(4)

Secondly, the parameters $k_{11},$ $k_{12}$ are computed utilizing $x_1\left(i\right)$.

$$\begin{gathered} k_{11}\left(i\right)=mod\left(floor\left(x_1\left(i\right)\times {10}^8\right),256\right) \\ {k}_{12}\left(i\right)=mod\left(floor\left(x_1\left(i\right)\times {10}^9\right),256\right) \end{gathered}$$

(5)

Thirdly, accomplish a bitwise XOR function on the expansion image $P_3$ with parameters $k_{11},$ $k_{12}.$

If $=r\left(i\right)$, then

$$\begin{gathered} P_{30}\left(i,:\right)=P_3\left(i,:\right)\oplus k_{11}\left(i\right) \\ if \ne r\left(i\right), then \\ {P}_{30}\left(i,:\right)=P_3\left(i,:\right)\oplus k_{11}\left(i\right) \\ {P}_{30}\left(r\left(i\right),:\right)=P_3\left(r\left(i\right),:\right)\oplus k_{12}\left(i\right) \end{gathered}$$

(6)

At the fourth stage, swap the $i$th and $r\left(i\right)$th row of $P_{30}$ for obtaining $P_{31}.$

$$\begin{gathered} temp=P_{30}\left(i,:\right) \\ {P}_{30}\left(i,:\right)=P_{30}\left(r\left(i\right),:\right) \\ {P}_{30}\left(r\left(i\right),:\right)=temp \\ {P}_{31}=P_{30} \end{gathered}$$

(7)

In the fifth, the first and last columns of $P_{31}$ can be computed to obtain $P_4.$

$$P_4\left(i, 1\right)=mod \left(P_{31}\left(i, 1\right)+P_{31}\left(i, N+4\right),256\right)$$

(8)

At the sixth stage, the other columns of $P_{31}$ and $P_4$ can be computed.

$$P_4\left(i,j\right)=mod \left(P_{31}\left(i,j\right)+P_4\left(i,j-1\right),256\right)$$

(9)

The diffusion and confusion of columns are related to the row, but that sequence $y_1\left(i\right)$ was utilized rather than sequence $x_1\left(i\right)$. The particular computation process was projected in Algorithm 1.

Algorithm 1: Column confusion and diffusion

Input: Image $P_4$ and pre-processed chaotic sequence $y_1\left(i\right)$ Output: Image $P_5$ for $j=1$ to $N+4$    $q\left(j\right)=ceil\left(\left(N+4\right)\cdot y_1\left(j\right)\right)$,     $k_{21}\left(j\right)=mod \left(floor\left({10}^8\times y_1\left(j\right)\right),2^8\right)$,     $k_{22}\left(j\right)=mod \left(floor\left({10}^9\times y_1\left(j\right)\right),2^8\right)$,    if $q\left(j\right)<j$ then                         $q\left(j\right)=j,$    end if    if $q\left(j\right)=j$ then         $P_4\left(:,j\right)=k_{21}\left(j\right)\oplus P_4\left(:,j\right)$,    else if     $P_4\left(:,j\right)=k_{21}\left(j\right)\oplus P_4\left(:,j\right)$, $P_4\left(:,q\left(j\right)\right)=k_{22}\left(j\right)\oplus P_4$ $q\left(j\right))$, end if $temp=P_4\left(:,j\right)$, $P_4\left(:,j\right)=P_4\left(:,q\left(j\right)\right)$,               $P_4\left(:,q\left(j\right)\right)=temp,$                   $P_{41}=P_{4;}$    for $i=1 to M+4$        $P_5\left(1,j\right)=mod \left(P_{41}\left(1,j\right)+P_{41}\left(M+4,j\right),2^8\right)$,        $P_5\left(i,j\right)=mod \left(P_5\left(i-1,j\right)+P_{41}\left(i,j\right),2^8\right)$,   end for end for

3.2. Key Generation Process

The DOA is used for an effective key generation process. The DOA is a metaheuristic approach stimulated by the hunting behaviours of dingo. DOA is chosen for key generation due to its following advantages: high convergence, robust, global optimization, a smaller number of parameters, simplicity, and highly versatile. This strategy includes scavenging nature, attack by persecution, and assembling procedures [24]. Australian dingo dogs are in danger of extermination. Consequently, the survival rate of dingo is regarded in the DOA. The mathematical expression of DOA is given in the following. In general, dingoes meet in groups during hunting. They then find the prey location and surround it using the following equation:

$${\overrightarrow{x}}_i\left(t+1\right)={\beta }_1{\displaystyle \sum }_{k=1}^{na}\frac{\left[\overrightarrow{{\phi }_k\left(t\right)}-{\overrightarrow{x}}_i\left(t\right)\right]\frac{\backslash }{{\varphi }_k\left(t\right)}}{na}-{\overrightarrow{x}}_i{}_{\ast }\left(t\right)$$

(10)

In Equation (10), $\overrightarrow{x}\left(t+1\right)$ represents the new prey location of the searching agent, $na$ denotes the random integer generated within $[$2, $\frac{SizePop}{2}]$, where SizePop indicates overall dingo population size. ${\overrightarrow{\phi }}_k\left(t\right)$ shows the subset of search agent where $\varphi \subset X,$ $X$ denotes the randomly generated dingo population, ${\overrightarrow{x}}_i\left(t\right)$ specifies the existing search agent, ${\overrightarrow{x}}_i\left(t\right)$ signifies the best possible searching agent attained from prior iteration, and ${\beta }_1$ is a consistently produced arbitrary number within [−2, 2]. Typically, dingoes hunt tiny prey and chase it till it gets caught. These characteristics are expressed as follows:

$${\overrightarrow{x}}_i\left(t+1\right)={\overrightarrow{x}}_{\ast }\left(t\right)+{\beta }_1\ast e^{{\beta }_2}\ast \left({\overrightarrow{x}}_{r_1}\left(t\right)-{\overrightarrow{x}}_i\left(t\right)\right)$$

(11)

In Equation (11), $\overrightarrow{x}\left(t+1\right)$ describes the movement of the dingo, ${\overrightarrow{x}}_i\left(t\right)$ shows existing search agents, ${\overrightarrow{x}}_{\ast }\left(t\right)$ means best possible search agent obtained from the previous iteration, $r_1$ represents randomly produced numbers from the interval 1 to the size of maximal of the search agent, and ${\overrightarrow{x}}_{r1}\left(t\right)$ shows the $r_1-\mathrm{th}$ selected search agent, where $i\ne r_1$.

Scavenger is characterized as a dingo finding meat to eat if they get a random walk in the habitat.

$${\overrightarrow{x}}_i\left(t+1\right)=\frac{1}{2}[e^{{\beta }_2}\ast {\overrightarrow{x}}_{r_1}\left(t\right)-\left(-1{)}^{\sigma }\ast {\overrightarrow{x}}_i\left(t\right)\right]$$

(12)

In Equation (12), $\overrightarrow{x}\left(t+1\right)$ denotes the dingo progress, ${\beta }_2$ has equivalent value as in Equation (12), $r_1$ represents the randomly generated number within [1, max_size of searching agent] interval, ${\overrightarrow{x}}_{r_1}\left(t\right)$ indicates the $r_1^{th}$ selected search agent, ${\overrightarrow{x}}_i\left(t\right)$ denotes the existing search agent, where $i\ne r_1$, and $\sigma$ signifies the arbitrarily created binary number. Finally, the survival rate of the dingoes is expressed as follows:

$$survival \left(i\right)=\frac{fitnes{s}_{ \max }-fitness\left(i\right)}{fitnes{s}_{ \max }-fitnes{s}_{ \min }}$$

(13)

In Equation (13), $fitnes{s}_{ \max }$ and $fitnes{s}_{ \min }$ correspondingly represent poor and optimum fitness values in the present round. $fitness\left(i\right)$ signifies existing fitness value of $i$-$th$ searching agent. The survival vector in Equation (13) encompasses the normalizing fitness value within $\left[0, 1\right]$. Equation (14) is used for attaining lower survival rate.

$${\overrightarrow{x}}_i\left(t\right)={\overrightarrow{x}}_{\ast }\left(t\right)+\frac{1}{2}[{\overrightarrow{x}}_{r_1}\left(t\right)-\left(-1{)}^{\sigma }\ast {\overrightarrow{x}}_{r_2}\left(t\right)\right]$$

(14)

In Equation (14), ${\overrightarrow{x}}_i\left(t\right)$ represents that search agent with minimal survival rate is upgraded. In addition, $r_1$ and $r_2$ denote the randomly produced numbers within [1, max_size of searching agent] interval, ${\overrightarrow{x}}_{\ast }\left(t\right)$ specifies best possible searching agent accomplished from previous iteration, and $\sigma$ showing binary number of agents, with $r_1\ne r_2,$ ${\overrightarrow{x}}_{r_1}\left(t\right)$ and ${\overrightarrow{x}}_{r_2}\left(t\right)$, describes $r_1$, $r_2$ selected searching agent, ${\overrightarrow{x}}_{\ast }\left(t\right)$ indicates the best possible searching agent accomplished from previous iteration, and $\sigma$ shows the randomly generated number.

The set of keys is preferred by considering the “fitness function” as a max key using peak signal-to-noise ratio (PSNR) for scrambling and unscrambling data from medical images. With the help of hybrid optimization, the organization has been developed, and it is given in the following:

$$Fitness=\max \left\{PSNR\right\}$$

(15)

3.3. Blockchain Technology

The proposed BSHS-EODL technique used BC technology for secure data transmission in the medical field. A BC is distributed data where a novel time-stamped transaction is grouped and appended to a hash-chain of blocks [25]. The BSHS-EODL technique comprises a data processing section, application server for data transmission and reception, BC enabled decentralized databases, application programming interface (API) management element, and data analytics unit. A few processes which take place in the system are Create_Patient_Data, Grant_Access_ToHCP, and Revoke_Access. The structured data of the patient gets saved in the classical dataset and the unstructured data gets stored in the data warehouse. The encrypted data gets saved in the distributed BC using preferrable smart contract. After the storage of data in the allotted BC, BSHS-EODL technique uses VELM classifier for classification process. The medical image is loaded into the decentralized BC, and the BSHS-EODL technique can be employed to the data fetched from the decentralized network. The BSHS-EODL technique operates in the following way. Ethereum BC network can be employed for patient data distribution. Each individual actor carries out various activities in the network and has access to the data for which they received access. The patients can generate the information and commit the transaction. When the transactions are committed in the BC, the altered transaction is dispersed over the Internet, verifying that each data existing in the network can be accessed by every actor in the network and cannot be changed by unintentional persons. The medical personnel can access the data only when the respective user provides access permissions. Healthcare professionals can access the patient data and perform disease diagnostic processes. If the healthcare professional receives a request from the patient, they can accept it and send a request to access the data to the specific person. Upon the acceptance of the request, they investigate the medical data for disease detection purposes.

3.4. Disease Classification Model

In this work, the BSHS-EODL technique performs disease diagnosis comprising SqueezeNet, BO based parameter tuning, and VELM.

3.4.1. Feature Extraction Using SqueezeNet

To produce feature vectors, the SqueezeNet model is used in this work. SqueezeNet is a small, efficient deep neural network structure [26]. It is intended to be faster and smaller than other architectures while accomplishing higher accuracy on image classification tasks. SqueezeNet exploits a technique named “squeeze-and-excitation” to decrease the parameter count in the network, enabling it to be more effective in terms of memory and computational requirements. It was specifically designed for use on embedded and mobile devices. The SqueezeNet architecture comprises a series of layers, including the following:

• Pooling layers, decrease the spatial dimension of the feature maps.
• The input layer takes in the image dataset.
• A sequence of FC layers categorises the image based on the extracted features through the convolution layer.
• A sequence of convolutional layers extracts features from the image. This layer uses “fire modules” that comprise the “expand” layer with a larger number of filters, followed by “squeeze” layer with smaller number of filters. This enables the network to maintain fewer parameters while still extracting relevant features from the image.

The architecture also includes a dropout layer and a softmax layer. Dropout is a regularization technique that prevents overfitting by randomly dropping out some neurons during training. The softmax layer creates a probability distribution over the feasible classes used to classify the image. The SqueezeNet architecture is designed to be small and efficient, with a total of only 1.2 million parameters. This makes it better suited for use on embedded and mobile devices with limited computational resources.

Here, the BO is utilized for the hyperparameter selection of SqueezeNet. A probabilistic method of the objective function $\left(x\right)$ called the surrogate function can be created using BO technique [27]. Bayes’ Theorem is the core of BO technique and computes the conditional probability of event $A$ given another event $B, P(A|B)$,

$$P\left(A|B\right)=P\left(B|A\right)\ast \frac{P\left(A\right)}{P\left(B\right)}$$

(16)

Bayes’ theorem is capable of being adjusted by neglecting the $P\left(B\right)$ marginal probability from the conditional probability for optimization problem using Equation (17):

$$P\left(A|B\right)=P\left(B|A\right)\ast P\left(A\right)$$

(17)

A new version of Bayes’ theorem is given as follows:

$$Posterior=Likelihood \ast Prior$$

(18)

The conditional probability is a function that estimates the objective function and is utilized for sampling the searching space. The searching space in these problems is the SqueezeNet hyperparameter. BO algorithm, as an informed search technique, can be differentiated by using an acquisition function that exploits the posterior for sampling the searching area and selecting the succeeding sample to evaluate the objective function. In this study, the objective function can be denoted as a Gaussian method with the Matern 5/2 kernel. At first, random samples from the search space $\left(x_1, x_2, \dots , x_n\right)$ are exploited for determining the $F\left(x\right)$ objective function at these samples. The assessments and samples are gathered in a consecutive way, which leads to a sequence of data points $S=\left\{x_i, F\left(x_j\right), \dots x_n, F\left(x_n\right)\right\}$, where $n$ denotes the number of samples. The set $S$ defines the likelihood, and prior function can be described as follows:

$$P(F|S)=P(S|F)\ast P\left(S\right)$$

(19)

The posterior is updated afterwards with the evaluation of prior and probability. The acquisition function, $C$, is enhanced over the Gaussian algorithm for selecting the subsequent sample $x_n$, which can be represented as follows:

$$x_n={ \mathrm{argmax}}_{x}C(x|S_{1:n-1})$$

(20)

In this study, the acquisition function can be executed by the expected improvement algorithm, as defined below.

$$C\left(x\right)=E\left[\max \left(F\left(x\right)-P\left(x^{+}\right),0\right)\right]$$

(21)

In Equation (21), $F\left(x\right)$ indicates the value of objective function for the better sample, $E$ denotes the expectation operator, and $x^{+}$ shows the better sample location in the search range. Then, the sample selected can be assessed by the objective function, and these processes are repeated until the objective function attains its least or minimum objective within the given run time.

3.4.2. Image Classification Using VELM Model

Finally, the classification of medical images is performed by the VELM model. The VELM was utilized as a classifier in this work. The VELM is a significant ML model which enhances classification accuracy while maintaining high processing speeds and robustness to noise and outliers in the input data. An ELM is a type of artificial neural network (ANN) with a single hidden layer (HL) [28]. Here, the weight that connects input to the HL and HL to biases are randomized. The weights between the output and HLs are computed by the Moore–Penrose inverse, making the training model faster. Several ELMs can be used for classification to increase detection accuracy. Each individual ELM is trained using similar data. In the process of detection, the sample is used for all the ELMs and output is computed. Based on the majority voting, the last output is computed. Assume, an ELM with activation functions $f$ and $l$ hidden neurons in HL. If there is $N$ training sample of the form $\left(x_i, t_i\right)$, where $x_i={[x_{i1}, x_{i2}, \dots , x_{in}]}^T\in R^n$ and $t_i={[t_{i1}, t_{i2}, \dots , t_{im}]}^T\in R^m$ ($m=2$) then the output can be represented as

$$0_i={\displaystyle \sum }_{j=1}^1{v}_{j}f\left(u_j, b_j, x_i\right)$$

(22)

for, $i=1,2,3,\dots ,N$.

Where $u_j\in R^n$ and $b_j\in R$ denote the learning parameters of jth hidden neuron. $v_j={[{\nu }_{j1}, {\nu }_{j2}, \dots , {\nu }_{jm}]}^T$ indicates the weight vector that connects jth hidden neurons to output neurons. This can be represented as follows:

$$O=HV$$

(23)

where,

$$H=\left[\begin{array}{ccc}f\left(u_1,b_1,x_1\right)& \dots & f\left(u_l,b_l,x_1\right)\\ ⋮& ⋮& ⋮\\ f\left(u_1,b_1,x_N\right)& \dots & f\left(u_l,b_{|},x_N\right)\end{array}\right],V=\left[\begin{array}{l}{v}_1^T\hfill \\ ⋮\hfill \\ v_l^T\hfill \end{array}\right]\mathrm{and} O=\left[\begin{array}{l}{o}_1^T\hfill \\ ⋮\hfill \\ o_N^T\hfill \end{array}\right]$$

The $u_j$ and $b_j$ parameters are randomly initialized for minimizing the error $\left|\left|O-T\right|\right|$, where $T=\left(t_1, t_2,\dots ,t_N\right)$, that is independent of input dataset. The output weights can be expressed by finding the least square solution,

$$V=H^{+}T$$

(24)

where the symbol $“+”$ characterizes the Moore–Penrose generalized inverse of matrix. It implies ELM is trained. In $V$-ELM, $k$-$\mathrm{th}$ ELM is used. The equivalent number of hidden layers initialized this ELM. The learning parameter $u_j$ and $b_j$ of each ELM is initialized in a random fashion. Next, each ELM is trained on a similar dataset and the results are computed. In detection stage, a set of samples of the form $y_i=$ $\left[y_{i1}, y_{i2}, \dots , y_{in}\right]$ is used for each ELM. The output $0_i=\left[0, 1\right]$ or $0_i=\left[1, 0\right]$ of every individual ELM is taken, and majority voting receives the last output. For every $i$ sample, a vector $C_i\in Z_{>=0}^2$ has been used for storing the class labels recognized by dissimilar ELMs. At first, $C_i$ is initialized to zero $\left(C_i=\left[0,0\right]\right)$ once an ELM output takes place; the value of equivalent location in $C_i$ can be raised by 1. For instance, assume output of $EL{M}_1$ is [1, 0] now $C_i$ become [1, 0]. Output of $EL{M}_2$ is again $\left[1, 0\right]$, then $C_i$ becomes $\left[2, 0\right]$. Output of $EL{M}_3$ is $\left[0, 1\right]$, then $C_i$ becomes $\left[2, 1\right]$. Once each $k$ output is reached, then the concluding output is evaluated.

4. Performance Validation

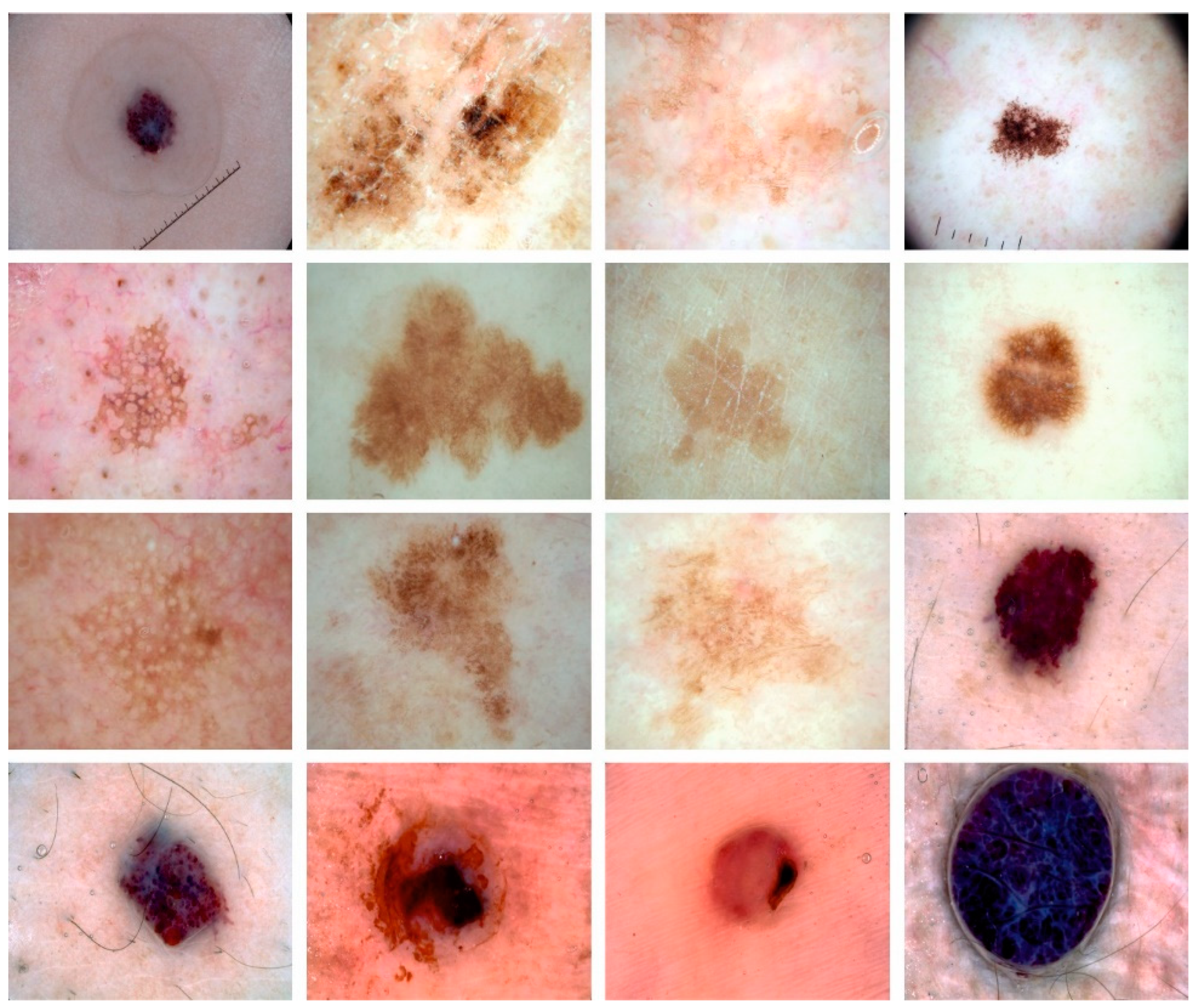
In this section, the experimental outcome of the BSHS-EODL technique is well studied on skin lesion images in the ISIC database. Figure 2 illustrates the sample images.

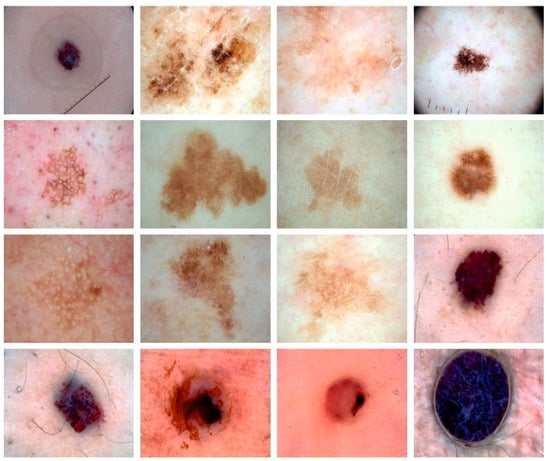
Figure 2. Sample Images.

Figure 3 shows the histogram analysis of the BSHS-EODL technique. Figure 3a,b show the original images and their corresponding histogram images. Similarly, Figure 3c,d demonstrate the encrypted images and their respective histograms.

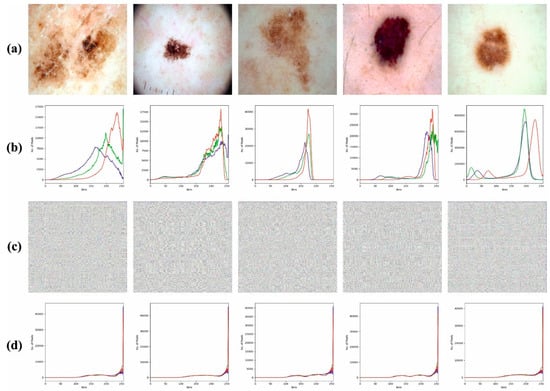
Figure 3. (a) Original Images (b) Histogram of Original Images (c) Encrypted Images (d) Histogram of Encrypted Images.

Table 1 represents the comparative MSE and PSNR examination of the BSHS-EODL technique with existing techniques [17,29] on different images. The results indicate that the GWO and GO-PSO algorithms resulted in higher MSE values, while the GO-FFO and HOCE-ECC techniques led to considerable MSE values. However, the BSHS-EODL technique gains effective performance over other models with minimal MSE of 0.072, 0.057, 0.078, 0.102, and 0.071 under test images 1–5, respectively. The experimental outcomes indicate that the GWO and GO-PSO algorithms represented lower PSNR values than existing ones. Although the GO-FFO and HOCE-ECC models reach moderately improved PSNR values, the BSHS-EODL technique outperformed the existing models with a higher PSNR of 59.56 dB, 60.57 dB, 59.21 dB, 58.04 dB, and 59.62 dB under images 1–5 respectively.

Table 1. MSE and PSNR analysis BSHS-EODL approach with other systems under varying images.

Sample Images	BSHS-EODL		HOCE-ECC [29]		GO-FFO [17]		GO-PSO [17]		GWO [17]
	MSE	PSNR	MSE	PSNR	MSE	PSNR	MSE	PSNR	MSE	PSNR
Image 1	0.072	59.56	0.112	57.64	0.132	56.93	0.171	55.80	0.197	55.19
Image 2	0.057	60.57	0.083	58.94	0.119	57.38	0.152	56.31	0.172	55.78
Image 3	0.078	59.21	0.118	57.41	0.152	56.31	0.188	55.39	0.220	54.71
Image 4	0.102	58.04	0.13	56.99	0.157	56.17	0.184	55.48	0.210	54.91
Image 5	0.071	59.62	0.107	57.84	0.128	57.06	0.165	55.96	0.186	55.44

Table 2 shows a brief CC outcome of the BSHS-EODL system under several images. The experimental outcome stated that the GWO and GO-PSO algorithms represented lesser CC values over existing ones. However, the GO-FFO and HOCE-ECC models reach moderately enhanced CC values, and the BSHS-EODL approach outperformed the existing techniques with maximal CC of 99.42, 99.63, 99.21, 99.72, and 99.68 under images 1–5 correspondingly.

Table 2. CC analysis of BSHS-EODL approach with other techniques under varying images.

Sample Images	BSHS-EODL	HOCE-ECC [29]	GO-FFO [17]	GO-PSO [17]	GWO [17]
Image 1	99.42	98.93	98.49	98.16	97.7
Image 2	99.63	99.22	98.84	98.53	98.18
Image 3	99.21	98.76	98.45	97.98	97.54
Image 4	99.72	99.33	99.01	98.65	98.19
Image 5	99.68	99.37	99.04	98.54	98.22

Table 3 represents the encryption outcomes of the BSHS-EODL method with existing models under the presence of attacks in terms of computation time (CT) and PSNR. The outcome inferred that the GWO and GO-PSO algorithms resulted in higher CT values, while the GO-FFO and HOCE-ECC approaches led to considerable CT values. The BSHS-EODL algorithm attains effectual performance over other systems with minimal CT of 0.20 s, 0.13 s, 0.16 s, 0.11 s, and 0.15 s under test images 1–5 correspondingly.

Table 3. CT and PSNR outcome of BSHS-EODL approach with other techniques under varying images.

Computation Time (s)
Sample Images	BSHS-EODL	HOCE-ECC [29]	GO-FFO [17]	GO-PSO [17]	GWO [17]
Image 1	0.20	0.50	0.78	0.94	1.29
Image 2	0.13	0.31	0.51	0.70	1.05
Image 3	0.16	0.48	0.72	0.92	1.07
Image 4	0.11	0.45	0.59	0.89	1.03
Image 5	0.15	0.41	0.68	1.00	1.31
PSNR During Attacks (dB)
Sample Images	BSHS-EODL	HOCE-ECC [29]	GO-FFO [17]	GO-PSO [17]	GWO [17]
Image 1	59.21	57.08	56.47	55.29	54.66
Image 2	60.17	58.34	56.90	56.01	55.48
Image 3	58.80	57.01	55.74	54.84	54.38
Image 4	57.71	56.44	55.61	54.91	54.44
Image 5	59.31	57.43	56.59	55.42	55.09

The experimental outcomes implied that the GWO and GO-PSO algorithms represented minimal PSNR values over existing ones. However, the GO-FFO and HOCE-ECC models reached moderately greater PSNR values, and the BSHS-EODL approach outperformed the existing approaches with enhanced PSNR of 59.21 dB, 60.17 dB, 58.80 dB, 57.71 dB, and 59.31 dB under images 1–5 correspondingly.

The classification performance of the BSHS-EODL technique can be tested on the ISIC 2017 Dataset, comprising 318 samples with seven classes, as defined in Table 4.

Table 4. Details of dataset.

Labels	Class	No. of Images
C-0	Angioma	21
C-1	Nevus	46
C-2	Lentigo NOS	41
C-3	Solar Lentigo	68
C-4	Melanoma	51
C-5	Seborrheic Keratosis	54
C-6	BCC	37
Total count of Images		318

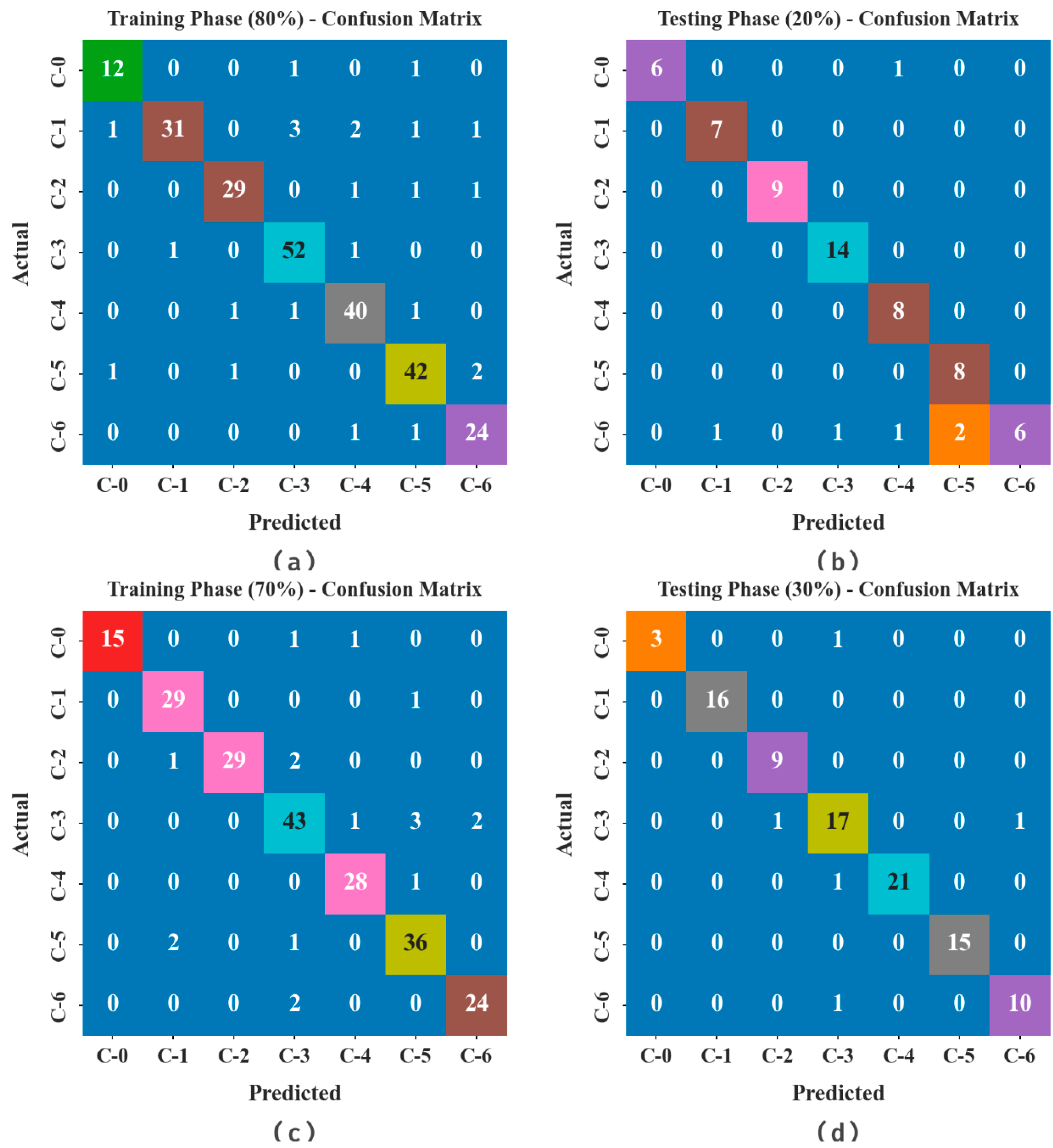
The confusion matrices of the BSHS-EODL method are investigated under distinct sizes of TRS and TSS in Figure 4. The results demonstrated that the BSHS-EODL technique properly recognizes the samples under every class.

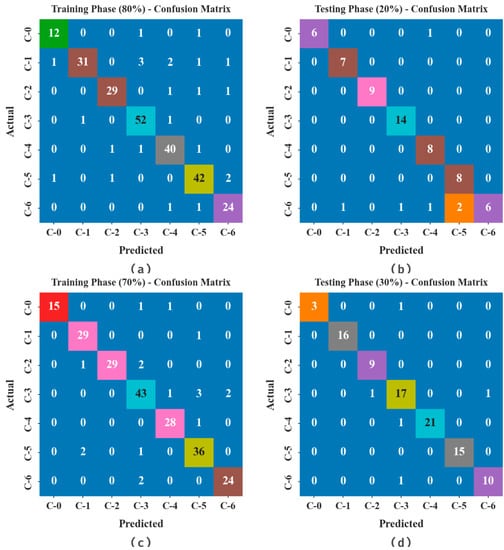
Figure 4. Confusion matrices of BSHS-EODL approach (a,b) TRS/TSS of 80:20 and (c,d) TRS/TSS of 70:30.

In Table 5, the overall results of the BSHS-EODL technique are demonstrated. The results indicate that the BSHS-EODL technique properly classified the images under all classes. For instance, with 80% of TRS, the BSHS-EODL technique reaches average $acc{u}_{bal}$ of 97.30%. In addition, with 20% of TSS, the BSHS-EODL approach attains average $acc{u}_{bal}$ of 97.32%. Meanwhile, with 70% of TRS, the BSHS-EODL system attains average $acc{u}_{bal}$ of 97.68%. Finally, with 30% of TSS, the BSHS-EODL algorithm obtains average $acc{u}_{bal}$ of 98.51%.

Table 5. Classifier outcome of BSHS-EODL approach with different metrics.

Labels	$\mathit{A}\mathit{c}\mathit{c}{\mathit{u}}_{\mathit{y}}$	$\mathit{S}\mathit{e}\mathit{n}{\mathit{s}}_{\mathit{y}}$	$\mathit{S}\mathit{p}\mathit{e}{\mathit{c}}_{\mathit{y}}$	${\mathit{F}}_{\mathit{s}\mathit{c}\mathit{o}\mathit{r}\mathit{e}}$	MCC
Training Phase (80%)
C-0	98.43	85.71	99.17	85.71	84.88
C-1	96.46	79.49	99.53	87.32	85.85
C-2	98.03	90.62	99.10	92.06	90.96
C-3	97.24	96.30	97.50	93.69	91.99
C-4	96.85	93.02	97.63	90.91	89.04
C-5	96.46	91.30	97.60	90.32	88.16
C-6	97.64	92.31	98.25	88.89	87.64
Average	97.30	89.82	98.40	89.85	88.36
Testing Phase (20%)
C-0	98.44	85.71	100.00	92.31	91.78
C-1	98.44	100.00	98.25	93.33	92.72
C-2	100.00	100.00	100.00	100.00	100.00
C-3	98.44	100.00	98.00	96.55	95.64
C-4	96.88	100.00	96.43	88.89	87.83
C-5	96.88	100.00	96.43	88.89	87.83
C-6	92.19	54.55	100.00	70.59	70.60
Average	97.32	91.47	98.44	90.08	89.49
Training Phase (70%)
C-0	99.10	88.24	100.00	93.75	93.48
C-1	98.20	96.67	98.44	93.55	92.57
C-2	98.65	90.62	100.00	95.08	94.45
C-3	94.59	87.76	96.53	87.76	84.29
C-4	98.65	96.55	98.96	94.92	94.15
C-5	96.40	92.31	97.27	90.00	87.84
C-6	98.20	92.31	98.98	92.31	91.29
Average	97.68	92.06	98.60	92.48	91.15
Testing Phase (30%)
C-0	98.96	75.00	100.00	85.71	86.14
C-1	100.00	100.00	100.00	100.00	100.00
C-2	98.96	100.00	98.85	94.74	94.32
C-3	94.79	89.47	96.10	87.18	83.96
C-4	98.96	95.45	100.00	97.67	97.05
C-5	100.00	100.00	100.00	100.00	100.00
C-6	97.92	90.91	98.82	90.91	89.73
Average	98.51	92.98	99.11	93.74	93.03

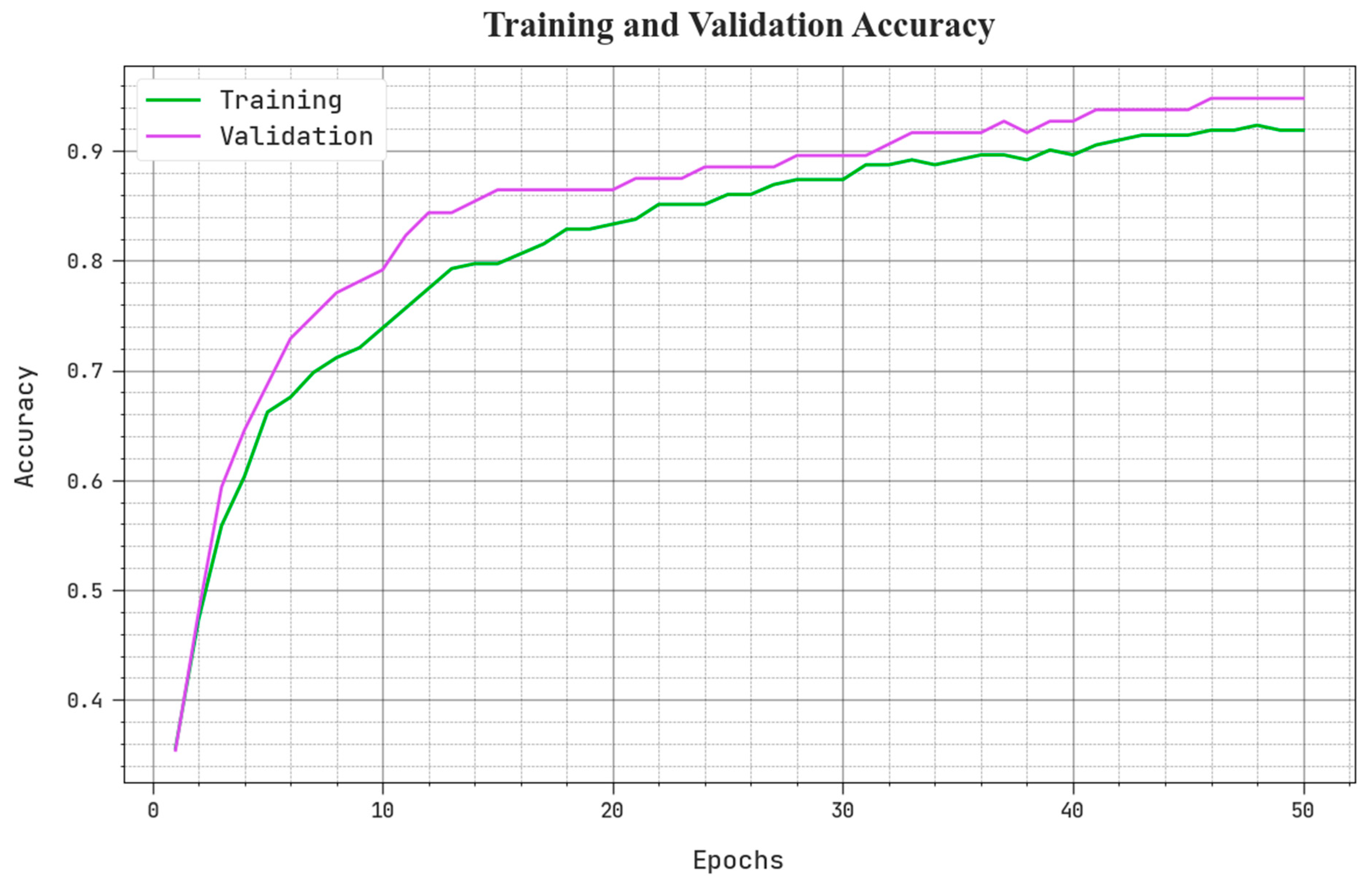
The training accuracy (TACY) and validation accuracy (VACY) of the BSHS-EODL method can be assessed in Figure 5. The figure inferred that the BSHS-EODL algorithm has demonstrated greater results with enhanced values of TACY and VACY. It can be noted that the BSHS-EODL system has obtained maximal TACY outcomes.

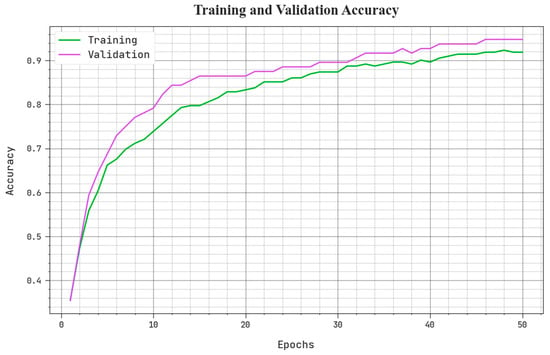
Figure 5. TACY and VACY analysis of BSHS-EODL method.

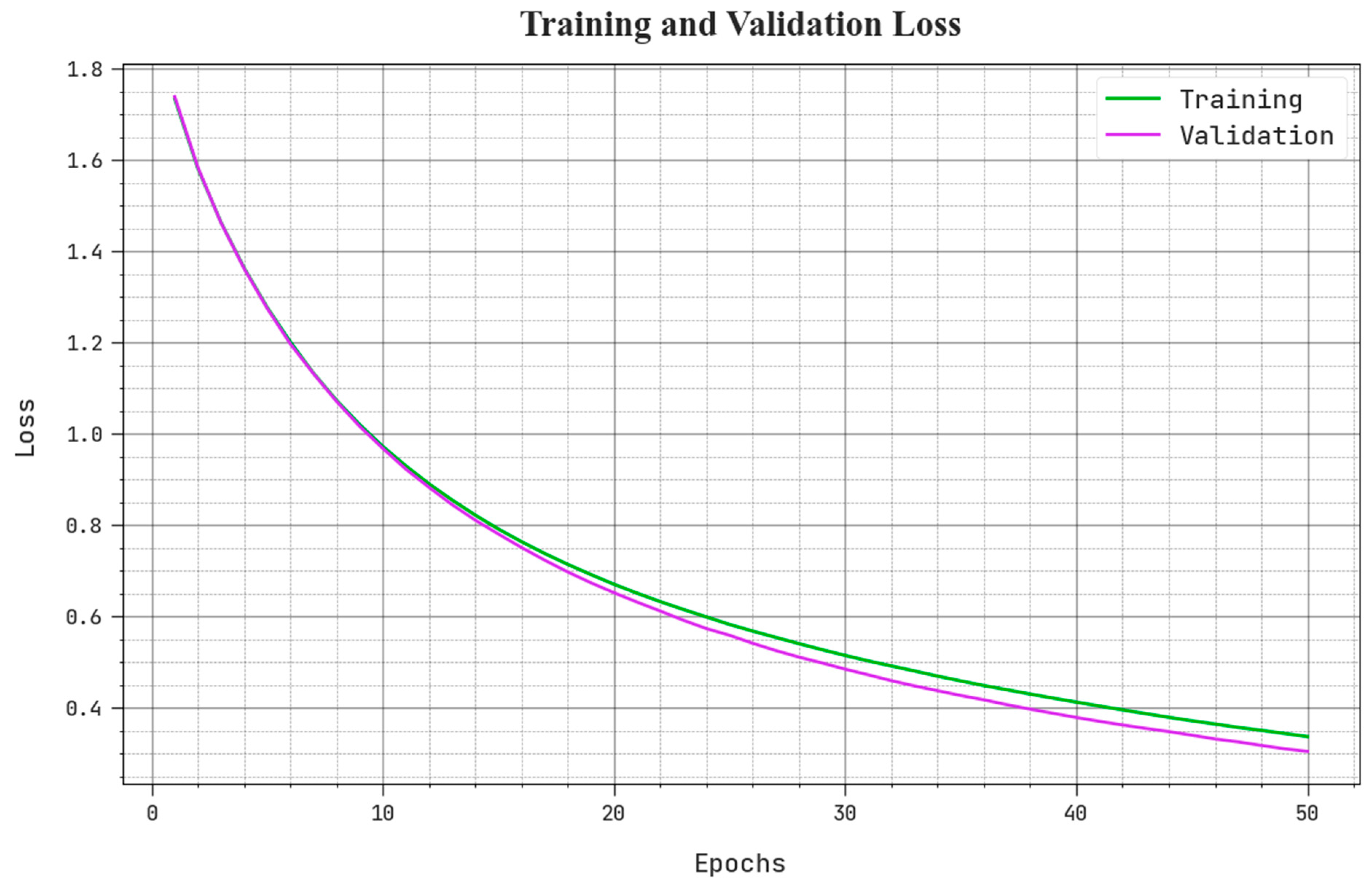
The training loss (TLOS) and validation loss (VLOS) of the BSHS-EODL approach are tested in Figure 6. The figure stated that the BSHS-EODL approach has demonstrated higher performance with decreasing TLOS and VLOS. Evidently, the BSHS-EODL algorithm has resulted in lesser VLOS outcomes.

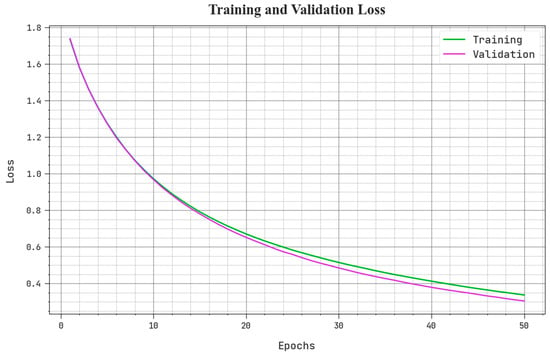
Figure 6. TLOS and VLOS analysis of BSHS-EODL approach.

The extensive comparative study of the BSHS-EODL technique takes place in Table 6 [17,30]. The results highlighted that the VGG-19 model shows least performance, whereas the DBN and YOLO-GC techniques reported moderately similar outcomes. In comparison, the ResNet and CDNN models attain a reasonable performance.

Table 6. Comparative outcome of BSHS-EODL method with other DL techniques.

Methods	Accuracy	Sensitivity	Specificity
BSHS-EODL	98.51	92.98	99.11
DBN [17]	94.15	91.40	90.98
YOLO-GC [17]	94.24	89.30	90.77
ResNet Model [17]	96.19	90.44	91.03
VGG-19 [30]	91.19	90.20	93.73
CDNN [17]	95.29	91.19	92.77

However, the BSHS-EODL technique gains maximum classification performance with $acc{u}_y$ of 98.51%, $sen{s}_y$ of 92.98%, and $spe{c}_y$ of 99.11%. These outcomes ensured the betterment of the BSHS-EODL method over other existing techniques in the IoMT environment.

5. Conclusions

This article introduces a new BSHS-EODL technique for secure medical image transmission and analysis in the IoMT environment. The presented BSHS-EODL technique enables BC assisted secured image transmission and diagnosis models for the IoMT platform. The proposed method includes data classification, data collection, and image encryption. At the initial stage, the IoMT devices enable data collection processes, and the gathered images are stored in BC for security. Subsequently, image encryption is applied to encrypt the data and the key generation process is performed via the DOA. Finally, the BSHS-EODL technique performs disease diagnosis comprising SqueezeNet, BO based parameter tuning, and VELM. A comprehensive set of simulation analyses on medical datasets highlights the supremacy of the BSHS-EODL technique. In upcoming years, the performance of the proposed method can be tested on other disease diagnoses.