Detection and Characterization of Artificial Porosity and Impact Damage in Aerospace Carbon Fiber Composites by Pulsed and Line Scan Thermography
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Samples
2.2. Data Acquisition
2.2.1. Pulsed Thermography (PT)
2.2.2. Line Scan Thermography (LST)
2.3. Data Processing
2.3.1. Pulsed Thermography (PT)
2.3.2. Line Scan Thermography (LST)
2.3.3. Contrast-to-Noise Ratio (CNR)
2.3.4. Estimation of Thermal Diffusivity, α
2.3.5. Depth Estimation with the Phase
3. Results and Discussion
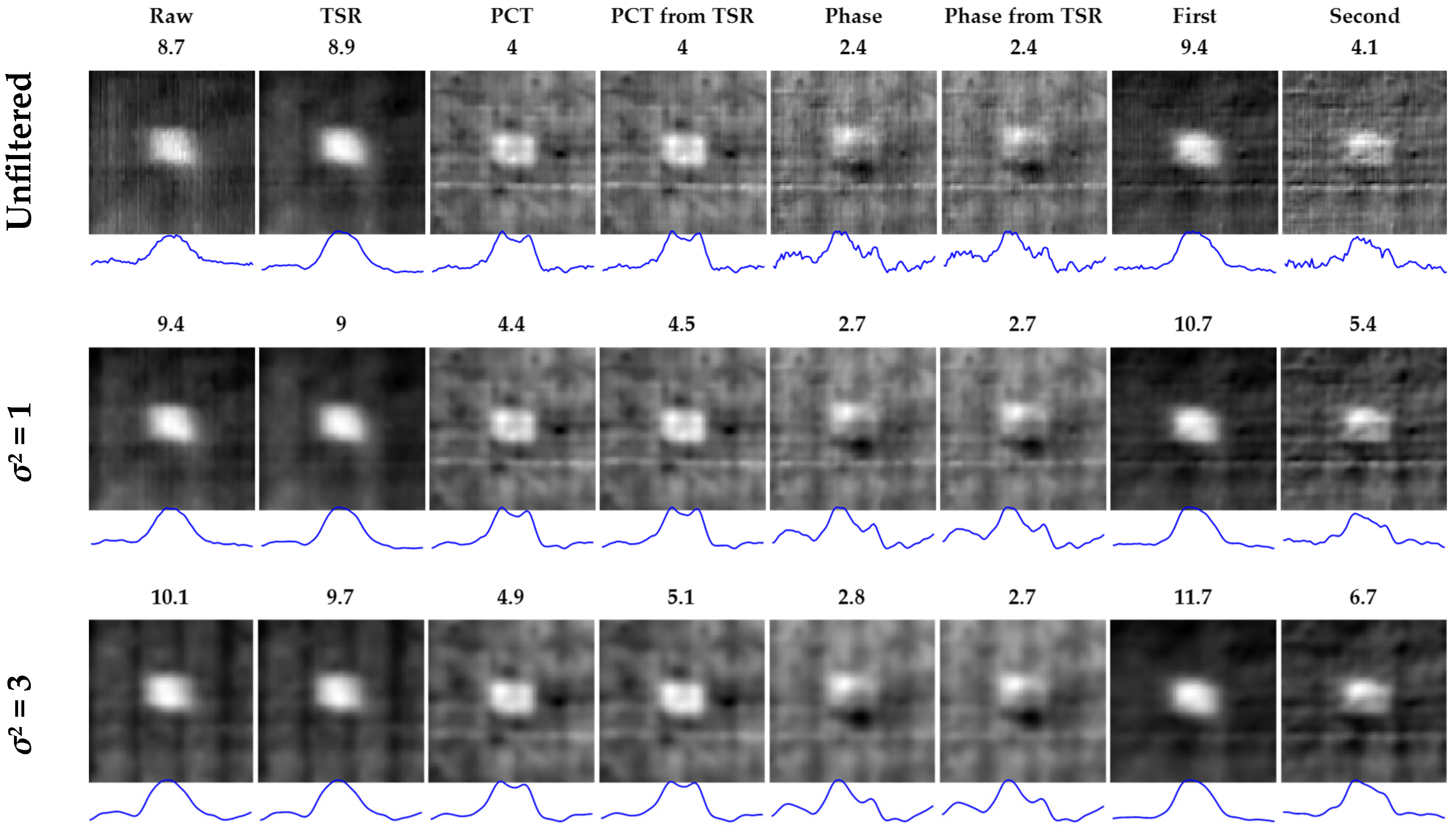
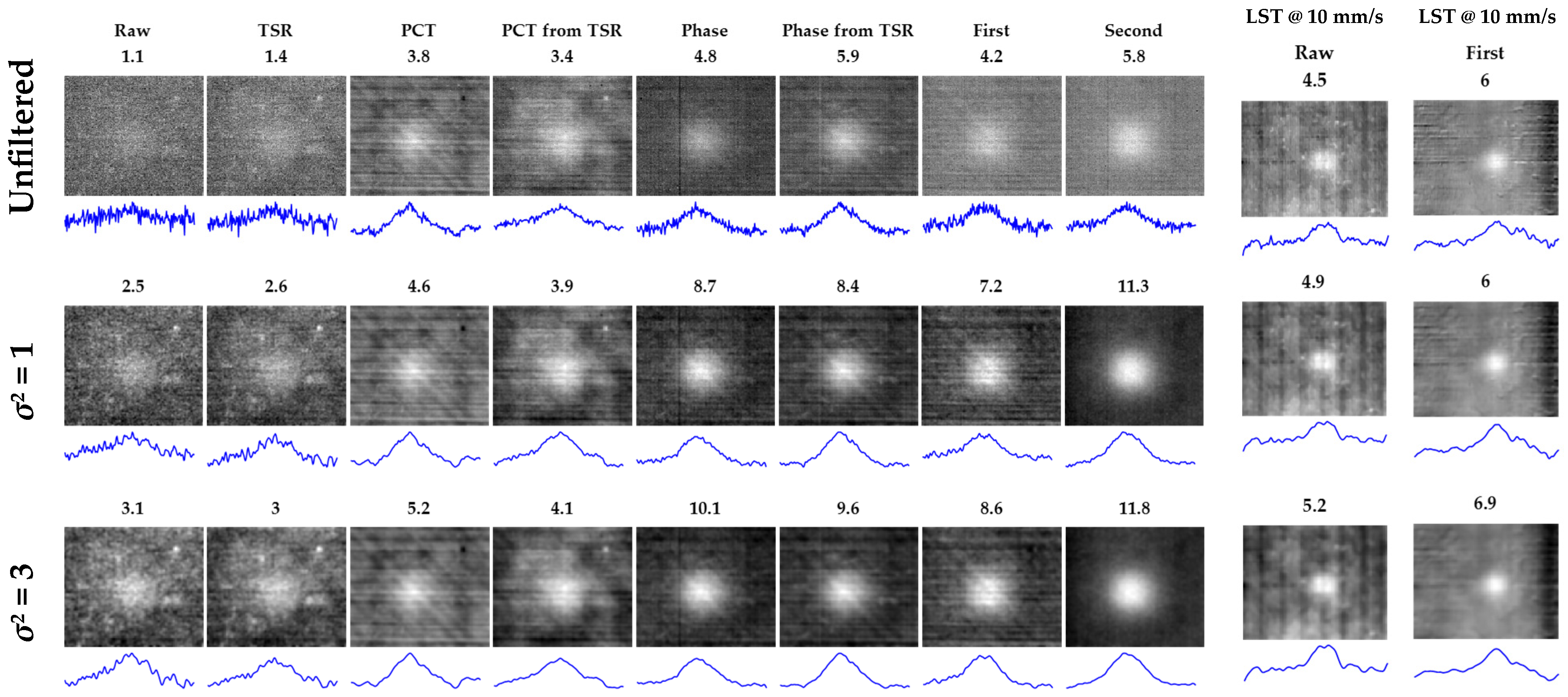
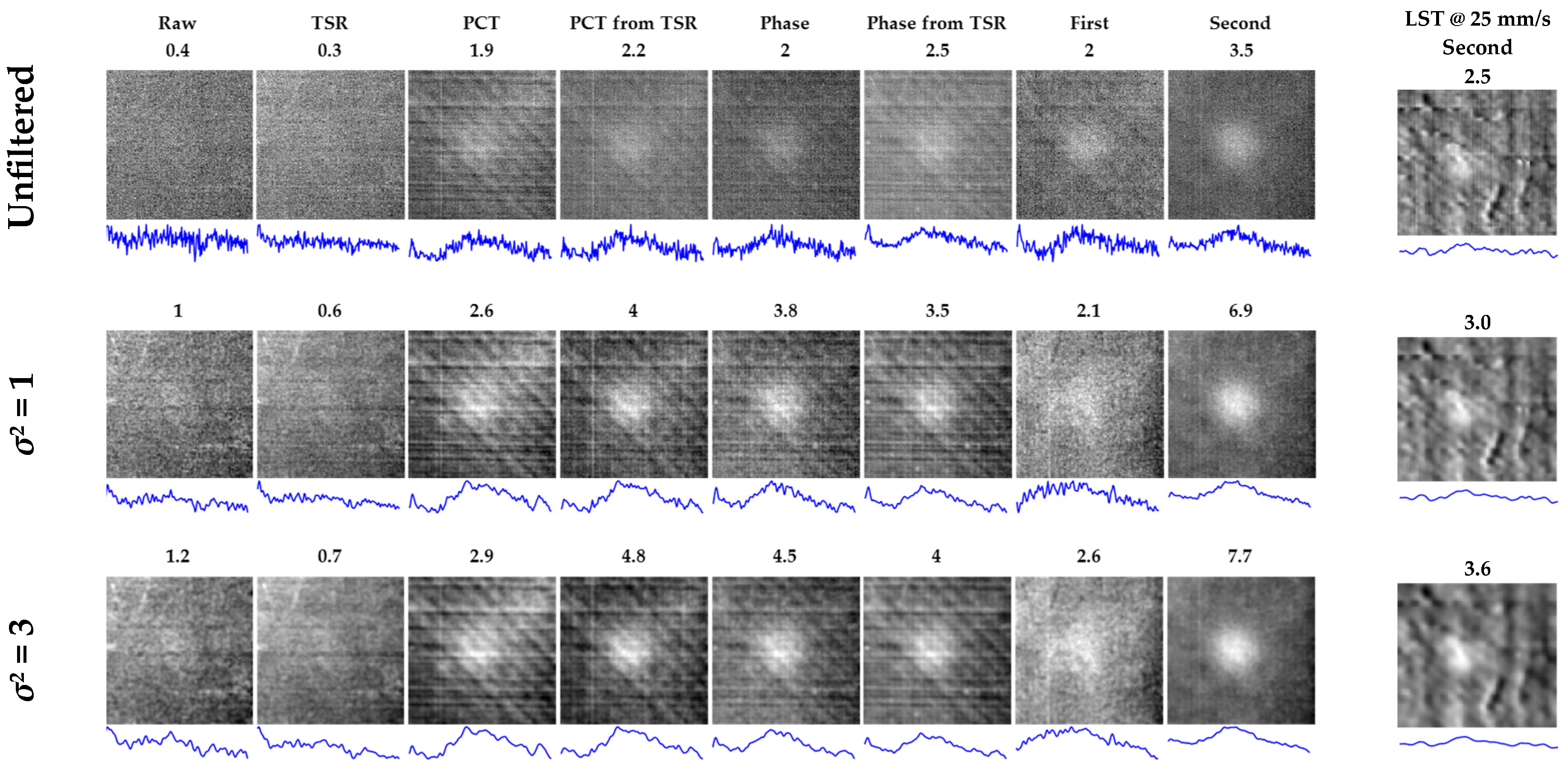
3.1. Comparison of PT and LST through CNR Analysis
3.2. Thermal Diffusivity by the Flash Method
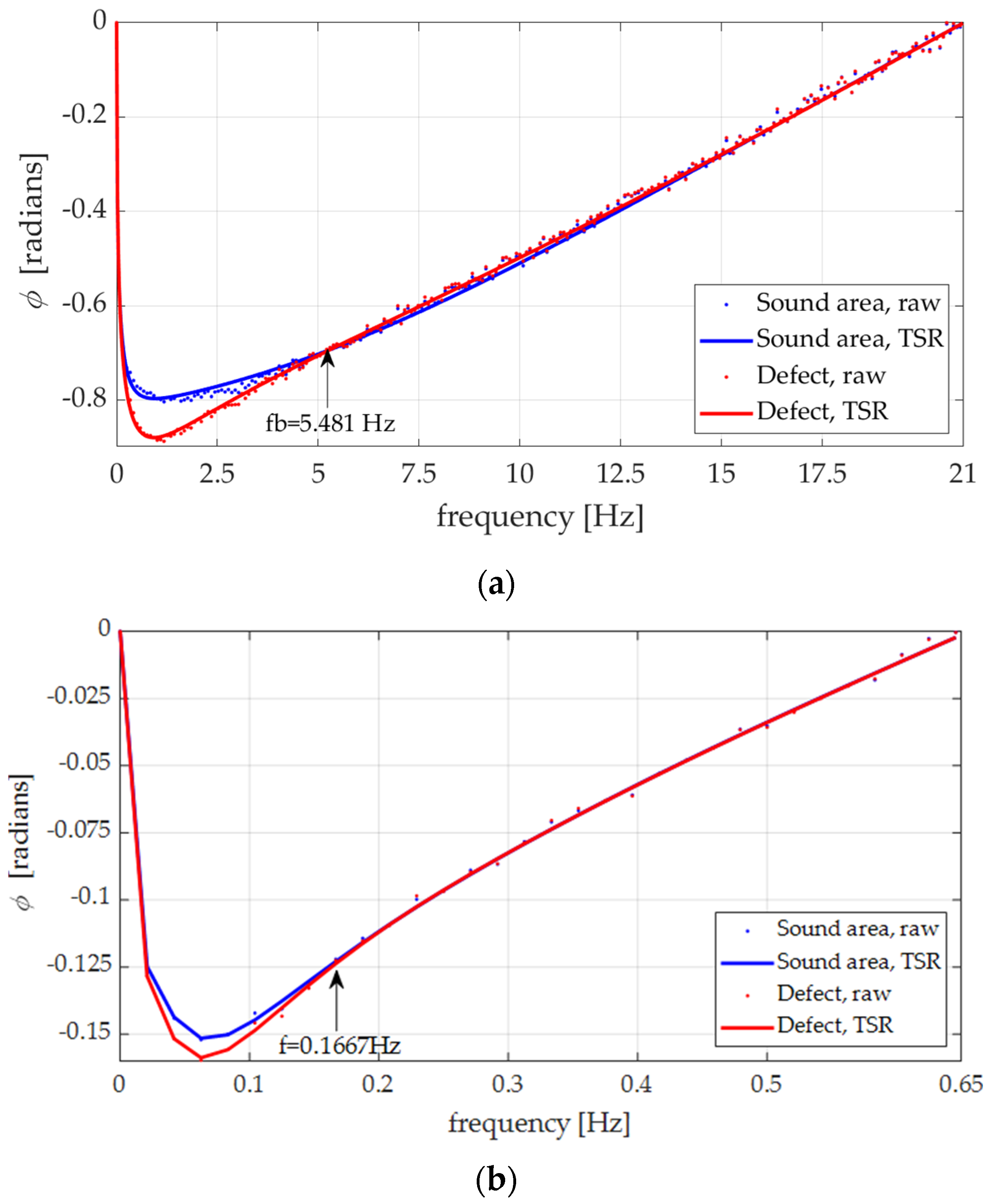
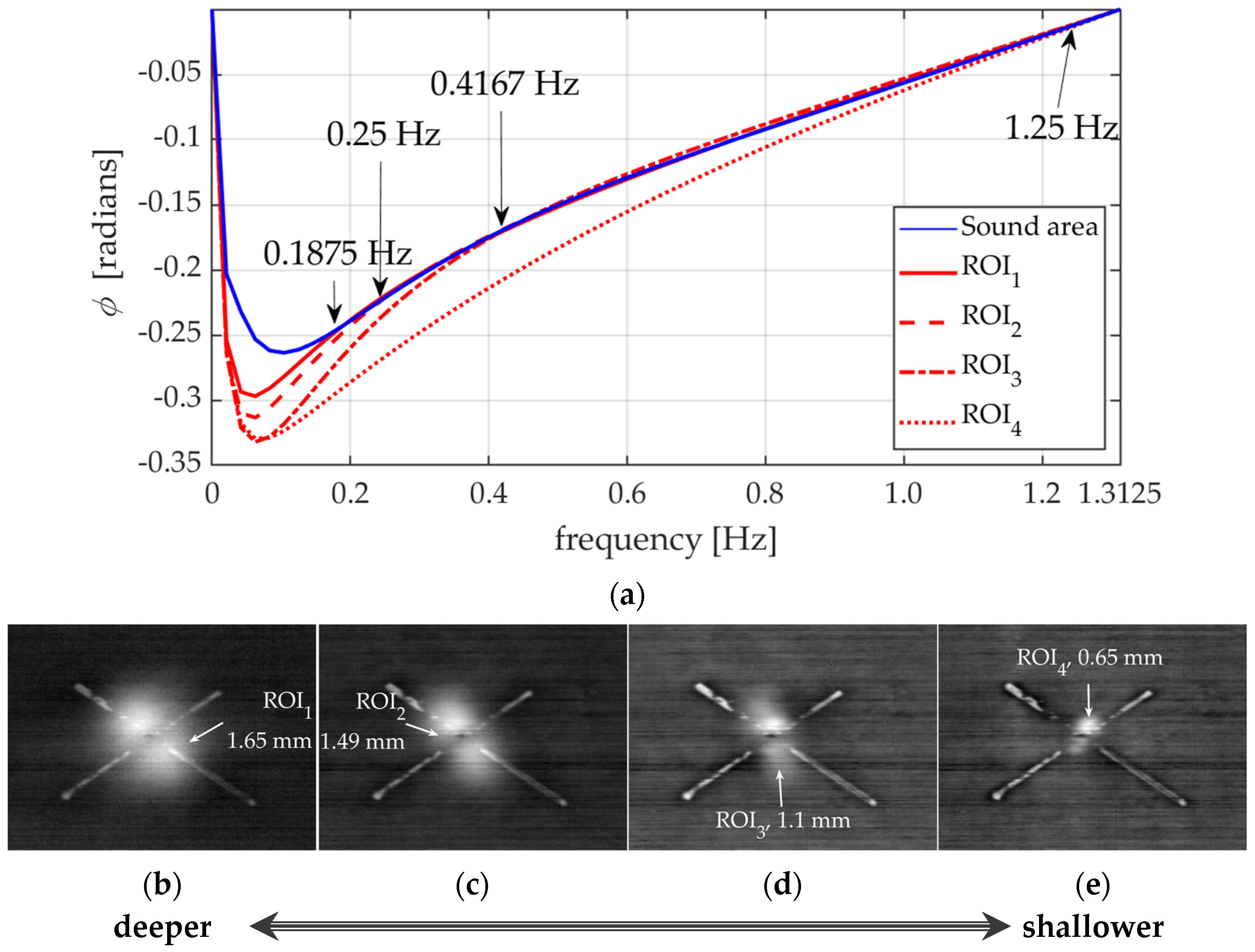
3.3. Depth Estimation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Park, S.-J.; Seo, M.-K. Chapter 8-Composite Characterization. Interface Sci. Technol. 2011, 18, 631–738. [Google Scholar] [CrossRef]
- Madenci, E.; Onuralp Ozkili, Y. Free vibration analysis of open-cell FG porous beams: Analytical, numerical and ANN approaches. Steel Compos. Struct. 2021, 40, 157–173. [Google Scholar] [CrossRef]
- Katunin, A.; Wronkowicz-Katunin, A.; Danek, W.; Wyleżoł, M. Modeling of a realistic barely visible impact damage in composite structures based on NDT techniques and numerical simulations. Compos. Struct. 2021, 267, 113889. [Google Scholar] [CrossRef]
- Daniel, I.M.; Wooh, S.C.; Komsky, I. Quantitative porosity characterization of composite materials by means of ultrasonic attenuation measurements. J. Nondestruct. Eval. 1992, 11, 1–8. [Google Scholar] [CrossRef]
- Gusenbauer, C.; Reiter, M.; Plank, B.; Salaberger, D.; Senck, S.; Kastner, J. Porosity Determination of Carbon and Glass Fibre Reinforced Polymers Using Phase-Contrast Imaging. J. Nondestruct. Eval. 2018, 38, 1–10. [Google Scholar] [CrossRef]
- Francesconi, L.; Taylor, M.; Bertoldi, K.; Baldi, A. Static and Modal Analysis of Low Porosity Thin Metallic Auxetic Structures Using Speckle Interferometry and Digital Image Correlation. Exp. Mech. 2017, 58, 283–300. [Google Scholar] [CrossRef]
- Scislo, L. Single-Point and Surface Quality Assessment Algorithm in Continuous Production with the Use of 3D Laser Doppler Scanning Vibrometry System. Sensors 2023, 23, 1263. [Google Scholar] [CrossRef]
- Hendorfer, G.; Mayr, G.; Zauner, G.; Haslhofer, M.; Pree, R. Quantitative determination of porosity by active thermography. AIP Conf. Proc. 2007, 894, 702–708. [Google Scholar] [CrossRef]
- Moran, J.; Rajic, N. Remote line scan thermography for the rapid inspection of composite impact damage. Compos. Struct. 2018, 208, 442–453. [Google Scholar] [CrossRef]
- Ibarra-Castanedo, C.; Maldague, X.P.V. Infrared Thermography. In Handbook of Technical Diagnostics; Czichos, H., Ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Maldague, X.P. Nondestructive Testing Handbook. 3. Infrared and Thermal Testing; American Society for Nondestructive Testing: Columbus, OH, USA, 2001. [Google Scholar]
- Ley, O.; Godinez-Azcuaga, V. Line scanning thermography and its application inspecting aerospace composites. In Proceedings of the 5th International Symposium on NDT in Aerospace, Singapore, 13–15 November 2013; pp. 13–15. Available online: http://www.ndt.net/article/aero2013/content/papers/48_Godinez-Azcuaga.pdf (accessed on 9 May 2023).
- Ibarra-Castanedo, C.; Maldague, X. Pulsed phase thermography reviewed. Quant. InfraRed Thermogr. J. 2004, 1, 47–70. [Google Scholar] [CrossRef]
- ASTM D7136/D7136M−15; Standard Test Method for Measuring the Damage Resistance of a Fiber-Reinforced Polymer Matrix Composite to a Drop-Weight Impact Event. ASTM International: West Conshohocken, PA, USA, 2022. [CrossRef]
- Usamentiaga, R.; Ibarra-Castanedo, C.; Maldague, X. More than Fifty Shades of Grey: Quantitative Characterization of Defects and Interpretation Using SNR and CNR. J. Nondestruct. Eval. 2018, 37, 25. [Google Scholar] [CrossRef]
- Ibarra-Castanedo, C.; Piau, J.M.; Guilbert, S.; Avdelidis, N.P.; Genest, M.; Bendada, A.; Maldague, X.P. Comparative study of active thermography techniques for the nondestructive evaluation of honeycomb structures. Res. Nondestruct. Eval. 2009, 20, 1–31. [Google Scholar] [CrossRef]
- Shepard, S.M.; Lhota, J.R.; Rubadeux, B.A.; Wang, D.; Ahmed, T. Reconstruction and enhancement of active thermographic image sequences. Opt. Eng. 2003, 42, 1337–1342. [Google Scholar] [CrossRef]
- Balageas, D.L. Defense and illustration of time-resolved pulsed thermography for NDE. Quant. InfraRed Thermogr. J. 2012, 9, 3–32. [Google Scholar] [CrossRef]
- Rajic, N. Principal component thermography for flaw contrast enhancement and flaw depth characterisation in composite structures. Compos. Struct. 2002, 58, 521–528. [Google Scholar] [CrossRef]
- Maldague, X.P.; Marinetti, S. Pulse Phase Infrared Thermography. J. Appl. Phys. 1996, 79, 2694–2698. [Google Scholar] [CrossRef]
- Ibarra-Castanedo, C.; Servais, P.; Ziadi, A.; Klein, M.; Maldague, X. RITA-Robotized Inspection by Thermography and Advanced processing for the inspection of aeronautical components. In Proceedings of the 12th International Conference on Quantitative Infrared Thermography, Bordeaux, France, 7–11 July 2014; Available online: https://www.ndt.net/?id=17748 (accessed on 9 May 2023).
- Khodayar, F.; Lopez, F.; Ibarra-Castanedo, C.; Maldague, X. Optimization of the inspection of large composite materials using robotized line scan thermography. J. Nondestruct. Eval. 2017, 36, 32. [Google Scholar] [CrossRef]
- Gray, J.; Woodrow, M.; Rosalie, C.; Rajic, N. Comparative Evaluation of a High Operating Temperature Midwave Infrared Detector for Automated Non-Destructive Inspection of Composite Damage. Mater. Res. Proc. 2021, 18, 29–36. [Google Scholar] [CrossRef]
- ASTM E2737−10; Standard Practice for Digital Detector Array Performance Evaluation and Long-Term Stability. ASTM International: West Conshohocken, PA, USA, 2018. [CrossRef]
- Parker, W.J.; Jenkins, R.J.; Butler, C.P.; Abbott, G.L. Flash Method of Determining Thermal Diffusivity, Heat Capacity, and Thermal Conductivity. J. Appl. Phys. 1961, 32, 1679. [Google Scholar] [CrossRef]
- ASTM E1461−13; Standard Test Method for Thermal Diffusivity by the Flash Method. ASTM International: West Conshohocken, PA, USA, 2022. [CrossRef]
- ASTM E2585−09; Standard Practice for Thermal Diffusivity by the Flash Method. ASTM International: West Conshohocken, PA, USA, 2022. [CrossRef]
- Degiovanni, A. Diffusivité et méthode flash. Rev. Générale Therm. 1977, 185, 420–442. [Google Scholar]
- Balageas, D.L. Nouvelle méthode d’interprétation des thermogrammes pour la détermination de la diffusivité thermique par la méthode impulsionnelle (méthode “flash”). Rev. Phys. Appl. 1982, 17, 227–237. [Google Scholar] [CrossRef]
- Hay, B.; Filtz, J.-R.; Batsale, J.-C. Mesure de la diffusivité thermique par la méthode flash. Tech. Ing. 2004, R2955, V1. [Google Scholar] [CrossRef]
- Thomas, R.L.; Pouch, J.J.; Wong, Y.H.; Favro, L.D.; Kuo, P.K. Subsurface Flaw Detection in Metals by Photoacustic Microscopy. J. Appl. Phys. 1980, 51, 1152–1156. [Google Scholar] [CrossRef]







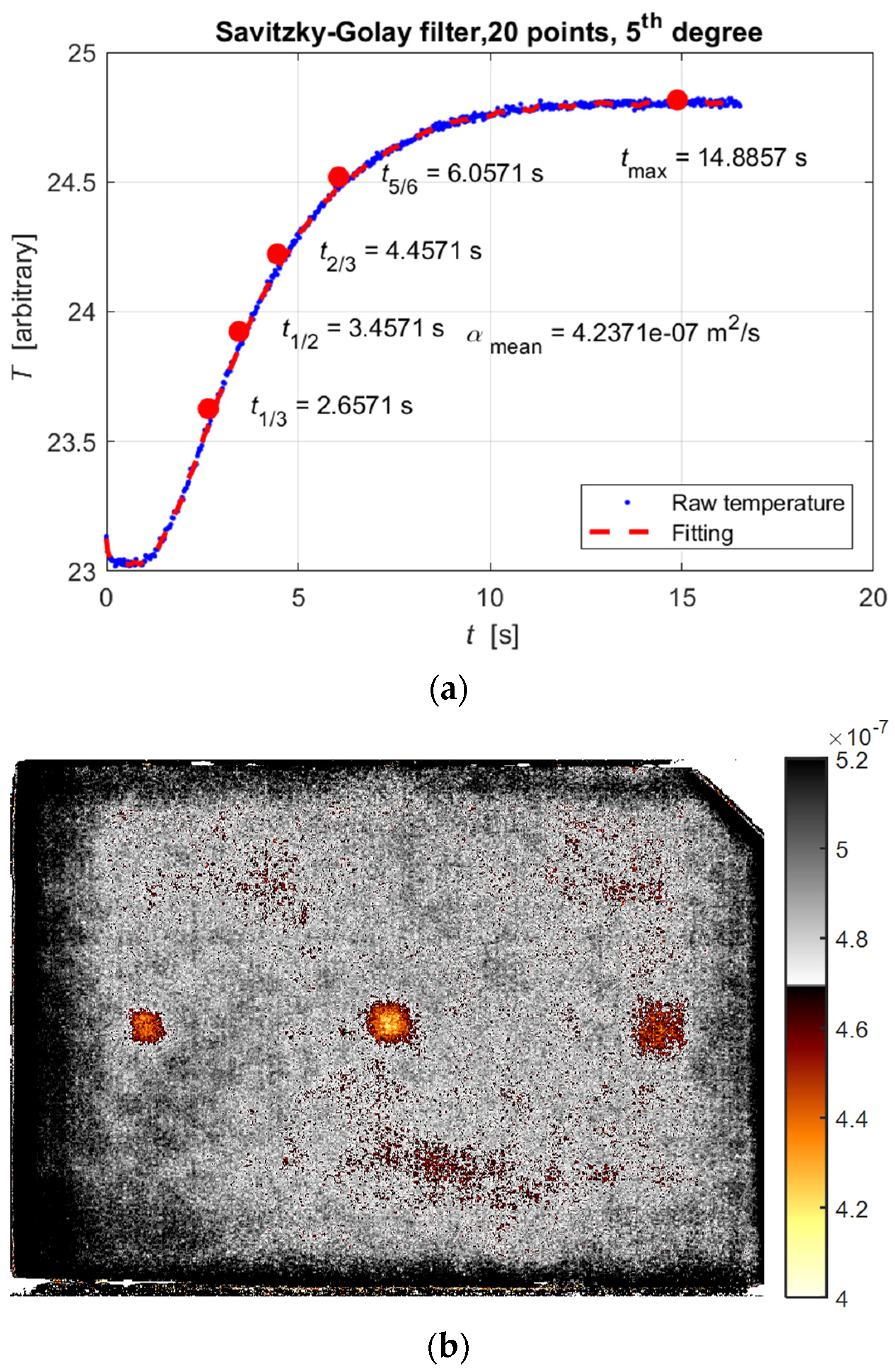

| Sample | Type | Width (mm) × Height (mm) | Thickness L (mm) | α (m2/s) × 10−7 |
|---|---|---|---|---|
| S44 | porosity | 180 × 120 | 3.4 | 4.869 |
| S45 | porosity | 180 × 120 | 3.4 | 4.935 |
| S48 | porosity | 180 × 120 | 3.4 | 4.829 |
| S5 | impact, 10 J | 150 × 100 | 3.33 | 4.961 |
| S9 | impact, 10 J | 150 × 100 | 3.3 | 4.586 |
| S28 | impact, 12 J | 150 × 100 | 3.27 | 5.092 |
| S29 | impact, 15 J | 150 × 100 | 3.27 | 5.889 |
| Porosity Samples | Unfiltered | Gaussian Filter, σ2 = 1 | Gaussian Filter, σ2 = 3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sample | Method | Processing | Defect1 | Defect2 | Defect3 | Defect1 | Defect2 | Defect3 | Defect1 | Defect2 | Defect3 |
| S44 front depths (mm) = | 0.287 | 1.7 | 3.115 | 0.287 | 1.7 | 3.115 | 0.287 | 1.7 | 3.115 | ||
| S44 | PT | raw | 5.2 | 0.8 | NOT DETECTED | 5.7 | 1.6 | NOT DETECTED | 5.8 | 1.8 | NOT DETECTED |
| S44 | PT | tsr | 5.2 | 0.9 | 5.6 | 1.5 | 5.6 | 1.7 | |||
| S44 | PT | pct | 5.9 | 4.4 | 7.9 | 5.2 | 8.2 | 5.5 | |||
| S44 | PT | pct tsr | 6.0 | 4.6 | 7.6 | 5.7 | 7.9 | 6.0 | |||
| S44 | PT | phase | 8.8 | 3.9 | 13.1 | 5.3 | 15.9 | 5.8 | |||
| S44 | PT | phase tsr | 11.5 | 4.2 | 14.3 | 5.6 | 17.2 | 6.0 | |||
| S44 | PT | first | 10.7 | 3.1 | 14.9 | 6.3 | 18.1 | 7.3 | |||
| S44 | PT | second | 16.0 | 5.3 | 21.2 | 8.7 | 24.5 | 9.4 | |||
| S44 | LST 25 mm/s | raw | 6.1 | 1.7 | NOT DETECTED | 6.6 | 2.1 | NOT DETECTED | 6.9 | 2.3 | NOT DETECTED |
| S44 | LST 25 mm/s | tsr | 6.2 | 1.5 | 6.4 | 1.6 | 6.7 | 1.7 | |||
| S44 | LST 25 mm/s | pct | 6.2 | 1.3 | 6.8 | 1.7 | 7.3 | 2.0 | |||
| S44 | LST 25 mm/s | pct tsr | 5.9 | 1.4 | 6.5 | 1.8 | 7.1 | 2.2 | |||
| S44 | LST 25 mm/s | phase | 2.1 | 1.1 | 2.2 | 1.3 | 2.2 | 1.6 | |||
| S44 | LST 25 mm/s | phase tsr | 1.8 | 1.1 | 1.9 | 1.3 | 1.9 | 1.5 | |||
| S44 | LST 25 mm/s | first | 6.7 | 1.4 | 7.3 | 1.6 | 7.6 | 1.7 | |||
| S44 | LST 25 mm/s | second | 3.3 | 1.7 | 3.7 | 2.2 | 4.0 | 2.9 | |||
| S45 front depths (mm) = | 0.287 | 1.7 | 3.115 | 0.287 | 1.7 | 3.115 | 0.287 | 1.7 | 3.115 | ||
| S45 | PT | raw | 8.9 | 0.6 | NOT DETECTED | 11.6 | 1.5 | NOT DETECTED | 12.3 | 1.8 | NOT DETECTED |
| S45 | PT | tsr | 9.1 | 0.6 | 11.5 | 0.9 | 12.1 | 1.0 | |||
| S45 | PT | pct | 10.1 | 2.6 | 11.6 | 3.3 | 12.0 | 3.4 | |||
| S45 | PT | pct tsr | 10.0 | 3.4 | 11.4 | 4.8 | 11.8 | 5.0 | |||
| S45 | PT | phase | 5.9 | 2.3 | 14.4 | 4.2 | 19.0 | 4.8 | |||
| S45 | PT | phase tsr | 14.9 | 2.7 | 19.6 | 3.7 | 22.7 | 4.0 | |||
| S45 | PT | first | 11.1 | 2.4 | 15.8 | 5.2 | 18.0 | 6.1 | |||
| S45 | PT | second | 8.7 | 4.0 | 17.2 | 6.6 | 20.5 | 7.1 | |||
| S45 | LST 25 mm/s | raw | 8.7 | 1.2 | 0.0 | 9.4 | 1.3 | 0.0 | 10.1 | 1.3 | 0.0 |
| S45 | LST 25 mm/s | tsr | 8.9 | 0.7 | −0.4 | 9.0 | 0.7 | −0.5 | 9.7 | 0.7 | −0.4 |
| S45 | LST 25 mm/s | pct | 4.0 | 2.7 | 2.8 | 4.4 | 3.0 | 3.3 | 4.9 | 3.0 | 3.6 |
| S45 | LST 25 mm/s | pct tsr | 4.0 | 3.2 | 2.0 | 4.5 | 3.6 | 2.2 | 5.1 | 3.7 | 2.3 |
| S45 | LST 25 mm/s | phase | 2.4 | 1.9 | 0.9 | 2.7 | 2.1 | 1.4 | 2.8 | 2.2 | 1.6 |
| S45 | LST 25 mm/s | phase tsr | 2.4 | 1.8 | 0.9 | 2.7 | 2.0 | 1.3 | 2.7 | 2.1 | 1.5 |
| S45 | LST 25 mm/s | first | 9.4 | 1.8 | 1.3 | 10.7 | 1.9 | 1.4 | 11.7 | 2.0 | 1.4 |
| S45 | LST 25 mm/s | second | 4.1 | 3.4 | 1.9 | 5.4 | 3.9 | 2.0 | 6.7 | 4.0 | 2.1 |
| S48 front depths (mm) = | 1.69 | 1.41 | 1.41 | 1.69 | 1.41 | 1.41 | 1.69 | 1.41 | 1.41 | ||
| 2nd insert (mm) = | 1.98 | 1.69 | 1.42 | 1.69 | 1.42 | 1.69 | |||||
| 3rd insert (mm) = | 1.98 | 1.98 | 1.98 | ||||||||
| S48 | PT | raw | 1.1 | 1.1 | 0.4 | 2.5 | 2.2 | 1.0 | 3.1 | 2.5 | 1.2 |
| S48 | PT | tsr | 2.4 | 1.3 | 0.3 | 2.6 | 2.2 | 0.6 | 3.0 | 2.3 | 0.7 |
| S48 | PT | pct | 3.8 | 5.3 | 1.9 | 4.6 | 6.8 | 2.6 | 5.2 | 7.7 | 2.9 |
| S48 | PT | pct tsr | 3.4 | 5.0 | 2.2 | 3.9 | 6.2 | 4.0 | 4.1 | 6.9 | 4.8 |
| S48 | PT | phase | 4.8 | 4.1 | 2.0 | 8.7 | 7.6 | 3.8 | 10.1 | 9.1 | 4.5 |
| S48 | PT | phase tsr | 5.9 | 5.4 | 2.5 | 8.4 | 7.5 | 3.5 | 9.6 | 8.7 | 4.0 |
| S48 | PT | first | 4.2 | 3.5 | 2.0 | 7.2 | 8.3 | 2.1 | 8.6 | 9.8 | 2.6 |
| S48 | PT | second | 7.5 | 5.0 | 3.5 | 11.3 | 11.4 | 6.9 | 11.8 | 12.0 | 7.7 |
| S48 | LST 25 mm/s | raw | 2.5 | 2.9 | 1.3 | 2.7 | 3.4 | 1.6 | 2.8 | 3.7 | 1.8 |
| S48 | LST 25 mm/s | tsr | 2.3 | 3.1 | 1.1 | 2.4 | 3.3 | 1.1 | 2.4 | 3.5 | 1.2 |
| S48 | LST 25 mm/s | pct | 2.4 | 2.5 | 1.8 | 2.7 | 2.6 | 2.2 | 2.9 | 2.7 | 2.7 |
| S48 | LST 25 mm/s | pct tsr | 2.2 | 2.4 | 2.2 | 2.6 | 2.5 | 2.5 | 3.1 | 2.6 | 2.8 |
| S48 | LST 25 mm/s | phase | 2.8 | 2.3 | 1.6 | 3.2 | 2.7 | 1.8 | 3.6 | 3.1 | 2.2 |
| S48 | LST 25 mm/s | phase tsr | 2.7 | 2.4 | 1.6 | 3.2 | 2.8 | 1.8 | 3.6 | 3.1 | 2.1 |
| S48 | LST 25 mm/s | first | 3.7 | 4.2 | 2.3 | 4.3 | 4.9 | 2.7 | 4.8 | 5.4 | 3.2 |
| S48 | LST 25 mm/s | second | 3.3 | 2.4 | 2.5 | 3.8 | 2.6 | 3.0 | 4.0 | 2.6 | 3.6 |
| S48 | LST 10 mm/s | raw | 4.5 | 3.2 | NOT DETECTED | 4.9 | 3.4 | NOT DETECTED | 5.2 | 3.5 | NOT DETECTED |
| S48 | LST 10 mm/s | tsr | 4.3 | 3.1 | 4.5 | 3.2 | 4.6 | 3.4 | |||
| S48 | LST 10 mm/s | pct | 2.1 | 2.1 | 2.6 | 2.5 | 2.8 | 2.8 | |||
| S48 | LST 10 mm/s | pct tsr | 2.2 | 2.4 | 3.4 | 2.7 | 4.4 | 2.9 | |||
| S48 | LST 10 mm/s | phase | 1.6 | 1.2 | 2.0 | 1.7 | 2.2 | 2.1 | |||
| S48 | LST 10 mm/s | phase tsr | 1.7 | 1.0 | 2.0 | 1.2 | 2.2 | 1.4 | |||
| S48 | LST 10 mm/s | first | 6.0 | 3.5 | 6.7 | 4.0 | 6.9 | 4.5 | |||
| S48 | LST 10 mm/s | second | 2.2 | 1.4 | 2.4 | 1.8 | 2.7 | 2.1 | |||
| S48 | LST 5 mm/s | raw | 3.7 | NOT DETECTED | NOT DETECTED | 4.2 | NOT DETECTED | NOT DETECTED | 4.6 | NOT DETECTED | NOT DETECTED |
| S48 | LST 5 mm/s | tsr | 3.6 | 4.1 | 4.5 | ||||||
| S48 | LST 5 mm/s | pct | 3.2 | 4.0 | 4.6 | ||||||
| S48 | LST 5 mm/s | pct tsr | 3.2 | 4.0 | 4.6 | ||||||
| S48 | LST 5 mm/s | phase | 0.7 | 1.2 | 1.6 | ||||||
| S48 | LST 5 mm/s | phase tsr | 0.7 | 0.8 | 1.0 | ||||||
| S48 | LST 5 mm/s | first | 3.0 | 3.4 | 3.7 | ||||||
| S48 | LST 5 mm/s | second | 1.4 | 1.7 | 2.0 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibarra-Castanedo, C.; Servais, P.; Klein, M.; Boulanger, T.; Kinard, A.; Hoffait, S.; Maldague, X.P.V. Detection and Characterization of Artificial Porosity and Impact Damage in Aerospace Carbon Fiber Composites by Pulsed and Line Scan Thermography. Appl. Sci. 2023, 13, 6135. https://doi.org/10.3390/app13106135
Ibarra-Castanedo C, Servais P, Klein M, Boulanger T, Kinard A, Hoffait S, Maldague XPV. Detection and Characterization of Artificial Porosity and Impact Damage in Aerospace Carbon Fiber Composites by Pulsed and Line Scan Thermography. Applied Sciences. 2023; 13(10):6135. https://doi.org/10.3390/app13106135
Chicago/Turabian StyleIbarra-Castanedo, Clemente, Pierre Servais, Matthieu Klein, Thibault Boulanger, Alain Kinard, Sébastien Hoffait, and Xavier P. V. Maldague. 2023. "Detection and Characterization of Artificial Porosity and Impact Damage in Aerospace Carbon Fiber Composites by Pulsed and Line Scan Thermography" Applied Sciences 13, no. 10: 6135. https://doi.org/10.3390/app13106135
APA StyleIbarra-Castanedo, C., Servais, P., Klein, M., Boulanger, T., Kinard, A., Hoffait, S., & Maldague, X. P. V. (2023). Detection and Characterization of Artificial Porosity and Impact Damage in Aerospace Carbon Fiber Composites by Pulsed and Line Scan Thermography. Applied Sciences, 13(10), 6135. https://doi.org/10.3390/app13106135







