Abstract
This paper proposes a distributed algorithm for games with shared coupling constraints based on the variational approach and the proximal-point algorithm. The paper demonstrates the effectiveness of the proximal-point algorithm in distributed computing of generalized Nash equilibrium (GNE) problems using local data and communication with neighbors in any networked game. The algorithm achieves the goal of reflecting local decisions in the Nash–Cournot game under partial-decision information while maintaining the distributed nature and convergence of the algorithm.
1. Introduction
The problem of finding a generalized Nash equilibrium (GNE) for networked systems has gained significant interest recently owing to its applicability to multi-agent decision-making scenarios, such as demand-side management in intelligent grids [1], demand response in competitive markets [2], and electric vehicle charging [3]. In such systems, the agents aim to minimize cost functions under joint feasibility constraints with non-cooperative settings. They cannot reduce their local costs by unilaterally changing their decisions but by relying on the decisions of the other agents. The GNE is a self-executing outcome, and once computed, all agents execute it to achieve their own minimum cost. In these systems, each user has a local cost function to minimize, which is a function of their own and other users’ decisions. Moreover, each user’s feasible decision set is coupled with other users’ decisions due to the limited network resources. A natural solution concept for such systems is the GNE, which captures the non-cooperative behavior of multiple interacting agents. A GNE is a vector of decisions such that no user can reduce their local cost by unilaterally deviating from it, given the decisions of other users. Hence, a GNE is a self-enforcing outcome that all agents will implement once computed, as it achieves their individual minimum costs.
To compute GNE introspectively, most algorithms for finding Nash equilibrium require a central information center to collect and store all game information such as cost functions, coupling constraints, and feasible local sets in a traditional computing environment. However, this approach is not suitable for large-scale network games because it is difficult to observe the true decisions of all other players in this type of game. Additionally, having a central coordinator node may be impractical due to technical, geographical, or game-related reasons. In this case, each player needs to compute their local decision corresponding to GNE in a distributed way by utilizing their local objective function, local feasible set, and possibly local data related to the coupling constraints and communicating with their neighbors. Therefore, our goal is to develop a distributed algorithm that estimates the strategies of all other agents only by communicating with adjacent agents. This algorithm can achieve the goal of reflecting local decisions in the absence of global information and eventually reconstructing actual value.
The proximal-point algorithm has been widely used in distributed computing of GNE problems. In our study, we demonstrate that it can achieve the goal of reflecting local decisions in the absence of global information while maintaining the distributed nature and convergence of the algorithm. That is to say, in the absence of a central coordinator, the generalized Nash equilibrium point is calculated by each participant using local information and communication with neighbors. This approach enables each player to compute a local decision corresponding to GNE by utilizing its local objective function, local feasible set, and possibly local data related to the coupling constraints and communicating with its neighbors. By continuously updating the proximal point, the proximal-point algorithm can achieve the convergence of restricted monotone and Lipschitz continuous pseudo-gradient games under appropriate fixed step size conditions. Our study proposes a new distributed GNE algorithm for games with shared biomimetic coupling constraints, which is based on the variational GNE approach and the proximal-point algorithm. Our results demonstrate the effectiveness of the proposed algorithm in achieving GNE in a distributed manner in the presence of shared constraints.
1.1. Literature Review
The research of GNE was initiated by the seminal works of [4,5]. In recent years, the computation of distributed GNE in monotone games has received considerable interest. However, most existing studies rely on the assumption that every agent in the system has access to the decision information of other agents, i.e., by employing a central node coordinator to orchestrate the information processing. The initial approach was based on the variational inequality method [6]. The variational inequality framework for generalized Nash equilibrium problems established in [6] has been extended to more general settings, such as time-dependent or stochastic problems in [7]. Ref. [8] developed a Tikhonov-regularized primal-dual algorithm, and [9] devised a primal-dual gradient method, which can reduce the compensation and assumed that it can acquire the decisions of all adversaries that influence each cost. In ref. [10], a payoff-based GNE algorithm was introduced, which has a diminishing step size and converges to a class of convex games. Recently, an operator-splitting method has emerged as a very powerful design technique, which ensures global convergence and features a fixed step size and succinct convergence analysis. However, most GNE application scenarios are aggregative games, such as [3,11,12,13,14]. In refs. [12,13], the algorithms are semi-decentralized, requiring a central node to disseminate the common multipliers and aggregate variables, thus resulting in a star topology. In ref. [14], this is relaxed by a projection gradient algorithm based on two-layer consensus, both of which are only suitable for aggregative games.
In networked non-cooperative games, a distributed forward-backward operator-splitting algorithm for seeking the GNE has been proposed by Yi and Pavel [15], based on the convex analysis framework of Bauschke and Combettes [16]. Under partial information, the algorithm requires only local objective function, feasible set, and block of affine constraints for each agent. It also introduces a local estimate of all agents’ decisions. They further extended their algorithm to an asynchronous setting by using auxiliary variables associated with Graphology [17]. In this setting, each agent uses private data and delay information from their neighbors’ latency information to iterate asynchronously. They proved the convergence and effectiveness of their algorithm under mild assumptions. Ref. [18] investigated a generalized Nash equilibrium problem in which players are modeled as nodes of a network and each player’s utility function depends on its own and its neighbors’ actions, and derived a variational decomposition of the game under a quadratic reference model with shared constraints, which is illustrated with numerical examples. Bianchi et al. [19] has developed a novel algorithm that differs from the existing projective pseudo gradient dynamics in that it is fully distributed, one-layer, and uses a proximal best response with consensus terms. It can overcome the limitations of double-layer iterations or conservative step sizes of the gradient-based methods. It can also extend the applicability of the proximal point method by analyzing the restricted monotonicity property. Pavel [20] applied a preconditioned proximal point algorithm (PPPA) that decomposes the merit-seeking task into Nash equilibrium (NE) computation of regularised subgame sequences based on local information. The PPPA also performs distributed updates of multipliers and auxiliary variables, which require multiple communications among agents to solve the subgame. For games with general coupling costs and affine coupling constraints, [15,21] adopt operator methods to perform distributed decentralized GNE optimization: forward-backward optimization algorithm for strongly monotone games [15] and preconditioned proximal optimization algorithm for monotone games [21]. The players exchange local multipliers over the network with arbitrary topology, but each user can access all the agent decisions that affect its cost, thus obtaining complete decision information.
1.2. Contributions
Compared with most existing distributed optimization algorithms, the main contributions of this paper are summarized as follows:
- The proposal of a GNE algorithm for games with shared biomimetic coupling constraints. The algorithm is based on the variational GNE approach and the proximal-point algorithm, and is improved by introducing two choice matrices to enhance its accuracy, as in [22,23], where we design a novel preconditioning matrix to distribute the computation and obtain a single-layer iteration. Each player has an auxiliary variable to estimate the decisions of other agents. The algorithm is distributed, where each player only utilizes its local objective function, local feasible set, and local data related to the coupling constraints, and there is no centralized coordinator to update and propagate dual variables.
- An original dual analysis of the Karush–Kuhn–Tucker (KKT) conditions of the variational inequality (VI) is conducted, which introduces a local copy of the multiplier and an auxiliary variable for each player. It is observed that the KKT conditions mandate consensus among all agents on the multiplier for shared constraints. By reformulating the original problem as finding the zero point of a monotone operator that includes the Laplacian matrix of the connected graph, the consistency of local multipliers is enhanced.
This paper presents global and distributed methods for finding GNE in games with shared affine coupling constraints under partial decision information. Section 2 introduces the game model and formulates the GNE problem. Section 3 proposes a global GNE-seeking method based on the proximal-point algorithm with global information. Section 4 develops a distributed GNE-finding method with partial information and proves its convergence and implementation feasibility. Section 5 illustrates the performance of our methods through numerical simulations. Finally, Section 6 concludes the paper and discusses some future work directions.
2. Game Formulation
We study a non-cooperative generalized game with a crowd of agents. Each agent has a local decision set and chooses its own decision , where is the set of real numbers and is the dimension of agent i’s decision-making. The global decision space is where and the stacked vector of all agents’ decisions is . Let denote the decision profile of all other agents except for agent i, then . The feasible set for any agent depends on the coupling constraints shared with other agents and their own decisions. Each agent aims to minimize its objective function over this feasible set as follows:
The objective function (1) can describe how multiple participants can optimize their interests in a non-cooperative situation while being affected by sharing constraints. This model can be applied to a variety of practical scenarios, such as smart grids, competitive markets, and electric vehicle charging.
Assumption 1.
The cost functions and of each agent are convex. The common cost function is continuously differentiable and the local idiosyncratic cost function is lower semicontinuous. is bounded and closed for any .
We denote and , where and are local parameters. By the affine function above, the set of overall feasible decisions via affine coupling constraints and cost functions is denoted as follows:
where is a closed and convex set of decisions that is nonempty. It is used to simulate some phenomena in nature, such as group behavior, competition, and cooperation. Such constraints can reflect the interactions and dependencies among participants, making the game more complex and interesting.
Assumption 2.
Slater’s constraint qualification holds for the collective set . Therefore, each agent in the generalized game tries to solve this interdependent optimization problem as follows:
To obtain the primal-dual characterization of each agent , we define a Lagrangian function with dual variable multiplier as follows:
We call a decision that satisfies (3) a GNE of the game. This implies that for any agent ,
where .
If satisfies the KKT conditions below with , then it is an optimal solution to (3).
We reformulate the KKT condition using the normal cone operator as follows:
We denote the pseudogradient of as . Denote the pseudogradient of as .
Let denote the vector of Lagrangian multipliers associated with each agent . A variational GNE is a decision that satisfies the variational inequality problem and has equal Lagrangian multipliers ().
3. Iterative Algorithms with Global Information
We propose a distributed algorithm based on preconditioned proximal-point algorithms that use full-decision information. This means that every agent can access the decisions of all other agents that affect its local objective function directly.
3.1. Communication Graph
Let and . We define as the set of edges adjacent to i, which consists of (the incoming edges) and (the outgoing edges). Let be the symmetric weight matrix of , where if and otherwise. We also set for all agents. The Laplacian matrix of is denoted by , where is the degree matrix and for all .
Assumption 3.
is a connected and undirected graph.
3.2. Algorithm Development
Assumption 4.
is a μ-strongly monotone function, meaning that , and a -Lipschitz continuous function, implying that .
The strong monotonicity of implies that a v-GNE exists and is unique. We can write the variational problem for the original game problem as follows:
The objective function is defined by the following Lagrangian function:
Let be a global Lagrangian multiplier. To design distributed optimization algorithms, we impose the consistency constraints , i.e., , where is an identity matrix of order m. Define , , , and . Then,
Its corresponding saddle point problem would be
Let , and , the Lagrangian function that defines this saddle point problem is . The optimal conditions for this problem are obtained by sequentially finding the partial derivatives of the variables , , and as follows:
It follows from Lagrange’s dual theorem that the variational problem has an optimal solution only when satisfies the KKT conditions (13).
Let and consider the following operator:
We regard the iterative algorithm as a special case of proximal-point algorithms (PPA) [16] for finding a zero of . The general form of PPA can be written as
where .
We apply the interaction rule (9) to the operator , where is defined as the following:
We choose the step sizes , and such that .The next lemma provides sufficient conditions for based on Gershgorin’s circle theorem.
Lemma 2.
For any agent and any , the preconditioning matrix Φ in (16) is positive definite if
Assuming that for all chosen step sizes, we can state the following results.
Lemma 3.
4. Distributed Algorithm with Partial Information
In a distributed setting, it is challenging to access the decisions of all other agents requiring a central coordinator to collect and deliver information from all participants, as assumed in the previous section. The global information assumptions in Section 3 are relaxed in this section, allowing each participant to iteratively update their decisions, multipliers, and auxiliary variables using only their own local information and the estimates exchanged with their neighbors. Therefore, this section proposes a distributed GNE-seeking algorithm that uses partial information based on the preconditioned proximal-point algorithm.
4.1. Algorithm Development
This section presents an algorithm for GNE-seeking in game (3) in a fully distributed manner.
Each agent i has a cost function and a feasible set but does not know the full state of other agents. Agent i can only exchange information with its neighboring agents over a network . The edge belongs to if agents i and j can exchange information mutually. is defined as agent i’s estimate of agent j’s decision. Then and denotes j’s estimate of all other agents except i. If , we can replace the cost function of agent i with . Then, we equivalently transform the game (3) as the following:
It is worth noting that problems (3) and (22) are equivalent under a certain condition. We will explain this point below.
Let be the set of feasible solutions for agent i under a consistency constraint. Then, agent i’s cost function only depends on its own local information .
We introduce matrices and to develop a distributed algorithm that uses partial decision information for game (22).
where . Then, and . Let , . Hence and . Moreover, .
Similar to (13), we design sufficient conditions of (22) as follows:
where , , , , Moreover, c is a parameter about the dual variable associated with the constraint .
Define the following operator:
The variables and satisfy condition (25) if where .
Lemma 4.
Proof of Lemma 4.
By applying the definition of inverse operations, we obtain that
By , , and , we have
Hence, by the property that the subdifferential of a convex function contains only zeros at its minima [16], we can reformulate (30) as follows.
□
Write (31) as a distributed algorithm as Algorithm 1.
4.2. Convergence Analysis
In this section, we will prove that Algorithm 1 applying the game (22) converges to the variational GNE through a rigorous mathematical analysis. We show that any limit point of Algorithm 1 satisfies and has certain properties. Moreover, we demonstrate that every such zero is in the consensus subspace and solves .
| Algorithm 1. Distributed Algorithm with Partial Information |
| Initialize: For all , set ,, , |
| for do |
| end for |
| Retuen: The sequence will eventually approximate the optimal solution. |
Assumption 5.
is a Lipschitz continuous mapping, which implies that there exists a positive constant θ such that for any and , we have .
Define the operator:
From (26), we know
Lemma 5.
Define .
When , we have and is restricted monotone if Assumptions 1–5 hold.
Proof of Lemma 5.
Let be any zero of , which exists by Lemma 4. From (33), we can decompose as a sum of three operators, two of which are monotone. Moreover, for any , we have for all by Lemma 1. Then,
Hence, for any , with , we obtain . □
Lemma 6.
Define as a restricted monotone in and is firmly quasinonexpansive in , where is the Hilbert space induced by the inner product . Then for any , , it holds that
Proof of Lemma 6.
Lemma 7.
Let by Lemma 6. For ,we assume that and such that . If ,
Then we obtain Algorithm 1 by applying (13) to the operator , where
is called a preconditioning matrix. It ensures that the agents will be able to compute the resulting iteration in a fully distributed manner.
We choose the step sizes , and such that . This implies that . The next lemma provides sufficient conditions for based on Gershgorin’s circle theorem.
Lemma 8.
For any agent and any , the preconditioning matrix Φ in (38) is positive definite if
Using Lemma 4 and Assumption 4, we can show that is single-valued by applying Equation (28) to .
Lemma 9.
Let as in Lemma 3. Then is restricted monotone in .
It means that finding a zero point of is equivalent to finding a variational GNE for problem (3). Moreover, since , we have by Lemma 9. Therefore, finding a zero point of is also equivalent to finding a variational GNE for problem (3). This establishes the equivalence between problems (3) and (22) under the condition that as in Lemma 3.
Theorem 1.
Assume that are as defined in Lemma 8 and that the step sizes satisfy Lemma 5. Then, Algorithm 1 generates a sequence that converges to an equilibrium .
Proof of Theorem 1.
The set of inequalities (29) is equivalent to Equation (37) when , for all . By applying Lemma 9, we deduce that is restricted monotone on . Then, we define
By Lemma 9, is restricted monotone in , which implies .
Let , so that . For all ,
Then by Lemma 7, we have
By the Cauchy–Schwarz inequality, it holds that
By (43), the sequence is bounded so that there is at least one cluster point such as . Define:
consists of the sum of the first two equations of . By (29) and (44), it holds that
Let and , for all . Then, . Moreover, for all we have
Followed by recursion, it holds that
5. Numerical Studies
In this section, we will explore a network-based Nash–Cournot game [21] that is used to model the competition between N companies in m markets. This game is of particular interest because it has been shown to be an effective tool for analyzing competition between companies. The markets have shared affine constraints or equivalent global coupling affine constraints, which makes it possible to model the interactions between the companies in a realistic way. It is important to note that in this game, the agents can only communicate with their neighbors, and there is no central node with bidirectional communication to all participants. This makes the game even more challenging, as the agents must rely on their own resources to make decisions.
Although this game has been applied in networked Cournot games [15], it is worth noting that it assumes that the agents’ decision information is global. However, in contrast, our work considers network structure and partial decision information, which leads to a more accurate representation of the real-world dynamics of competition between companies. This means that our research is more relevant to the real world, and can help us gain a deeper understanding of the complex interactions between the agents. By incorporating the network structure and partial decision information, we are able to gain a deeper understanding of the complex interactions between the agents, which can have significant implications for the overall performance of the companies in the markets. Additionally, our research can help to inform future policy decisions, as it provides a more accurate picture of the dynamics of competition between companies in networked markets.
5.1. Cournot Market Competition
Each firm i decides the quantity of the commodity for markets, subject to . The maximum capacity of each market is . Hence, we have a shared affine constraint , where and . The matrix indicates which markets firm i enters. Specifically, if firm i enters market l, and otherwise, for all and .The profit function of each firm i is , where and . is the production cost of firm i, and are given parameters. The market price for each market and is given by , where are constants.
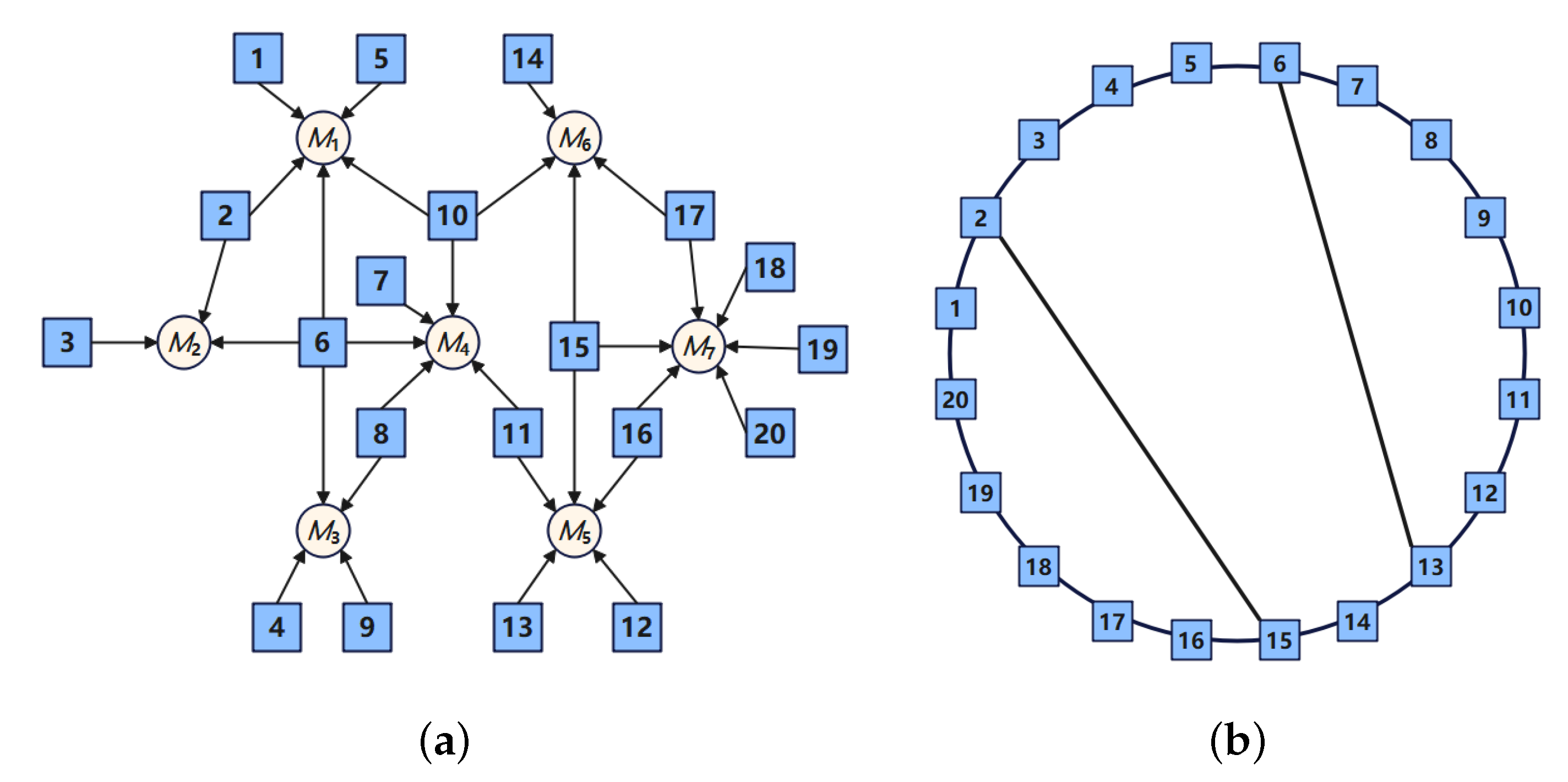
In this simulation, we set the total number of participants to 20 and the number of markets to 7, i.e., . We defined the market structure using Figure 1a, which does not show the actual spatial relationships and distances among markets and firms. We also set for all . Then the arrows in Figure 1a represent only the participation of firms in the markets; therefore, we have .
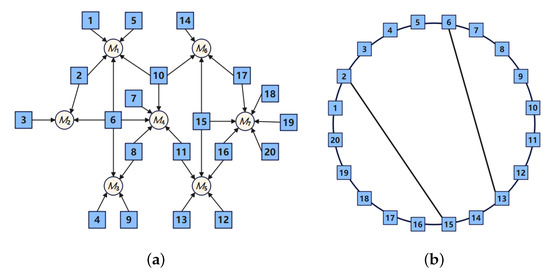
Figure 1.
(a) Network Nash–Cournot game. (b) Communication graph .
We considered m markets distributed across seven continents. Individual firms could not communicate with all other firms because of geographical location, communication technology, or company systems. The firms could communicate only with their neighbors on the communication graph , shown in Figure 1b. Only connected firms i and j in the undirected communication graph could exchange their information. We randomly selected , Q with diagonal elements in [1,8], , , , and for all and .
5.2. Numerical Results
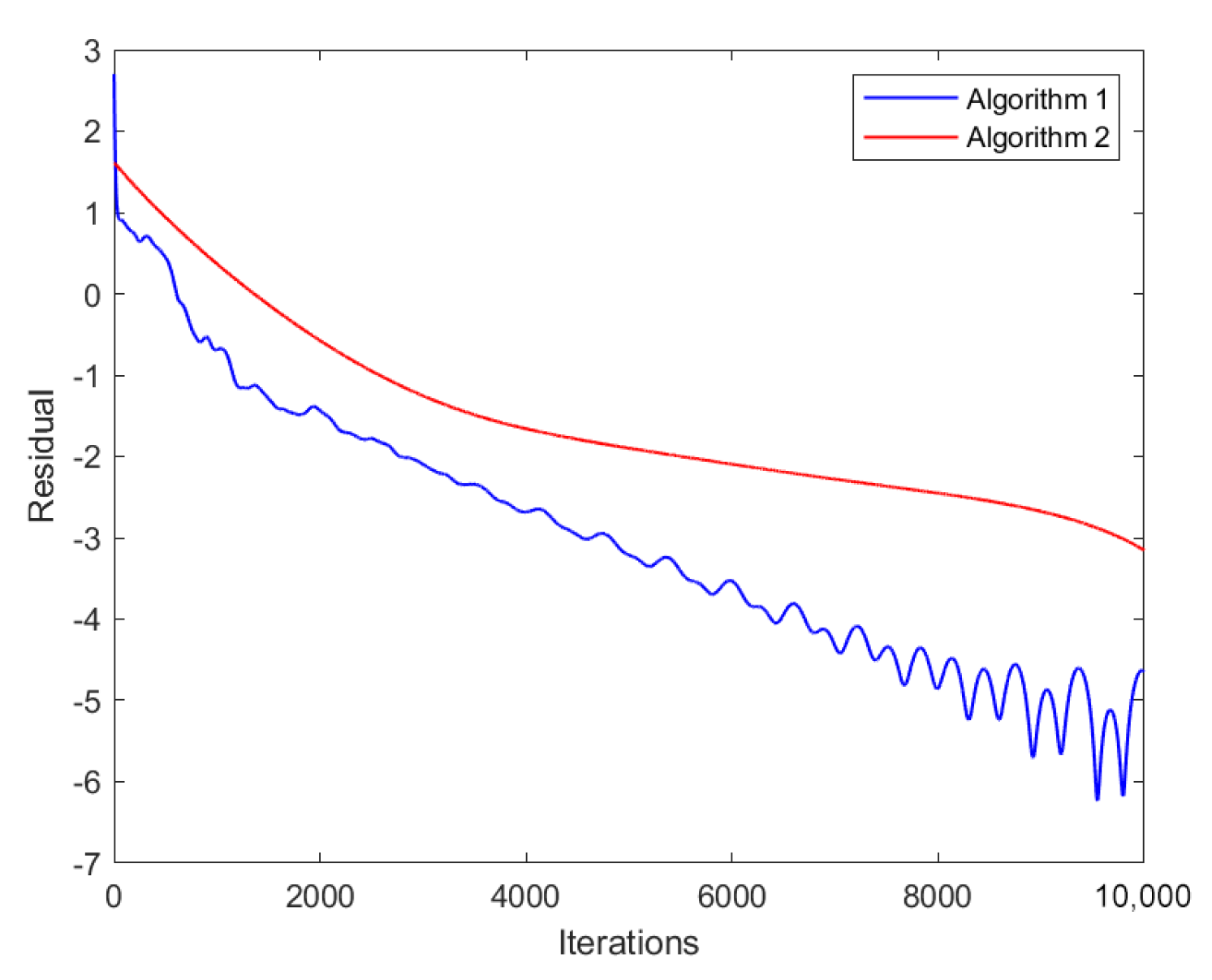
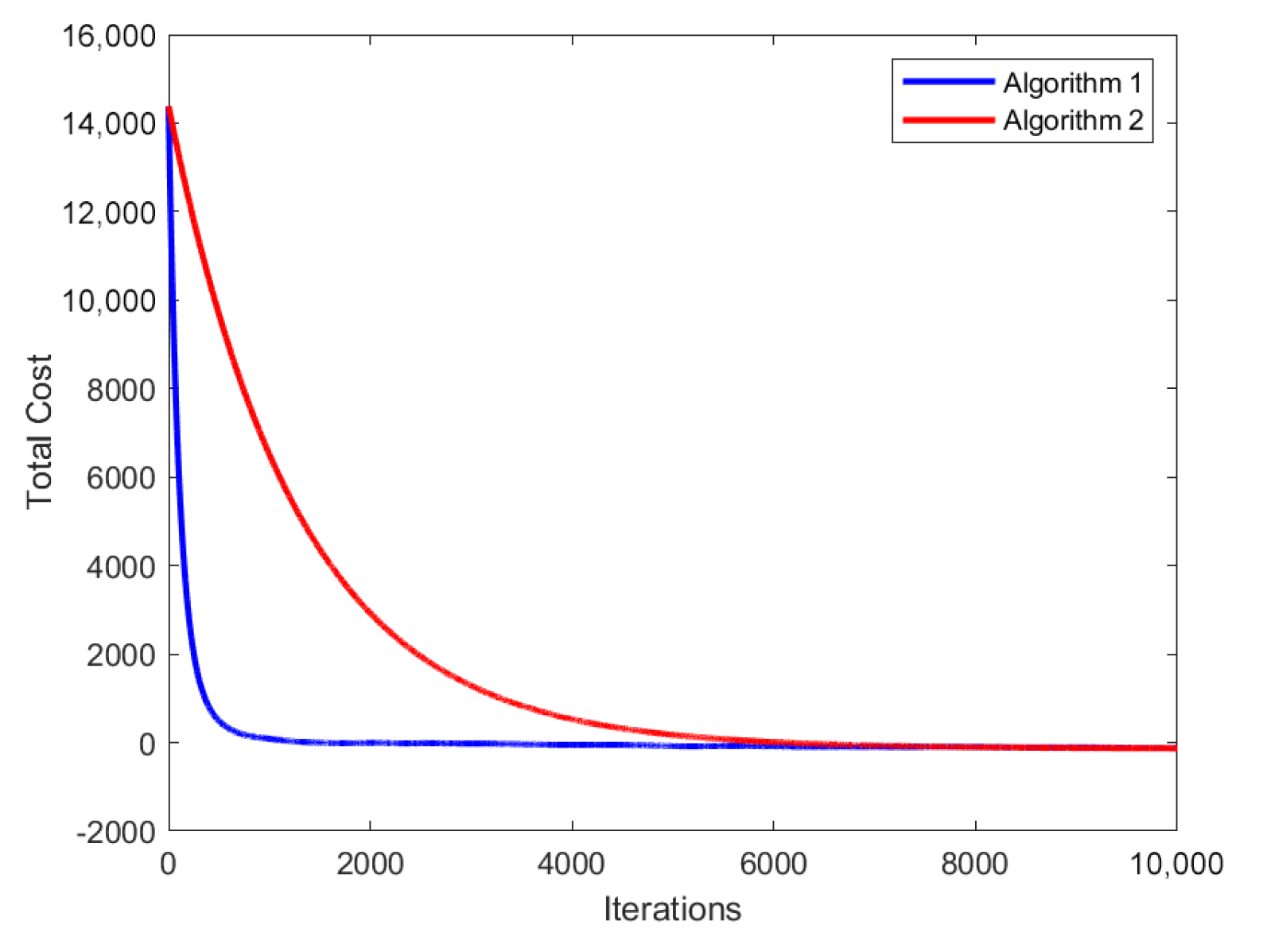
The experimental settings described above satisfy all assumptions presented in [21]. We selected the step size in Lemma 8 to fulfill all conditions required by Theorem 1. To compare the performance of Algorithm 1 and the algorithm in [21], we conducted experiments using the same random initial condition for both algorithms. As shown in Figure 2 and Figure 3, Algorithm 1 proposed in this paper converges faster than the algorithm in [21], which is referred to as Algorithm 2 in the following text.
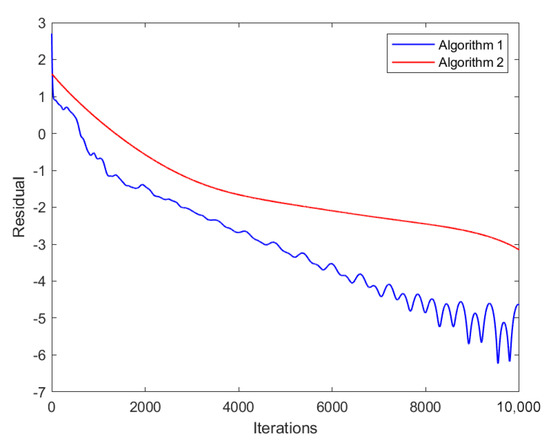
Figure 2.
Relative error plot generated by Algorithm 1 and Algorithm 2 (the algorithm in [21]).
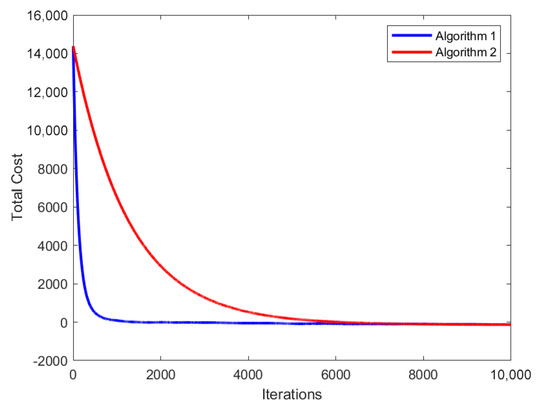
Figure 3.
The total cost of all agents generated by Algorithm 1 and Algorithm 2 (the algorithm in [21]).
Figure 2 compares the convergence of the two algorithms under the partial decision setting by plotting the relative error of their decisions. The results show that Algorithm 1 has smaller relative errors than Algorithm 2 (the algorithm in [21]) for the same number of iterations, indicating a faster convergence rate for Algorithm 1.
Figure 3 illustrates the trajectory of the total cost of all agents in the market corresponding to Algorithm 1 and Algorithm 2 (the algorithm in [21]), where the total cost is generated by . The trajectory eventually converges to the same minimum value, indicating the correctness and accuracy of Algorithm 1. Furthermore, the convergence of the trajectory represents the effectiveness of the algorithm in terms of optimizing the total cost of all agents in the market.
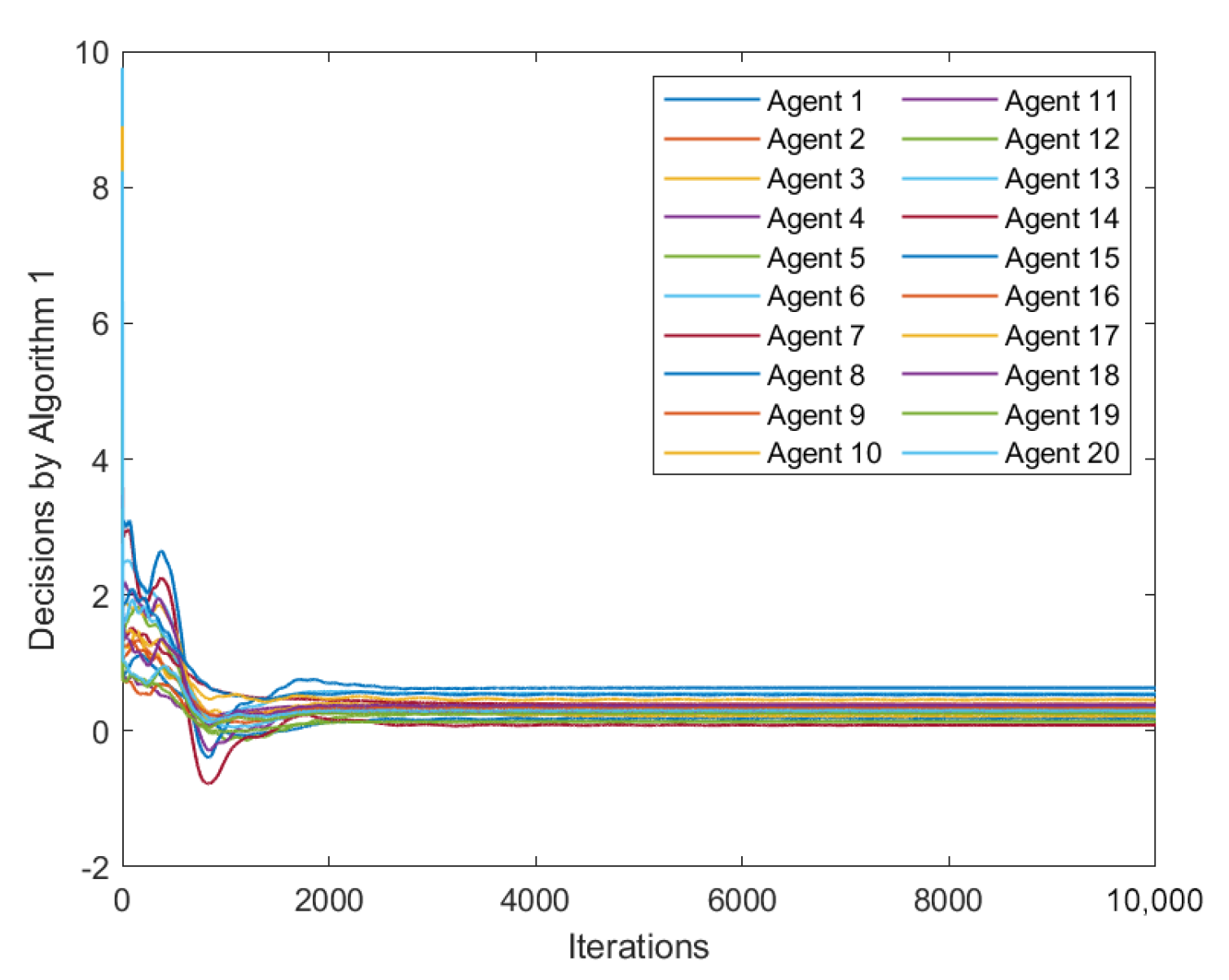
In Figure 4, we can observe the trajectory of each agent’s decision in the Cournot market game, which has been solved by Algorithm 1. As we can see from the graph, the decision trajectories of all agents converge, which is a strong indication that the GNE obtained by executing Algorithm 1 can effectively minimize the cost incurred by each agent. It is worth noting that the convergence of decision trajectories is a critical aspect of the game theory that is often used to evaluate the effectiveness of a given algorithm. Therefore, the observed convergence in Figure 4 is an encouraging sign that Algorithm 1 can be a viable approach for solving similar problems in the future.
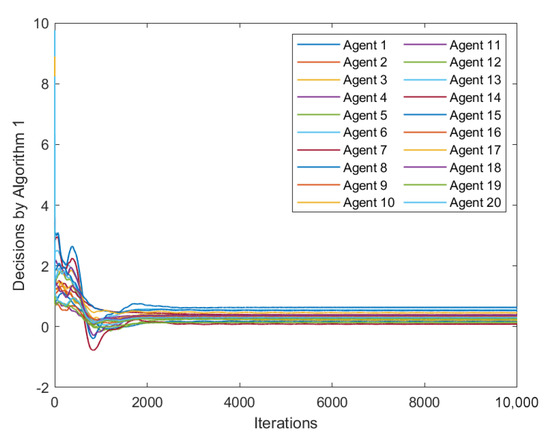
Figure 4.
Trajectories of every agent’s decision generated by Algorithm 1.
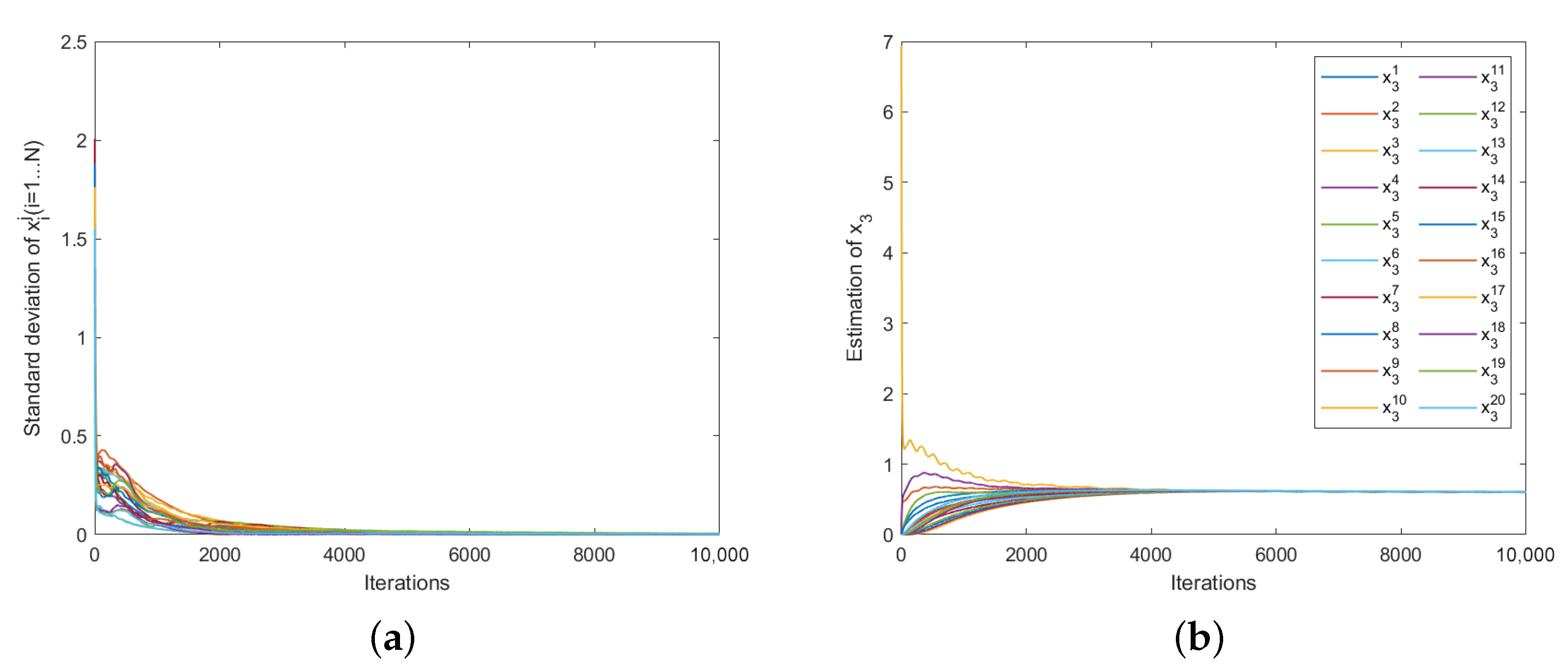
During the iterative process of Algorithm 1, the estimated value of each agent’s decision for all other agents is first obtained according to the formula . This formula is used to compute the value of . Subsequently, the estimated decision value is used for the iteration of , which is a mathematical notation used to represent the values of the decision variables. When the algorithm converges, i.e., when the GNE is obtained, the estimated decision value of each agent for is equal to the actual decision value of , i.e., for . Figure 5a shows the trajectory of the standard deviation of each agent’s estimated decision set for with increasing iteration times, which is generated by for . It can be seen that the standard deviation of the estimated decision set for each agent eventually converges to 0. This indicates that the results satisfy the condition that the estimated value of each agent’s decision for is equal to the actual decision value of . As shown in Figure 5b, taking agent 3 as an example, the trajectory plot of all agents’ estimated decision values for agent 3 is displayed, where represents the actual value of agent 3’s decision. The trajectory plot eventually converges to the same value, visually confirming the accuracy of Algorithm 1.
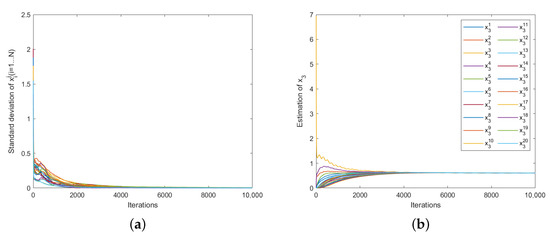
Figure 5.
(a) Trajectories of the standard deviation of agents’ estimations of generated by Algorithm 1. (b) Trajectories of agents’ estimations of generated by Algorithm 1.
6. Conclusions
In this paper, we propose a distributed algorithm for games with shared coupling constraints based on the preconditioned proximal-point algorithm under partial decision information, which can converge with a fixed step size on arbitrarily connected graphs and is successfully applied to the GNE computation of the Cournot Market competition under partial decision information with a relatively fast convergence rate. A possible direction for future work is to study partial decision information sets and their impact on the memory efficiency of the algorithm. We will also explore how to predict only a subset of agents’ decisions rather than all agents’ decisions and study the convergence properties of the algorithm. Future work will further investigate this direction.
Author Contributions
Methodology, H.L. and Y.S.; Software, Z.W., M.C. and J.C.; Formal analysis, Z.W., H.L. and M.C.; Investigation, Z.W. and Y.S.; Resources, Z.W. and Y.S.; Data curation, Z.W., H.L. and J.T.; Writing—original draft, Z.W.; Supervision, Y.S.; Project administration, Z.W. and Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Saad, W.; Han, Z.; Poor, H.V.; Basar, T. Game-theoretic methods for the smart grid: An overview of microgrid systems, demand-side management, and smart grid communications. IEEE Signal Process. Mag. 2012, 29, 86–105. [Google Scholar] [CrossRef]
- Li, N.; Chen, L.; Dahleh, M.A. Demand response using linear supply function bidding. IEEE Trans. Smart Grid 2015, 6, 1827–1838. [Google Scholar] [CrossRef]
- Grammatico, S. Dynamic control of agents playing aggregative games with coupling constraints. IEEE Trans. Autom. Control 2017, 62, 4537–4548. [Google Scholar] [CrossRef]
- Debreu, G. A social equilibrium existence theorem. Proc. Natl. Acad. Sci. USA 1952, 38, 886–893. [Google Scholar] [CrossRef] [PubMed]
- Rosen, J.B. Existence and uniqueness of equilibrium points for concave n-person games. Econom. J. Econom. Soc. 1965, 33, 520–534. [Google Scholar] [CrossRef]
- Facchinei, F.; Kanzow, C. Generalized Nash equilibrium problems. Ann. Oper. Res. 2010, 175, 177–211. [Google Scholar] [CrossRef]
- Mastroeni, G.; Pappalardo, M.; Raciti, F. Generalized Nash equilibrium problems and variational inequalities in Lebesgue spaces. Minimax Theory Appl. 2020, 5, 47–64. [Google Scholar]
- Yin, H.; Shanbhag, U.V.; Mehta, P.G. Nash equilibrium problems with congestion costs and shared constraints. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC) Held Jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 4649–4654. [Google Scholar]
- Zhu, M.; Frazzoli, E. Distributed robust adaptive equilibrium computation for generalized convex games. Automatica 2016, 63, 82–91. [Google Scholar] [CrossRef]
- Tatarenko, T.; Kamgarpour, M. Learning generalized Nash equilibria in a class of convex games. IEEE Trans. Autom. Control 2018, 64, 1426–1439. [Google Scholar] [CrossRef]
- Paccagnan, D.; Gentile, B.; Parise, F.; Kamgarpour, M.; Lygeros, J. Distributed computation of generalized Nash equilibria in quadratic aggregative games with affine coupling constraints. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 6123–6128. [Google Scholar]
- Belgioioso, G.; Grammatico, S. Semi-decentralized Nash equilibrium seeking in aggregative games with separable coupling constraints and non-differentiable cost functions. IEEE Control. Syst. Lett. 2017, 1, 400–405. [Google Scholar] [CrossRef]
- Belgioioso, G.; Grammatico, S. Projected-gradient algorithms for generalized equilibrium seeking in aggregative games arepreconditioned forward-backward methods. In Proceedings of the 2018 European Control Conference (ECC), Limassol, Cyprus, 12–15 June 2018; IEEE: Piscataway, NJ, USA; pp. 2188–2193. [Google Scholar]
- Parise, F.; Gentile, B.; Lygeros, J. A distributed algorithm for average aggregative games with coupling constraints. IEEE Trans. Control. Netw. Syst. 2020, 7, 770–782. [Google Scholar] [CrossRef]
- Yi, P.; Pavel, L. An operator splitting approach for distributed generalized Nash equilibria computation. Automatica 2019, 102, 111–121. [Google Scholar] [CrossRef]
- Bauschke, H.H.; Combettes, P.L. Convex Analysis and Monotone Operator Theory in Hilbert Spaces; Springer: Berlin/Heidelberg, Germany, 2011; Volume 408. [Google Scholar]
- Yi, P.; Pavel, L. Asynchronous distributed algorithms for seeking generalized Nash equilibria under full and partial-decision information. IEEE Trans. Cybern. 2019, 50, 2514–2526. [Google Scholar] [CrossRef] [PubMed]
- Passacantando, M.; Raciti, F. A note on generalized Nash games played on networks. In Nonlinear Analysis, Differential Equations, and Applications; Springer: Berlin/Heidelberg, Germany, 2021; pp. 365–380. [Google Scholar]
- Bianchi, M.; Belgioioso, G.; Grammatico, S. Fast generalized Nash equilibrium seeking under partial-decision information. Automatica 2022, 136, 110080. [Google Scholar] [CrossRef]
- Yi, P.; Pavel, L. Distributed generalized Nash equilibria computation of monotone games via double-layer preconditioned proximal-point algorithms. IEEE Trans. Control. Netw. Syst. 2018, 6, 299–311. [Google Scholar] [CrossRef]
- Pavel, L. Distributed GNE seeking under partial-decision information over networks via a doubly-augmented operator splitting approach. IEEE Trans. Autom. Control. 2019, 65, 1584–1597. [Google Scholar] [CrossRef]
- Gadjov, D.; Pavel, L. A passivity-based approach to Nash equilibrium seeking over networks. IEEE Trans. Autom. Control. 2018, 64, 1077–1092. [Google Scholar] [CrossRef]
- Salehisadaghiani, F.; Shi, W.; Pavel, L. Distributed Nash equilibrium seeking under partial-decision information via the alternating direction method of multipliers. Automatica 2019, 103, 27–35. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).