Scene Reconstruction Algorithm for Unstructured Weak-Texture Regions Based on Stereo Vision
Abstract
:Featured Application
Abstract
1. Introduction
- Based on the FAST feature detection algorithm, a SAD-FAST feature detection algorithm with newer and smarter decision conditions is proposed. This algorithm changes the fixed grayscale difference threshold used by the traditional FAST detection into a self-adaptive grayscale difference threshold based on the light and dark stretch contrast of the image to avoid missing the necessary feature points and improves the feature point judgment conditions to screen the feature points with higher quality;
- In this study, the three-step correlation algorithm in the stereo-matching system based on feature points was adopted to “select the essence and discard the dross”, and a combination method of FAST feature detection + SURF feature description + FLANN feature matching is proposed. Furthermore, the Mahalanobis distance was used to reduce the mismatching between different dimensions when matching, which ensured efficiency and accuracy when facing complex texture scenes. We propose a GVDS feature extraction algorithm to adjust the distribution of feature points, avoiding the loss of 3D information caused by the absence of feature points in part of the scene to be reconstructed and thus making the final reconstruction effect more realistic and improving the reconstruction efficiency.
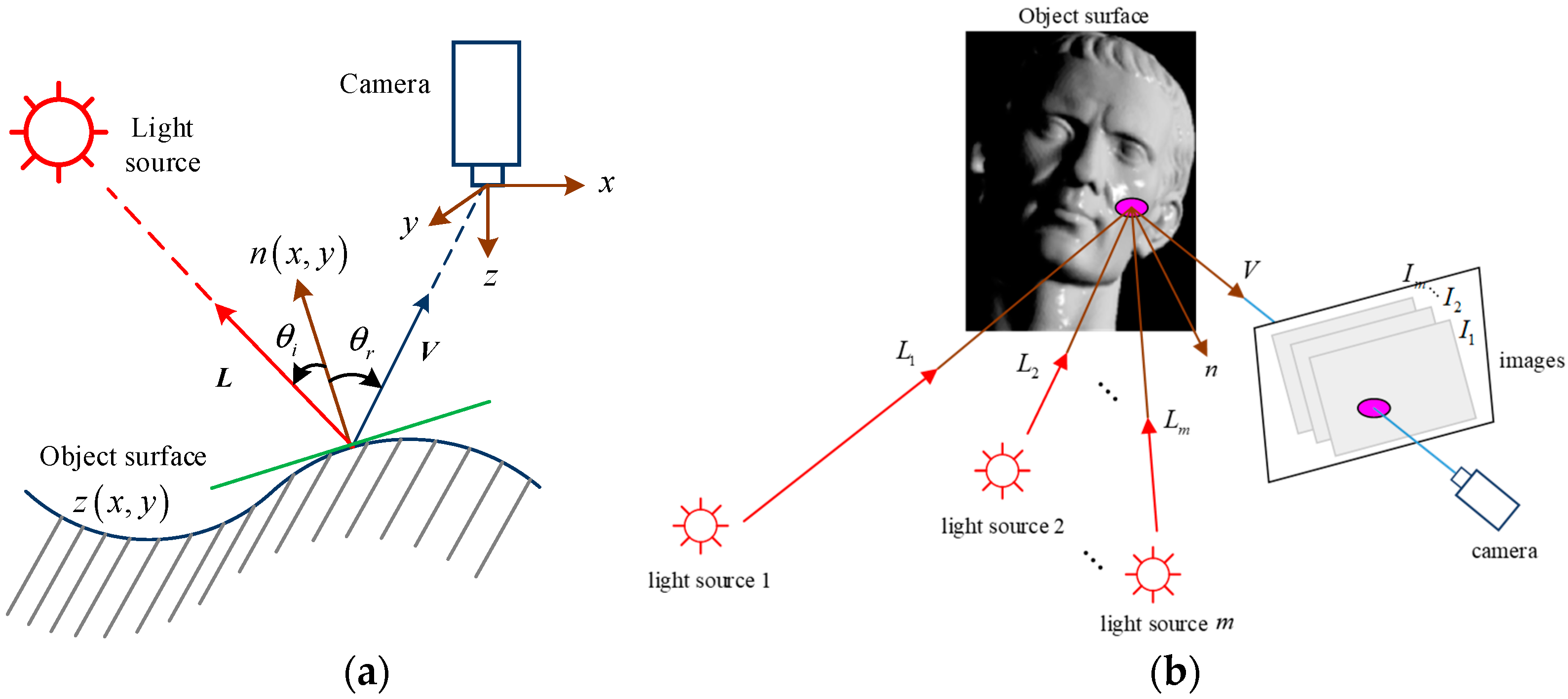
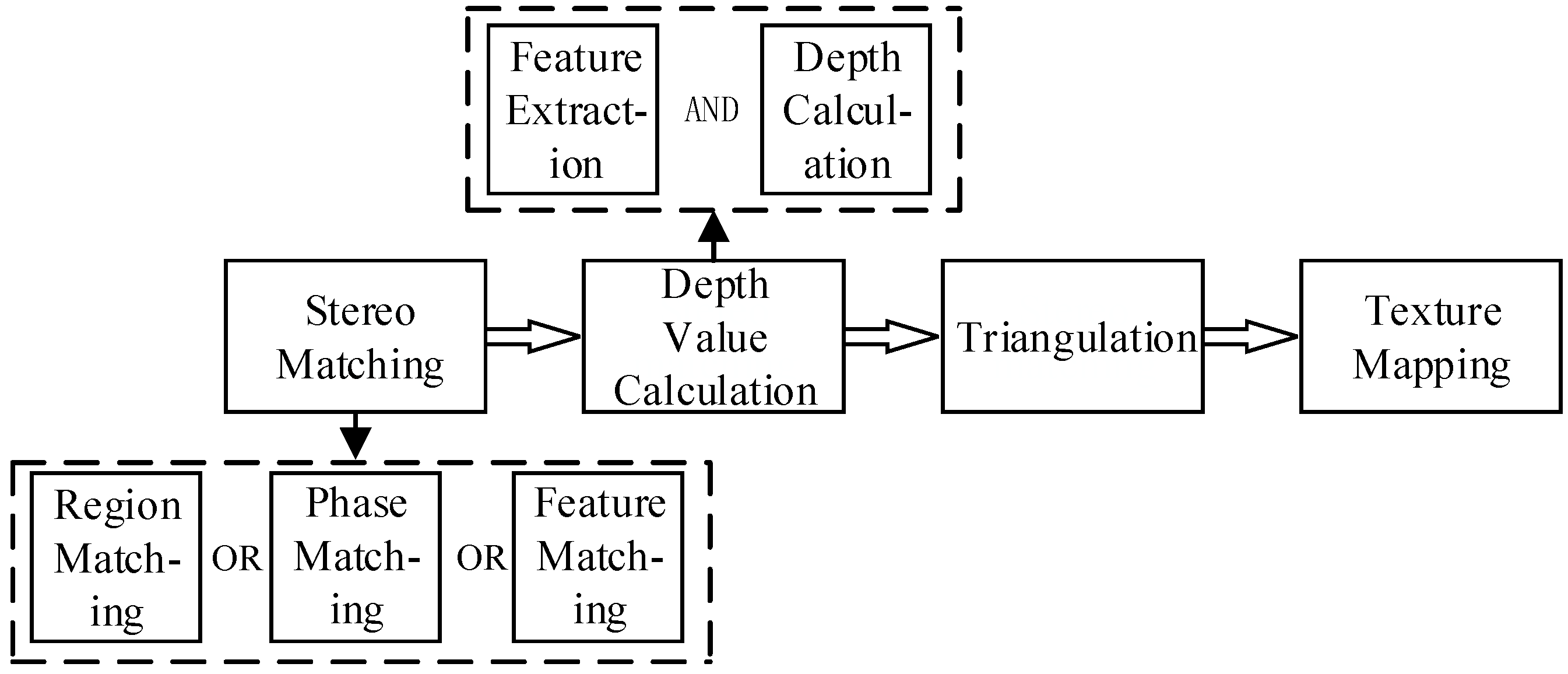
2. Stereo Reconstruction Algorithm for Unstructured Scenes
2.1. SAD-FAST Feature Detection and Recombination Stereo-Matching System
2.1.1. SAD-FAST Feature Detection
- , and point is brighter than point ;
- , and point is darker than point ;
- , and the two points are of equal brightness.
2.1.2. SURF Descriptor
2.1.3. FLANN Feature Matching
2.1.4. Mahalanobis Distance
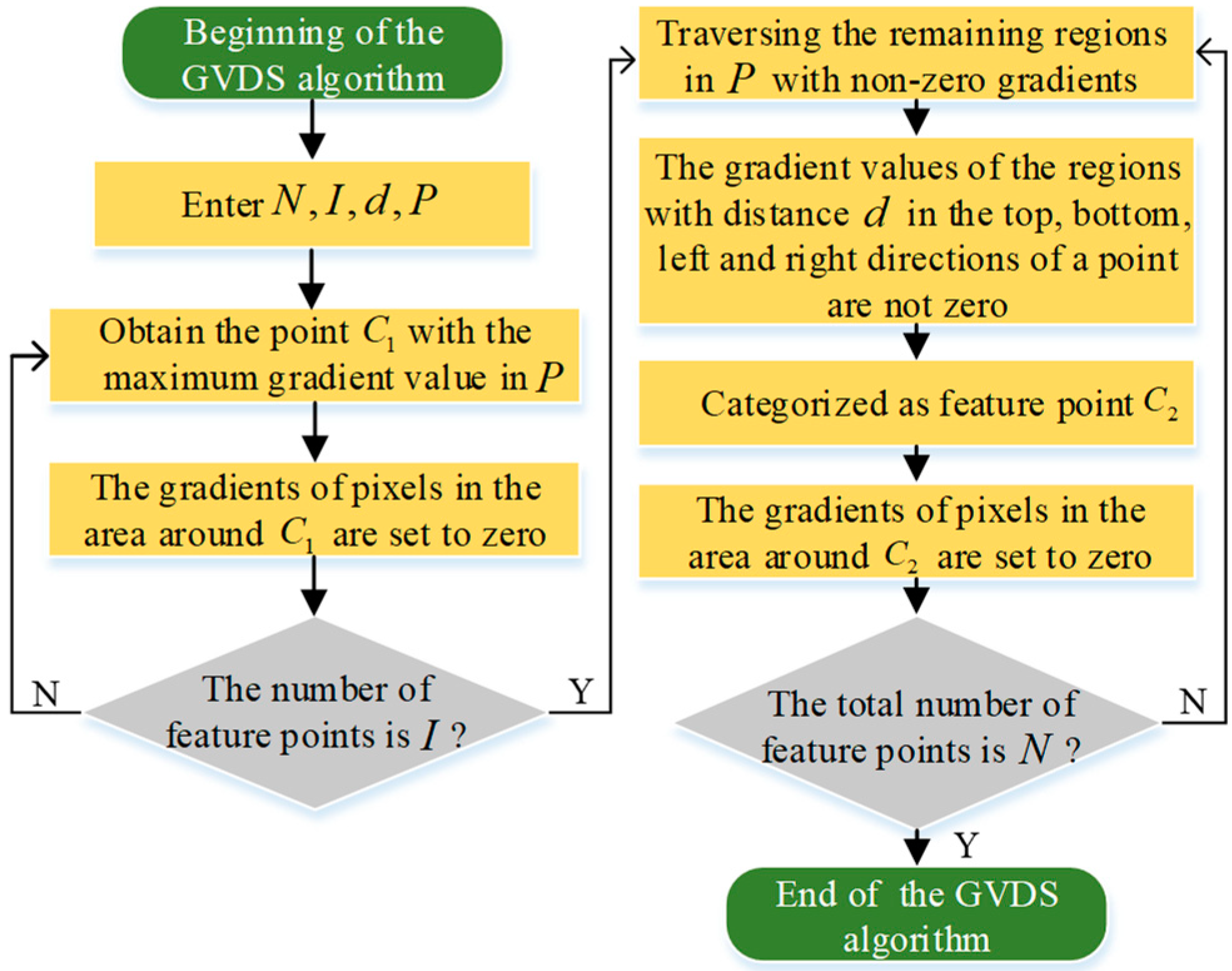
2.2. GVDS Feature Extraction Algorithm
- (1)
- Set the total number of feature extraction points as , the number of feature points with strong depth variation as , the shortest Euclidean distance between adjacent feature points as , and the disparity map derived from stereo matching as ;
- (2)
- Calculate the gradient value for the disparity map , and then the point with the largest gradient value can be found, which is the first feature point selected;
- (3)
- In order to avoid too dense a distribution of feature points, the gradient of the surrounding pixels within a certain range should be set to zero after a feature point is selected. In the disparity map , the gradient-zeroing operation is carried out in the surrounding area with point as the center of the circle and as the radius;
- (4)
- Repeat steps (2) and (3) until the number of selected feature points is not less than ;
- (5)
- Feature point extraction is performed for the remaining scattered regions with low depth variation in the disparity map . A pixel coordinate in the disparity map is defined as so that it traverses the region with a non-zero gradient value starting from the top left of the disparity map . If the gradient values of the pixels with distances of in the top, bottom, left, and right directions are not zero when the traversal reaches a certain point, the point is selected as the feature point and is called ;
- (6)
- The gradient of the surrounding area with point as the center and as the radius is set to zero;
- (7)
- Repeat steps (5) and (6) until the total number of feature points that have been selected is .
2.3. Triangulation and Texture Mapping
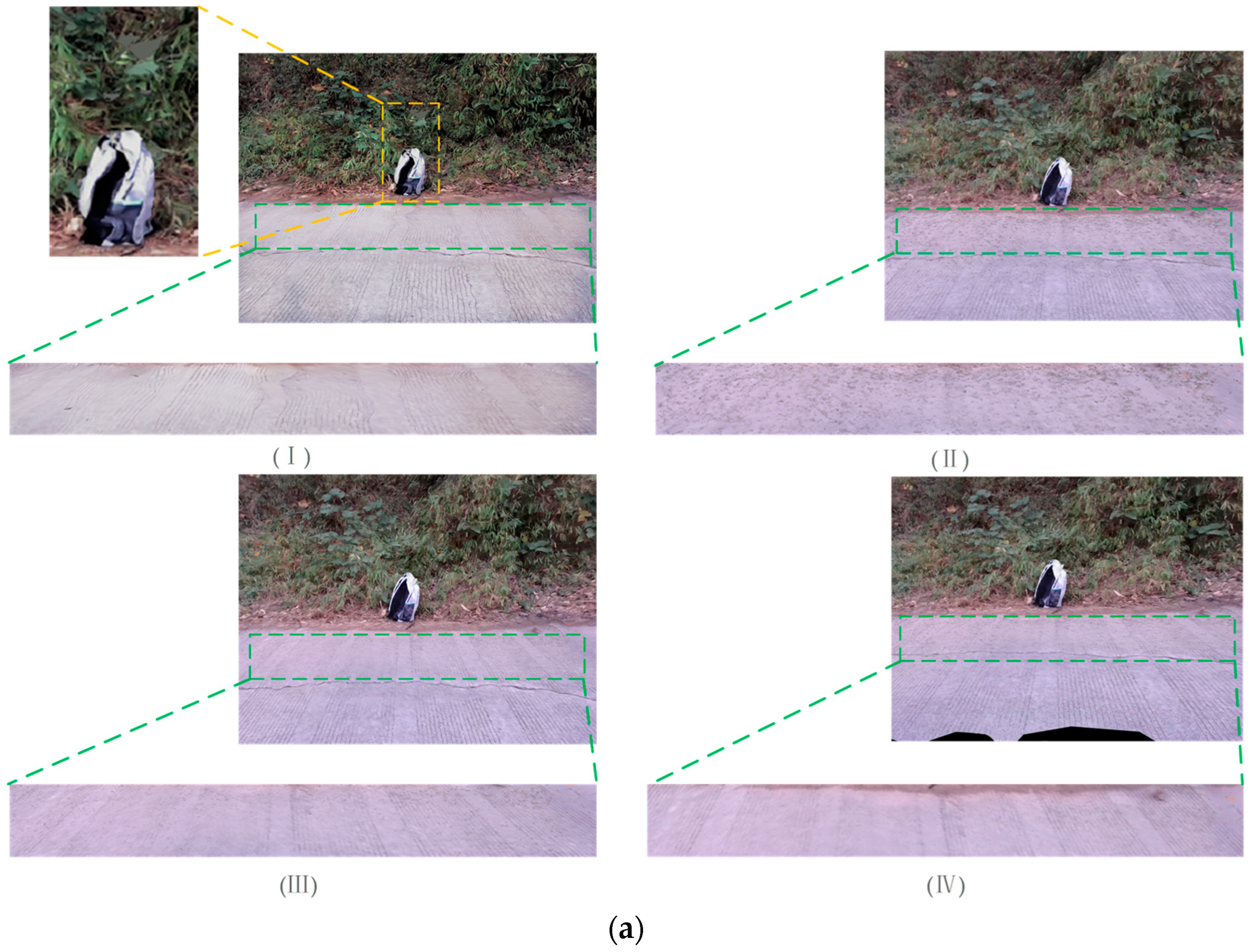
3. Experimental Results and Analysis
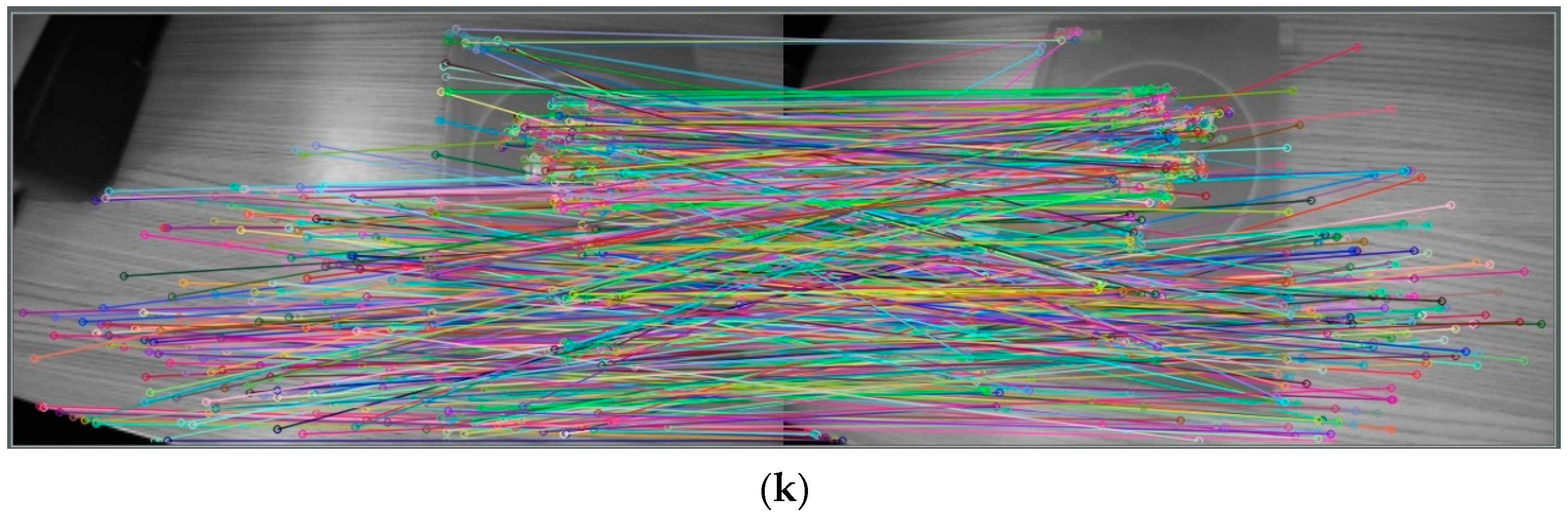
3.1. Stereo-Matching Experiments
3.2. Experimental Results for Feature Extraction with Depth Value Calculation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.; Wu, Z.; Wang, Z.; Song, Y.B.; Ling, Y.G.; Bao, L.C. Self-supervised learning of detailed 3D face reconstruction. IEEE Trans. Image Process. 2019, 29, 8696–8705. [Google Scholar] [CrossRef] [PubMed]
- Zheng, T.X.; Huang, S.; Li, Y.F.; Feng, M.C. Key techniques for vision based 3D reconstruction: A review. Acta Autom. Sin. 2020, 46, 631–652. [Google Scholar]
- Tewari, A.; Zollhöfer, M.; Bernard, F.; Garrido, P.; Kim, H.; Perez, P.; Theobalt, C. High-Fidelity Monocular Face Reconstruction Based on an Unsupervised Model-Based Face Autoencoder. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 357–370. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.; Wang, S.; Xie, S. 3D Scene Reconstruction with Sparse LiDAR Data and Monocular Image in Single Frame. SAE Int. J. Passeng. Cars-Electron. Electr. Syst. 2017, 11, 48–56. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Z.; Zeng, T. Research and Design of 3D Reconstruction System Based on Binocular Vision. Int. Core J. Eng. 2019, 5, 29–35. [Google Scholar]
- Jian, X.; Chen, X.; He, W.; Gong, X. Outdoor 3D reconstruction method based on multi-line laser and binocular vision. IFAC-PapersOnLine 2020, 53, 9554–9559. [Google Scholar] [CrossRef]
- Hsu, G.J.; Liu, Y.; Peng, H. RGB-D-Based Face Reconstruction and Recognition. IEEE Trans. Inf. Forensics Secur. 2014, 9, 2110–2118. [Google Scholar] [CrossRef]
- Gao, Y.P.; Leif, K.; Hu, S.M. Real-Time High-Accuracy Three-Dimensional Reconstruction with Consumer RGB-D Cameras. ACM Trans. Graph. 2018, 37, 1–16. [Google Scholar]
- Huan, L.; Zheng, X.; Gong, J. GeoRec: Geometry-enhanced semantic 3D reconstruction of RGB-D indoor scenes. ISPRS J. Photogramm. Remote Sens. 2022, 186, 301–314. [Google Scholar] [CrossRef]
- Wang, D.; Deng, H.; Li, X.; Tian, X. 3D reconstruction of intelligent driving high-precision maps with location information convergence. J. Guilin Univ. Electron. Technol. 2019, 39, 182–186. [Google Scholar]
- Cai, Y.; Lin, X. Design of 3D reconstruction system for laser Doppler image based on virtual reality technology. Laser J. 2017, 38, 122–126. [Google Scholar]
- Lu, S.; Luo, H.; Chen, J.; Gao, M.; Liang, J. Application of 3D printing technology in the repair and reconstruction of bone defect in knee joint: One clinical case report. Chin. J. Clin. Anat. 2021, 39, 732–736. [Google Scholar]
- Shah, F.M. Condition assessment of ship structure using robot assisted 3D-reconstruction. Ship Technol. Res. 2021, 68, 129–146. [Google Scholar] [CrossRef]
- Fahim, G.; Min, K.; Zarif, S. Single-View 3D Reconstruction: A Survey of Deep Learning Methods. Comput. Graph. 2021, 94, 164–190. [Google Scholar] [CrossRef]
- Gao, X.; Hen, S.; Zhu, L.; Shi, T.X.; Wang, Z.H.; Hu, Z.Y. Complete Scene Reconstruction by Merging Images and Laser Scans. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 3688–3701. [Google Scholar] [CrossRef]
- Pepe, M.; Alfio, V.S.; Costantino, D. UAV Platforms and the SfM-MVS Approach in the 3D Surveys and Modelling: A Review in the Cultural Heritage field. Appl. Sci. 2023, 12, 886. [Google Scholar] [CrossRef]
- Kumar, S.; Dai, Y.; Li, H. Monocular Dense 3D Reconstruction of a Complex Dynamic Scene from Two Perspective Frames. In Proceedings of the ICCV, Honolulu, HI, USA, 21–26 July 2017; pp. 4659–4667. [Google Scholar]
- Chen, H.C. Monocular Vision-Based Obstacle Detection and Avoidance for a Multicopter. IEEE Access 2019, 7, 16786–16883. [Google Scholar] [CrossRef]
- Wan, Y.; Shi, M.; Nong, X. UAV 3D Reconstruction System Based on ZED Camera. China New Telecommun. 2019, 21, 155–157. [Google Scholar]
- Wu, X.; Wen, F.; Wen, P. Hole-Filling Algorithm in Multi-View Stereo Reconstruction. In Proceedings of the CVMP, London, UK, 24–25 November 2015; Volume 24, pp. 1–8. [Google Scholar]
- Wang, Z.W.; Wang, H.; Li, J. Research On 3D Reconstruction of Face Based on Binocualr Stereo Vision. In Proceedings of the 2019 International Conference, Beijing, China, 18–20 October 2019. [Google Scholar] [CrossRef]
- Han, R.; Yan, H.; Ma, L. Research on 3D Reconstruction methods Based on Binocular Structured Light Vision. Proc. J. Phys. Conf. Ser. 2021, 1744, 032002. [Google Scholar] [CrossRef]
- Carolina, M.; Weibel, J.A.; Vlachos, P.P.; Garimella, S.V. Three-dimensional liquid-vapor interface reconstruction from high-speed stereo images during pool boiling. Int. J. Heat Mass Transf. 2020, 136, 265–275. [Google Scholar]
- Zhou, J.; Han, S.; Zheng, Y.; Wu, Z.; Yang, Y. Three-Dimensional Reconstruction of Retinal Vessels Based on Binocular Vision. Chin. J. Med. 2020, 44, 13–19. [Google Scholar]
- Cai, Y.T.; Liu, X.Q.; Xiong, Y.J.; Wu, X. Three-Dimensional Sound Field Reconstruction and Sound Power Estimation by Stereo Vision and Beamforming Technology. Appl. Sci. 2021, 11, 92. [Google Scholar] [CrossRef]
- Zhai, G.; Zhang, W.; Hu, W.; Ji, Z. Coal Mine Rescue Robots Based on Binocular Vision: A Review of the State of the Art. IEEE Access 2020, 8, 130561–130575. [Google Scholar] [CrossRef]
- Wang, Y.; Deng, N.; Xin, B.J.; Wang, W.Z.; Xing, W.Y.; Lu, S.G. A novel three-dimensional surface reconstruction method for the complex fabrics based on the MVS. Opt. Laser Technol. 2020, 131, 106415. [Google Scholar] [CrossRef]
- Furukawa, Y.; Curless, B. Towards Internet-scale multi-view stereo. In Proceedings of the CVPR, San Francisco, CA, USA, 13–18 June 2010; pp. 1434–1441. [Google Scholar]
- Mnich, C.; Al-Bayat, F. In situ weld pool measurement using stereovision. In Proceedings of the ASME, Denver, CO, USA, 19–21 July 2014; pp. 19–21. [Google Scholar]
- Liang, Z.M.; Chang, H.X.; Wang, Q.Y.; Wang, D.L.; Zhang, Y.M. 3D Reconstruction of Weld Pool Surface in Pulsed GMAW by Passive Biprism Stereo Vision. IEEE Robot. Autom. Lett. 2019, 4, 3091–3097. [Google Scholar] [CrossRef]
- Jiang, G. A Practical 3D Reconstruction Method for Weak Texture Scenes. Remote Sens. 2021, 13, 3103. [Google Scholar]
- Stathopoulou, E.K.; Battisti, R.; Dan, C.; Remondino, F.; Georgopoulos, A. Semantically Derived Geometric Constraints for MVS Reconstruction of Textureless Areas. Remote Sens. 2021, 13, 1053. [Google Scholar] [CrossRef]
- Wang, G.H.; Han, J.Q.; Zhang, X.M. A New Three-Dimensional Reconstruction Algorithm of the Lunar Surface based on Shape from Shading Method. J. Astronaut. 2009, 30, 2265–2269. [Google Scholar]
- Woodham, R.J. Photometric Method for Determining Surface Orientation from Multiple Images. Opt. Eng. 1980, 19, 139–144. [Google Scholar] [CrossRef]
- Horn, B.K.P.; Brooks, M.J. The Variational Approach to Shape from Shading. Comput. Vis. Graph. Image Process. 1986, 33, 174–208. [Google Scholar] [CrossRef]
- Frankot, R.T.; Chellappa, R. A Method for Enforcing Integrability in Shape from Shading Algorithms. IEEE Trans. Pattern Anal. Mach. Intell. 1988, 10, 439–451. [Google Scholar] [CrossRef]
- Agrawal, A.; Raskar, R.; Chellappa, R. What Is the Range of Surface Reconstructions from a Gradient Field. In Proceedings of the ECCV, Graz, Austria, 7–13 May 2006; pp. 578–591. [Google Scholar]
- Harker, M.; O’Leary, P. Regularized Reconstruction of a Surface from its Measured Gradient Field: Algorithms for Spectral, Tikhonov, Constrained, and Weighted Regularization. J. Math. Imaging Vis. 2015, 51, 46–70. [Google Scholar] [CrossRef]
- Queau, Y.; Durou, J.D.; Aujol, J.-F. Variational Methods for Normal Integration. J. Math. Imaging Vis. 2018, 60, 609–632. [Google Scholar] [CrossRef]
- Queau, Y.; Durou, J.D.; Aujol, J.-F. Normal Integration: A Survey. J. Math. Imaging Vis. 2018, 60, 576–593. [Google Scholar] [CrossRef]
- Zhang, Y.; Weiwei, X.U.; Tong, Y. Online Structure Analysis for Real-Time Indoor Scene Reconstruction. ACM Trans. Graph. 2015, 34, 1–13. [Google Scholar] [CrossRef]
- Kim, J.; Hong, S.; Hwang, S. Automatic waterline detection and 3D reconstruction in model ship tests using stereo visive. Electron. Lett. 2019, 55, 527–529. [Google Scholar]
- Peng, F.; Tan, Y.; Zhang, C. Exploiting Semantic and Boundary Information for Stereo Matching. J. Signal Process. Syst. 2021, 95, 379–391. [Google Scholar] [CrossRef]
- Wang, D.; Hu, L. Improved Feature Stereo Matching Method Based on Binocular Vision. Acta Electron. Sin. 2022, 50, 157–166. [Google Scholar]
- Haq, Q.M.; Lin, C.H.; Ruan, S.J.; Gregor, D. An edge-aware based adaptive multi-feature set extraction for stereo matching of binocular images. J. Ambient. Intell. Humaniz. Comput. 2022, 13, 1953–1967. [Google Scholar] [CrossRef]
- Li, H.; Chen, L.; Li, F. An Efficient Dense Stereo Matching Method for Planetary Rover. IEEE Access 2019, 7, 48551–48564. [Google Scholar] [CrossRef]
- Candès, E.; Tao, T. Signal recovery from incomplete and inaccurate measurement. Commun. Pure Appl. Math. 2005, 59, 1207–1223. [Google Scholar] [CrossRef]
- Kong, D.W. Triangulation and Computer Three-Dimensional Reconstruction of Point Cloud Data. J. Southwest China Norm. Univ. (Nat. Sci. Ed.) 2019, 44, 87–92. [Google Scholar]
- Dai, G. Automatic, Multiview, Coplanar Extraction for CityGML Building Model Texture Mapping. Remote Sens. 2021, 14, 50. [Google Scholar]
- Peng, X.; Guo, X.; Centre, L. The Research on Texture Extraction and Mapping Implementation in 3D Building Reconstruction. Bull. Sci. Technol. 2014, 30, 77–81. [Google Scholar]
- Bernardini, F.; Martin, I.M.; Rushmeier, H. High-quality texture reconstruction from multiple scans. IEEE Trans. Vis. Comput. Graph. 2001, 7, 318–322. [Google Scholar] [CrossRef]
- Muja, M.; Lowe, D.G. Fast Approximate Nearest Neighbors with Automaticalgorithm Configuration. In Proceedings of the ICCV, Kyoto, Japan, 29 September–2 October 2009; pp. 331–340. [Google Scholar]
- Pablo, F.A.; Adrien, B.; Andrew, J.D. KAZE Features. In Proceedings of the ECCV, Florence, Italy, 7–13 October 2012; pp. 214–227. [Google Scholar]
- Pablo, F.A.; Nuevo, J.; Adrien, B. Fast Explicit Diffusion for Accelerated Features in Nonlinear Scale Spaces. In Proceedings of the BMVC, Bristol, UK, 9–13 September 2013. [Google Scholar] [CrossRef]
- Leutenegger, S.; Chli, M.; Siegwart, R.Y. BRISK: Binary Robust Invariant scalable keypoints. In Proceedings of the ICCV, Barcelona, Spain, 6–13 November 2011; pp. 2548–2555. [Google Scholar]
- Alahi, A.; Ortiz, R.; Vandergheynst, P. FREAK: Fast Retina Keypoint. In Proceedings of the CVPR, Providence, RI, USA, 16–21 June 2012; pp. 510–517. [Google Scholar]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Gool, L.V. SURF: Speeded Up Robust Features. In Proceedings of the ECCV, Graz, Austria, 7–13 May 2006; pp. 404–417. [Google Scholar]
- Calonder, M.; Lepetit, V.; Strecha, C. BRIEF: Binary Robust Independent Elementary Feature. In Proceedings of the ECCV, Hersonissos, Greece, 5–11 September 2010; pp. 778–792. [Google Scholar]
- Rosten, E.; Drummond, T. Machine Learning for High-Speed Corner Detection. In Proceedings of the ECCV, Graz, Austria, 7–13 May 2006; pp. 430–443. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G.R. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the ICCV, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Yang, G.S.; Manela, J.; Happold, M.; Ramanan, D. Hierarchical Deep Stereo Matching on High-Resolution Images. In Proceedings of the CVPR, Long Beach, CA, USA, 16–20 June 2019. [Google Scholar] [CrossRef]
- Xu, G.W.; Cheng, J.D.; Peng, G.; Yang, X. Attention Concatenation Volume for Accurate and Efficient Stereo Matching. In Proceedings of the CVPR, New Orleans, LA, USA, 19–24 June 2022; pp. 12981–12990. [Google Scholar]
- Liu, B.Y.; Yu, H.M.; Long, Y.Q. Local Similarity Pattern and Cost Self-Reassembling for Deep Stereo Matching Networks. In Proceedings of the AAAI, Vancouver, BC, Canada, 22 February–1 March 2022; pp. 1647–1655. [Google Scholar]














| Detection Algorithms | Number of Feature Points Detected by Image Pair/Points | Time Consumption for Feature Point Detection/ms |
|---|---|---|
| KAZE [53] | 275 | 141 |
| AKAZE [54] | 222 | 120 |
| BRISK [55] | 311 | 276 |
| FREAK [56] | 98 | 56 |
| SIFT [57] | 406 | 952 |
| SURF [58] | 601 | 174 |
| BRIEF [59] | 98 | 92 |
| FAST-50 [60] | 514 | 19 |
| FAST-40 | 602 | 27 |
| SAD-FAST- | 874 | 32 |
| Algorithms | Matching Success Rate/% | Matching Time/ms |
|---|---|---|
| ORB [61] | 64 | 36.6 |
| SIFT [57] | 87.7 | 156.7 |
| SURF [58] | 79.4 | 312.1 |
| AKAZE [54] | 71.6 | 41.7 |
| BRISK [55] | 75.2 | 46.3 |
| ORB + SURF | 81.4 | 73.2 |
| AKAZE + SURF | 82.1 | 149.4 |
| SIFT + SURF | 76.7 | 243.9 |
| BRISK + SURF | 79.6 | 376.1 |
| KAZE + SURF | 81.9 | 69.4 |
| SAD-FAST- + SURF | 85.1 | 57.9 |
| 3D Reconstruction Steps | Traditional Algorithms/ms | Our Algorithm/ms | ||
|---|---|---|---|---|
| SURF [58] | SIFT [57] | ORB [61] | SAD-FAST + SURF + GVDS | |
| Camera and image pretreatments | 47.361 + 51.12 | 47.361 + 51.12 | 47.361 + 51.12 | 47.361 + 51.12 |
| Stereo-matching experiment | 336.27 | 182.61 | 61.632 | 64.301 |
| Depth value calculation | 57.94 | 42.46 | 25.73 | 17.82 |
| Triangulation and texture mapping | --- | --- | --- | 35.134 |
| 3D Reconstruction Steps | Traditional Algorithms/ms | Our Algorithm/ms | ||
|---|---|---|---|---|
| [62] | [63] | [64] | ||
| Camera and image pretreatments | 47.361 + 51.12 | 47.361 + 51.12 | 47.361 + 51.12 | 47.361 + 51.12 |
| Stereo-matching experiment | 137 | 263.2 | 243 | 64.301 |
| Triangulation and texture mapping | 32.17 | 35.784 | 37.263 | 35.134 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.; Duan, Z.; Lan, Z.; Yi, S. Scene Reconstruction Algorithm for Unstructured Weak-Texture Regions Based on Stereo Vision. Appl. Sci. 2023, 13, 6407. https://doi.org/10.3390/app13116407
Chen M, Duan Z, Lan Z, Yi S. Scene Reconstruction Algorithm for Unstructured Weak-Texture Regions Based on Stereo Vision. Applied Sciences. 2023; 13(11):6407. https://doi.org/10.3390/app13116407
Chicago/Turabian StyleChen, Mingju, Zhengxu Duan, Zhongxiao Lan, and Sihang Yi. 2023. "Scene Reconstruction Algorithm for Unstructured Weak-Texture Regions Based on Stereo Vision" Applied Sciences 13, no. 11: 6407. https://doi.org/10.3390/app13116407
APA StyleChen, M., Duan, Z., Lan, Z., & Yi, S. (2023). Scene Reconstruction Algorithm for Unstructured Weak-Texture Regions Based on Stereo Vision. Applied Sciences, 13(11), 6407. https://doi.org/10.3390/app13116407







