Effect of Partially Correlated Wind Loading on the Response of Two-Way Asymmetric Systems: The Impact of Torsional Sensitivity and Nonlinear Effects
Abstract
1. Introduction
2. Structural Model, Wind-Loading Model, and Analysis Procedure
2.1. Equation of Motion and Instantaneous Loads Eccentricities (A-Δ Effect)
2.2. Wind-Loading Model
2.3. Analysis Procedure
- (1)
- Simulate , and by using Equation (8);
- (2)
- Solve Equation (5) for the structure without and with the A-Δ effect to obtain the time history of the responses using Gear’s method [12];
- (3)
- Evaluate the response ratios (i.e., , , , and ) defined in Equation (10);
- (4)
- Repeat steps 1 to 3 for all the structures considered.
3. Parametric Analysis and Results
3.1. Structural Characteristics and Peak Responses
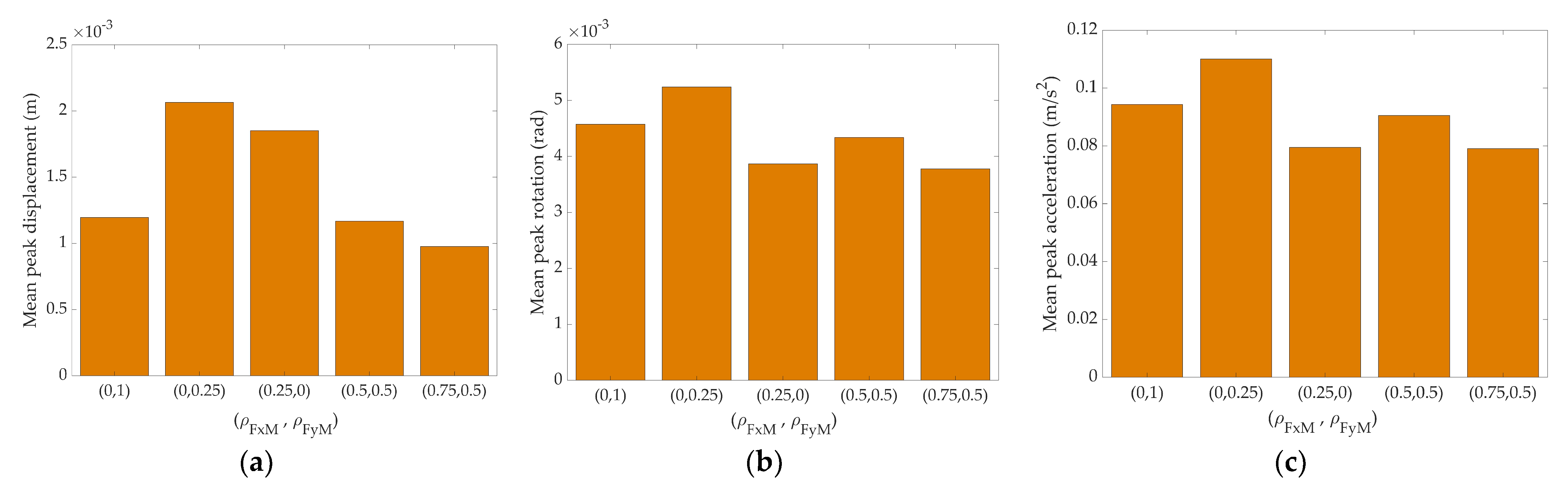
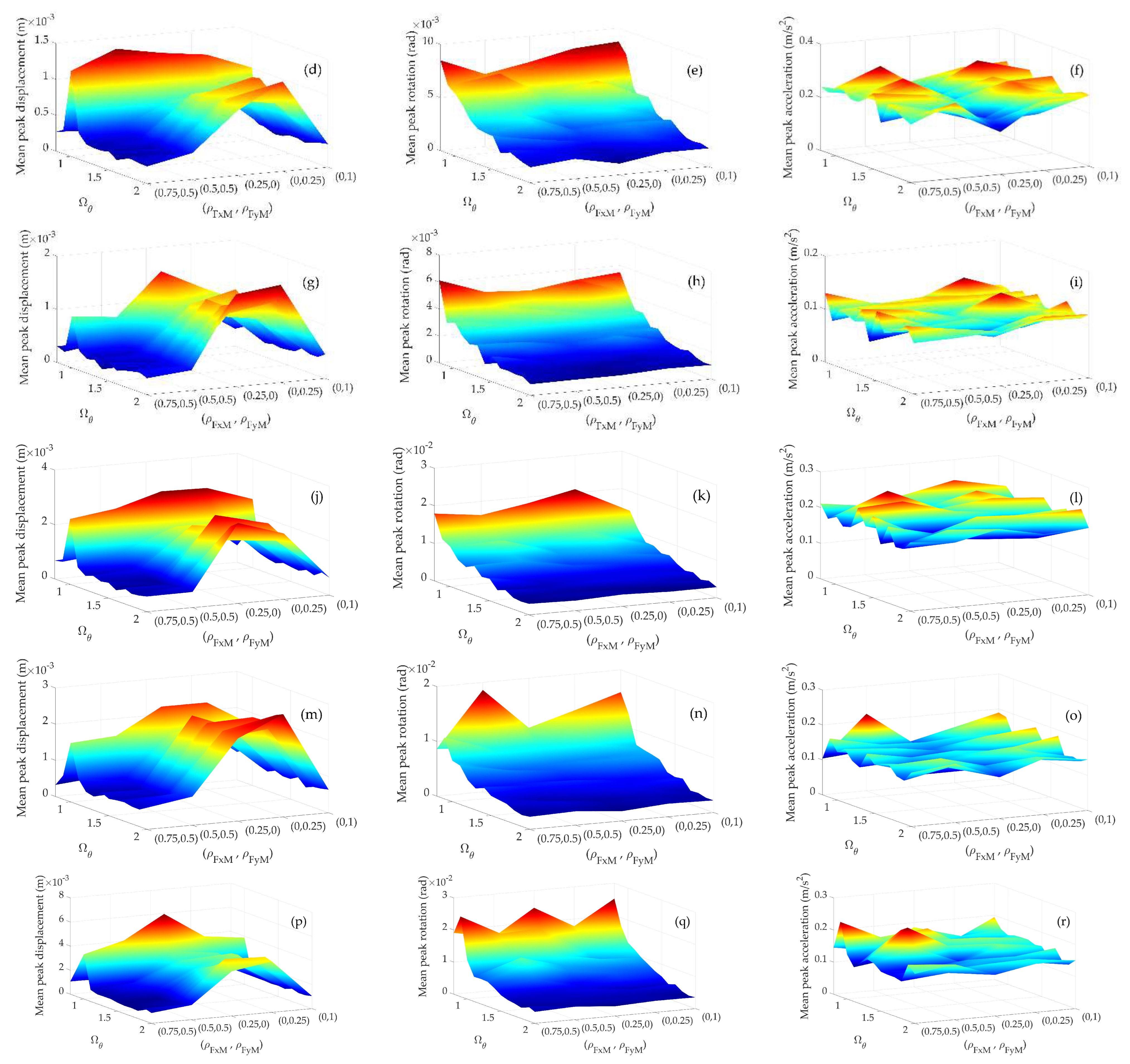
3.1.1. Impact of and (, ) on the Mean Peak Responses
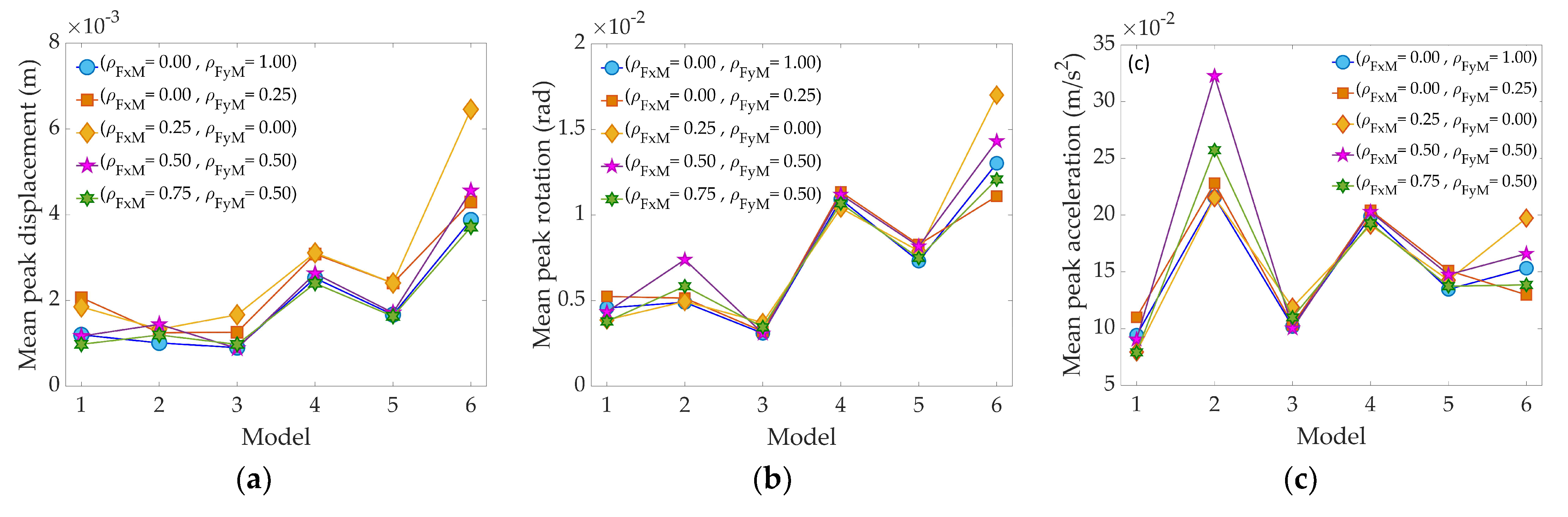
3.1.2. Impact of the A-Δ effect, , and (, ) on the Peak Responses
4. Conclusions
- ▪
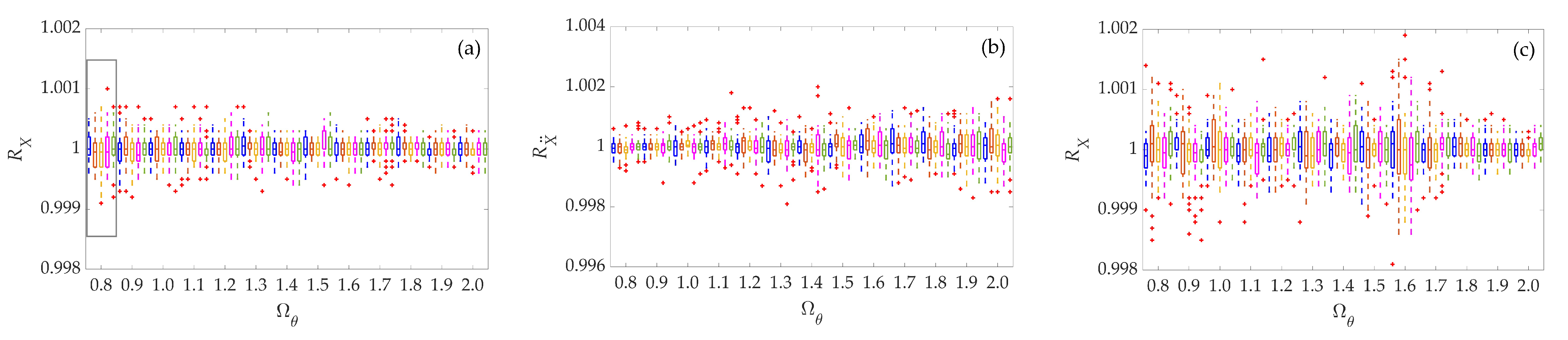
- In all the structural models analyzed, the median and the extreme data, as well as the outliers of the response ratio (RX, , , and ) values are very close to one for all the values considered of Ωθ. The latter indicates that the A-Δ effect does not have an important impact on wind-induced displacement and acceleration.
- ▪
- The correlation coefficient between the wind forces (i.e., and ) has the most important impact on the response, indicating that different levels of correlation of the wind forces and the torsional moment have to be considered in the evaluation of the wind-induced response.
- ▪
- The wind-induced rotational velocity with and without the A-Δ effect is practically the same, indicating that the A-Δ effect has a marginal impact on it.
- ▪
- The results presented in this study show that the A-Δ effect has a marginal impact on the wind-induced response; however, the evaluation of the wind-induced response considering the nonlinear behavior of the structure (i.e., material or element nonlinearity) is very scarce in the relevant literature. Different to the nonlinear response of structures under seismic action, where the nonlinear response is likely to reduce compared to the linear response, wind-induced response will not necessarily behave in the same way, as nonlinearity may cause the structure to become more flexible with a consequent increase in the dynamic response of the structure. Further analyses are required to evaluate the impact of the material and element nonlinearity on tall buildings subjected to partially correlated wind loads.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Kareem, A. Lateral-torsional motion of tall buildings to wind loads. J. Struct. Eng. 1985, 111, 2479–2496. [Google Scholar] [CrossRef]
- Holmes, J.D. Distribution of Peak Wind Loads on a Low-Rise Building. J. Wind Eng. Ind. Aerodyn. 2013, 122, 1. [Google Scholar] [CrossRef]
- Kwok, K.C.C.; Burton, M.D.; Abdelrazaq, A.K. Wind-Induced Motion of Tall Buildings: Designing for Habitability, 1st ed.; ASCE: Reston, VA, USA, 2015; pp. 1–65. [Google Scholar] [CrossRef]
- Isyumov, N.; Kilpatrick, J. Full-scale experience with wind-induced motions of tall buildings. In Proceedings of the 67th Regional Conference Council on Tall Buildings and Urban Habitat, Chicago, IL, USA, 15–18 April 1996. [Google Scholar]
- Burton, M.; Kwok, K.C.; Hitchcock, P.A.; Denoon, R.O. Frequency Dependence of Human Response to Wind-Induced Building Motion. J. Struct. Eng. 2006, 132, 296–303. [Google Scholar] [CrossRef]
- Burton, M.; Kwok, K.C.S.; Abdelrazaq, A. Wind-Induced Motion of Tall Buildings: Designing for Occupant Comfort. Int. J. High-Rise Build. 2015, 4, 1–8. [Google Scholar]
- Pozos-Estrada, A. A simple procedure to evaluate the wind-induced acceleration in tall buildings: An application to Mexico, JCR. Wind Struct. Int. J. 2018, 27, 337–345. [Google Scholar] [CrossRef]
- Wu, J.R.; Li, Q.S. Wind-induced lateral-torsional coupled responses of tall buildings. Wind Struct. 2008, 11, 153–178. [Google Scholar] [CrossRef]
- Elsharawy, M.; Stathopoulos, T.; Galal, K. Wind-Induced Torsional Aerodynamic Loads on Low and Medium Height Buildings. In Proceedings of the The Seventh International Colloquium on Bluff Body Aerodynamics and Applications, Shanghai, China, 2–6 September 2012. [Google Scholar]
- Guzmán-Solis, V.; Pozos-Estrada, A.; Gómez-Martínez, R. Experimental study of wind-induced shear, bending, and torsional loads on rectangular tall buildings. Adv. Struct. Eng. 2020, 23, 2982–2995. [Google Scholar] [CrossRef]
- Hong, H.P. Torsional Responses under Bidirectional Seismic Excitations: Effect of Instantaneous Load Eccentricities. J. Struct. Eng. 2013, 139, 133–143. [Google Scholar] [CrossRef]
- Shampine, L.F.; Reichelt, M.W. The MATLAB ode suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]
- Pozos-Estrada, A.; Hong, H.P.; Galsworthy, J.K. Serviceability design factors for wind-sensitive structures. Can. J. Civil Eng. 2010, 37, 728–738. [Google Scholar] [CrossRef]
- Pozos-Estrada, A.; Hong, H.P. Sensitivity analysis of the effectiveness of tuned mass dampers to reduce the wind-induced torsional responses. Lat. Am. J. Solids Struct. 2015, 12, 2520–2538. [Google Scholar] [CrossRef]
- Tamura, Y.; Kikuchi, H.; Hibi, K. Quasi-static wind load combinations for low- and middle-rise buildings. J. Wind Eng. Ind. Aerodyn. 2003, 91, 1613–1625. [Google Scholar] [CrossRef]
- Tamura, Y.; Kikuchi, H.; Hibi, K. Peak normal stresses and effects of wind direction on wind load combinations for medium-rise buildings. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1043–1057. [Google Scholar] [CrossRef]
- Tamura, Y.; Kim, Y.C.; Kikuchi, H.; Hibi, K. Correlation and combination of wind force components and responses. J. Wind Eng. Ind. Aerodyn. 2014, 125, 81–93. [Google Scholar] [CrossRef]
- Shinozuka, M. Monte Carlo Solution of Structural Dynamics. Comput. Struct. 1972, 2, 855–874. [Google Scholar] [CrossRef]
- Hong, H.P. Modeling of Nonstationary Winds and its Applications. J. Eng. Mech. 2016, 142, 04016004. [Google Scholar] [CrossRef]
- Griffis, L.G. Serviceability limit states under wind load. Eng. J. 1993, 30, 1–16. [Google Scholar]
- MATLAB. Version R2022b; The MathWorks Inc.: Natick, MA, USA, 2022. [Google Scholar]
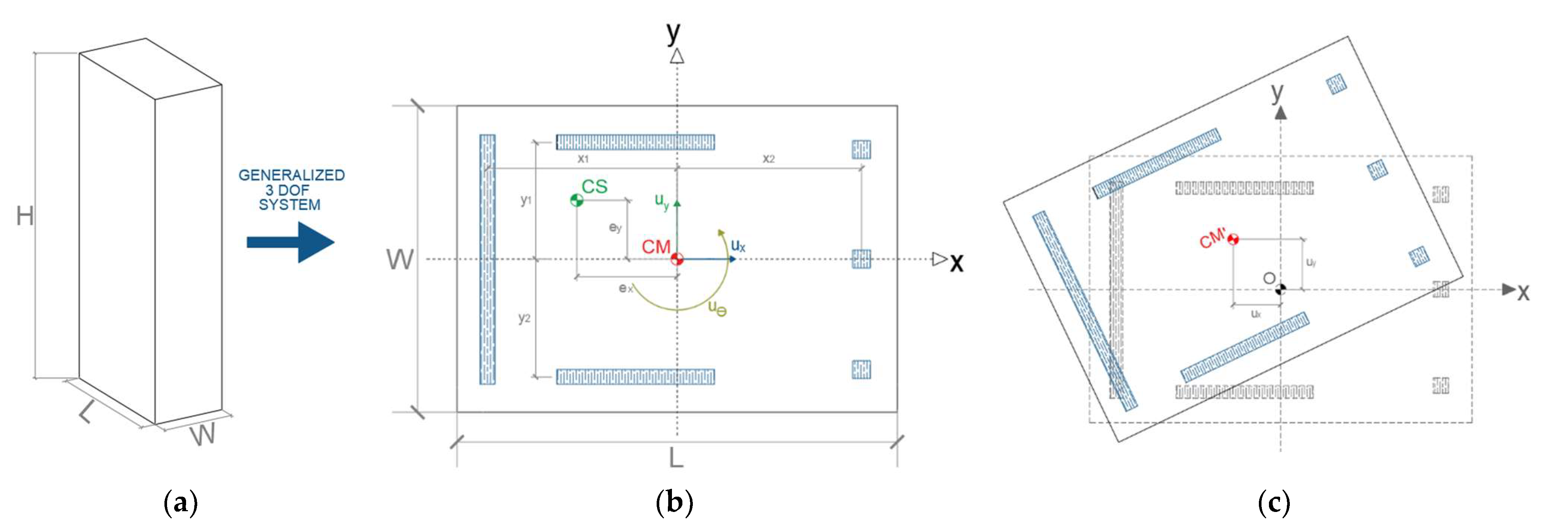
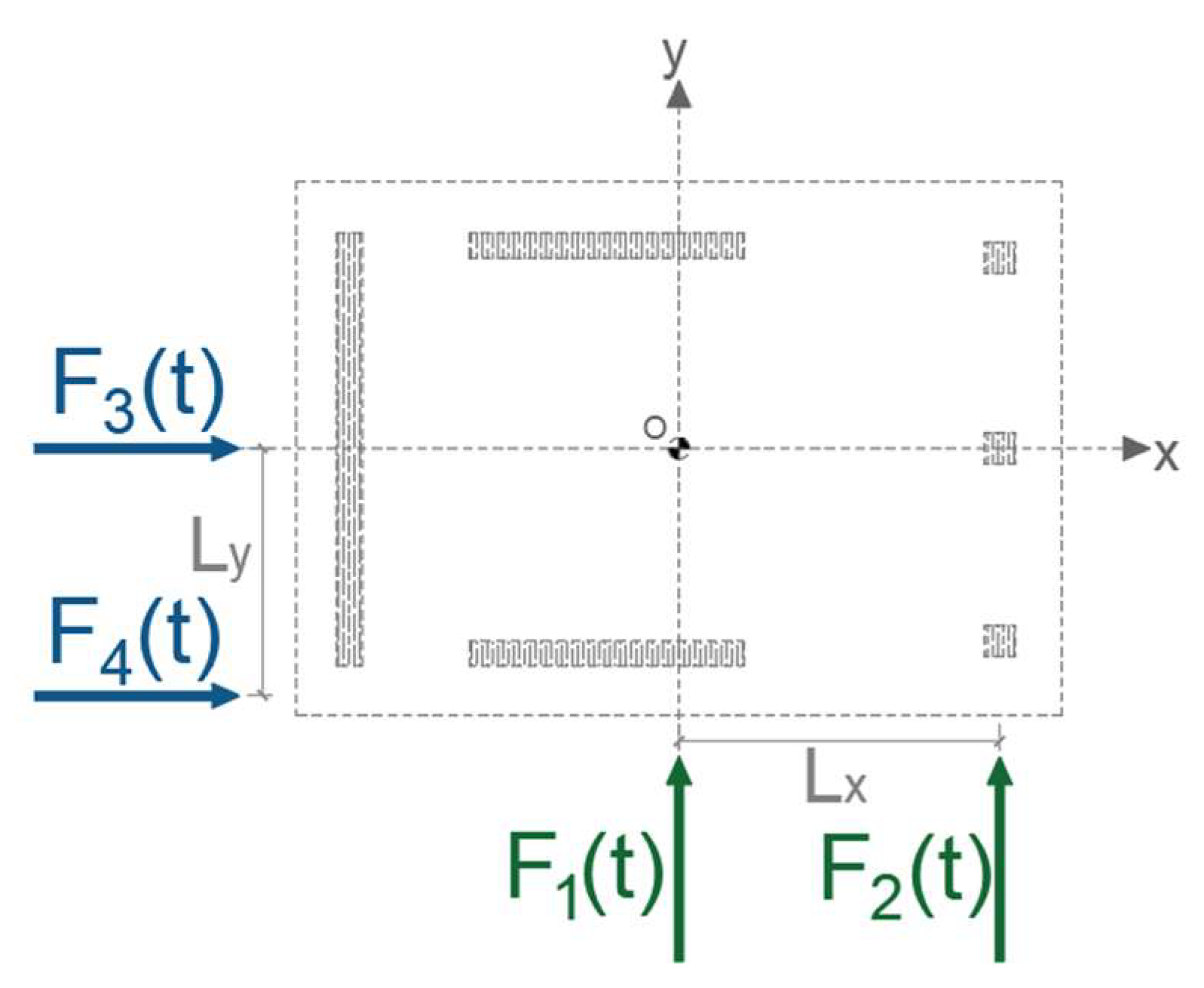


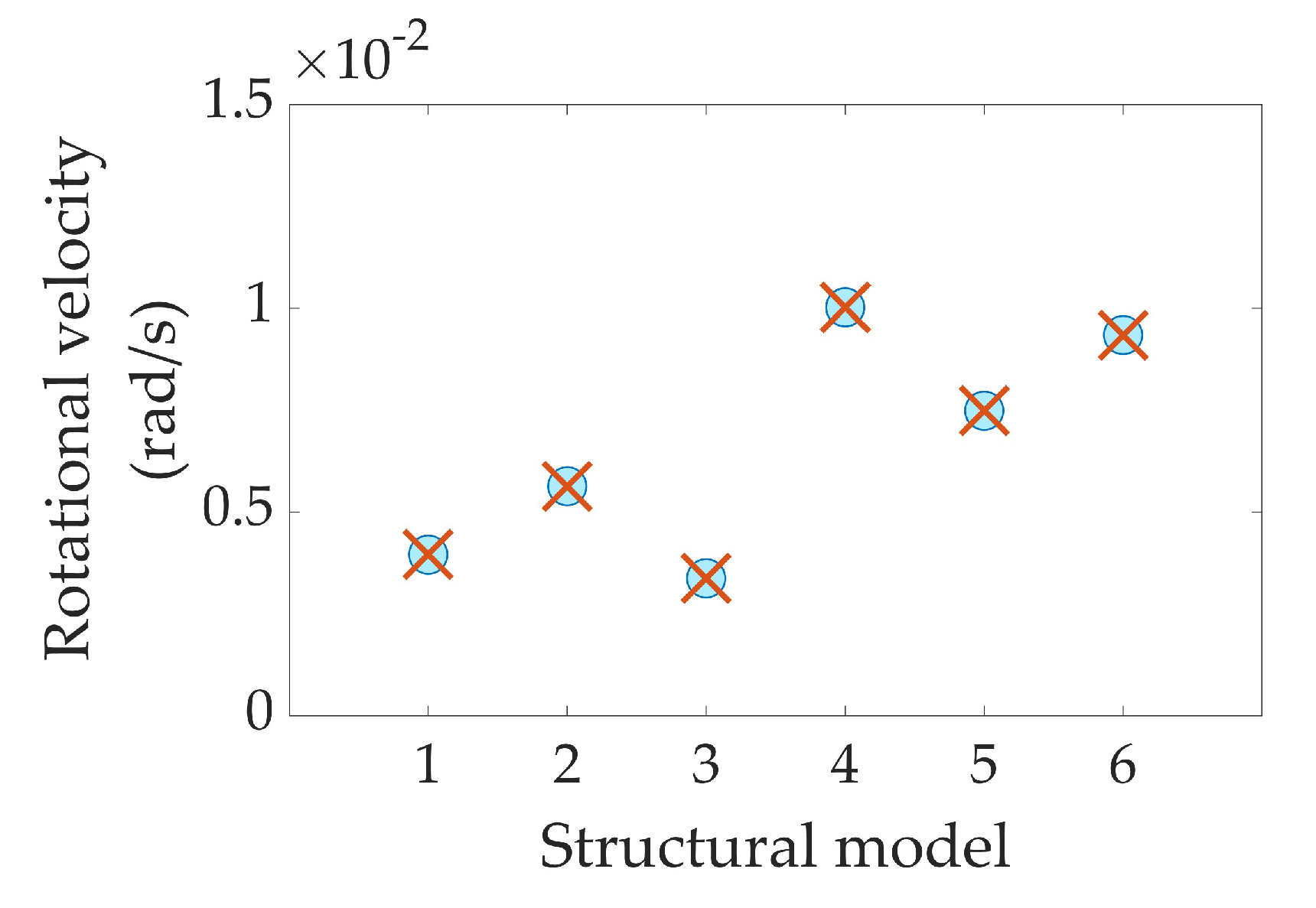
| Model | Mass (kg) | ωx (rad/s) | ωy (rad/s) | H (m) | L (m) | W (m) | H/L | H/W | Lx (m) | Ly (m) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2,281,509 | 0.925 | 0.945 | 170 | 40 | 33 | 4.3 | 5.2 | 12 | 11 | 1.09 |
| 2 | 3,516,347 | 1.259 | 0.788 | 262 | 55 | 25 | 4.8 | 10.5 | 35 | 30 | 1.17 |
| 3 | 2,180,727 | 1.179 | 1.033 | 140 | 38 | 34 | 3.7 | 4.1 | 15 | 13 | 1.15 |
| 4 | 827,663 | 0.980 | 1.045 | 116 | 36 | 19 | 3.2 | 6.1 | 28 | 25 | 1.12 |
| 5 | 479,315 | 1.098 | 1.559 | 101 | 29 | 14 | 3.5 | 7.2 | 20 | 18 | 1.11 |
| 6 | 2,519,208 | 0.753 | 0.753 | 200 | 30 | 30 | 6.7 | 6.7 | 20 | 20 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Ibarra, A.; Pozos-Estrada, A.; Nava-González, R. Effect of Partially Correlated Wind Loading on the Response of Two-Way Asymmetric Systems: The Impact of Torsional Sensitivity and Nonlinear Effects. Appl. Sci. 2023, 13, 6421. https://doi.org/10.3390/app13116421
López-Ibarra A, Pozos-Estrada A, Nava-González R. Effect of Partially Correlated Wind Loading on the Response of Two-Way Asymmetric Systems: The Impact of Torsional Sensitivity and Nonlinear Effects. Applied Sciences. 2023; 13(11):6421. https://doi.org/10.3390/app13116421
Chicago/Turabian StyleLópez-Ibarra, Adrián, Adrián Pozos-Estrada, and Rigoberto Nava-González. 2023. "Effect of Partially Correlated Wind Loading on the Response of Two-Way Asymmetric Systems: The Impact of Torsional Sensitivity and Nonlinear Effects" Applied Sciences 13, no. 11: 6421. https://doi.org/10.3390/app13116421
APA StyleLópez-Ibarra, A., Pozos-Estrada, A., & Nava-González, R. (2023). Effect of Partially Correlated Wind Loading on the Response of Two-Way Asymmetric Systems: The Impact of Torsional Sensitivity and Nonlinear Effects. Applied Sciences, 13(11), 6421. https://doi.org/10.3390/app13116421








