Numerical Simulation and Analysis of the Causes and Distribution of Secondary Lining Cracks in Overlapping Railway Tunnels
Abstract
:1. Introduction
2. Methodology
2.1. Project Overview
2.2. Methods of on-Site Investigation of Cracks
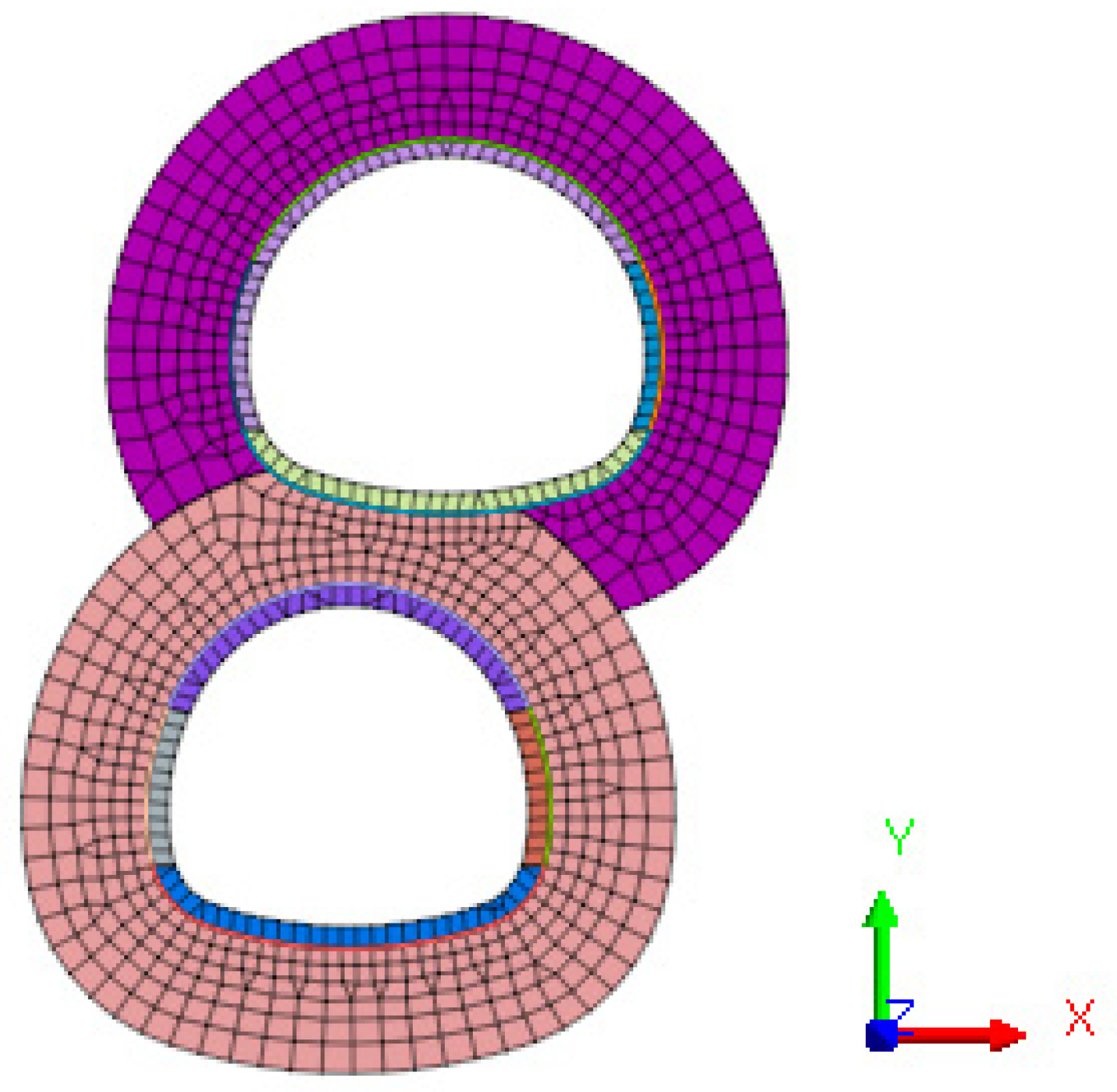
2.3. Numerical Simulation Calculation Method of Cracks
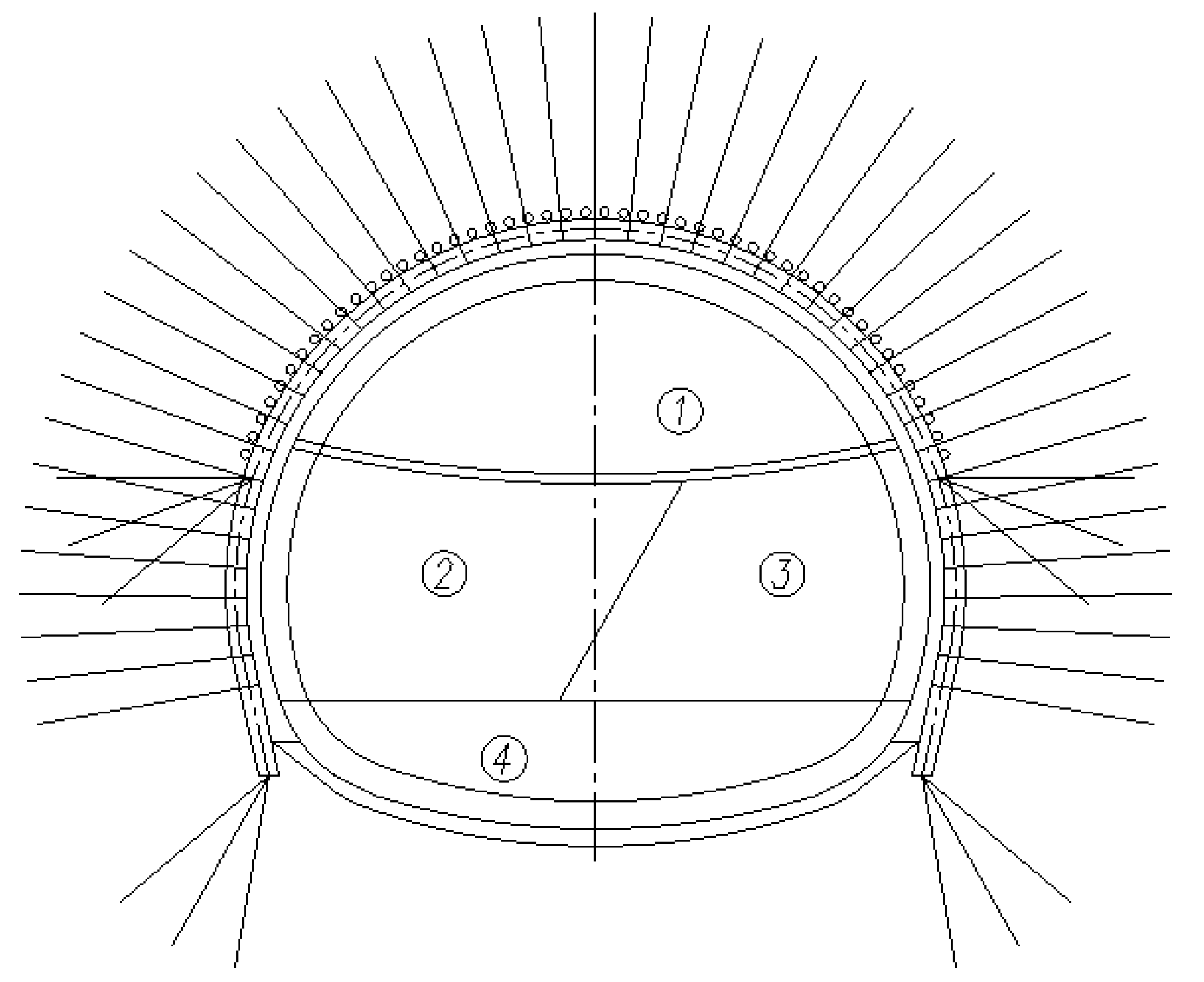
2.3.1. Parameter Delineation
2.3.2. Boundary Conditions
2.3.3. Excavation Process Simulation
2.4. Analysis Method of the Cause and Distribution of Cracks
3. Results
3.1. On-Site Crack Investigation
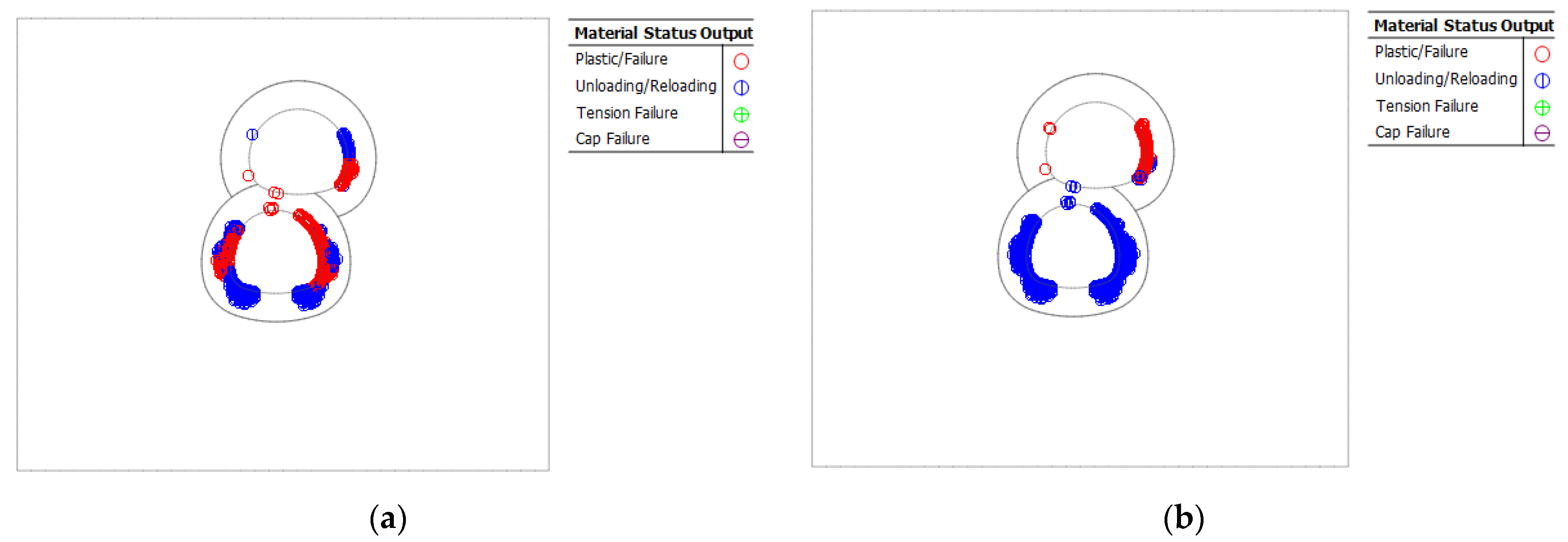
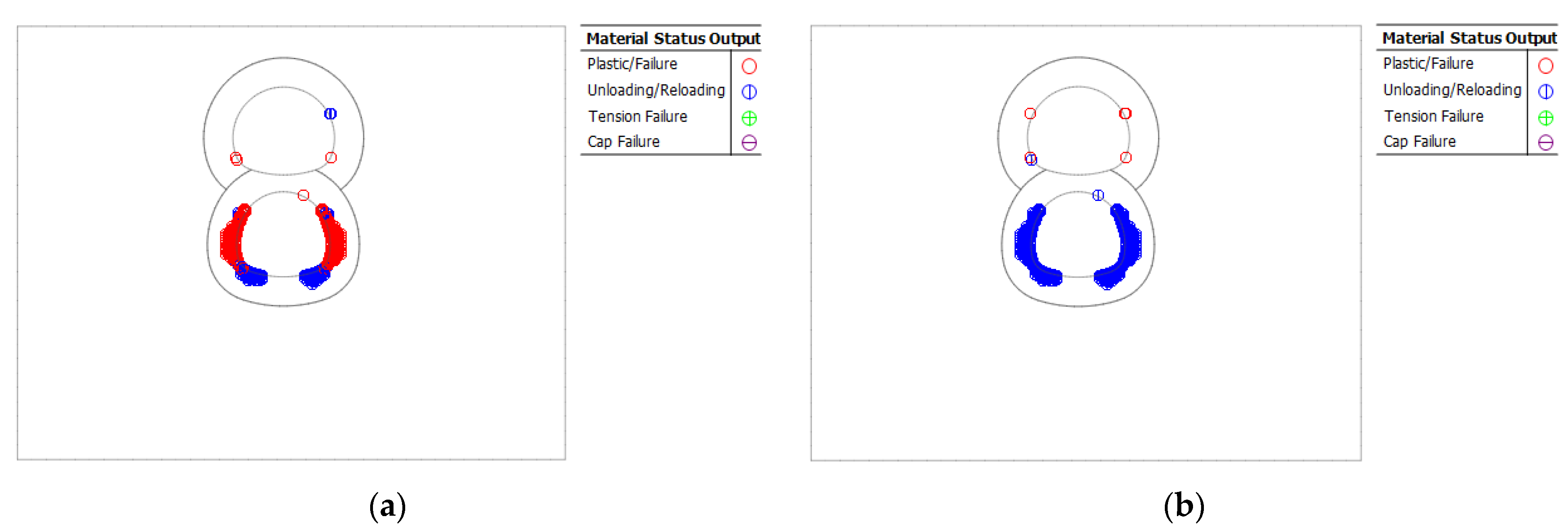
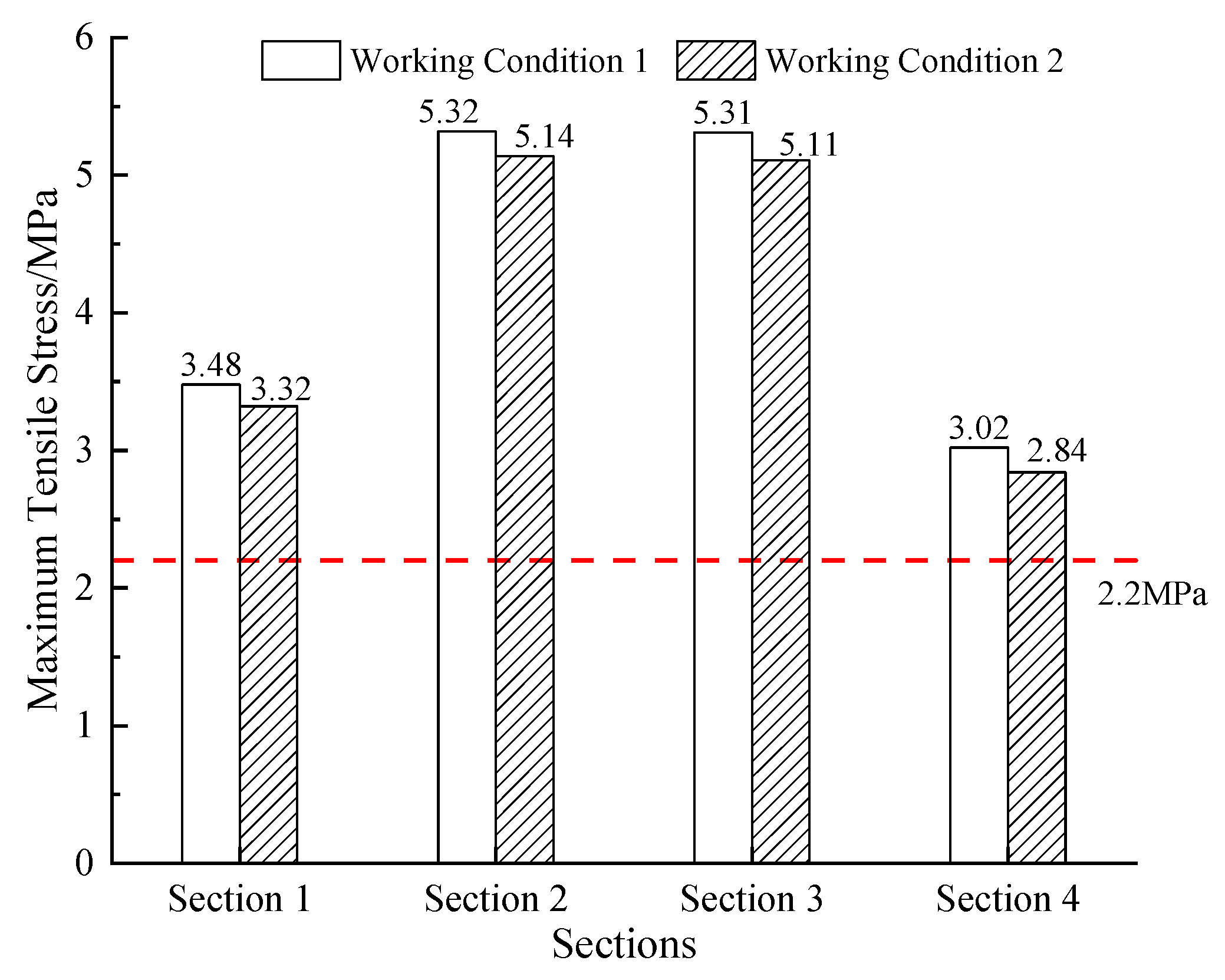
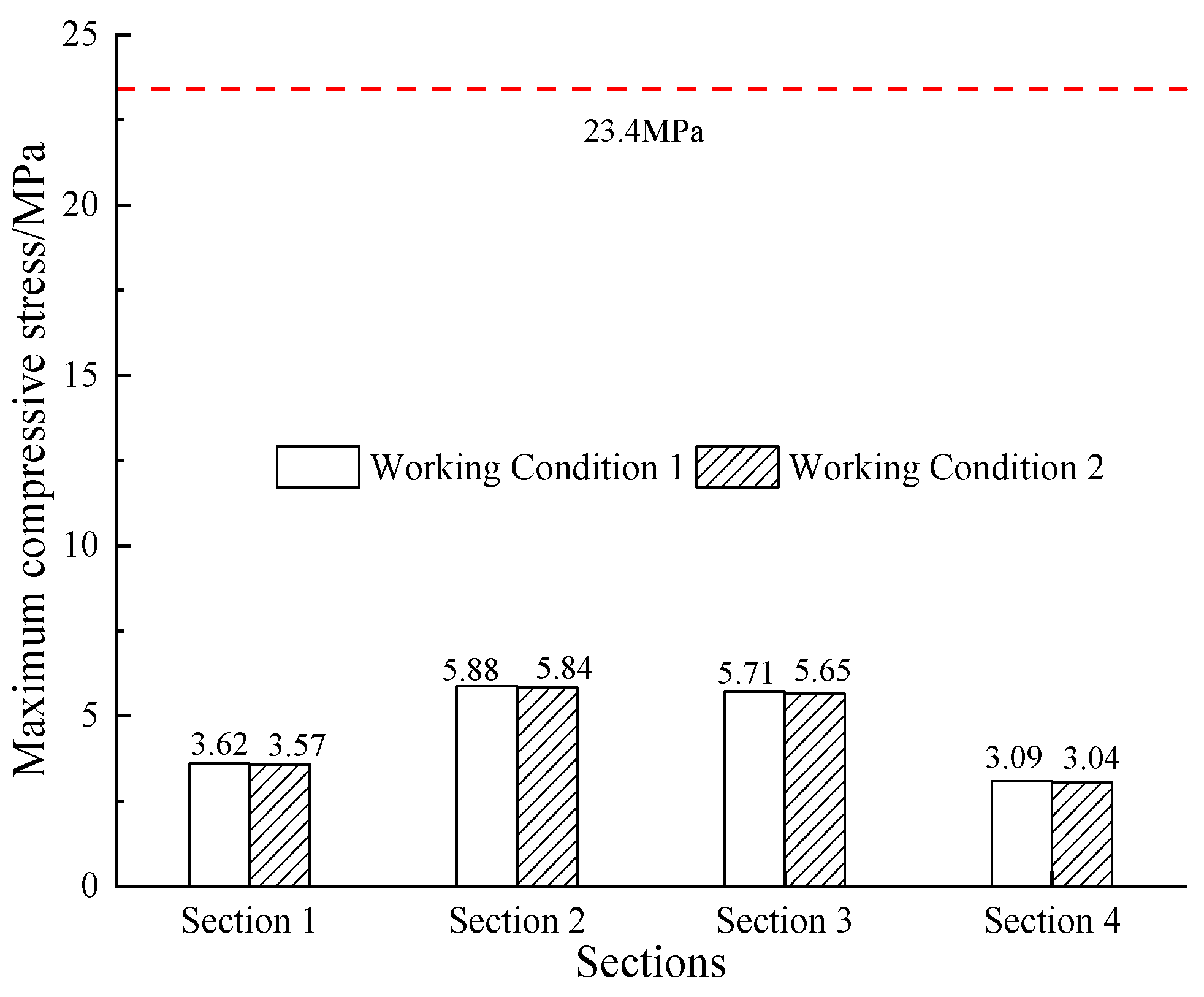
3.2. Calculation of Stress and Plastic Zone
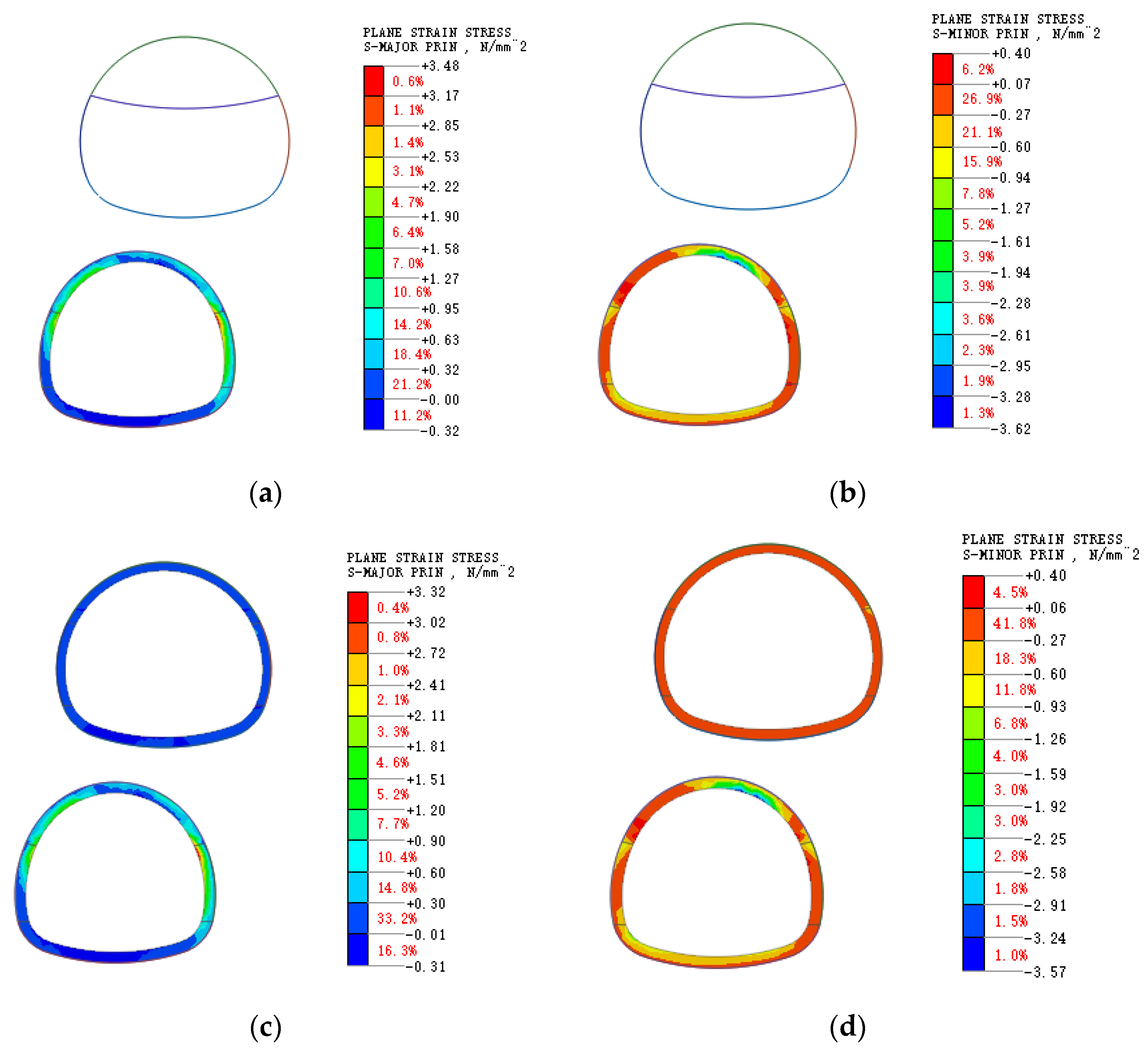
3.2.1. Stress Distribution
3.2.2. Plastic Zone Distribution
4. Discussion
4.1. Statistics on the on-Site Distribution of Cracks
4.2. Discussions on the Theoretical Causes and Distribution of Cracks
4.3. Suggestions on Cracks in the Secondary Lining
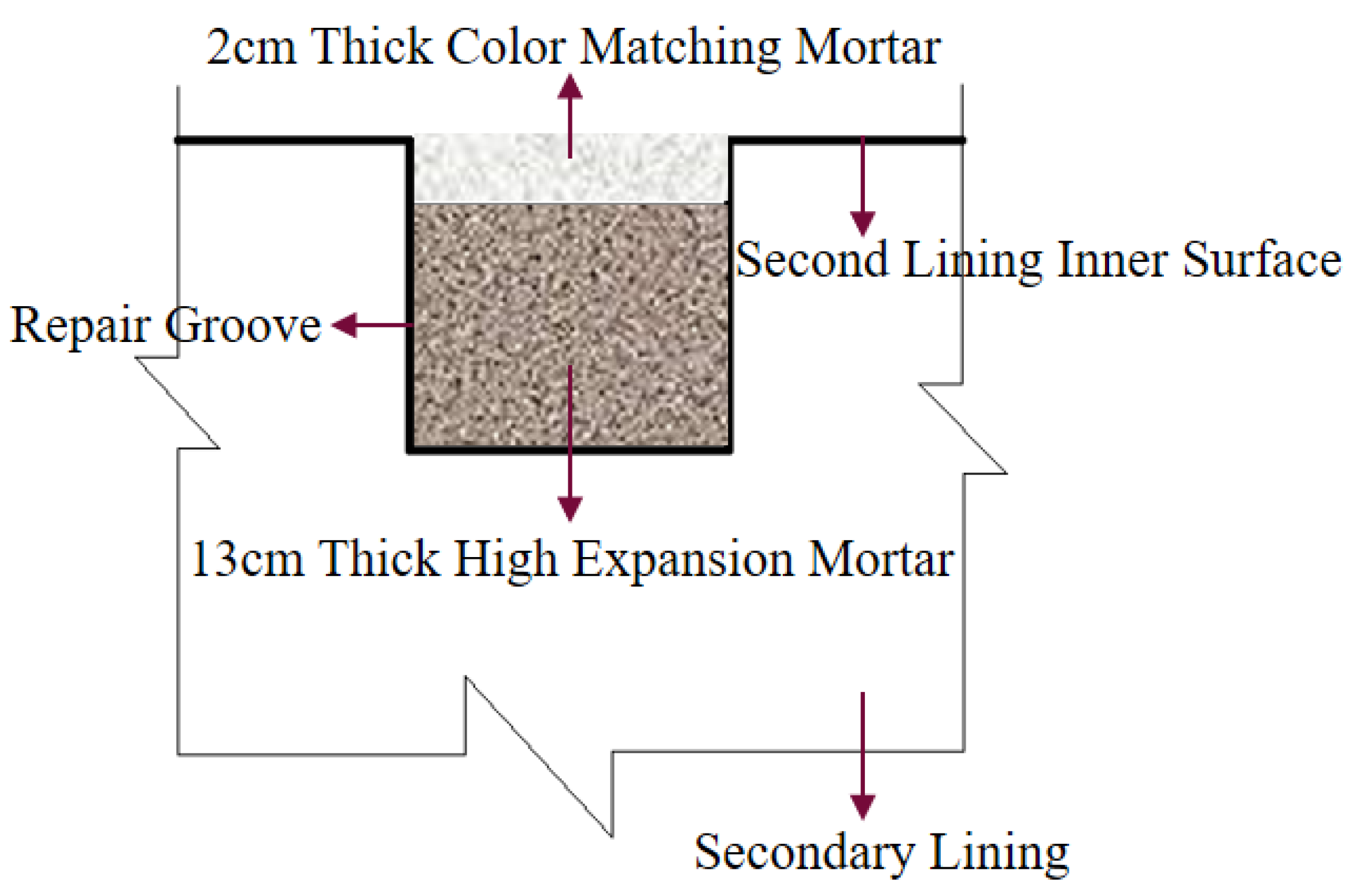
4.3.1. Tunnel Crack Treatment Measures
4.3.2. Suggestions for the Treatment of Cracks in the Lower Tunnel
4.4. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tonon, F. Sequential excavation, NATM and ADECO: What they have in common and how they differ. Tunn. Undergr. Space Technol. 2010, 25, 245–265. [Google Scholar] [CrossRef]
- Xu, G.; He, C.; Chen, Z.; Liu, C.; Wang, B.; Zou, Y. Mechanical behavior of secondary tunnel lining with longitudinal crack. Eng. Fail. Anal. 2020, 113, 104543. [Google Scholar] [CrossRef]
- Zhu, C.; Karakus, M.; He, M.; Meng, Q.; Shang, J.; Wang, Y.; Yin, Q. Volumetric deformation and damage evolution of Tibet interbedded skarn under multistage constant-amplitude-cyclic loading. Int. J. Rock Mech. Min. Sci. 2022, 152, 105066. [Google Scholar] [CrossRef]
- Lai, J.; Qiu, J.; Fan, H.; Chen, J.; Hu, Z.; Zhang, Q.; Wang, J. Structural Safety Assessment of Existing Multiarch Tunnel: A Case Study. Adv. Mater. Sci. Eng. 2017, 2017, 1697041. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, C.; Zhou, H.; Liu, N.; Zhang, Y.; Azhar, M.U.; Dai, F. The long-term safety of a deeply buried soft rock tunnel lining under inside-to-outside seepage conditions. Tunn. Undergr. Space Technol. 2017, 67, 132–146. [Google Scholar] [CrossRef]
- Fang, Y.; Guo, J.; Grasmick, J.; Mooney, M. The effect of external water pressure on the liner behavior of large cross-section tunnels. Tunn. Undergr. Space Technol. 2016, 60, 80–95. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, L.; Zhu, H.; Gong, Z.; Liu, J.; Zhu, Y. Laboratory tests on conditioning the sandy cobble soil for EPB shield tunnelling and its field application. Tunn. Undergr. Space Technol. 2020, 105, 103512. [Google Scholar] [CrossRef]
- Yun, H.-B.; Park, S.-H.; Mehdawi, N.; Mokhtari, S.; Chopra, M.; Reddi, L.N.; Park, K.-T. Monitoring for close proximity tunneling effects on an existing tunnel using principal component analysis technique with limited sensor data. Tunn. Undergr. Space Technol. 2014, 43, 398–412. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, M. Geotechnical influence on existing subway tunnels induced by multiline tunneling in Shanghai soft soil. Comput. Geotech. 2014, 56, 121–132. [Google Scholar] [CrossRef]
- Liang, Q.; Li, J.; Li, D.; Ou, E. Effect of Blast-Induced Vibration from New Railway Tunnel on Existing Adjacent Railway Tunnel in Xinjiang, China. Rock Mech. Rock Eng. 2013, 46, 19–39. [Google Scholar] [CrossRef]
- Ukritchon, B.; Yingchaloenkitkhajorn, K.; Keawsawasvong, S. Three-dimensional undrained tunnel face stability in clay with a linearly increasing shear strength with depth. Comput. Geotech. 2017, 88, 146–151. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, J.; Lin, B. Study on calculation of rock pressure for ultra-shallow tunnel in poor surrounding rock and its tunneling procedure. J. Mod. Transp. 2014, 22, 1–11. [Google Scholar] [CrossRef]
- Xiao, J.Z.; Dai, F.C.; Wei, Y.Q.; Xing, Y.C.; Cai, H.; Xu, C. Analysis of mechanical behavior in a pipe roof during excavation of a shallow bias tunnel in loose deposits. Environ. Earth Sci. 2016, 75, 293. [Google Scholar] [CrossRef]
- Yang, C.; Hu, Z.; Huang, D.; Guo, F. Failure Mechanism of Primary Support for a Shallow and Asymmetrically Loaded Tunnel Portal and Treatment Measures. J. Perform. Constr. Facil. 2020, 34, 04019105. [Google Scholar] [CrossRef]
- Kong, C.; Gao, X.; Cao, L.; Liu, K. Analysis of the failure of primary support of a deep-buried railway tunnel in silty clay. Eng. Fail. Anal. 2016, 66, 259–273. [Google Scholar] [CrossRef]
- Yang, C.; Zhang, Y.-X.; Huang, D.; Zhu, Q. Deformation Behavior of Topographic Unsymmetrical Loaded Tunnels and Their Pre-Reinforcements after Excavation. J. Highw. Transp. Res. Dev. 2013, 7, 69–75. [Google Scholar] [CrossRef]
- Zhou, Y.-Y.; Feng, X.-T.; Xu, D.-P.; Fan, Q.-X. An enhanced equivalent continuum model for layered rock mass incorporating bedding structure and stress dependence. Int. J. Rock Mech. Min. Sci. 2017, 97, 75–98. [Google Scholar] [CrossRef]
- Simanjuntak, T.; Marence, M.; Mynett, A.; Schleiss, A. Pressure tunnels in non-uniform in situ stress conditions. Tunn. Undergr. Space Technol. 2014, 42, 227–236. [Google Scholar] [CrossRef]
- Lei, M.; Peng, L.; Shi, C. Model test to investigate the failure mechanisms and lining stress characteristics of shallow buried tunnels under unsymmetrical loading. Tunn. Undergr. Space Technol. 2015, 46, 64–75. [Google Scholar] [CrossRef]
- Rosso, M.M.; Marasco, G.; Aiello, S.; Aloisio, A.; Chiaia, B.; Marano, G.C. Convolutional networks and transformers for intelligent road tunnel investigations. Comput. Struct. 2023, 275, 106918. [Google Scholar] [CrossRef]
- Marano, G.C.; Rosso, M.M.; Aloisio, A.; Cirrincione, G. Generative adversarial networks review in earthquake-related engineering fields. Bull. Earthq. Eng. 2023, 1–52. [Google Scholar] [CrossRef]
- Ngamkhanong, C.; Keawsawasvong, S.; Jearsiripongkul, T.; Cabangon, L.T.; Payan, M.; Sangjinda, K.; Banyong, R.; Thongchom, C. Data-Driven Prediction of Stability of Rock Tunnel Heading: An Application of Machine Learning Models. Infrastructures 2022, 7, 148. [Google Scholar] [CrossRef]
- Yuan, F.; Liu, Y.; Xu, Q.; Zheng, Y.; Hu, L.; Zhao, P.; Cui, Y. Study on Mechanical Characteristics and Construction Control of the Railway Overlapping Tunnels. Front. Earth Sci. 2022, 10, 721. [Google Scholar] [CrossRef]
- Li, G.; Zhu, C.; He, M.; Zuo, Y.; Gong, F.; Xue, Y.; Feng, G. Intelligent method for parameters optimization of cable in soft rock tunnel base on longitudinal wave velocity. Tunn. Undergr. Space Technol. 2023, 133, 104905. [Google Scholar] [CrossRef]
- Ren, F.; Zhu, C.; He, M.; Shang, J.; Feng, G.; Bai, J. Characteristics and Precursor of Static and Dynamic Triggered Rockburst: Insight from Multifractal. Rock Mech. Rock Eng. 2023, 56, 1945–1967. [Google Scholar] [CrossRef]
- Qu, Z.; Chen, S.Q.; Liu, Y.Q.; Liu, L. Linear seam elimination of tunnel crack images based on statistical specific pixels ratio and adaptive fragmented segmentation. IEEE Trans. Intell. Transp. Syst. 2020, 21, 3599–3607. [Google Scholar] [CrossRef]

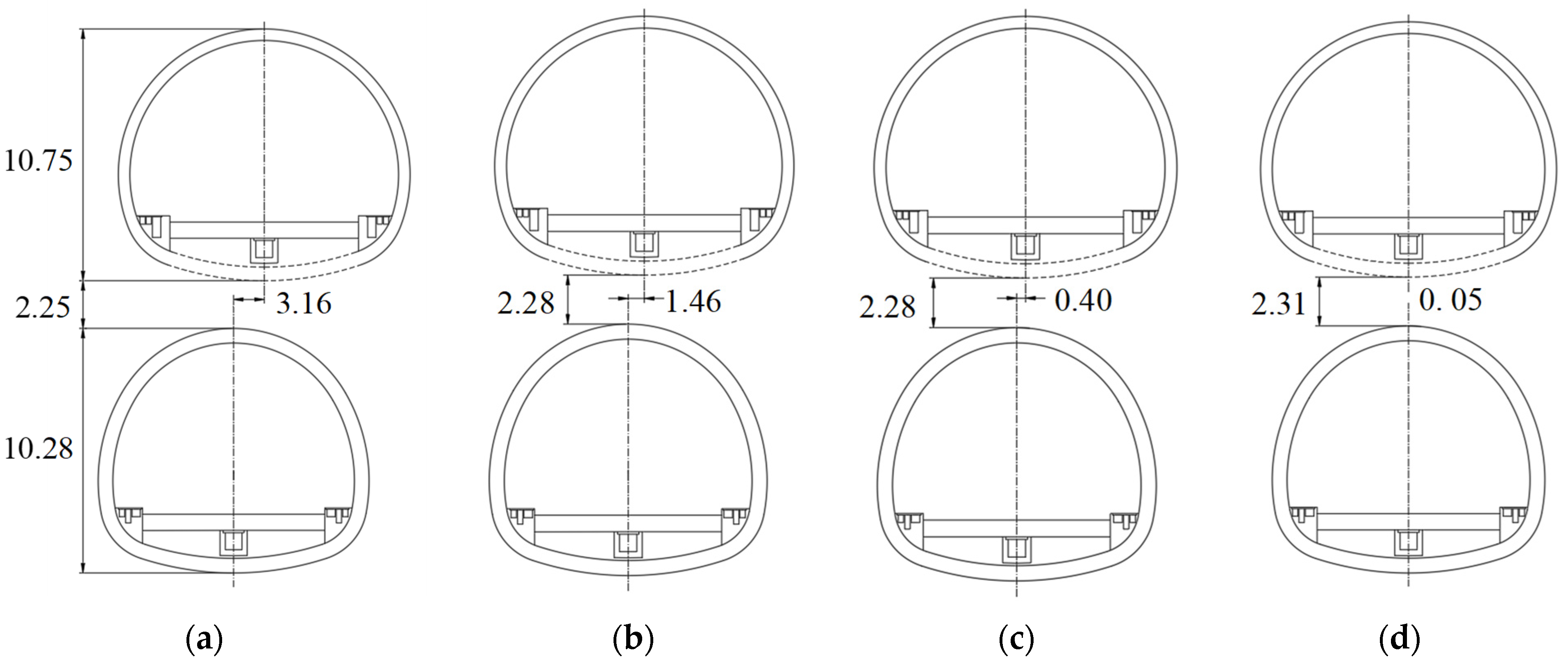




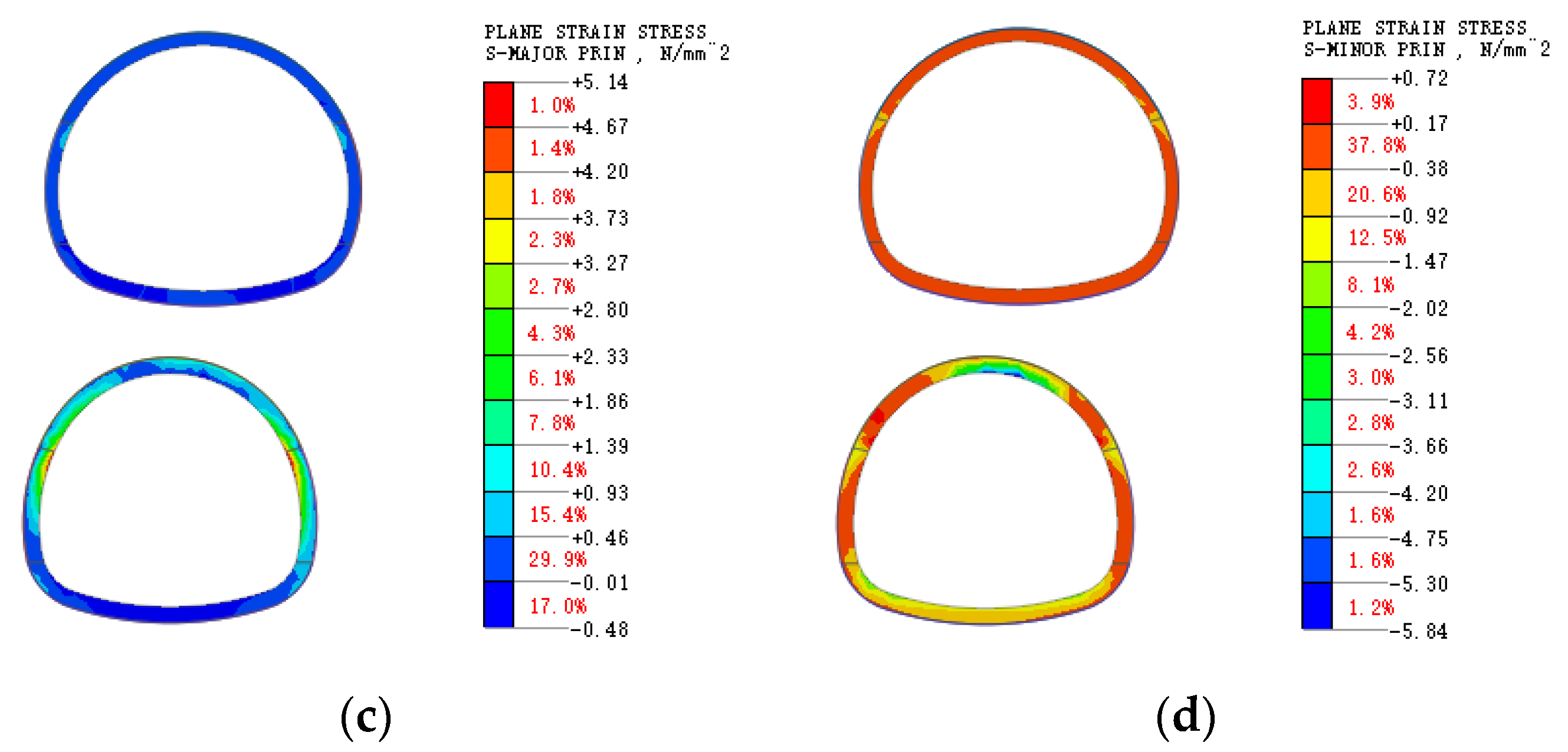

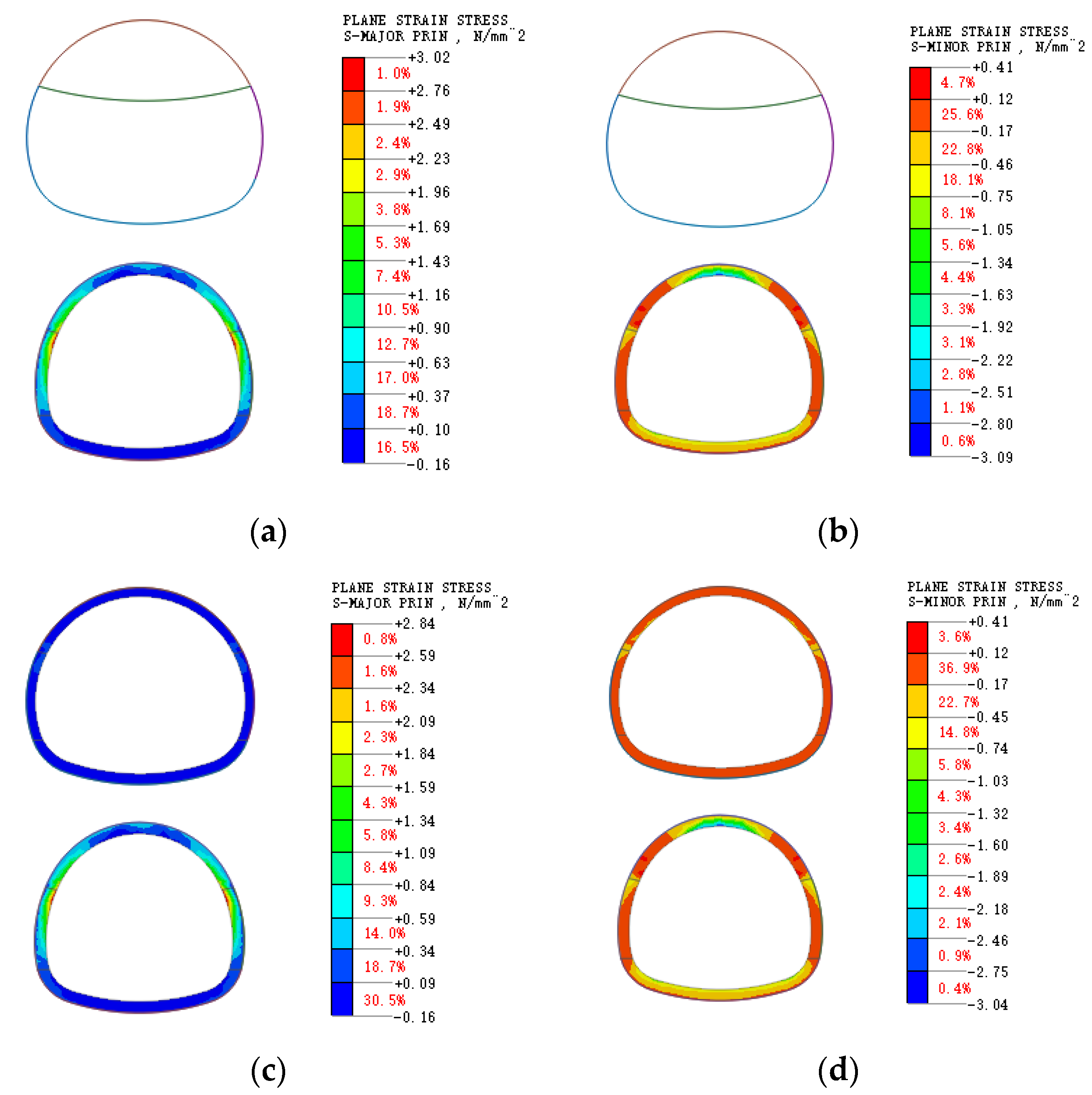


| Category | Section 1 | Section 2 | Section 3 | Section 4 |
|---|---|---|---|---|
| Mileage | DK63 + 900 | DK63 + 950 | DK64 + 000 | DK64 + 050 |
| Buried depth of upper tunnel (m) | 12.8 | 26.6 | 25.8 | 8.3 |
| The vertical distance between upper and lower tunnels (m) | 2.25 | 2.28 | 2.28 | 2.31 |
| The horizontal distance between upper and lower tunnels (m) | 3.16 | 1.46 | 0.4 | 0.05 |
| Category | Section 1 | Section 2 | Section 3 | Section 4 |
|---|---|---|---|---|
| Mileage | DK63 + 900 | DK63 + 950 | DK64 + 000 | DK64 + 050 |
| Length of the model (m) | 75 | 75 | 75 | 75 |
| Height of the model (m) | 65 | 80 | 75 | 60 |
| Material Name | Gravity (kN/m3) | Poisson Ratio | Cohesion (kPa) | Internal Friction Angle (°) | Deformation Modulus (GPa) |
|---|---|---|---|---|---|
| Grade V surrounding rock | 26 | 0.42 | 160 | 24.5 | 1.65 |
| Bolt reinforcement area | 28.6 | 0.42 | 176.0 | 27.0 | 1.8 |
| C25 concrete | 25 | 0.2 | / | / | 28 |
| C35 concrete | 25 | 0.2 | / | / | 31.5 |
| Steel | 78.5 | 0.25 | / | / | 200 |
| Working Condition | Construction Content | Remarks |
|---|---|---|
| 1 | Initial ground stress | Activating of all soil elements and application of boundary conditions and gravity loads. |
| 2 | Displacement clearing | / |
| 3 | Construction of the lower tunnel | Excavating the hole ①, spraying the area with mix and anchors and constructing temporary cross bracing. |
| 4 | Construction of the lower tunnel | Excavating the cave ②, spraying the area with the mix, and anchoring the rods. |
| 5 | Construction of the lower tunnel | Excavating the cave ③, spraying the area with the mix, and anchoring the rods. |
| 6 | Construction of the lower tunnel | Excavating the cave ④, spraying the area with the mix, and anchoring the rods. |
| 7 | Construction of the lower tunnel | Construction of secondary lining and removal of temporary cross bracings. |
| 8 | Construction of the upper tunnel | Excavating the cave ①, spraying the area with the mix, and anchoring the rods. |
| 9 | Construction of the upper tunnel | Excavating the cave ②, spraying the area with the mix, and anchoring the rods. |
| 10 | Construction of the upper tunnel | Excavating the cave ③, spraying the area with the mix, and anchoring the rods. |
| 11 | Construction of the upper tunnel | Excavating the cave ④, spraying the area with the mix, and anchoring the rods. |
| 12 | Construction of the upper tunnel | Construction of secondary lining and removal of temporary cross bracings. |
| Mileage | Crack Length (m) | Crack Width (mm) | Maximum Crack Depth (cm) | Crack Type |
|---|---|---|---|---|
| DK63 + 905 | 12 | 0.3 | 11.8 | Longitudinal direction |
| DK63 + 905 | 12 | 0.2 | 7.7 | Longitudinal direction |
| DK63 + 932 | 12 | 0.3 | 9 | Longitudinal direction |
| DK63 + 933 | 12 | 0.3 | 10.9 | Longitudinal direction |
| DK63 + 936 | 12 | 0.4 | 11.9 | Longitudinal direction |
| DK63 + 934.5 | 12 | 0.2 | 12.5 | Longitudinal direction |
| DK63 + 934.5 | 12 | 0.3 | 11.2 | Longitudinal direction |
| DK64 + 140 | 2 | 0.3 | 7.8 | Circumferential direction |
| DK64 + 026 | 12 | 0.3 | 8.4 | Longitudinal direction |
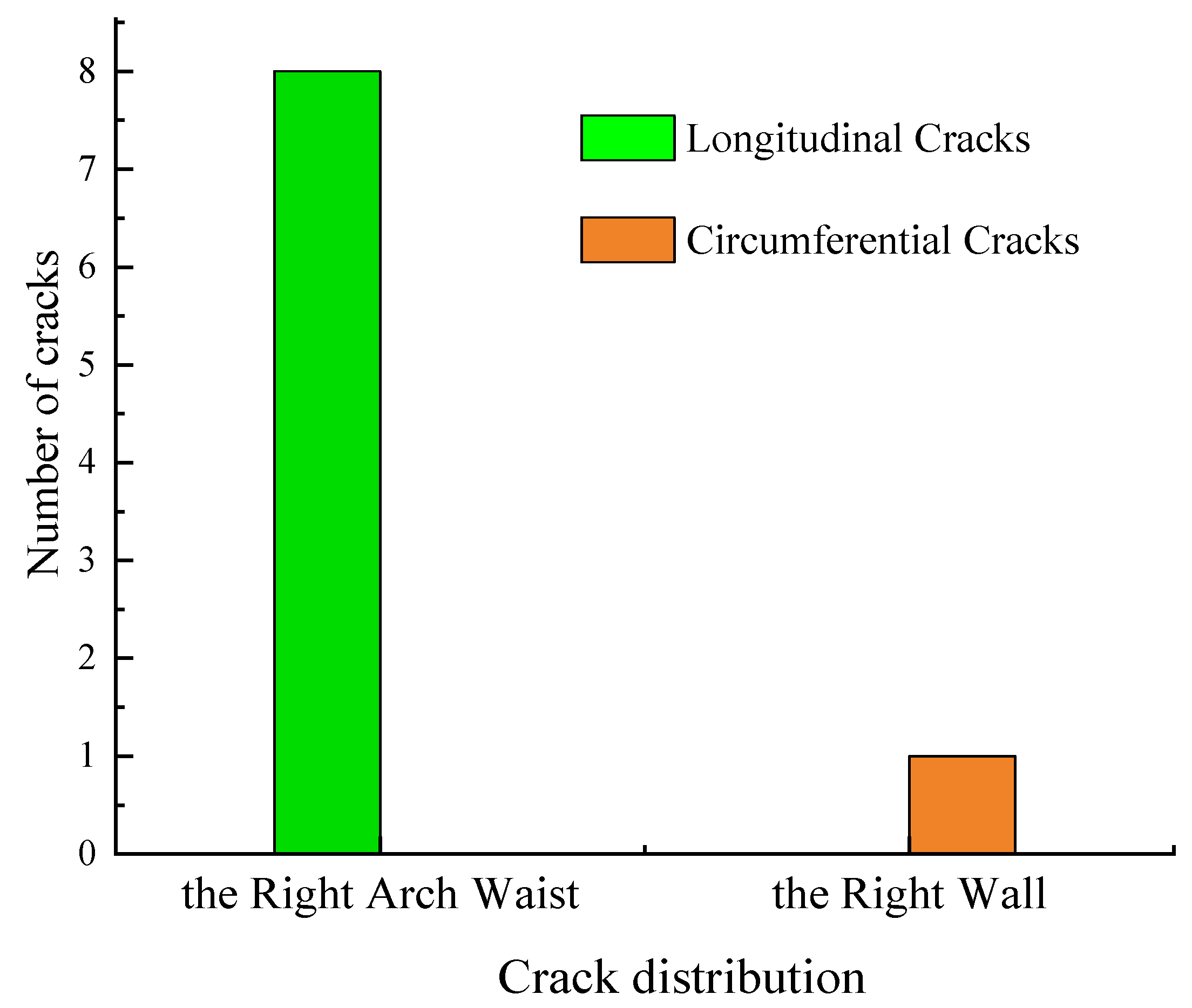
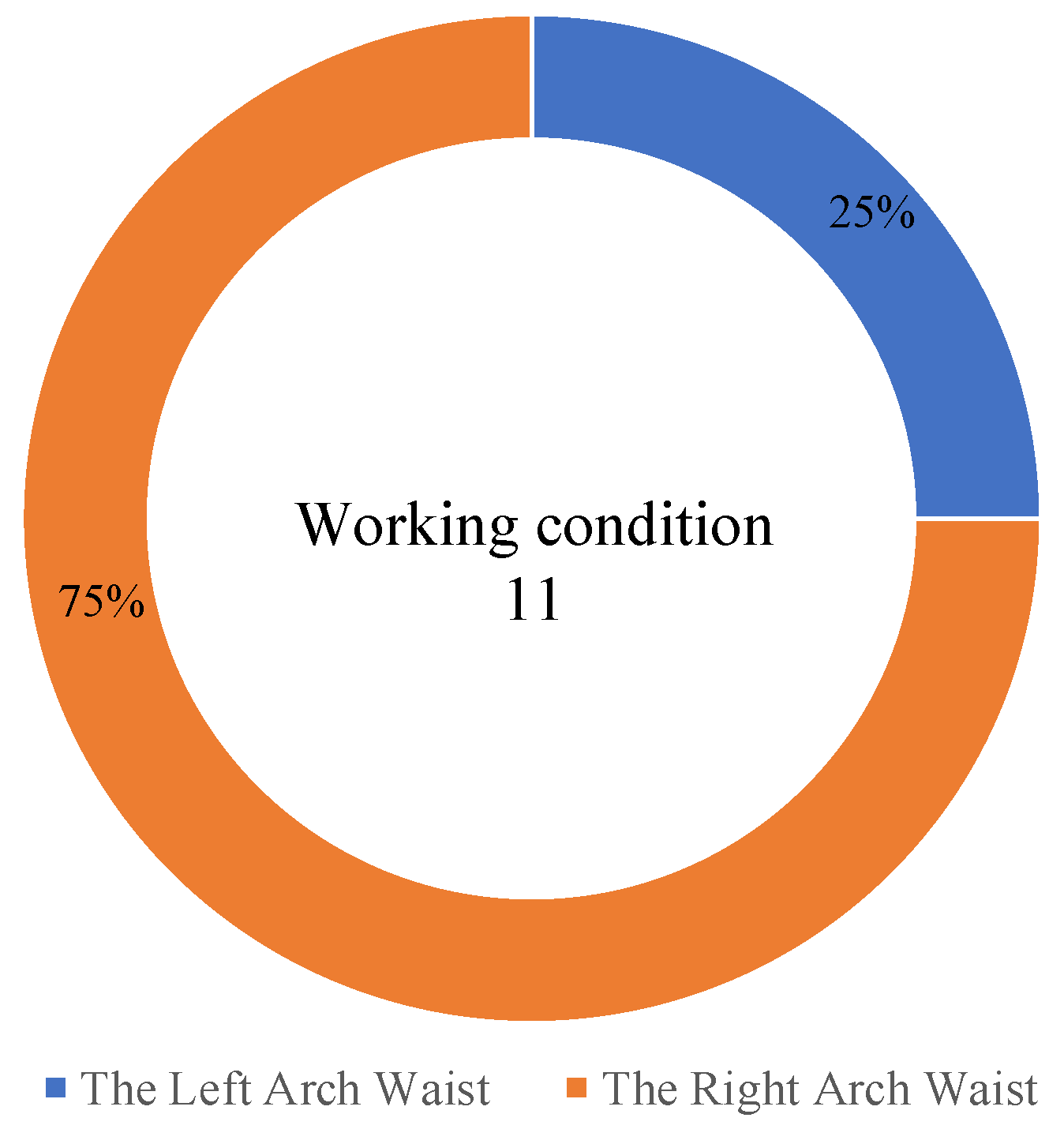
| Crack Type | Proportion/Number of Articles | Location | Proportion/Number of Articles |
|---|---|---|---|
| Longitudinal | 88.89%/8 | Right arch waist | 100%/8 |
| Circumferential | 11.11%/1 | Right side wall | 100%/1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Q.; Xie, J.; Zhou, F.; Tang, Z. Numerical Simulation and Analysis of the Causes and Distribution of Secondary Lining Cracks in Overlapping Railway Tunnels. Appl. Sci. 2023, 13, 6436. https://doi.org/10.3390/app13116436
Xu Q, Xie J, Zhou F, Tang Z. Numerical Simulation and Analysis of the Causes and Distribution of Secondary Lining Cracks in Overlapping Railway Tunnels. Applied Sciences. 2023; 13(11):6436. https://doi.org/10.3390/app13116436
Chicago/Turabian StyleXu, Qianwei, Jinli Xie, Feng Zhou, and Zhuohua Tang. 2023. "Numerical Simulation and Analysis of the Causes and Distribution of Secondary Lining Cracks in Overlapping Railway Tunnels" Applied Sciences 13, no. 11: 6436. https://doi.org/10.3390/app13116436
APA StyleXu, Q., Xie, J., Zhou, F., & Tang, Z. (2023). Numerical Simulation and Analysis of the Causes and Distribution of Secondary Lining Cracks in Overlapping Railway Tunnels. Applied Sciences, 13(11), 6436. https://doi.org/10.3390/app13116436





