Numerical Study on Cooling Performance of a Steam-Cooled Blade Based on Response Surface Method
Abstract
:1. Introduction
2. Numerical Methods
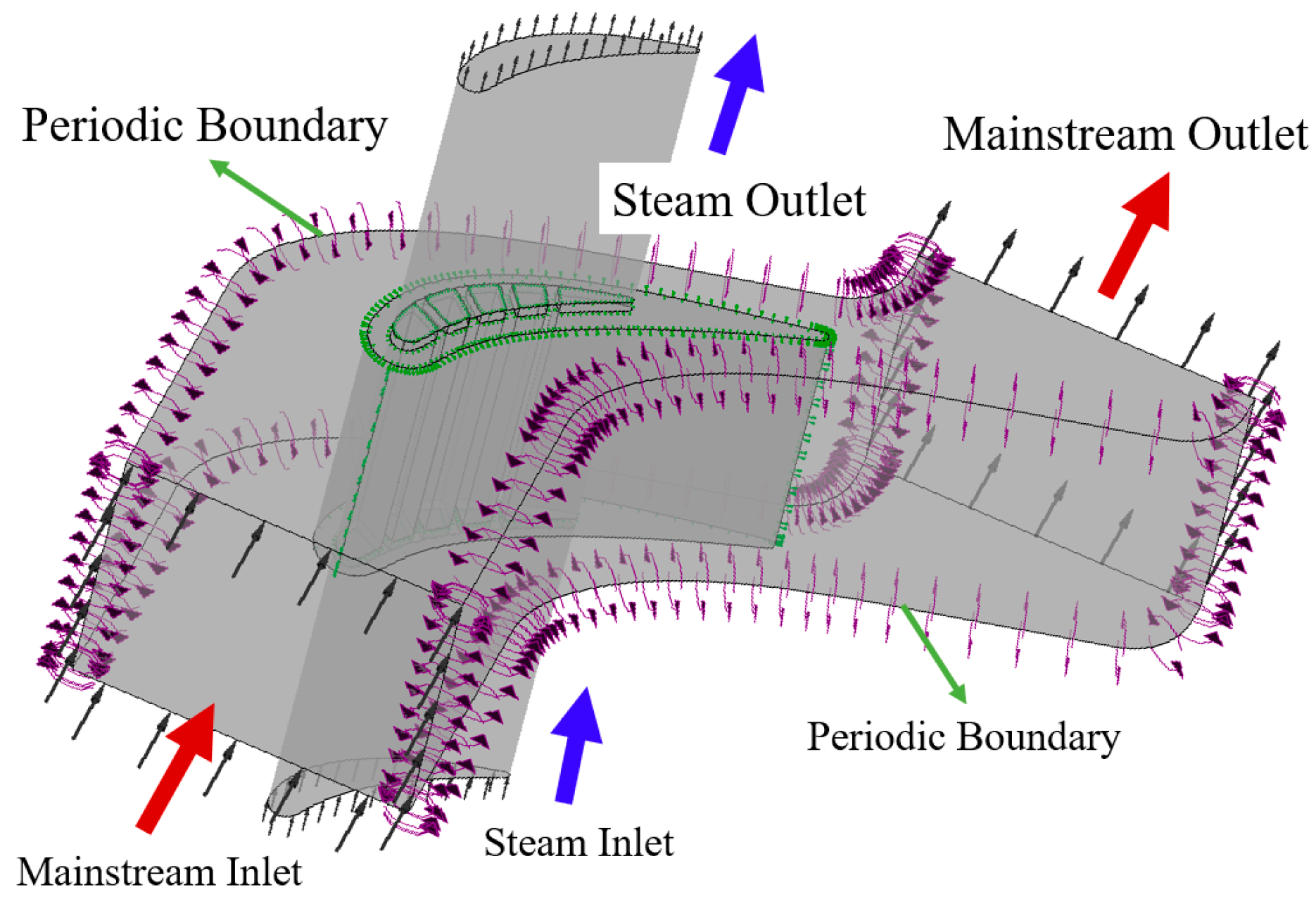
2.1. Subsection Physical Model
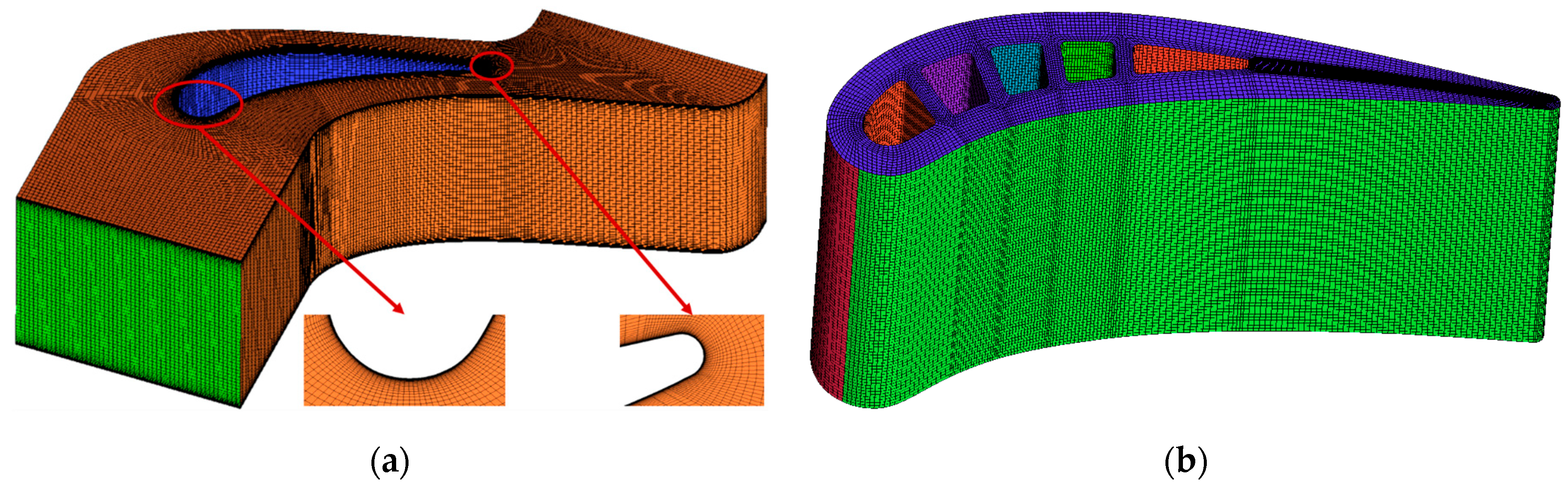
2.2. Numerical Methods
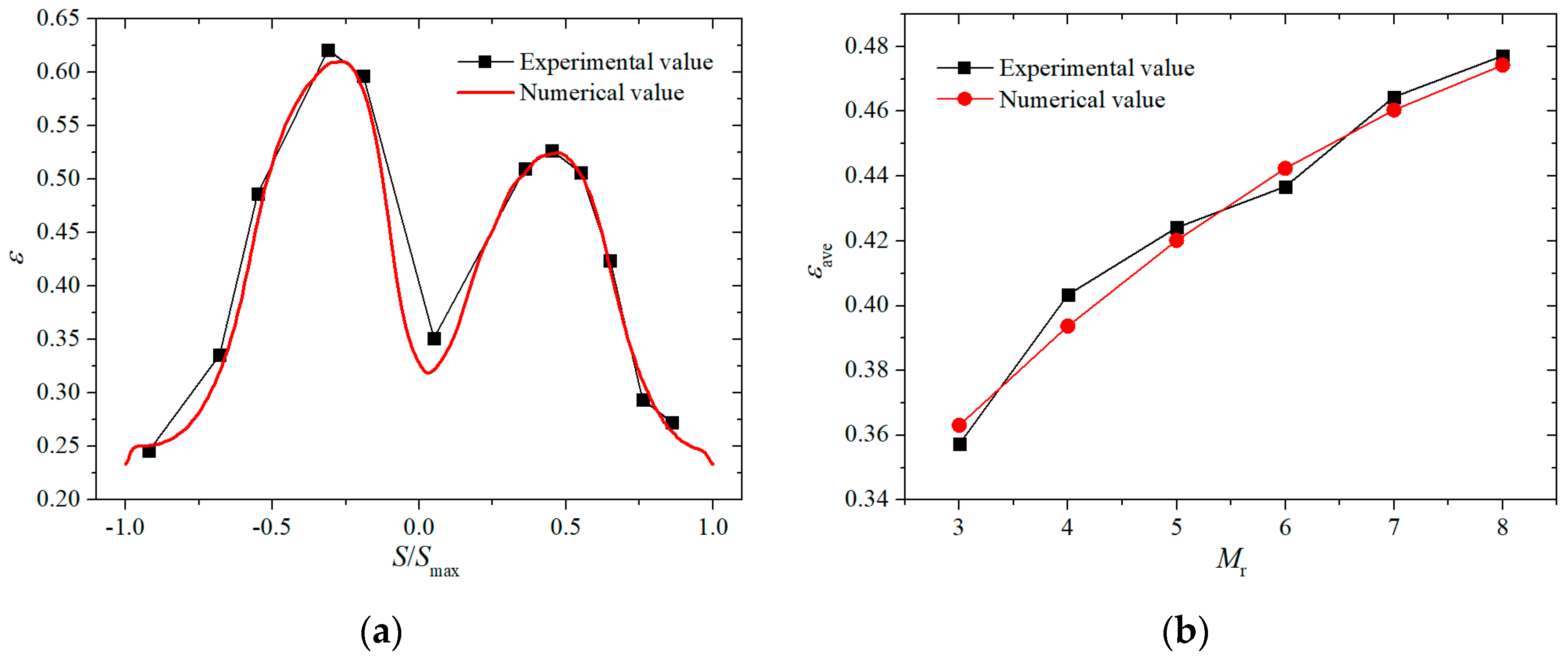
2.3. Numerical Verification
2.4. Data Reduction
3. Effect of Working Parameters on the Cooling Performance of the Blade
3.1. Influence of Mainstream Inlet Temperature
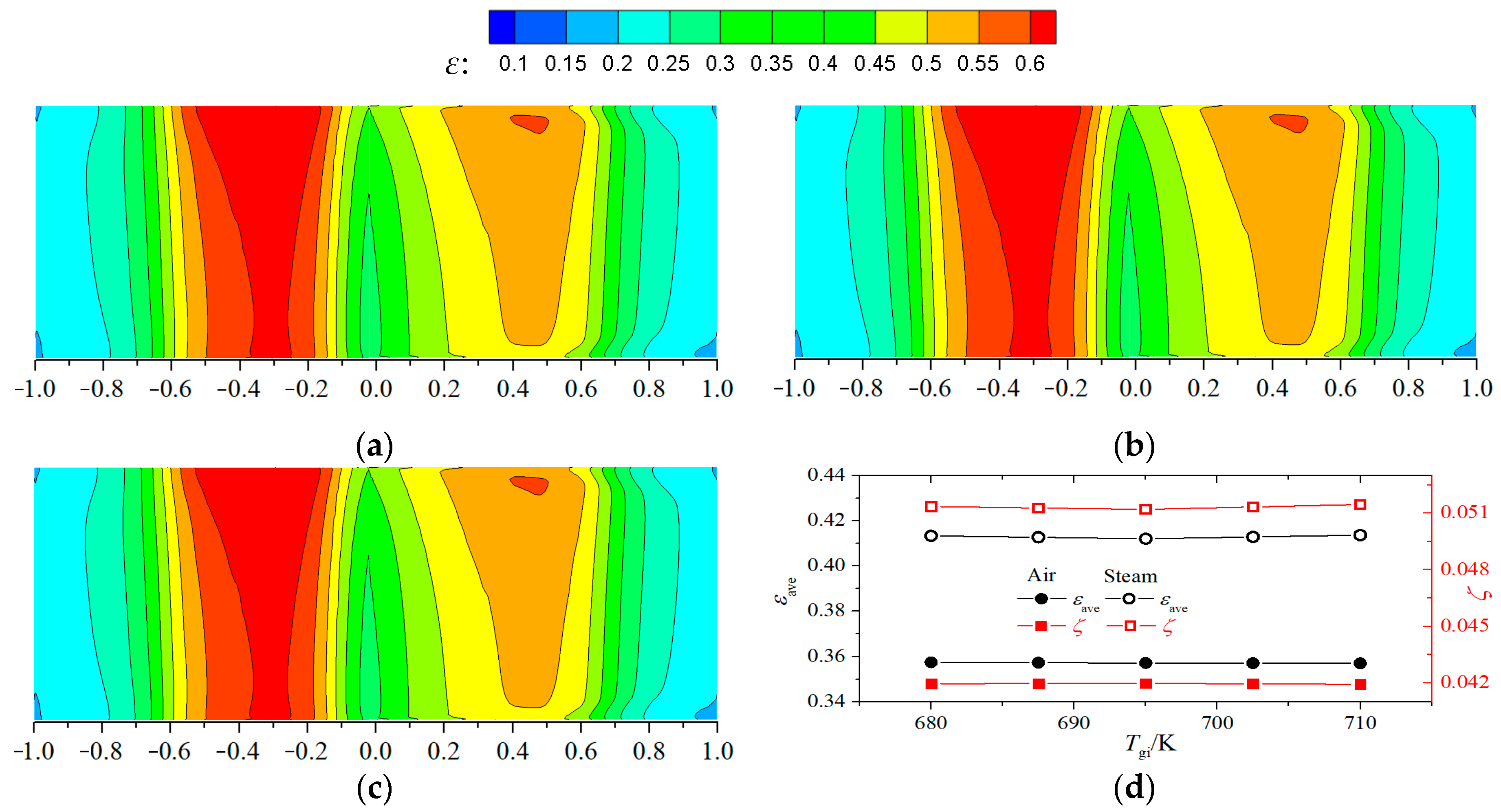

3.2. Influence of Mainstream Outlet Pressure
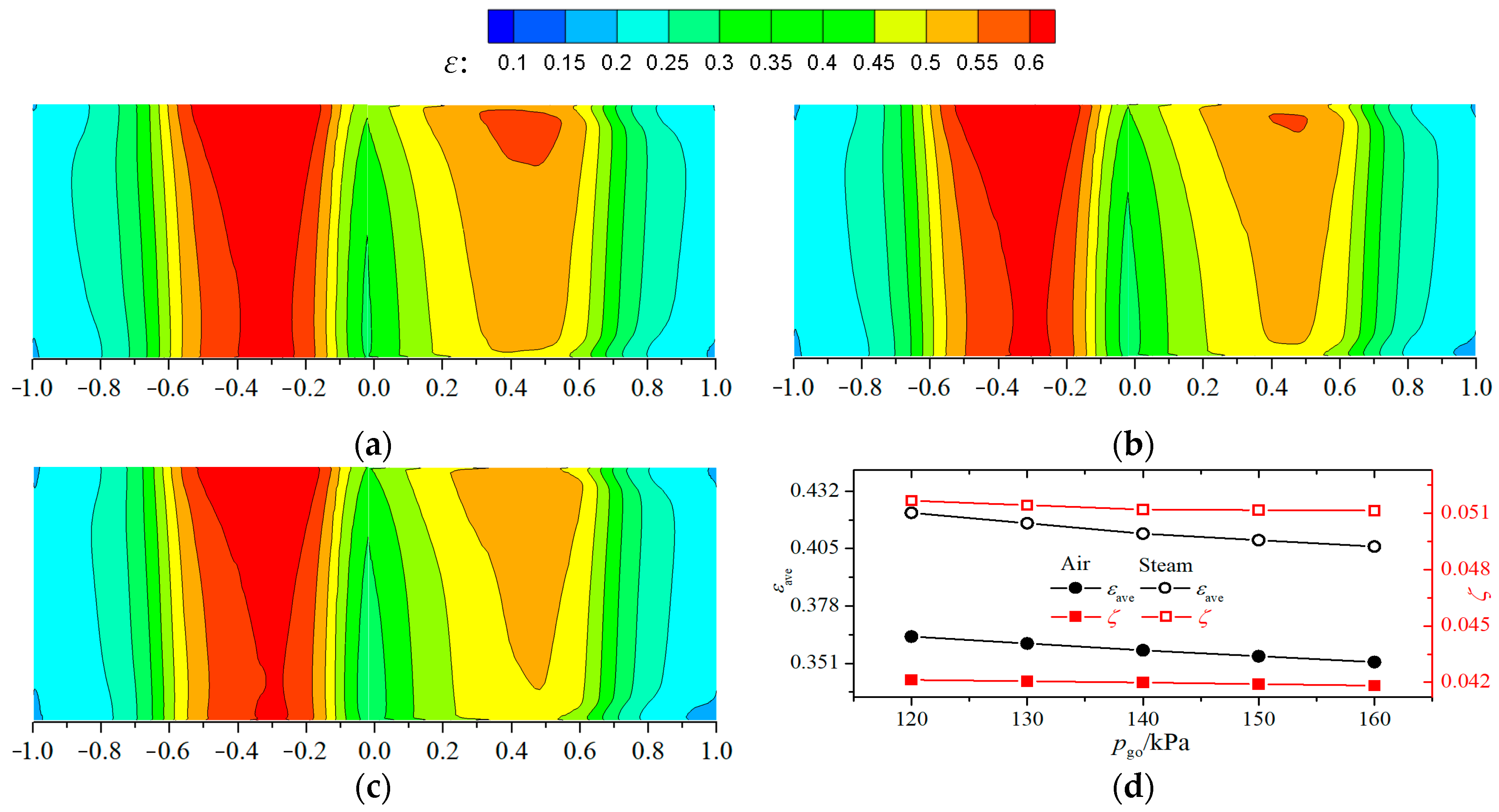


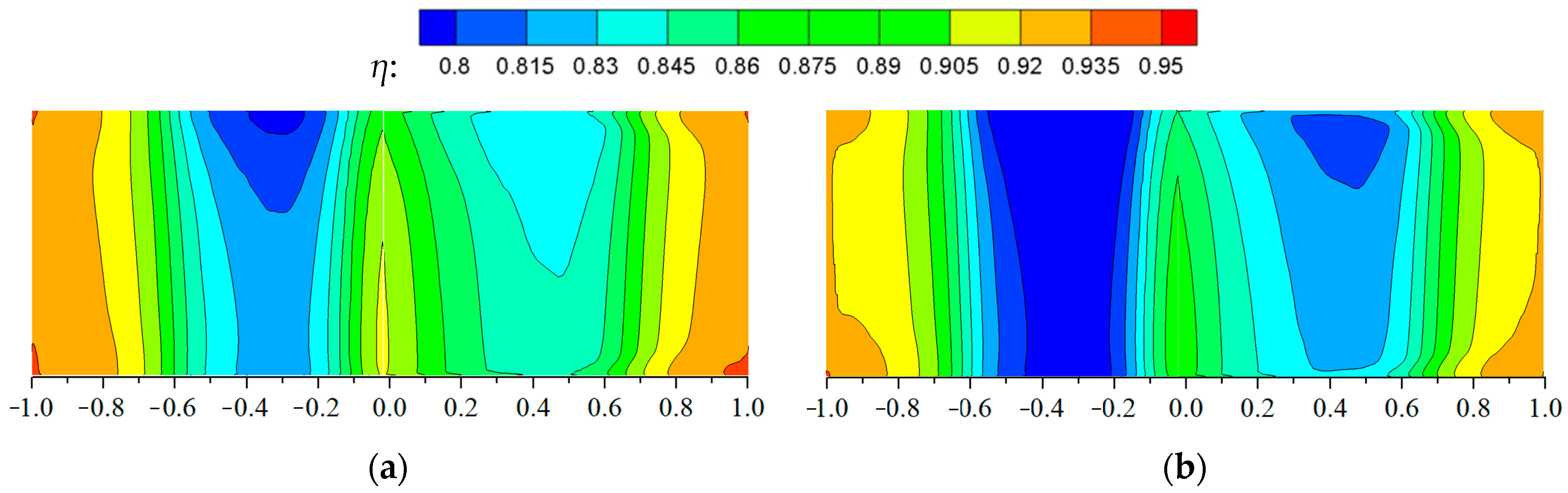
3.3. Influence of Mainstream Inlet to Outlet Pressure Ratio
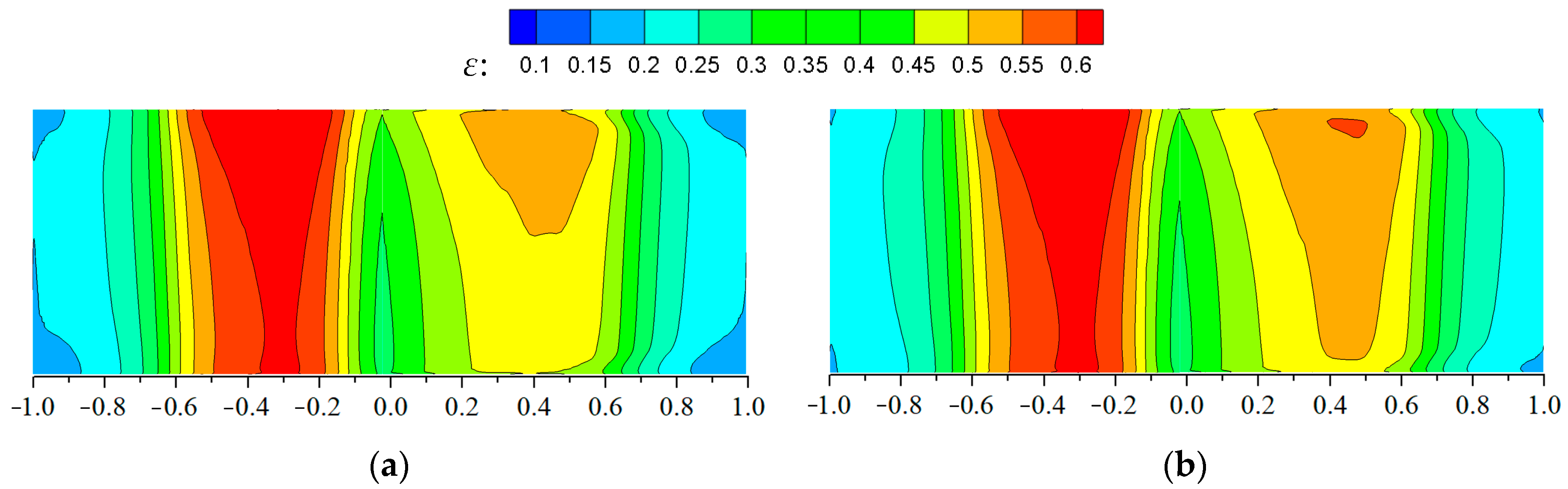
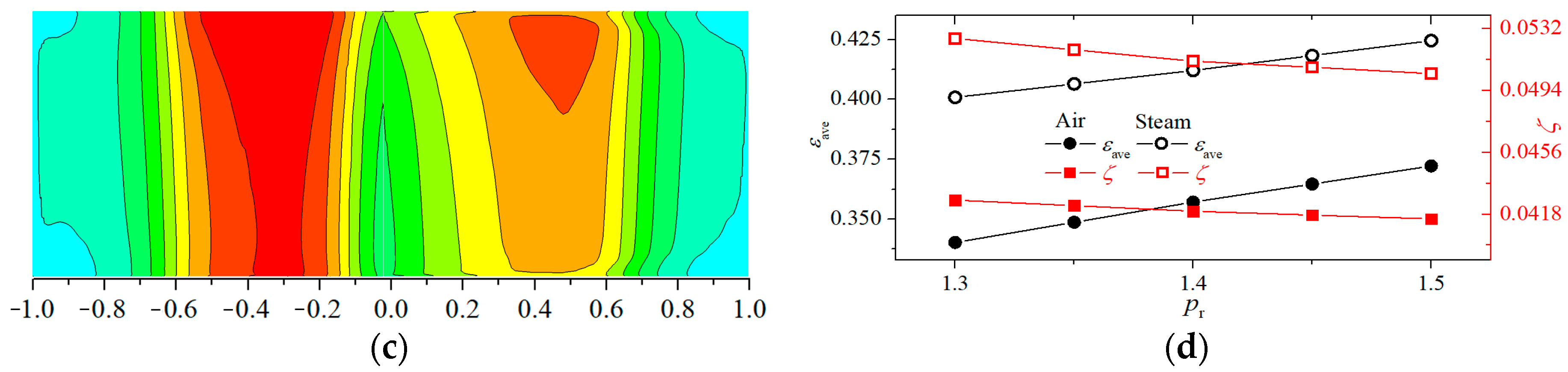
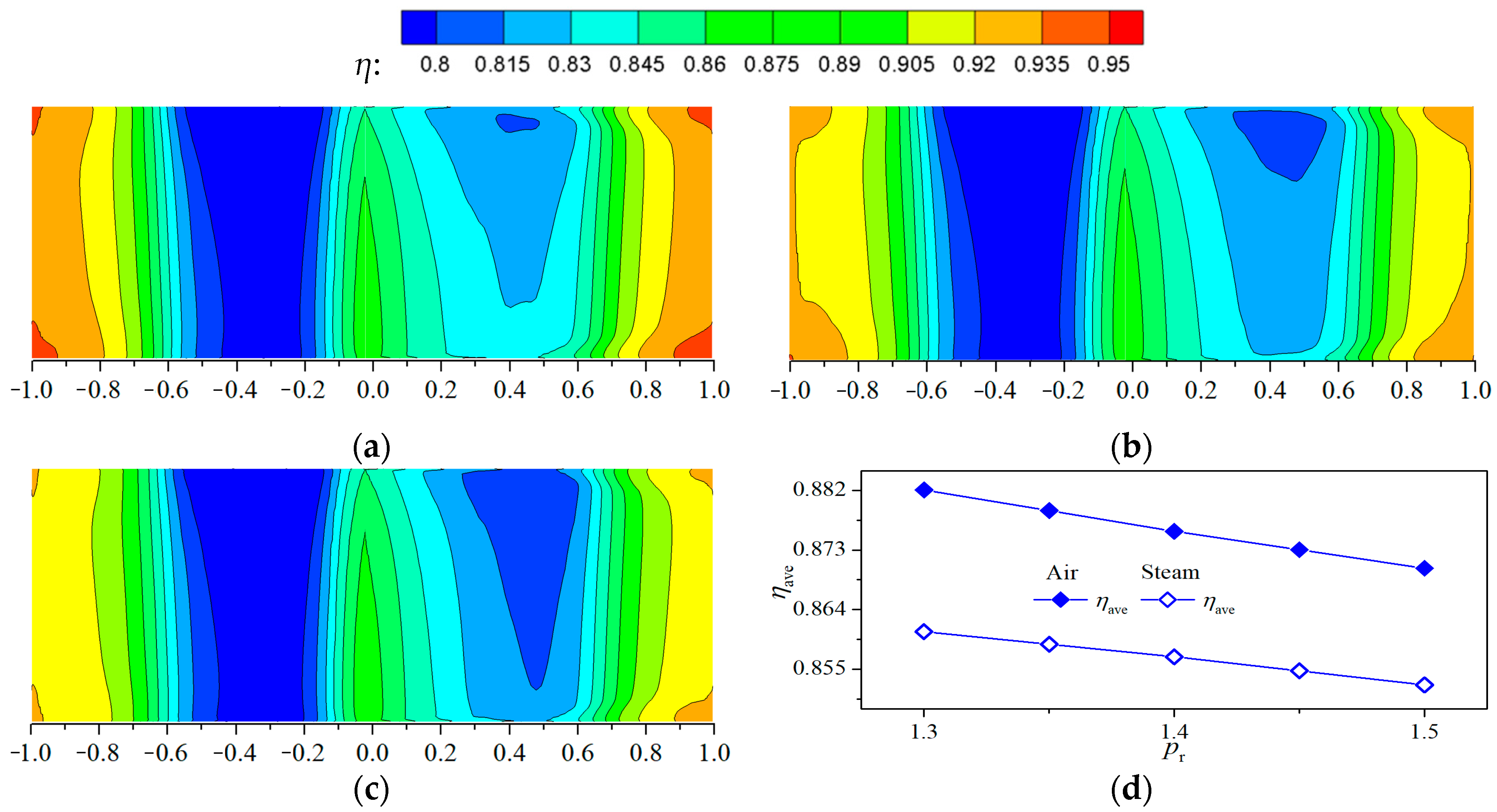
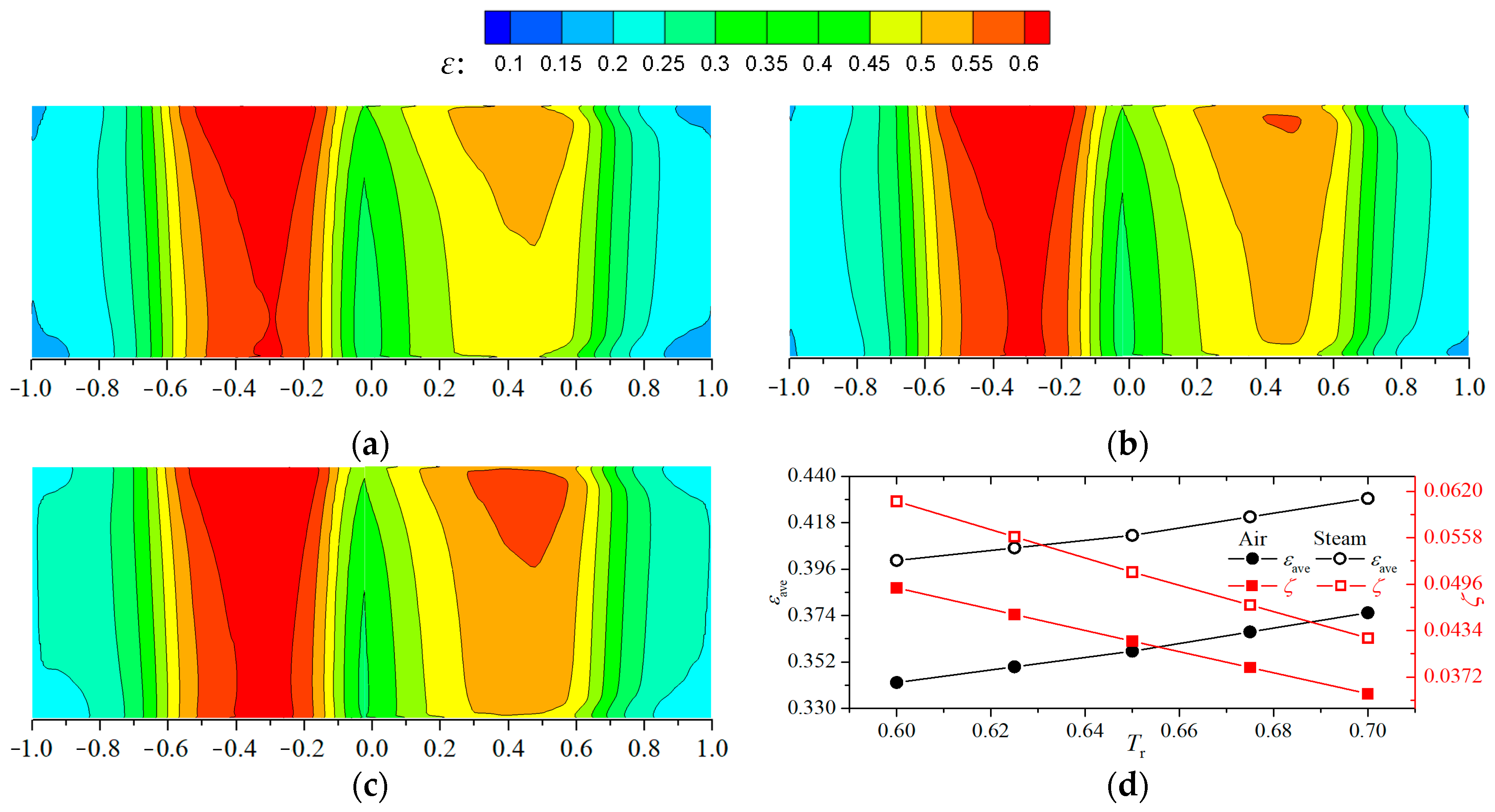
3.4. Influence of Temperature Ratio of Steam to Mainstream

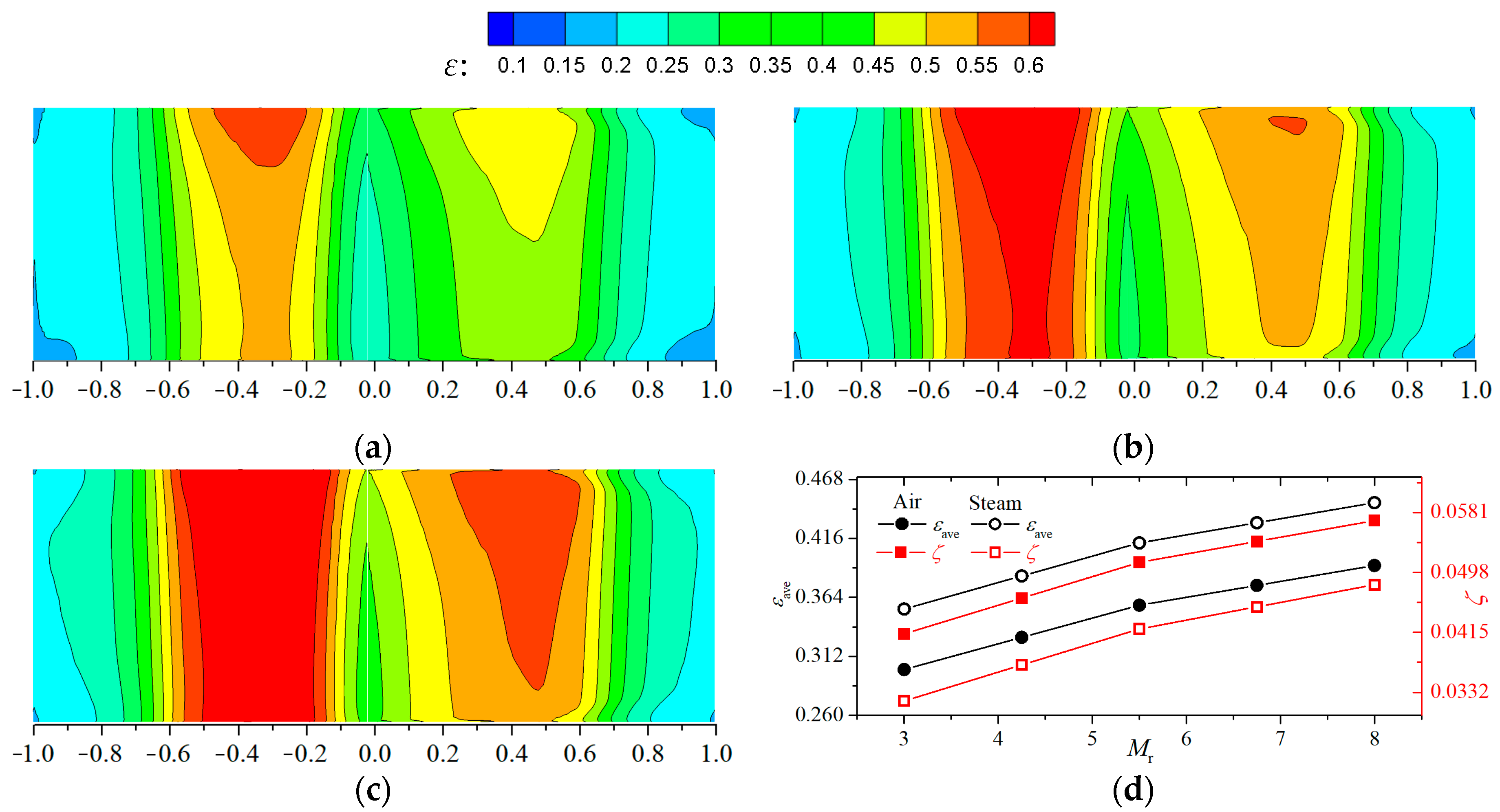
3.5. Influence of Flow Ratio of Steam to Mainstream
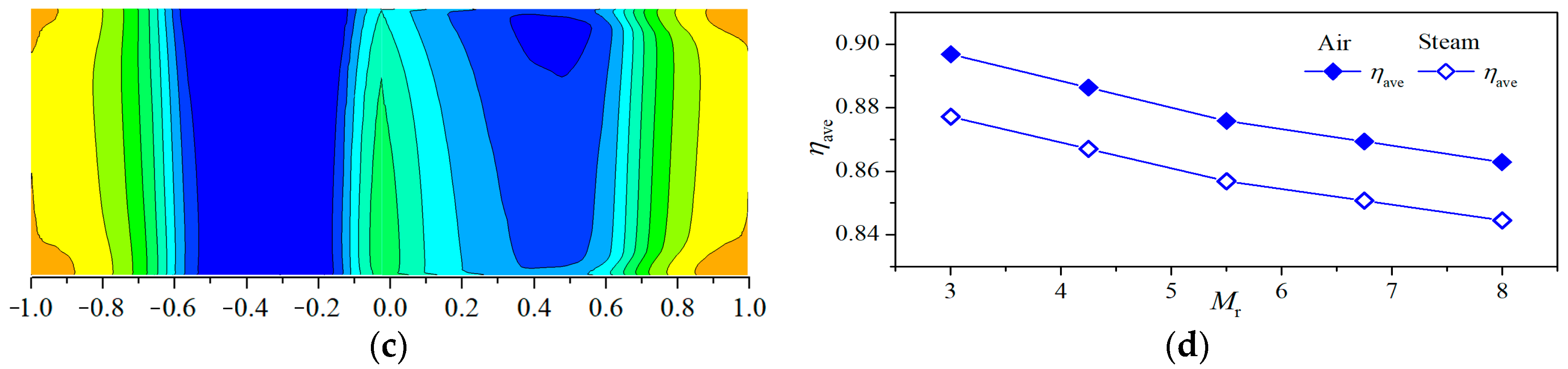
4. Analysis of the Results of the Response Surface Model Fitting
4.1. Experimental Design of Working Parameters
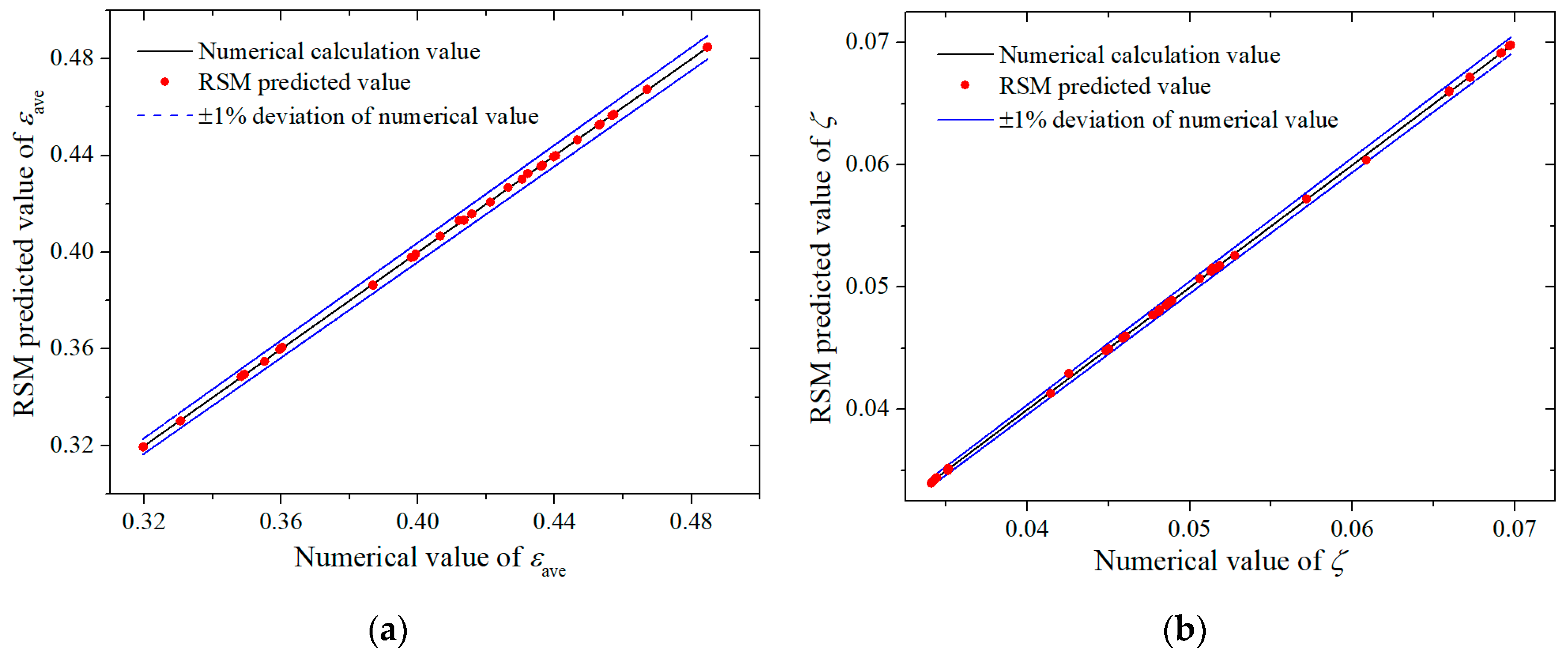
4.2. Correlation Fitting Based on Response Surface Model
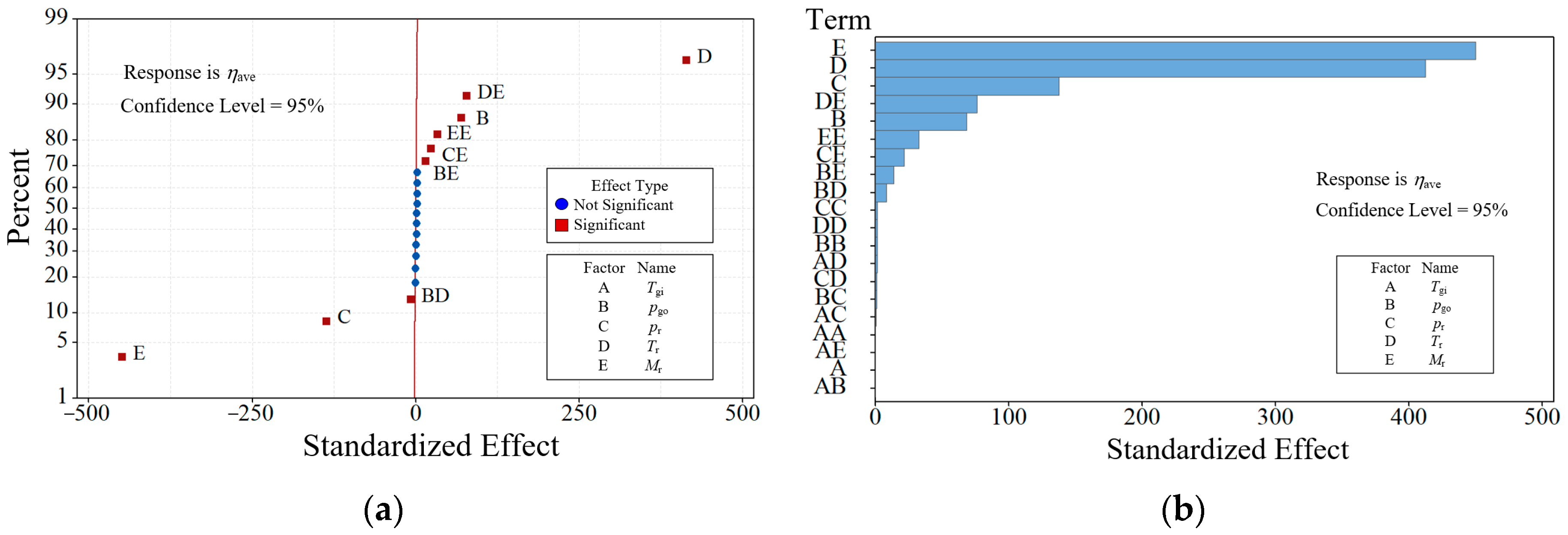
4.3. Significance Analysis of Working Parameters
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Surface area of the blade |
| CCD | Central composite design |
| CCF | Central composite face-centered design |
| Mr | Flow ratio of steam to mainstream multiplied by 100 |
| N–S | Navier Stokes |
| pgo | Mainstream outlet pressure (kPa) |
| pr | Mainstream inlet to outlet pressure ratio |
| RSM | Response Surface Model |
| RMSE | Root mean square errors |
| R2 | Determination coefficients |
| Tw | Temperature of blade surface (K) |
| Twave | Average temperature of the blade (K) |
| Tci | Inlet temperature of steam flow (K) |
| Tgi | Mainstream inlet temperature (K) |
| Tr | Temperature ratio of steam to mainstream |
| y | Response value |
| ω | Prediction error |
| ε | Cooling efficiency |
| εave | Average cooling efficiency |
| ζ | Temperature nonuniformity |
| η | Dimensionless temperature |
| ηave | Average dimensionless temperature |
References
- Xu, L.; Sun, Z.; Ruan, Q.; Xi, L.; Gao, J.; Li, Y. Development Trend of Cooling Technology for Turbine Blades at Super-High Temperature of above 2000 K. Energies 2023, 16, 668. [Google Scholar] [CrossRef]
- Nourin, F.N.; Amano, R.S. Review of Gas Turbine Internal Cooling Improvement Technology. J. Energy Resour. Technol. 2020, 143, 8. [Google Scholar] [CrossRef]
- Yeranee, K.; Rao, Y. A review of recent studies on rotating internal cooling for gas turbine blades. Chin. J. Aeronaut. 2021, 34, 85–113. [Google Scholar] [CrossRef]
- Zhang, L.; Cao, G.; Feng, K.; Jia, Y.; Zhang, Z. Improvement of Multi-Hole Airflow Impingement on Flow and Heat Transfer Characteristics Inside a Turbine Vane Cavity. Appl. Sci. 2021, 11, 9924. [Google Scholar] [CrossRef]
- Du, W.; Luo, L.; Jiao, Y.; Wang, S.; Li, X.; Sunden, B. Heat transfer in the trailing region of gas turbines–A state-of-the-art review. Appl. Therm. Eng. 2021, 199, 117614. [Google Scholar] [CrossRef]
- Ngetich, G.C.; Murray, A.V.; Ireland, P.T.; Romero, E. A Three-Dimensional Conjugate Approach for Analyzing a Double-Walled Effusion-Cooled Turbine Blade. J. Turbomach. 2018, 141, 1. [Google Scholar] [CrossRef]
- Luo, J.; Razinsky, E.H. Conjugate Heat Transfer Analysis of a Cooled Turbine Vane Using the V2F Turbulence Model. J. Turbomach. 2006, 129, 773–781. [Google Scholar] [CrossRef]
- John, B.; Senthilkumar, P.; Sadasivan, S. Applied and Theoretical Aspects of Conjugate Heat Transfer Analysis: A Review. Arch. Comput. Methods Eng. 2019, 26, 475–489. [Google Scholar] [CrossRef]
- Prapamonthon, P.; Yooyen, S.; Sleesongsom, S.; Dipasquale, D.; Xu, H.; Wang, J.; Ke, Z. Investigation of Cooling Performances of a Non-Film-Cooled Turbine Vane Coated with a Thermal Barrier Coating Using Conjugate Heat Transfer. Energies 2018, 11, 1000. [Google Scholar] [CrossRef]
- Nowak, G.; Wróblewski, W.; Nowak, I. Convective cooling optimization of a blade for a supercritical steam turbine. Int. J. Heat Mass Transf. 2012, 55, 4511–4520. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, J.W.; Yang, L.; Zhou, Y.C.; Wei, Y.G.; Wu, R.T. Modeling and simulation of the temperature and stress fields in a 3D turbine blade coated with thermal barrier coatings. Surf. Coat. Technol. 2017, 315, 443–453. [Google Scholar] [CrossRef]
- Zhang, G.; Zhu, R.; Xie, G.; Li, S.; SundÉN, B. Optimization of cooling structures in gas turbines: A review. Chin. J. Aeronaut. 2022, 35, 18–46. [Google Scholar] [CrossRef]
- Liu, Z.; Karimi, I.A. Gas turbine performance prediction via machine learning. Energy 2020, 192, 116627. [Google Scholar] [CrossRef]
- Abbasi, S.; Gholamalipour, A. Performance optimization of an axial turbine with a casing injection based on response surface methodology. J Braz. Soc. Mech. Sci. 2021, 43, 435. [Google Scholar] [CrossRef]
- Lakzian, E.; Yazdani, S.; Lee, B.J. Passive control optimization of condensation flow in steam turbine blades. Int. J. Mech. Sci. 2023, 237, 107804. [Google Scholar] [CrossRef]
- Mahdavi, N.; Mojaver, P.; Khalilarya, S. Multi-objective optimization of power, CO2 emission and exergy efficiency of a novel solar-assisted CCHP system using RSM and TOPSIS coupled method. Renew. Energ. 2022, 185, 506–524. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, L.; Huang, K. Fast prediction and sensitivity analysis of gas turbine cooling performance using supervised learning approaches. Energy 2022, 246, 123373. [Google Scholar] [CrossRef]
- Maheshwari, M.; Singh, O. Comparative evaluation of different combined cycle configurations having simple gas turbine, steam turbine and ammonia water turbine. Energy 2019, 168, 1217–1236. [Google Scholar] [CrossRef]
- Sanjay; Singh, O.; Prasad, B.N. Influence of different means of turbine blade cooling on the thermodynamic performance of combined cycle. Appl. Therm. Eng. 2008, 28, 2315–2326. [Google Scholar] [CrossRef]
- Xing, J.; Han, S.; Song, Y.; An, N.; Zhou, L.; Li, L.; Zhang, H.; Du, X. Improving internal cooling performance of turbine blade with steam in channel with rhombus-patterned biomimetic ribs: A numerical investigation. Therm. Sci. Eng. Prog. 2023, 40, 101789. [Google Scholar] [CrossRef]
- Najjar, Y.S.H.; Alghamdi, A.S.; Al-Beirutty, M.H. Comparative performance of combined gas turbine systems under three different blade cooling schemes. Appl. Therm. Eng. 2004, 24, 1919–1934. [Google Scholar] [CrossRef]
- Wang, W. Efficiency study of a gas turbine guide vane with a newly designed combined cooling structure. Int. J. Heat Mass Transf. 2015, 80, 217–226. [Google Scholar] [CrossRef]
- Xu, L.; Wang, W.; Gao, T.; Shi, X.; Gao, J.; Liang, W. Experimental study on cooling performance of a steam-cooled turbine blade with five internal cooling smooth channels. Exp. Therm. Fluid Sci. 2014, 58, 180–187. [Google Scholar] [CrossRef]
- Xi, L.; Xu, L.; Gao, J.; Zhao, Z.; Li, Y. Numerical analysis and optimization on flow and heat transfer performance of a steam-cooled ribbed channel. Case Stud. Therm. Eng. 2021, 28, 101442. [Google Scholar] [CrossRef]
- Xi, L.; Gao, J.; Xu, L.; Zhao, Z.; Ruan, Q.; Li, Y. Numerical Investigation and Parameter Sensitivity Analysis on Flow and Heat Transfer Performance of Jet Array Impingement Cooling in a Quasi-Leading-Edge Channel. Aerospace 2022, 9, 87. [Google Scholar] [CrossRef]
- Khan, M.S.; Hamdan, M.O.; Al-Omari, S.A.B.; Elnajjar, E. A comparison of oscillating sweeping jet and steady normal jet in cooling gas turbine leading edge: Numerical analysis. Int. J. Heat Mass Transf. 2023, 208, 124041. [Google Scholar] [CrossRef]
- Rathore, M.M.; Kapuno, R. Engineering Heat Transfer, Second Edition; Jones and Bartlett Publishers, Inc.: Sudbury, MA, USA, 2010. [Google Scholar]
- Xu, L.; Shui, L.; Gao, J.; Shi, X.; Wang, W.; Li, X. Investigation on Optimal Allocation of Mass Flow and Direction for Binary Cooling Turbine Test Blades. J. Xi’an Jiaotong Univ. 2012, 46, 7–12+90. (In Chinese) [Google Scholar]
- Jiang, G.; Gao, J.; Shi, X.; Li, F.; Xu, L. Flow and Heat Transfer Characteristics of the Mist/Steam Two-Phase Flow Cooling the Rectangular Channel with Column-Row-Ribs. Int. J. Heat Mass Transf. 2020, 156, 119737. [Google Scholar] [CrossRef]
- Zhao, Z.; Gao, J.; Xu, L.; Xi, L.; Li, Y. Numerical simulation on structural parameter optimization of heat exchanger with frustum of a cone. J. Xi’an Jiaotong Univ. 2021, 55, 35–46. (In Chinese) [Google Scholar]
- Mishra, S.; Sharma, A.; Kumari, A.; Sanjay. Response surface methodology based optimization of air-film blade cooled gas turbine cycle for thermal performance prediction. Appl. Therm. Eng. 2020, 164, 114425. [Google Scholar] [CrossRef]
- Courand, A.; Metz, M.; Héran, D.; Feilhes, C.; Prezman, F.; Serrano, E.; Bendoula, R.; Ryckewaert, M. Evaluation of a robust regression method (RoBoost-PLSR) to predict biochemical variables for agronomic applications: Case study of grape berry maturity monitoring. Chemom. Intell. Lab. Syst. 2022, 221, 104485. [Google Scholar] [CrossRef]


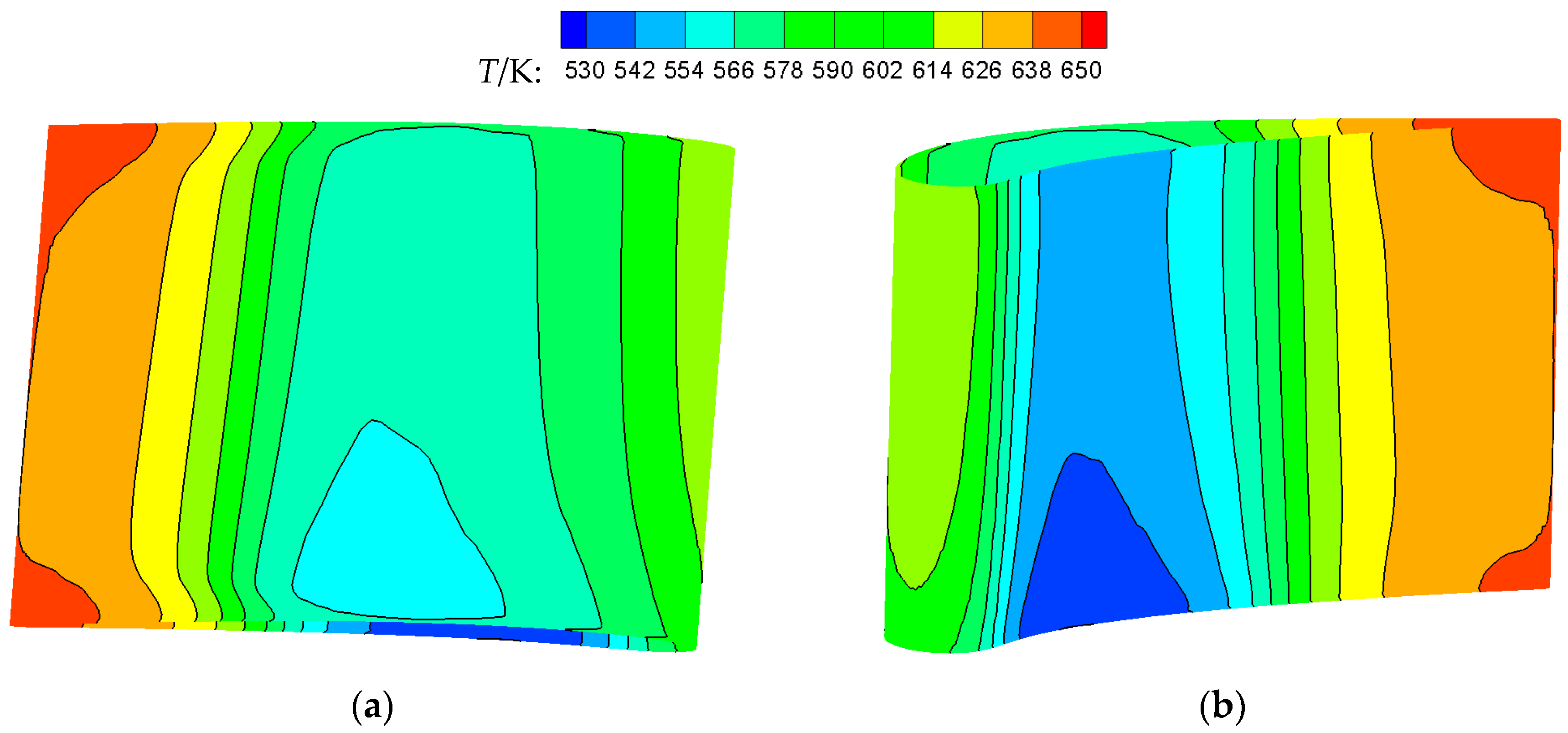




| Fluid Domain Mesh | Solid Domain Mesh | Total Mesh Number | εave | ηave |
|---|---|---|---|---|
| 1,098,756 | 118,740 | 1,217,496 | 0.355 | 0.799 |
| 1,617,840 | 209,874 | 1,827,714 | 0.384 | 0.812 |
| 2,014,780 | 319,871 | 2,334,651 | 0.411 | 0.834 |
| 2,478,210 | 422,968 | 2,901,178 | 0.431 | 0.849 |
| 3,047,180 | 512,950 | 3,560,130 | 0.433 | 0.853 |
| Working Parameters | Variation Range |
|---|---|
| Mainstream inlet temperature Tgi/K | 680 to 710 |
| Mainstream outlet pressure pgo/kPa | 120 to 160 |
| Mainstream inlet to outlet pressure ratio pr | 0.6 to 0.7 |
| Temperature ratio of steam to mainstream Tr | 1.3 to 1.5 |
| Flow ratio of steam to mainstream multiplied by 100 Mr | 3 to 8 |
| Order | Design Variables | Responses | ||||||
|---|---|---|---|---|---|---|---|---|
| Tgi/K | pgo/kPa | pr | Tr | Mr | εave | ζ | ηave | |
| 1 | 710 | 160 | 1.3 | 0.7 | 3 | 0.349 | 0.035 | 0.898 |
| 2 | 695 | 140 | 1.5 | 0.65 | 5.5 | 0.426 | 0.051 | 0.852 |
| 3 | 710 | 120 | 1.5 | 0.6 | 3 | 0.360 | 0.048 | 0.857 |
| 4 | 680 | 120 | 1.3 | 0.6 | 8 | 0.432 | 0.070 | 0.827 |
| 5 | 710 | 160 | 1.5 | 0.6 | 3 | 0.348 | 0.048 | 0.862 |
| 6 | 680 | 120 | 1.5 | 0.7 | 8 | 0.485 | 0.046 | 0.856 |
| 7 | 680 | 120 | 1.3 | 0.7 | 8 | 0.457 | 0.049 | 0.864 |
| 8 | 695 | 140 | 1.4 | 0.65 | 5.5 | 0.412 | 0.051 | 0.857 |
| 9 | 710 | 160 | 1.5 | 0.6 | 8 | 0.436 | 0.066 | 0.825 |
| 10 | 710 | 120 | 1.3 | 0.6 | 8 | 0.432 | 0.070 | 0.827 |
| 11 | 710 | 120 | 1.3 | 0.7 | 8 | 0.457 | 0.049 | 0.864 |
| 12 | 710 | 160 | 1.3 | 0.7 | 8 | 0.440 | 0.048 | 0.870 |
| 13 | 680 | 160 | 1.5 | 0.6 | 3 | 0.349 | 0.048 | 0.862 |
| 14 | 710 | 120 | 1.5 | 0.7 | 3 | 0.398 | 0.034 | 0.883 |
| 15 | 680 | 160 | 1.3 | 0.7 | 8 | 0.440 | 0.048 | 0.870 |
| 16 | 680 | 120 | 1.5 | 0.6 | 8 | 0.453 | 0.067 | 0.818 |
| 17 | 695 | 120 | 1.4 | 0.65 | 5.5 | 0.421 | 0.052 | 0.853 |
| 18 | 710 | 160 | 1.5 | 0.7 | 8 | 0.467 | 0.045 | 0.861 |
| 19 | 710 | 120 | 1.3 | 0.6 | 3 | 0.331 | 0.049 | 0.870 |
| 20 | 710 | 160 | 1.3 | 0.6 | 8 | 0.416 | 0.069 | 0.834 |
| 21 | 695 | 160 | 1.4 | 0.65 | 5.5 | 0.407 | 0.051 | 0.859 |
| 22 | 680 | 160 | 1.3 | 0.6 | 3 | 0.320 | 0.049 | 0.874 |
| 23 | 710 | 120 | 1.3 | 0.7 | 3 | 0.360 | 0.035 | 0.895 |
| 24 | 680 | 140 | 1.4 | 0.65 | 5.5 | 0.413 | 0.052 | 0.856 |
| 25 | 695 | 140 | 1.4 | 0.65 | 3 | 0.355 | 0.041 | 0.878 |
| 26 | 680 | 160 | 1.3 | 0.7 | 3 | 0.349 | 0.035 | 0.899 |
| 27 | 710 | 160 | 1.5 | 0.7 | 3 | 0.387 | 0.034 | 0.887 |
| 28 | 680 | 120 | 1.3 | 0.6 | 3 | 0.331 | 0.049 | 0.869 |
| 29 | 710 | 140 | 1.4 | 0.65 | 5.5 | 0.413 | 0.052 | 0.856 |
| 30 | 710 | 160 | 1.3 | 0.6 | 3 | 0.320 | 0.049 | 0.874 |
| 31 | 695 | 140 | 1.4 | 0.6 | 5.5 | 0.399 | 0.061 | 0.840 |
| 32 | 695 | 140 | 1.4 | 0.65 | 8 | 0.447 | 0.057 | 0.844 |
| 33 | 680 | 120 | 1.3 | 0.7 | 3 | 0.360 | 0.035 | 0.895 |
| 34 | 695 | 140 | 1.4 | 0.7 | 5.5 | 0.430 | 0.043 | 0.873 |
| 35 | 710 | 120 | 1.5 | 0.6 | 8 | 0.453 | 0.067 | 0.818 |
| 36 | 680 | 120 | 1.5 | 0.7 | 3 | 0.398 | 0.034 | 0.883 |
| 37 | 710 | 120 | 1.5 | 0.7 | 8 | 0.485 | 0.046 | 0.856 |
| 38 | 695 | 140 | 1.3 | 0.65 | 5.5 | 0.399 | 0.053 | 0.862 |
| 39 | 680 | 160 | 1.5 | 0.7 | 3 | 0.387 | 0.034 | 0.887 |
| 40 | 680 | 160 | 1.3 | 0.6 | 8 | 0.416 | 0.069 | 0.834 |
| 41 | 680 | 160 | 1.5 | 0.6 | 8 | 0.436 | 0.066 | 0.825 |
| 42 | 680 | 120 | 1.5 | 0.6 | 3 | 0.360 | 0.048 | 0.857 |
| 43 | 680 | 160 | 1.5 | 0.7 | 8 | 0.467 | 0.045 | 0.861 |
| Coefficients | εave | ζ | ηave |
|---|---|---|---|
| B0 | 0.285 | −0.008 | 0.999 |
| B1 | −0.00048 | 0.000216 | 0.000188 |
| B2 | 0.000036 | 0.000135 | 0.00018 |
| B3 | −1.229 | −1.023 | 0.0413 |
| B4 | 0.317 | −0.0224 | −0.2213 |
| B5 | 0.06165 | 0.018726 | −0.034086 |
| B11 | 0 | 0 | 0 |
| B22 | 0.000001 | 0 | 0 |
| B33 | 0.694 | 0.0187 | 0.1034 |
| B44 | −0.0983 | 0.01049 | 0.0342 |
| B55 | −0.001819 | −0.000304 | 0.000636 |
| B12 | 0 | 0 | 0 |
| B13 | 0.000106 | 0.000018 | −0.000043 |
| B14 | −0.000148 | 0.000007 | 0.000051 |
| B15 | 0 | 0 | 0 |
| B23 | −0.000043 | 0.000015 | −0.00028 |
| B24 | −0.000116 | −0.000059 | 0.000041 |
| B25 | −0.000033 | −0.000003 | 0.000011 |
| B34 | 0.4615 | 0.00586 | 0.01224 |
| B35 | −0.007777 | −0.014006 | 0.022025 |
| B45 | −0.008928 | −0.002077 | 0.003074 |
| Evaluation Index | εave | ζ | ηave |
|---|---|---|---|
| RMSE | 0.00053 | 0.00015 | 0.00023 |
| R2 | 0.9999 | 0.9999 | 0.9999 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Xi, L.; Gao, J.; Xu, L.; Li, Y. Numerical Study on Cooling Performance of a Steam-Cooled Blade Based on Response Surface Method. Appl. Sci. 2023, 13, 6625. https://doi.org/10.3390/app13116625
Zhao Z, Xi L, Gao J, Xu L, Li Y. Numerical Study on Cooling Performance of a Steam-Cooled Blade Based on Response Surface Method. Applied Sciences. 2023; 13(11):6625. https://doi.org/10.3390/app13116625
Chicago/Turabian StyleZhao, Zhen, Lei Xi, Jianmin Gao, Liang Xu, and Yunlong Li. 2023. "Numerical Study on Cooling Performance of a Steam-Cooled Blade Based on Response Surface Method" Applied Sciences 13, no. 11: 6625. https://doi.org/10.3390/app13116625





