Double-Bend and Semi-Spherical Energy Deflectors’ Blast Load Efficiency—A Comparative Study
Abstract
1. Introduction
- Increasing the distance from the explosive;
- Using energy-absorbing panels;
- Appropriate shaping of the vehicle bottom—the use of deflectors.
2. Materials and Methods
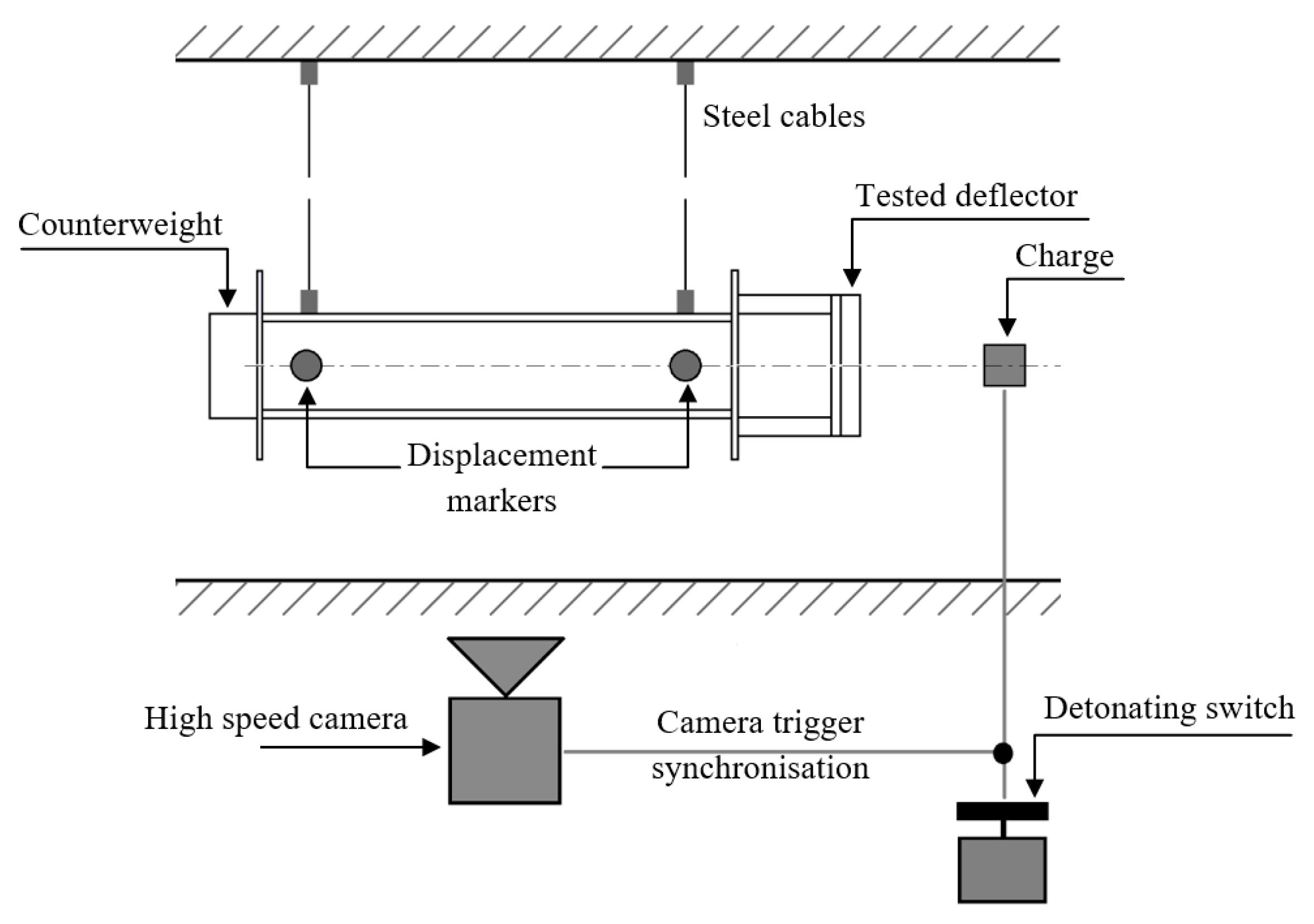
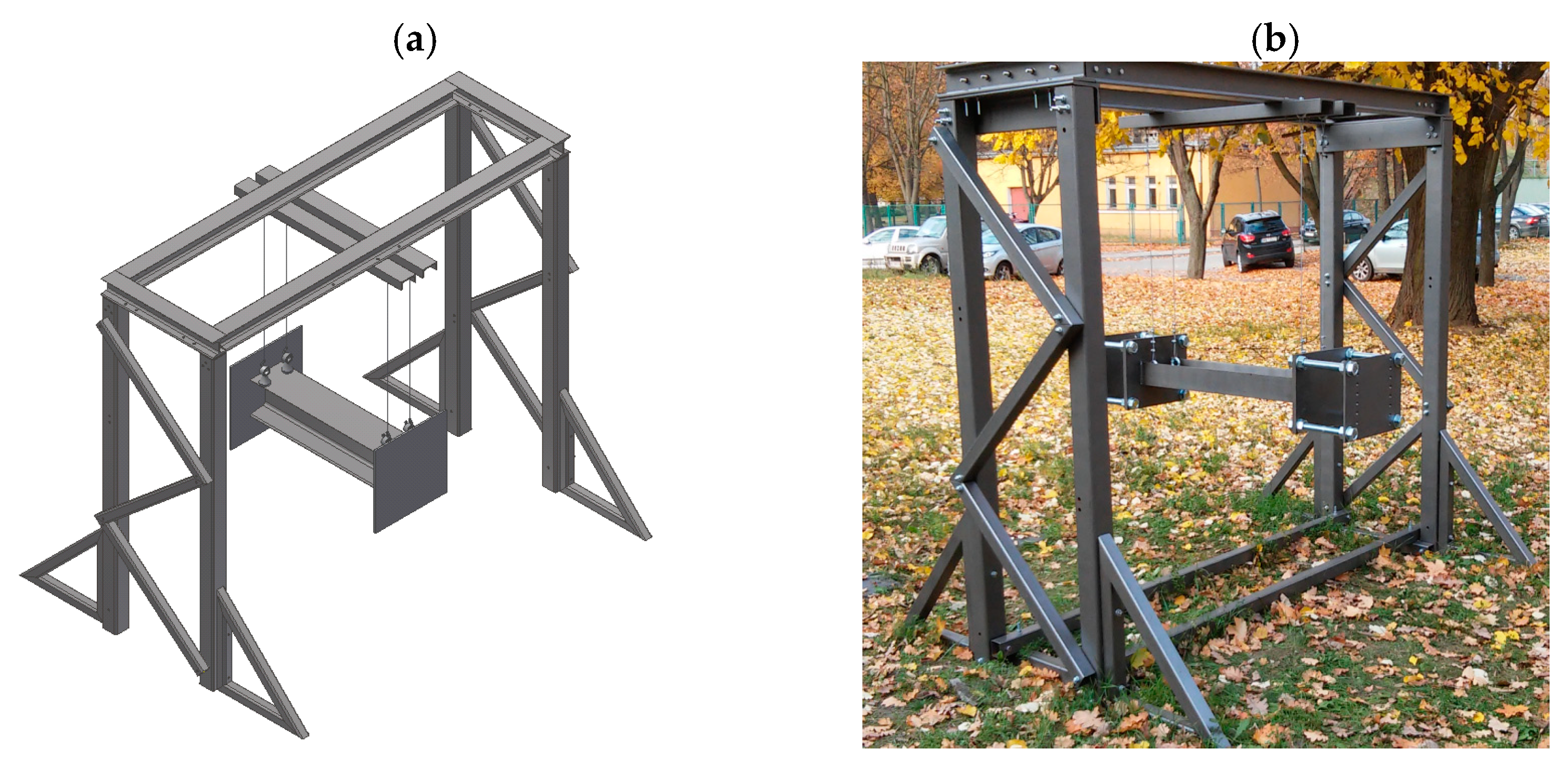
2.1. Ballistic Pendulum
- The main pendulum beam, made of I-beam 220;
- Steel plates (10 mm thick) attached directly to the pendulum beam at both ends;
- Spacers (200 mm long) made of 24 mm diameter threaded rod;
- Steel plates (20 mm) attached to the spacers and placed at the ends of the pendulum.
2.2. Energy-Dissipating Systems under Study
3. Numerical Modelling
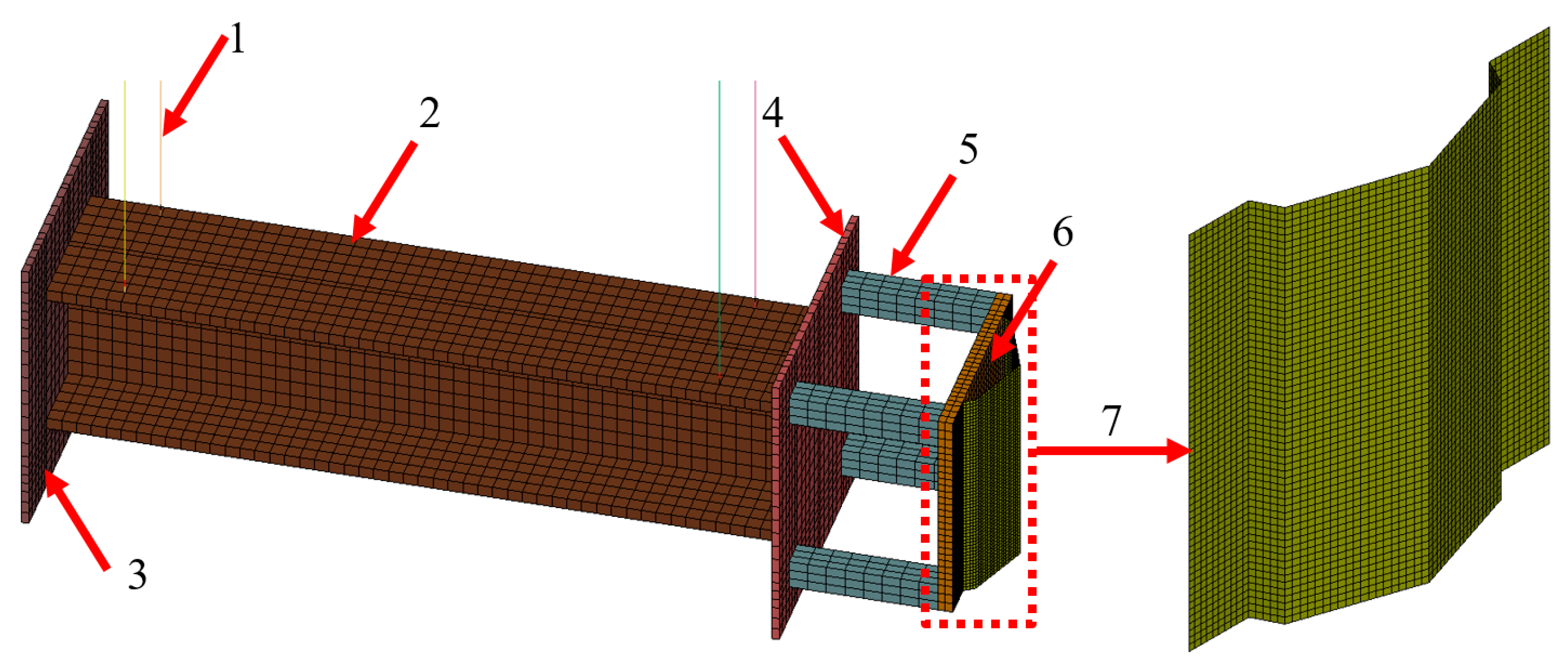
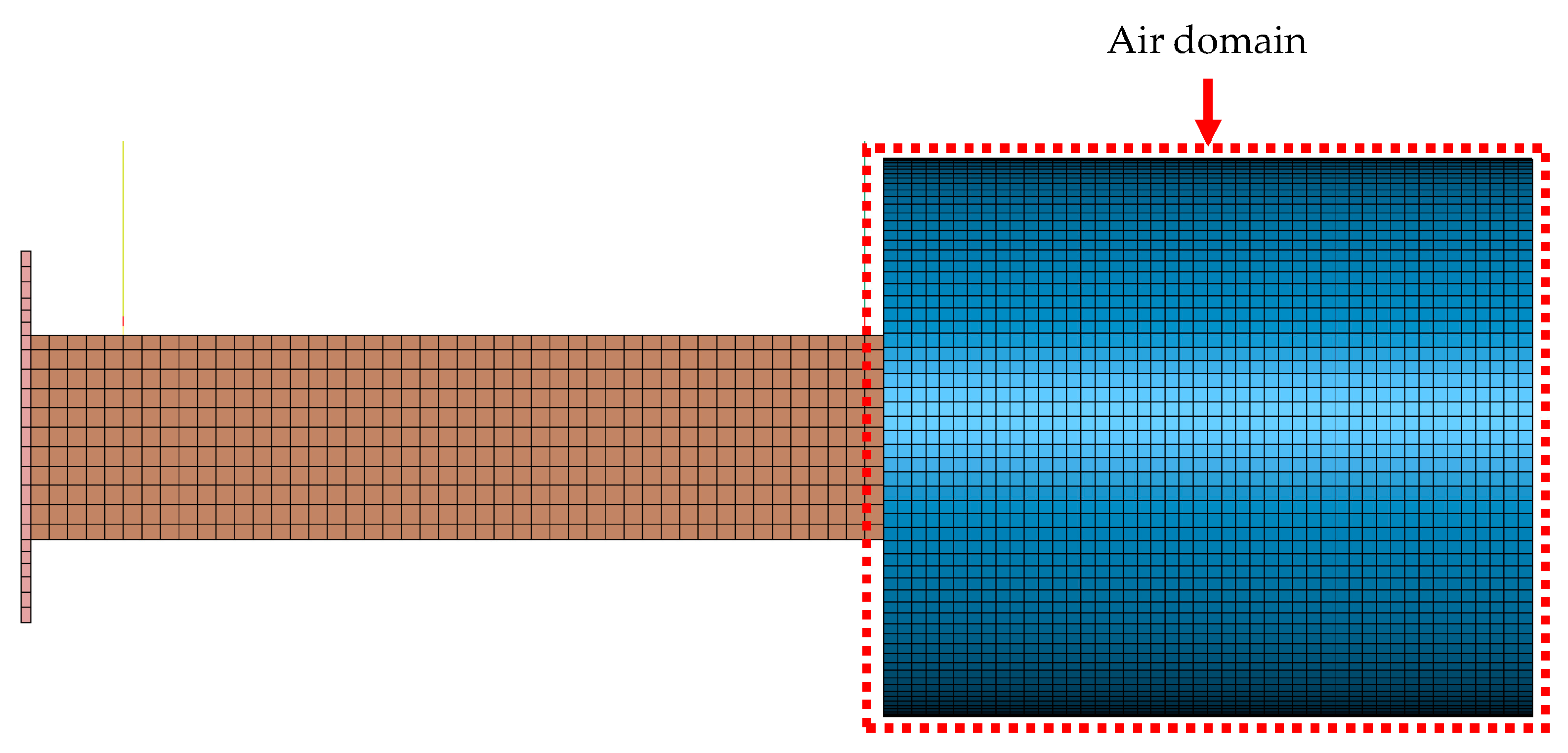
3.1. Ballistic Pendulum Modelling
3.2. Material Parameters
3.3. Boundary Conditions
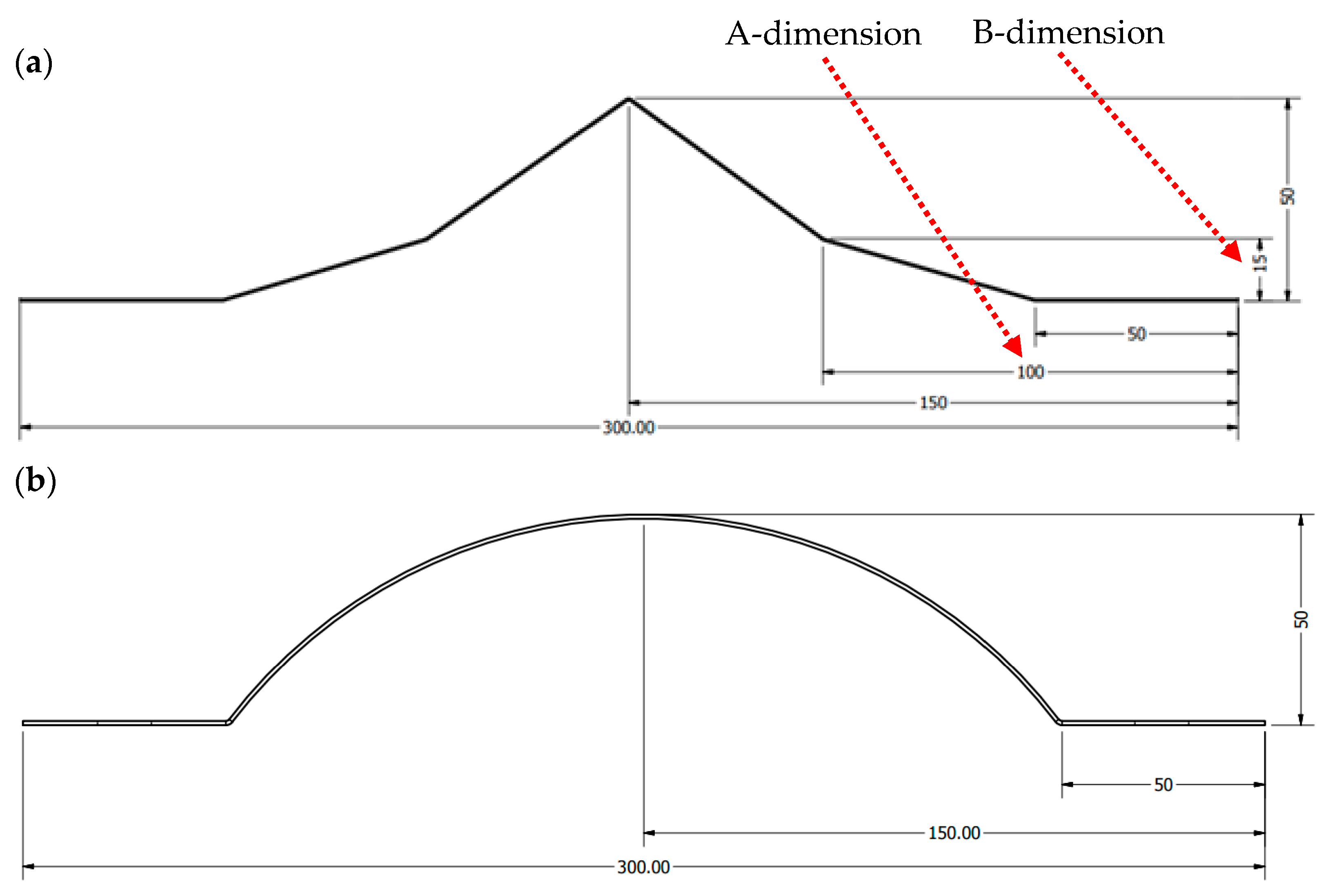
3.4. Variants of the Deflector Geometry
4. Results and Discussion
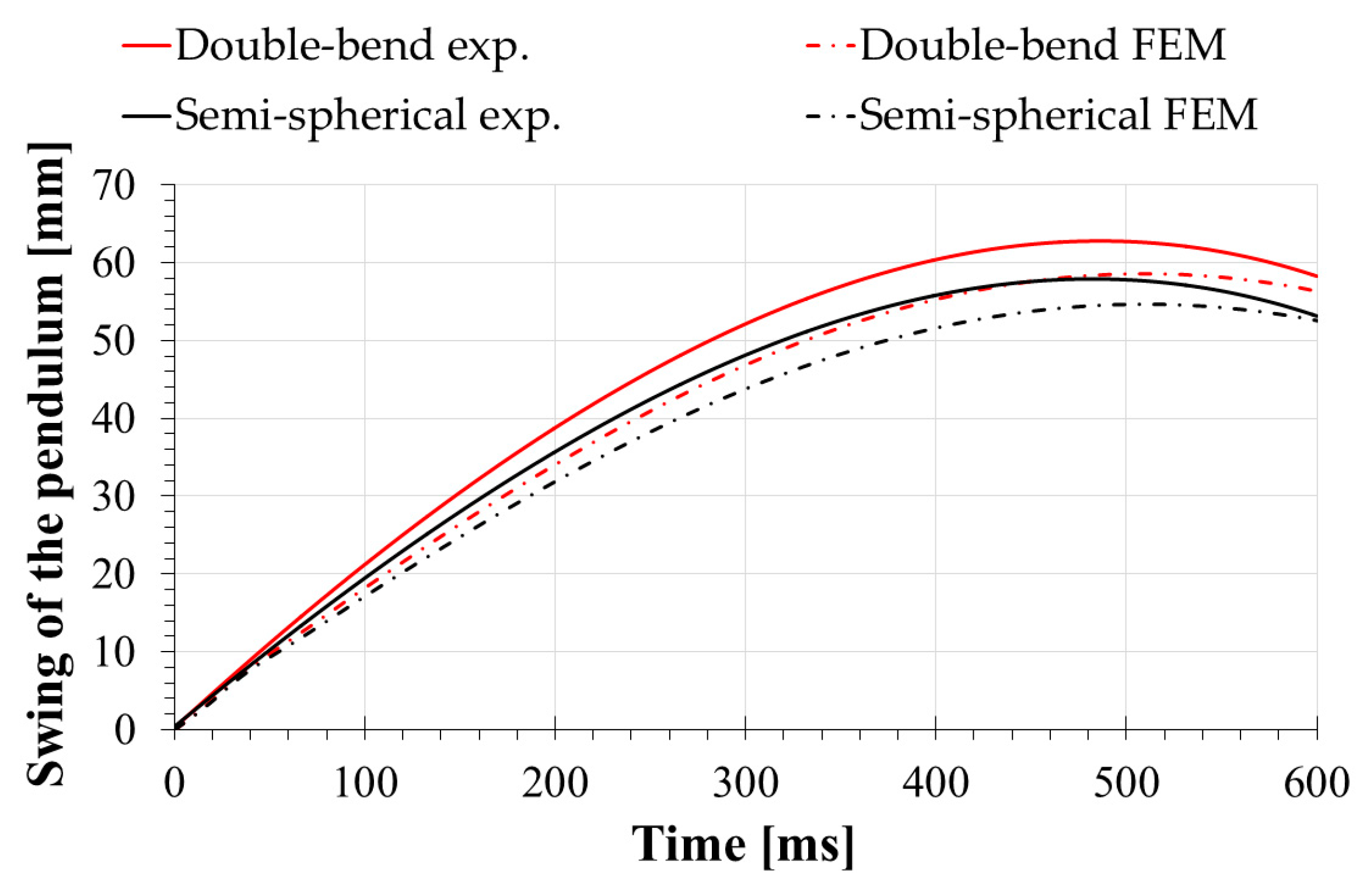
4.1. Validation of the Numerical Model
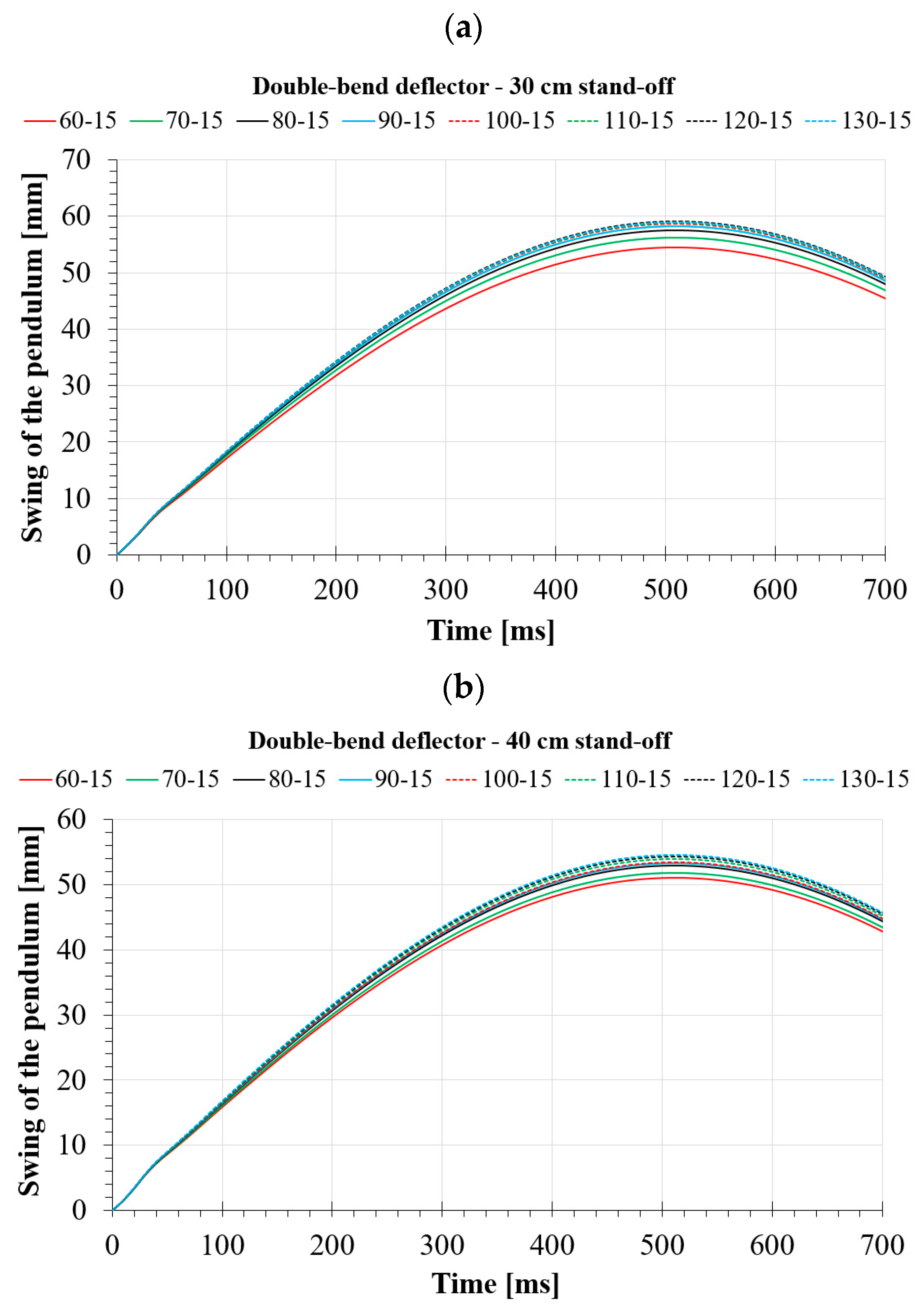
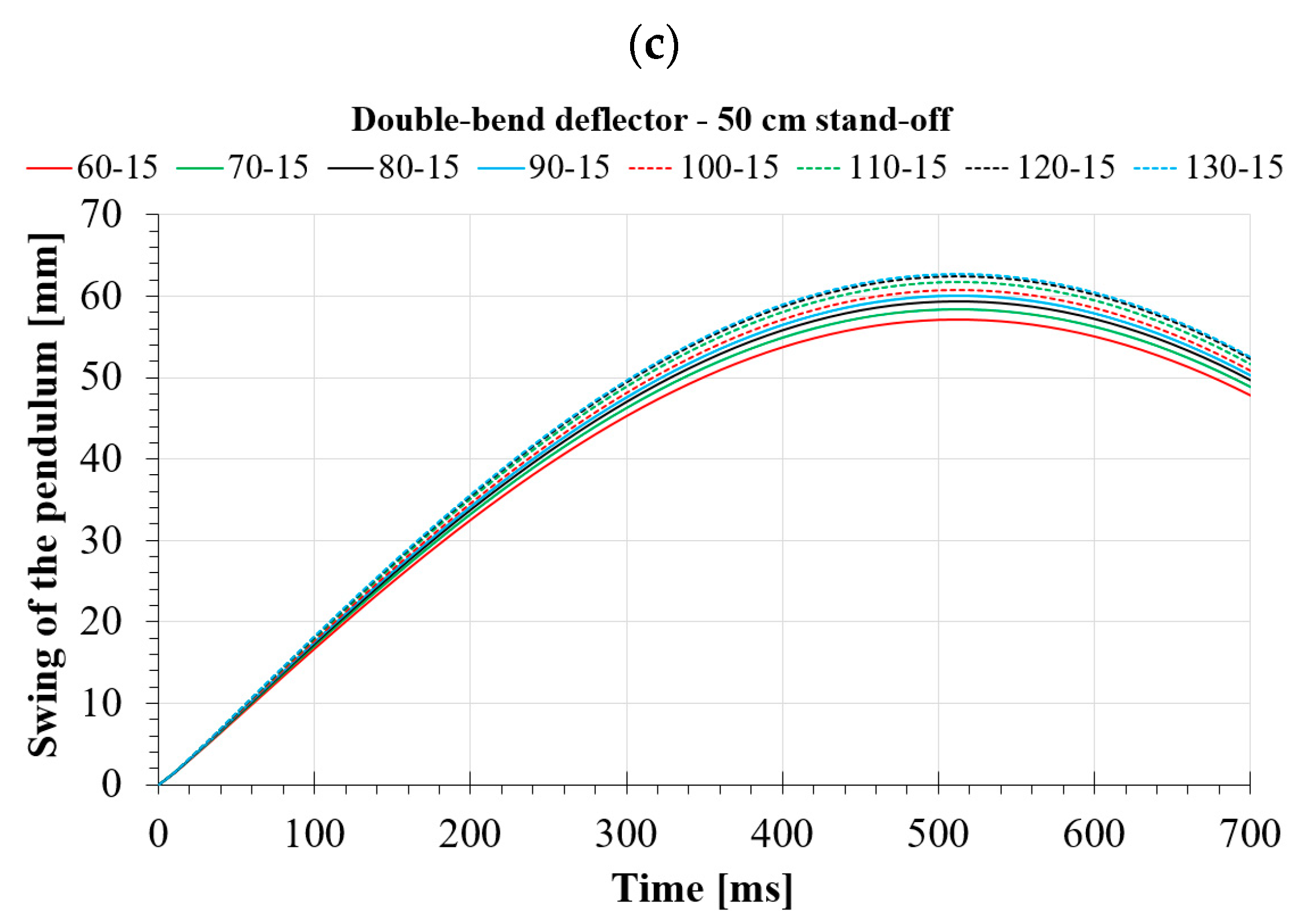
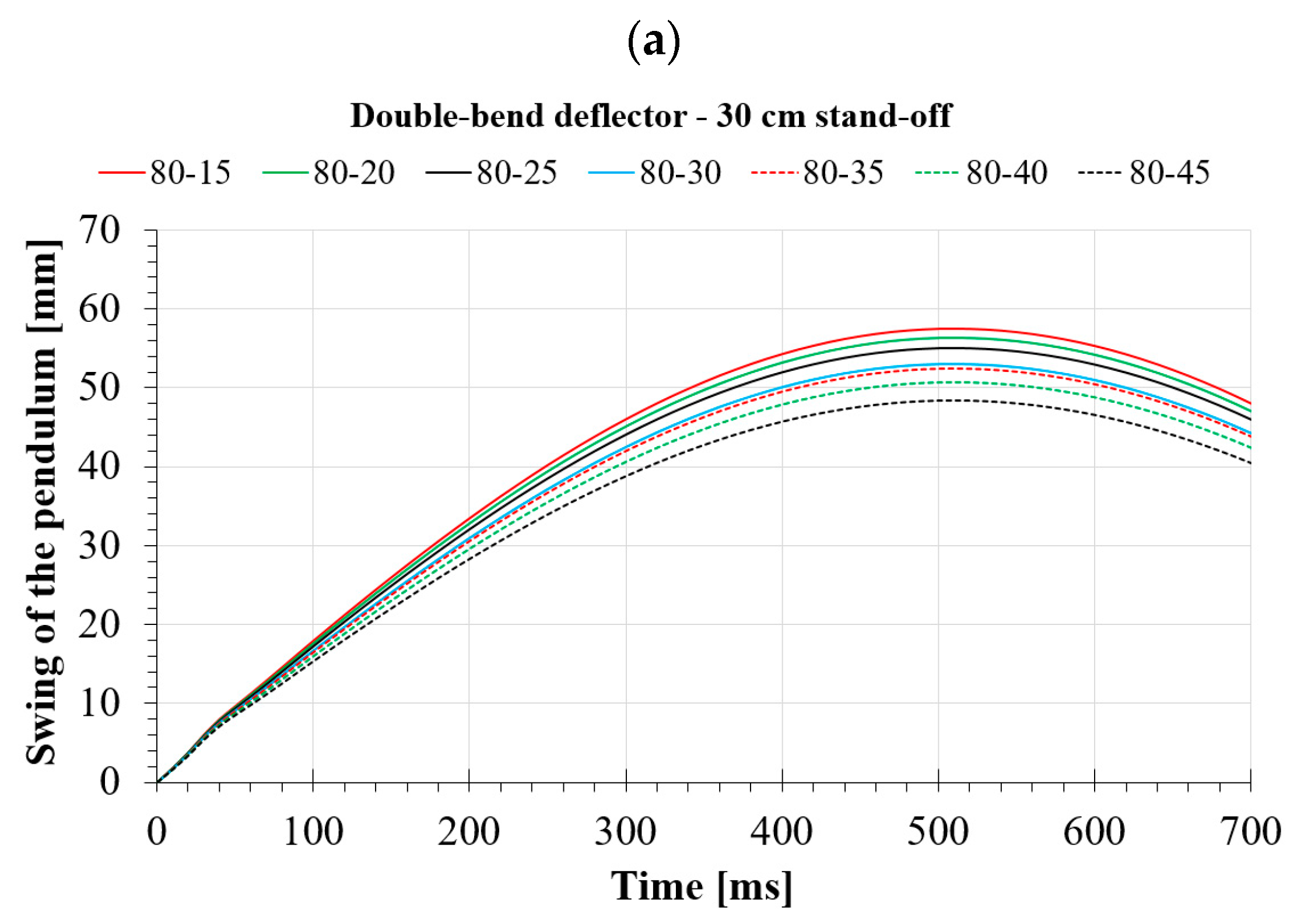
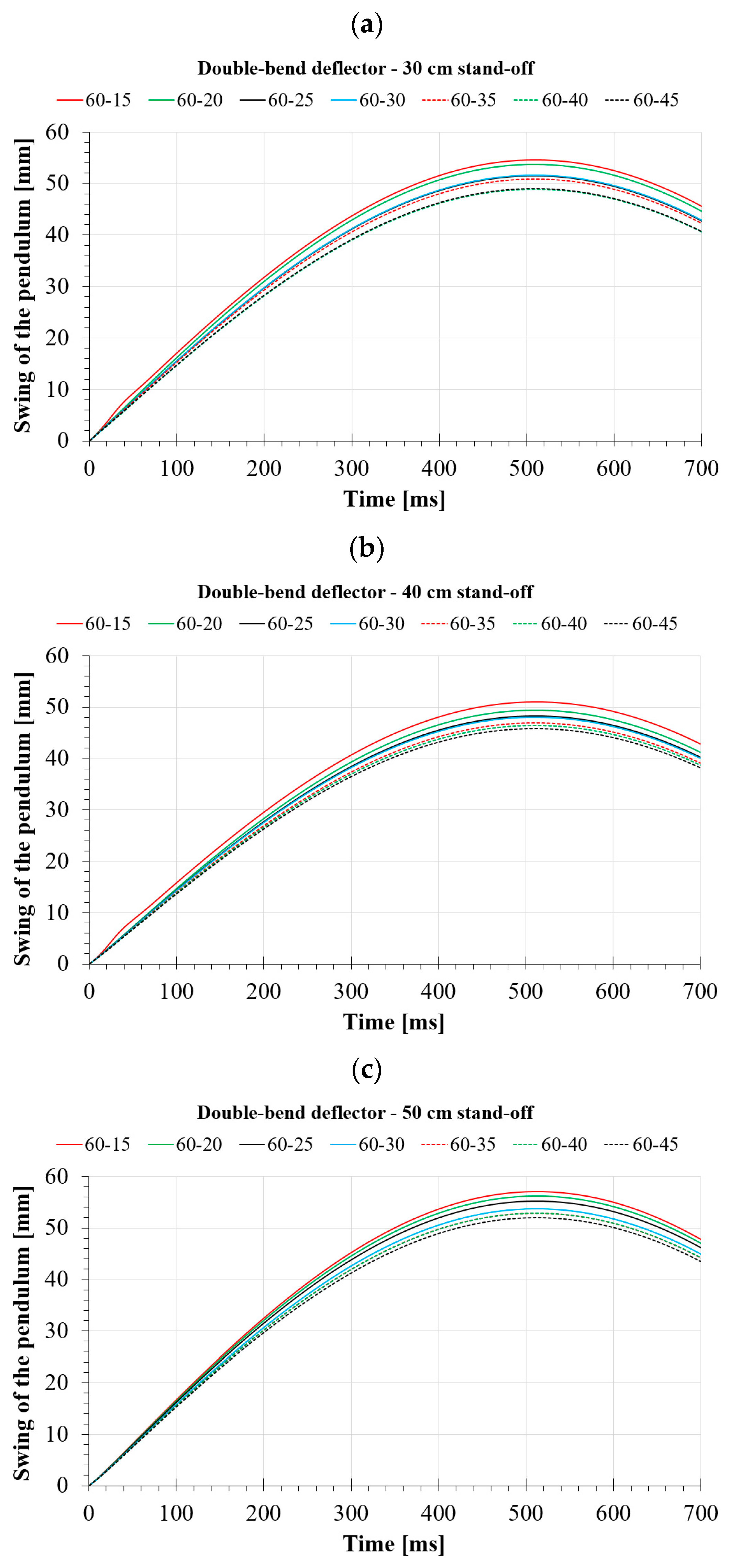
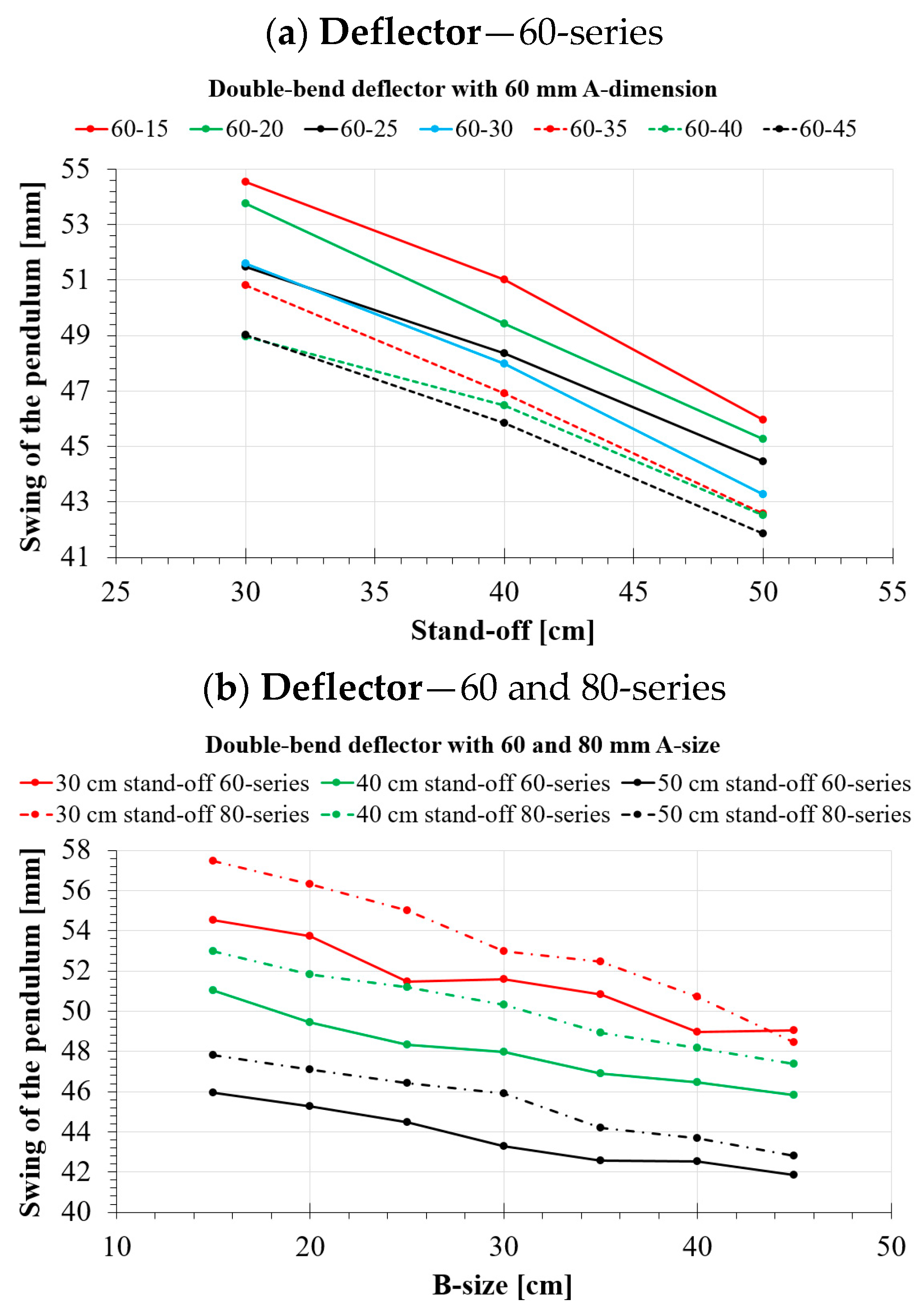
4.2. Numerical Analyses of the Double-Bend Deflector
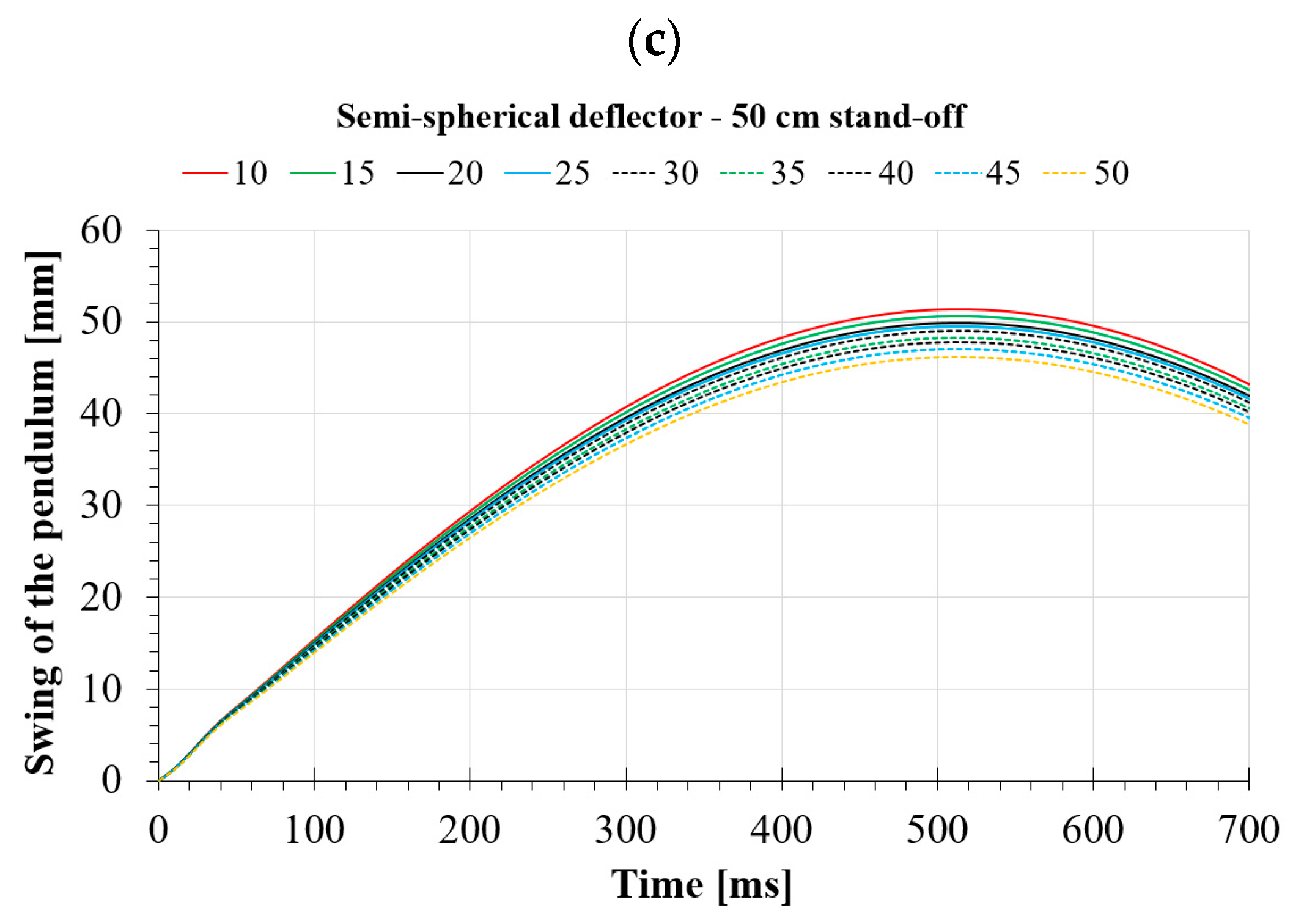
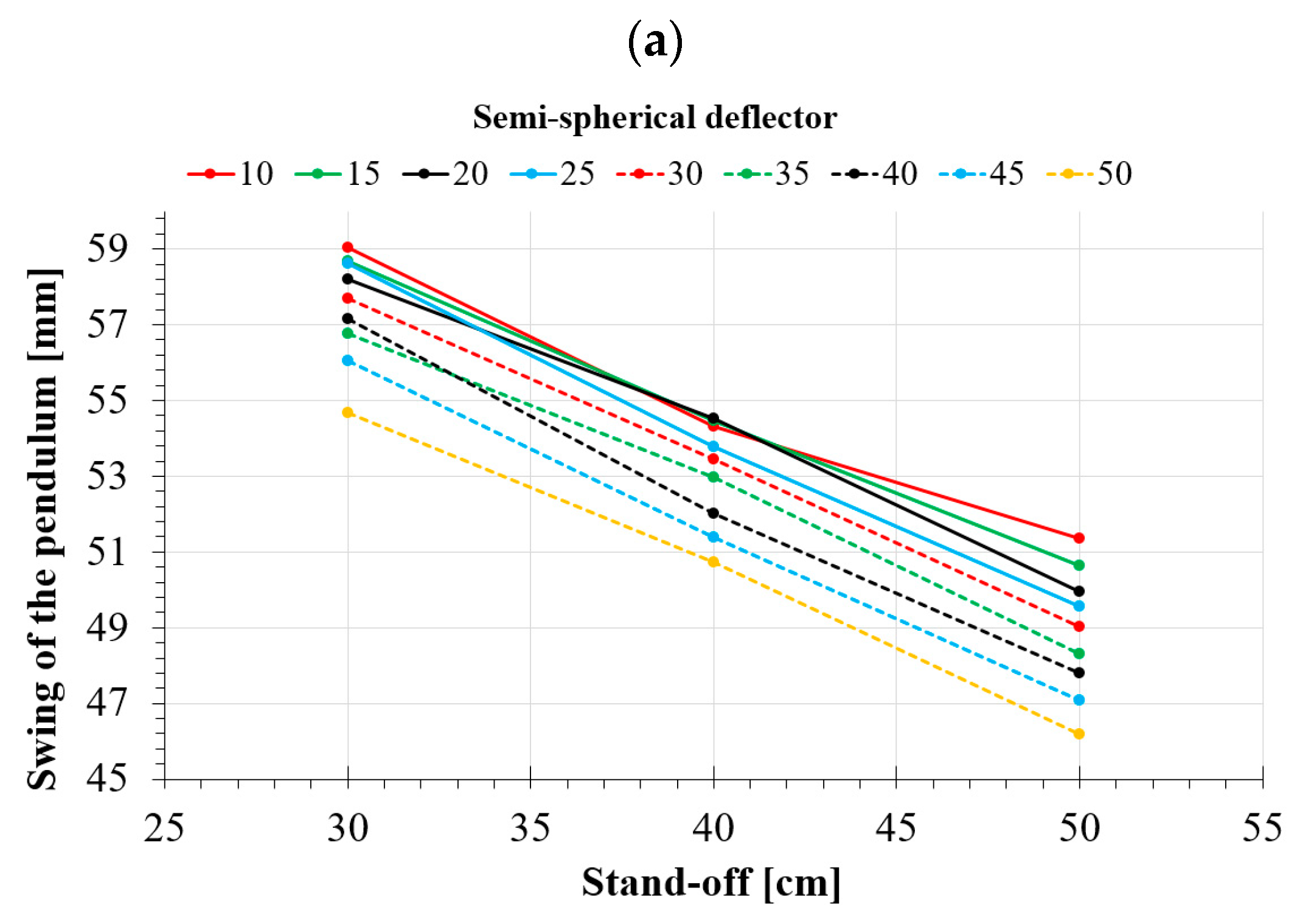
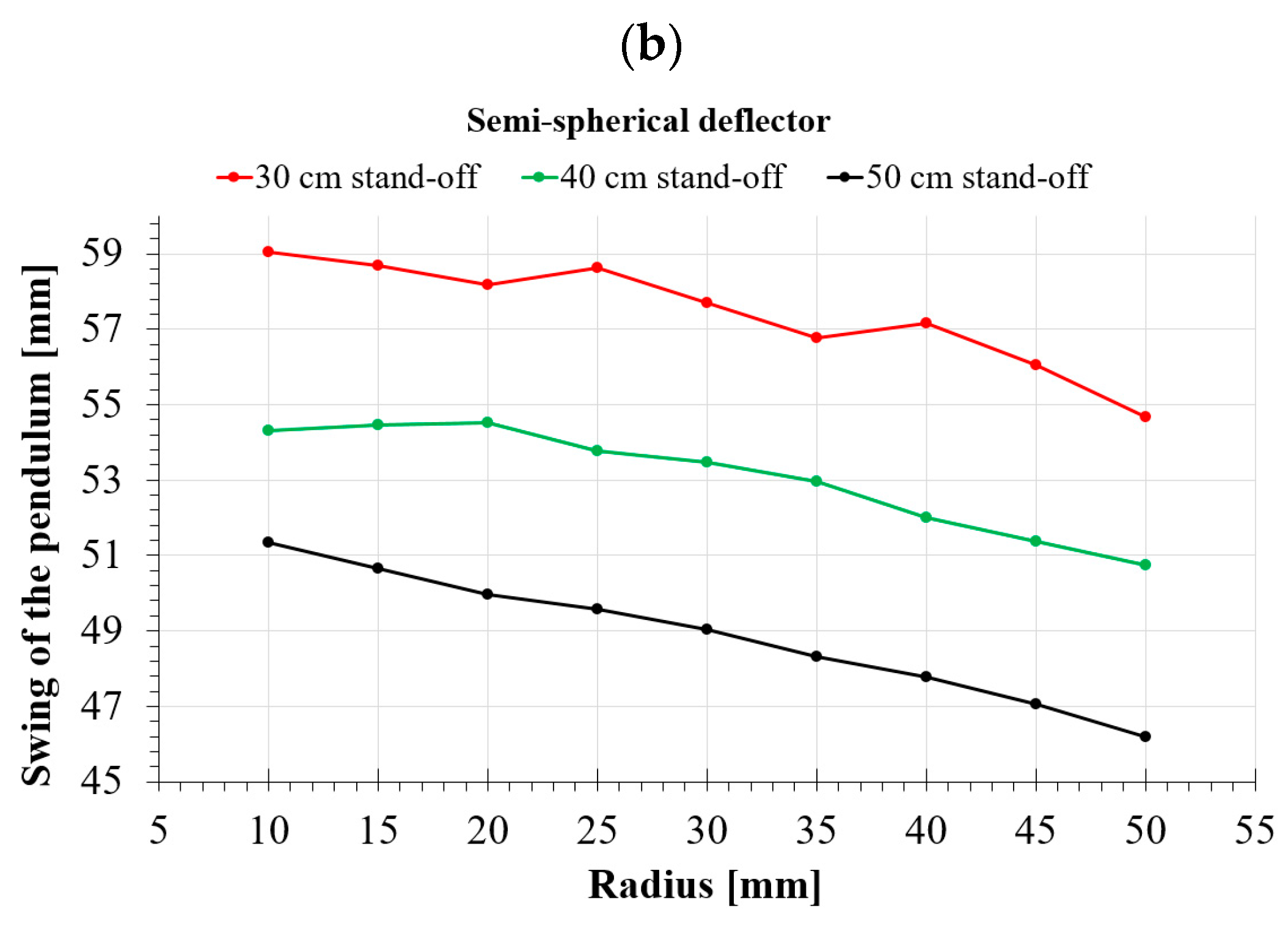
4.3. Numerical Analyses of the Semi-Spherical Deflector
5. Summary
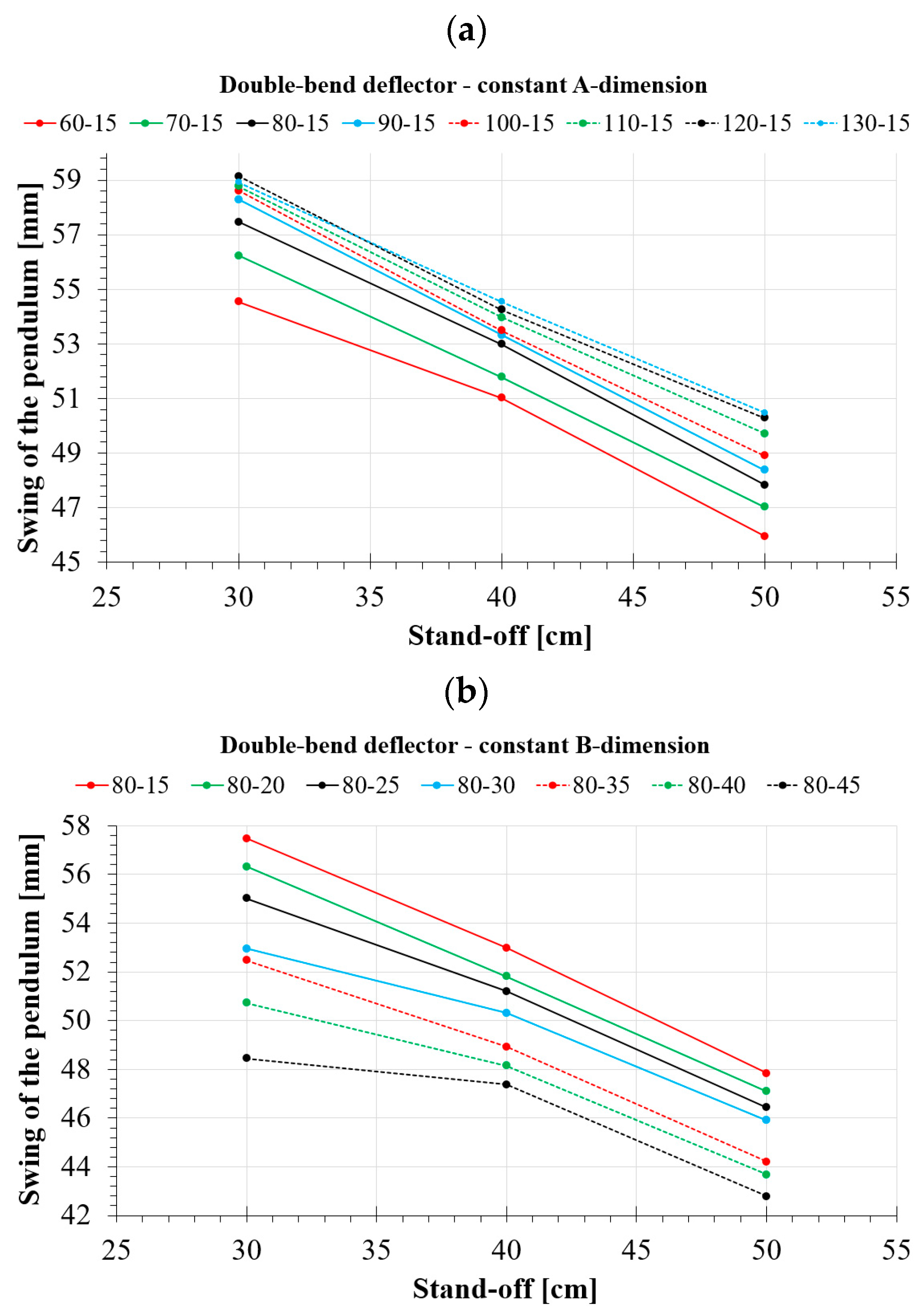
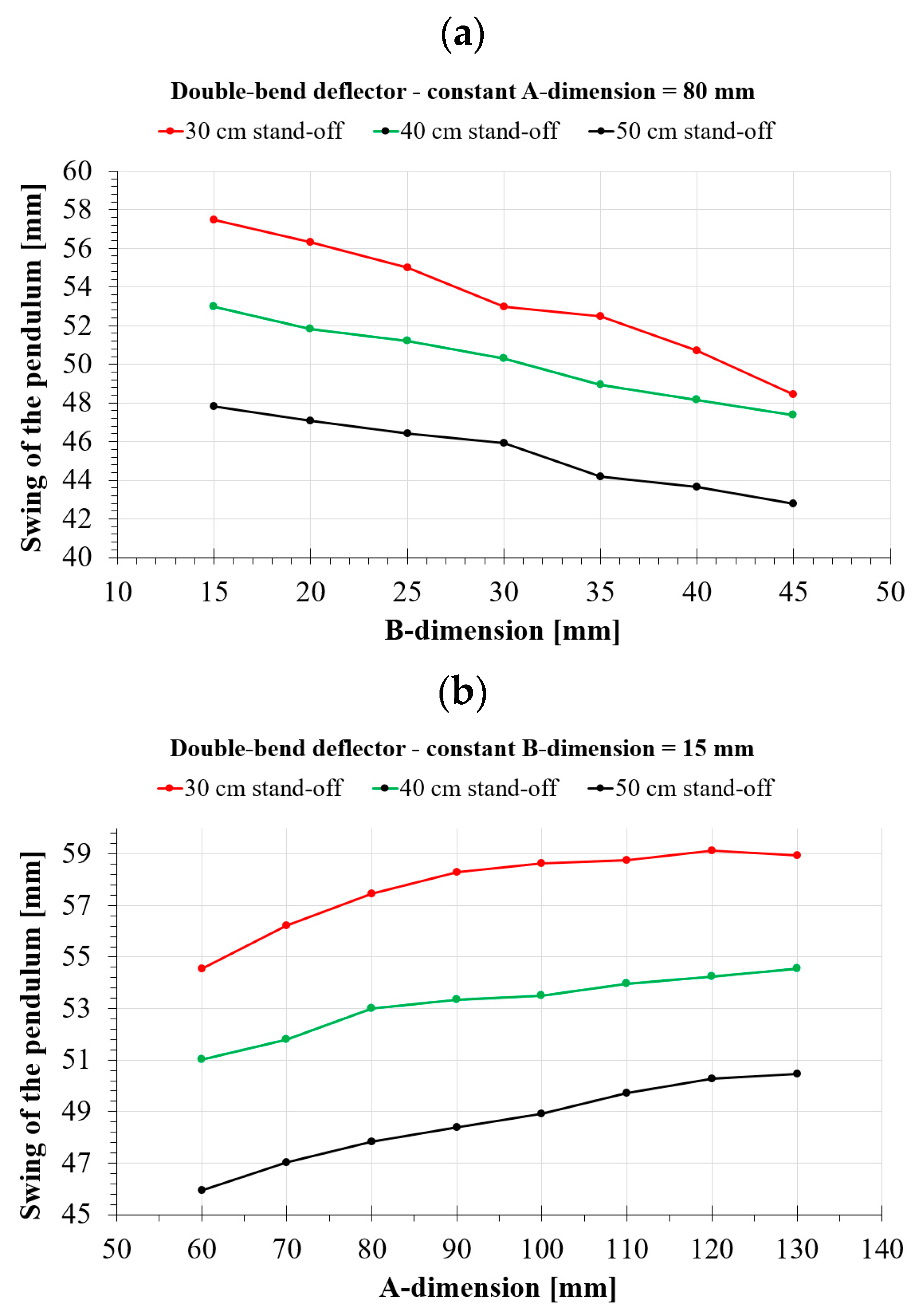
- For a double-bend deflector, an increasing A-size results in a deterioration of its energy dissipation capability. An increasing B-size, on the other hand, results in the opposite situation, i.e., the performance is improved;
- Increasing the A-size from 60 mm to 130 mm results in a 7.4% deterioration in effectiveness for a 30 cm stand-off. When the distance is increased, the deterioration in effectiveness increases slightly to 8.9%;
- The deflector effectiveness increases by as much as 15.6% for a 30 cm stand-off, increasing the B-size from 15 mm to 45 mm. For greater distances, the effectiveness increase decreases to 10.5%;
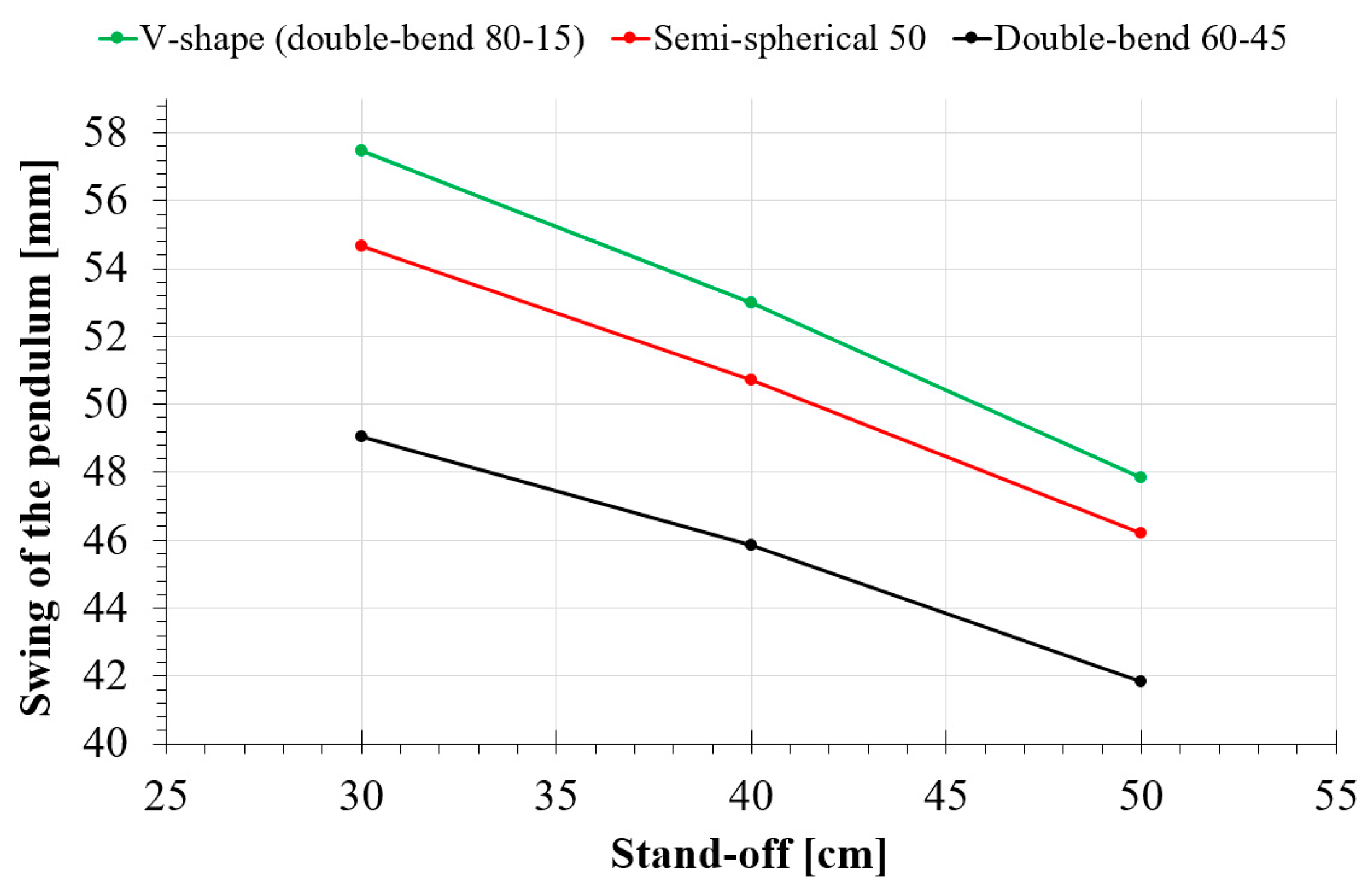
- Using semi-spherical deflectors is more effective, by up to 5%, than a typical V-shaped deflector, whereas for double-bend deflectors, the difference increases to 14.5%
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miller, E.; Distler, M. Mass Casualty Explosives Attacks in Iraq and Afghanistan; START: College Park, MD, USA, 2017. [Google Scholar]
- Taylor, G. The Pressure and Impulse of Submarine Explosion Waves on Plates. Sci. Pap. G Taylor 1941, III, 287–303. [Google Scholar]
- Cole, R. Underwater Explosions; Princeton University Press: Princeton, NJ, USA, 1948. [Google Scholar]
- Kambouchev, N.; Noels, L.; Radovitzky, R. Nonlinear Compressibility Effects in Fluid-Structure Interaction and Their Implications on the Air-Blast Loading of Structures. J. Appl. Phys. 2006, 100, 063519. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Energy and Momentum Transfer in Air Shocks. J. Appl. Mech. 2009, 76, 051307. [Google Scholar] [CrossRef]
- Wang, E.; Wright, J.; Shukla, A. Analytical and Experimental Study on the Fluid Structure Interaction during Air Blast Loading. J. Appl. Phys. 2011, 110, 114901. [Google Scholar] [CrossRef]
- Dharmasena, K.P.; Wadley, H.N.G.; Xue, Z.; Hutchinson, J.W. Mechanical Response of Metallic Honeycomb Sandwich Panel Structures to High-Intensity Dynamic Loading. Int. J. Impact Eng. 2008, 35, 1063–1074. [Google Scholar] [CrossRef]
- Xue, Z.; Hutchinson, J.W. A Comparative Study of Impulse-Resistant Metal Sandwich Plates. Int. J. Impact Eng. 2004, 30, 1283–1305. [Google Scholar] [CrossRef]
- Shen, J.; Lu, G.; Wang, Z.; Zhao, L. Experiments on Curved Sandwich Panels under Blast Loading. Int. J. Impact Eng. 2010, 37, 960–970. [Google Scholar] [CrossRef]
- Studziński, R.; Gajewski, T.; Malendowski, M.; Sumelka, W.; Al-Rifaie, H.; Peksa, P.; Sielicki, P.W. Blast Test and Failure Mechanisms of Soft-Core Sandwich Panels for Storage Halls Applications. Materials 2021, 14, 70. [Google Scholar] [CrossRef]
- Li, W.; Huang, G.; Bai, Y.; Dong, Y.; Feng, S. Dynamic Response of Spherical Sandwich Shells with Metallic Foam Core under External Air Blast Loading—Numerical Simulation. Compos. Struct. 2014, 116, 612–625. [Google Scholar] [CrossRef]
- Li, X.; Zhang, P.; Wang, Z.; Wu, G.; Zhao, L. Dynamic Behavior of Aluminum Honeycomb Sandwich Panels under Air Blast: Experiment and Numerical Analysis. Compos. Struct. 2014, 108, 1001–1008. [Google Scholar] [CrossRef]
- Cui, X.; Zhao, L.; Wang, Z.; Zhao, H.; Fang, D. Dynamic Response of Metallic Lattice Sandwich Structures to Impulsive Loading. Int. J. Impact Eng. 2012, 43, 1–5. [Google Scholar] [CrossRef]
- Barnat, W.; Dziewulski, P.; Niezgoda, T.; Panowicz, R. Application of Composites to Impact Energy Absorption. Comput. Mater. Sci. 2011, 50, 1233–1237. [Google Scholar] [CrossRef]
- Zhang, C.; Cheng, Y.; Zhang, P.; Duan, X.; Liu, J.; Li, Y. Numerical Investigation of the Response of I-Core Sandwich Panels Subjected to Combined Blast and Fragment Loading. Eng. Struct. 2017, 151, 459–471. [Google Scholar] [CrossRef]
- Dmitruk, A.; Naplocha, K.; Pach, J.; Pyka, D.; Ziółkowski, G.; Bocian, M.; Jamroziak, K. Experimental and Numerical Study of Ballistic Resistance of Composites Based on Sandwich Metallic Foams. Appl. Compos. Mater. 2021, 28, 2021–2044. [Google Scholar] [CrossRef]
- Ziętala, M.; Durejko, T.; Panowicz, R.; Konarzewski, M. Microstructure Evolution of 316L Steel Prepared with the Use of Additive and Conventional Methods and Subjected to Dynamic Loads: A Comparative Study. Materials 2020, 13, 4893. [Google Scholar] [CrossRef] [PubMed]
- Płatek, P.; Rajkowski, K.; Cieplak, K.; Sarzyński, M.; Małachowski, J.; Woźniak, R.; Janiszewski, J. Deformation Process of 3D Printed Structures Made from Flexible Material with Different Values of Relative Density. Polymers 2020, 12, 2120. [Google Scholar] [CrossRef]
- Dutkiewicz, J.; Rogal, Ł.; Kalita, D.; Węglowski, M.; Błacha, S.; Berent, K.; Czeppe, T.; Antolak-Dudka, A.; Durejko, T.; Czujko, T. Superelastic Effect in NiTi Alloys Manufactured Using Electron Beam and Focused Laser Rapid Manufacturing Methods. J. Mater. Eng. Perform. 2020, 29, 4463–4473. [Google Scholar] [CrossRef]
- Dutkiewicz, J.; Rogal, Ł.; Kalita, D.; Berent, K.; Antoszewski, B.; Danielewski, H.; Węglowski, M.S.; Łazińska, M.; Durejko, T.; Czujko, T. Microstructure and Properties of Inconel 625 Fabricated Using Two Types of Laser Metal Deposition Methods. Materials 2020, 13, 5050. [Google Scholar] [CrossRef] [PubMed]
- Antolak-Dudka, A.; Płatek, P.; Durejko, T.; Baranowski, P.; Małachowski, J.; Sarzyński, M.; Czujko, T. Static and Dynamic Loading Behavior of Ti6Al4V Honeycomb Structures Manufactured by Laser Engineered Net Shaping (LENSTM) Technology. Materials 2019, 12, 1225. [Google Scholar] [CrossRef]
- Novak, N.; Vesenjak, M.; Ren, Z. Crush Behaviour of Auxetic Cellular Structures. Spec. Issue Cell. Mater. 2018, 30, 4–7. [Google Scholar] [CrossRef]
- Qi, C.; Remennikov, A.; Pei, L.-Z.; Yang, S.; Yu, Z.-H.; Ngo, T.D. Impact and Close-in Blast Response of Auxetic Honeycomb-Cored Sandwich Panels: Experimental Tests and Numerical Simulations. Compos. Struct. 2017, 180, 161–178. [Google Scholar] [CrossRef]
- Deshpande, V.S.; McMeeking, R.M.; Wadley, H.N.G.; Evans, A.G. Constitutive Model for Predicting Dynamic Interactions between Soil Ejecta and Structural Panels. J. Mech. Phys. Solids 2009, 57, 1139–1164. [Google Scholar] [CrossRef]
- Dharmasena, K.P.; Wadley, H.N.G.; Liu, T.; Deshpande, V.S. The Dynamic Response of Edge Clamped Plates Loaded by Spherically Expanding Sand Shells. Int. J. Impact Eng. 2013, 62, 182–195. [Google Scholar] [CrossRef]
- Kyner, A.; Dharmasena, K.; Williams, K.; Deshpande, V.; Wadley, H. Response of Square Honeycomb Core Sandwich Panels to Granular Matter Impact. Int. J. Impact Eng. 2018, 117, 13–31. [Google Scholar] [CrossRef]
- Nurick, G.N.; Lockley, J.P. Experimental Investigation to Evaluate the Effect of the Included Angle of a Folded “V” Shape Plate for Blast Resistance. In Proceedings of the 1st International Conference on Integrity, Reliabaliry and Failure, Porto, Portugal, 19–22 July 1999. [Google Scholar]
- Chung Kim Yuen, S.; Langdon, G.S.; Nurick, G.N.; Pickering, E.G.; Balden, V.H. Response of V-Shape Plates to Localised Blast Load: Experiments and Numerical Simulation. Int. J. Impact Eng. 2012, 46, 97–109. [Google Scholar] [CrossRef]
- Zhao, X.; Shultis, G.; Hurley, R.; Sutton, M.; Fourney, W.; Leiste, U.; Deng, X. Small Scale Models Subjected to Buried Blast Loading Part I: Floorboard Accelerations and Related Passenger Injury Metrics with Protective Hulls. Exp. Mech. 2014, 54, 539–555. [Google Scholar] [CrossRef]
- Zhao, X.; Hurley, R.; Sutton, M.; Fourney, W.; Leiste, U.; Deng, X. Small Scale Models Subjected to Buried Blast Loading Part II: Frame Accelerations with Hulls and Additional Mitigation Methods. Exp. Mech. 2014, 54, 857–869. [Google Scholar] [CrossRef]
- Anderson, C.E.; Behner, T.; Weiss, C.E. Mine Blast Loading Experiments. Int. J. Impact Eng. 2011, 38, 697–706. [Google Scholar] [CrossRef]
- Markose, A.; Rao, C.L. Mechanical Response of V Shaped Plates under Blast Loading. Thin-Walled Struct. 2017, 115, 12–20. [Google Scholar] [CrossRef]
- Trajkovski, J.; Kunc, R.; Prebil, I. Blast Response of Centrally and Eccentrically Loaded Flat-, U-, and V-Shaped Armored Plates: Comparative Study. Shock. Waves 2017, 27, 583–591. [Google Scholar] [CrossRef]
- Li, Y.; Lv, Z.; Wang, Y. Blast Response of Aluminum Foam Sandwich Panel with Double V-Shaped Face Plate. Int. J. Impact Eng. 2020, 144, 103666. [Google Scholar] [CrossRef]
- Stanisławek, S.; Morka, A. On the Blast Mitigation Ability of Multiple V-Shape Deflectors. Shock. Vib. 2020, 2020, 8708974. [Google Scholar] [CrossRef]
- Erdik, A.; Uçar, V. On Evaluation and Comparison of Blast Loading Methods Used in Numerical Simulations. Sak. Üniversitesi Fen Bilim. Enstitüsü Derg. 2018, 22, 1385–1391. [Google Scholar] [CrossRef]
- Vannucci, P.; Masi, F.; Stefanou, I. A Study on the Simulation of Blast Actions on a Monument Structure. 2017. Available online: https://hal.science/hal-01447783v3/document (accessed on 10 February 2023).
- Souli, M.; Ouahsine, A.; Lewin, L. ALE Formulation for Fluid–Structure Interaction Problems. Comput. Methods Appl. Mech. Eng. 2000, 190, 659–675. [Google Scholar] [CrossRef]
- Jin, S.Y.; Majumder, A.; Altenhof, W.; Green, D. Axial Cutting of AA6061-T6 Circular Extrusions under Impact Using Single-and Dual-Cutter Configurations. Int. J. Impact Eng. 2010, 37, 735–753. [Google Scholar] [CrossRef]
- Johnson, G.R. A Constitutive Model and Data for Materials Subjected to Large Strains, High Strain Rates, and High Temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, the Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Ludwik, P. Elemente Der Technologischen Mechanik; Springer: Berlin/Heidelberg, Germany, 1909. [Google Scholar]
- Wuertemberger, L.; Palazotto, A.N. Evaluation of Flow and Failure Properties of Treated 4130 Steel. J. Dyn. Behav. Mater. 2016, 2, 207–222. [Google Scholar] [CrossRef]
- Zhang, D.-N.; Shangguan, Q.-Q.; Xie, C.-J.; Liu, F. A Modified Johnson–Cook Model of Dynamic Tensile Behaviors for 7075-T6 Aluminum Alloy. J. Alloys Compd. 2015, 619, 186–194. [Google Scholar] [CrossRef]
- Tao, Z.; Fan, X.; He, Y.; Jun, M.; Heng, L. A Modified Johnson–Cook Model for NC Warm Bending of Large Diameter Thin-Walled Ti–6Al–4V Tube in Wide Ranges of Strain Rates and Temperatures. Trans. Nonferrous Met. Soc. China 2018, 28, 298–308. [Google Scholar] [CrossRef]
- Hallquist, J. LS-DYNA Theory Manual 680; Livermore Software Technology Corporation: Livermore, CA, USA, 2005. [Google Scholar]
- Włodarczyk, E. Wstęp Do Mechaniki Wybuchu; Polish Wydawnictwo Naukowe PWN: Warsaw, Poland, 1994. [Google Scholar]
- Zhang, G. Experimental Study on Shock Wave Propagation of the Explosion in a Pipe with Holes by High-Speed Schlieren Method. Shock. Vib. 2020, 2020, 8850443. [Google Scholar] [CrossRef]
- Bae, D.-M.; Zakki, A.F. Comparisons of Multi Material ALE and Single Material ALE in LS-DYNA for Estimation of Acceleration Response of Free-Fall Lifeboat. J. Soc. Nav. Archit. Korea 2011, 48, 552–559. [Google Scholar] [CrossRef]

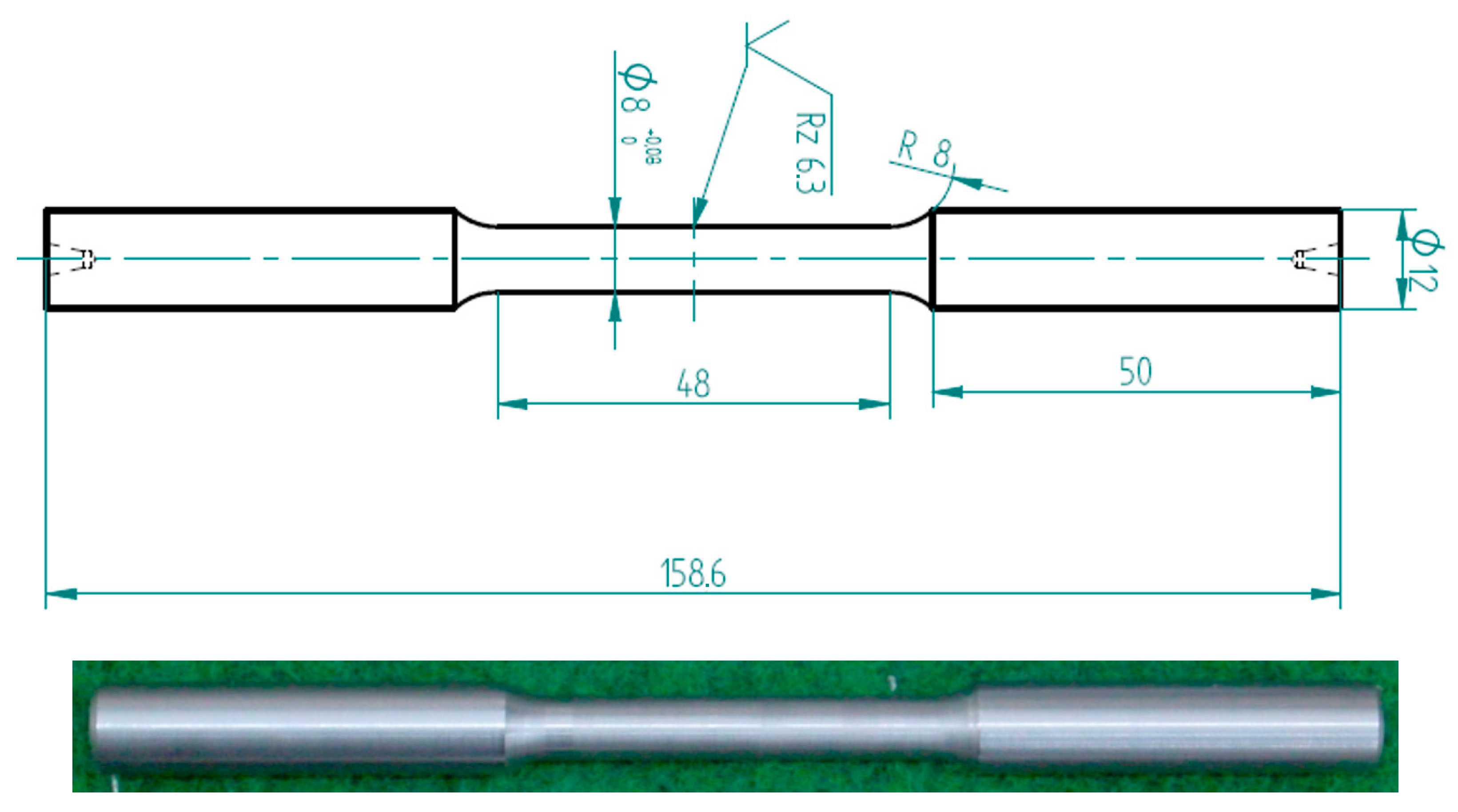
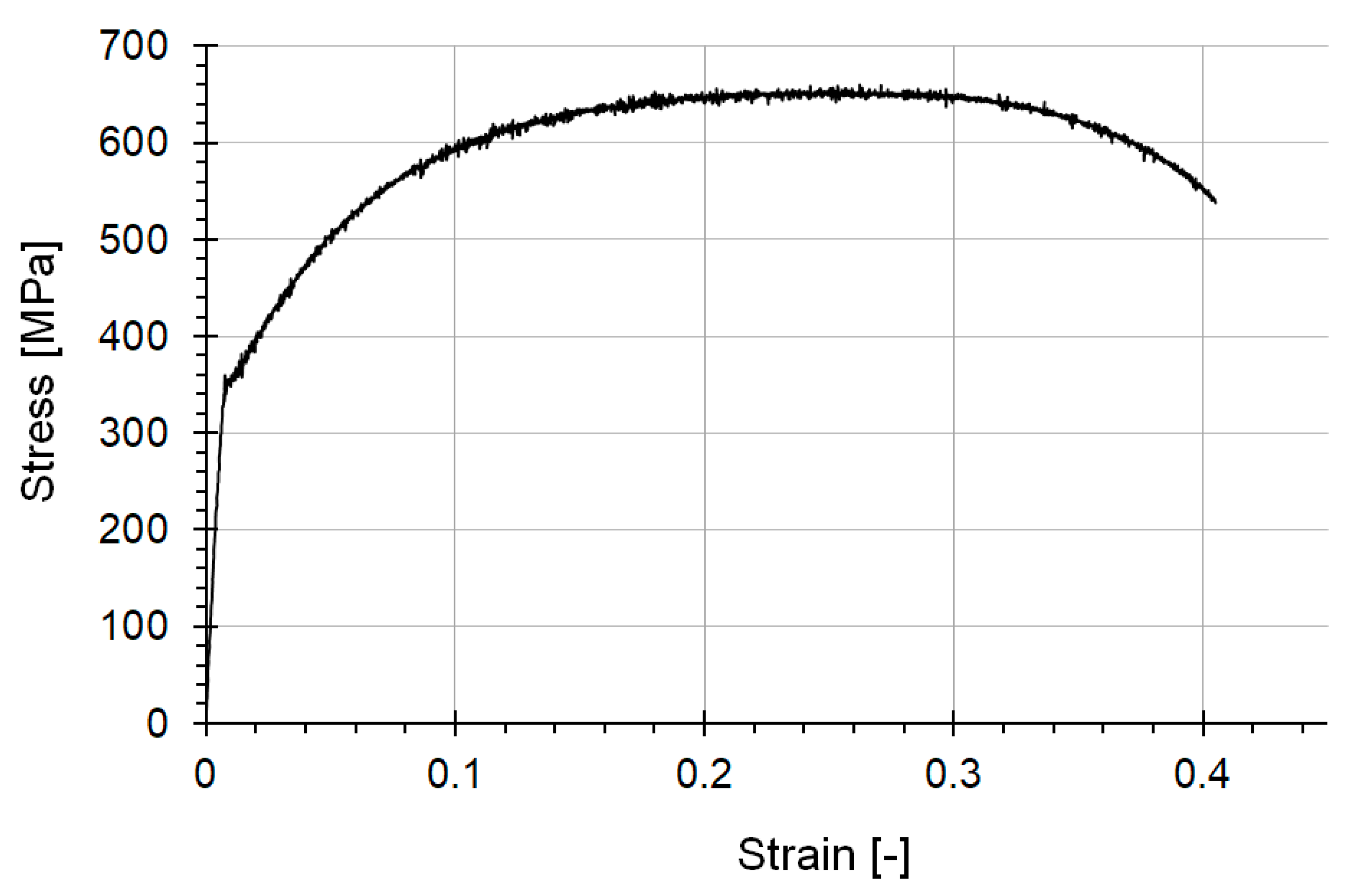
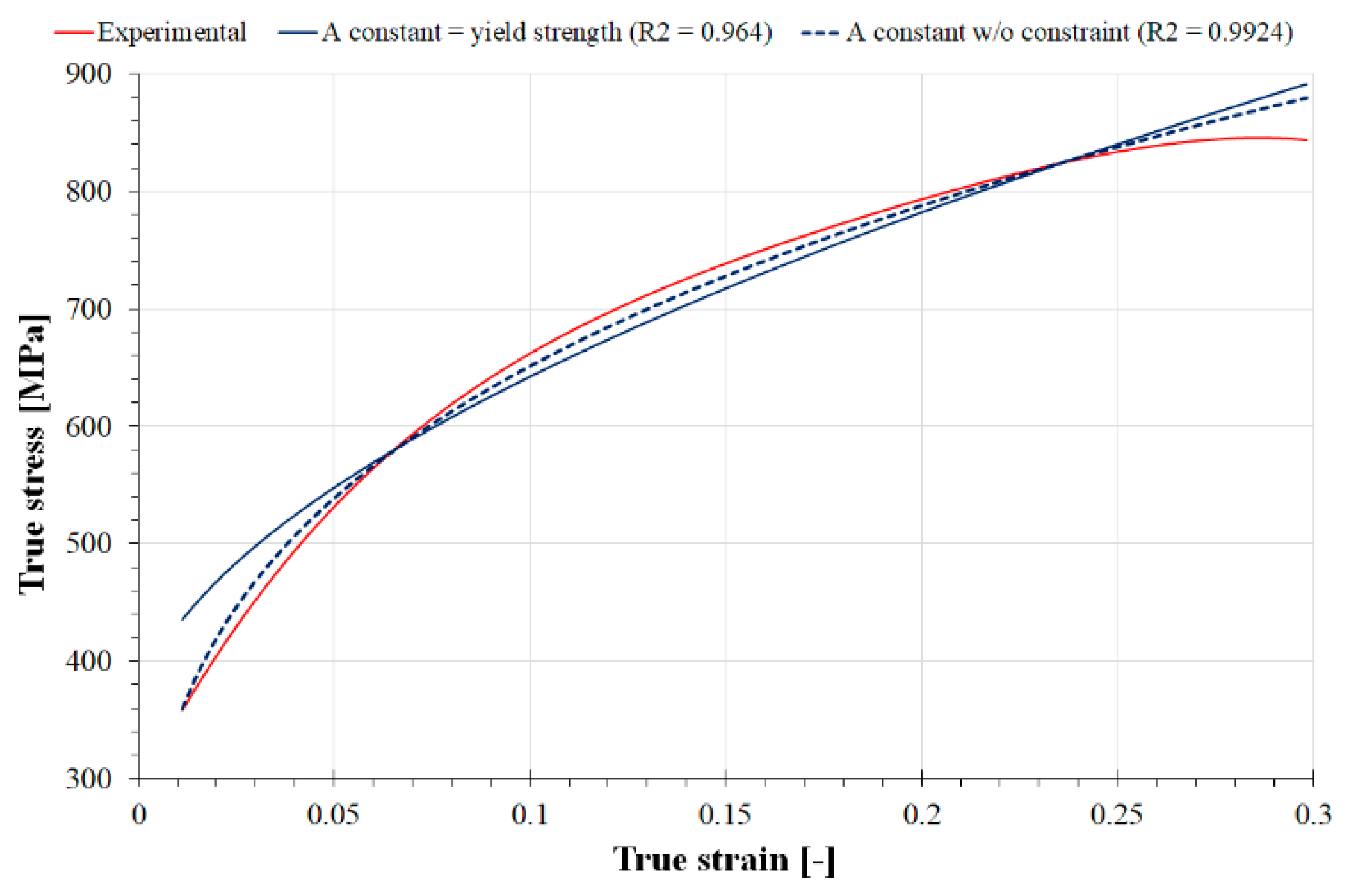



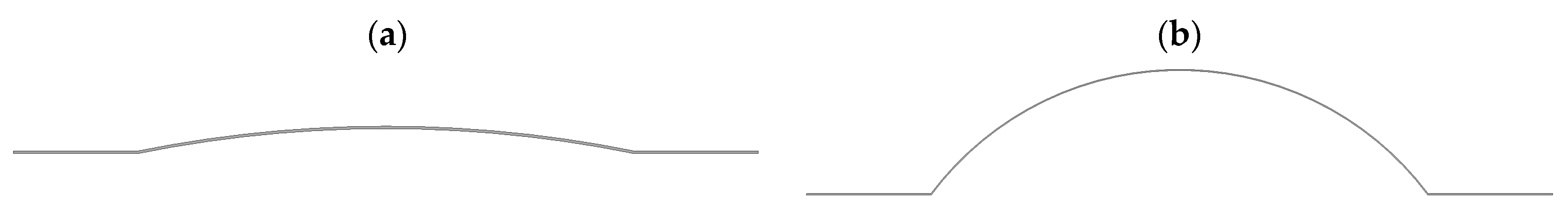


| Rupture [MPa] | Yield Strength [MPa] | Ultimate Strength [MPa] | Strain at Failure [-] | Young’s Modulus [GPa] | Poisson’s Ratio [-] |
|---|---|---|---|---|---|
| 536.7 | 353.3 | 623.2 | 0.308 | 209.6 | 0.307 |
| Parameter | Description | Unit | Value |
|---|---|---|---|
| Density | g/cm3 | 7.89 | |
| E | Young’s modulus | MPa | 209,600 |
| υ | Poisson’s coefficient | - | 0.307 |
| Material constant | MPa | 14 | |
| Material constant | MPa | 1214 | |
| Material constant | - | 0.28 | |
| Material constant | - | 0.0936 | |
| Plastic strain at the failure | - | 0.308 |
| Parameter | Description | Unit | Value |
|---|---|---|---|
| Density | kg/mm3 | 1.42 × 10−6 | |
| D | Detonation velocity | mm/ms | 7200 |
| PCJ | C-J pressure | GPa | 28 |
| A | Explosive charge constant | GPa | 609 |
| B | Explosive charge constant | GPa | 12.95 |
| R1 | Explosive charge constant | - | 4.5 |
| R2 | Explosive charge constant | - | 1.4 |
| ω | Explosive charge constant | - | 0.25 |
| Parameter | Description | Unit | Value |
|---|---|---|---|
| Density | kg/mm3 | 1.2 × 10−9 | |
| C4 | Constant | - | 0.4 |
| C5 | Constant | - | 0.4 |
| Deflector Type | Pendulum Swing—Experiment [mm] | Pendulum Swing—Numerical [mm] | Difference [%] |
|---|---|---|---|
| Double-bend 100-15 | 62.79 | 58.62 | 6.64 |
| Semi-spherical 50 | 57.91 | 54.66 | 5.61 |
| Max. Swing of the Pendulum [mm] | |||
|---|---|---|---|
| Deflector Size | 30 cm Stand-Off | 40 cm Stand-Off | 50 cm Stand-Off |
| 60-15 | 54.54 | 51.02 | 45.95 |
| 70-15 | 56.23 | 51.78 | 47.03 |
| 80-15 | 57.47 | 52.99 | 47.83 |
| 90-15 | 58.29 | 53.33 | 48.38 |
| 100-15 | 58.62 | 53.49 | 48.91 |
| 110-15 | 58.77 | 53.97 | 49.71 |
| 120-15 | 59.14 | 54.25 | 50.28 |
| 130-15 | 58.93 | 54.55 | 50.47 |
| 80-15 | 57.47 | 52.99 | 47.83 |
| 80-20 | 56.32 | 51.82 | 47.10 |
| 80-25 | 55.02 | 51.20 | 46.43 |
| 80-30 | 52.96 | 50.31 | 45.91 |
| 80-35 | 52.47 | 48.93 | 44.21 |
| 80-40 | 50.72 | 48.15 | 43.67 |
| 80-45 | 48.45 | 47.38 | 42.79 |
| Max. Swing of the Pendulum [mm] | |||
|---|---|---|---|
| Deflector Size | 30 cm Stand-Off | 40 cm Stand-Off | 50 cm Stand-Off |
| 60-15 | 54.54 | 51.02 | 45.95 |
| 60-20 | 53.75 | 49.43 | 45.26 |
| 60-25 | 51.46 | 48.34 | 44.46 |
| 60-30 | 51.58 | 47.98 | 43.28 |
| 60-35 | 50.82 | 46.91 | 42.58 |
| 60-40 | 48.96 | 46.48 | 42.51 |
| 60-45 | 49.03 | 45.84 | 41.84 |
| Max. Swing of the Pendulum [mm] | |||
|---|---|---|---|
| Deflector Size | 30 cm Stand-Off | 40 cm Stand-Off | 50 cm Stand-Off |
| 10 | 59.04 | 54.31 | 51.34 |
| 15 | 58.69 | 54.46 | 50.65 |
| 20 | 58.19 | 54.52 | 49.95 |
| 25 | 58.62 | 53.76 | 49.57 |
| 30 | 57.69 | 53.46 | 49.03 |
| 35 | 56.77 | 52.97 | 48.31 |
| 40 | 57.15 | 52.01 | 47.79 |
| 45 | 56.05 | 51.37 | 47.07 |
| 50 | 54.66 | 50.73 | 46.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konarzewski, M.; Panowicz, R.; Jeschke, A. Double-Bend and Semi-Spherical Energy Deflectors’ Blast Load Efficiency—A Comparative Study. Appl. Sci. 2023, 13, 6752. https://doi.org/10.3390/app13116752
Konarzewski M, Panowicz R, Jeschke A. Double-Bend and Semi-Spherical Energy Deflectors’ Blast Load Efficiency—A Comparative Study. Applied Sciences. 2023; 13(11):6752. https://doi.org/10.3390/app13116752
Chicago/Turabian StyleKonarzewski, Marcin, Robert Panowicz, and Adam Jeschke. 2023. "Double-Bend and Semi-Spherical Energy Deflectors’ Blast Load Efficiency—A Comparative Study" Applied Sciences 13, no. 11: 6752. https://doi.org/10.3390/app13116752
APA StyleKonarzewski, M., Panowicz, R., & Jeschke, A. (2023). Double-Bend and Semi-Spherical Energy Deflectors’ Blast Load Efficiency—A Comparative Study. Applied Sciences, 13(11), 6752. https://doi.org/10.3390/app13116752






