Construct the Optimum Process Model for Transistor Gaskets with Six-Sigma DMAIC
Abstract
:1. Introduction
2. Research Methods
2.1. Define
2.2. Measure
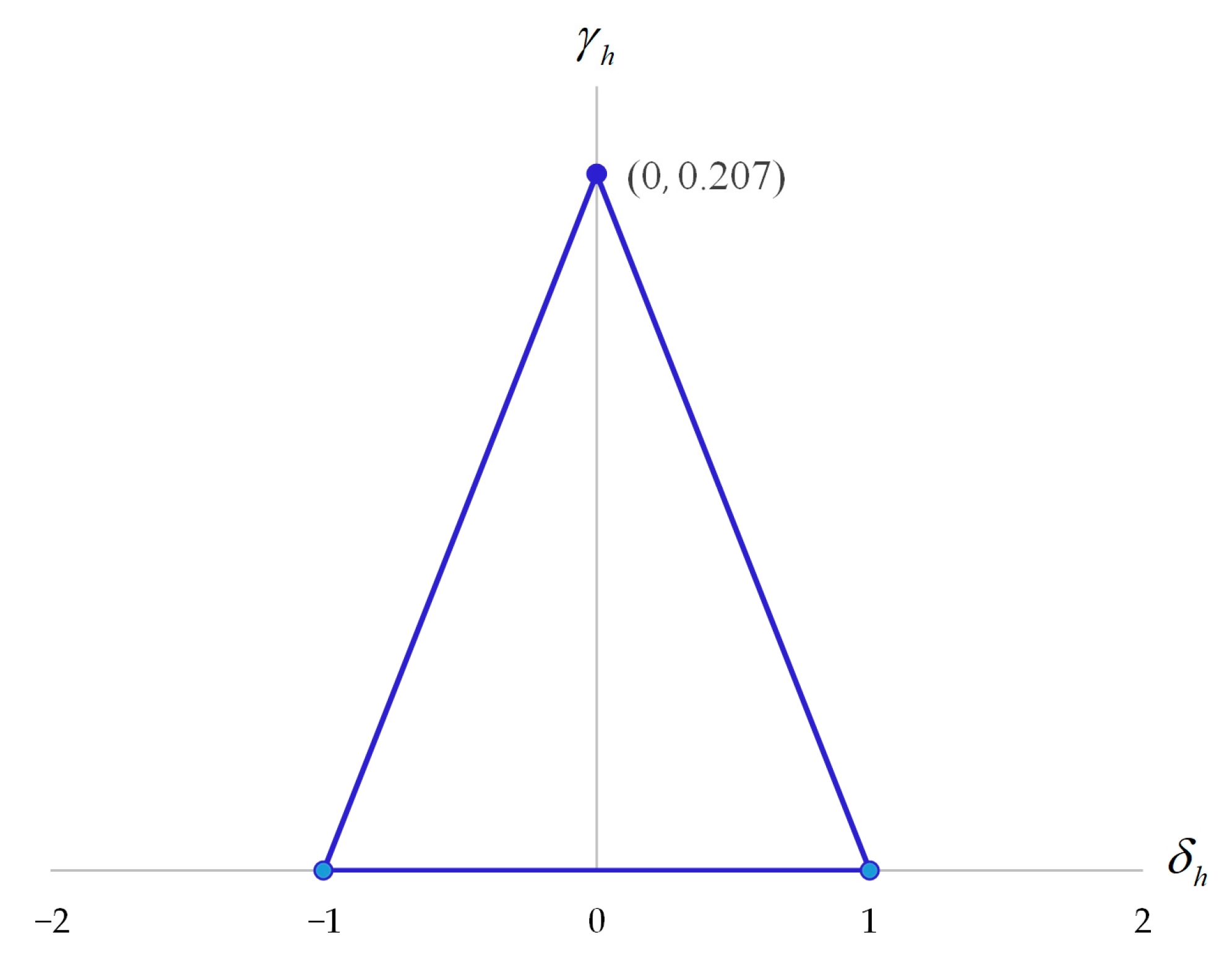
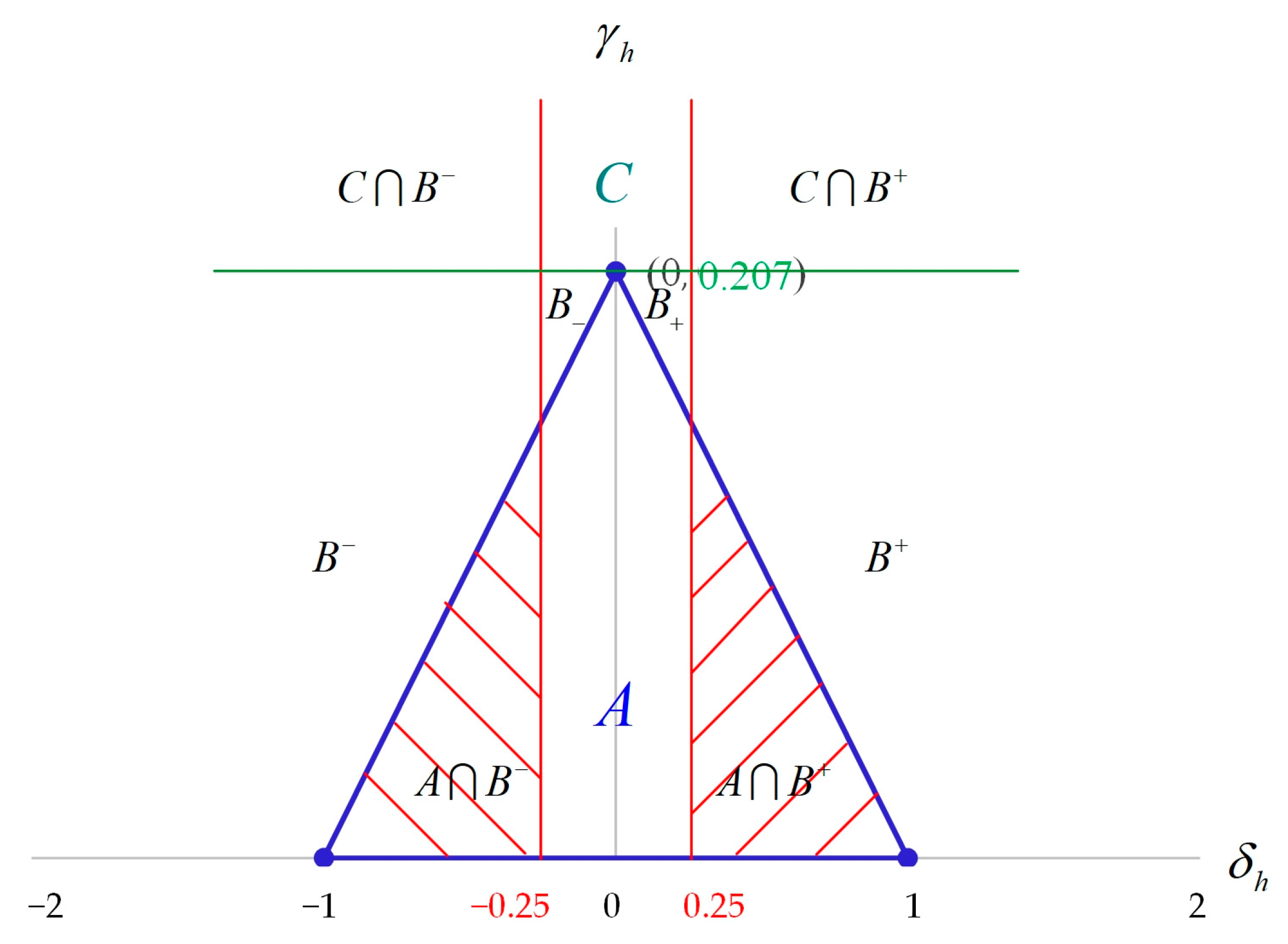
2.3. Analyze
- (1)
- When , the process capability has attained the required quality level but the process is still in a state of right deviation. As long as the machine parameters are adjusted, the process accuracy can be raised and the process quality level can be greatly lifted.
- (2)
- When , the process capability has met the requirements of the quality level but the process is still in a state of left deviation. As long as the machine parameters are modified, the process accuracy can be enhanced and the process quality level can be significantly boosted.
- (3)
- When , the process capability does not get to the required quality level. Thus, we need to adjust the machine parameters to improve the right deviation of the process or conduct Taguchi experiments to moderately reduce the process variation, thereby raising the process quality level.
- (4)
- When , the process capability does not attain the required quality level. Therefore, it is necessary to adjust the machine parameters to better the left deviation of the process or carry out Taguchi experiments to moderately decrease the process variation, thereby advancing the process quality level.
- (5)
- When , the process capability does not attain the required quality level and the process variation is too large. Therefore, we need to lower the process variation and increase the process accuracy, thereby raising the process quality level.
- (6)
- When , the process capability does not attain the required quality level, the process variation is too large, and the process is in a state of right deviation. Consequently, we need to reduce the process variation and ameliorate the correct deviation of the process so as to level up the precision and accuracy of the process and increase the process quality level.
- (7)
- When , the process capability does not attain the required quality level, the process variation is too large, and the process is in a state of left deviation. Accordingly, we need to reduce the process variation and ameliorate the left deviation of the process in order to raise the precision and accuracy of the process and further enhance the process quality level.
2.4. Improve and Control
3. A Practical Example
3.1. Define
3.2. Measure
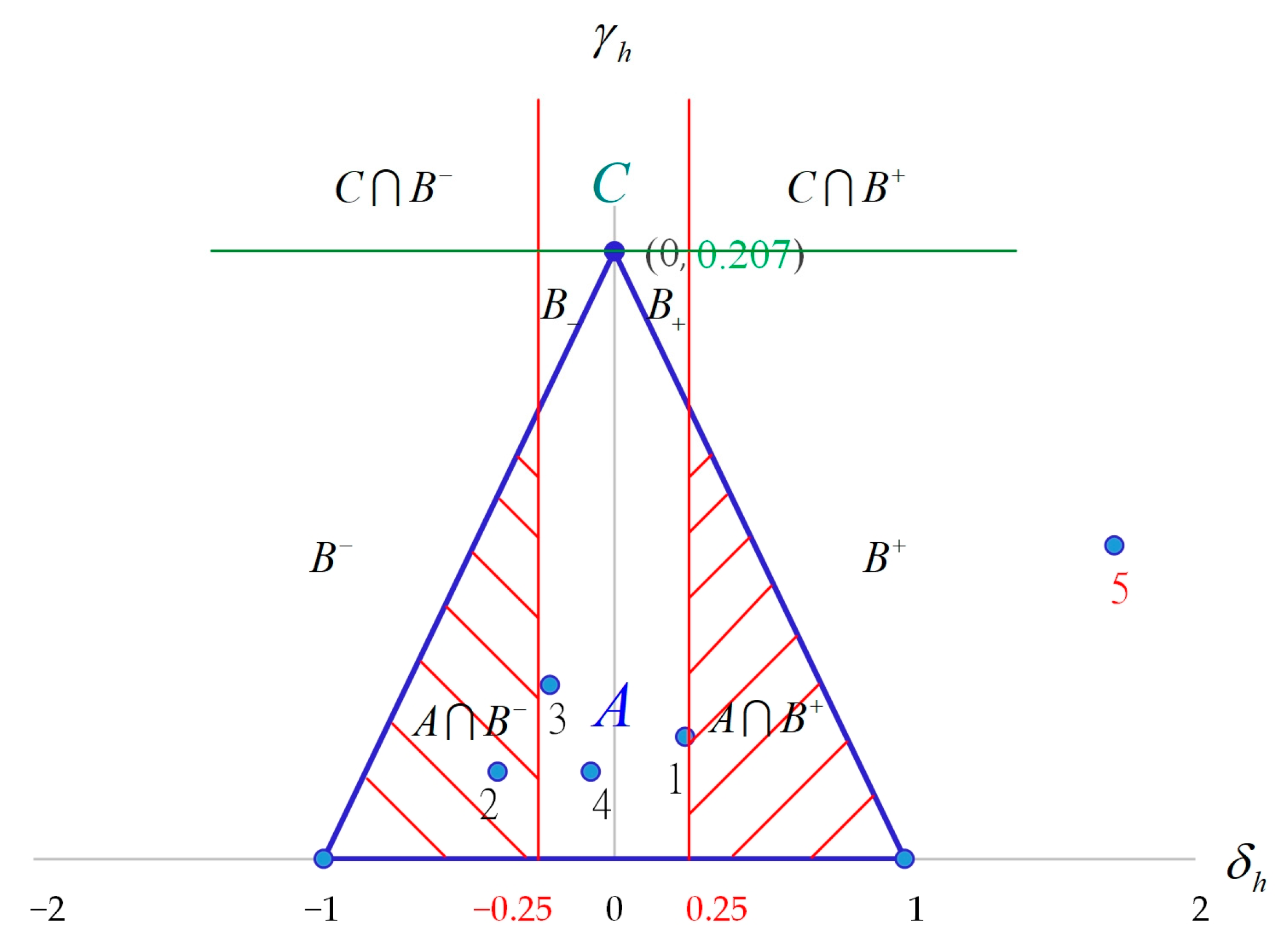
3.3. Analyze
3.4. Improve and Control
4. Conclusions
5. Research Limitation
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hoskin, J.; Stuart, B.; Taylor, J. A Motorola Commitment: A Six Sigma Mandate, The Motorola Guide to Statistical Process Control for Continuous Improvement Towards Six Sigma Quality; Morotola Co.: Chicago, IL, USA, 1988. [Google Scholar]
- Noguera, J.; Nielsen, T. Implement six sigma for interconnect technology. In Proceedings of the ASQC Quality Congress Transactions, Nashville, TN, USA, 18–20 May 1992; pp. 538–544. [Google Scholar]
- Pande, P.S.; Neuman, R.P.; Cavanagh, R.R. The Six Sigma Way: How GE Motorola and Other Top Companies Are Honing Their Performance; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Antony, J. Six sigma for service processes. Bus. Process Manag. J. 2006, 12, 234–248. [Google Scholar] [CrossRef]
- Bilgin Turna, G. Application of lean six sigma for yield improvement in the stainless steel industry: A recipe from Türkiye. Int. J. Lean Six Sigma 2023, 14, 534–554. [Google Scholar] [CrossRef]
- Aktar Demirtas, E.; Gultekin, O.S.; Uskup, C. A case study for surgical mask production during the COVID-19 pandemic: Continuous improvement with kaizen and 5S applications. Int. J. Lean Six Sigma 2023, 14, 679–703. [Google Scholar] [CrossRef]
- Kregel, I.; Stemann, D.; Koch, J.; Coners, A. Process mining for six sigma: Utilising digital traces. Comput. Ind. Eng. 2021, 153, 107083. [Google Scholar] [CrossRef]
- Nikzad, E.; Amiri, A.; Amirkhani, F. Estimating total and specific process capability indices in three-stage processes with measurement errors. J. Stat. Comput. Simul. 2018, 88, 3033–3064. [Google Scholar] [CrossRef]
- De-Felipe, D.; Benedito, E. Monitoring high complex production processes using process capability indices. Int. J. Adv. Manuf. Technol. 2017, 93, 1257–1267. [Google Scholar] [CrossRef] [Green Version]
- Otsuka, A.; Nagata, F. Quality design method using process capability index based on Monte-Carlo method and real-coded genetic algorithm. Int. J. Prod. Econ. 2018, 204, 358–364. [Google Scholar] [CrossRef]
- Liao, M.Y.; Wu, C.W. Process capability monitoring and change-point analysis for S-type quality characteristic. Qual. Technol. Quant. Manag. 2023. [Google Scholar] [CrossRef]
- Chatterjee, M.; Chakraborty, A.K. Distributions and process capability control charts for CPU and CPL using subgroup information. Commun. Stat. Theory Methods 2015, 44, 4333–4353. [Google Scholar] [CrossRef]
- Yu, C.M.; Huang, T.H.; Chen, K.S.; Huang, T.Y. Construct Six Sigma DMAIC Improvement Model for Manufacturing Process Quality of Multi-Characteristic Products. Mathematics 2022, 10, 814. [Google Scholar] [CrossRef]
- Chen, K.S.; Chang, T.C. A modified approach for six sigma quality assessment of product with multiple characteristics in intelligent manufacturing environments. J. Test. Eval. 2022, 50, 3035–3053. [Google Scholar] [CrossRef]
- Almazah, M.M.A.; Ali, F.A.M.; Eltayeb, M.M.; Atta, A. Comparative analysis four different ways of calculating yield index SSSpk based on information of control chart, and six sigma, to measuring the process performance in industries: Case study in Aden’s oil refinery, Yemen. IEEE Access 2021, 9, 134005–134021. [Google Scholar] [CrossRef]
- Suppipat, S.; Hu, A.H. Achieving sustainable industrial ecosystems by design: A study of the ICT and electronics industry in Taiwan. J. Clean Prod. 2022, 369, 133393. [Google Scholar] [CrossRef]
- Kao, F.C.; Huang, S.C.; Lo, H.W. A rough-fermatean DEMATEL approach for sustainable development evaluation for the manufacturing industry. Int. J. Fuzzy Syst. 2022, 24, 3244–3264. [Google Scholar] [CrossRef]
- Liao, R.; He, Y.; Feng, T.; Yang, X.; Dai, W.; Zhang, W. Mission reliability-driven risk-based predictive maintenance approach of multistate manufacturing system. Reliab. Eng. Syst. Saf. 2023, 236, 109273. [Google Scholar] [CrossRef]
- Wan, Q.; Chen, L.; Zhu, M. A reliability-oriented integration model of production control, adaptive quality control policy and maintenance planning for continuous flow processes. Comput. Ind. Eng. 2023, 176, 108985. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, Y.; Meng, X.; Zhang, D.; Ding, N.; Ren, Z.; Gao, W.; Sun, Z. Life cycle assessment on the vanadium production process: A multi-objective assessment under environmental and economic perspectives. Resour. Conserv. Recycl. 2023, 192, 106926. [Google Scholar] [CrossRef]
- Feng, Y.; Hong, Z.; Tian, G.; Li, Z.; Tan, J.; Hu, H. Environmentally friendly MCDM of reliability-based product optimisation combining DEMATEL-based ANP, interval uncertainty and vlse kriterijumska optimizacija kompromisno resenje (VIKOR). Inf. Sci. 2018, 442–443, 128–144. [Google Scholar] [CrossRef]
- Kane, V.E. Process capability indices. J. Qual. Technol. 1986, 18, 41–52. [Google Scholar] [CrossRef]
- Boyles, R.A. The Taguchi capability index. J. Qual. Technol. 1991, 23, 17–26. [Google Scholar] [CrossRef]
- Kumar, P.; Singh, D.; Bhamu, J. Development and validation of DMAIC based framework for process improvement: A case study of indian manufacturing organization. Int. J. Qual. Reliab. Manag. 2021, 38, 1964–1991. [Google Scholar] [CrossRef]
- Hollingshed, M. Standardizing six sigma green belt training: Identification of the most frequently used measure phase DMAIC tools. Int. J. Lean Six Sigma 2022, 13, 276–294. [Google Scholar] [CrossRef]
- Chen, K.S.; Hung, Y.H.; Su, Y.T. Multiple manufacturing processing target value setting models: A case study on grinding and polishing processes of the electric vehicle motor shaft. J. Test. Eval. 2022, 50, 1468–1484. [Google Scholar] [CrossRef]
- Wu, M.F.; Chen, H.Y.; Chang, T.C.; Wu, C.F. Quality evaluation of internal cylindrical grinding process with multiple quality characteristics for gear products. Int. J. Prod. Res. 2019, 57, 6687–6701. [Google Scholar] [CrossRef]
- Lin, C.J.; Pearn, W.L.; Huang, J.Y.; Chen, Y.H. Group selection for processes with multiple quality characteristics. Commun. Stat. Theory Methods 2018, 47, 3923–3934. [Google Scholar] [CrossRef]
| Item (h) | Quality Characteristics | Type | Tolerance Spec. | Unit | Inspection Equipment |
|---|---|---|---|---|---|
| 1 | Diameter of fitting assembly parts | NTB | 4.5 ± 0.2 | mm | PIN gauge |
| 2 | Diameter of fitting assembly hole | NTB | 9.8 ± 0.2 | mm | Caliper |
| 3 | Height of fitting assembly parts | NTB | 10.3 + 0/−0.3 | mm | Caliper |
| 4 | Spacing | NTB | 2 ± 0.2 | mm | Caliper |
| 5 | Eccentric control | STB | <0.1 | mm | 2.5D optical projector |
| Item | Quality Characteristics | ||||
|---|---|---|---|---|---|
| h = 1 | Diameter of fitting assembly parts | ||||
| h = 2 | Diameter of fitting assembly hole | ||||
| h = 3 | Height of fitting assembly parts | ||||
| h = 4 | Spacing | ||||
| h = 5 | Eccentric control |
| Quality Characteristic h | Quality Zone | |||
|---|---|---|---|---|
| h = 1 | 0.27 | 0.07 | (0.244, 0.056) | A |
| h = 2 | −0.42 | 0.05 | (−0.401, 0.040) | A |
| h = 3 | −0.26 | 0.10 | (−0.222, 0.080) | A |
| h = 4 | −0.10 | 0.05 | (−0.081, 0.040) | A |
| h = 5 | 1.79 | 0.18 | (1.722, 0.144) |
| Injection speed (Control factors) | The injection screw advances to push the hot melt adhesive forward and inject it. It is best to fill the mold cavity as quickly as possible so that weld lines can have better consistency. |
| Barrel temperature (Control factors) | This mainly affects the difficulty in product processing. If the temperature of the hot melt adhesive is too low, then the viscosity of plastics will be higher. The finished product is difficult to process, so it is prone to short shots. |
| Hold pressure (Control factors) | When the melted adhesive has completely filled the mold cavity, it continues to maintain a state of high pressure in order to supplement the shrinkage of the plastic volume caused by cooling. Additionally, if the plastics are insufficient, more are added to ensure that the mold cavity is completely filled. |
| Mold temperature (Control factors) | The mold temperature distribution and the plastic heat transfer behavior are mainly affected. If the mold temperature is too low, then plastics will be more likely to cool and condense earlier, which will cause short shots of the finished goods. |
| Injection pressure (Fixed factors) | This refers to the plastic pressure at the front end of the screw, which is the pressure generated by the hydraulic cylinder and formed on the injection rod. |
| Hold time (Fixed factors) | It is continuously effective time, of which the length will affect burr and the change of product size. |
| Factor | Level 1 | Level 2 | Level 3 |
|---|---|---|---|
| Injection speed (mm/s) | 20 | 40 | 60 |
| Barrel temperature (°C) | 250 | 260 | 270 |
| Hold pressure (kg/cm2) | 15 | 25 | 35 |
| Mold temperature (°C) | 75 | 85 | 95 |
| Experiment No. | 1 | 2 | 3 | 4 | A | B | C | D |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 20 | 250 | 15 | 75 |
| 2 | 1 | 2 | 2 | 2 | 20 | 250 | 15 | 75 |
| 3 | 1 | 3 | 3 | 3 | 20 | 250 | 15 | 75 |
| 4 | 2 | 1 | 2 | 3 | 40 | 260 | 25 | 85 |
| 5 | 2 | 2 | 3 | 1 | 40 | 260 | 25 | 85 |
| 6 | 2 | 3 | 1 | 2 | 40 | 260 | 25 | 85 |
| 7 | 3 | 1 | 3 | 2 | 60 | 270 | 35 | 95 |
| 8 | 3 | 2 | 1 | 3 | 60 | 270 | 35 | 95 |
| 9 | 3 | 3 | 2 | 1 | 60 | 270 | 35 | 95 |
| No. | A | B | C | D | Y1 | Y2 | Y3 | Y4 | SN |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 0.187 | 0.200 | 0.152 | 0.204 | 14.569 |
| 2 | 1 | 2 | 2 | 2 | 0.205 | 0.184 | 0.183 | 0.164 | 14.677 |
| 3 | 1 | 3 | 3 | 3 | 0.192 | 0.164 | 0.159 | 0.163 | 15.391 |
| 4 | 2 | 1 | 2 | 3 | 0.154 | 0.163 | 0.186 | 0.166 | 15.554 |
| 5 | 2 | 2 | 3 | 1 | 0.152 | 0.152 | 0.181 | 0.203 | 15.222 |
| 6 | 2 | 3 | 1 | 2 | 0.183 | 0.154 | 0.176 | 0.187 | 15.116 |
| 7 | 3 | 1 | 3 | 2 | 0.159 | 0.192 | 0.164 | 0.204 | 14.859 |
| 8 | 3 | 2 | 1 | 3 | 0.154 | 0.184 | 0.154 | 0.184 | 15.408 |
| 9 | 3 | 3 | 2 | 1 | 0.176 | 0.187 | 0.203 | 0.200 | 14.343 |
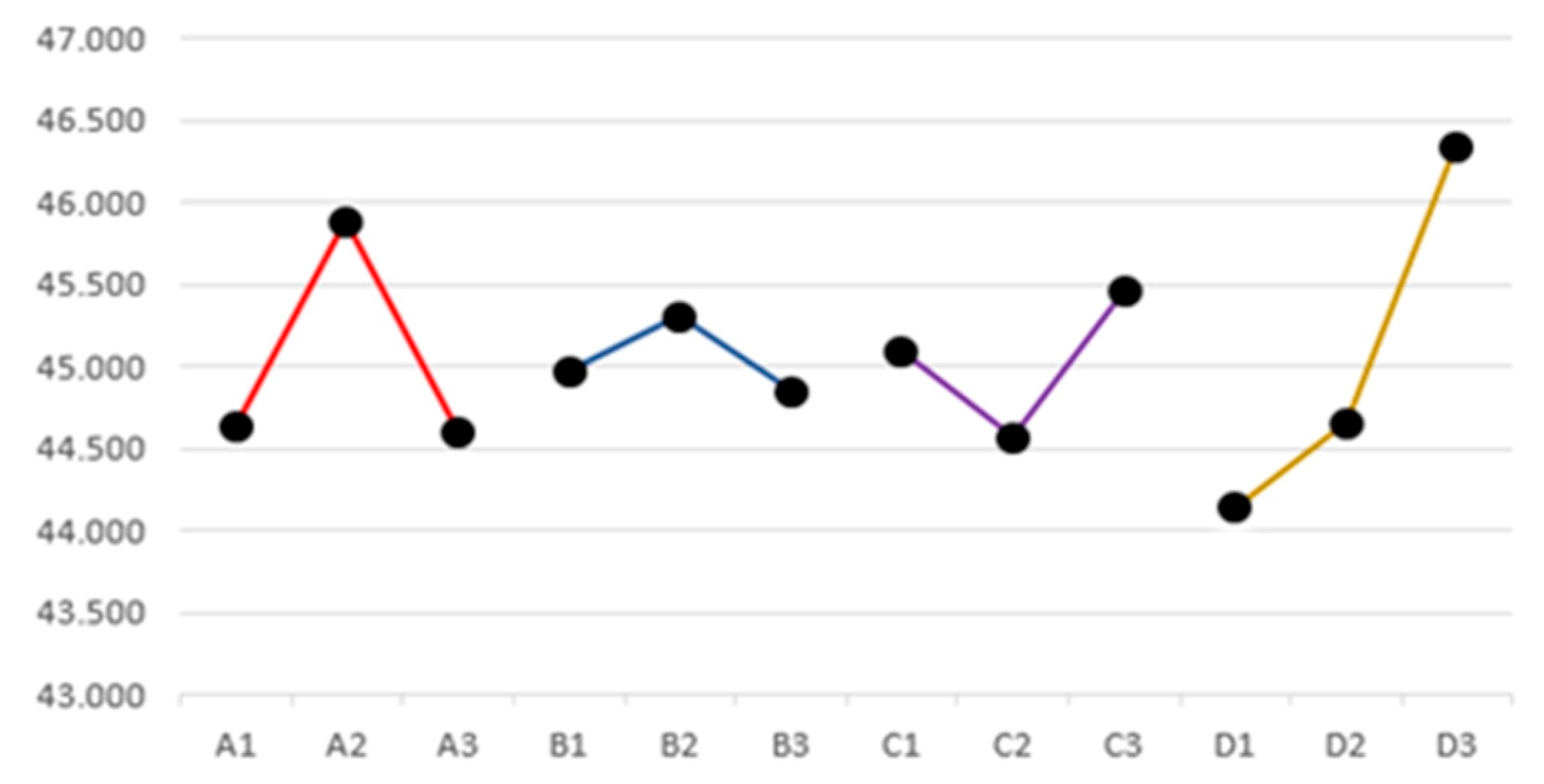
| Level | A. Injection Speed | B. Barrel Temperature | C. Hold Pressure | D. Mold Temperature |
|---|---|---|---|---|
| Level 1 | 44.636 | 44.983 | 45.093 | 44.134 |
| Level 2 | 45.893 | 45.307 | 44.574 | 44.652 |
| Level 3 | 44.610 | 44.850 | 45.472 | 46.353 |
| Difference | 1.283 | 0.457 | 0.898 | 2.219 |
| Rank | 2 | 4 | 3 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.-S.; Ye, G.-P.; Yu, C.-M.; Yu, C.-H. Construct the Optimum Process Model for Transistor Gaskets with Six-Sigma DMAIC. Appl. Sci. 2023, 13, 6895. https://doi.org/10.3390/app13126895
Chen K-S, Ye G-P, Yu C-M, Yu C-H. Construct the Optimum Process Model for Transistor Gaskets with Six-Sigma DMAIC. Applied Sciences. 2023; 13(12):6895. https://doi.org/10.3390/app13126895
Chicago/Turabian StyleChen, Kuen-Suan, Guo-Ping Ye, Chun-Min Yu, and Chun-Hung Yu. 2023. "Construct the Optimum Process Model for Transistor Gaskets with Six-Sigma DMAIC" Applied Sciences 13, no. 12: 6895. https://doi.org/10.3390/app13126895
APA StyleChen, K.-S., Ye, G.-P., Yu, C.-M., & Yu, C.-H. (2023). Construct the Optimum Process Model for Transistor Gaskets with Six-Sigma DMAIC. Applied Sciences, 13(12), 6895. https://doi.org/10.3390/app13126895







