Comparison of Single Control Loop Performance Monitoring Methods
Abstract
:1. Introduction
2. Materials and Methods
2.1. Implemented CPM Indices
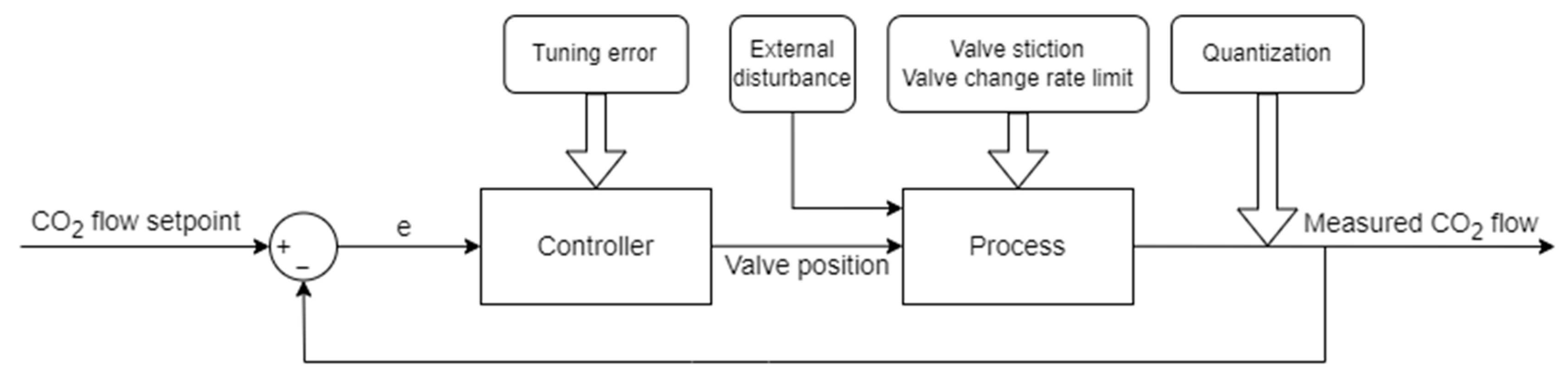
2.2. Simulated Process
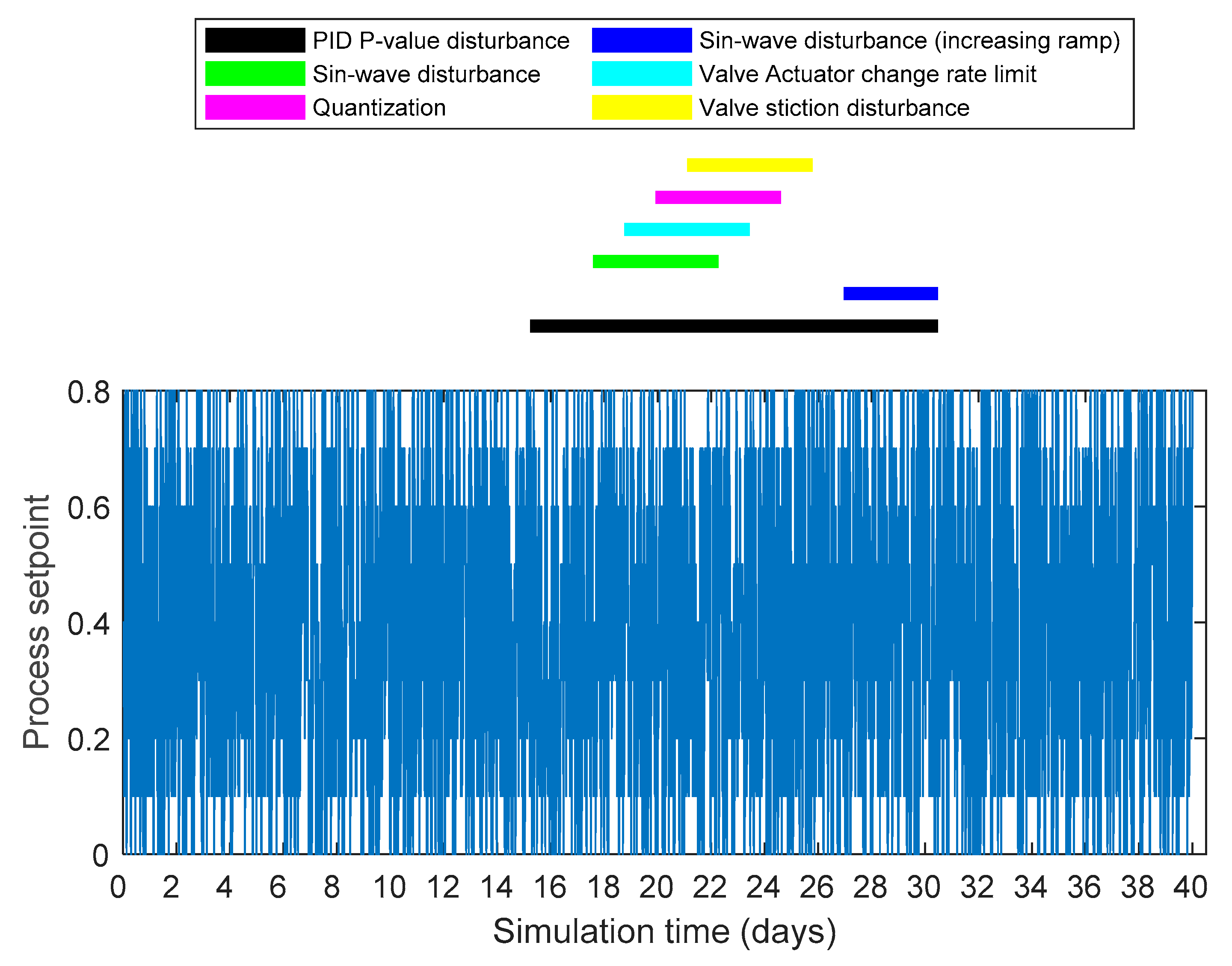
2.3. Simulated Faults
- Valve stiction, where a certain difference between the previous and new controller output is required in order to have an effect on the actuator position. Nominally, the valve stiction in a faulty situation was set to 0.002.
- Valve change rate limit—simulating a scenario where the motor controlling the valve has a sudden fault limiting the speed of the valve change. In this case, the speed is limited to 0.04 valve rotations/s.
- Sin-wave with a constant amplitude of 75 bar, a frequency of 0.00002 Hz, and a rising amplitude (from 0 to 141.6 bar), with a frequency of 0.0001 Hz representing an external disturbance to the process. This disturbance acts as the second input variable in the state-space model (pressure error), as described in Section 2.2.
- Quantization, where the measured process value fed back for the controller is quantized within an accuracy of 0.08 L/min instead of a floating number. This value was selected to produce a noticeable effect on the process control behavior.
- PID controller tuning error, where the value of the P-parameter is changed from 8 to 0.8 for the duration of the fault.
3. Results
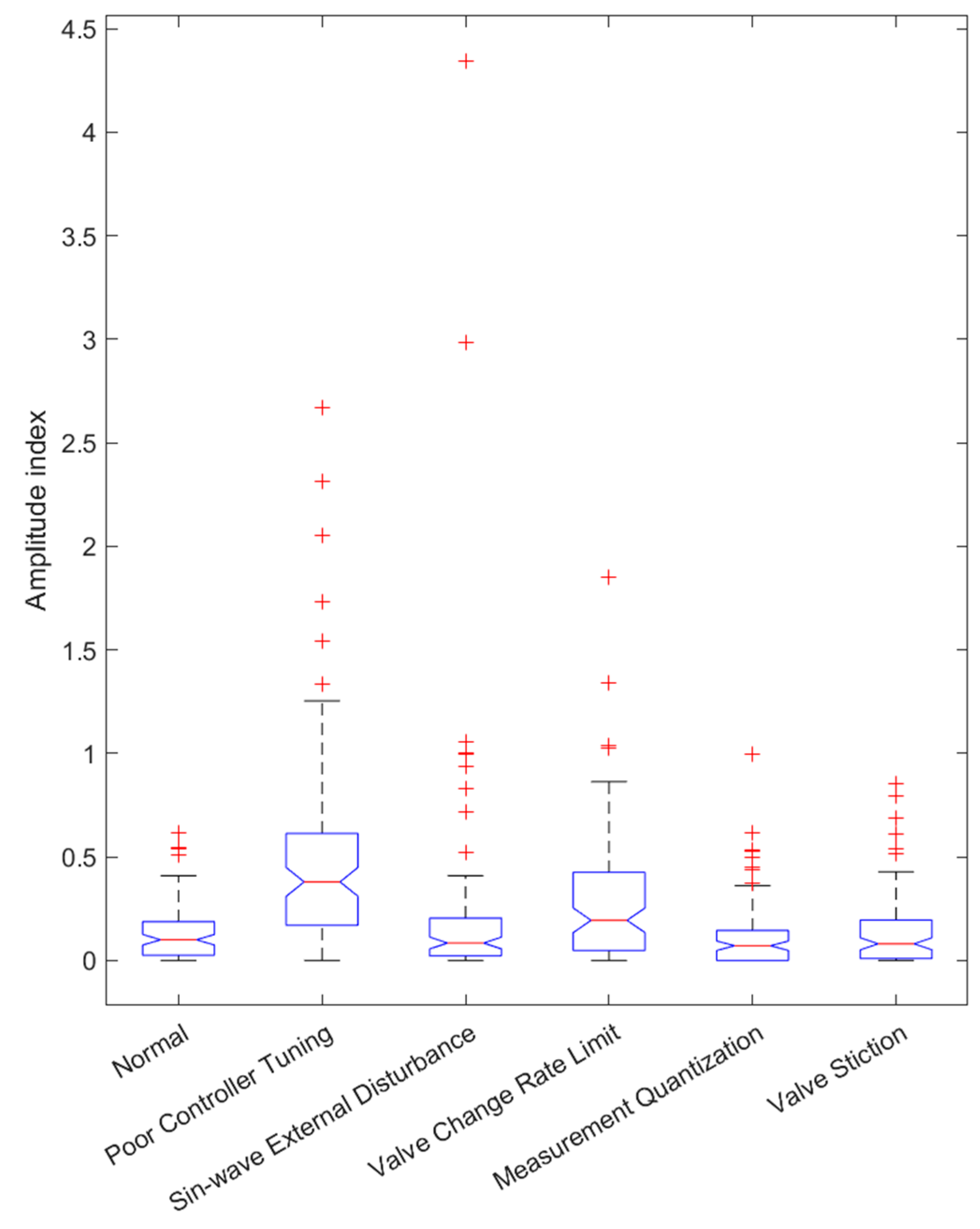
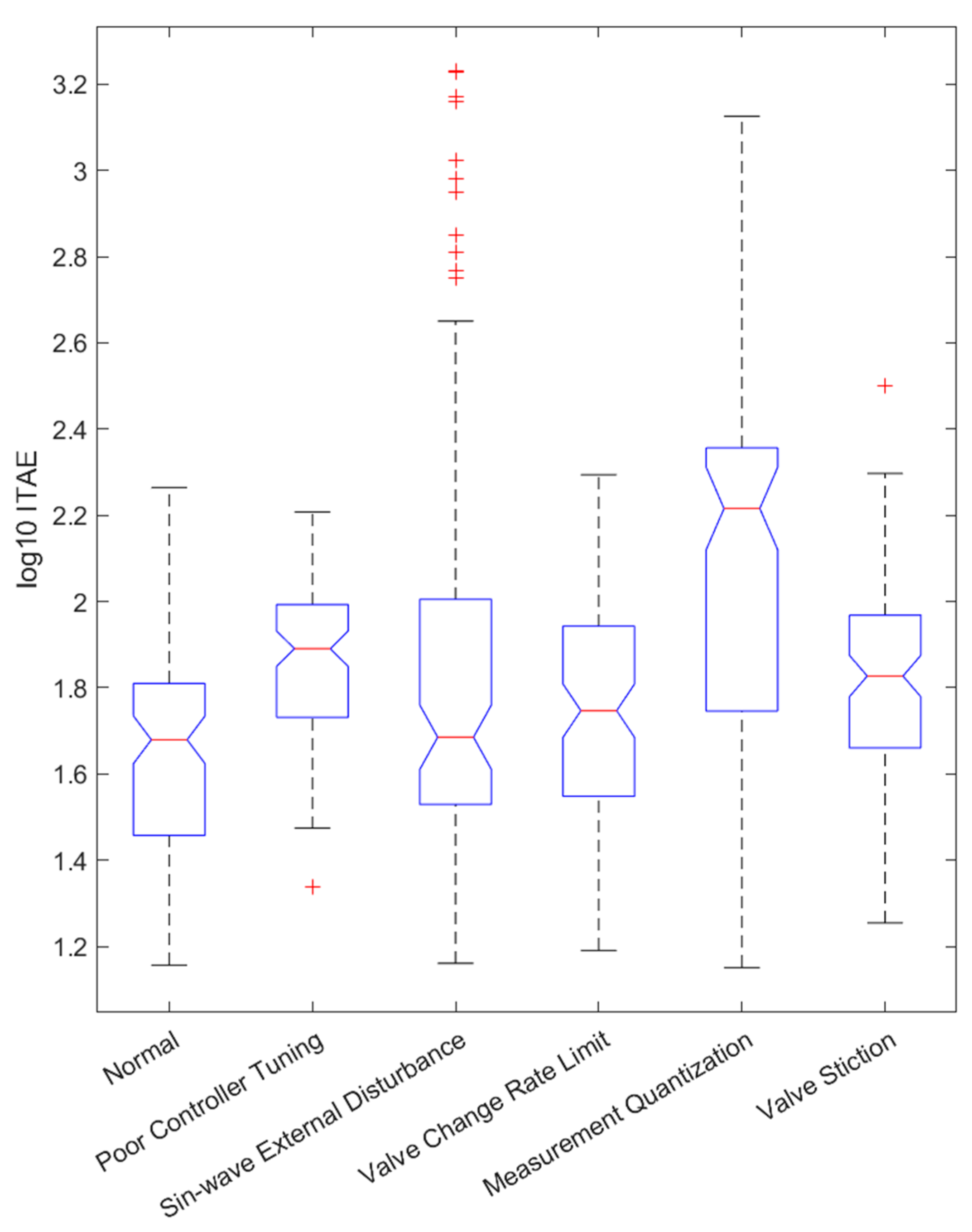
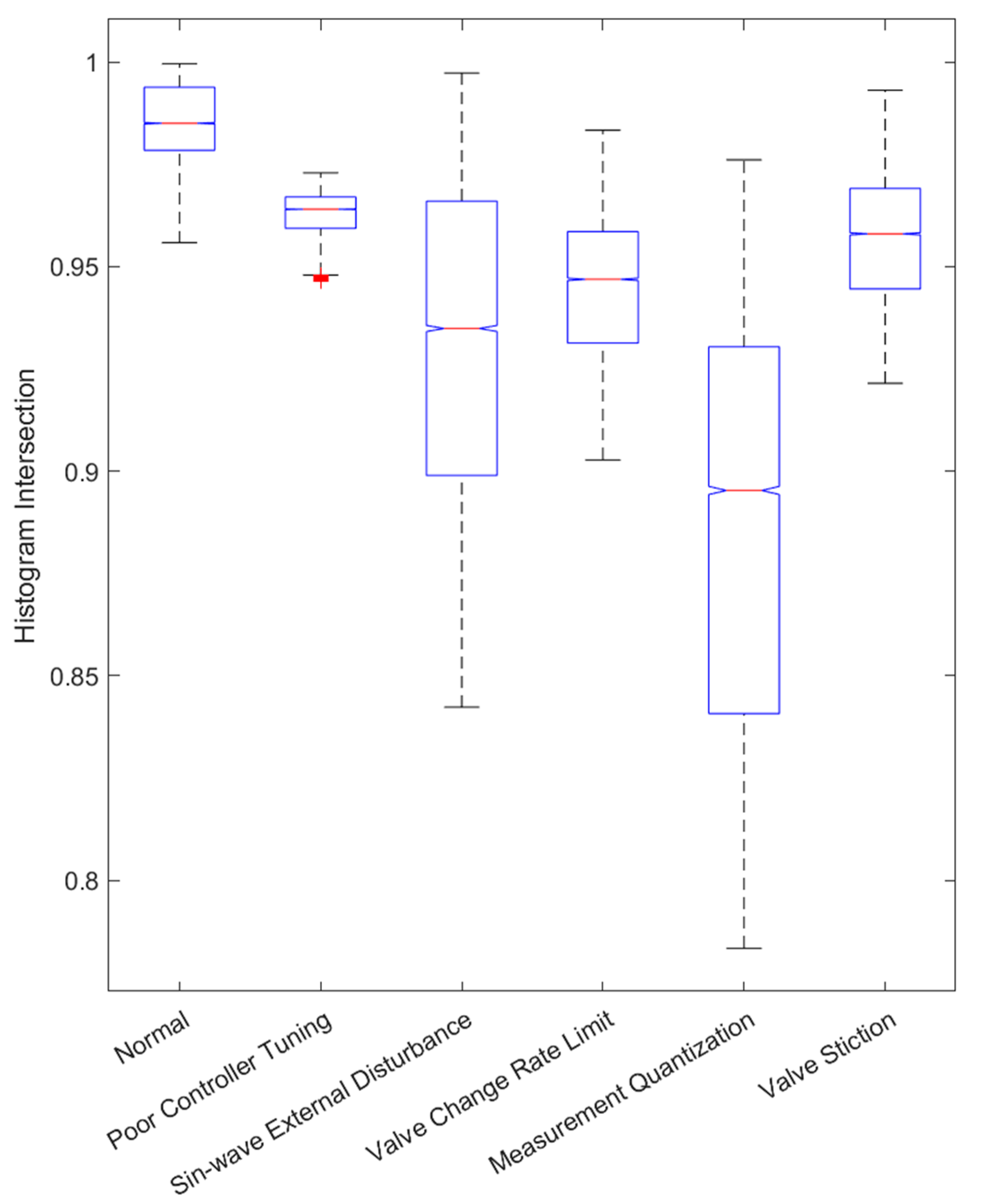
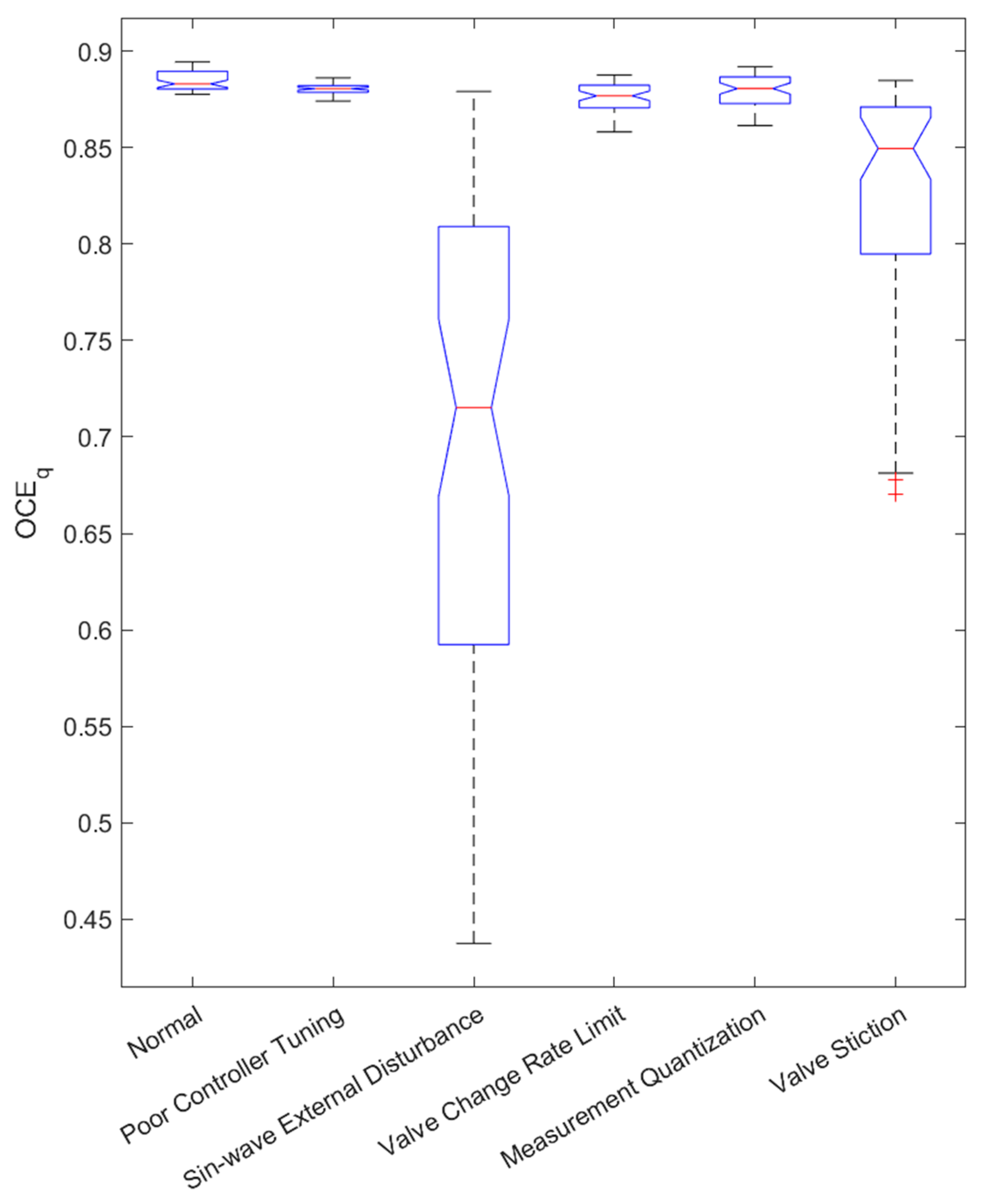
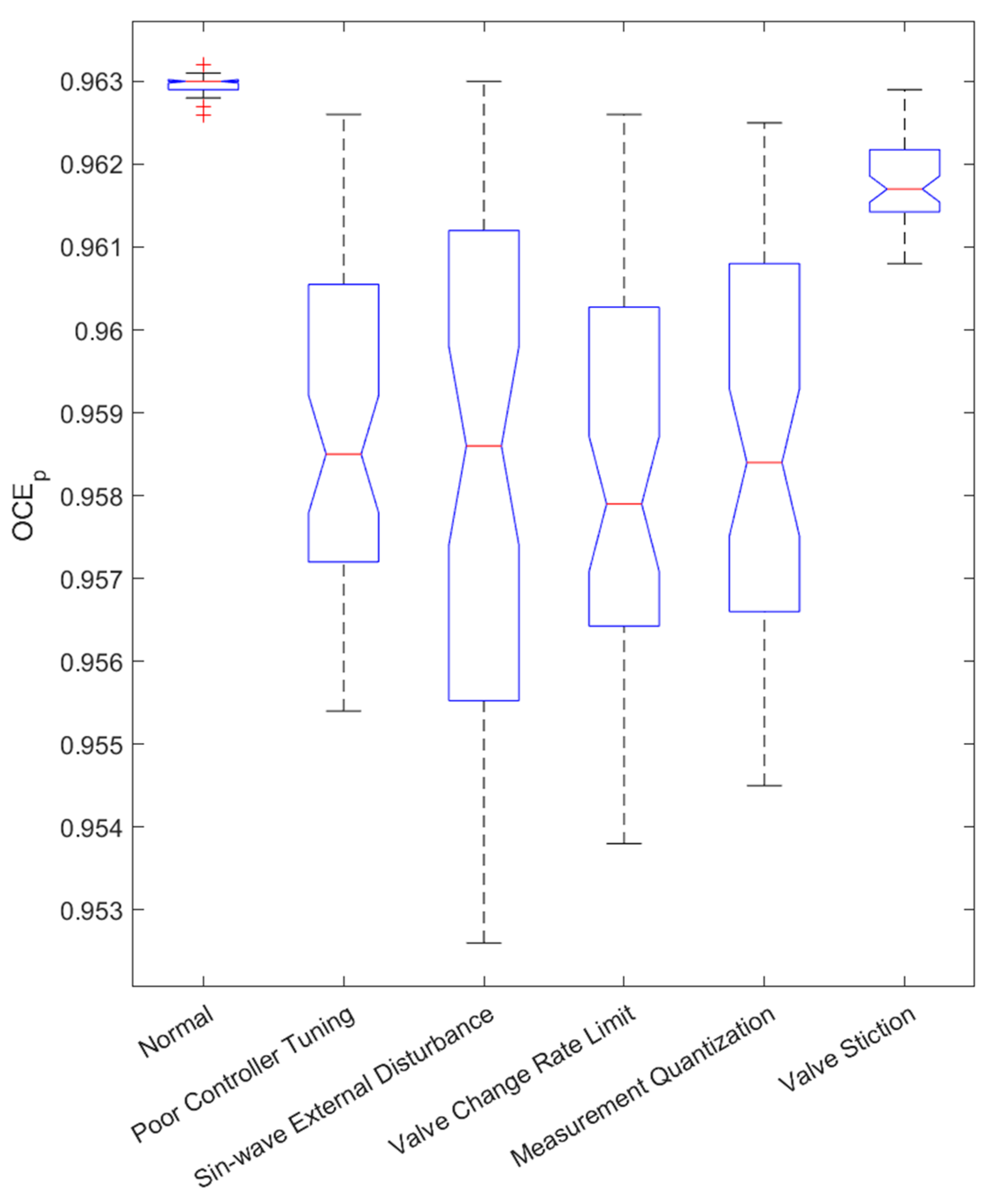
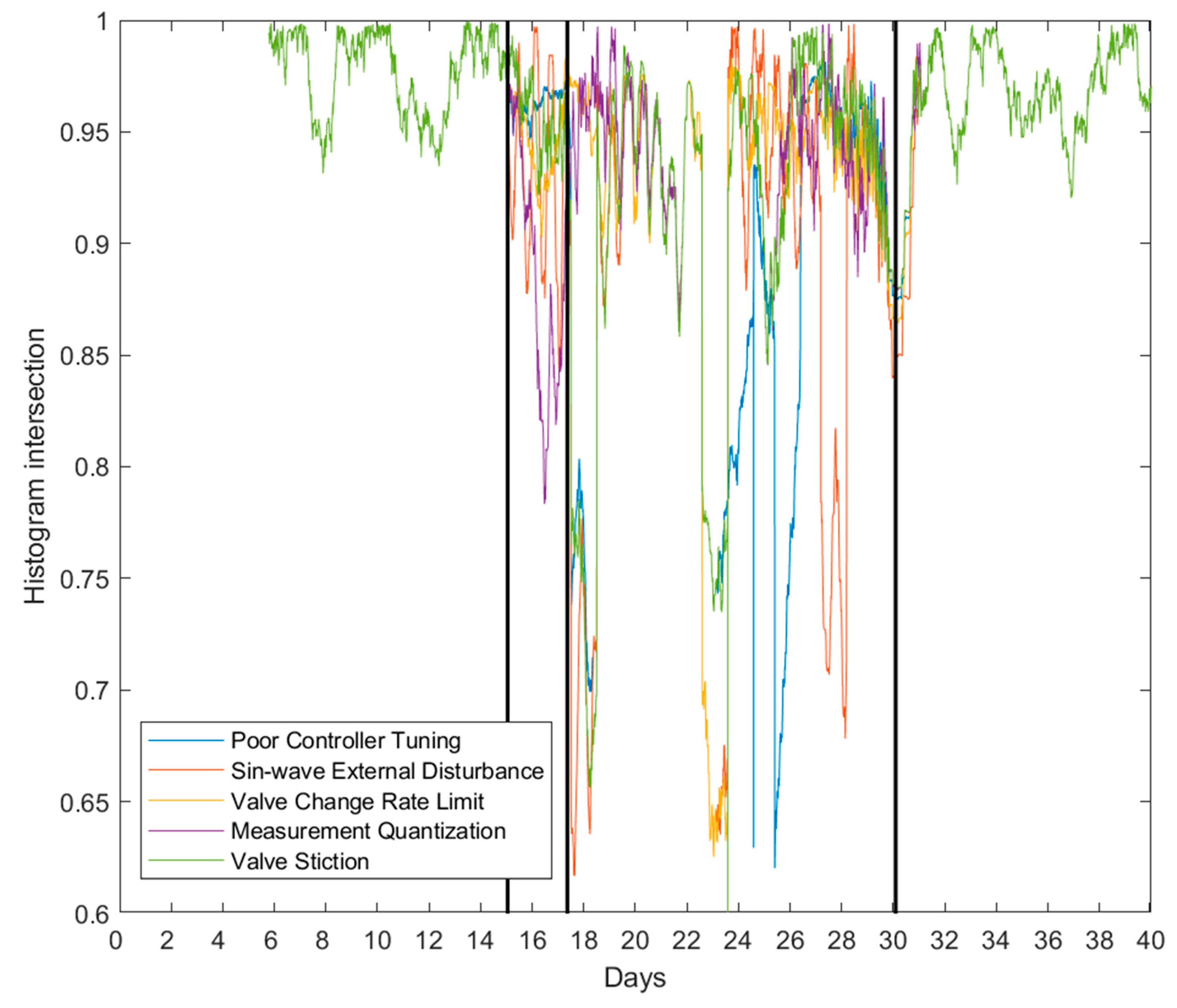
3.1. Case 1. Identification of Faults with Different CPM Methods
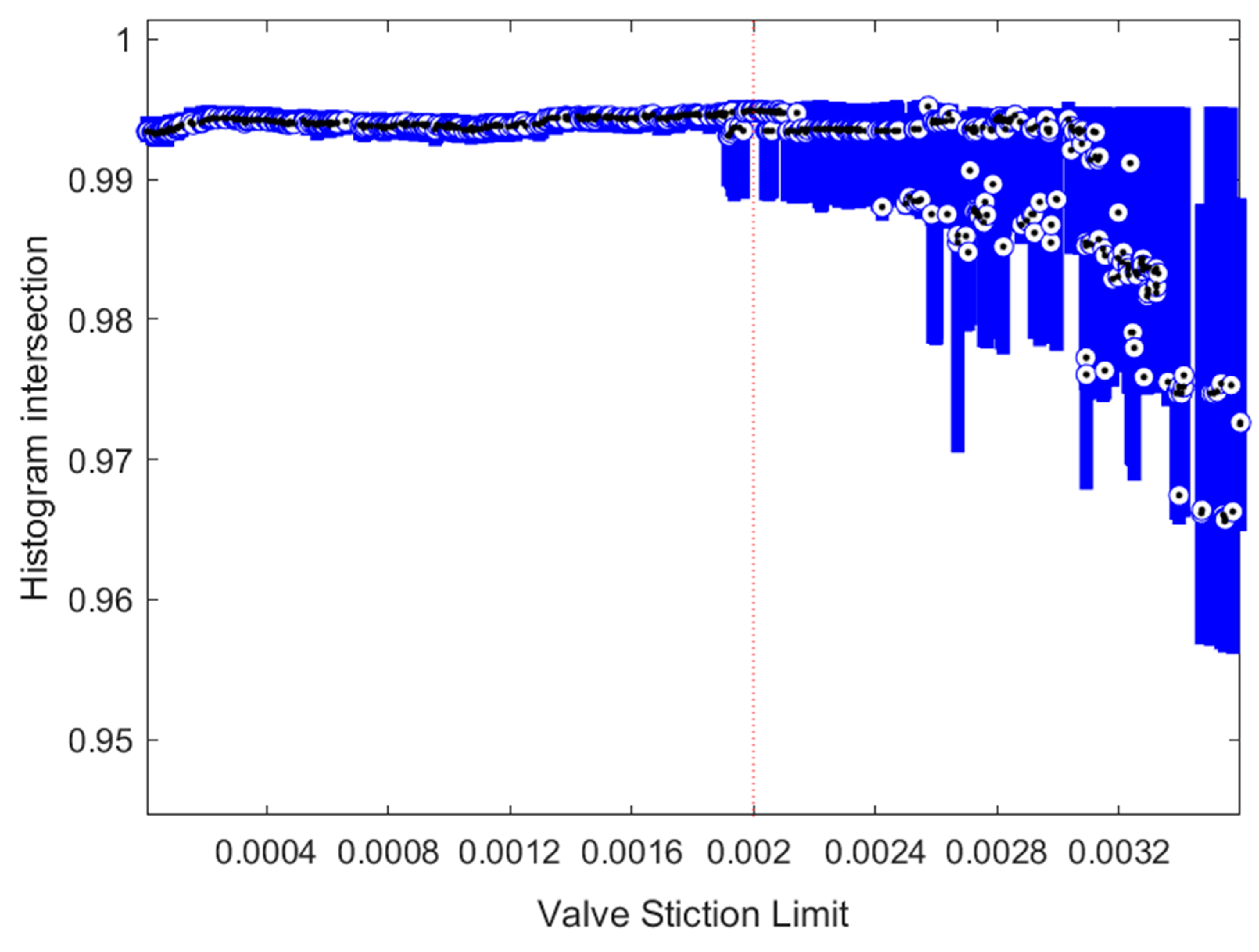
3.2. Case 2. Robustness of the Methods with Varying Fault Intensities
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A


References
- Domański, P.D. Performance Assessment of Predictive Control—A Survey. Algorithms 2020, 13, 97. [Google Scholar] [CrossRef] [Green Version]
- Al Soraihi, H.G. Control Loop Performance Monitoring in an Industrial Setting. Master’s Thesis, RMIT University, Melbourne, VIC, Australia, 2006. [Google Scholar]
- Jamsa-Jounela, S.-L.; Poikonen, R.; Georgiev, Z.; Zuehlke, U.; Halmevaara, K. Evaluation of control performance: Methods and applications. In Proceedings of the International Conference on Control Applications, Glasgow, UK, 18–20 September 2002; Volume 2, pp. 681–686. [Google Scholar] [CrossRef]
- Starr, K.D.; Petersen, H.; Bauer, M. Control loop performance monitoring—ABB’s experience over two decades. IFAC-PapersOnLine 2016, 49, 526–532. [Google Scholar] [CrossRef]
- Bauer, M.; Horch, A.; Xie, L.; Jelali, M.; Thornhill, N. The current state of control loop performance monitoring—A survey of application in industry. J. Process Control 2016, 38, 1–10. [Google Scholar] [CrossRef]
- Holstein, F. Control Loop Performance Monitor. Lund Institute of Technology. 2004. Available online: https://lup.lub.lu.se/luur/download?func=downloadFile&recordOId=8848037&fileOId=8859439 (accessed on 16 June 2022).
- Múnera, J.G.; Jiménez-Cabas, J.; Díaz-Charris, L. User Interface-Based in Machine Learning as Tool in the Analysis of Control Loops Performance and Robustness. In Computer Information Systems and Industrial Management; Saeed, K., Dvorský, J., Eds.; In Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2022; pp. 214–230. [Google Scholar] [CrossRef]
- Grelewicz, P.; Khuat, T.T.; Czeczot, J.; Nowak, P.; Klopot, T.; Gabrys, B. Application of Machine Learning to Performance Assessment for a Class of PID-Based Control Systems. IEEE Trans. Syst. Man Cybern. Syst. 2023, 2023, 1–13. [Google Scholar] [CrossRef]
- Stamatis, D.H. The OEE Primer: Understanding Overall Equipment Effectiveness, Reliability, and Maintainability; Productivity Press: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Vorne Industries, Inc. What Is OEE (Overall Equipment Effectiveness)?|OEE. 2022. Available online: https://www.oee.com/ (accessed on 4 November 2022).
- Ghaleb, M.; Taghipour, S. Assessing the impact of maintenance practices on asset’s sustainability. Reliab. Eng. Syst. Saf. 2022, 228, 108810. [Google Scholar] [CrossRef]
- Choudhury, M.A.A.S.; Shah, S.L.; Thornhill, N.F. Diagnosis of poor control-loop performance using higher-order statistics. Automatica 2004, 40, 1719–1728. [Google Scholar] [CrossRef] [Green Version]
- Horch, A. A simple method for detection of stiction in control valves. Control Eng. Pract. 1999, 7, 1221–1231. [Google Scholar] [CrossRef]
- Howard, R.; Cooper, D. A novel pattern-based approach for diagnostic controller performance monitoring. Control Eng. Pract. 2010, 18, 279–288. [Google Scholar] [CrossRef]
- Mok, R.; Ahmad, M.A. Fast and optimal tuning of fractional order PID controller for AVR system based on memorizable-smoothed functional algorithm. Eng. Sci. Technol. Int. J. 2022, 35, 101264. [Google Scholar] [CrossRef]
- Ekinci, S.; Hekimoğlu, B. Improved Kidney-Inspired Algorithm Approach for Tuning of PID Controller in AVR System. IEEE Access 2019, 7, 39935–39947. [Google Scholar] [CrossRef]
- Ziane, M.A.; Pera, M.C.; Join, C.; Benne, M.; Chabriat, J.P.; Steiner, N.Y.; Damour, C. On-line implementation of model free controller for oxygen stoichiometry and pressure difference control of polymer electrolyte fuel cell. Int. J. Hydrogen Energy 2022, 47, 38311–38326. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, C.; Lu, J. Parameter Self-Tuning of SISO Compact-Form Model-Free Adaptive Controller Based on Long Short-Term Memory Neural Network. IEEE Access 2020, 8, 151926–151937. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Wu, P. Performance monitoring of MIMO control system using Kullback-Leibler divergence. Can. J. Chem. Eng. 2018, 96, 1559–1565. [Google Scholar] [CrossRef]
- Patacchiola, M. The Simplest Classifier: Histogram Comparison. Mpatacchiola’s Blog. 12 November 2016. Available online: https://mpatacchiola.github.io/blog/2016/11/12/the-simplest-classifier-histogram-intersection.html (accessed on 1 July 2021).
- Cha, S.-H. Taxonomy of Nominal Type Histogram Distance Measures. In Proceedings of the MATH ’08, Harvard, MA, USA, 24–26 March 2008; p. 6. [Google Scholar]
- Hämäläinen, H. Identification and Energy Optimization of Supercritical Carbon Dioxide Batch Extraction. Ph.D. Thesis, University of Oulu, Oulu, Finland, 2020. [Google Scholar]
- Hämäläinen, H.; Ruusunen, M. Identification of a supercritical fluid extraction process for modelling the energy consumption. Energy 2022, 252, 124033. [Google Scholar] [CrossRef]


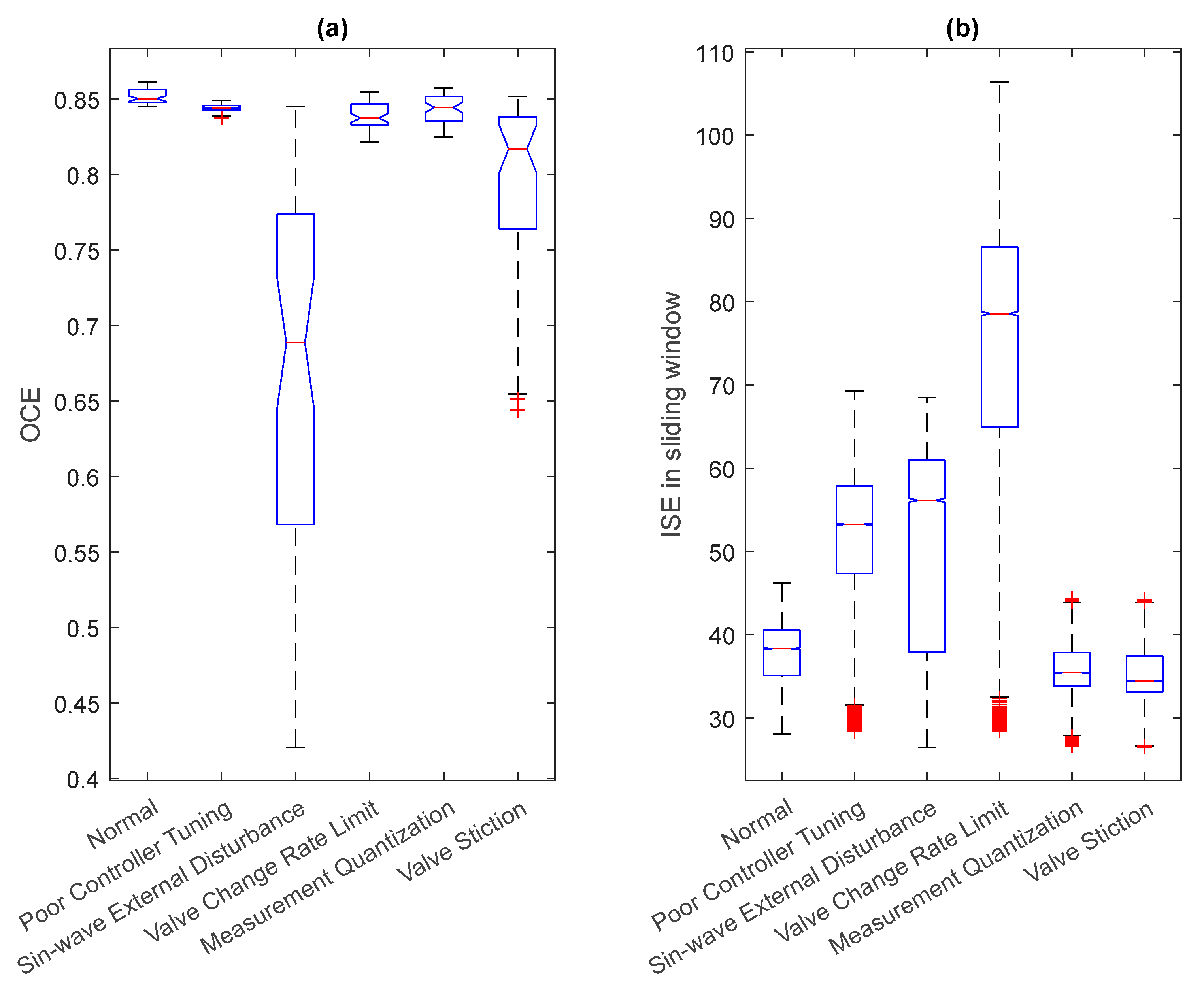


| CPM Index | Cont. Tuning | Ext. Dist. | Rate Limit | Quant. | Valve Stiction |
|---|---|---|---|---|---|
| ISE | X | X | X | - | - |
| ITAE | X | - | - | X | X |
| AMP | X | - | X | - | - |
| KL | X | X | X | X | X |
| ED | X | X | X | X | X |
| HI | X | X | X | X | X |
| OCEp | X | X | X | X | X |
| OCEq | - | X | X | - | X |
| OCEtotal | X | X | X | X | X |
| CPM Index | Lowest Identified Fault Intensity | Highest Non-Identified Fault Intensity | Identified Fault Intensities | Identification Percentage |
|---|---|---|---|---|
| ISE | 1.4 × 10−3 | 0.0015 | 307/500 | 61.4% |
| AMP | - | - | 0/500 | 0% |
| ITAE | 1.1 × 10−3 | 0.0014 | 345/500 | 69% |
| KL | 6.9 × 10−6 | 0.0026 | 447/500 | 89.4% |
| HI | 2.5 × 10−5 | 0.0031 | 194/500 | 38.8% |
| ED | 2.5 × 10−5 | 0.0031 | 194/500 | 38.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pätsi, T.; Ohenoja, M.; Kukkasniemi, H.; Vuolio, T.; Österberg, P.; Merikoski, S.; Joutsijoki, H.; Ruusunen, M. Comparison of Single Control Loop Performance Monitoring Methods. Appl. Sci. 2023, 13, 6945. https://doi.org/10.3390/app13126945
Pätsi T, Ohenoja M, Kukkasniemi H, Vuolio T, Österberg P, Merikoski S, Joutsijoki H, Ruusunen M. Comparison of Single Control Loop Performance Monitoring Methods. Applied Sciences. 2023; 13(12):6945. https://doi.org/10.3390/app13126945
Chicago/Turabian StylePätsi, Teemu, Markku Ohenoja, Harri Kukkasniemi, Tero Vuolio, Petri Österberg, Seppo Merikoski, Henry Joutsijoki, and Mika Ruusunen. 2023. "Comparison of Single Control Loop Performance Monitoring Methods" Applied Sciences 13, no. 12: 6945. https://doi.org/10.3390/app13126945
APA StylePätsi, T., Ohenoja, M., Kukkasniemi, H., Vuolio, T., Österberg, P., Merikoski, S., Joutsijoki, H., & Ruusunen, M. (2023). Comparison of Single Control Loop Performance Monitoring Methods. Applied Sciences, 13(12), 6945. https://doi.org/10.3390/app13126945








