Research on Real-Time Obstacle Avoidance Motion Planning of Industrial Robotic Arm Based on Artificial Potential Field Method in Joint Space

Abstract

The artificial potential field method is a highly popular obstacle avoidance algorithm which is widely used in the field of industrial robotics due to its high efficiency. However, the traditional artificial potential field method has poor real-time performance, making it less suitable for modern factory work patterns, and it is difficult to handle situations when the robotic arm encounters singular configurations. In this paper, we propose an improved artificial potential field method in joint space, which effectively improves the real-time performance of the algorithm, and still performs well when the robotic arm falls into a singular configuration. This method solves the gradient of the repulsive potential field in advance by defining the shortest distance from each joint of the robotic arm to the obstacle, and only needs to calculate potential field function once per cycle, which significantly reduces the calculation time. In addition, when a robotic arm falls into a local minimum position in potential field, the algorithm adds a virtual obstacle to make it leave the position, while this virtual obstacle does not require additional input information. Experimental results show that the algorithm obtains short movement paths and requires very little computing time in the face of different obstacles.

1. Introduction

The utilization of robotic manipulators enhances the efficiency and automation of industrial manufacturing processes. In the 3c industry (computer, communication, consumer electronics), rapidly updated products and complex production patterns require highly flexible robotic arms to complete tasks. In the process of performing the task, the robotic arm may collide with obstacles, so a real-time obstacle avoidance algorithm is needed to control the robotic arm [1,2,3,4,5,6].

The obstacle avoidance algorithm is widely studied in the field of robot motion planning, and it is a computational method to find the path from the starting point to the target point without colliding with obstacles when the robotic manipulator is working in an environment with obstacles. At present, researchers have proposed various obstacle-avoidance algorithms, such as genetic algorithm, rapidly exploring random tree (RRT), and probabilistic roadmap (PRM). However, they all have limitations in practical applications [7].

The RRT algorithm begins by selecting the starting point as the root node and proceeds to generate a randomly expanded tree structure by iteratively sampling and adding leaf nodes, and the shortest path from the starting point along the leaf node to the target position is the obstacle avoidance path. Nevertheless, the calculation speed of RRT is slow, and the smoothness of the trajectory obtained by this algorithm is unsatisfactory, which makes the manipulator shake easily [8]. The genetic algorithm finds an intermediate point with position and velocity information, and connects the starting position to the intermediate point and the intermediate point to the target position through two polynomial paths. The two paths are concatenated to obtain an obstacle avoidance path. Although the genetic algorithm can obtain a smooth obstacle avoidance trajectory, the computational efficiency is very low [9,10]. The PRM algorithm establishes a complete undirected graph by sampling and collision detection, and then obtains a feasible obstacle avoidance path through a graph search algorithm (such as the A* algorithm). However, the process of establishing the map using the PRM algorithm is complex and time-consuming. Moreover, the connection between two nodes in the undirected graph does not take into account the robot’s motion model [11,12]. Although the above algorithms can obtain obstacle avoidance trajectories, their real-time performance is weaker than the artificial potential field method. This paper only discusses the artificial potential field method.

The artificial potential field (APF) method is a widely recognized motion planning strategy in the field of robotics. In 1986, Oussama Khatib first proposed the artificial potential field method (APF) for the motion planning of robots [13]. The APF method extensively borrows the concept of potential fields from physics and transforms the path planning problem of robots or moving objects into a problem of searching for the optimal path in a virtual potential field. The core idea is to consider the target location as an attractive source and obstacles or infeasible areas as repulsive sources. High potential fields are assigned around obstacles, while low potential fields are assigned around the target location. By calculating the forces and directions, the APF guides the robot or object to move along the direction of decreasing potential energy, thereby achieving the goal of avoiding obstacles and reaching the target location.

The APF method is characterized by its simplicity, intuitiveness, ease of implementation, and real-time capabilities. As a result, it has been widely applied in the industrial field. For example, in automated warehousing systems, robots utilize the APF method to navigate around obstacles and find the shortest path based on the layout and obstacle positions within the warehouse. This potential field guidance enables them to efficiently and swiftly accomplish tasks such as cargo handling [14,15]. In the field of autonomous driving, the APF method establishes a potential field within the road network. It considers other vehicles, pedestrians and obstacles as repulsive sources while regarding the target destination as an attractive source. This enables vehicles to navigate to their destination safely and smoothly [16,17]. In multi-agent cooperation, the APF method guides robots to avoid collisions and collaboratively accomplish complex production tasks. It achieves this by considering robots and target positions as attractive sources, and other robots as repulsive sources [18,19]. These application cases highlight the significant role of the APF method in achieving efficient, safe, and flexible industrial operations.

The coordinate systems of the APF method can be divided into two categories: Cartesian space and joint space. If attraction and repulsion forces are calculated in Cartesian space, the coordinate system for this method is the Cartesian space. If attraction and repulsion forces are calculated in joint space, the coordinate system for this method is the joint space.

In studies based on Cartesian space, Hui Zhang et al. proposed an obstacle avoidance strategy for the dual-arm robot by improving the potential field into a velocity field [20]. Sun-Oh Park et al. proposed a numerical method based on a Jacobian matrix to solve the obstacle avoidance problem of a redundant robotic arm [21]. All the above obstacle avoidance strategies in Cartesian space need to be mapped to joint space, and the inverse of the Jacobian matrix cannot be solved when the robotic arm falls into a singular configuration. In studies based on joint space, Lufeng Luo et al. uses a sampling method to generate anti-collision path points [22]. Anoush Sepehri et al. used a numerical method to solve the gradient of potential field [23]. All of the above obstacle avoidance strategies in joint space require the multiple calculations of the potential field function, so the real-time performance is low. In Section 3, we introduced these above algorithms and compared them with the algorithm in this paper.

In an intelligent workshop, the robotic arm is required to grip the workpieces on the conveyor belt and move them to the target position without collisions. Due to the uncertain initial position of the workpieces, a real-time obstacle avoidance algorithm is needed. This paper proposes an improved artificial potential field method specifically designed for the aforementioned industrial scenario. The algorithm generates a suitable trajectory for the robotic arm, so that it can start from any specified starting point and reach the target point without colliding with obstacles in the process. We propose a way to calculate the shortest distance from the obstacle to the joint of the robotic arm, whereby an analytic formula for the gradient of repulsive potential field can be solved in advance. In addition, we propose a way to make the robotic arm jump out of the local minimum.

The contributions of this study are novel and unique in various aspects. (1) Compared with the APF method in Cartesian space, this algorithm does not need to calculate the inverse of the Jacobian matrix. (2) Compared with others’ studies on the APF method in joint space, this algorithm only needs to calculate the potential field function once during each cycle. Therefore, the algorithm has a very high real-time performance. (3) In addition, the algorithm provides an effective way to avoid the robotic arm falling into the local optimum by introducing a virtual obstacle, which does not need additional information.

The subsequent sections of this paper are structured as follows: in Section 2, the D-H parameters and kinematic model of the robot are presented. Section 3 describes the principle and flow of the algorithm, which is the focus of this paper. In Section 4, the simulations and experiments are presented. Section 5 discusses the advantages and disadvantages of the algorithm proposed in this paper compared to other algorithms. Section 6 summarizes the conclusions.

2. Kinematics Model of n-DOF Robot

It is firstly necessary to establish the kinematics model of the robotic manipulator to prevent collision.

To describe the structure and coordinate system of robot, we used 1-n to represent each joint of the manipulator, and x1y1z1-xnynzn to represent the coordinate systems of each link. We used the modified D-H parameter method to establish the kinematics model of the robotic manipulator. Equation (1) describes the relationship between any two adjacent joints.

$$\begin{gathered} {}_{i-1}{}^{i}T={Rot}_{x_{i-1}}\left({\alpha }_{i-1}\right)\times {Trans}_{x_{i-1}}\left(a_{i-1}\right)\times {Rot}_{z_i}\left({\theta }_i\right)\times {Trans}_{z_i}\left(d_i\right)= \\ \left[\begin{array}{ccc}\begin{array}{c}C{\theta }_i\\ S{\theta }_i{C\alpha }_{i-1}\\ \begin{array}{c}S{\theta }_i{S\alpha }_{i-1}\\ 0\end{array}\end{array}& \begin{array}{c}-S{\theta }_i\\ C{\theta }_{i}C{\alpha }_{i-1}\\ \begin{array}{c}C{\theta }_{i}S{\alpha }_{i-1}\\ 0\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ -S{\alpha }_{i-1}\\ \begin{array}{c}C{\alpha }_{i-1}\\ 0\end{array}\end{array}& \begin{array}{c}{a}_{i-1}\\ -S{\alpha }_{i-1}{d}_i\\ \begin{array}{c}C{\alpha }_{i-1}{d}_i\\ 1\end{array}\end{array}\end{array}\end{array}\right] \end{gathered}$$

(1)

where ${\theta }_i$ represents the angle of rotation of the i-th joint, $S{\theta }_i=sin{\theta }_i,C{\theta }_i=cos{\theta }_i$, and ${}_{i-1}{}^{i}T,i=\mathrm{1,2},\cdots ,n$ is the homogeneous transformation matrix built from D-H parameters. If the D-H parameters of the n-DOF robot are known, the homogeneous transformation matrix of each link can be obtained by substituting these parameters into Equation (1), so that the coordinate system transformation from the base to the end of the manipulator can be expressed as Equation (2):

$${}_n{}^{0}T={}_1{}^{0}T\times {}_2{}^{1}T\times {}_3{}^{2}T\times \cdots \times {}_n{}^{n-1}T$$

(2)

${}_n{}^{0}T$ represents the position and orientation of the end-effector in Cartesian space, and it can be expressed as (3):

$${}_n{}^{0}T=\left[\begin{array}{ccc}\begin{array}{c}{n}_x\\ n_y\\ \begin{array}{c}{n}_z\\ 0\end{array}\end{array}& \begin{array}{c}{o}_x\\ o_y\\ \begin{array}{c}{o}_z\\ 0\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}{a}_x\\ a_y\\ \begin{array}{c}{a}_z\\ 0\end{array}\end{array}& \begin{array}{c}{p}_x\\ p_y\\ \begin{array}{c}{p}_z\\ 1\end{array}\end{array}\end{array}\end{array}\right]$$

(3)

where n, o, a denote the orientation and p denotes the position. Our industrial background involves a robotic arm gripping objects on a conveyor belt in workshops and moving them to the end position. In order to maintain a stable grip and prevent object dropping, the robotic arm’s end-effector should predominantly move along the z axis of Cartesian space when approaching and placing the objects [24]. According to the requirements of the industrial task, the positions and orientations of both the starting point and the endpoint of the task are known. The Cartesian coordinates of the task starting point and goal point can be mapped to joint space by inverse kinematics.

As evidenced from (1) and (2), the position of joint i depends on a series of variables related to joint angles ${\theta }_i,i=1,\cdots ,n$, with these variables ranging from ${\theta }_1$ to ${\theta }_{i-1}$, so the position of joint i can be expressed as $\left\{x(\theta ),y(\theta ),z(\theta )\right\}$.

3. Improved Artificial Potential Field Method Based on Joint Space

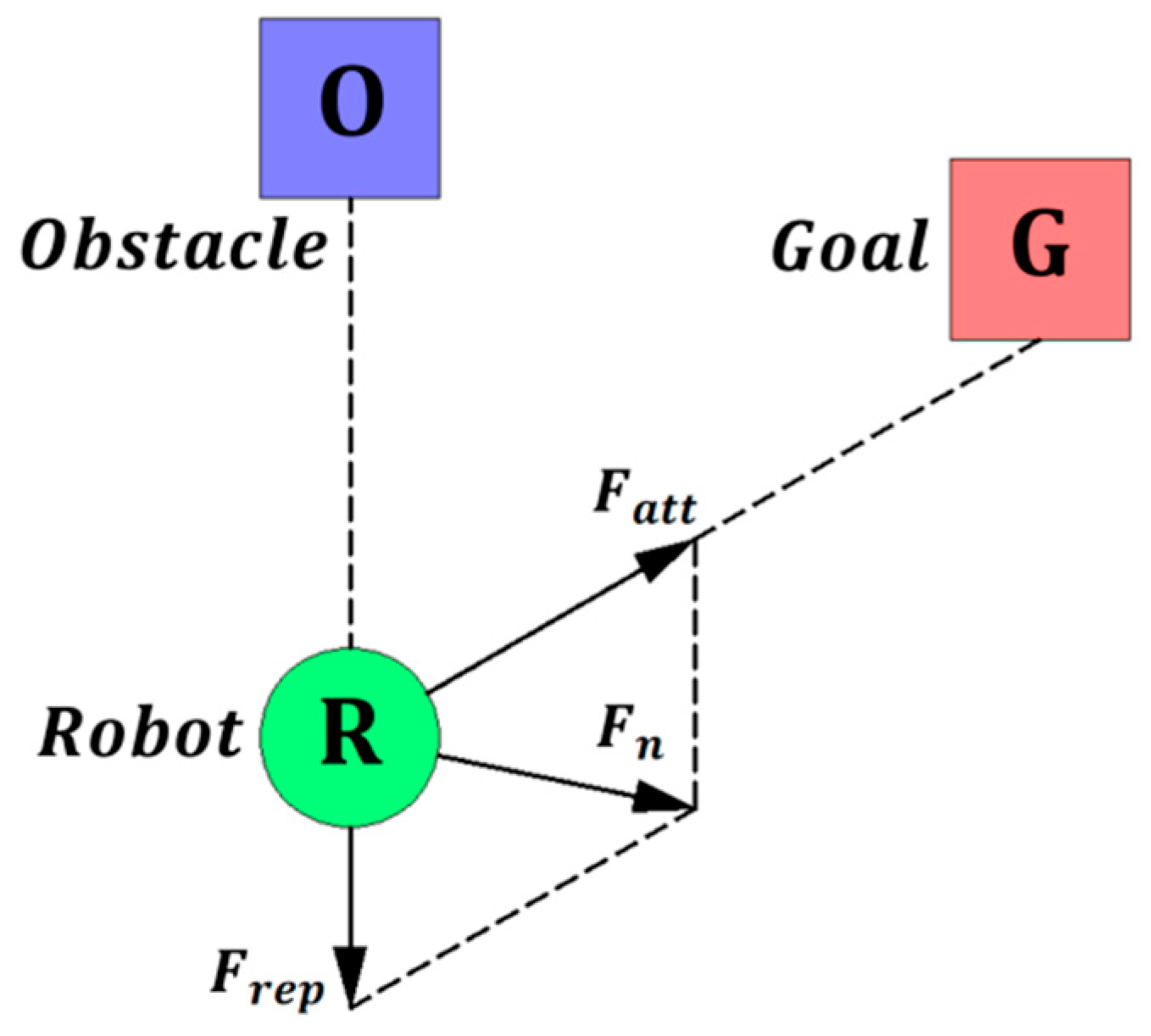
3.1. Traditional Artificial Potential Field Algorithm

In APF, the robotic arm is subjected to two forces when moving to the target point. One force is the attractive force that pulls the robot towards the target position, while the other force is the repulsive force exerted by obstacles on the robot. Under the combined force of these two forces, the robotic arm can quickly reach the target position without colliding with obstacles in this process. The force analysis of the robotic arm in the potential field is shown in Figure 1. The force on each joint and link of the robotic arm is shown in Figure 2.

$F_{rep}$ represents the repulsive force; $F_{att}$ represents the attractive force; and $F_n$ is the combined force of the two forces, which makes the manipulator reach the target position.

The attraction field produced by $F_{att}$ can be obtained by Equation (4):

$$U_{att}\left({\theta }_1,\cdots ,{\theta }_n\right)=\frac{1}{2}\mu d^2\left(q,q_{goal}\right)$$

(4)

where $U_{att}\left({\theta }_1,\cdots ,{\theta }_n\right)$ is the attraction field, $\mu$ is the correction coefficient of the attractive potential field, q represents the current position configuration of the robot, $q_{goal}$ represents the position configuration of the robot when reaching the target position, and $d\left(q,q_{goal}\right)$ is the distance between the robot and the target position.

The repulsive potential field produced by $F_{rep}$ can be obtained by Equation (5):

$$U_{rep}\left({\theta }_1,\cdots ,{\theta }_n\right)=\left\{\begin{array}{c}\frac{1}{2}k{\left(\frac{1}{d\left(q,q_{obs}\right)}-\frac{1}{d_0}\right)}^2,d\left(q,q_{obs}\right)\le d_0\\ 0,d\left(q,q_{obs}\right)>d_0\end{array}\right.$$

(5)

where $U_{rep}\left({\theta }_1,\cdots ,{\theta }_n\right)$ is the repulsive potential field, k is the correction coefficient of the repulsion potential field, $q_{obs}$ represents the position configuration of the robot when colliding with an obstacle, $d\left(q,q_{obs}\right)$ is the real-time distance between the robotic arm and the obstacle, and $d_0$ represents the influence radius of the obstacle. When $d\left(q,q_{obs}\right)>d_0$, the repulsion field will not affect the movement of the robot.

The total potential energy function can be expressed as Equation (6):

$$U\left({\theta }_1,\cdots ,{\theta }_n\right)=U_{att}\left({\theta }_1,\cdots ,{\theta }_n\right)+U_{rep}\left({\theta }_1,\cdots ,{\theta }_n\right)$$

(6)

3.2. The Gradient of the Potential Field Function

The potential energy function is only dependent on joint angles $\left({\theta }_1,\cdots ,{\theta }_n\right)$ for a robotic arm. We use the gradient descent method to minimize the potential energy function and determine a set of angles so that the robotic arm can reach the target position in the direction of the fastest potential energy descent without a collision with obstacles.

The attraction $F_{att}$ is the negative of the gradient of the attraction potential field $U_{att}$, and it can be expressed as (7):

$$F_{att}=-\nabla U_{att}\left({\theta }_1,\cdots ,{\theta }_n\right)=-\mu d\left(q,q_{goal}\right)\nabla d(q,q_{goal})$$

(7)

q is the current position configuration of the robot, and $q_{goal}$ is the position configuration of the robot when reaching the goal position. If the manipulator is entirely composed of revolute joints, q can be assumed to be $\left[{\theta }_1,\cdots ,{\theta }_n\right]$, and $q_{goal}$ can be assumed to be $\left[{\theta }_1^{\ast },\cdots ,{\theta }_n^{\ast }\right]$. Then, $d\left(q,q_{goal}\right)$ can be expressed as (8):

$$d\left(q,q_{goal}\right)=\sqrt{{\sum }_{i=1}^n{\left({\theta }_i-{\theta }_i^{\ast }\right)}^2}$$

(8)

If the manipulator comprises both prismatic joints (from joint 1 to joint j) and revolute joints (from joint j + 1 to joint n), in this case, q can be assumed to be $\left[d_1,\cdots ,d_j,{\theta }_{j+1},\cdots ,{\theta }_n\right]$, q_goal can be assumed to be $\left[d_1^{\ast },\cdots ,d_j^{\ast },{\theta }_{j+1}^{\ast },\cdots ,{\theta }_n^{\ast }\right]$, and we assign a weight ${\omega }_1$ to the prismatic joint and a weight ${\omega }_2$ to the revolute joint to eliminate the units of nonhomogeneous form. Then, $d\left(q,q_{goal}\right)$ can be expressed as (9):

$$d\left(q,q_{goal}\right)={\omega }_1\times \sqrt{{\sum }_{i=1}^j{\left(d_i-d_i^{\ast }\right)}^2}+{\omega }_2\times \sqrt{{\sum }_{i=j+1}^n{\left({\theta }_i-{\theta }_i^{\ast }\right)}^2}$$

(9)

The repulsive force $F_{rep}$ is the negative of the gradient of the repulsive potential field $U_{rep}$ can be expressed as (10):

$$F_{rep}=-\nabla U_{rep}\left({\theta }_1,\cdots ,{\theta }_n\right)=\left\{\begin{array}{c}k\left(\frac{1}{d\left(q,q_{obs}\right)}-\frac{1}{d_0}\right)\frac{1}{d^2(q,q_{obs})}\nabla d\left(q,q_{obs}\right),d\left(q,q_{obs}\right)\le d_0\\ 0,d\left(q,q_{obs}\right)>d_0\end{array}\right.$$

(10)

We use the gradient descent to minimize the potential energy function in Equation (6). Equation (11) presents the generalized formula utilized for the sth iteration of gradient descent. and Equation (12) shows how the learning rate $\lambda$ is calculated. $q_s$ represents the position configuration of the robot arm at the sth cycle.

$$q_s=q_{s-1}-\lambda \times \nabla U\left({\theta }_1,\cdots ,{\theta }_n\right)$$

(11)

$$\lambda =ϵ1+ϵ2\times d\left(q,q_{goal}\right)+ϵ3\times d\left(q,q_{obs}\right)$$

(12)

The learning rate $\lambda$ is dynamic, and it depends on the distance between the end-effector and goal point and the distance between the joints of robot and obstacle. $ϵ1,ϵ2,ϵ3$ are positive constants. $ϵ$1 specifies the basic learning rate and $ϵ2,ϵ3$ specify the sensitivity to the position of manipulator. As the end-effector approaches the goal point and the joint of the robot approaches the obstacle, the learning rate decreases. This is performed to avoid collision with obstacles and reach the goal point more accurately. If faster algorithm execution is desired, the values of $ϵ1$, $ϵ2$, and $ϵ3$ can be increased accordingly. In this paper, $ϵ$1, $ϵ2$, and $ϵ3$ are adjusted within the range of 0.5–1.

The gradient of the attractive potential field is easy to calculate, while the gradient of the repulsive potential field is difficult to calculate, because the shortest distance $d\left(q,q_{obs}\right)$ between the robotic arm and the obstacle is difficult to calculate. This section focuses on the calculation of the shortest distance $d\left(q,q_{obs}\right)$ when facing different obstacles.

There are two types of obstacles on the factory assembly line usually, which are obstacles with complex shapes and obstacles with regular shapes. The obstacle can be simulated using the ball envelope method [25], as shown in Figure 3 and Figure 4.

The parameters describing the obstacle are $\left\{a,b,c,r\right\}$, where a, b, c represent the spatial location coordinates of the obstacle and r represents the radius of the ball envelope obstacle.

For an obstacle with a complex shape, it can be enveloped by a single sphere. According to the conclusion of Section 2, the position configuration coordinates of q are determined by a series variable of the joint angle, and can be solved by kinematics. Therefore, the coordinates of q can be expressed as $q:\{x(\theta ),y(\theta ),z(\theta )\}$. Then, the shortest distance between the joint of the robot and the obstacle can be expressed as (13):

$$d\left(q,q_{obs}\right)=\sqrt{{\left(x(\theta )-a\right)}^2+{\left(y(\theta )-b\right)}^2+{\left(z(\theta )-c\right)}^2}-r_1-r_2$$

(13)

where r₁ denotes the radius of the enveloping obstacle sphere and r₂ denotes the thickness of the joint.

For an obstacle with a regular shape, it can be enveloped by a series of spheres whose coordinate parameters are denoted by $\left\{a_i,b_i,c_i,r_i\right\}$. The distance between the joint and the nearest sphere is the shortest distance $d(q,q_{obs})$ between the joint and the obstacle with a regular shape. In order to make the motion of the robotic arm smooth, the manipulator receives repulsive forces from the two sources, one is the nearest ball, and the other is the ball adjacent to the nearest ball.

On the left side of Figure 5, ball 2 is closest to the joint, and the robotic arm is subject to the repulsive force of ball 2 and the adjacent ball 1. When the robotic arm moves to the next state, as shown in the right side of Figure 5, ball 3 is closest to the joint and the robot is subject to the repulsive force of ball 3 and the adjacent ball 2.

The derivative of Equation (13) can lead to Equation (14):

$$\nabla d\left(q,q_{obs}\right)=\frac{\left(x-a\right)\frac{\partial x\left(\theta \right)}{\partial \theta }+\left(y-b\right)\frac{\partial y\left(\theta \right)}{\partial \theta }+\left(z-c\right)\frac{\partial z\left(\theta \right)}{\partial \theta }}{\sqrt{{\left(x-a\right)}^2+{\left(y-b\right)}^2+{\left(z-c\right)}^2}}$$

(14)

The analytic formula of the gradient of the repulsive potential field $\nabla U_{rep}$ can be obtained by substituting Equations (13) and (14) into Equation (10), and it is determined by the series variable of the joint angle. This algorithm has a very high real-time performance because it only needs to calculate the potential field function once per cycle.

3.3. The Virtual Obstacle

Sometimes, the robotic arm has not reached the target, but the resultant force is zero. At this time, the robotic arm falls into the local minimum state, and it can be expressed as (15):

$$-\nabla U\left({\theta }_1,\cdots ,{\theta }_n\right)=F_{att}+F_{rep}=0$$

(15)

We make the robotic arm jump out of the local minimum state by adding a virtual obstacle. In Figure 6, we treat the center of the ball which envelops the obstacle as a virtual obstacle, and q₁ is the position configuration of the robot when colliding with the center of the ball. The position coordinates of this virtual obstacle come from the obstacle, so there is no need to introduce additional information. $F_{rep\_vir}$ is the repulsive force generated by q₁ when the robot is trapped in a local minimum state, and it is calculated as shown in (16) and (17).

$$F_{rep\_vir}=k\left(\frac{1}{d\left(q,q_1\right)}-\frac{1}{d_0}\right)\frac{1}{d^2\left(q,q_1\right)}\nabla d\left(q,q_1\right)$$

(16)

$$d\left(q,q_1\right)=\sqrt{{\left(x\left(\theta \right)-a\right)}^2+{\left(y\left(\theta \right)-b\right)}^2+{\left(z\left(\theta \right)-c\right)}^2}$$

(17)

To ensure successful obstacle avoidance, the repulsion coefficient k of the virtual obstacle is set to 1–10³ times the general obstacle, and the influence radius of the virtual obstacle is set as 1.5–3 times that of general obstacles [26].

3.4. Joint Angle Constraints

Typically, each joint of a robotic arm has angle limitations. To ensure that the joint angles of the robotic arm do not exceed their respective limits during obstacle avoidance, the algorithm proposed in this paper must satisfy the following requirements.

Taking an n-degree-of-freedom robotic arm as an example, we assume that the joint angle limits for each joint of the robotic arm are in the range of [${\theta }_{i\_min}$, ${\theta }_{i\_max}$].

Solution 1: In the first step of the algorithm, the initial and target positions of the robotic arm can be transformed from Cartesian space to joint space using inverse kinematics. $q_{start}$ can be assumed to be $\left[{\theta }_1,\cdots ,{\theta }_n\right]$ and $q_{goal}$ can be assumed to be $\left[{\theta }_1^{\ast },\cdots ,{\theta }_n^{\ast }\right]$. Due to the existence of multiple solutions in inverse kinematics, it is necessary to select an appropriate solution in this step, ensuring that ${\theta }_{i\_min}<{\theta }_i<{\theta }_{i\_max}$ and ${\theta }_{i\_min}<{\theta }_i^{\ast }<{\theta }_{i\_max}$.

Solution 2: The algorithm imposes limitations on the magnitude of attraction Fatt and repulsion forces Frep during the computation (such as $F_{att}\le 0.1,F_{rep}\le 0.1$). This serves to prevent the joint angles from exceeding the constraint range.

Solution 3: During obstacle avoidance, it is possible that the strong repulsive force from an obstacle may cause one of the joint angles of the robotic arm to exceed the specified limit. In the case depicted in Figure 7, we can appropriately reduce the repulsive force by adjusting the repulsion coefficient k. This allows the robotic arm to complete the obstacle avoidance task while ensuring that the joint angles remain within the allowed range.

3.5. Algorithm Comparison

The flowchart of the artificial potential field algorithm in joint space is shown in Figure 8, and the pseudocode is shown in Algorithm 1. The values of $\epsilon 1$, $\epsilon 2$, and $\epsilon 3$ can be adjusted appropriately according to the requirements. It can be seen that each iteration only requires the calculation of the potential field function once from the algorithm flowchart. The configuration at the starting position and the target position are obtained by inverse kinematics. In order to obtain a smooth obstacle avoidance trajectory, the values of $F_{rep}$ and $F_{rep\_vir}$ are limited to less than $\epsilon 3$.

Algorithm 1 The pseudocode of the algorithm.

Algorithm 1: Improved artificial potential field

1: Set Start position: qstart and Goal position: qgoal

2: ${q_{start}=\left[{\theta }_1,\cdots ,{\theta }_n\right]}_{start},{q_{goal}=\left[{\theta }_1,\cdots ,{\theta }_n\right]}_{goal}$ by inverse kinematics

3: While $d(q,q_{goal})>\epsilon 1$ %Determine whether the target point has been reached

4: For $i=1:n$ %Calculate the attraction and repulsive forces on each joint

5: $F_{att}(i)=-\mu d\left(q,q_{goal}\right)$; $d\left(q,q_{obs}\right)=\sqrt{{\left(x(\theta )-a\right)}^2+{\left(y(\theta )-b\right)}^2+{\left(z(\theta )-c\right)}^2}-r1-r2$

6: $F_{rep}(i)=\left\{\begin{array}{c}k\left(\frac{1}{d\left(q,q_{obs}\right)}-\frac{1}{d_0}\right)\frac{1}{d^2(q,q_{obs})}\nabla d\left(q,q_{obs}\right),d\left(q,q_{obs}\right)\le d_0\\ 0,d\left(q,q_{obs}\right)>d_0\end{array}\right.$

7:  if $F_{rep}$ > $\epsilon 3$ $F_{rep}$ = $\epsilon 3$ end %Ensure smooth trajectory

8: $F_{att}=\mathrm{s}\mathrm{u}\mathrm{m}(F_{att}(i)$), $F_{rep}=\mathrm{s}\mathrm{u}\mathrm{m}(F_{rep}(i))$ end

9:  $\nabla U({\theta }_1,\cdots ,{\theta }_n)=F_{att}+F_{rep}$

10:    if $\nabla U({\theta }_1,\cdots ,{\theta }_n)<\epsilon 2$ %Determine whether the robot falls into local optimum

11:    $d\left(q,q_1\right)=\sqrt{{\left(x(\theta )-a\right)}^2+{\left(y(\theta )-b\right)}^2+{\left(z(\theta )-c\right)}^2}$

12:   $F_{rep\_vir}=k\left(\frac{1}{d\left(q,q_1\right)}-\frac{1}{d_0}\right)\frac{1}{d^2\left(q,q_1\right)}\nabla d\left(q,q_1\right)$ %adding a virtual obstacle

13:   $\nabla U({\theta }_1,\cdots ,{\theta }_6)=F_{att}+F_{rep}+F_{vir\_rep}$ end

14: $\lambda =ϵ1+ϵ2\times d\left(q,q_{goal}\right)+ϵ3\times d\left(q,q_{obs}\right)$ %Determine iteration step size

15: $q_s=q_{s-1}-\lambda \times \nabla U\left({\theta }_1,\cdots ,{\theta }_n\right)$ %Update joint angles using gradient descent method

16: end

3.5.1. Comparison with APF Algorithm in Cartesian Space

This type of method [20] calculates repulsion and attraction in Cartesian space, and maps the resultant force from Cartesian space to joint space using the Jacobian matrix. The process of this type of method is as Algorithm 2 follows:

Algorithm 2: APF in Cartesian space

STEP1: Calculate the coordinates of each joint using kinematics

STEP2: Calculate attraction Fa and repulsive forces Fr in the Cartesian space, and convert them into the velocity $V=[v_x,v_y,v_z]$ of the end-effector

STEP3: Calculate the Jacobian matrix  $J(q)$and its inverse $J^{-1}(q)$

STEP4: Converting velocity V into joint space using Jacobian matrix  $\dot{q}=J^{-1}(q)V$

STEP5: $q_{s+1}=q_s+h\times \dot{q}$ %h is the iteration step size

The coordinate system of this method is constantly transformed between Cartesian space and joint space, and this method cannot solve the inverse matrix of the Jacobian matrix when the robotic arm falls into a singular configuration ($J(\theta )=0$). Because the algorithm in this paper is directly in joint space so that it does not require STEP3 and STEP4. It has much higher real-time performance and efficiency than the APF algorithm in Cartesian space.

3.5.2. Comparison with APF Algorithm Using a Sampling Method

This type of methods [22] uses a sampling method to calculate the fastest decreasing direction of the potential field function. Its process is as Algorithm 3 follows:

Algorithm 3: APF using a sampling method

STEP1: Each joint angle ${\theta }_i$ has three variations in the next moment For example: ${\theta }_1^{\prime }\leftarrow \left\{{\theta }_1-h,{\theta }_1,{\theta }_1+h\right\}$ %h is the iteration step size

STEP2: Calculate all cases of $U({\theta }^{\prime })$ and find the lowest value of $U({\theta }^{\prime })$

%${\theta }^{\prime }=[{\theta }_1^{\prime },{\theta }_2^{\prime },{\theta }_3^{\prime },\cdots ,{\theta }_n^{\prime }]$. The joint angle  $\theta$ changes to ${\theta }^{\prime }$ along the negative gradient direction of the potential field function.

STEP3: Update joint angle from $\theta$  to  ${\theta }^{\prime }$

This type of method needs to calculate the potential field function $3^n$ times in each cycle, while our algorithm only needs to calculate the potential field function once in each cycle. Thus, the algorithm in this paper has a higher real-time performance.

3.5.3. Comparison with APF Algorithm Using a Numerical Method

This type of method [23] uses the Euler method to calculate the gradient of the potential field function, as shown in Equations (18) and (19):

$$\nabla U({\theta }_1,\cdots {\theta }_n)=(\frac{\partial U}{\partial {\theta }_1},\cdots ,\frac{\partial U}{\partial {\theta }_n})$$

(18)

$$\frac{\partial U}{\partial {\theta }_i}=\frac{U({\theta }_i+h\cdots ,{\theta }_n)-U({\theta }_i-h\cdots ,{\theta }_n)}{2h}$$

(19)

h is the iteration step size. This method requires calculating the potential field function twice to obtain the gradient direction of a joint angle, and each cycle requires calculating the gradient of six joint angles. Therefore, the method requires 2n calculations of the potential field function per cycle, while our algorithm only needs to calculate the potential field function once in each cycle. Thus, the algorithm in this paper has a higher real-time performance.

4. Experiment and Result

In this paper, the ROCR6 is our research object. ROCR6 is a six-axis robotic arm developed by a Chinese company, Si Valley. Figure 9 shows the structure and coordinate system of the robot, and

Table 1. Modified D-H parameters of the 6-DOF robot.

Joint	${\mathit{\theta }}_{\mathit{i}}$	${\mathit{\alpha }}_{\mathit{i}-1}$	${\mathit{a}}_{\mathit{i}-1}$$(\mathbf{mm})$	${\mathit{d}}_{\mathit{i}}$$(\mathbf{mm})$
1	${\theta }_1$	0	0	122.3
2	${\theta }_2-\pi /2$	$\pi /2$	0	0
3	${\theta }_3$	0	−270	0
4	${\theta }_4-\pi /2$	0	−253	123.3
5	${\theta }_5$	$\pi /2$	0	207.1
6	${\theta }_6$	$-\pi /2$	0	99.1

shows the modified D-H parameters of the 6-DOF robot.

We performed kinematic simulations in Simscape in Matlab, and these simulations were divided into two cases, namely obstacle avoidance for a sphere and obstacle avoidance for a rectangular beam. To demonstrate the real-time capability of our algorithm in this paper, we compared it with the algorithms discussed in Section 3.5. Additionally, we compared it with the genetic algorithm to showcase the performance of the results obtained by our algorithm.

4.1. The Obstacle Avoidance for a Sphere

Table 2. The information of the spherical obstacle and the configuration of the robot.

Spherical Obstacle and Robot	Information
Starting position	[590,−131,112] (mm)
The configuration at the starting position	$\left[\begin{array}{c}-0.0130,-1.0585,-0.6853\\ \mathrm{0.1730,1.5780,1.5578}\end{array}\right]$ (rad)
Target position	[104,−600,120] (mm)
The configuration at the target position	$\left[\begin{array}{c}-1.1953,-1.0796,-0.6122\\ \mathrm{0.1210,1.5780,0.3755}\end{array}\right]$ (rad)
Obstacle coordinates	[250,−300,112] (mm)
Obstacle radius	75 mm

shows the task information and the parameter details of the spherical obstacle. The motion process of the robotic arm using the APF algorithm is shown in Figure 10, where the red trajectory represents the running trajectory of the middle joint and end-effector. The change in each joint angle using the improved APF algorithm is shown in Figure 11, and the change in each joint angle using the genetic algorithm is shown in Figure 12, and their operation indexes are shown in

Table 3. The performance of algorithms result.

Algorithm	Improved APF	Genetic
Joint angle increment	2.9510 (rad)	10.8894 (rad)
Path length	880.6657 (mm)	895.9892 (mm)

.

Table 4. The run time of algorithms.

Algorithm	Run Time
Improved APF	0.3558 (s)
APF in Cartesian space	8.8696 (s)
APF using a sampling method	260.3108 (s)
APF using a numerical method	6.2696 (s)

compares the running time of our algorithm with each of the algorithms in Section 3.5.

4.2. The Obstacle Avoidance for a Rectangular Beam

Table 5. The information of the rectangular beam and the configuration of the robot.

Rectangular Beam Obstacle and Robot	Information
Starting position	[590,−131,110] (mm)
The configuration at the starting position	$\left[\begin{array}{c}-0.0130,-1.0716,-0.7080\\ \mathrm{0.2088,1.5780,1.5578}\end{array}\right]$ (rad)
Target position	[104,−600,160] (mm)
The configuration at the target position	$\left[\begin{array}{c}-1.1953,-1.0659,-0.4804\\ \mathrm{0.0245,1.5780,0.3755}\end{array}\right]$ (rad)
Obstacle coordinates	[250,−300,0] (mm)
Obstacle bottom edge	60 $\times$ 60 (mm)
Obstacle height	300 mm

shows the parameter details of the rectangular beam. The motion process of the robotic arm using the APF algorithm is shown in Figure 13, where magenta trajectory represents the running trajectory of the middle joint and end-effector. The change of each joint angle using the improved APF algorithm is shown in Figure 14, the change of each joint angle using genetic algorithm is shown in Figure 15, and their operation indexes are shown in

Table 6. The performance of the algorithms.

Algorithm	Improved APF	Genetic
Joint angle increment	4.1690 (rad)	10.1739 (rad)
Path length	1246.6496 (mm)	838.3892 (mm)

.

Table 7. The run time of algorithms.

Algorithm	Run Time
Improved APF	0.3912 (s)
APF in Cartesian space	9.7521 (s)
APF using a sampling method	286.2102 (s)
APF using a numerical method	6.8694 (s)

shows the running time of each algorithm.

4.3. Experimentation in the Real World

The improved APF algorithm has now been tested in the real world for the rectangular beam obstacle in Section 4.2. Figure 16 shows each joint of the real robotic arm and the obstacle. Figure 17 shows the experimental result in the real world, and the robot avoids the obstacle and reaches the target position.

5. Discussions

In smart factories, trajectory planning algorithms require high real-time capability to adapt to complex and dynamic industrial tasks. The algorithm proposed in this paper meets this requirement by demonstrating an excellent real-time performance. As evident in Table 4 and Table 7, the improved artificial potential field method presented in this paper outperforms other APF methods in terms of real-time performance, as it can complete trajectory planning tasks within a mere 0.4 s.

The algorithm should strive to compute excellent trajectories, as excellent trajectories can save the energy consumed by the robotic arm, reduce the impacts during motion, and enhance the operational efficiency. From Table 4 and Table 7, it can be observed that the algorithm presented in this paper exhibits smaller joint angle variations compared with the genetic algorithm. This indicates that using the algorithm proposed in this paper can reduce the energy consumption during the operation of the robotic arm. However, the algorithm proposed in this paper still has some drawbacks. In comparison to the genetic algorithm, this algorithm may cause the robotic arm’s end effector to move slightly further, thereby reducing the efficiency of the robotic arm’s operation. Additionally, the smoothness of the paths obtained by this algorithm is lower than that of the genetic algorithm, which may result in a greater impact on the robotic arm. Lastly, taking the rectangular beam obstacle in Section 4.2 as a case study, we conducted real-world testing using the algorithm presented in this paper. It can be observed that the robotic arm can effectively avoid obstacles.

6. Conclusions

Robotic arms are widely used in factory assembly lines. A real-time obstacle avoidance algorithm that can adapt to changes in the starting position and goal position at any time is needed. In this paper, we propose an improved artificial potential field method in joint space, which can realize the real-time obstacle avoidance of the robotic arm. The experimental results show that the algorithm can achieve good performance under different obstacles. The algorithm completes the computation very quickly, and the performance of the obstacle avoidance trajectory obtained by this algorithm is higher than the trajectory obtained by genetic algorithm. Its main advantages are as follows:

• The algorithm prevents the transformation of coordinate system from Cartesian space into joint space, and the robotic arm still performs well when it is caught in a singular configuration.
• The algorithm can solve the gradient expression of repulsive potential field in advance. The potential field function only needs to be calculated once during each iteration, and the calculation efficiency is very fast.
• The algorithm proposes an effective method to prevent the robotic arm falling into a local minimum state without introducing additional information.

In future work, we will further improve this algorithm to make the motion trajectory smoother. In addition, the algorithm can obtain the angle, velocity, and acceleration information of each joint during operation. We intend to combine this algorithm with dynamics to control robotic arms in the future.