Abstract
With the increasing utilization of intelligent mobile devices for online inspection of electrical equipment in smart grids, the limited computing power and storage capacity of these devices pose challenges for deploying large algorithm models, and it is also difficult to obtain a substantial number of images of electrical equipment in public. In this paper, we propose a novel distillation method that compresses the knowledge of teacher networks into a compact few-shot classification network, employing a global and local knowledge distillation strategy. Central to our method is exploiting the global and local relationships between the features exacted by the backbone of the teacher network and the student network. We compared our method with recent state-of-the-art (SOTA) methods on three public datasets, and we achieved superior performance. Additionally, we contribute a new dataset, namely, EEI-100, which is specifically designed for electrical equipment image classification. We validated our method on this dataset and demonstrated its exceptional prediction accuracy of 94.12% when utilizing only 5-shot images.
1. Introduction
As an essential component of the power system, daily inspection of electrical equipment is imperative to ensure the secure and stable operation of the power system [1]. Image classification is a crucial prerequisite for monitoring the condition of electrical equipment based on image information. In recent years, machine learning has made significant progress in the field of image classification for electrical equipment. Bogdann presented a machine learning method for determining the state of each switch by analyzing images of the switches in power distribution substations [2]. Zhang implemented FINet based on improved YOLOv5 to inspect the insulators and their defects in order to ensure the safety and stability of the power system [3]. To address the few fault cases and deficient monitoring information in transformer diagnostic tasks, Xu provides an improved few-shot learning method based on approximation space and belief functions [4]. Yi proposed a label distribution CNNs classifier to estimate the aging time of the conductor morphology of the high-voltage transmission line [5]. It is noteworthy that the majority of these investigations have concentrated on a restricted range of electrical apparatus. These models necessitate a substantial quantity of training data to guarantee optimal performance. Nevertheless, acquiring adequate electrical equipment images in a practical setting may prove challenging, and the proportion of labeled samples is minimal. To a certain extent, the classification of electrical equipment images is not really a big data problem; rather, it belongs to the few-shot learning (FSL) domains.
Few-shot classification (FSC) is the task of classifying samples with a limited number of instances while showcasing rapid generalization capabilities. Recently, a large number of few-shot image classification algorithms have been proposed. Depending on the learning paradigm used, these methods can be broadly divided into two categories: (1) meta-learning-based methods and (2) transfer-based learning methods. Meta-learning is a promising approach that leverages episodic training to simulate the real test environment by randomly selecting several subtasks. Optimization-based meta-learning methods employ a two-tier optimization process to learn the optimizer for quickly processing new tasks. Model-Agnostic Meta-Learning (MAML) [6] obtains the optimal initialization parameters of the model through meta-training, enabling the model to adapt to new tasks after a few gradient updates. In addition, the learning rate and gradient direction are also important factors for the optimizer [7,8]. However, these methods require the storage and computation of higher-order derivatives, resulting in high memory and computational costs. On the other hand, metric-based methods use nonparametric classifiers as the basic learners, avoiding the aforementioned issues. The key factors of these methods are feature extraction and similarity measurement, which offer ample room for improvement. PARN [9] proposed a feature extractor that learned an offset for each cell in the convolution kernel in order to extract more efficient features, building deformable convolutional layers. CC+rot [10] improved the transfer ability of feature extractors by adopting auxiliary self-supervised tasks. Zhang et al. [11] used the pre-trained visual saliency detection model to segment the foreground and background of the image and then extract the foreground and background features, respectively. With the proven effectiveness of attention mechanisms in extracting discriminating features, several few-shot classification (FSC) tasks have adopted this method, including CAN [12], AWGIM [13], and CTM [14]. Additionally, in metric-based meta-learning methods, the measurement of similarity is also crucial. SEN [15] combines Euclidean distance and norm distance to improve the effectiveness of Euclidean distance measurement in high-dimensional spaces. FPN [16] calculated the reconstruction error between the support sample and the query sample as the similarity score. DN4 [17] and Deep EMD [18] obtain rich similarity measures directly from local features.
Recent studies have indicated that the FSC of the transfer-learning method can attain comparable performance to that of the meta-learning method with complex episodic training. Such methods typically combine pre-trained feature extractors on all base-class datasets with arbitrary traditional classifiers to make classification decisions for query samples of unknown classes. It has been shown that pre-training the entire base class dataset using the cross-entropy loss function followed by fine-tuning the pre-trained model using support samples of the visible class can provide a powerful baseline for FSC tasks [19]. Since then, several efforts have been proposed to improve the representation performance of feature extractors. For example, Neg-Cosin [20] proposed the use of the non-negative interval Cosine loss function to optimize the model, thereby increasing the distance between the training sample and its corresponding parametric prototype, which can effectively improve the generalization performance of the model. S2M2 [21] used manifold mixing as an effective regularization method to improve the generalization performance of the model. Refs. [22,23] used rotation prediction and mirror prediction as self-supervised tasks to add to the pre-training process, and experimental results showed that self-supervised tasks are effective methods to improve feature representation performance.
In the pursuit of high-accuracy classification performance, many studies tend to employ highly complex networks to enhance the representation of features. As a result, deploying these methods in real-world applications often requires significant computing resources (such as storage space and computing power) and leads to significant time delays. However, power inspection heavily relies on intelligent mobile devices, including inspection robots and UAVs. Considering the limited storage capacity of these devices, it is essential to ensure that the classification model’s size is not excessively large. Therefore, in this study, we utilize a knowledge distillation-based model compression algorithm to achieve few-shot image classification, aiming to reduce the number of model parameters.
Knowledge distillation [24,25] is one of the most effective model compression methods and has garnered significant research interest in both industry and academia due to its simple training strategy and effective performance. It leverages the knowledge acquired by a teacher network to guide the training of a small-scale student network, enabling the latter to achieve comparable performance despite having fewer parameters. In order to make better use of the knowledge information contained in the teacher network, AT [26] proposed to take the spatial attention of the hidden layer features of the teacher network as knowledge and instruct the student network to imitate its attention feature map. RKD [27] proposed a relational knowledge distillation method, which used distance and angle to measure the relationship between sample features, as a valid type of knowledge during distillation. Peng et al. [28] used the kernel function to obtain higher-order relationships between the features of samples as effective distillation knowledge. Although the model compression methods based on feature relation knowledge mentioned above can effectively improve the performance of small-capacity student networks, the current work only focuses on the local relationship between individual sample features, ignoring the global relationship between the features of samples. Therefore, this paper proposes a method based on global and local knowledge distillation and applies it to the task of FSC for electrical equipment images.
In this paper, we propose three main contributions:
- We present a novel distillation approach that compresses the knowledge of teacher networks into a compact student network, enabling efficient few-shot classification. The incorporation of global and local relationship strategies during the distillation process effectively directs the student network towards achieving performance levels akin to those of the teacher network.
- We contribute a new dataset that contains 100 classes of electrical equipment with 4000 images. The dataset contains a wide range of various pieces of electrical equipment, including power generation equipment, distribution equipment, industrial electrical equipment, and household electrical equipment.
- We demonstrate the effectiveness of our proposed method by validating it on three public datasets and comparing it with the SOTA methods on the electrical image dataset we introduced. Our proposed method outperforms all other methods and achieves the best performance.
2. Methodology
2.1. Problem Definition
In few-shot image classification tasks, given a certain size of image dataset I, it is randomly divided into three subsets: Itrain, Ival, and Itest. Itrain is used as the base dataset for pre-training the classification model. Assuming that the pre-training set has Cb categories, the m-th image sample is denoted as xm, and its corresponding label is represented as ym. Ival is used for validation, while Itest is used as the new class dataset for testing the trained model. For Ival and Itest, multiple N-way-K-shot subtasks are randomly sampled, with each task consisting of a support sample set (IS) and a query sample set (IQ). IS is constructed by randomly selecting N categories from Ival or Itest, and then randomly selecting K samples from each category. The set of the n-th category is denoted as , and the k-th image in the n-th category is denoted as Ik. IQ is composed of Q samples randomly selected from each residual sample category, denoted as , where Iq represents the q-th query sample. Therefore, the problem of few-shot image classification can be described as using the model trained on the base class dataset and the support sample set to make classification decisions for query samples.
2.2. FSC Network Based on Global and Local Knowledge Distillation
We propose a novel few-shot electrical image classification algorithm based on knowledge distillation. Figure 1 shows the overall architecture of our network. We first trained a high-performance teacher network through self-supervised learning, and we then guided the training of the student network by the teacher network. To fully utilize the prior knowledge of the teacher network, we designed a knowledge distillation method based on global and local relationships. This method can transfer the global and local features of the images extracted by the teacher network to the student network, enabling the compact student network to learn more effective features about the images and achieve better image classification.
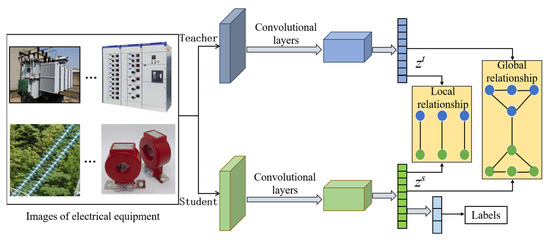
Figure 1.
Network architecture of our proposed method. The input pairs that produce activations in the pre-trained teacher network produce similar activations in the student network. Global and local distillation bridges the gap between the feature representation of the student and teacher.
2.2.1. Pre-Train of Teacher Network
The teacher model consists of a backbone convolutional neural network and two linear classifiers. The backbone network fθ(•) is used for feature extraction of images, one classifier Lw(•) is used for predicting the base class of image samples, and the other classifier Lr(•) is used for predicting the rotation category in self-supervised tasks. Additionally, each classifier is followed by a Softmax layer. M image samples are randomly selected from the base class dataset, and each image is rotated at 0°, 90°, 180°, and 270°, with its corresponding rotation label as = [0, 1, 2, 3].
When image xm is fed into the teacher network, the d-dimensional feature representation fθ(xm) is extracted by the backbone network. The classification scores of the base class prediction classifier and the rotation prediction classifier for the features are expressed as Sb and Sr, as shown in Equation (1):
Furthermore, the aforementioned classification scores are transformed into base class and rotation class prediction probabilities through a Softmax layer, as shown in Equation (2):
where Sbc denotes the c-th element of the score vector Sb, Srr denotes the r-th element of the score vector Sr, Cb denotes the number of base class labels, and and are the probability output values of the base classifier and the rotation classifier, respectively. The cross-entropy loss function and the self-supervised loss function are calculated to obtain the training loss function, as shown in Equation (3):
where ymc denotes the c-th element of the one-hot encoded vector of ym, and denotes the c-th element of the one-hot encoded vector of . Based on the loss function in Equation (3), the parameters of the teacher network are optimized to complete the pre-training process.
2.2.2. Global and Local Knowledge Distillation
Firstly, a student network is constructed, which consists of a backbone neural network BΦ(•) composed of a small number of convolutional layers and a linear classifier CH(•). Next, a batch of M images randomly selected from the base dataset Itrain is inputted into both the teacher network and the student network. The m-th image is represented by feature maps and obtained from the backbone of the teacher network and the student network, respectively. Finally, the features are fed into the linear classifier to obtain the output value of the student network, as shown in Equation (4):
Furthermore, the above output classification scores are transformed into classification prediction probabilities through the Softmax layer, as shown in Equation (5):
where Smc denotes the c-th element of the score vector Sm.
The equation for calculating the cross-entropy loss function between the output values of a student network and the true labels is shown in Equation (6):
In order to enable students to learn the representation of global features of images by the teacher network through online learning, we adopt the maximum mean discrepancy between the feature spaces of the two networks as the global loss function, which is calculated by Equation (7):
In addition, we calculate the Euclidean distance between each sample feature in the two networks as the local loss function, and its calculation formula is shown in Equation (8):
In summary, the total loss function for the student network is shown in Equation (9). Based on Equation (9), the student network is trained, and the parameters in the network are updated until optimal, thereby completing the knowledge distillation process from the teacher network to the student network.
2.2.3. Few-Shot Evaluation
After completing the knowledge distillation task in Section 2.2.2, the base classifiers in the student network are first removed. Furthermore, the parameters of the backbone neural network BΦ(•) are fixed, and features are extracted from both the support and query samples. Finally, based on the N-way-K-shot method, the query samples are classified using Equation (10), where the features of the k-th support sample and the q-th query sample are denoted as BΦ(Ik) and BΦ(Iq), respectively, and gφ{•} is a classifier with parameters φ. Any traditional classifier can be used to complete the classification prediction task.
3. Experiments
3.1. EEI-100 Dataset
We invested a substantial amount of time in constructing a dataset for electrical equipment image classification, EEI-100. It contains 100 classes of electrical equipment with 4000 images. The majority of the images were obtained through on-site collection, with a small number of images sourced from online platforms. To the best of our knowledge, this is one of the first datasets specifically designed for the classification of electrical equipment. This dataset is an extension of our previous EEI-40 [29]. It includes substation equipment, distribution station equipment, and common electrical equipment, ranging from large-scale equipment such as heavy-duty transformers to small-scale equipment such as circuit breakers. A few images from the proposed dataset are illustrated in Figure 2 (more images are illustrated in Appendix A).

Figure 2.
Some images of EEI-100 dataset. They represent different electrical equipment. (a) wind power tower; (b) heavy-duty transformer; (c) heavy-duty distribution cabinet; (d) energy storage battery pack; (e) electrical insulator; (f) split-core current transformer; (g) three-phase moto; (h) heavy-duty circuit breaker; (i) contactor; (j) cooling fan; (k) electric energy meter; (l) dragline board.
3.2. Experiments on Public Datasets
3.2.1. Experiment Setup
We evaluate our knowledge distillation method on three widely used public datasets, namely MiniImageNet, CIFAR-FS, and CUB. The experiments were conducted on a workstation equipped with an NVIDIA 3090Ti GPU and implemented using Pytorch software. To ensure a fair comparison with current few-shot image classification methods, a commonly used 4-layer convolutional neural network (CNN) and ResNet12 were adopted as the student network and teacher network, respectively. During the training phase, we used the SGD optimizer to optimize our models in all experiments, where momentum was set to 0.9 and weight decay was set to 5 × 10−4. We trained for 100 epochs with an initial learning rate of 0.025, which was reduced by half after 60 epochs. In the testing phase, we conducted 5-way-1-shot and 5-way-5-shot tests. Specifically, we randomly performed 2000 classification subtasks on the testing dataset. In each subtask, 15 images were randomly selected from each class as query images for testing. The evaluation criterion for the algorithm’s classification performance was the average accuracy of all subtasks, and the standard deviation of the accuracy under a 95% confidence interval should also be provided.
Please note that we also conducted a similar experiment on the 1080Ti GPU and achieved comparable performance. This significantly alleviates the economic burden associated with model training. Leveraging a 4-layer CNN architecture, the student model occupies a mere 2 MB in size, which is approximately 50 times smaller than the teacher model. This lightweight model can be deployed on diverse edge processors, substantially lowering the hardware requirements for its implementation.
3.2.2. Parametric Analysis Experiment
It can be seen from Equation (9) that α1 and α2 are important hyperparameters in the process of distilling the student network. Initially, we conducted experiments in which we temporarily ignored the influence of global knowledge by setting α1 to 0. Through this analysis, we observed that α2 near 1 yielded the best model’s performance. Building upon this observation, we proceeded to fix α2 at 1, and the value of parameter α1 was varied with a step size of 0.1 within the range of [0, 1]. The test accuracy of the student network under different values of α1 is shown in Figure 3a,b. The results indicate that the model performance is optimal when the value of α1 is 0.5. Therefore, the value of α1 was set to 0.5, and then α2 was varied with a step size of 0.01 within the range of [0, 0.1]. The test accuracy of the student network under different values of α2 is shown in Figure 3c,d. The results reveal that the optimal value for α2 is 0.1.
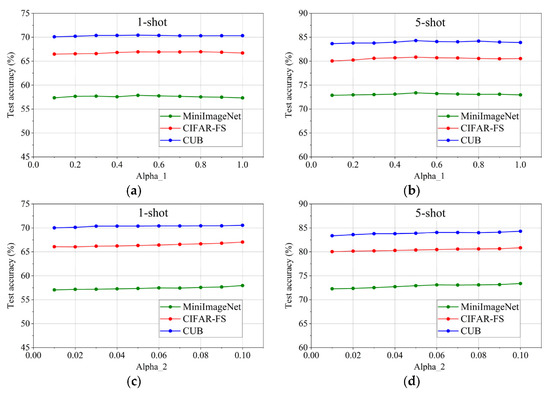
Figure 3.
Test experiments under different values of α1 and α2 on three public datasets. (a) 1-shot test accuracy under different values of α1; (b) 5-shot test accuracy under different values of α1; (c) 1-shot test accuracy under different values of α2; (d) 5-shot test accuracy under different values of α2.
Additionally, after completing the search for α1 and α2 within their respective ranges, we extended our exploration beyond the boundaries of [0, 1] and [0, 0.1]. However, we found that no values outside of these ranges yielded superior results.
3.2.3. Ablation Studies
The innovation of this work lies in proposing a knowledge distillation algorithm for global and local relationships. In order to verify the effectiveness of the proposed method, detailed ablation experiments were conducted on three public datasets. The knowledge distillation algorithms using only global and local relationships are denoted as Global and Local, respectively, and their fusion is denoted as Global-Local. The classification accuracies of these methods on 5-way-1-shot and 5-way-5-shot tasks are shown in Table 1.

Table 1.
Results (%) of ablation experiment.
The results in Table 1 indicate that for both 5-way 1-shot and 5-way 5-shot tasks on all datasets, the classification accuracy of Global-Local is consistently higher than that of Global and Local. The experiments demonstrate that global and local relationships are complementary, and their fusion can extract richer image features. Therefore, the knowledge distillation algorithm based on global and local relationships can further improve the performance of knowledge distillation.
3.2.4. Comparison Experiment Compared with Existing Methods
This paper compares our method with the SOTA methods in recent years, which are mainly divided into two categories: meta-learning-based methods and transfer learning-based methods. The comparison results with these methods are shown in Table 2.

Table 2.
Comparison results (%) of the experiment on three public datasets.
According to the results in Table 2, the following observations can be made:
- On the MiniImageNet dataset, our proposed method achieves the best classification performance. Compared with the best-performing method in the meta-learning-based category, HGNN, our method outperforms it by 2.23% and 0.9% on 1-shot and 5-shot classification tasks, respectively. In the transfer learning-based category, compared with the best performing method, CGCS, our method outperforms it by 2.33% and 1.26% on 1-shot and 5-shot classification tasks, respectively.
- On the CIFAR-FS dataset, our proposed method also achieves top performance. Our method outperforms the best-performing method, PSST, by 2.67% and 0.42% on 1-shot and 5-shot classification tasks, respectively.
- On the CUB-200-2011 dataset, our proposed method achieves the highest classification performance. Our method outperforms the best-performing method, HGNN, by 1.42% and 0.99% on 1-shot and 5-shot classification tasks, respectively.
3.3. Experiments on EEI-100 Dataset
Furthermore, we compare the performance of our proposed method with the SOTA methods on the EEI-100 dataset. The experimental process employs the same parameter selection strategy as before.
3.3.1. Parametric Analysis Experiment
By following the approach outlined in Section 3.2.2, the values of parameters α1 and α2 are determined to optimize the performance of the model on EEI-100. Experimental results show that α1 has the optimal value of 0.6 within the range of [0.1, 1], as illustrated in Figure 4a. Similarly, α2 has the optimal value of 0.1 within the range of [0.01, 0.1], as illustrated in Figure 4b.
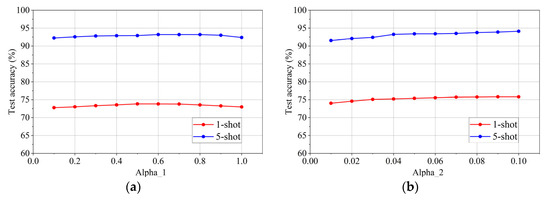
Figure 4.
Test experiments under different values of α1 and α2 on EEI-100 dataset. (a) 1-shot and 5-shot test accuracy under different values of α1; (b) 1-shot and 5-shot test accuracy under different values of α2.
3.3.2. Comparison Experiment with Existing Methods
To demonstrate the superiority of our proposed method in the classification of electrical equipment images, this section presents a comparative experiment with three existing methods, namely, CGCS, Neg-Cosine, and HGNN, on the EEI-100 dataset. These three methods have recently achieved good performance on public datasets. The classification accuracy of the test set is presented in Table 3. Specifically, our method achieves the highest classification accuracy (up to 94.12%) compared with the other methods.

Table 3.
Comparison result (%) of the experiment on EEI-100 dataset.
4. Conclusions and Future Work
In conclusion, this paper proposes a novel few-shot electrical image classification algorithm based on knowledge distillation. By leveraging the few-shot learning method and employing global and local knowledge distillation, our algorithm achieves high classification accuracy with only a limited number of image samples. The results obtained on the newly introduced EEI-100 dataset demonstrate that our method achieves a remarkable prediction accuracy of 94.12% using just 5-shot images. The lightweight and high-performance nature of our model enables its practical application in the online inspection of electrical equipment in smart grids, effectively enhancing the efficiency of detection and maintenance in the power system. Furthermore, the training and deployment of our model do not impose significant hardware requirements, making it accessible to a wide range of researchers.
Regarding future work, we plan to explore a pre-training method to separate the foreground and background, as different backgrounds may negatively affect distillation. Additionally, we plan to use a multi-stage fusion of global and local features during the distillation process. This can provide a better understanding of the underlying structure of the complex model and the relationship between different stages of the model.
Author Contributions
Conceptualization, B.Z. and J.G.; methodology, B.Z.; software, C.Y.; validation, B.Z. and J.Z.; formal analysis, B.Z.; investigation, X.Z.; resources, J.Z.; data curation, X.Z.; writing—original draft preparation, B.Z.; writing—review and editing, J.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the National Natural Science Foundation of China under Grant No. U2066203 and No. 61973178, and in part by the Key Research & Development Program of Jiangsu Province under Grant No. BE2021063.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The dataset proposed in this paper can be obtained from the author with a reasonable request.
Conflicts of Interest
The authors declare no conflict of interest in preparing this article.
Abbreviations
| SOTA | State-of-the-art |
| UAV | Unmanned aerial vehicle |
| CNN | convolutional neural network |
| FSL | Few-shot learning |
| FSC | Few-shot classification |
Appendix A
In this appendix, more images of the EEI-100 dataset proposed by us are presented. However, we regret to inform that due to the fact that some image data were collected in specific scenarios, the device information in the pictures cannot be disclosed. Therefore, we are unable to fully release the entire dataset here.

Figure A1.
Few images of EEI-100 dataset.
References
- Peng, J.; Sun, L.; Wang, K.; Song, L. ED-YOLO power inspection UAV obstacle avoidance target detection algorithm based on model compression. Chin. J. Sci. Instrum. 2021, 10, 161–170. [Google Scholar]
- Bogdan, T.N.; Bruno, M.; Rafael, W.; Victor, B.G.; Vanderlei, Z.; Lourival, L. A Computer Vision System for Monitoring Disconnect Switches in Distribution Substations. IEEE Trans. Power Deliv. 2022, 37, 833–841. [Google Scholar]
- Zhang, Z.D.; Zhang, B.; Lan, Z.C.; Lu, H.C.; Li, D.Y.; Pei, L.; Yu, W.X. FINet: An Insulator Dataset and Detection Benchmark Based on Synthetic Fog and Improved YOLOv5. IEEE Trans. Instrum. Meas. 2022, 71, 6006508. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Wang, Y.; Zhong, D.; Zhang, G. Improved few-shot learning method for transformer fault diagnosis based on approximation space and belief functions. Expert Syst. Appl. 2021, 167, 114105. [Google Scholar] [CrossRef]
- Yi, Y.; Chen, Z.; Wang, L. Intelligent Aging Diagnosis of Conductor in Smart Grid Using Label-Distribution Deep Convolutional Neural Networks. IEEE Trans. Instrum. Meas. 2022, 71, 3501308. [Google Scholar] [CrossRef]
- Finn, C.; Abbeel, P.; Levine, S. Model-Agnostic Meta-Learning for Fast Adaptation of Deep Network. In Proceedings of the 34th International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Li, Z.; Zhou, F.; Chen, F.; Li, H. Meta-SGD: Learning to Learn Quickly for Few-Shot Learning. arXiv 2017, arXiv:1707.09835. [Google Scholar]
- Ravi, S.; Larochelle, H. Optimization as a model for few-shot learning. In Proceedings of the 5th International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Wu, Z.; Li, Y.; Guo, L.; Jia, K. PARN: Position-Aware Relation Networks for few-shot learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Gidaris, S.; Bursuc, A.; Komodakis, N.; Perez, P.; Cord, M.; Ecole, L. Boosting few-shot visual learning with self-supervision. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Zhang, H.; Zhang, J.; Koniusz, P. Few-shot learning via saliency-guided hallucination of samples. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Hou, R.; Chang, H.; Ma, B.; Shan, S.; Chen, X. Cross attention network for few-shot classification. In Proceedings of the 33rd International Conference on Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Guo, Y.; Cheung, N. Attentive weights generation for few shot learning via information maximization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Li, H.; Eigen, D.; Dodge, S.; Zeiler, M.; Wang, X. Finding task-relevant features for few-shot learning by category traversal. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Nguyen, V.N.; Løkse, S.; Wickstrøm, K.; Kampffmeyer, M.; Roverso, D.; Jenssen, R. SEN: A novel feature normalization dissimilarity measure for prototypical few-Shot learning networks. In Proceedings of the 16th European Conference on Computer Vision (ECCV), Glasgow, Scotland, 23–28 August 2020. [Google Scholar]
- Wertheime, D.; Tang, L.; Hariharan, B. Few-shot classification with feature map reconstruction networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Virtual Conference, 19–25 June 2021. [Google Scholar]
- Li, W.; Wang, L.; Xu, J.; Huo, J.; Gao, Y.; Luo, J. Revisiting local descriptor based image-to-class measure for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Zhang, C.; Cai, Y.; Lin, G.; Shen, C. DeepEMD: Few-shot image classification with differentiable Earth Mover’s distance and structured classifiers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Chen, Y.; Liu, Y.; Kira, Z.; Wang, Y.F.; Huang, J. A closer look at few-shot classification. In Proceedings of the 7th International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Liu, B.; Cao, Y.; Lin, Y.; Zhang, Z.; Long, M.; Hu, H. Negative margin matters: Understanding margin in few-shot classification. In Proceedings of the 16th European conference on computer vision (ECCV), Glasgow, Scotland, 23–23 August 2020. [Google Scholar]
- Mangla, P.; Singh, M.; Sinha, A.; Kumari, N.; Balasubramanian, V.; Krishnamurthy, B. Charting the right manifold: Manifold mixup for few-shot learning. In Proceedings of the the IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–7 January 2020. [Google Scholar]
- Su, J.; Maji, S.; Hariharan, B. When does self-supervision improve few-shot learning. In Proceedings of the 16th European conference on computer vision (ECCV), Glasgow, Scotland, 23–23 August 2020. [Google Scholar]
- Shao, S.; Xing, L.; Wang, Y.; Xu, R.; Zhao, C.; Wang, Y.J.; Liu, B. MHFC: Multi-head feature collaboration for few-shot learning. In Proceedings of the 29th ACM International Conference on Multimedia (MM), Virtual Conference, 20–24 October 2021. [Google Scholar]
- Geoffrey, H.; Oriol, V.; Jeff, D. Distilling the Knowledge in a Neural Network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Adriana, R.; Nicolas, B.; Samira, E.K.; Antoine, C.; Carlo, G.; Yoshua, B. FitNets: Hints for Thin Deep Nets. arXiv 2014, arXiv:1412.6550. [Google Scholar]
- Zagoruyko, S.; Komodakis, N. Paying more attention to attention: Improving the performance of convolutional neural networks via attention transfer. In Proceedings of the 5th International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Park, W.; Kim, D.; Lu, Y.; Cho, M. Relational knowledge distillation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Peng, B.; Jin, X.; Liu, J.; Zhou, S.; Wu, Y.; Liu, Y.; Li, D.; Zhang, Z. Correlation congruence for knowledge distillation. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Zhou, B.; Zhang, X.; Zhao, J.; Zhao, F.; Yan, C.; Xu, Y.; Gu, J. Few-shot electric equipment classification via mutual learning of transfer-learning model. In Proceedings of the IEEE 5th International Electrical and Energy Conference (CIEEC), Nanjing, China, 27–29 May 2022. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).