Mesoscopic Effects of Interfacial Thermal Conductance during Fast Pre-Melting and Melting of Metal Microparticles
Abstract
:Featured Application
Abstract
1. Introduction
2. Interfacial Adhesion and Dispersion Forces
3. Photon and Phonon Tunneling through a Vacuum Gap
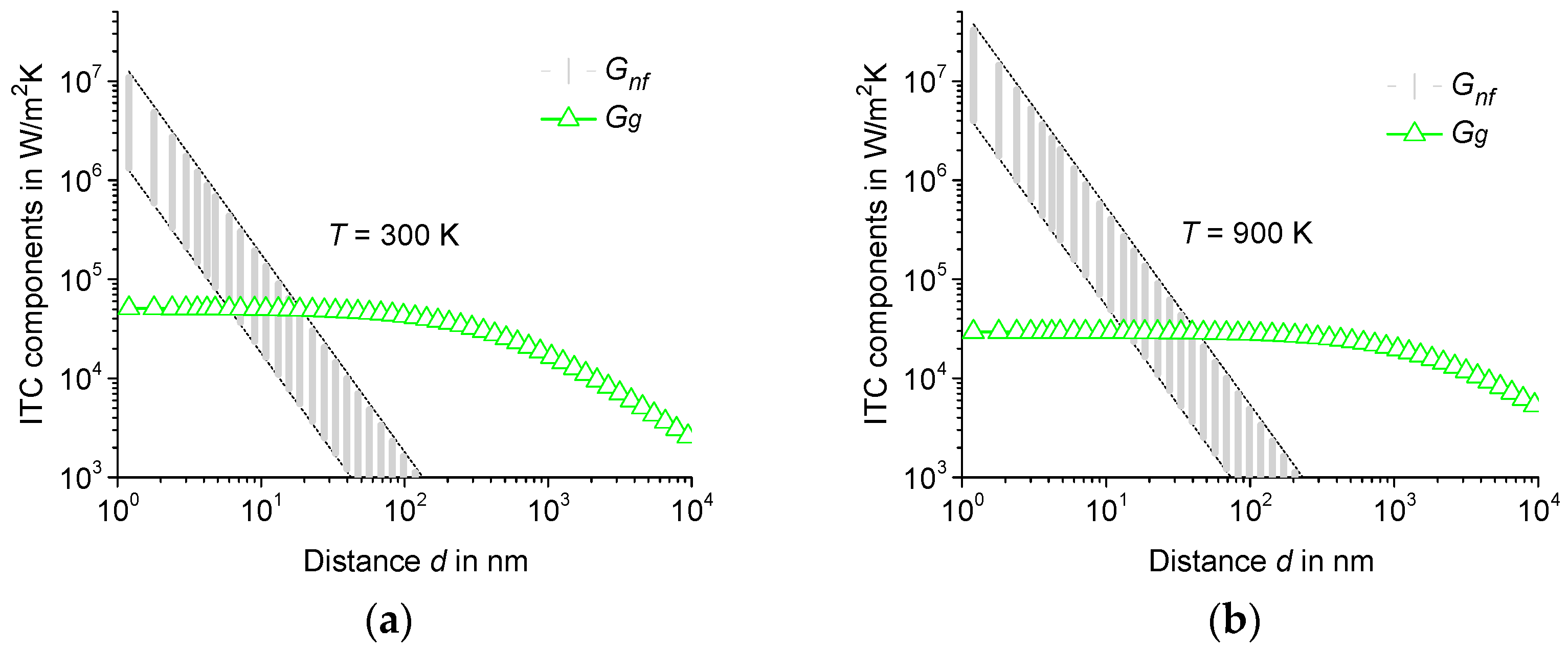
3.1. Nanoscale Radiative Heat Transfer
3.2. Photon Tunneling through a Vacuum Gap
3.3. Phonon Coupling at Sub-Nanometer Gaps
4. Heat Transfer through the Gas Gap
5. Heat Transfer across Liquid-Solid Interfaces
5.1. Effective Gap Thickness at the Liquid-Solid Interface
5.2. Evolution of Thermal Contact Conductance during the Pre-Melting Process
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Latin Symbols | |
| Hamaker constant (J) | |
| interatomic distance (m) | |
| the speed of light in vacuum (m/s) | |
| heat capacity per one molecule at a constant volume (J/K) | |
| effective size of the interfacial gap (m) | |
| characteristic length of nonlocal effects in metals (m) | |
| interfacial thermal conductance (W/m2K) | |
| ITC associated with black-body radiation limit (W/m2K) | |
| ITC due to heat transfer through gas (W/m2K) | |
| maximum possible ITC due to heat transfer through gas (W/m2K) | |
| ITC due to near-field heat transfer (W/m2K) | |
| maximum possible ITC due to near-field heat transfer (W/m2K) | |
| ITC due to phonon tunneling (W/m2K) | |
| ITC of liquid-solid interface (W/m2K) | |
| ITC of solid-solid interface (W/m2K) | |
| ITC at pre-melting process (W/m2K) | |
| Grashof number (dimensionless) | |
| Boltzmann constant (J/K) | |
| wave vector (m−1) | |
| component of the wave vector parallel to the surface (m−1) | |
| component of the wave vector perpendicular to the surface (m−1) | |
| mean-free-path of gas molecules (m) | |
| electron mean free path (m) | |
| mass of a gas molecule (kg) | |
| number of molecules per unit volume (m−3) | |
| Nusselt number (dimensionless) | |
| Prandtl number (dimensionless) | |
| interfacial contact pressure (Pa) | |
| gas pressure (Pa) | |
| heat flux through the gas (W/m2) | |
| temperature scan rate (K/s) | |
| arithmetic average of surface roughness (m) | |
| melting point (K) | |
| liquidus temperature (K) | |
| solidus temperature (K) | |
| sample temperature (K) | |
| membrane temperature (K) | |
| intermediate temperature between and (K) | |
| and | temperatures of plate 1 and plate 2 (K) |
| Fermi velocity (m/s) | |
| average velocity of gas molecules (m/s) | |
| number of molecules striking unit area of the surface per unit time (m−2s−1) | |
| Greek Symbols | |
| specific heats ratio (dimensionless) | |
| distance associated with the surface temperature jump (m) | |
| complex dielectric constant (dimensionless) | |
| gas thermal conductivity (Wm−1K−1) | |
| mean free pass of gas molecules (m) | |
| characteristic wavelength of the absorption spectra (m) | |
| characteristic wavelength of thermal radiation (m) | |
| kinematic viscosity of the gas (m2/s) | |
| gas density (kg/m3) | |
| thermal accommodation coefficient (dimensionless) | |
| angular frequency of electromagnetic waves (rad/s) | |
| characteristic frequency of absorption spectra (rad/s) | |
| Special Symbols | |
| reduced Planck constant (J⸱s) | |
References
- Chen, J.; Xu, X.; Zhou, J.; Li, B. Interfacial thermal resistance: Past, present, and future. Rev. Mod. Phys. 2022, 94, 025002. [Google Scholar] [CrossRef]
- Swamy, M.C.K.; Satyanarayan. A Review of the Performance and Characterization of Conventional and Promising Thermal Interface Materials for Electronic Package Applications. J. Electron. Mater. 2019, 48, 7623–7634. [Google Scholar] [CrossRef]
- Oliveira, J.P.; Santos, T.G.; Miranda, R.M. Revisiting fundamental welding concepts to improve additive manufacturing: From theory to practice. Prog. Mater. Sci. 2020, 107, 100590. [Google Scholar] [CrossRef]
- Mukherjee, T.; Wei, H.; De, A.; DebRoy, T. Heat and fluid flow in additive manufacturing—Part I: Modeling of powder bed fusion. Comput. Mater. Sci. 2018, 150, 304–313. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Jiang, Q.; Huo, J.; Zhang, Y.; Yang, W.; Li, X. Crystallization in additive manufacturing of metallic glasses: A review. Addit. Manuf. 2020, 36, 101568. [Google Scholar] [CrossRef]
- Zhang, J.; Song, B.; Wei, Q.; Bourell, D.; Shi, Y. A review of selective laser melting of aluminum alloys: Processing, microstructure, property and developing trends. J. Mater. Sci. Technol. 2019, 35, 270–284. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, Y.; Liu, J.; Wang, L.; Chen, Z.; Wang, M.; Zhong, S.; Wu, Y.; Wang, H. Microstructure evolution of the rapidly solidified alloy powders and composite powders. Mater. Des. 2019, 182, 108045. [Google Scholar] [CrossRef]
- Liu, H.; Yang, D.; Jiang, Q.; Jiang, Y.; Yang, W.; Liu, L.; Zhang, L.-C. Additive manufacturing of metallic glasses and high-entropy alloys: Significance, unsettled issues, and future directions. J. Mater. Sci. Technol. 2023, 140, 79–120. [Google Scholar] [CrossRef]
- Kürnsteiner, P.; Wilms, M.B.; Weisheit, A.; Gault, B.; Jägle, E.A.; Raabe, D. High-strength Damascus steel by additive manufacturing. Nature 2020, 582, 515–519. [Google Scholar] [CrossRef]
- Rittinghaus, S.-K.; Jägle, E.A.; Schmid, M.; Gökce, B. New Frontiers in Materials Design for Laser Additive Manufacturing. Materials 2022, 15, 6172. [Google Scholar] [CrossRef]
- Madhusudana, C.V. Thermal Contact Conductance. In Mechanical Engineering Series, 2nd ed.; Springer: Cham, Switzerland, 2014; ISBN 978-1-4612-3978-9. [Google Scholar]
- Liu, D.; Xie, R.; Yang, N.; Li, B.; Thong, J.T.L. Profiling Nanowire Thermal Resistance with a Spatial Resolution of Nanometers. Nano Lett. 2014, 14, 806–812. [Google Scholar] [CrossRef] [PubMed]
- Ye, N.; Feser, J.P.; Sadasivam, S.; Fisher, T.S.; Wang, T.; Ni, C.; Janotti, A. Thermal transport across metal silicide-silicon interfaces: An experimental comparison between epitaxial and nonepitaxial interfaces. Phys. Rev. B 2017, 95, 085430. [Google Scholar] [CrossRef] [Green Version]
- Chiloyan, V.; Garg, J.; Esfarjani, K.; Chen, G. Transition from near-field thermal radiation to phonon heat conduction at sub-nanometre gaps. Nat. Commun. 2015, 6, 6755. [Google Scholar] [CrossRef] [Green Version]
- Hamdan, A.; Sahli, F.; Richards, R. Characterization of a dielectric microdroplet thermal interface material with dispersed nanoparticles. J. Nanopart. Res. 2012, 14, 1250–1254. [Google Scholar] [CrossRef]
- Ge, Z.; Cahill, D.G.; Braun, P.V. Thermal Conductance of Hydrophilic and Hydrophobic Interfaces. Phys. Rev. Lett. 2006, 96, 186101. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Israelachvili, J.N., Ed.; Academic Press: San Diego, CA, USA, 2011; pp. 253–289. ISBN 978-0-12-375182-9. [Google Scholar]
- Han, Z.; Fina, A. Thermal conductivity of carbon nanotubes and their polymer nanocomposites: A review. Prog. Polym. Sci. 2011, 36, 914–944. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Wang, Y.; Wang, C.M.; Gu, Y. Thermal Conductivity of Graphene and its Polymer Nanocomposites: A Review. In Advanced Computational Nanomechanics, 1st ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2016; ISBN 978-1-119-06893-8. [Google Scholar]
- Rashidi, M.; Nazari, M.A.; Mahariq, I.; Ali, N. Modeling and Sensitivity Analysis of Thermal Conductivity of Ethylene Glycol-Water Based Nanofluids with Alumina Nanoparticles. Exp. Tech. 2023, 47, 83–90. [Google Scholar] [CrossRef]
- Izadi, M.; Sheremet, M.; Hajjar, A.; Galal, A.M.; Mahariq, I.; Jarad, F.; Ben Hamida, M.B. Numerical investigation of magneto-thermal-convection impact on phase change phenomenon of Nano-PCM within a hexagonal shaped thermal energy storage. Appl. Therm. Eng. 2023, 223, 119984. [Google Scholar] [CrossRef]
- Dash, J.G. History of the search for continuous melting. Rev. Mod. Phys. 1999, 71, 1737–1743. [Google Scholar] [CrossRef]
- Wang, G.-X.; Matthys, E. Experimental determination of the interfacial heat transfer during cooling and solidification of molten metal droplets impacting on a metallic substrate: Effect of roughness and superheat. Int. J. Heat Mass Transf. 2002, 45, 4967–4981. [Google Scholar] [CrossRef]
- Minakov, A.; Morikawa, J.; Zhuravlev, E.; Ryu, M.; Schick, C. Thermal contact conductance at melting and crystallization of metal micro-droplets. Mater. Res. Express 2020, 7, 066524. [Google Scholar] [CrossRef]
- Minakov, A.; Morikawa, J.; Ryu, M.; Zhuravlev, E.; Schick, C. Interfacial thermal conductance of 7075 aluminum alloy microdroplets in contact with a solid at fast melting and crystallization. Mater. Res. Express 2022, 9, 086503. [Google Scholar] [CrossRef]
- Minakov, A.; Morikawa, J.; Ryu, M.; Zhuravlev, E.; Schick, C. Variations of interfacial thermal conductance at melting and crystallization of an indium micro-particle in contact with a solid. Mater. Des. 2021, 201, 109475. [Google Scholar] [CrossRef]
- Lifshitz, E.; Hamermesh, M. The theory of molecular attractive forces between solids. In Perspectives in Theoretical Physics, The Collected Papers of E.M. Lifshitz; Pergamon Press: Oxford, UK; Frankfurt, Germany, 1992; pp. 329–349. [Google Scholar] [CrossRef]
- Dzyaloshinskii, I.E.; Lifshitz, E.M.; Pitaevskii, L.P. General theory of Van der Waals forces. Sov. Phys. Uspekhi 1961, 4, 153–176. [Google Scholar] [CrossRef]
- Pitaevskii, L.P.; Lifshitz, E.M. Course of Theoretical Physics 9: Statistical Physics, Part 2, 3rd ed.; Pergamon Press: Oxford, UK; Frankfurt, Germany, 1980; ISBN 13: 9780080230726. [Google Scholar]
- Casimir, H.B.G. On the attraction between two perfectly conducting plates. Proc. K. Ned. Akad. Wet. 1948, 51, 793–795. Available online: https://inspirehep.net/literature/24990 (accessed on 29 January 2023).
- Winterton, R.H.S. Van der Waals forces. Contemp. Phys. 1970, 11, 559–574. [Google Scholar] [CrossRef]
- Bergström, L. Hamaker constants of inorganic materials. Adv. Colloid Interface Sci. 1997, 70, 125–169. [Google Scholar] [CrossRef]
- Leite, F.L.; Bueno, C.C.; Da Róz, A.L.; Ziemath, E.C.; Oliveira, J.O.N. Theoretical Models for Surface Forces and Adhesion and Their Measurement Using Atomic Force Microscopy. Int. J. Mol. Sci. 2012, 13, 12773–12856. [Google Scholar] [CrossRef]
- Mohideen, U.; Roy, A. Precision Measurement of the Casimir Force from 0.1 to 0.9 µm. Phys. Rev. Lett. 1998, 81, 4549–4552. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez, A.W.; Capasso, F.; Johnson, S. The Casimir effect in microstructured geometries. Nat. Photon 2011, 5, 211–221. [Google Scholar] [CrossRef]
- Volokitin, A.; Persson, B. Near-field radiative heat transfer and noncontact friction. Rev. Mod. Phys. 2007, 79, 1291–1329. [Google Scholar] [CrossRef]
- Biehs, S.-A.; Messina, R.; Venkataram, P.S.; Rodriguez, A.W.; Cuevas, J.C.; Ben-Abdallah, P. Near-field radiative heat transfer in many-body systems. Rev. Mod. Phys. 2021, 93, 025009. [Google Scholar] [CrossRef]
- Mulet, J.-P.; Joulain, K.; Carminati, R.; Greffet, J.-J. Enhanced radiative heat transfer at nanometric distances. Microscale Thermophys. Eng. 2002, 6, 209–222. [Google Scholar] [CrossRef]
- Joulain, K.; Mulet, J.-P.; Marquier, F.; Carminati, R.; Greffet, J.-J. Surface electromagnetic waves thermally excited: Radiative heat transfer, coherence properties and Casimir forces revisited in the near field. Surf. Sci. Rep. 2005, 57, 59–112. [Google Scholar] [CrossRef] [Green Version]
- Jones, A.C.; O’callahan, B.T.; Yang, H.U.; Raschke, M.B. The thermal near-field: Coherence, spectroscopy, heat-transfer, and optical forces. Prog. Surf. Sci. 2013, 88, 349–392. [Google Scholar] [CrossRef]
- Francoeur, M. Near-Field Thermal Radiation. In Handbook of Thermal Science and Engineering; Kulacki, F.A., Ed.; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Chapuis, P.-O.; Volz, S.; Henkel, C.; Joulain, K.; Greffet, J.-J. Effects of spatial dispersion in near-field radiative heat transfer between two parallel metallic surfaces. Phys. Rev. B 2008, 77, 035431. [Google Scholar] [CrossRef] [Green Version]
- Landau, L.D.; Lifshitz, E.M.; Pitaevskii, L.P. Statistical Physics Part 2, Theory of the Condensed State V. 9; Butterworth-Heinemann: Oxford, UK, 1980; ISBN 0750626364. ISBN-13: 9780750626361. [Google Scholar]
- Gall, D. Electron mean free path in elemental metals. J. Appl. Phys. 2016, 119, 085101. [Google Scholar] [CrossRef] [Green Version]
- Song, B.; Fiorino, A.; Meyhofer, E.; Reddy, P. Near-field radiative thermal transport: From theory to experiment. AIP Adv. 2015, 5, 053503. [Google Scholar] [CrossRef] [Green Version]
- Cuevas, J.C.; García-Vidal, F.J. Radiative Heat Transfer. ACS Photon 2018, 5, 3896–3915. [Google Scholar] [CrossRef]
- Hu, L.; Narayanaswamy, A.; Chen, X.; Chen, G. Near-field thermal radiation between two closely spaced glass plates exceeding Planck’s blackbody radiation law. Appl. Phys. Lett. 2008, 92, 133106. [Google Scholar] [CrossRef] [Green Version]
- Ying, X.; Sabbaghi, P.; Sluder, N.; Wang, L. Super-Planckian Radiative Heat Transfer between Macroscale Surfaces with Vacuum Gaps Down to 190 nm Directly Created by SU-8 Posts and Characterized by Capacitance Method. ACS Photon 2019, 7, 190–196. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, R.; Zhang, Z. Near-field radiative heat transfer with doped-silicon nanostructured metamaterials. Int. J. Heat Mass Transf. 2014, 73, 389–398. [Google Scholar] [CrossRef]
- Basu, S.; Lee, B.J.; Zhang, Z.M. Near-Field Radiation Calculated with an Improved Dielectric Function Model for Doped Silicon. J. Heat Transf. 2010, 132, 023302. [Google Scholar] [CrossRef]
- Park, K.; Zhang, Z. Fundamentals and Applications of Near-Field Radiative Energy Transfer. Front. Heat Mass Transf. 2013, 4, 013001. [Google Scholar] [CrossRef] [Green Version]
- van Zwol, P.J.; Thiele, S.; Berger, C.; de Heer, W.A.; Chevrier, J. Nanoscale Radiative Heat Flow due to Surface Plasmons in Graphene and Doped Silicon. Phys. Rev. Lett. 2012, 109, 264301. [Google Scholar] [CrossRef] [Green Version]
- Králík, T.; Hanzelka, P.; Zobač, M.; Musilová, V.; Fořt, T.; Horak, M. Strong Near-Field Enhancement of Radiative Heat Transfer between Metallic Surfaces. Phys. Rev. Lett. 2012, 109, 224302. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Bie, M.; Cai, W.; Ge, L.; Ji, Z.; Jia, Y.; Gong, K.; Zhang, X.; Wang, J.; Xu, J. Giant near-field radiative heat transfer between ultrathin metallic films. Opt. Express 2019, 27, 36790–36798. [Google Scholar] [CrossRef]
- Shen, S.; Mavrokefalos, A.; Sambegoro, P.; Chen, G. Nanoscale thermal radiation between two gold surfaces. Appl. Phys. Lett. 2012, 100, 233114. [Google Scholar] [CrossRef]
- Tang, L.; DeSutter, J.; Francoeur, M. Near-Field Radiative Heat Transfer between Dissimilar Materials Mediated by Coupled Surface Phonon- and Plasmon-Polaritons. ACS Photon 2020, 7, 1304–1311. [Google Scholar] [CrossRef]
- Volokitin, A.I.; Persson, B.N.J. Resonant photon tunneling enhancement of the radiative heat transfer. Phys. Rev. B 2004, 69, 045417. [Google Scholar] [CrossRef] [Green Version]
- Lide, D.R.; Haynes, W.M.M. CRC Handbook of Chemistry and Physics, 90th ed.; CRC Press: Boca Raton, FL, USA, 2010; ISBN 13: 9781420090840. [Google Scholar]
- Minakov, A. Temperature gradients in ultrafast thin-film nanocalorimetry. Thermochim. Acta 2019, 677, 32–41. [Google Scholar] [CrossRef]
- Landau, L.; Lifshitz, E. Fluid Mechanics, Course of Theoretical Physics, 2nd ed.; Pergamon: Oxford, UK; Frankfurt, Germany, 1987; Volume 6, ISBN 978-0-08-033933-7. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Physical Kinetics, Course of Theoretical Physics, 1st ed.; Pergamon Press: Oxford, UK; Frankfurt, Germany, 1981; Volume 10. [Google Scholar] [CrossRef]
- Kennard, E.H. Kinetic Theory of Gases with Introduction to Statistical Mechanics; Wiley & Sons: New York, NY, USA, 1938. [Google Scholar] [CrossRef]
- Kogan, E.Y.; Malnev, V.N. Accommodation coefficient of a diatomic molecular gas. Zh. Eksp. Teor. Fiz. 1978, 74, 525–532. [Google Scholar]
- Burghold, E.; Frekers, Y.; Kneer, R. Determination of time-dependent thermal contact conductance through IR-thermography. Int. J. Therm. Sci. 2015, 98, 148–155. [Google Scholar] [CrossRef]
- Minakov, A.; Morikawa, J.; Zhuravlev, E.; Ryu, M.; van Herwaarden, A.W.; Schick, C. High-speed dynamics of temperature distribution in ultrafast (up to 108 K/s) chip-nanocalorimeters, measured by infrared thermography of high resolution. J. Appl. Phys. 2019, 125, 054501. [Google Scholar] [CrossRef]
- Schick, C.; Mathot, V. Fast Scanning Calorimetry; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- La Spina, L.; Ovchinnikov, D.; Wien, W.H.; van Herwaarden, A.W.; Goudena, E.J.; Loos, J.; Nanver, L.K. Reduction of surface roughness of a silicon chip for advanced nanocalorimetry. Sensors Actuators A Phys. 2008, 144, 403–409. [Google Scholar] [CrossRef]
- Ni, H.; Lee, H.-J.; Ramirez, A.G. A robust two-step etching process for large-scale microfabricated SiO2 and Si3N4 MEMS membranes. Sensors Actuators A Phys. 2005, 119, 553–558. [Google Scholar] [CrossRef]
- Smallman, R.; Ngan, A. Modern Physical Metallurgy, 8th ed.; Butterworth-Heinemann: Oxford, UK, 2014; ISBN 978-0-08-098204-5. [Google Scholar] [CrossRef]
- Montanari, R.; Varone, A. Synergic Role of Self-Interstitials and Vacancies in Indium Melting. Metals 2015, 5, 1061–1072. [Google Scholar] [CrossRef]
- Goncharova, E.V.; Makarov, A.; Konchakov, R.A.; Kobelev, N.P.; Khonik, V.A. Premelting generation of interstitial defects in polycrystalline indium. JETP Lett. 2017, 106, 35–39. [Google Scholar] [CrossRef]
- Rühm, A.; Reichert, H.; Donner, W.; Dosch, H.; Grütter, C.; Bilgram, J. Bulk and surface premelting phenomena in a-gallium. Phys. Rev. B 2003, 68, 224110. [Google Scholar] [CrossRef]
| Contact Pressure MPa | ITC W/m2K | Effective Thickness μm | Temperature Jump Distance μm | Temperature K | Gas Pressure Pa | Gas Thermal Conductivity W/m·K |
|---|---|---|---|---|---|---|
| 25.8 | 0.8⸱104 | 3.0 | 0.3 | 350 | 105 | 0.029 |
| 120 | 3.2⸱104 | 0.3 | 0.3 | 350 | 105 | 0.029 |
| ITC W/m2K | ITC Component W/m2K | ITC Component W/m2K | Effective Thickness nm | Temperature K | Gas Pressure Pa |
|---|---|---|---|---|---|
| 106 | 25 | 106 | 1–5 | 450 | 60 |
| Surface Roughness μm | ITC W/m2K | ITC Component W/m2K | ITC Component W/m2K | Effective Thickness nm |
|---|---|---|---|---|
| 7.7 | 4.8∙104 | 2.5⸱104 | 2.3⸱104 | 20–62 |
| 0.07 | 9∙104 | 2.5⸱104 | 6.5⸱104 | 12–37 |
| Sample Temperature K | Intermediate Temperature K | ITC W/m2K | ITC Component W/m2K | ITC Component W/m2K | Effective Thickness nm |
|---|---|---|---|---|---|
| 420 | 4.1∙103 | 4.1∙103 | <0.5 | 7400 | |
| 433 | 5∙104 | 4⸱104 | 1⸱104 | 17–50 |
| Sample Temperature K | Intermediate Temperature K | ITC W/m2K | ITC Component W/m2K | ITC Component W/m2K | Effective Thickness nm |
|---|---|---|---|---|---|
| 805 K | 820 | 3∙104 | 2.9∙104 | 103 | 90–160 |
| 901 K | 433 | 1.8∙105 | 3⸱104 | 1.5⸱105 | 6–20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minakov, A.; Schick, C. Mesoscopic Effects of Interfacial Thermal Conductance during Fast Pre-Melting and Melting of Metal Microparticles. Appl. Sci. 2023, 13, 7019. https://doi.org/10.3390/app13127019
Minakov A, Schick C. Mesoscopic Effects of Interfacial Thermal Conductance during Fast Pre-Melting and Melting of Metal Microparticles. Applied Sciences. 2023; 13(12):7019. https://doi.org/10.3390/app13127019
Chicago/Turabian StyleMinakov, Alexander, and Christoph Schick. 2023. "Mesoscopic Effects of Interfacial Thermal Conductance during Fast Pre-Melting and Melting of Metal Microparticles" Applied Sciences 13, no. 12: 7019. https://doi.org/10.3390/app13127019
APA StyleMinakov, A., & Schick, C. (2023). Mesoscopic Effects of Interfacial Thermal Conductance during Fast Pre-Melting and Melting of Metal Microparticles. Applied Sciences, 13(12), 7019. https://doi.org/10.3390/app13127019








