Author Contributions
Conceptualization, J.Z., K.S. and H.M.; methodology, J.Z., K.S. and H.S.; software, J.Z.; validation, J.Z., R.S., T.F., Z.L. and H.M.; investigation, J.Z. and K.S.; data curation, J.Z., H.M. and Z.L.; writing—original draft preparation, J.Z. and K.S.; supervision, K.S.; funding acquisition, K.S. and J.Z. All authors have read and agreed to the published version of the manuscript.
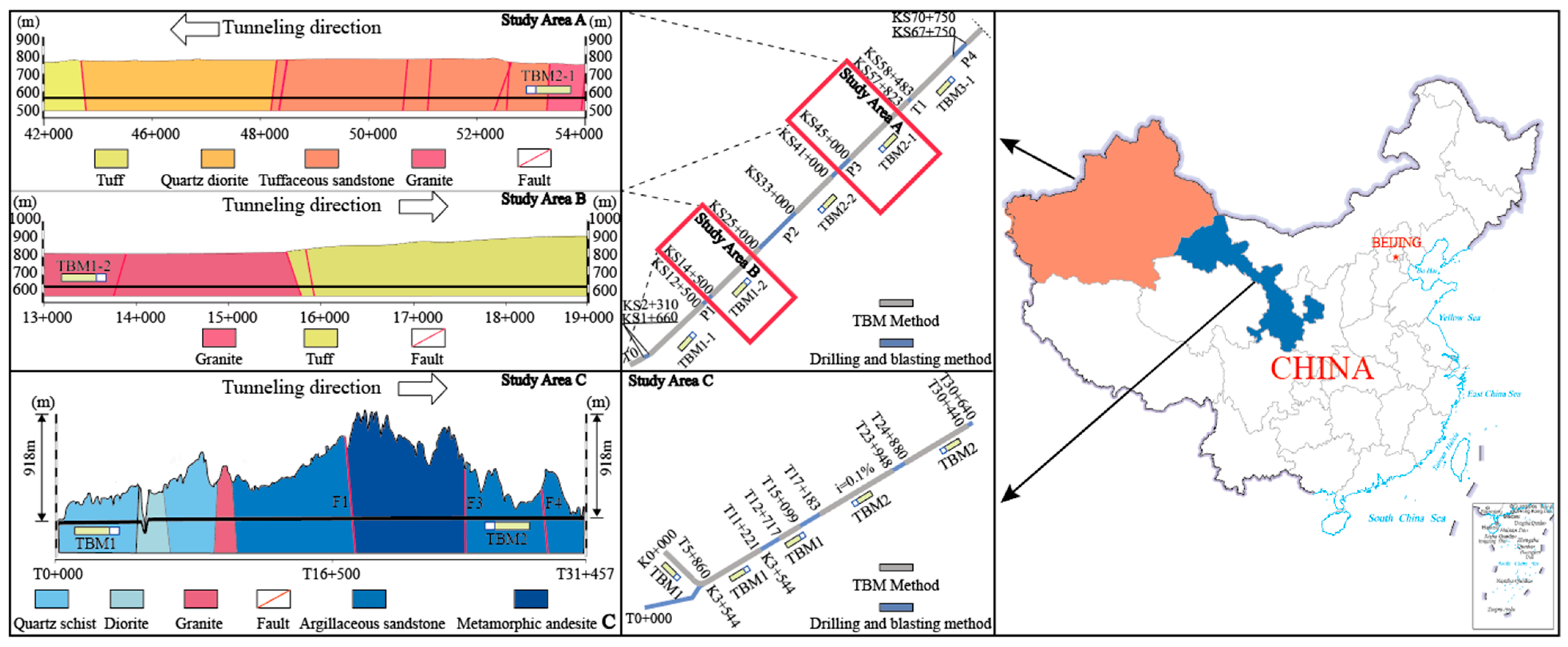
Figure 1.
Geological profiles of the study area.
Figure 1.
Geological profiles of the study area.
Figure 2.
Processes of acquiring parameters related to the uniaxial compressive strength of rock: (a) field sampling; (b) rock core samples; (c) laboratory tests.
Figure 2.
Processes of acquiring parameters related to the uniaxial compressive strength of rock: (a) field sampling; (b) rock core samples; (c) laboratory tests.
Figure 3.
Multiple TBM tunneling phases and shutdown phases.
Figure 3.
Multiple TBM tunneling phases and shutdown phases.
Figure 4.
The first three segments of the TBM operation segment (start-up, ascending, and stable).
Figure 4.
The first three segments of the TBM operation segment (start-up, ascending, and stable).
Figure 5.
Visualization of the K-means clustering principle.
Figure 5.
Visualization of the K-means clustering principle.
Figure 6.
K-means clustering example (cutterhead torque as an example).
Figure 6.
K-means clustering example (cutterhead torque as an example).
Figure 7.
Normality test of four TBM tunneling indexes: (a) cutterhead torque; (b) cutterhead rotational speed; (c) advance rate; (d) total thrust.
Figure 7.
Normality test of four TBM tunneling indexes: (a) cutterhead torque; (b) cutterhead rotational speed; (c) advance rate; (d) total thrust.
Figure 8.
Principle of the box plot method.
Figure 8.
Principle of the box plot method.
Figure 9.
Box plot method used to identify outliers of the cutterhead torque in
Figure 4.
Figure 9.
Box plot method used to identify outliers of the cutterhead torque in
Figure 4.
Figure 10.
Multi-granularity scanning structure (three classifications).
Figure 10.
Multi-granularity scanning structure (three classifications).
Figure 11.
Cascade forest structure.
Figure 11.
Cascade forest structure.
Figure 12.
Forest decision process (three classifications).
Figure 12.
Forest decision process (three classifications).
Figure 13.
Surrounding rock excavatability classification process.
Figure 13.
Surrounding rock excavatability classification process.
Figure 14.
Distribution characteristics of SER and the total thrust of five different surrounding rock classifications.
Figure 14.
Distribution characteristics of SER and the total thrust of five different surrounding rock classifications.
Figure 15.
Correlation between Rc and PR.
Figure 15.
Correlation between Rc and PR.
Figure 16.
Correlation between Kv and PR.
Figure 16.
Correlation between Kv and PR.
Figure 17.
Penetration Pareto charts of different surrounding rock classifications: (a) Class II; (b) Class IIIa; (c) Class IIIb; (d) Class IV; (e) Class V.
Figure 17.
Penetration Pareto charts of different surrounding rock classifications: (a) Class II; (b) Class IIIa; (c) Class IIIb; (d) Class IV; (e) Class V.
Figure 18.
Correlation between penetration and BQ.
Figure 18.
Correlation between penetration and BQ.
Figure 19.
Correlation between SER and BQ.
Figure 19.
Correlation between SER and BQ.
Figure 20.
Correlation between PR and BQ.
Figure 20.
Correlation between PR and BQ.
Figure 21.
TOPSIS surrounding rock excavatability classification criteria.
Figure 21.
TOPSIS surrounding rock excavatability classification criteria.
Figure 22.
Comparison of the surrounding rock excavatability and actual surrounding rock classification.
Figure 22.
Comparison of the surrounding rock excavatability and actual surrounding rock classification.
Figure 23.
Five surrounding rock classes at construction sites: (a) Class V; (b) Class IV (c) Class IIIb; (d) Class IIIa; (e) Class II.
Figure 23.
Five surrounding rock classes at construction sites: (a) Class V; (b) Class IV (c) Class IIIb; (d) Class IIIa; (e) Class II.
Figure 24.
Hyperparameter optimization process.
Figure 24.
Hyperparameter optimization process.
Figure 25.
Five-fold cross-validation structure.
Figure 25.
Five-fold cross-validation structure.
Figure 26.
Hyperparameter six-round iterative process.
Figure 26.
Hyperparameter six-round iterative process.
Figure 27.
Optimal accuracies for individual iterations.
Figure 27.
Optimal accuracies for individual iterations.
Figure 28.
Confusion matrix for DF test set.
Figure 28.
Confusion matrix for DF test set.
Figure 29.
Importance scores of different input features for surrounding rock excavatability prediction.
Figure 29.
Importance scores of different input features for surrounding rock excavatability prediction.
Figure 30.
The confusion matrices of the four models on the test set: (a) DT; (b) RF; (c) SVC; (d) DNN.
Figure 30.
The confusion matrices of the four models on the test set: (a) DT; (b) RF; (c) SVC; (d) DNN.
Figure 31.
Classification performances of DT, RF, SVC, DNN, and DF.
Figure 31.
Classification performances of DT, RF, SVC, DNN, and DF.
Table 1.
Geological characteristics and TBM parameters of tunnel projects.
Table 1.
Geological characteristics and TBM parameters of tunnel projects.
| Project Parameters | KS Tunnel in Xinjiang, China | Water Conveyance Tunnel Project in Lanzhou, China |
|---|
| Tunnel length/(km) | 283.41 | 31.57 |
| Mean buried depth/(m) | 428 | 500 |
| Rock types | Tuffaceous sandstone, granite, quartz diorite, andesite | Quartz diorite, quartz schist, granite, metamorphic andesite and sandstone |
| TBM types | Open full-face TBM | Double-shield TBM |
| Number of rolling cutters | 48 | 37 |
| Cutter diameter/(m) | 7 | 5.48 |
| Rated torque/(kN·m) | 4410 | 3458 |
| Maximum thrust/(kN) | 19,076 | 22,160 |
| Cutterhead rotating speed/(r/min) | 0~10.9 | 0~10.3 |
Table 2.
Penetration statistics table of different rock mass classes.
Table 2.
Penetration statistics table of different rock mass classes.
| Class | Data Size | Penetration Range/(mm/rev) | Mean/(mm/rev) | Standard Deviation
|
|---|
| II | 2297 | 1.01~8.74 | 3.76 | 1.41 |
| IIIa | 2170 | 2.21~10.89 | 6.65 | 1.44 |
| IIIb | 2085 | 4.01~14.87 | 9.8 | 1.9 |
| IV | 2175 | 6.08~19.49 | 12.58 | 1.84 |
| V | 2027 | 8.43~39.95 | 20.65 | 6.01 |
Table 3.
Penetration ranges for different rock mass classifications.
Table 3.
Penetration ranges for different rock mass classifications.
| Class | Range of Penetration/(mm/rev) | Mean/(mm/rev) |
|---|
| II | 1.38~5.82 | 3.55 |
| IIIa | 4.16–8.84 | 6.58 |
| IIIb | 7.13–12.85 | 9.86 |
| IV | 10.08–16.08 | 12.66 |
| V | 11.83–28.83 | 19.3 |
Table 4.
Surrounding rock excavatability grade classification based on the BQ value.
Table 4.
Surrounding rock excavatability grade classification based on the BQ value.
| BQ-Based Excavatability Classification | BQ |
|---|
| 1 | <200 |
| 2 | 325~200 |
| 3 | 397~325 |
| 4 | 507~397 |
| 5 | 657~507 |
| 6 | >657 |
Table 5.
Surrounding rock excavatability classification based on SER and PR.
Table 5.
Surrounding rock excavatability classification based on SER and PR.
| Excavatability Grade | BQ | SER/(m3·rev−1·cutter·kN−1) | PR/(m/h) | Excavatability Description |
|---|
| L-1 | <200 | >4.6 | >4.6 | excellent |
| L-2 | 325~200 | 4.6~2.3 | 4.6~3.7 | good |
| L-3 | 397~325 | 2.3~1.6 | 3.7~3.2 | fair |
| L-4 | 507~397 | 1.6~0.9 | 3.2~2.4 | poor |
| L-5 | 657~507 | 0.9~0.4 | 2.4~1.3 | very poor |
| L-6 | >657 | <0.4 | <1.3 | extremely poor |
Table 6.
Engineering validations.
Table 6.
Engineering validations.
| Sample | Mileage | Rock Types | SER/(m3·rev−1·Cutter·kN−1) | PR/(m/h) | Closeness | Grade |
|---|
| 1 | 64 + 781.46~64 + 786.52 | Tuffaceous sandstone | 11.0707 | 1.9747 | 0.6352 | L-1 |
| 2 | 68 + 415.99~68 + 694.9 | Glutenite | 2.1633 | 4.3026 | 0.4212 | L-2 |
| 3 | 64 + 497.34~64 + 499.9 | Tuffaceous sandstone | 5.1218 | 1.2231 | 0.4309 | L-2 |
| 4 | 64 + 499.9~64 + 506.1 | Tuffaceous sandstone | 5.4777 | 1.0423 | 0.4437 | L-2 |
| 5 | 68 + 285.55~68 + 310.98 | Glutenite | 2.0346 | 3.8760 | 0.3865 | L-3 |
| 6 | 68 + 585.69~68 + 602.26 | Glutenite | 2.1326 | 3.8556 | 0.3905 | L-3 |
| 7 | 68 + 735.53~68 + 751.03 | Glutenite | 2.4002 | 3.4125 | 0.3764 | L-3 |
| 8 | 64 + 709.74~64 + 728.58 | Tuffaceous sandstone | 1.9222 | 2.5992 | 0.2932 | L-4 |
| 9 | 64 + 865.99~64 + 877.1 | Tuffaceous sandstone | 2.6621 | 1.6782 | 0.2847 | L-4 |
| 10 | 64 + 877.1~64 + 888.66 | Tuffaceous sandstone | 1.6106 | 2.0212 | 0.2351 | L-4 |
| 11 | 59 + 198.28~59 + 205.67 | Tuffaceous sandstone | 0.9056 | 1.5410 | 0.1619 | L-5 |
| 12 | 59 + 205.67~59 + 222.28 | Tuffaceous sandstone | 0.8940 | 2.2756 | 0.2174 | L-5 |
| 13 | 45 + 274.00~45 + 280.16 | Granite | 0.1889 | 0.7560 | 0.0703 | L-6 |
| 14 | 45 + 714.69~45 + 722.97 | Granite | 0.2387 | 0.5400 | 0.0536 | L-6 |
| 15 | 46 + 223.21~46 + 231.43 | Andesite | 0.4915 | 1.3356 | 0.1279 | L-6 |
Table 7.
DF grid search and parameter optimization.
Table 7.
DF grid search and parameter optimization.
| Model | Parameters | Selected Values | Optimal Values |
|---|
| DF | nEstimators | 1~6 | 4 |
| nTrees | [60, 100, 140, 180, 200, 215, 220, 225, 226~234,
235, 240, 245, 250, 255, 260, 270, 280] | 227 |
| Max layer | 20 | 20 |
| Max depth | [5, 10, 13~20] | 16 |
| Min samples leaf | [1, 2, 3, 4, 7] | 1 |
Table 8.
Model final hyperparameters of DF.
Table 8.
Model final hyperparameters of DF.
| Model | Parameters | Values |
|---|
| DF | nEstimators | 4 |
| nTrees | 227 |
| Max layer | 20 |
| Max depth | 16 |
| Min samples leaf | 1 |
| Min samples split | 2 |
| Predictor | forest |
| Criterion | gini |
| Bin subsample | 200,000 |
| Bin type | percentile |
| nBins | 255 |
| nTolerant rounds | 2 |
Table 9.
Prediction results of surrounding rock excavatability.
Table 9.
Prediction results of surrounding rock excavatability.
| Grade | Recall | Precision | F1 Score |
|---|
| L-1 | 0.9209 | 0.9706 | 0.9451 |
| L-2 | 0.9277 | 0.9625 | 0.9448 |
| L-3 | 0.9720 | 0.9665 | 0.9692 |
| L-4 | 0.9543 | 0.9300 | 0.9419 |
| L-5 | 0.9666 | 0.9753 | 0.9709 |
| L-6 | 0.9872 | 0.9659 | 0.9764 |
| Average | 0.9548 | 0.9618 | 0.9581 |
Table 10.
Grid search and optimal parameters of classifiers.
Table 10.
Grid search and optimal parameters of classifiers.
| Model | Key Parameters | Selected Values | Optimal Values |
|---|
| DT | Max depth | [10, 15, 20, 25, 30] | 20 |
| Min samples leaf | [1, 2, 3, 4, 5] | 1 |
| Min samples split | [2, 3, 4, 5, 6] | 2 |
| RF | nEstimators | [50, 100, 150, 200, 300] | 150 |
| Max depth | [10, 15, 20, 25, 30] | 25 |
| Min samples split | [2, 3, 4] | 2 |
| Min samples leaf | [1, 2, 3, 5] | 1 |
| Max features | [auto,sqrt,log2] | auto |
| SVC | kernel | [Linear,poly,rbf,sigmoid] | poly |
| C | [0.25, 0.5, 1, 2, 4, 8, 16] | 16 |
| DNN | Hidden layer sizes | [(10,), (20,), (30,), (10, 10), (20, 10), (30, 20)] | (30, 20) |
| activation | [relu,tanh.logistic] | relu |
| learning_rate | [constant,invscaling,adaptive] | adaptive |
| alpha | [0.001, 0.01, 0.1] | 0.001 |
Table 11.
Hyperparameter values of DT, RF, SVC, and DNN.
Table 11.
Hyperparameter values of DT, RF, SVC, and DNN.
| Model | Parameters | Values |
|---|
| DT | Max depth | 20 |
| Min samples leaf | 1 |
| Min samples split | 2 |
| Max features | None |
| Criterion | gini |
| Class weight | None |
| Max leaf nodes | None |
| RF | nEstimators | 150 |
| Max depth | 25 |
| Min samples split | 2 |
| Min samples leaf | 1 |
| Max features | auto |
| Criterion | gini |
| Bootstrap | True |
| Class weight | None |
| Max leaf nodes | None |
| Max samples | None |
| Oob score | False |
| SVC | Kernel | poly |
| C | 16 |
| Gamma | scale |
| Degree | 3 |
| Class weight | None |
| Decision function shape | ovr |
| Tol | 0.001 |
| Max iter | −1 |
| DNN | Hidden layer sizes | (30, 20) |
| Activation | relu |
| Learning rate | adaptive |
| Alpha | 0.001 |
| Batch size | auto |
| Learning rate init | 0.001 |
| Solver | adam |
| Beta 1 | 0.9 |
| Beta 2 | 0.999 |
| Early stopping | False |
| Momentum | 0.9 |
| Nesterovs momentum | True |
| Tol | 0.0001 |