Research on the High Speed of Piston Pumps Based on Rapid Erecting of Launch Vehicles
Abstract
:1. Introduction
2. Methodology
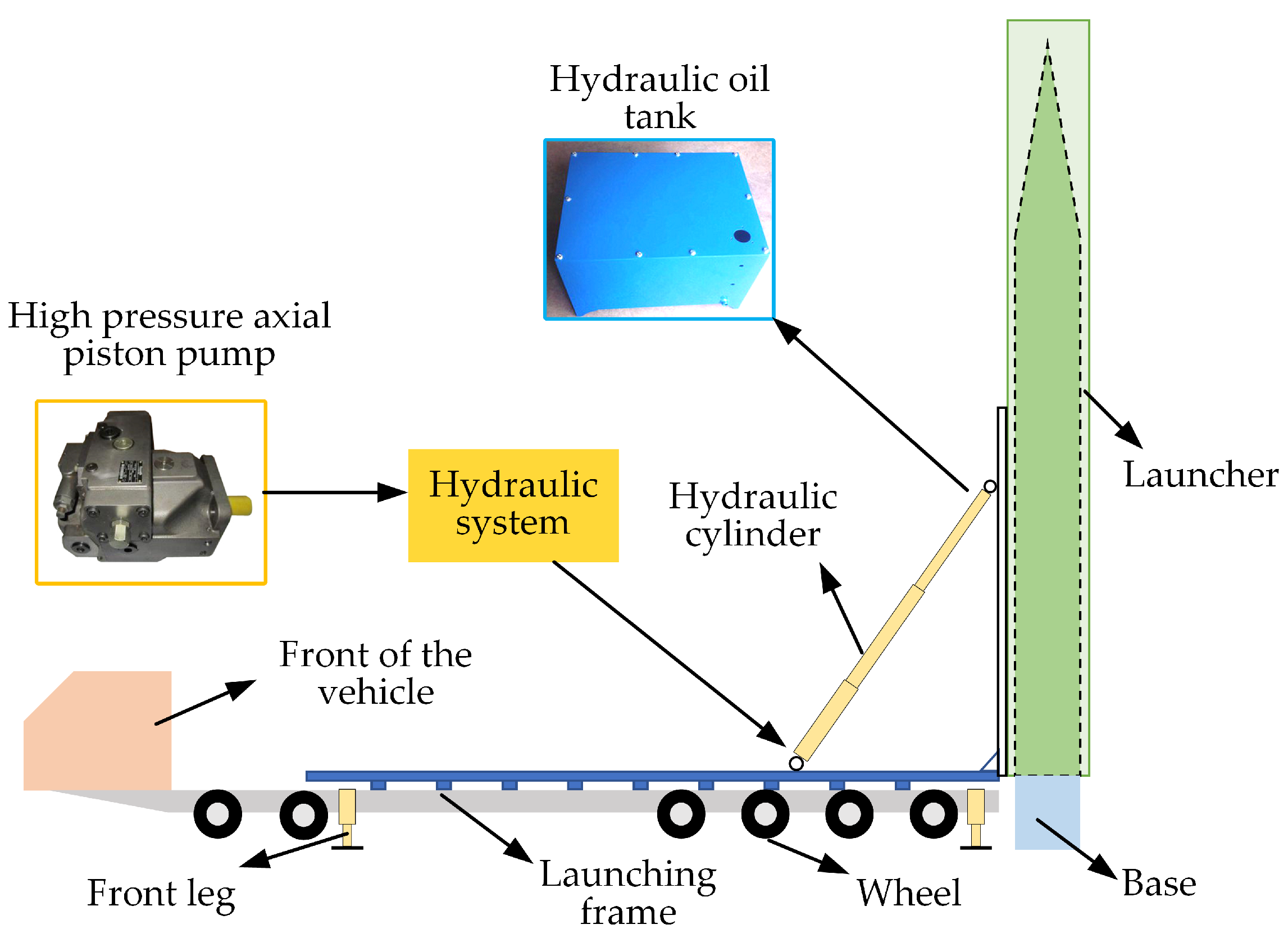
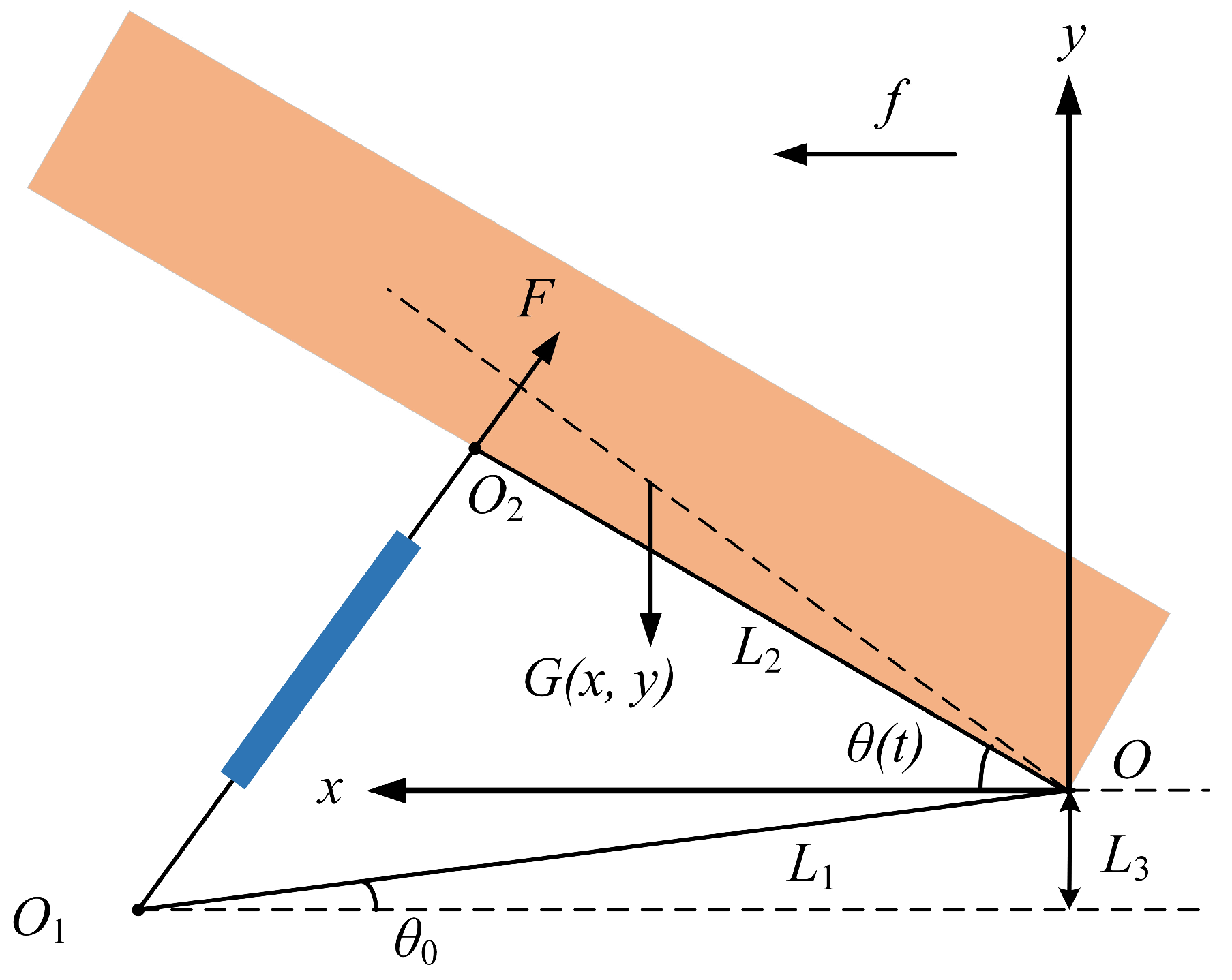
2.1. Erection Dynamics Model
- (1)
- Before erection, the missile is placed on the frame at a horizontal or slight inclination angle and is restrained by various means to ensure the safety of the transportation process and prevent the missile from fleeing forward or tumbling horizontally in the case of braking deceleration and sharp turning.
- (2)
- During erection, the hydraulic system is injected with oil by a high-pressure axial piston pump. The piston rods of the multi-stage hydraulic cylinder are forced to lengthen sequentially, causing the missile to spin around the bottom hinge with a specific motion law and gradually transition to a vertical state.
- (3)
- After erection, the missile is in a vertical state. The travel switch is triggered, the control system issues a stop command, the hydraulic cylinder is locked, and the launch procedure can be carried out.
2.2. Axial Piston Pump Model
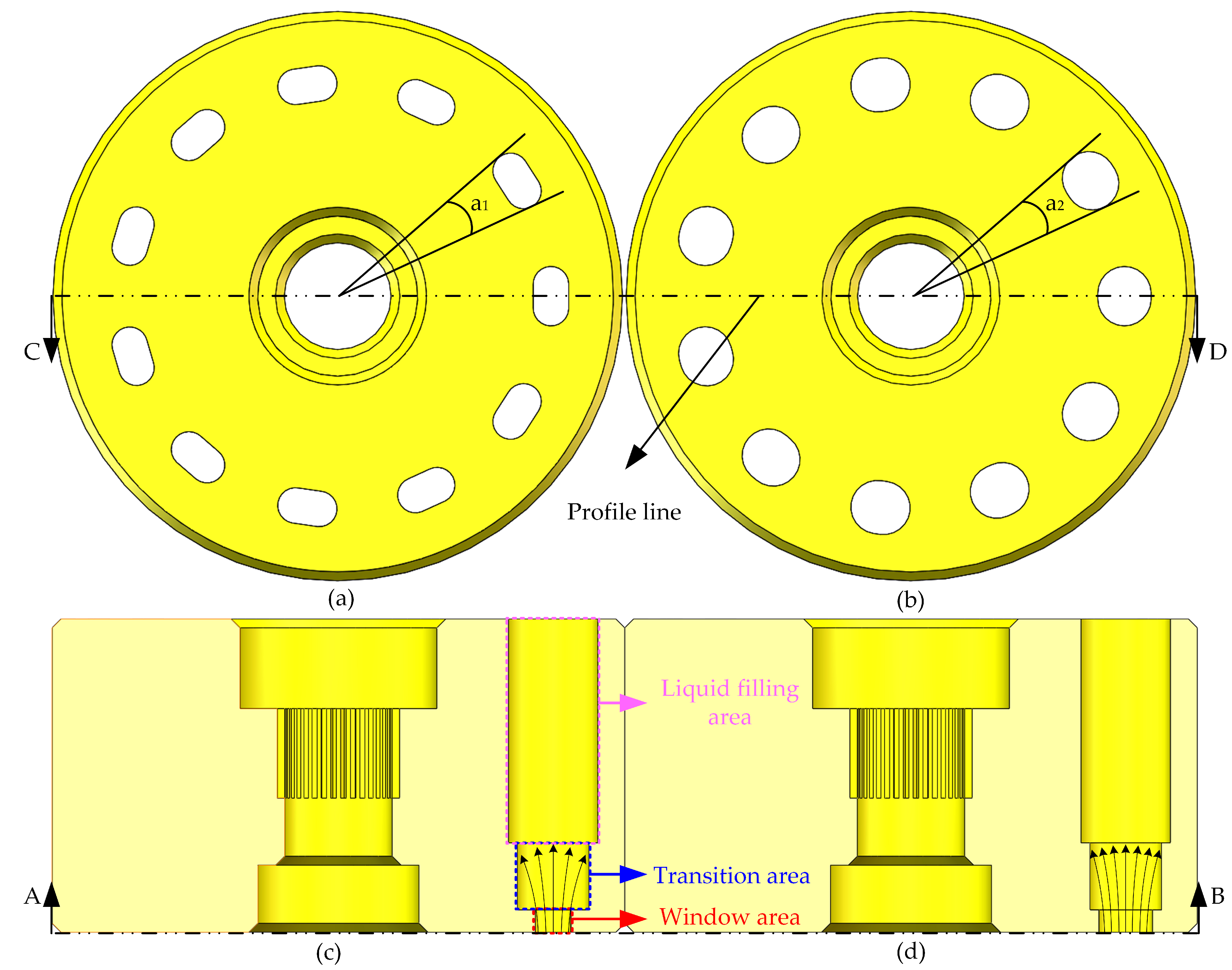
2.3. High-Speed Design of Piston Pumps
3. Validation of the Numerical Model
4. Results and Discussion
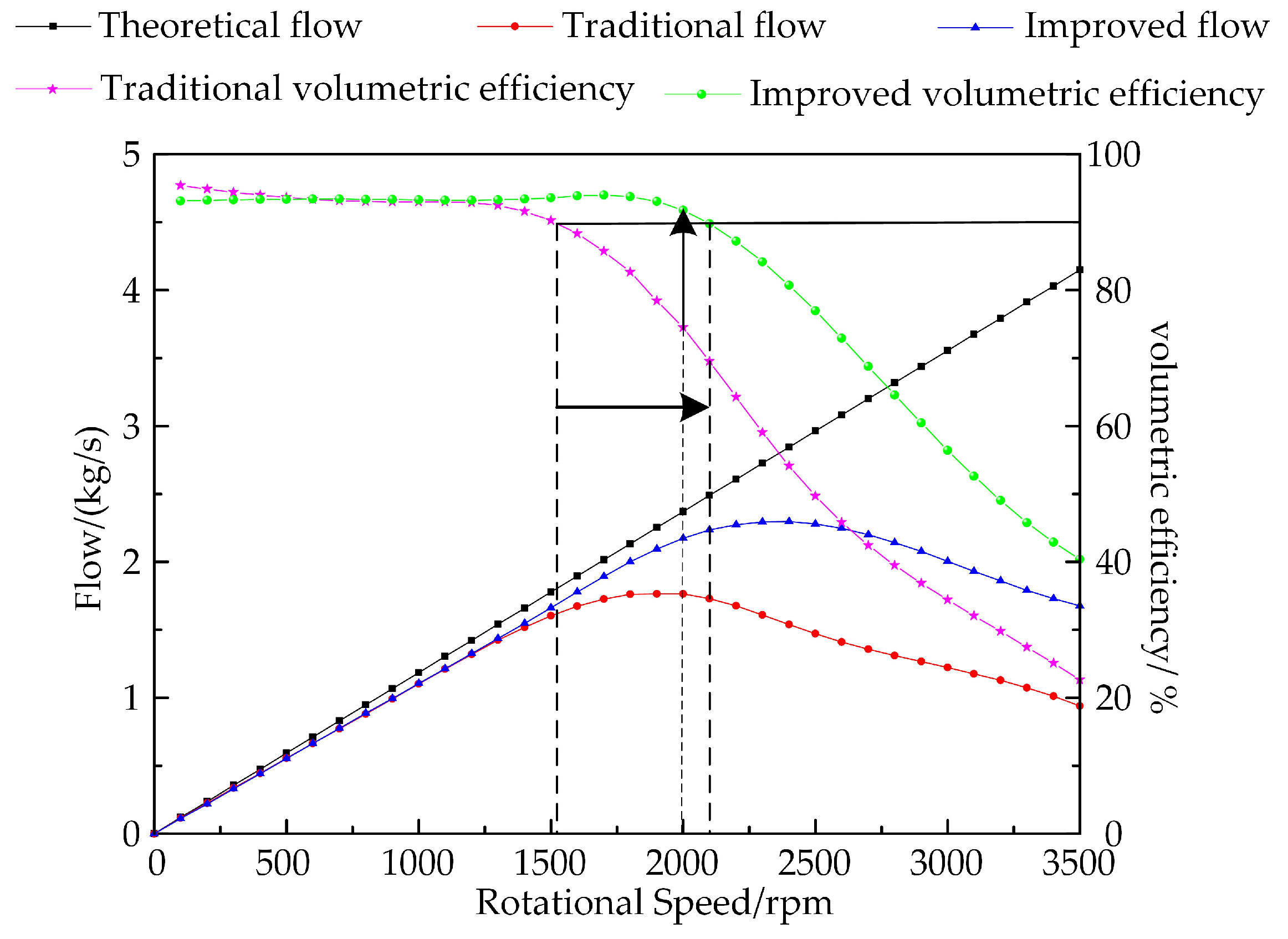
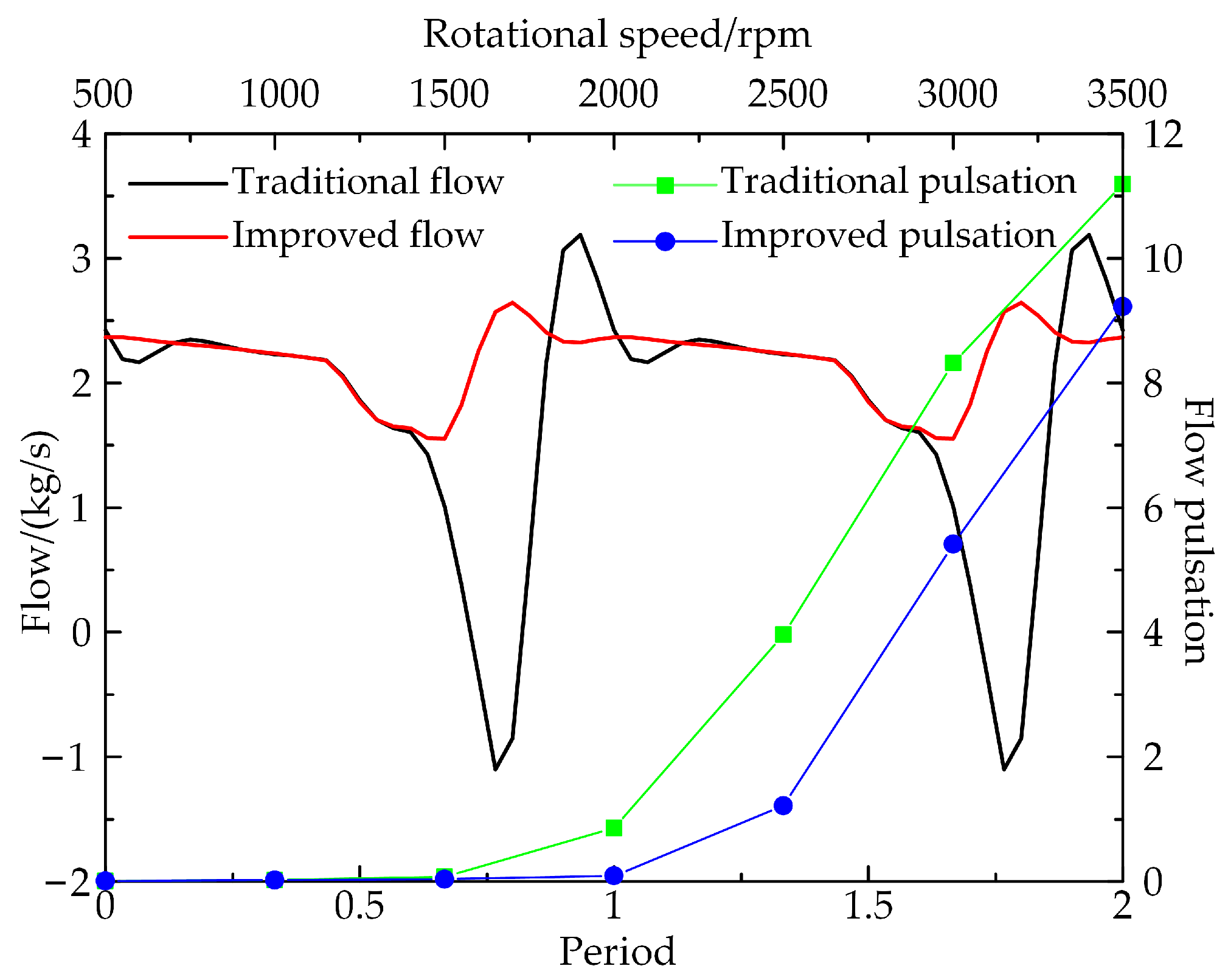
4.1. Flow Characteristics and Volumetric Efficiency of Piston Pumps
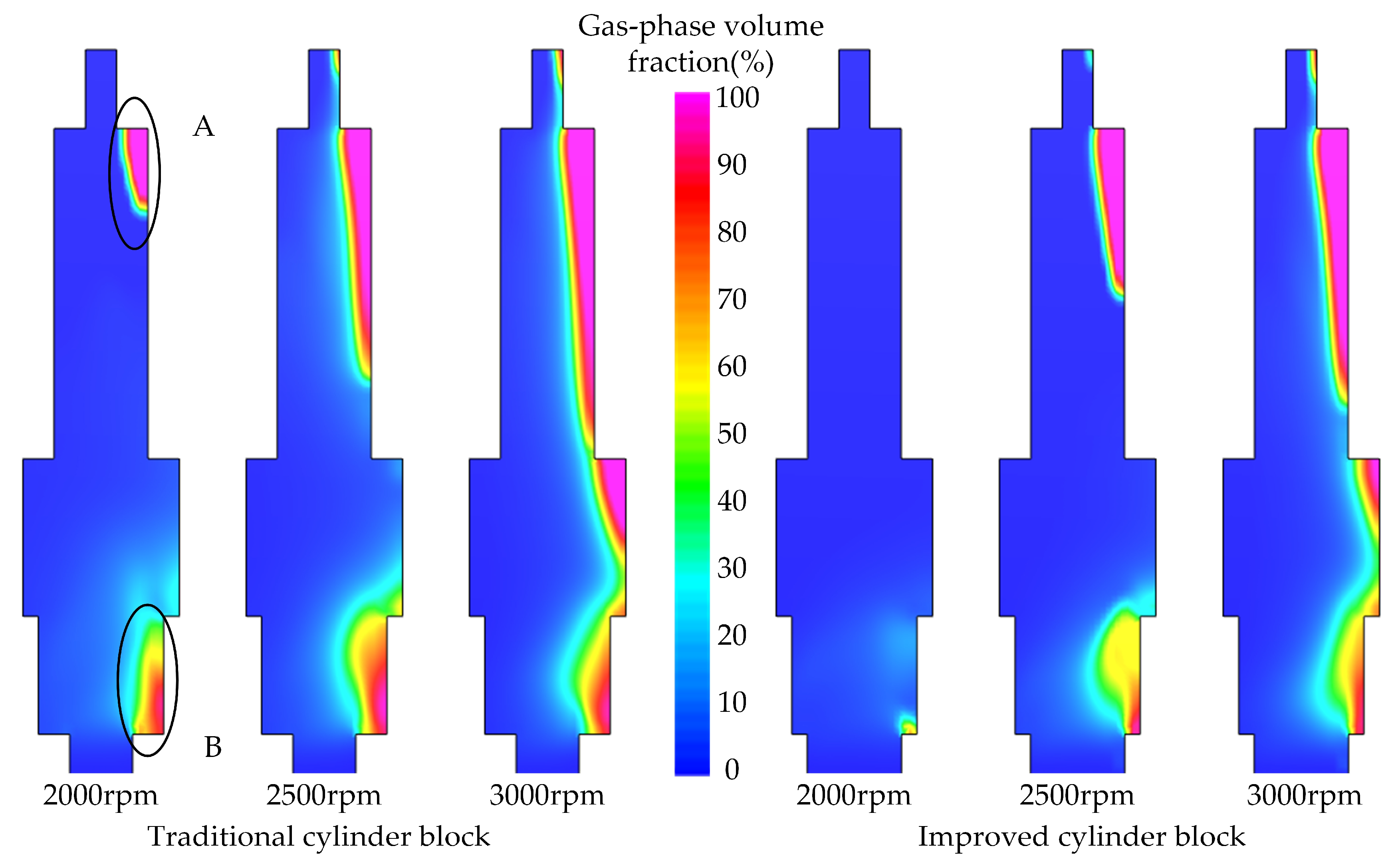
4.2. Mechanisms for Achieving High Speed of Piston Pumps
5. Conclusions
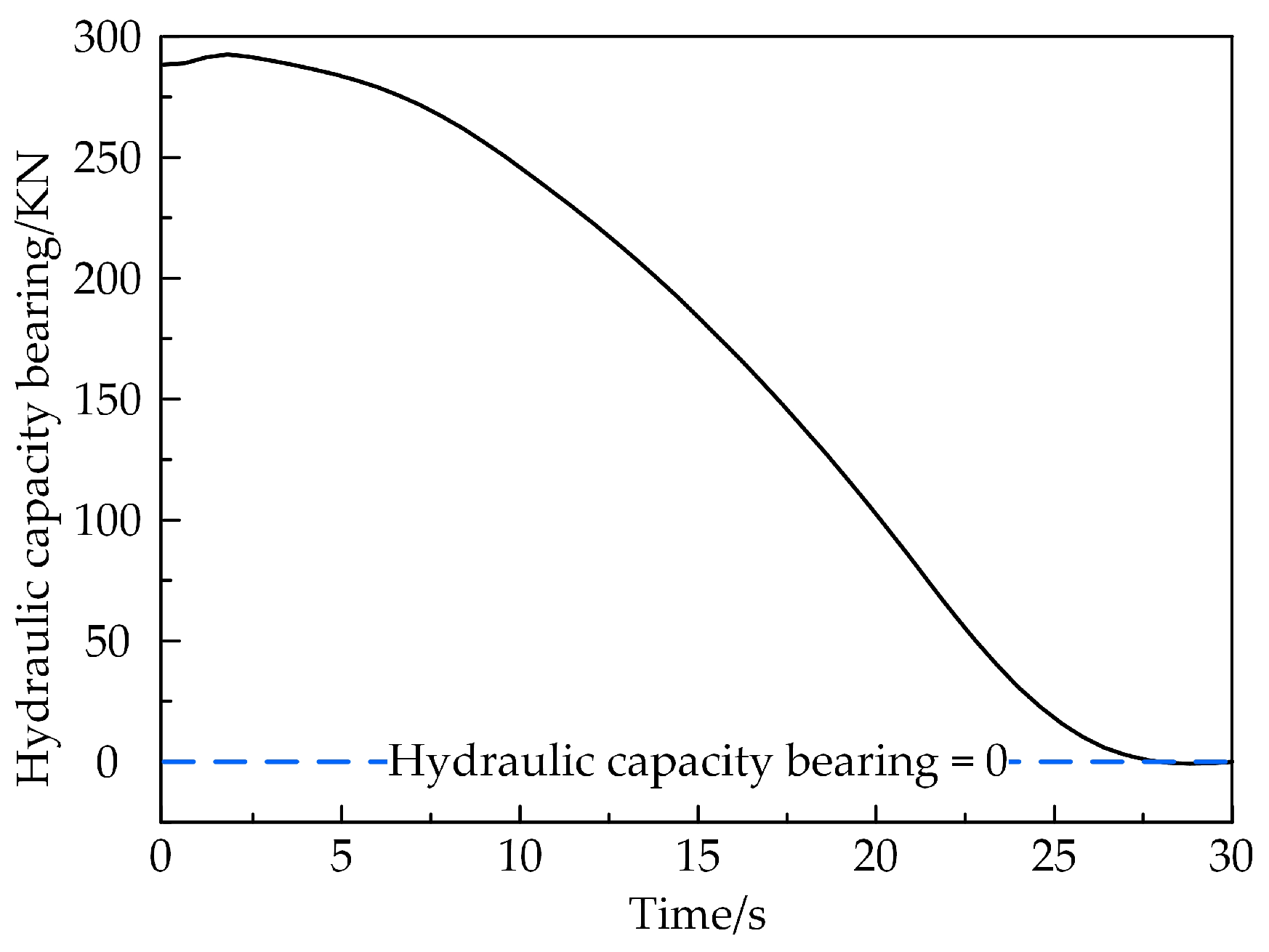
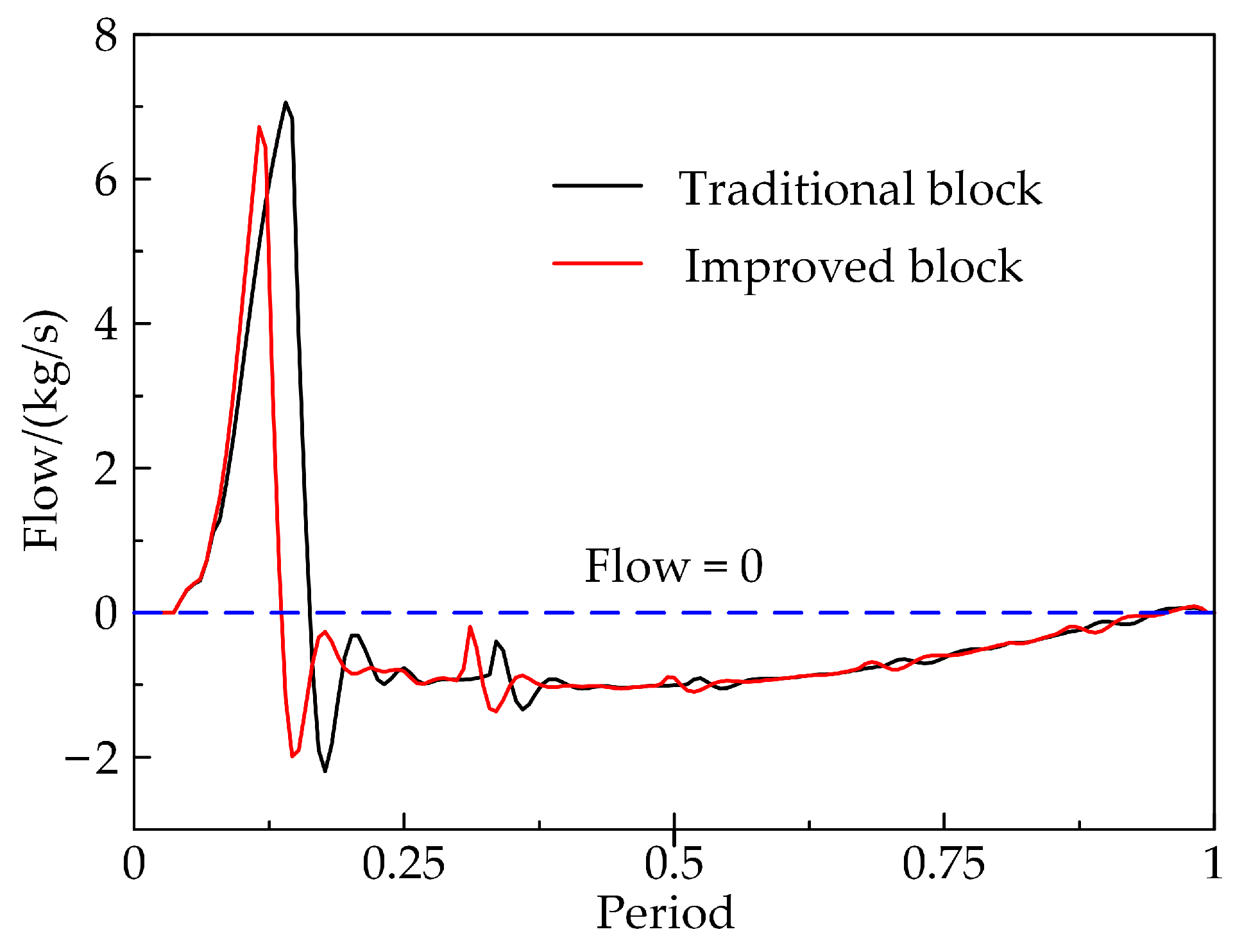
- The volumetric efficiency and flow rate of the improved cylinder block change slightly at low speeds but increase considerably at high speeds. The maximum speed at which the volumetric efficiency of a traditional axial piston pump remains above 90% is 1500 rpm, while the improved cylinder increases to 2100 rpm. At 2000 rpm, 2500 rpm, 3000 rpm and 3500 rpm, the volumetric efficiency is increased by 23.219%, 54.958%, 64.024% and 78.405%, respectively. The maximum flow rate of the improved piston pump rises from 1.765 kg/s to 2.295 kg/s with different speeds, an increase of 30.028%. When the speed is increased over 1500 rpm, the flow pulsation of the improved cylinder is also greatly reduced.
- The improved block can effectively inhibit the cavitation and backflow of the piston chamber. When rotational speeds at 2000 rpm, 2500 rpm and 3000 rpm, the peak gas phase volume fractions of the improved block are reduced by 3.508%, 9.423% and 6.962%, respectively, and the peak vapour volume fractions in the piston chamber are reduced by 0.492%, 1.498% and 4.250%, respectively, while the effective transport rates are increased by 11.064%, 23.208% and 22.401%, respectively, compared to the traditional blocks. Backflow and cavitation in the piston chambers will be reduced, which will help to increase the volumetric efficiency of the piston pump, reduce flow pulsation and reduce the vibration and noise of the pump body, resulting in smoother hydraulic system performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, B.; Hao, L. A review about missile unsupported combat and its capability requirements. Aerodyn. Missile J. 2017, 2017, 43–46+59. [Google Scholar] [CrossRef]
- Wu, X. Study on Electric Vertical Erection for Large Missile Launcher on Board. Ph.D. Thesis, Beijing Institute of Technology, Beijing, China, 2015. [Google Scholar]
- Feng, J.; Gao, Q.; Shao, Y.; Qian, W. Flow and pressure compound control strategy for missile hydraulic erection system. Acta Armamentarii 2018, 39, 209–216. [Google Scholar] [CrossRef]
- Feng, J.; Gao, Q.; Guan, W.; Li, L. Modeling of telescopic hydraulic cylinder and research on inter-stage buffer. Acta Armamentarii 2016, 37, 2268–2276. [Google Scholar] [CrossRef]
- Feng, J.; Gao, Q.; Guan, W.; Yao, X.; Li, L. Research on rapid missile erection system based on gas-hydraulic hybrid drive. Acta Armamentarii 2017, 38, 1348–1357. [Google Scholar] [CrossRef]
- Sao, Y.; Zhang, W.; Gao, Q.; Feng, J. Interior ballistics modeling and parameters optimization of erecting system with large inertia based on hybrid drive of gas and hydraulics. J. Propuls. Technol. 2018, 39, 751–759. [Google Scholar] [CrossRef]
- Ren, Y.; Gao, Q.; Tian, H. Optimization design and analysis of a rapid erection device based on gas-squeezer type power source. J. Vib. Shock. 2020, 39, 83–90. [Google Scholar] [CrossRef]
- Ren, Y.; Gao, Q.; Tian, H. Application of flow adjustable gas generator on missile erection device. J. Propuls. Technol. 2021, 42, 249–257. [Google Scholar] [CrossRef]
- Liu, X.; Li, M.; Hu, Y. Design of large hydraulic quick erecting system. Chin. Hydraul. Pneum. 2011, 6, 108–110. [Google Scholar]
- Chao, Q. Research on Some Key Technologies of High-Speed Rotation for Axial Piston Pumps Used in EHAs. Ph.D. Thesis, Zhejiang University, Zhejiang, China, 2019. [Google Scholar]
- Chao, Q.; Zhang, J.; Xu, B.; Huang, H.; Zhai, J. Centrifugal effects on cavitation in the cylinder chambers for high-speed axial piston pumps. Meccanica 2019, 54, 815–829. [Google Scholar] [CrossRef]
- Liu, C.; Wu, X.; Gan, X.; He, Y. Numerical simulation of cavitation flow in piston pump based on full cavitation model. China Mech. Eng. 2015, 26, 3341–3347. [Google Scholar]
- Chao, Q.; Tao, J.; Wei, X.; Wang, Y.; Meng, L.; Liu, C. Cavitation Intensity Recognition for High-Speed Axial Piston Pumps Using 1-D Convolutional Neural Networks with Multi-Channel Inputs of Vibration Signals. Alex. Eng. J. 2020, 59, 4463–4473. [Google Scholar] [CrossRef]
- Yin, F.; Nie, S.; Xiao, S.; Hou, W. Numerical and experimental study of cavitation performance in sea water hydraulic axial piston pump. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2016, 230, 716–735. [Google Scholar] [CrossRef]
- Han, J. Analysis of Flow Characteristic of Swashplate Axial Piston Pump. Master’s Thesis, Shandong University, Shandong, China, 2020. [Google Scholar]
- Tian, Z. Research on Cavitation Phenomenon of 250 cc/r Displacement Axial Piston Pump in the Process of Suction and Discharge. Master’s Thesis, Taiyuan University of Technology, Taiyuan, China, 2018. [Google Scholar]
- Ma, Y. Calculation and analysis of gas volume content in piston pump under different working conditions. Hydraul. Pneum. Seals 2020, 40, 18–22+26. [Google Scholar]
- Dong, H.; He, Y.; Wang, Y.; Kou, G. Numerical Investigation of Effect of a Centrifugal Boost Impeller on Suction Performance of an Aircraft Hydraulic Pump. Chin. J. Aeronaut. 2022, 35, 236–248. [Google Scholar] [CrossRef]
- Gao, D.; Suo, X.; Cai, Q.; Wu, S.; Liang, Y. Influence of key structural parameters of hydraulic piston pump on cavitation in pump. China Mech. Eng. 2018, 29, 434–440. [Google Scholar]
- Chao, Q.; Xu, Z.; Tao, J.; Liu, C. Capped Piston: A Promising Design to Reduce Compressibility Effects, Pressure Ripple and Cavitation for High-Speed and High-Pressure Axial Piston Pumps. Alex. Eng. J. 2023, 62, 509–521. [Google Scholar] [CrossRef]
- Ma, J.; Fang, Y.; Xu, B.; Yang, H. Optimization of cross angle based on the pumping dynamics model. J. Zhejiang Univ. Sci. A 2010, 11, 181–190. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, C.; Hong, H.; Cheng, G.; Yang, H.; Feng, S.; Zhai, J.; Xiao, W. Optimization of the Outlet Unloading Structure to Prevent Gaseous Cavitation in a High-Pressure Axial Piston Pump. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 3459–3473. [Google Scholar] [CrossRef]
- Zhang, H. Cavitation Characteristics Analysis of Distribution Pair of High Temperature Fuel Piston Pump. Master’s Thesis, Zhejiang University, Zhejiang, China, 2019. [Google Scholar]
- Tsukiji, T.; Takase, T.; Noguchi, E. Visualization analysis of cavitating jet flow issuing from notch in an axial piston pump. Trans. Jpn. Fluid Power Syst. Soc. 2011, 42, 7–12. [Google Scholar] [CrossRef] [Green Version]
- Tsukiji, T.; Chen, Z.; Chen, J. Visualized analysis of cavitation inside axial piston pump. Chin. Hydraul. Pneum. 2015, 2, 1–7. [Google Scholar]
- Yu, F.; Zhang, J.; Xu, B.; Zebing, M.; Li, C.; Huang, C.; Fei, L.; Zhimin, G. Raising the Speed Limit of Axial Piston Pumps by Optimizing the Suction Duct. Chin. J. Mech. Eng. Ji Xie Gong Cheng Xue Bao 2021, 34, 105. [Google Scholar] [CrossRef]
- Chao, Q.; Zhang, J.; Xu, B.; Huang, H.; Zhai, J. Effects of inclined cylinder ports on gaseous cavitation of high-speed electro-hydrostatic actuator pumps: A numerical study. Eng. Appl. Comput. Fluid Mech. 2019, 13, 245–253. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z. Study on Cavitation Resistance of Swash Plate Axial Piston Pump Cylinder and Valve Plate. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2017. [Google Scholar]
- Guan, C.; Jiao, Z.; He, S. Theoretical study of flow ripple for an aviation axial-piston pump with damping holes in the valve plate. Chin. J. Aeronaut. 2014, 27, 169–181. [Google Scholar] [CrossRef] [Green Version]
- Singhal, A.K.; Athavale, M.M.; Li, H.; Jiang, Y. Mathematical basis and validation of the full cavitation model. J. Fluids Eng. 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Iannetti, A.; Stickland, M.T.; Dempster, W.M. A CDF and experimental study on cavitation in positive displacement pumps: Benefits and drawbacks of the ‘full’ cavitation model. Eng. Appl. Comput. Fluid Mech. 2016, 10, 57–71. [Google Scholar] [CrossRef] [Green Version]
- Manring, N.D.; Mehta, V.S.; Nelson, B.E.; Graf, K.J.; Kuehn, J.L. Scaling the speed limitations for axial-piston swash-plate type hydrostatic machines. J. Dyn. Syst. Meas. Control 2014, 136, 031004. [Google Scholar] [CrossRef]
- Kunkis, M.; Weber, J. Experimental and Numerical Assessment of an Axial Piston Pump’s Speed Limit; American Society of Mechanical Engineers Digital Collection: Bath, UK, 2016. [Google Scholar]
- Suo, X.; Jiang, Y.; Wang, W.; Gao, D.; Zhang, X. Cavitation flow characteristics and optimization of high-pressure pumps in the hydraulic system of aircraft control surfaces. Acta Aeronaut. Astronaut. Sin. 2023, 44, 127402. [Google Scholar]

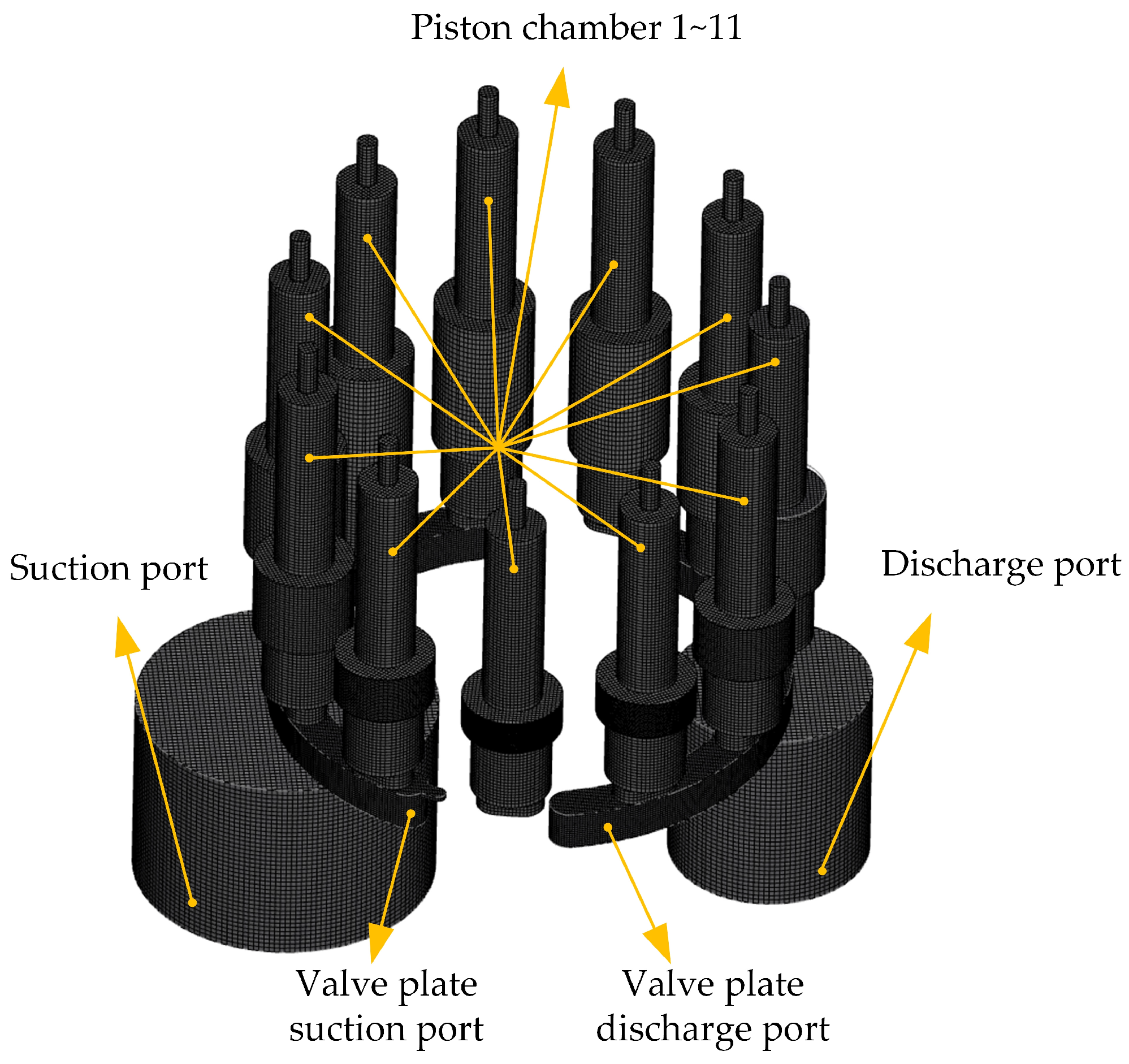





| Description | Value | Description | Value |
|---|---|---|---|
| Inlet pressure | 0.101325 MPa | Air dissolved volume | 13% |
| Outlet pressure | 25 MPa | Saturation vapour pressure | 400 Pa |
| Swash-plate angle | 15° | Hydraulic oil density | 800 kg/m3 |
| Air molar mass | 28.97 kg/kmol | Modulus of elasticity of hydraulic oil | 1.5 × 109 Pa |
| Number of pistons | 11 | Viscosity | 7 × 10−3 Pa·s |
| Outer radius of piston | 10 mm | Hydraulic oil temperature | 25 °C |
| Radius of piston distribution circle | 48 mm | - | - |
| Rotational Speed (rpm) | Traditional Cylinder Block | Improved Cylinder Block | ||||
|---|---|---|---|---|---|---|
| Filling Rate | Volume Efficiency | Effective Transportation Rate | Filling Rate | Volume Efficiency | Effective Transportation Rate | |
| 2000 | 89.703% | 74.465% | 83.013% | 97.532% | 91.755% | 94.077% |
| 2500 | 81.055% | 49.649% | 61.254% | 91.089% | 76.936% | 84.462% |
| 3000 | 75.148% | 34.390% | 45.763% | 82.753% | 56.408% | 68.164% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, M.; Jiang, Y. Research on the High Speed of Piston Pumps Based on Rapid Erecting of Launch Vehicles. Appl. Sci. 2023, 13, 7178. https://doi.org/10.3390/app13127178
Hu M, Jiang Y. Research on the High Speed of Piston Pumps Based on Rapid Erecting of Launch Vehicles. Applied Sciences. 2023; 13(12):7178. https://doi.org/10.3390/app13127178
Chicago/Turabian StyleHu, Mengya, and Yi Jiang. 2023. "Research on the High Speed of Piston Pumps Based on Rapid Erecting of Launch Vehicles" Applied Sciences 13, no. 12: 7178. https://doi.org/10.3390/app13127178
APA StyleHu, M., & Jiang, Y. (2023). Research on the High Speed of Piston Pumps Based on Rapid Erecting of Launch Vehicles. Applied Sciences, 13(12), 7178. https://doi.org/10.3390/app13127178





