A Novel Inverse Simulation Method of Helicopter Maneuvering Flight
Abstract
:1. Introduction
2. Degeneration Method
2.1. Degeneration Based on a Transitional Vector
2.2. Determination of the Transitional Vector
3. Application to the Helicopter System
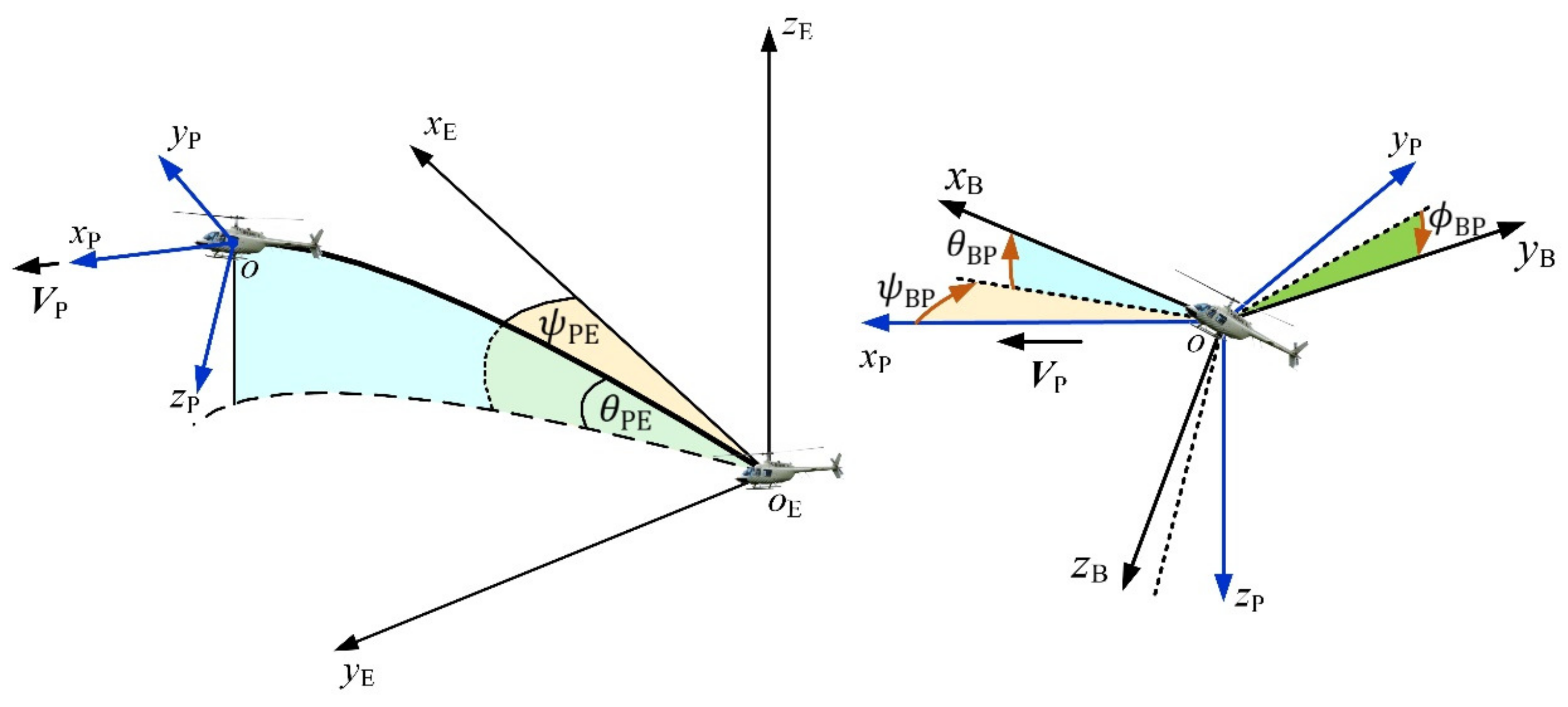
3.1. Construction of a Transitional Vector
- and indicate a maneuver with no sideslip; e.g., pull-up and hurdle-hop.
- and indicate a maneuver with a certain sideslip; e.g., sidestep and sideslip.
- indicates a maneuver with a certain yawing rate; e.g., hovering turn and pirouette.
3.2. Development of the Functional Forms of the State Vector
3.3. Degeneration of the First-Order Differential Equations
4. Case Studies and Results
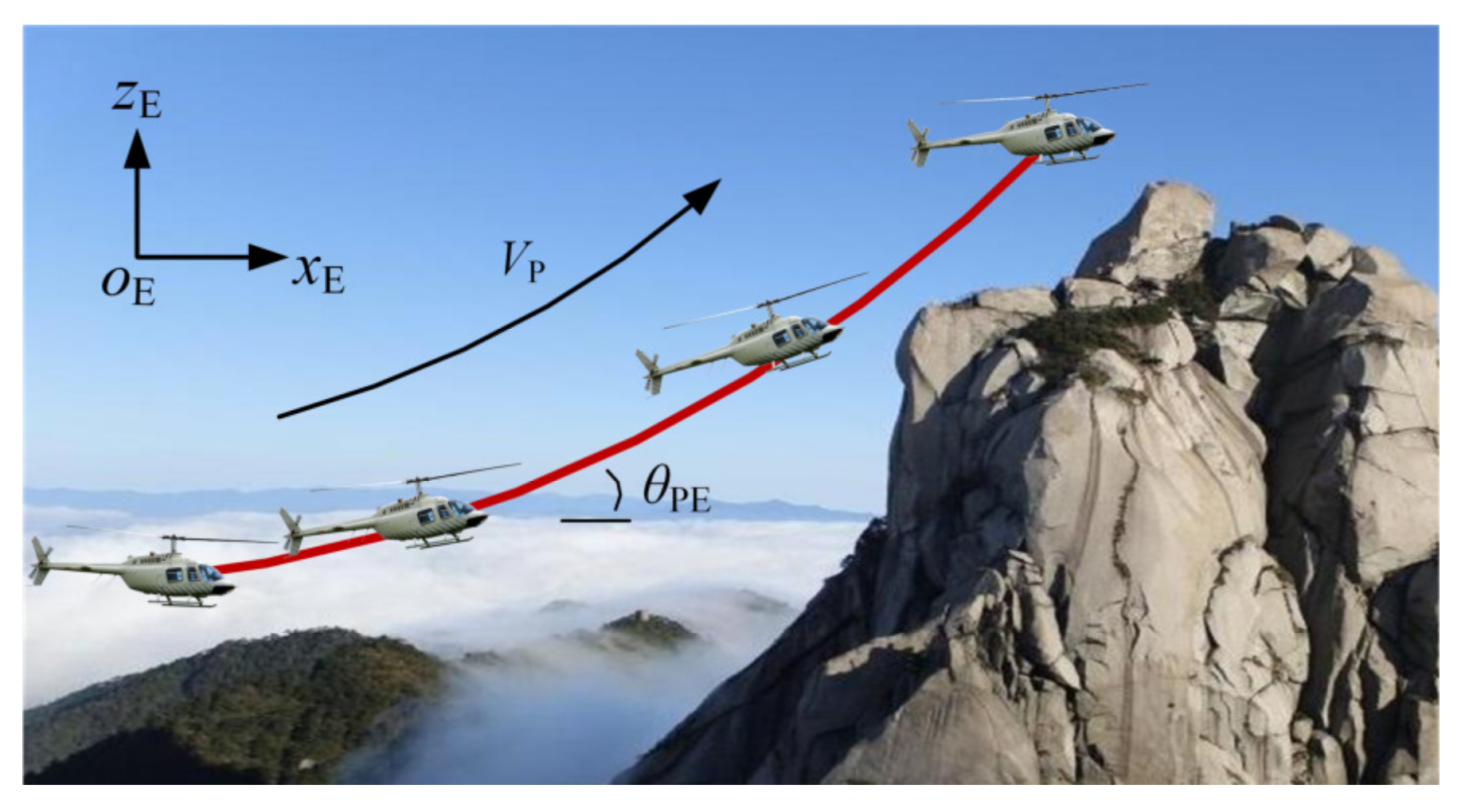
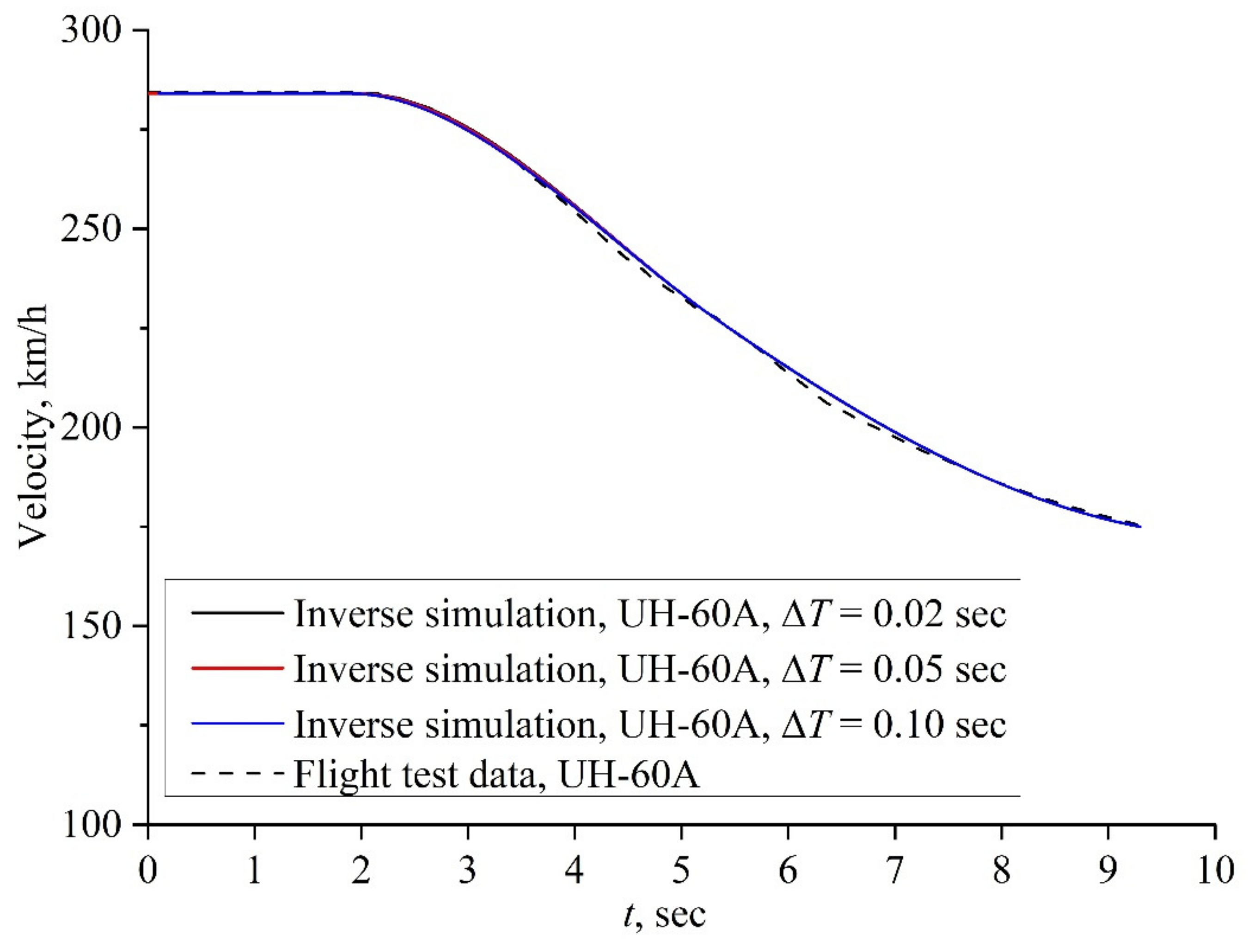
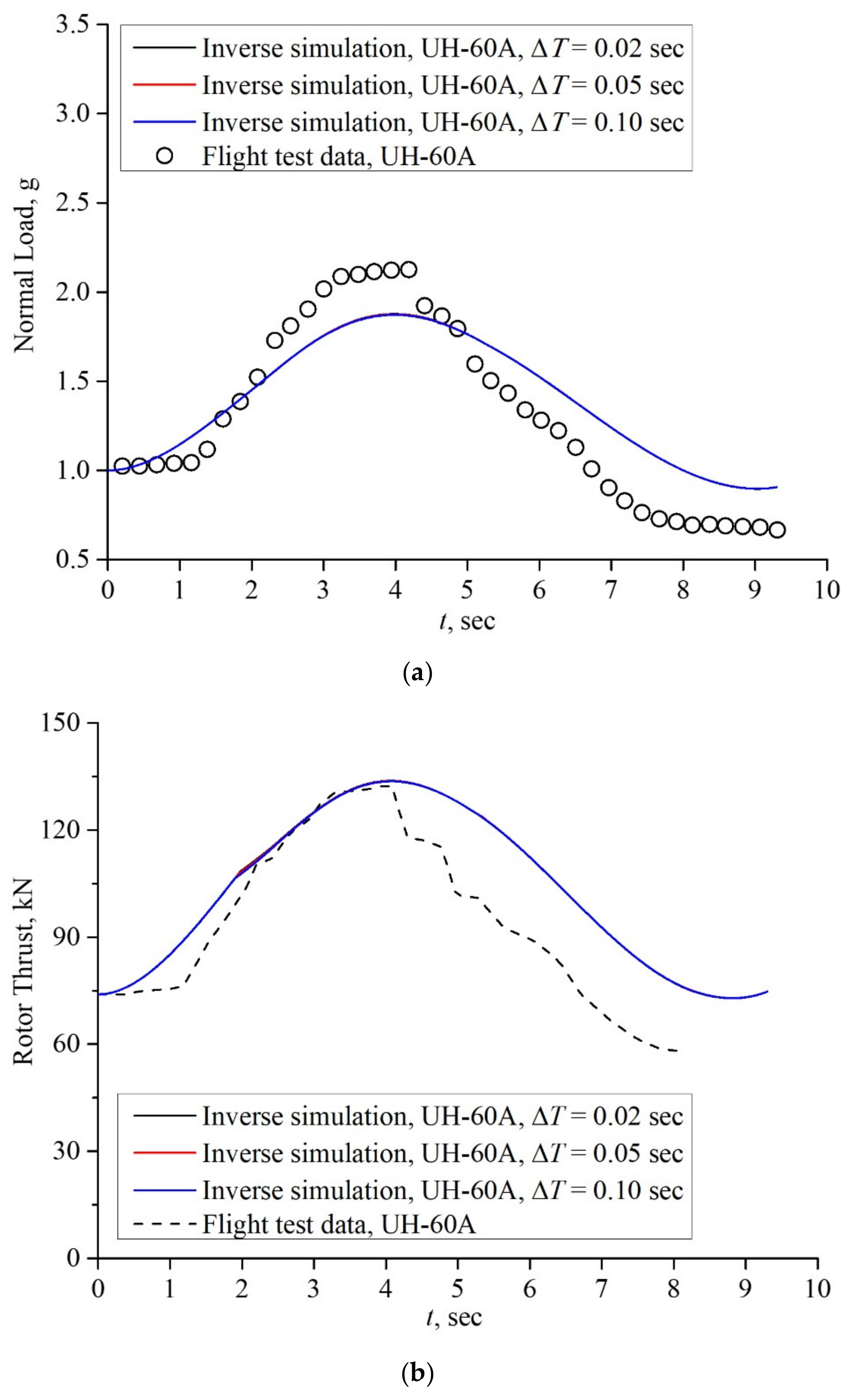
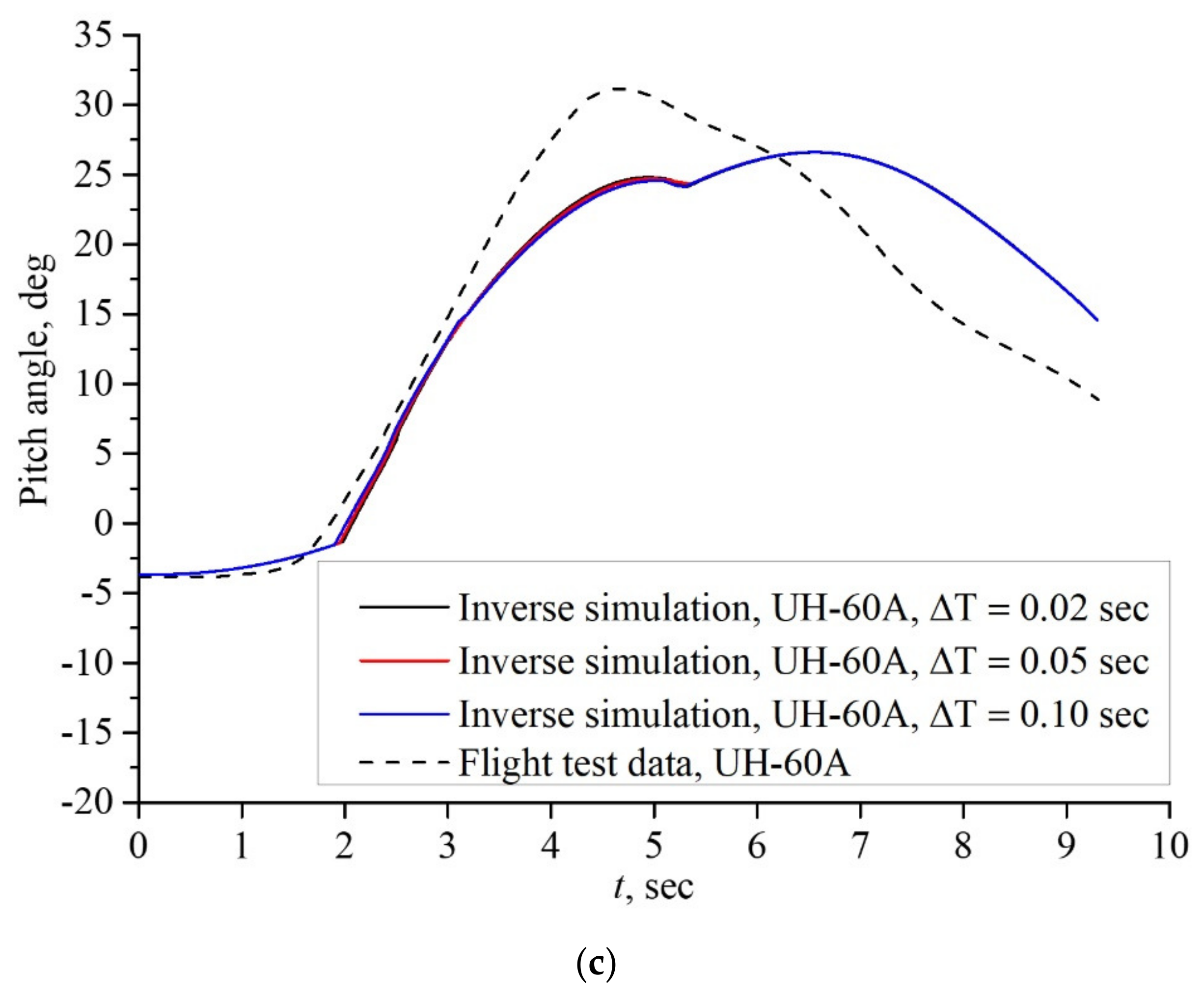
4.1. Case I: Pull-Up Maneuver
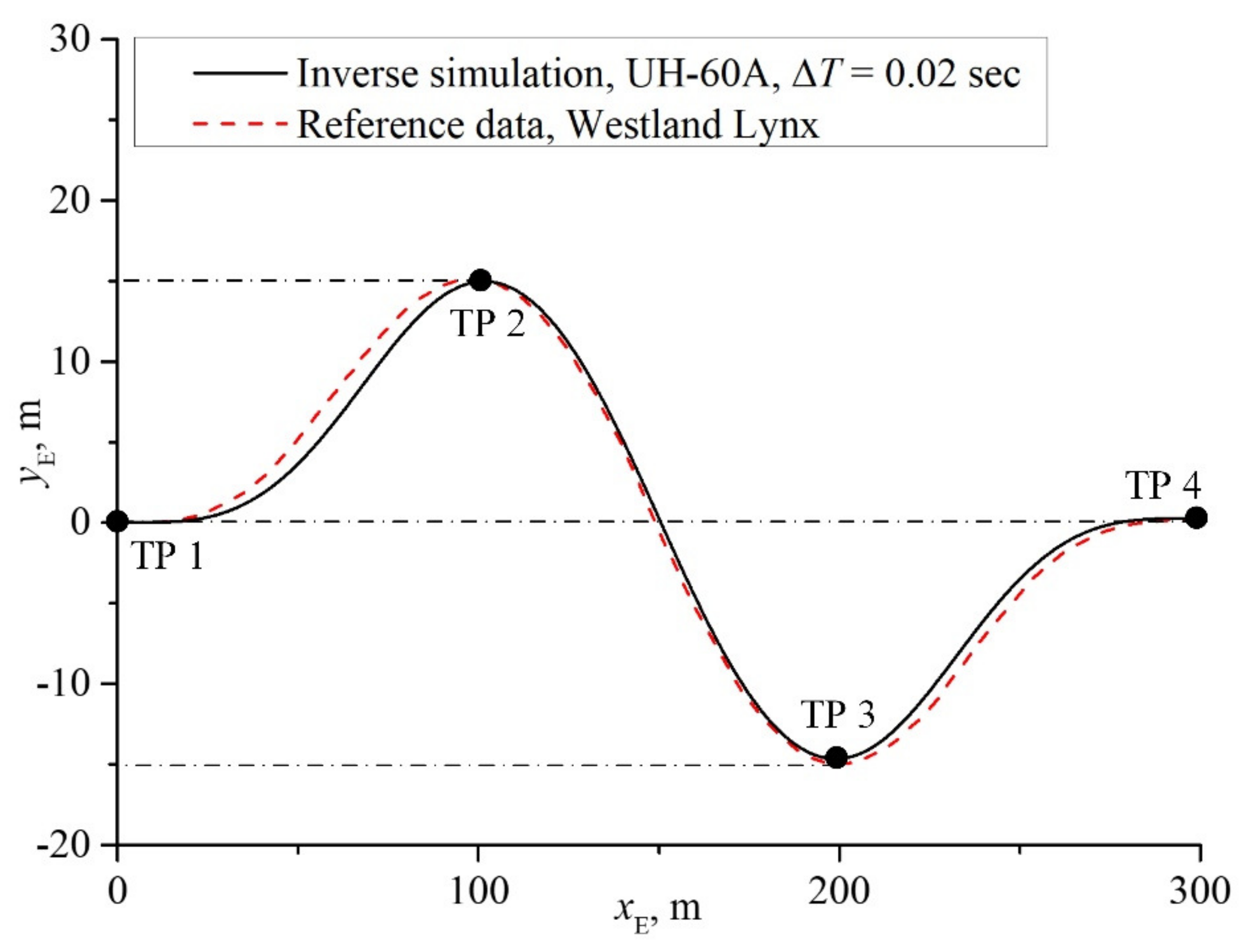
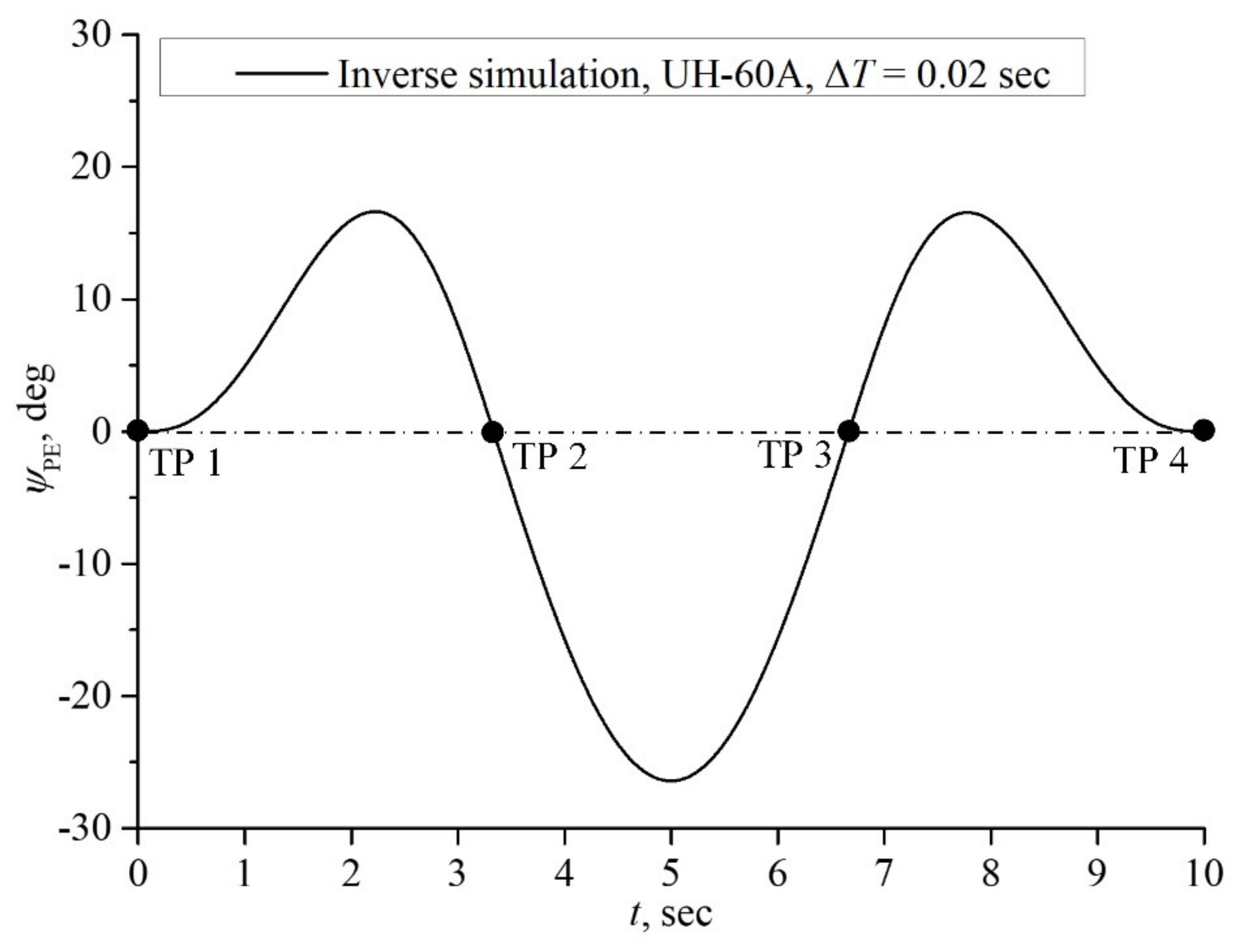
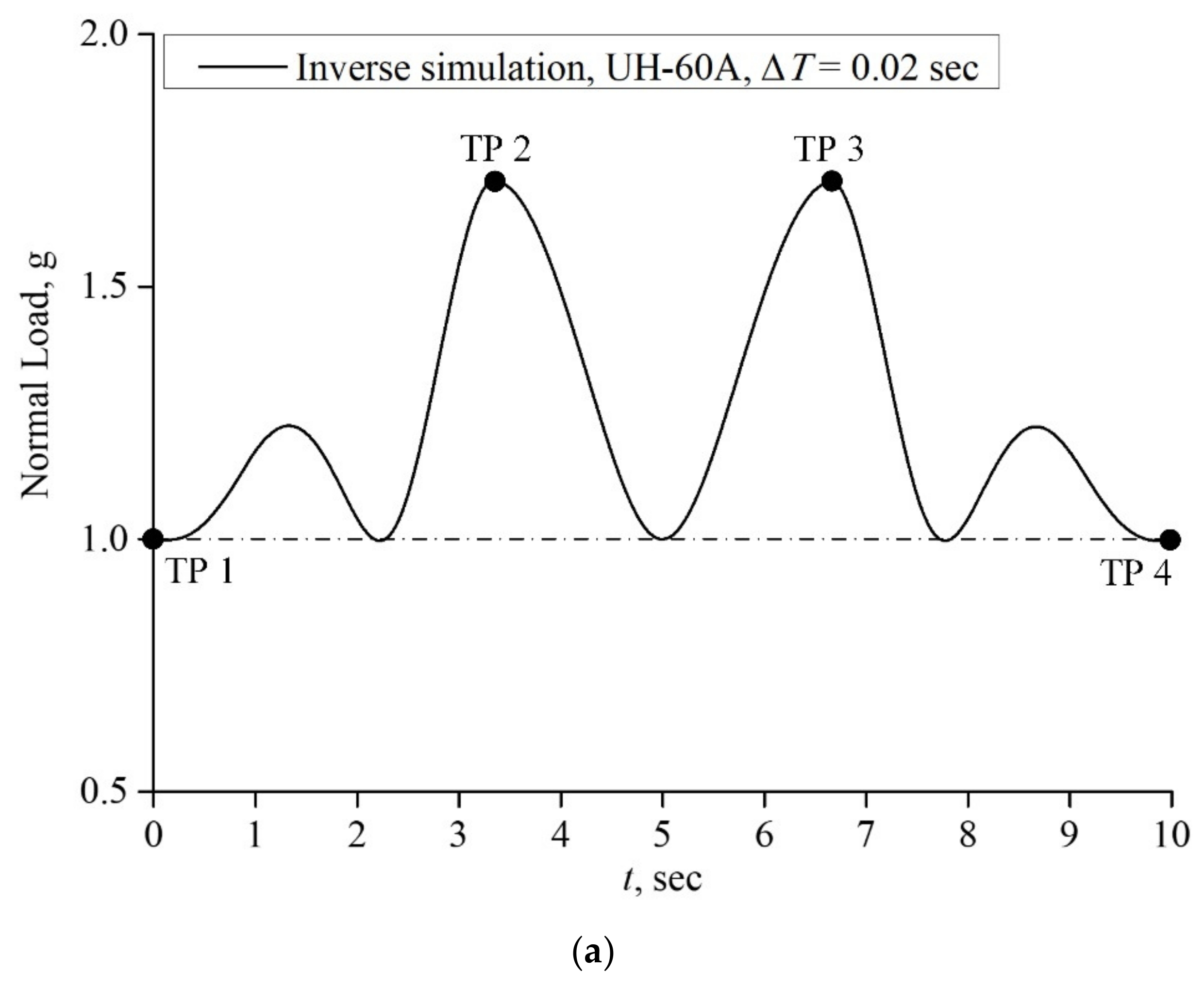
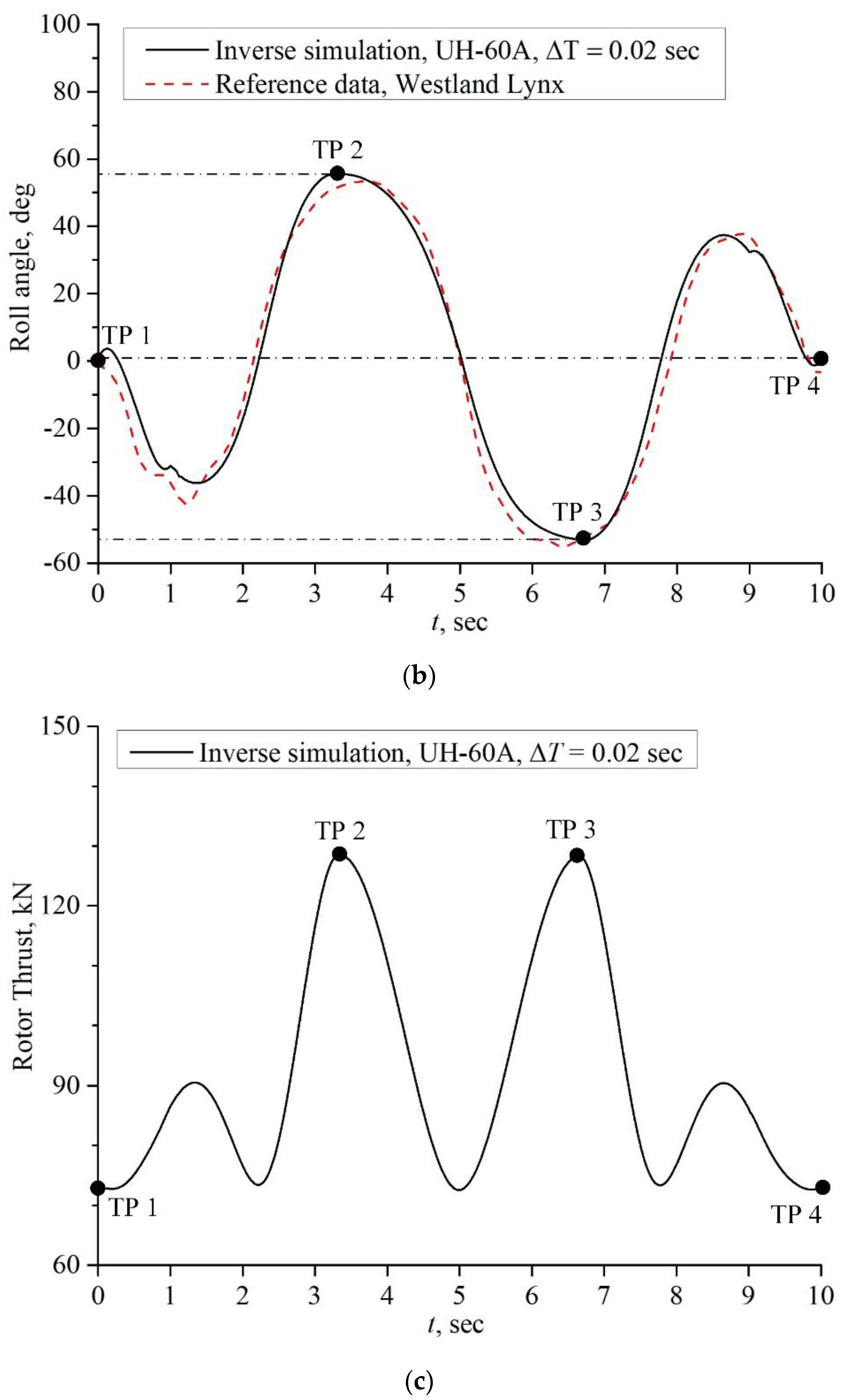
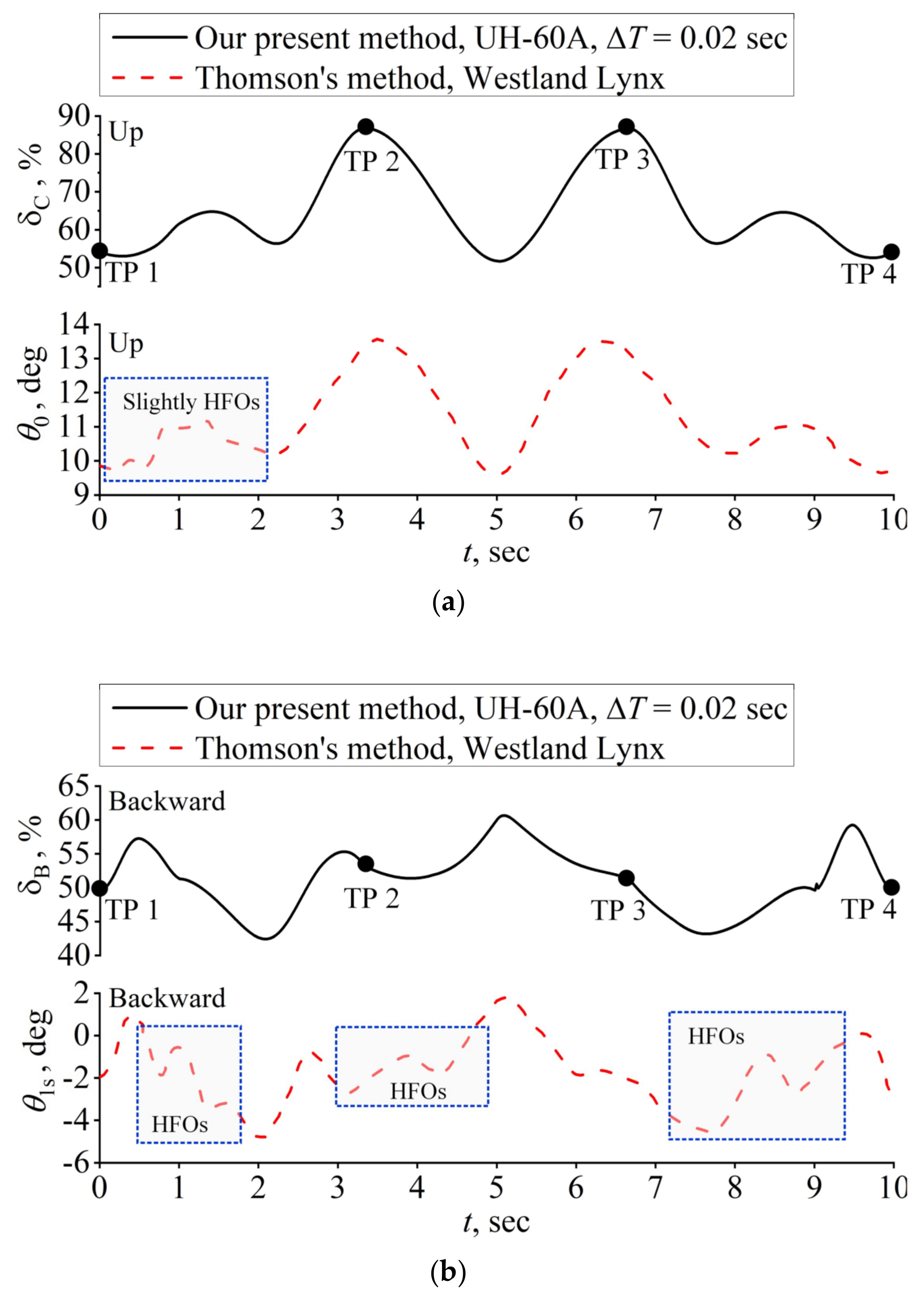
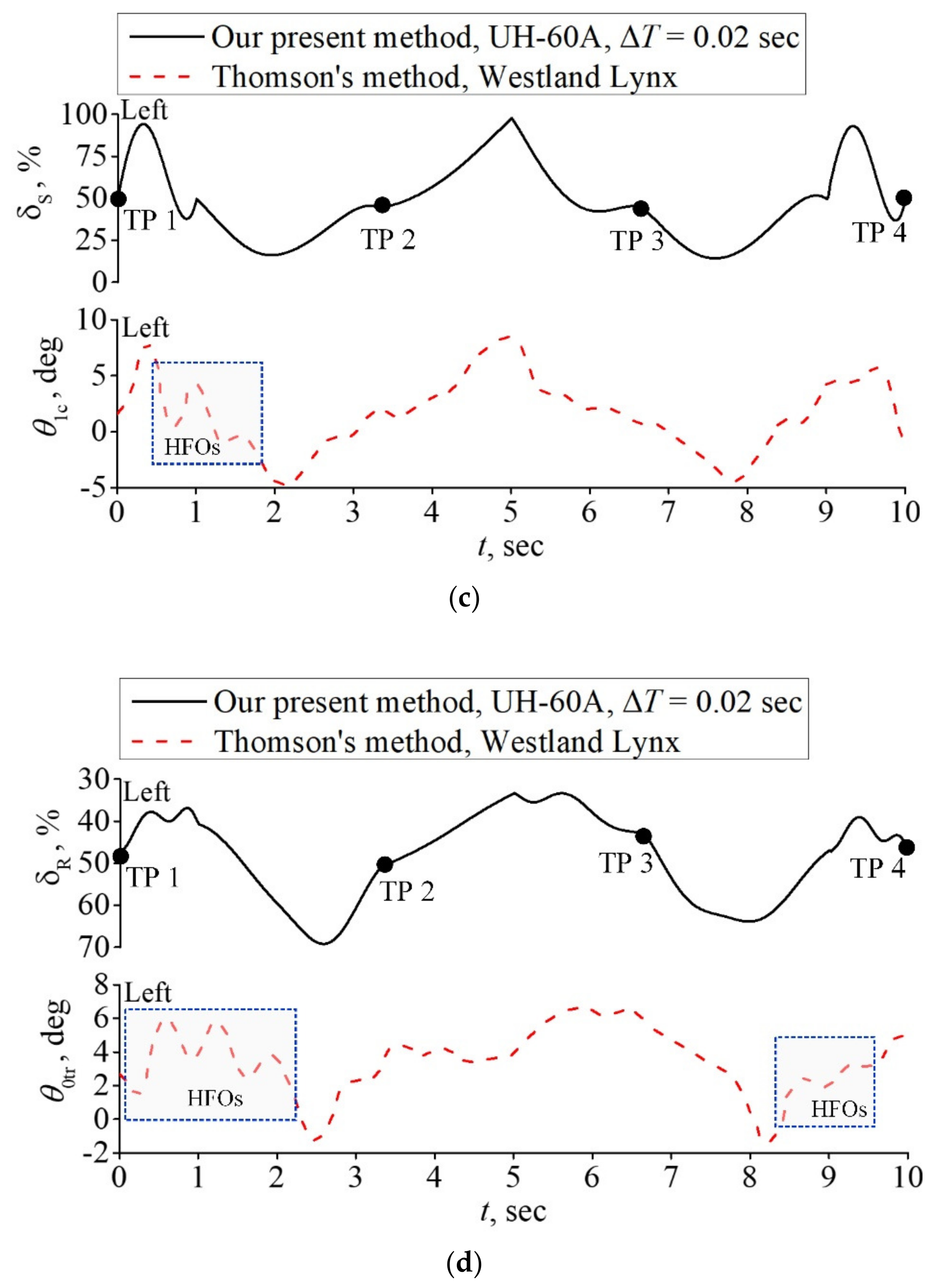
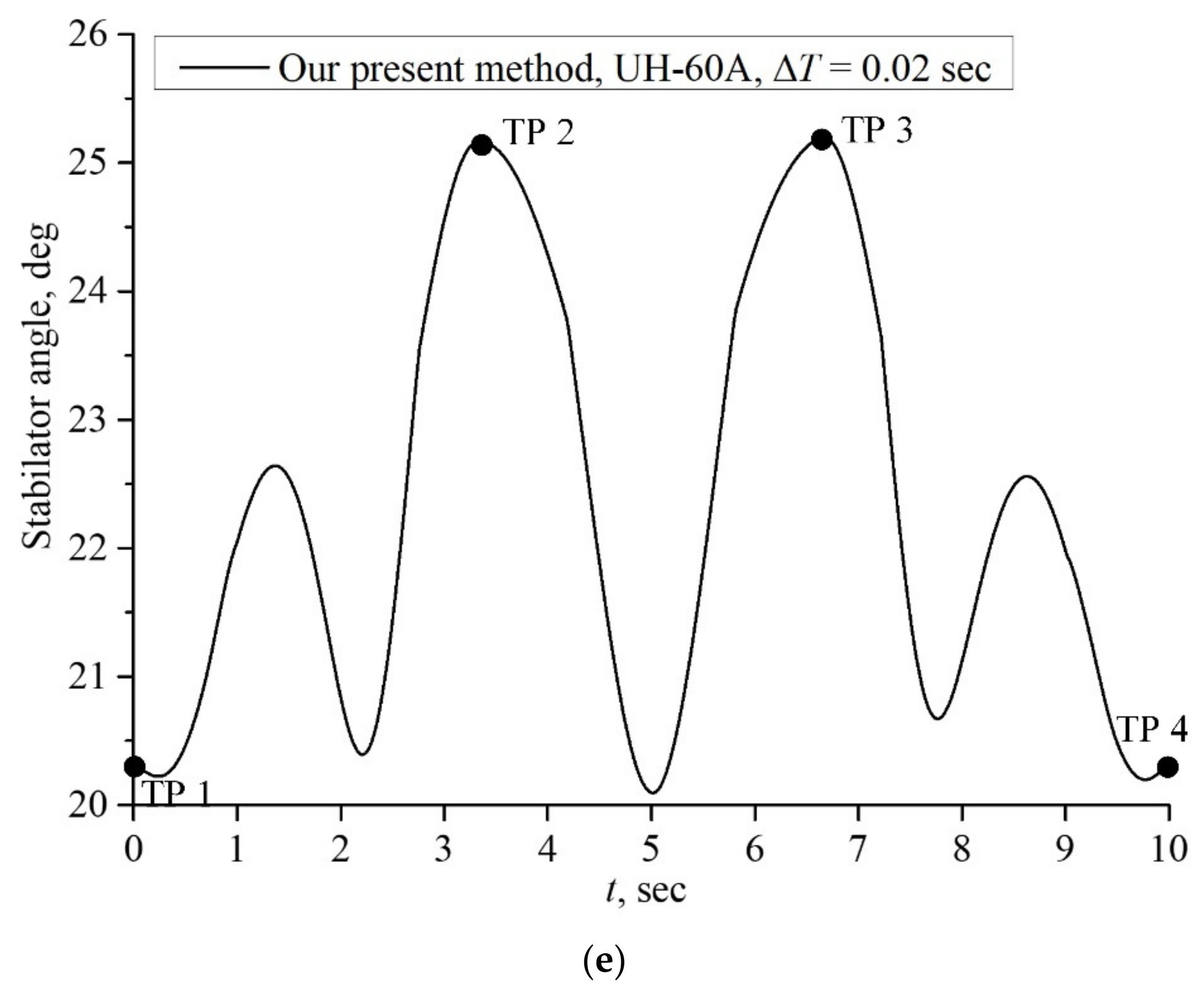
4.2. Case II: Slalom Maneuver
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Anderson, D. Modification of a generalized inverse simulation technique for rotorcraft flight. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2003, 217, 61–73. [Google Scholar] [CrossRef]
- Thomson, D.G.; Bradley, R. The use of inverse simulation for preliminary assessment of helicopter handling qualities. Aeronaut. J. 1997, 101, 287–294. [Google Scholar] [CrossRef]
- Bagiev, M.; Thomson, D.G. Handling Qualities Assessment of an Autogiro. J. Am. Helicopter Soc. 2010, 55, 32003. [Google Scholar] [CrossRef]
- Orike, S. The effects of genetic encoding on the realization of smooth trajectory for a helicopter pilot in flying a simple maneuver. In Proceedings of the IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Yuan, Y.; Thomson, D.; Chen, R. Variable rotor speed strategy for coaxial compound helicopters with lift–offset rotors. Aeronaut. J. 2019, 124, 96–120. [Google Scholar] [CrossRef]
- Yuan, Y.; Thomson, D.; Chen, R. Investigation of Lift Offset on Flight Dynamics Characteristics for Coaxial Compound Helicopters. J. Aircr. 2019, 56, 2210–2222. [Google Scholar] [CrossRef]
- Jones, R.T. A Simplified Application of the Method of Operators to the Calculation of Disturbed Motions of an Airplane; NACA TR560; 1936. Available online: https://ntrs.nasa.gov/citations/19930091636 (accessed on 18 June 2021).
- Etkin, B. Dynamics of Flight, Stability and Control, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1959; pp. 341–352. [Google Scholar]
- Wood, T.L.; Ford, D.G.; Brigman, G.H. Maneuver Evaluation Program, USAAMRDL-TR-74-32. 1974.
- Thomson, D.G. An Analytical Method of Quantifying Helicopter Agility. In Proceedings of the 12th European Rotorcraft Forum, Garmisch-Partenkirchen, Germany, 22–25 September 1986. [Google Scholar]
- Thomson, D.G.; Bradley, R. Development and Verification of an Algorithm for Helicopter Inverse Simulation. Vertica 1990, 14, 185–200. [Google Scholar]
- Thomson, D.; Bradley, R. Inverse simulation as a tool for flight dynamics research—Principles and applications. Prog. Aerosp. Sci. 2006, 42, 174–210. [Google Scholar] [CrossRef]
- Borri, M.; Bottasso, C.L.; Montelaghi, F. Numerical Approach to Inverse Flight Dynamics. J. Guid. Control. Dyn. 1997, 20, 742–747. [Google Scholar] [CrossRef]
- Cao, Y. A New Inverse Solution Technique for Studying Helicopter Maneuvering Flight. J. Am. Helicopter Soc. 2000, 45, 43–53. [Google Scholar] [CrossRef]
- Cao, Y.; Su, Y. Helicopter manoeuvre gaming simulation and mathematical inverse solution. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2002, 216, 41–49. [Google Scholar] [CrossRef]
- Hassan, S.; Amgad, M.A.; Gamal, E. Modeling and Inverse Simulation of Generic Helicopter Maneuvers. In Proceedings of the 2018 AIAA Modeling and Simulation Technologies Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Hassan, H.S.; Bayoumy, A.M.; El-Bayoumi, G.M.; Abdelrahman, M.M. Inverse Simulation of a Full-Scale Helicopter Using Finite Difference Technique. Int. Conf. Aerosp. Sci. Aviat. Technol. 2017, 17, 1–15. [Google Scholar] [CrossRef]
- Jafari, H.; Shahmiri, F. Examination of Quadrotor Inverse Simulation Problem Using Trust-Region Dogleg Solution Method. J. Aerosp. Sci. Technol. 2018, 12, 39–53. [Google Scholar]
- Hess, R.A.; Gao, C. A Generalized Algorithm for Inverse Simulation Applied to Helicopter Maneuvering Flight. J. Am. Helicopter Soc. 1993, 38, 3–15. [Google Scholar] [CrossRef]
- Rutherford, S.; Thomson, D. Improved methodology for inverse simulation. Aeronaut. J. 1996, 100, 79–86. [Google Scholar] [CrossRef]
- Doyle, S.A.; Thomson, D.G. Modification of a Helicopter Inverse Simulation to Include an Enhanced Rotor Model. J. Aircr. 2000, 37, 536–538. [Google Scholar] [CrossRef]
- Avanzini, G.; De Matteis, G.; Torasso, A. Assessment of Helicopter Model Accuracy Through Inverse Simulation. J. Aircr. 2017, 54, 535–547. [Google Scholar] [CrossRef]
- Abhishek, A.; Prasad, R. Helicopter Unsteady Maneuver Analysis Using Inverse Flight Dynamics Simulation and Comprehensive Analysis. J. Aircr. 2016, 53, 1614–1625. [Google Scholar] [CrossRef]
- Avanzini, G.; de Matteis, G. Two-Timescale Inverse Simulation of a Helicopter Model. J. Guid. Control. Dyn. 2001, 24, 330–339. [Google Scholar] [CrossRef]
- Avanzini, G.; de Matteis, G.; de Socio, L.M. Two-Timescale-Integration Method for Inverse Simulation. J. Guid. Control. Dyn. 1999, 22, 395–401. [Google Scholar] [CrossRef]
- Lin, K.; Lu, P. Inverse Simulation—An Error Analysis. Simulation 1995, 65, 385–392. [Google Scholar] [CrossRef]
- Transtrum, M.K.; Sethna, J.P. Improvements to the Levenberg-Marquardt Algorithm for Nonlinear Least-Squares Minimization. arXiv 2012, arXiv:1201.5885. [Google Scholar]
- Levi, M. Composition of rotations and parallel transport. Nonlinearity 1996, 9, 413–419. [Google Scholar] [CrossRef]
- Murray-Smith, D. The inverse simulation approach: A focused review of methods and applications. Math. Comput. Simul. 2000, 53, 239–247. [Google Scholar] [CrossRef]
- Abhishek, A.; Datta, A.; Ananthan, S.; Chopra, I. Prediction and Analysis of Main Rotor Loads in a Prescribed Pull-Up Maneuver. J. Aircr. 2010, 47, 1197–1215. [Google Scholar] [CrossRef]
- Prasad, R.; Abhishek, A. Development and Validation of Inverse Flight Dynamics Simulation for Helicopter Maneuver. In Proceedings of the 4th Asian/Australian Rotorcraft Forum, IISc, Bengaluru, India, 16–18 November 2015. [Google Scholar]
- Johnson, W. Helicopter Theory; Princeton University Press: Princeton, NJ, USA, 1980. [Google Scholar]
- Cao, Y.; Li, G.; Sheridan, J. Airflow hazard prediction for helicopter flight in icing condition. Proc. Inst. Mech. Eng. Part G: J. Aerosp. Eng. 2012, 228, 147–154. [Google Scholar] [CrossRef]
- Cao, Y.; Li, G.; Hess, R.A. Helicopter flight characteristics in icing conditions. Aeronaut. J. 2012, 116, 963–979. [Google Scholar] [CrossRef]
- Li, G.; Cao, Y. Numerical Simulation of the Wake Generated by a Helicopter Rotor in Icing Conditions. Fluid Dyn. Mater. Process. 2021, 17, 235–252. [Google Scholar] [CrossRef]
- Howlett, J.J. UH–60A Black Hawk Engineering Simulation Program: Mathematical Model; Report No. NASA CR-166309; National Aeronautics and Space Administration: Washington, DC, USA, 1981; Volume I. Available online: https://ntrs.nasa.gov/citations/19840020737 (accessed on 10 June 2023).
- Daniel, L.O. Handling Qualities Requirements for Military Rotorcraft: Aeronautical Design Standard ADS-33E-PRF; United States Army Aviation & Troop Command: 2000. Available online: https://www.robertheffley.com/docs/HQs/ADS-33E-PRF.pdf (accessed on 10 June 2023).




| Main Rotor | |
| Airfoil | SC 1095 |
| Number of Blades | 4 |
| Radius, m | 8.178 |
| Blade Chord, m | 0.5273 |
| Rotational Speed, rad/s | 27 |
| Longitudinal Shaft Tilt, deg | −3 |
| Linear Blade Twist, rad/m | −18 |
| Lock Number | 8.1936 |
| Flapping Hinge Offset, m | 0.381 |
| Mass Moment, | 385.66 |
| Inertia Moment, | 2050.81 |
| Fuselage | |
| Gross Weight, kg | 7876.18 |
| Roll Inertia, | 6316.8 |
| Pitch Inertia, | 52,215.6 |
| Yaw Inertia, | 49,889.0 |
| Product of Inertia, | 2551.7 |
| Tail Rotor | |
| Airfoil | SC 1095 |
| Number of Blades | 4 |
| Radius, m | 1.6764 |
| Blade Chord, m | 0.2469 |
| Rotational Speed, rad/s | 124.62 |
| Linear Blade Twist, rad/m | −18 |
| Lock Number | 3.3783 |
| Installation Angle, deg | 70 |
| Time Points (TPs) | ||||
|---|---|---|---|---|
| 1 | 0 | 0 | 284 | 0 |
| 2 | 2 | - | 284 | 0 |
| 3 | 5.34 | - | 227 | −18.52 |
| 4 | 9.3 | - | 175 | −5 |
| Time Points (TPs) | ||||
| 1 | 0 | 0 | 0 | 0 |
| 2 | 2 | - | - | - |
| 3 | 5.34 | - | - | - |
| 4 | 9.3 | 35 | 0 | 0 |
| Time Points (TP) | ||||
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 |
| 2 | 3.33 | 0 | −25.25 | 0 |
| 3 | 6.67 | 0 | 25.25 | 0 |
| 4 | 10 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Cao, Y. A Novel Inverse Simulation Method of Helicopter Maneuvering Flight. Appl. Sci. 2023, 13, 7214. https://doi.org/10.3390/app13127214
Li G, Cao Y. A Novel Inverse Simulation Method of Helicopter Maneuvering Flight. Applied Sciences. 2023; 13(12):7214. https://doi.org/10.3390/app13127214
Chicago/Turabian StyleLi, Guozhi, and Yihua Cao. 2023. "A Novel Inverse Simulation Method of Helicopter Maneuvering Flight" Applied Sciences 13, no. 12: 7214. https://doi.org/10.3390/app13127214
APA StyleLi, G., & Cao, Y. (2023). A Novel Inverse Simulation Method of Helicopter Maneuvering Flight. Applied Sciences, 13(12), 7214. https://doi.org/10.3390/app13127214






