LSTM Network for the Oxygen Concentration Modeling of a Wastewater Treatment Plant

Abstract

The activated sludge process is a well-known method used to treat municipal and industrial wastewater. In this complex process, the oxygen concentration in the reactors plays a key role in the plant efficiency. This paper proposes the use of a Long Short-Term Memory (LSTM) network to identify an input–output model suitable for the design of an oxygen concentration controller. The model is identified from easily accessible measures collected from a real plant. This dataset covers almost a month of data collected from the plant. The performances achieved with the proposed LSTM model are compared with those obtained with a standard AutoRegressive model with eXogenous input (ARX). Both models capture the oscillation frequencies and the overall behavior (ARX Pearson correlation coefficient $\rho$ = 0.833 , LSTM $\rho$ = 0.921), but, while the ARX model fails to reach the correct amplitude (index of fitting $FIT$ = 41.20%), the LSTM presents satisfactory performance ($FIT$ = 60.56%).

1. Introduction

A WasteWater Treatment Plant (WWTP) is a plant where wastewater is treated to remove pollutants, exploiting biological and chemical reactions, before being released back into the environment. The modeling and control of this process is not trivial, because the treatment depends on the nature and the characteristics of the wastewater. Wastewater usually firstly undergoes chemical–physical treatments in order to remove the solid part of the waste, and then biological treatments for the organic components. One of the most common biological treatments used in WWTPs is the Conventional Activated Sludge (CAS) process, in which bacteria are used to nitrify and denitrify wastewater.

Considering the complexity of the process, the control of a WWTP can be a challenging task: several flows may be involved, among with a huge variety of different biological and chemical reactions; it is necessary to provide a sufficient oxygen quantity but without an excess of aeration, reaching a trade-off between energy consumption and process demand, with a growing attention to environment-related problems. To design an optimal control strategy, it is necessary to have an accurate model of the process [1]. In [2], a review on the current state of the art regarding the modeling of activated sludge WWTPs is presented.

The model of the entire WWTP is usually composed of two main components: the hydraulic model that takes into account the different flows in input and output in the reactor, and the Activated Sludge Model (ASM) that models the biological and chemical reactions inside the tank due to the activated sludge process. The so-called Activated Sludge Model No. 1 (ASM1) [3] was extended in recent years to consider phosphorus dynamics in ASM2, [4] and to include the storage of organic substrates as a new process with an easier calibration in ASM3 [5]. ASM1 is still the most used model, and it can be considered the state of the art because several successive works are based on it [6,7,8]. However, complex and specialized models require the identification of more specific parameters subject to high sensitivity, with expensive and time-consuming procedures, far from practical applications. Hence, these specialized models are not a good choice for process design. For practical applications, in [9], the combination of the process knowledge with new artificial intelligence techniques is proposed. In [2], in addition to the most diffused WWTP white-box modeling, some black-box methodologies based on Neural Network (NN) techniques were presented with interesting results.

In view of all these considerations, in this work, an NN approach, in particular a Long Short-Term Memory (LSTM) network, is explored to model a WWTP located in Mortara (Pavia, Italy), managed by the company ASMortara S.p.A. The main goal was the development of a model for the biological reactor of the plant to improve several critical aspects of the process, such as the oxygen concentration regulation or the design of a fault detection system. The data used in this paper have been collected with a simple switching controller enabling (disabling) the input flow if the oxygen concentration inside the reactor is below (above) a certain threshold. The effect of this control strategy is an on/off oxygen flow rate that generates important oscillations in the oxygen concentration evolution. Having a better model of the system would make it possible to design a more advanced control strategy and to improve the energy consumption. In order to highlight the capabilities of the proposed approach, the LSTM performances are compared with those obtained with a standard AutoRegressive model with eXogenous input (ARX).

Because, in this kind of process, the knowledge of the biological reactions is limited, the NN approach can represent a promising alternative to the white-box one. Moreover, considering the large amount of input–output data that can be collected on the plant, these approaches are good candidates for control design. In several other similar cases, as reported in Section 2, the LSTM was found to be the best choice for model identification. In this work, the aim is to explore whether, for the considered WWTP process, the LSTM can also be trained to obtain satisfactory predicting capabilities for control purposes.

2. Related Works

Several works studied the possibility of using Recurrent Neural Network (RNN), and in particular LSTM, models to simulate the dynamical behavior of different processes, obtaining promising results. Recently, RNN has become a very popular research topic in the Machine Learning (ML) field, also because of these successful results. Forecasting time series data is an important subject in different fields, such as economics, business, finance, etc. It has been demonstrated [10] that deep NNs are effective model estimators from input–output data; therefore, the proposed work aims to evaluate the quality of LSTM architecture as a model for a WWTP. Similarly to [11], where several techniques to effectively forecast the next lag of time series were explored, in this work the LSTM is compared with the classic ARX model. Siami-Namini et al. in [11] proved how the LSTM outperforms traditionally-based algorithms, such as an ARIMA model, in terms of the average reduction in error rates obtained by an LSTM with respect to ARIMA, indicating the superiority of LSTM.

One promising field of application for the LSTM is represented by the modeling and identification of mechanical systems with the aim of designing control algorithms. In the mechanical world, in particular, friction characteristics often deteriorate the performance of control systems, causing overshoot, undershoot, etc. In the literature, some model structures have been proposed to overcome these issues, but the identification of the correct parameters for precise modeling remains a difficult task. In [12], the modeling of rolling friction based on an LSTM is proposed to precisely express the rolling friction characteristics, with satisfactory results when compared with conventional friction models using an actual experimental setup.

In [13], the authors considered two ML methods: the Extreme Gradient Boosting (XGBoost) method, which is based on decision trees that highly optimize the processing time and model complexity, and the LSTM model that is also considered in this work. The aim of the work was to provide useful predictions considering rare events, such as natural disasters, and in particular to obtain a data-driven decision-making approach for fire departments to forecast the number of interventions in the next hour. The work proved that predictions with good accuracy are possible and feasible for practical purposes.

A data-driven approach for modeling nonlinear dynamical systems using LSTM networks with output recurrence was proposed in [14]. This method can make full use of the data in establishing a dynamical system model. The considered system was a 42-story reinforced concrete frame-core tube building under seismic excitation. This work compared two types of LSTM models with different training strategies: one with output recurrence, which accepts the external excitation and the network outputs of the previous time step as inputs at the current time step and provides initial conditions at the first two time steps; the other one with teacher forcing, which takes the external excitation and true targets as the network inputs during training. The comparison proved that the latter network is not a feasible method for dynamical system modeling because it cannot guarantee long-term robustness.

The superiority of the LSTM method has been demonstrated in [15] for a different purpose. This paper compared the accuracy of missing stem water data for plants under different data filling methods to solve the problem of data loss in sensor data collection. Interpolation methods, time series statistical methods, RNN and LSTM neural networks were used to fill in the missing part. The results show that the LSTM network also has more accurate performance than the RNN in this kind of application.

However, in the case of very complex systems, the LSTM method may be insufficient to fully describe the dynamics of the process, and a more complicated architecture is required. In [16], for example, the LSTM network was combined with an NN, creating a hierarchical recurrent network with one multilayer perceptron to describe the system well.

Other studies have focused on the interpretation of the internal processes and weights in the LSTM network, which is one of the main limitations of this architecture connected to its structural complexity. In [17], the authors explored a new LSTM architecture to overcome this problem, representing the internal system processes in a manner that is analogous to a hydrological reservoir (HydroLSTM). The performances of the HydroLSTM and LSTM architectures were compared using data from hydroclimatically varied catchments. The HydroLSTM-based models require fewer cell states to obtain similar performance; the weights patterns associated with lagged input variables were interpreted, and the results were found to be consistent with regional hydroclimatic characteristics (snowmelt-dominated, recent rainfall-dominated, and historical rainfall-dominated).

A complete review of the LSTM network’s features, including a modern perspective on dynamical systems in the context of current goals and open challenges, can be found in [18].

3. Materials and Methods

This work is focused on modeling the dynamic of the oxygen in the reactor, in particular through the use of the LSTM structure because of the promising results it has obtained in several different fields. In the physical models ASM1, ASM2, and ASM3, the oxygen concentration (output), $O\left(t\right)$, is mainly connected to a few manipulable variables (input): the inlet flow of the wastewater, $q_{in}\left(t\right)$, and its Chemical Oxygen Demand, ($CO{D}_{in}\left(t\right)$); the oxygen inlet flow, $q_{oss}\left(t\right)$; the outlet flow of the clarified liquid filtered by the membrane, $q_{ol},\left(t\right)$, and the outlet flow manually removed from the reactor, $q_{om}\left(t\right)$.

Even if this notion is general, as clearly stated in the Introduction, every plant has its own peculiarities, due to the local law limits, design constraints, the average chemical composition of the waste and other factors [19]. This fact should require a model identification that is typically impossible in view of the limited number of variables measurable on a real plant. Black-box models, and in particular NNs, can be a reasonable compromise to overcome this limitation.

In the following, the plant is described in detail; then, the proposed LSTM is reported and compared with a classic ARX.

3.1. Plant Description

The considered WWTP is an industrial plant that is actually used to treat both municipal and industrial wastewater. The plant is composed of two different units (see [20]) dedicated to the two stages of treatment, called primary and secondary.

The industrial wastewater needs to be pre-treated before being accepted in municipal WWTP: it passes through Unit I to remove the solid part of the waste, exploiting chemical reactions. Firstly, the flow goes into a storage-equalization tank, with the goal of transforming a variable flow into a steady-state one that is then input to the treatment plant, optimizing the process in this way. The flow is then divided into two chemical–physical treatment lines: one dedicated to the light-strength aqueous wastes, and the second for the high-strength ones. The light-strength wastes are subjected to a chemical–physical treatment with classic procedures such as flocculation, coagulation and sedimentation. The wastes are put in sedimentation tanks, where the solid part is separated out by gravity; chemicals can be added to help coagulation, while with flocculation, the small colloidal particles are separated from the wastes and settle in the form of flocks. The high-strength aqueous wastes are instead fed into a Thermophilic Aerobic Membrane Reactor (TAMR). The plant has recently been equipped with this innovative reactor, built ad hoc to treat high-strength wastes. The advantage of the TAMR technology is the exploitation of biological reactions even during the pre-treating phase, considering that biological solutions are more affordable and sustainable than chemical ones. In practice, the waste undergoes aerobic reactions in thermophilic conditions, exploiting oxygen with temperatures greater than 45 °C [21,22].

After this phase, the pre-treated industrial wastewater is mixed with the municipal wastewater and flows into the biological reactor (Unit II), where the CAS process performs denitrification (DEN), oxidation and nitrification (OX-NIT). This paper focuses on the modeling of this part of the plant. The biological reactor is filled with oxygen, where aerobic micro-organisms are introduced to react with wastewater and to reduce its organic compounds. The overall flow goes to a settling tank (final settler), where the activated sludge settles because the micro-organisms create a biological flock, producing a liquid mostly free from suspended solids. The sludge is separated from the clarified water; the majority of the sludge is reintroduced into the CAS to treat the new wastewater, the remaining part is removed, while the cleared water is released into the environment. In the biological reactor, the wastewater is also subjected to the denitrification and nitrification processes to remove the nitrogen components from the wastewater. This is done before releasing the water back into the environment, because these components are dangerous for aquatic organisms and plants. Nitrification occurs in aerobic conditions and is the oxidation of ammonia into nitrite and nitrate by nitrifying autotrophic bacteria; denitrification happens in anaerobic conditions instead, reducing nitrite to nitrogen [23]. For this reason, nitrate recirculates from OX-NIT to DEN.

3.2. Long Short-Term Memory (LSTM) Network

The LSTM [24,25] network is a particular type of RNN characterized by a specific unit architecture, called a memory cell, that allows better learning of information dependencies compared with a simpler RNN. The LSTM memory cell presents an internal self-loop in addition to the outer feedback present in all RNNs, and a gating system that regulates the flow of information. In this way, the gradient flows over time, even for long periods, and its derivative remains computable (they neither vanish nor diverge). LSTM networks have been demonstrated to be able to dynamically map the input and output of a dynamical system; their use for learning the inherent properties of a given dynamical system has been studied in [14,17,18,24,26,27,28], obtaining promising results. They have proven to be powerful in representing long and short temporal dependencies in multiple examples with respect to other recurrent architectures, such as Gated Recurrent Unit (GRU), BIdirectional-LSTM (BI-LSTM), etc. [26]. For these reasons, the LSTM architecture was chosen as a promising candidate to model the process under study.

The mathematical formulation of a single memory cell is represented in Figure 1 and can be expressed as follows:

$$\begin{array}{cc}\hfill c_k& =f_k\times c_{k-1}+i_k\times {\tilde{c}}_k\hfill \\ \hfill h_k& =o_k\times tanh\left(c_k\right)\hfill \end{array}$$

(1)

where $c_k\in {\mathbb{R}}^n$ is the internal cell state at time k, $u_k\in {\mathbb{R}}^m$ is the input at time k, and $h_k\in {\mathbb{R}}^n$ is the hidden state at time k, with n the cell state dimension that corresponds to the number of LSTM neurons, m the number of features/input of the LSTM, × is the Hadamard product and $tanh$ is the hyperbolic tangent, used as an activation function.

Four structures, called gates, regulate the internal loop of the cell, adding or removing information to modify the value of the cell state at each time instant. The first gate is the forget gate, $f_k$; it decides which information is removed from the cell state $c_k$, multiplying it by its past value $c_{k-1}$, as can be seen in the first part of (1). Then, the input gate, $i_k$, chooses which value of the cell state is updated, while the input activation gate, ${\tilde{c}}_k$, creates a new candidate value of the cell state. The last gate is the output gate, $o_k$, which determines which information contained in the cell state is included in output. The hidden state is then defined in (1), where the output gate is multiplied by a transformation of the cell state through a hyperbolic tangent function. These gates are expressed as:

$$\begin{array}{cc}\hfill f_k& =\sigma (W_f{u}_k+U_f{h}_{k-1}+b_f)\hfill \\ \hfill i_k& =\sigma (W_i{u}_k+U_i{h}_{k-1}+b_i)\hfill \\ \hfill {\tilde{c}}_k& =tanh(W_{\tilde{c}}{u}_k+U_{\tilde{c}}{h}_{k-1}+b_{\tilde{c}})\hfill \\ \hfill o_k& =\sigma (W_o{u}_k+U_o{h}_{k-1}+b_o)\hfill \end{array}$$

(2)

where $W_f$, $W_i$, $W_o$, $W_{\tilde{c}}\in {\mathbb{R}}^{n\times m}$ are the input weight matrices, $U_f$, $U_i$, $U_o$, $U_{\tilde{c}}$$\in {\mathbb{R}}^{n\times n}$ are the previous output weight matrices, and $b_f,b_i,b_o,b_{\tilde{c}}\in {\mathbb{R}}^{n\times 1}$ are the biases. These quantities are specific to each gate and identified during the training of the network. The chosen activation functions are the hyperbolic tangent $tanh$ and $\sigma$, the sigmoid function, equal to:

$$\sigma \left(x\right)=\frac{1}{1+e^{-x}}.$$

(3)

Several LSTM cells are combined in the so-called LSTM layer, and the LSTM network can be composed of one or more stacked layers, representing the hidden layers. In regression applications, usually, the output of the last (if there is more than one) LSTM layer is passed to a fully connected layer without an activation function, which computes a linear combination, according to the following equation:

$$y_k=W_y{h}_k+b_y$$

(4)

where $W_y\in {\mathbb{R}}^{p\times n}$ is the matrix of the output weights, with p the number of outputs of the network, and $b_y\in {\mathbb{R}}^{p\times 1}$ the bias. $W_y$ and $b_y$ are determined during the training of the network as well.

Because of this structure, LSTMs show their strength especially when dealing with temporal data and when temporal lags must be taken into account [25,29,30,31,32]. The LSTM developed in this work considers three inputs ($m=3$): the ingoing oxygen flow rate $q_{oss}\left(t\right)$, the ingoing substrate flow rate $q_{in}\left(t\right)$, and the outgoing liquid substrate flow rate $q_{ol}\left(t\right)$, and one output ($p=1$), the oxygen concentration $O\left(t\right)$. In this case, the other inputs of the physical process, $q_{om}\left(t\right)$ and $CO{D}_{in}\left(t\right)$, are not considered in input because they are daily measurements, with very little variation, which can be considered almost constant signals not significantly contributing to the model. All the signals were rescaled using mean normalization before being used to train the LSTM network.

The simplest LSTM architecture, with a single layer, will be considered in order to minimize the complexity and computational burden.

3.3. AutoRegressive Model with eXogenous Input (ARX) Model

The ARX model family is the most used model structure to derive input–output models. According to this family [33], the process output y is given by three components: the autoregressive component (the previous value of the output), the exogenous input variable, u, and a white Gaussian additive noise, e. The process output can be defined as

$$y_k=\sum _{j=1}^{N_a}{\alpha }_k{y}_{k-j}+\sum _{j=1}^{N_b}{\beta }_k{u}_{k-d-j}+e_k$$

where the suffix indicates the time of the sample, $N_a$ and $N_b$ are the order of the autoregressives and of the input component respectively, and d is the input delay; those values as a whole are commonly referred to as the structure of the ARX model. In this scenario, the one-step predictor is given by the following:

$${\widehat{y}}_k^p=\sum _{j=1}^{N_a}{\alpha }_k{y}_{k-j}+\sum _{j=1}^{N_b}{\beta }_k{u}_{k-d-j}$$

where the prediction ${\widehat{y}}_k^p$ is also obtained using the last output values ($y_{k-j}$). For MISO systems, the former equation is usually provided in the following compact notation:

$${\widehat{y}}_k^p=\left(1-A\left(q\right)\right)y_k+\sum _{m=1}^M{B}_m\left(q\right)u_{m,k-d_m}$$

(5)

where M is the number of inputs, $u_{m,k}$ is the m-th input discrete signal at time k, $A\left(q\right)$ and $B_m\left(q\right)$ are polynomial in terms of the time-shift operator $q^{-1}$, and $d_m$ is the delay for the m-th input.

To estimate polynomial models, input delays and model orders have to be defined. If the physics of the system is known, the number of poles and zeros can be set accordingly. However, in most cases, the model orders are not known in advance. In those cases, the identification of an ARX model is a three-step procedure [33]: first, the data have to be conditioned, then the structure of the model (i.e., polynomials’ degrees and input delays) has to be identified, and finally the parameters (i.e., the polynomial’s coefficients) have to be estimated.

In control design, models are commonly used to simulate the behavior of the process, so that the previous outputs are not available. Hence, the final predictions ${\widehat{y}}_k$ will be obtained using the ARX model as

$${\widehat{y}}_k=\sum _{m=1}^M\frac{B_m\left(q\right)}{A\left(q\right)}{u}_{m,k-d}$$

(6)

in order to be compared with the LSTM ones (Equation (4)).

3.3.1. Data Conditioning

In order to identify a linear approximation around the working point of the system [34], a common precondition technique involves the use of the deviation with respect to the working point instead of the regular signal. The signal average values are used to approximate the plant working point. Hence, the signals in hand become:

$$\begin{array}{cc}\hfill \delta y_k& =y_k-\overline{y}\hfill \\ \hfill \delta u_{m,k}& =u_{m,k}-{\overline{u}}_m\hfill \end{array}$$

where $\overline{y}$ and ${\overline{u}}_m$ are the average values of the output and of the m-th input signal. Then, the ARX model predictor becomes:

$${\widehat{y}}_k^p=\overline{y}+\left(1-A\left(q\right)\right)\delta y_k+\sum _{m=1}^M{B}_m\left(q\right)\delta u_{m,k-d_m}.$$

3.3.2. Model Structure Estimation

In order to estimate the initial model orders and delays for the system, several ARX models can be estimated within a range of orders and delays, and then the performances of these models can be compared. The model orders that correspond to the best model performance are selected and used as an initial guess for the next phase.

To guarantee a fair comparison between models having different degrees of freedom, a simple validation approach is used [35]. According to this technique, the data are split into two sets: identification and validation. Each model is identified using the first set, while the performance of the model is evaluated on the second set. Then, the best model structure is the one that minimizes the prediction error computed on the validation dataset.

The ASM model family [3,4,5] was used to determine the ranges of the desired structure parameters. According to these models, the number of states ranges from 12 to 15, no delay is involved, and the proposed model is strictly proper. Starting from this consideration, the parameter space was determined. The main idea is that the research space has to include the structure proposed by the physical models. In particular, the degree of $A\left(q\right)$ is connected to the order of the system; then, it was supposed that $N_a>15$, and for each input, the sum of delay and order should also include the same limit, $d_m+N_{bm}>15$.

Table 1. Compared ARX structures.

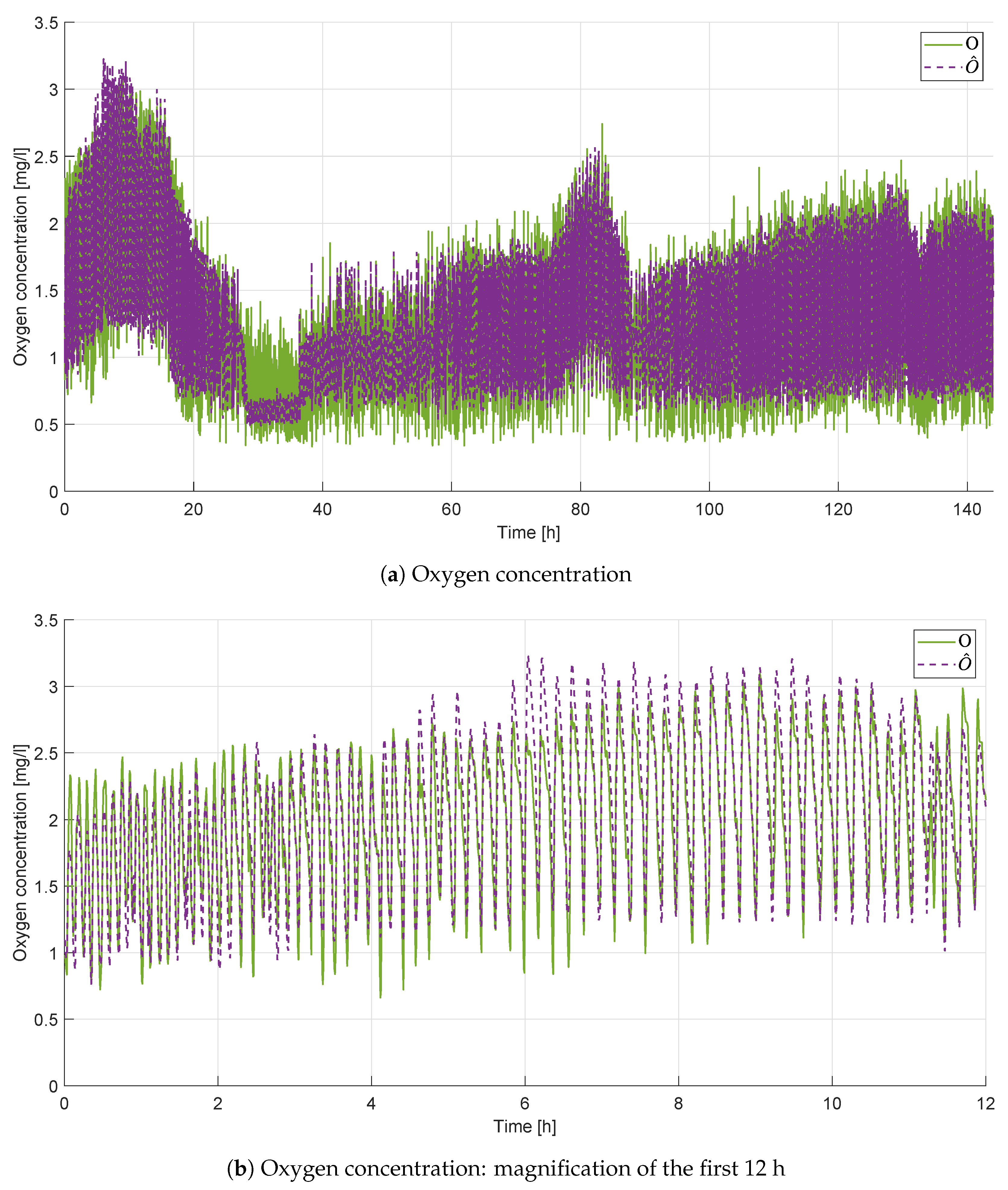
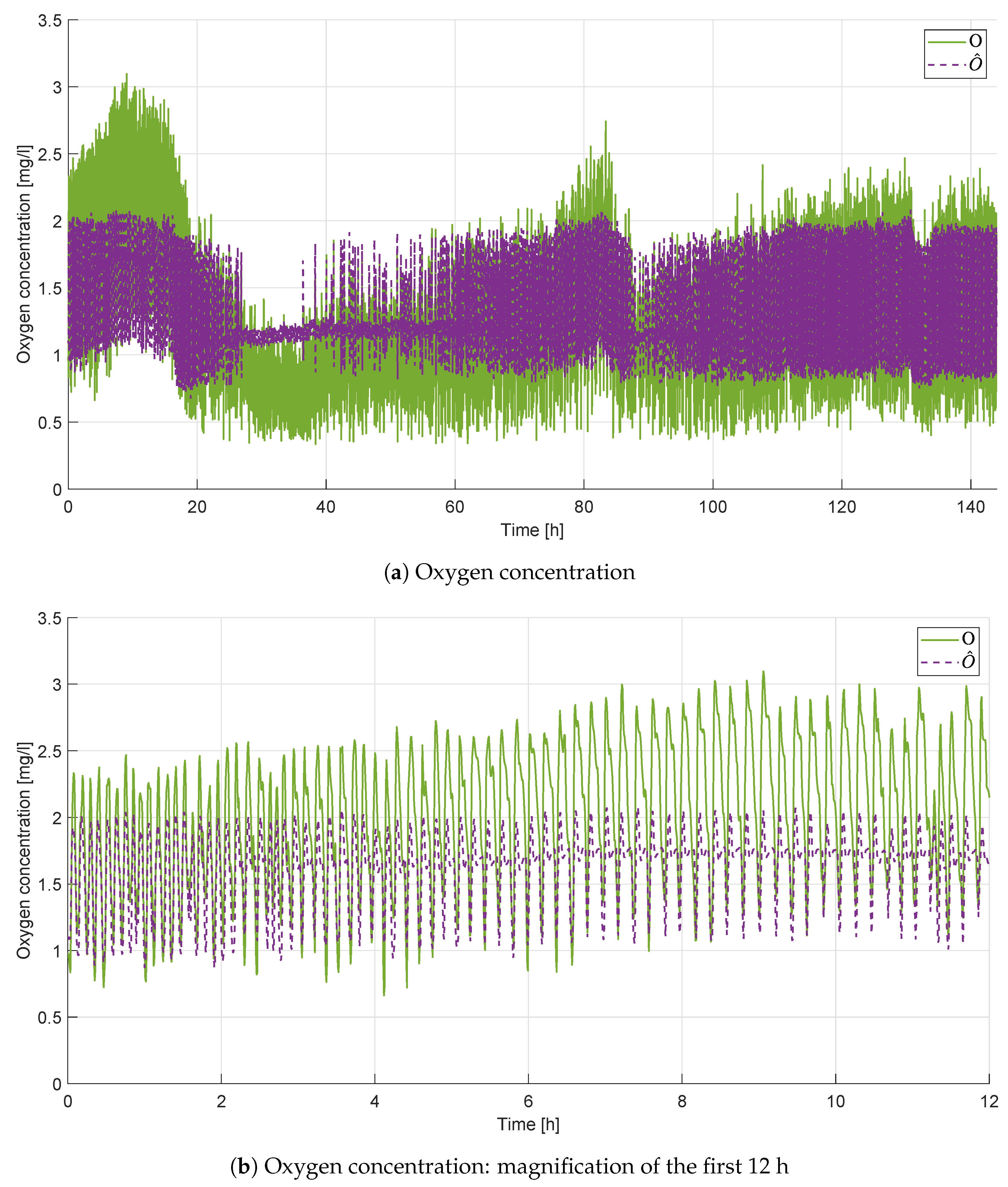
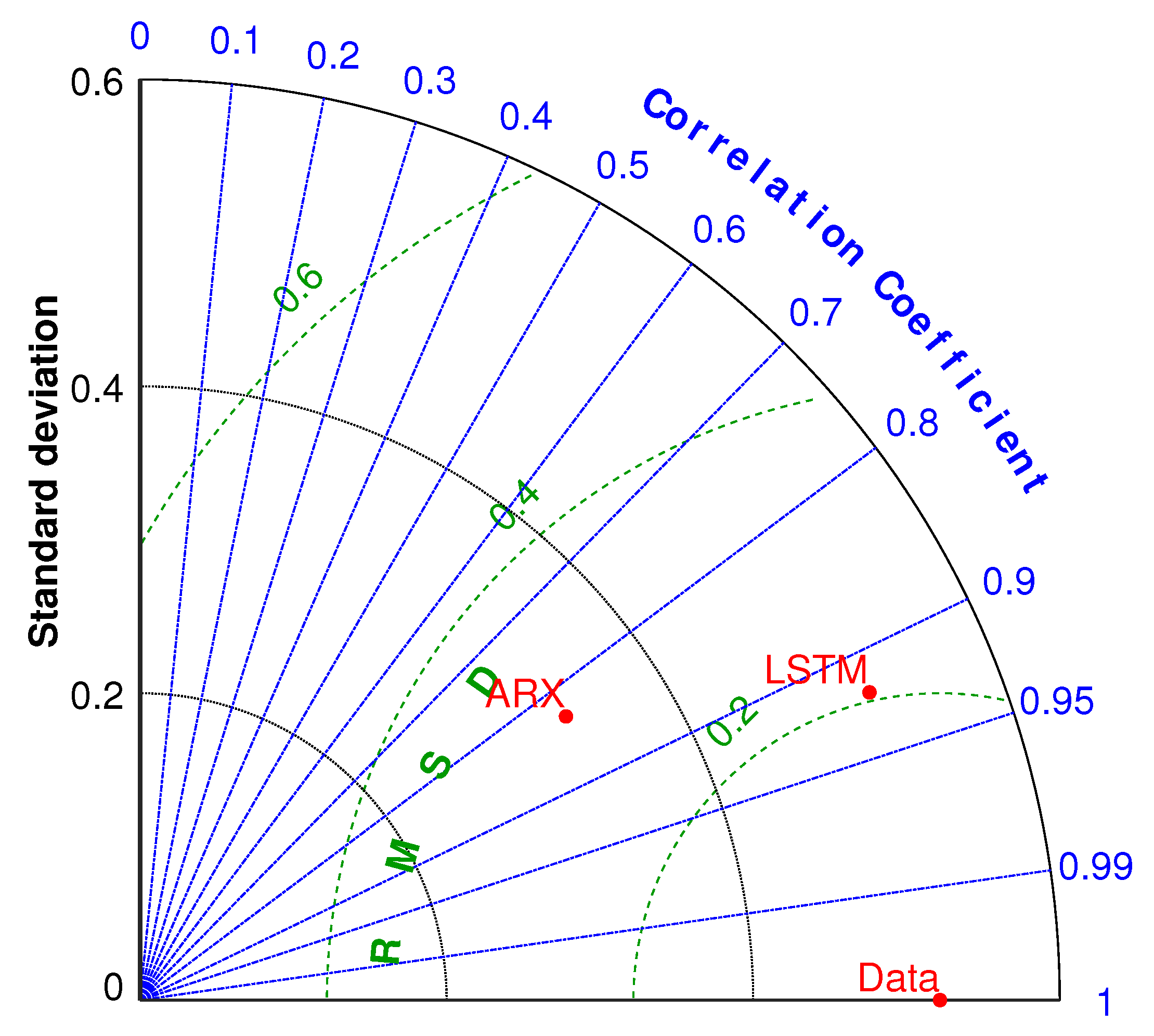
Signal	Component	Range	Selected
$O\left(t\right)$	order ($N_a$)	10–17	12
$q_{oss}\left(t\right)$	order ($N_{b1}$)	2–12	6
	delay ($d_1$)	0–5	2
$q_{in}\left(t\right)$	order ($N_{b2}$)	2–12	3
	delay ($d_2$)	0–10	5
$q_{ol}\left(t\right)$	order ($N_{b3}$)	3–9	7
	delay ($d_3$)	0–10	6

summarizes the proposed ranges.

3.3.3. Parameter Estimation

This final phase is devoted to determining the model. The structure is now known, so the whole dataset can be used to determine the best set of parameters. Moreover, this work aims to identify a model of a real plant which is intrinsically stable [3]. Therefore, the stability is enforced from a mathematical point of view, imposing:

$$(A,B)=\underset{A\left(q\right)\in H\left(N_a\right),B\left(q\right)}{arg\; min}\sum _k\parallel y_k-{\widehat{y}}_k^p\parallel$$

(7)

where $H\left(N_a\right)$ is set of the $N_a$-degree Hurwitz polynomial.

3.4. Description of Datasets

The WWTP is monitored through a Supervisory Control And Data Acquisition (SCADA) system used to manage the control protocols, alarm handling and also for data collection. From the SCADA interface, the user can have access to sensors equipped in the chemical–physical reactor (where the wastewater is pre-treated), in the biological reactor and in the two membrane bioreactors, called, respectively, MBR1 and MBR2.

In this way, the signals of interest can be downloaded. The value of $q_{in}\left(t\right)$ is obtained from the chemical–physical reactor, from which it goes as input into the biological reactor, after the preprocessing of the wastewater. In the reactor, the sensors measure the ingoing oxygen flow rate, $q_{oss}\left(t\right)$, and the oxygen concentration, $O\left(t\right)$, at a height of 4 m. Then, the measure of the output liquid substrate flow rate, $q_{ol}\left(t\right)$, is obtained from MBR1 and MBR2, as the sum of the two components that flow from the biological reactor into the two membrane bioreactors.

Lastly, $CO{D}_{in}$ is obtained through laboratory analysis, as well as $q_{om}\left(t\right)$, which is acquired daily by the operators who remove it from the reactor. These quantities are not considered in the models, not only because their values are constant, but also due to the difficulty of acquiring them. Six different datasets are collected, each one containing six days of data, as shown in

Table 2. Description of datasets.

Dataset Name	Start Date	End Date
Dataset 1	6 December 2021	11 December 2021
Dataset 2	15 December 2021	20 December 2021
Dataset 3	21 December 2021	26 December 2021
Dataset 4	27 December 2021	1 January 2022
Dataset 5	1 December 2022	6 May 2022

. All the datasets contain the three inputs and the output previously described. Dataset 1 is used as a testing dataset, while the remaining five datasets are used to train and validate the models. Because the plant’s dynamical behavior does not change during the time studied, the acquisition date of the datasets should not affect the input–output relationship. If the dynamic is correctly estimated by the models, they should present satisfactory results on all the acquired datasets, not being dependent on the acquisition date. For this reason, this partition between testing and training/validation results is reasonable.

Due to the privacy policy, the full description of the data is not available. Nevertheless, it is possible to present the conditioned data (see Section 3.3.1) without revealing the working point.

Table 3. Description of signals: mean (variance).

Dataset Name	$\mathit{\delta }\mathit{O}$	$\mathit{\delta }{\mathit{q}}_{\mathbf{oss}}$	$\mathit{\delta }{\mathit{q}}_{\mathbf{in}}$	$\mathit{\delta }{\mathit{q}}_{\mathbf{ol}}$
Dataset1	−0.0054 (0.2724)	−0.4061 (3355)	−0.5910 (25.58)	0.1471 (2.9851)
Dataset2	−0.3214 (0.1863)	24.0992 (1608)	−0.7720 (47.79)	−0.3733 (4.5006)
Dataset3	0.0618 (0.2406)	−14.1781 (3378)	−1.0119 (49.85)	−1.1114 (5.4282)
Dataset4	0.2023 (0.2633)	−25.0323 (3423)	−1.1772 (46.95)	−1.4870 (4.7857)
Dataset5	0.1414 (0.3130)	−4.2068 (4826)	0.8875 (48.54)	0.8547 (5.9122)
Dataset6	−0.0841 (0.2038)	19.3180 (3739)	2.0735 (85.26)	2.1169 (6.7172)

shows the average and the variance of such signals.

The first and second central moments of the six datasets, although similar, present differences that are not negligible. This fact can be explained by considering the normal data variability through the practice of a real plant. In fact, in the considered weeks, the waste showed different compositions, the membranes had different occlusions, the reactor had a small stop for maintenance, and these or other elements can affect the measurements.

3.5. Performance Indexes

Three performance indexes are considered:

• Index of fitting ($FIT$): normalized index that indicates how much the prediction matches the real data. For a perfect prediction, it is equal to 100%, and it can also be negative. It is expressed as:

  $$FIT=100(1-\frac{{\sum }_{k=1}^S||{\widehat{y}}_k-y_k||}{{\sum }_{k=1}^S||y_k-{\overline{y}}_k||})$$

  (8)
• Pearson correlation coefficient ($\rho$): measures the linear correlation between two variables and has a value between −1 (total negative correlation) and +1 (total positive correlation).

  $$\rho =\frac{{\sum }_{k=1}^S(y_k-\overline{y})({\widehat{y}}_k-\overline{\widehat{y}})}{||y_k-\overline{y}||||{\widehat{y}}_k-\overline{\widehat{y}}||}$$

  (9)
• Root Mean Squared Error ($RMSE$): shows the Euclidean distance of the predictions from the real data using

  $$RMSE=\sqrt{\frac{1}{S}{\displaystyle \sum _{k=1}^S}{(y_k-{\widehat{y}}_k)}^2}$$

  (10)

where y is the vector of the real data, $\widehat{y}$ of the predicted ones, containing S elements each, and $\overline{y}$ and $\overline{\widehat{y}}$ are their respective mean values.

The training and validation of the models are performed on five datasets (Dataset 2–Dataset 6) for a total amount of thirty days, and tested on the remaining one, Dataset 1.

4. Results

Due to privacy compliance, the working point of the plant is not made fully available: only the oxygen concentration is shown and available as full data ($\overline{O}=1.3167$ mg/L). This choice preserves the privacy of the company that provided the data, and allows a complete comparison of the results.

The performance of the two approaches will be presented individually and compared in the following sections.

4.1. LSTM Results

The LSTM network proposed in this work presents an architecture composed by a single-layer LSTM network with 160 neurons, trained for 1000 epochs, using the Adam optimizer with learning rate $\alpha =0.002$ and Mean Squared Error (MSE) loss function defined as:

$$MSE=\frac{1}{S}\sum _{k=1}^S{({\widehat{y}}_k-y_k)}^2$$

(11)

The values of the hyperparameters were obtained through an optimization procedure with KerasTuner [36], employing the $\mathtt{RandomSearch}$ algorithm, with the number of neurons spanning the range [32; 512] and the learning rate in the range [0.001; 0.01].

The LSTM architecture proposed in this work has the final goal of being used for control purposes, so the minimization of complexity is one of the required features, and only a single-layer LSTM network is considered. The selected LSTM network has 160 neurons and a learning rate of 0.002.

The training of the network is performed on a computer with an Intel i9-10920X CPU with 3.50 GHz, with a GPU NVIDIA GeForce RTX 2080Ti graphics processing unit; it was written in Python 3.9, using TensorFlow [37], Keras API [38] and KerasTuner [36]. The results are quite satisfying, with $FIT=60.56\%$, $\rho =0.921$ and $RMSE=0.206$ mg/L. An example of the prediction obtained with the LSTM network is reported in Figure 2, with a global overview in Figure 2a and a closer detail of the first 12 h in Figure 2b, to better emphasize the accuracy of the result. It can be observed that both the global dynamic of the signal and the oscillation frequencies are correctly reproduced, with an overall satisfactory outcome.

Between hours 30 and 37, the performances are degradated because the LSTM model underestimates the real data. Additional information on the plant could explain the sources of uncertainties or highlight additional inputs that affect the system behavior.

4.2. ARX

The procedure described in Section 3.3 was conducted using the System Identification Toolbox of Matlab [39].

Table 1 (last column) reports the structures of the model selected by the procedure. The identified model was used to simulate the testing dataset. Figure 3a shows the comparison between the actual oxygen concentration and the predicted one. The oscillation frequencies and the overall behavior are correctly estimated ($\rho =0.833>0.7$), but the model fails in reaching the correct amplitude ($FIT=41.20\%<60\%$ and $RMSE=0.307$ mg/L). These results are emphasized in the magnification reported in Figure 3b and summarized by the performance indicators.

4.3. Discussion

The performance indexes are reported in

Table 4. Model comparison, results from Dataset1 simulation.

Index	ARX	LSTM
$FIT$ [%]	41.20	60.56
$\rho$	0.833	0.921
$RMSE$ [mg/L]	0.307	0.206

for both of the presented techniques.

Figure 4 emphasizes the comparison of the two techniques by showing the first 6 h. This magnification makes it evident that the LSTM model is able to follow the peaks better with respect to the ARX model, which, in particular, underestimates the maximum values in this subsection.

The quality of the predictions can be evaluated through the use of different indices, but a compact way to represent them all together is proposed here. In order to compare the proposed LSTM and the classic ARX models, the Taylor diagram [40] is considered. It graphically summarizes the similarity between a predicted pattern and the observations. Their similarity is quantified in terms of their correlation, their centered Root-Mean-Square Difference (RMSD) and the amplitude of their variations (standard deviation). These diagrams are especially useful in evaluating multiple aspects of complex models at the same time, because the Taylor diagram can represent three different statistics simultaneously in a two-dimensional space. A point is assigned to each model, and its position quantifies how closely that model’s predictions match the observations. In the Taylor diagram, the model with better performance will lie nearest to the point marked “Data”, showing which prediction better represents the observations.

From this diagram, represented in Figure 5, it is clear that the LSTM model outperforms the ARX model: the LSTM model presents a lower correlation coefficient and lower RMSD, and has a standard deviation more similar to the observed one, with respect to the ARX model.

In Section 3.4, the variability of the datasets was attributed to different working conditions. Probably, a proper data classification that isolates plant stops and abnormal conditions will result in better performances for both models, and in particular, for linear models such as the ARX considered in this work. On the other hand, the nonlinearity of the LSTM can include and naturally estimate the different dynamics connected to abnormal but frequent conditions. In this case, the LSTM is able to represent the general dynamics of the process under study without requiring a working point estimation or a model switching.

5. Conclusions

This work proposes the use of an LSTM network to identify an input–output model suitable for the design of an oxygen concentration controller in an activated sludge process to treat municipal and industrial wastewater. Several ML methods present in the literature show that it is possible to maximize the knowledge extracted from data and operator experience; the idea of this paper is to identify an LSTM network for a specific WWTP and subsequently apply it to improve the control of the plant without the process knowledge required by white-box models.

The model is identified using easily accessible measures collected from a real plant located in Mortara, Italy. The LSTM network showed satisfactory performance, being able to capture both the oscillation frequencies and the overall behavior ($\rho =0.921$ and $FIT=60.56\%$). It also exceeds the performance of a classic ARX ($\rho =0.833$ and $FIT=41.20\%$), which is not able to reach the correct amplitude. The main limitation of this work lies in the use of datasets coming from a specific plant, which does not ensure generality. Moreover, other, more complex architectures could be used to obtain better results and are proposed as future development.

The design of a controller based on the LSTM model presented in this work is proposed as a future development. Moreover, the authors are exploring the possibility of properly classifying the dataset by labeling the data in collaboration with the company, in order to exclude abnormal events and then evaluate the improvements of the two models.