Optimizing the Powder Metallurgy Parameters to Enhance the Mechanical Properties of Al-4Cu/xAl2O3 Composites Using Machine Learning and Response Surface Approaches
Abstract
1. Introduction
2. Methodology
2.1. Experimental Design
2.2. Experimental Procedure
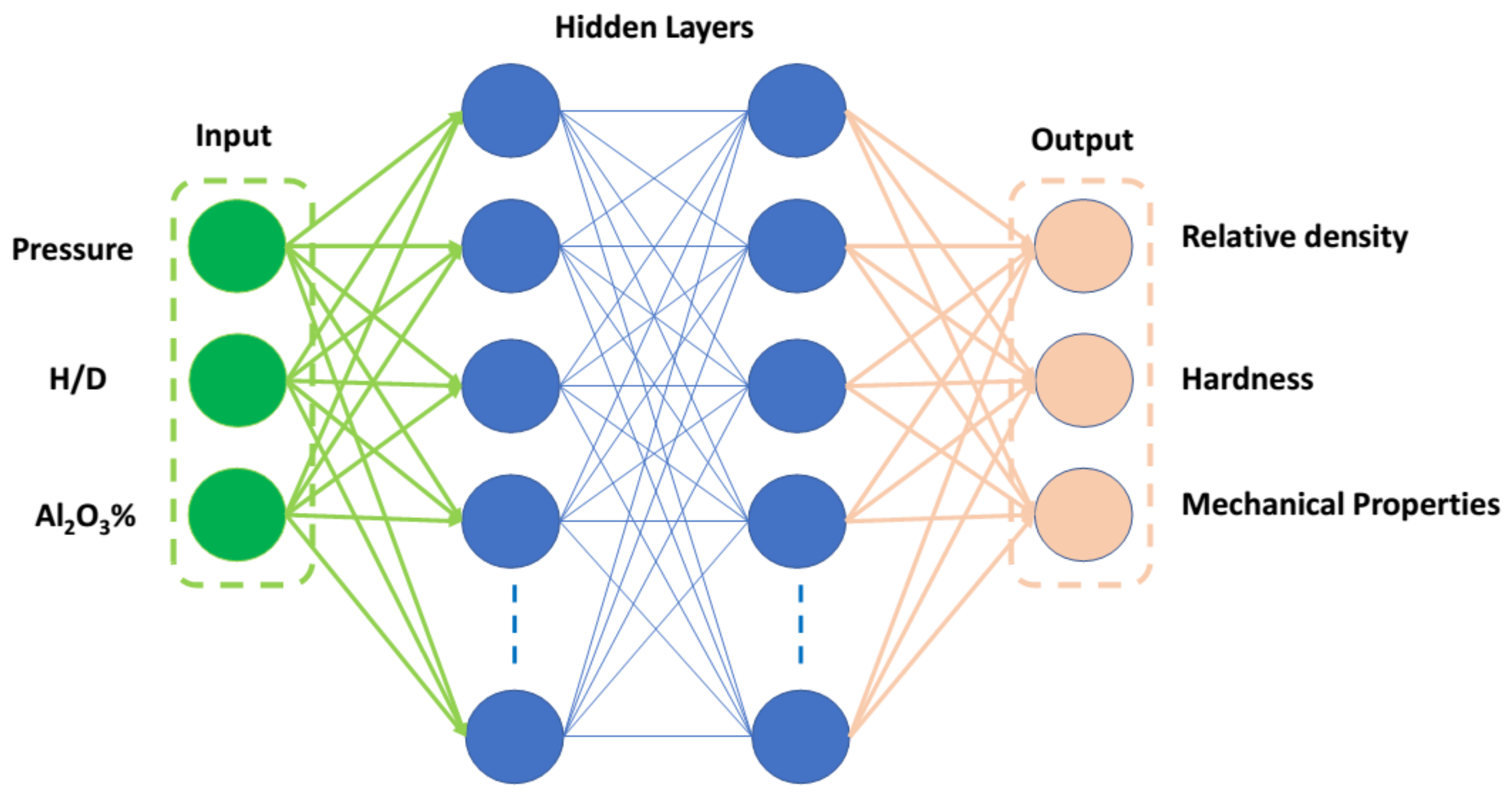
2.3. Machine Learning (ML)
2.3.1. Linear Regression
2.3.2. Regression Trees
2.3.3. Random Forest Regression
2.3.4. Gaussian Process Regression
2.3.5. Artificial Neural Networks
2.4. Statistical Analysis and Regression Model
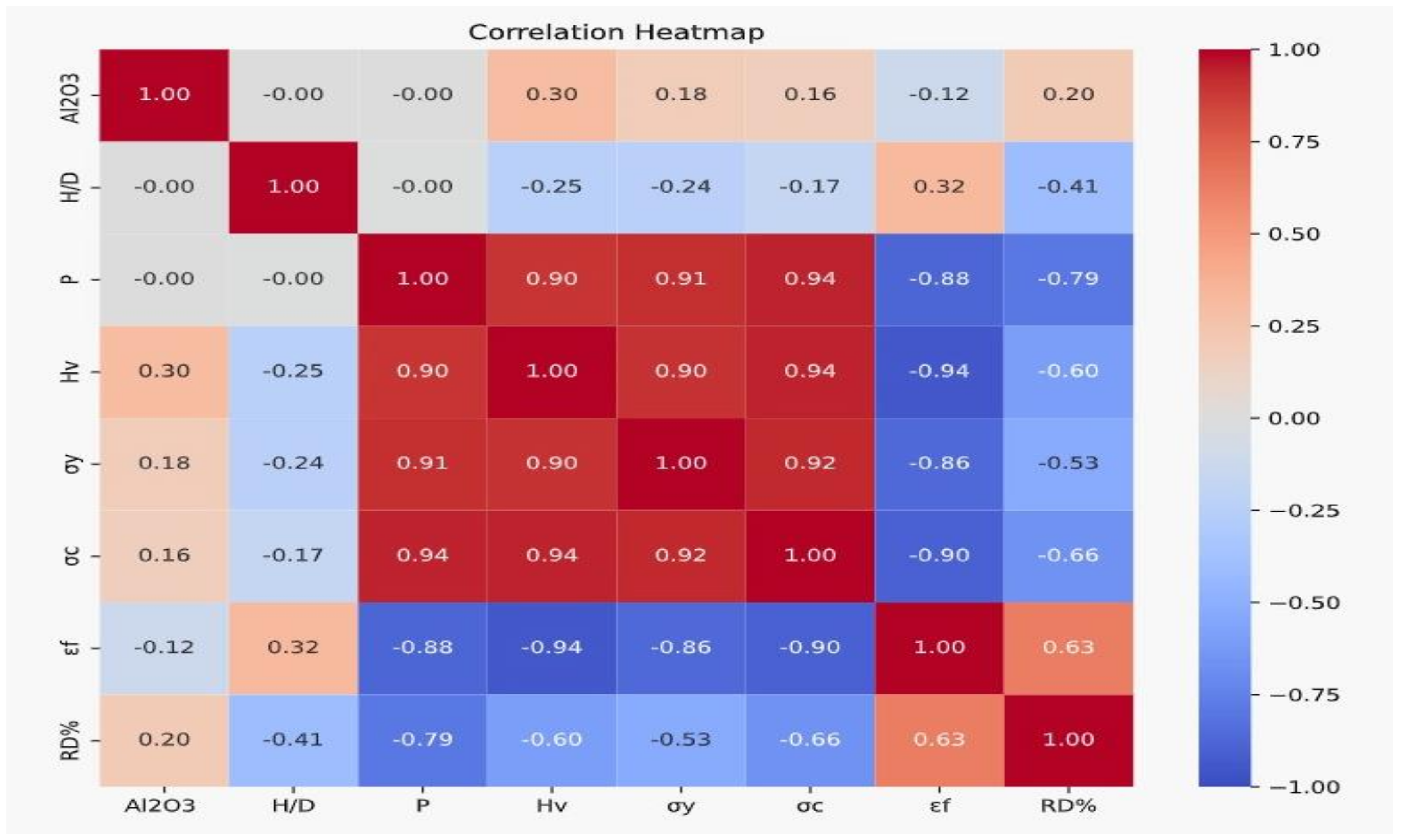
3. Results and Discussion
3.1. Relative Density (RD)
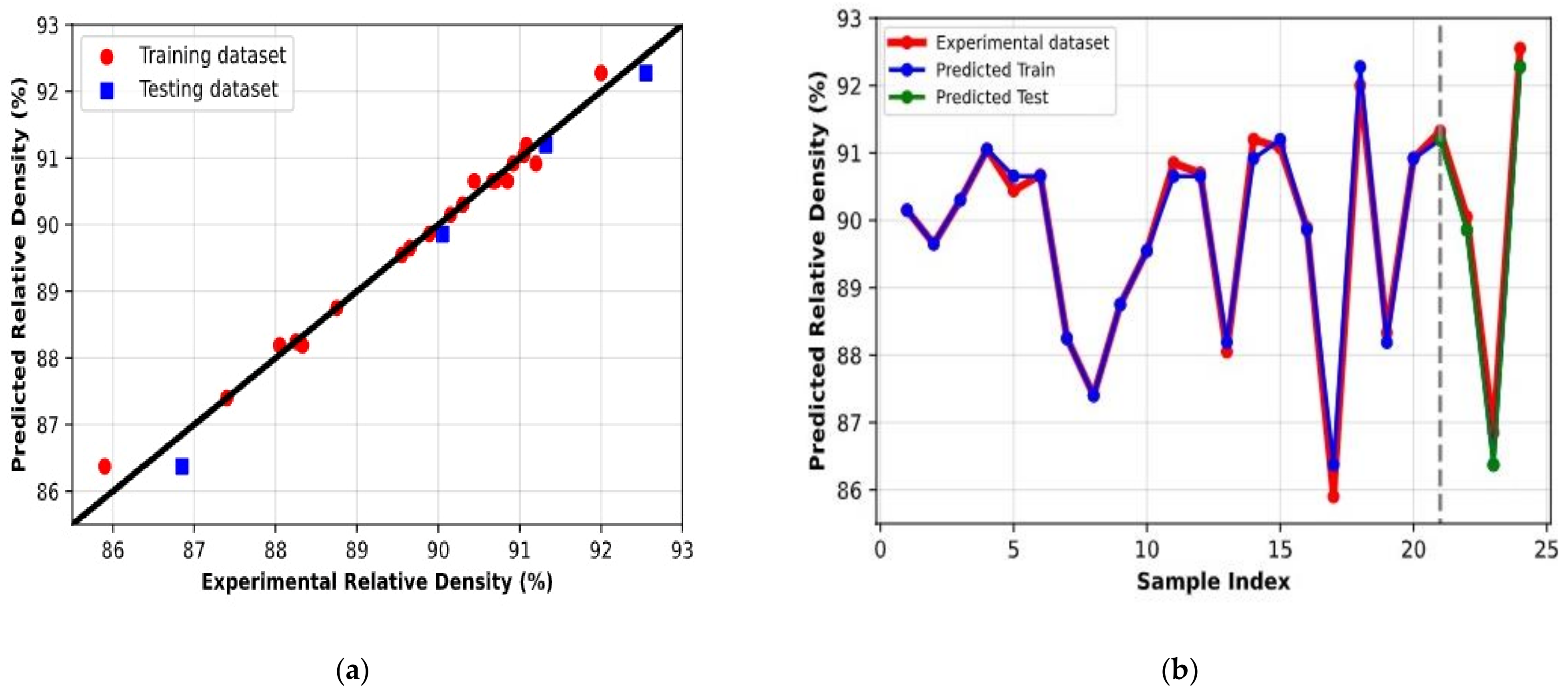
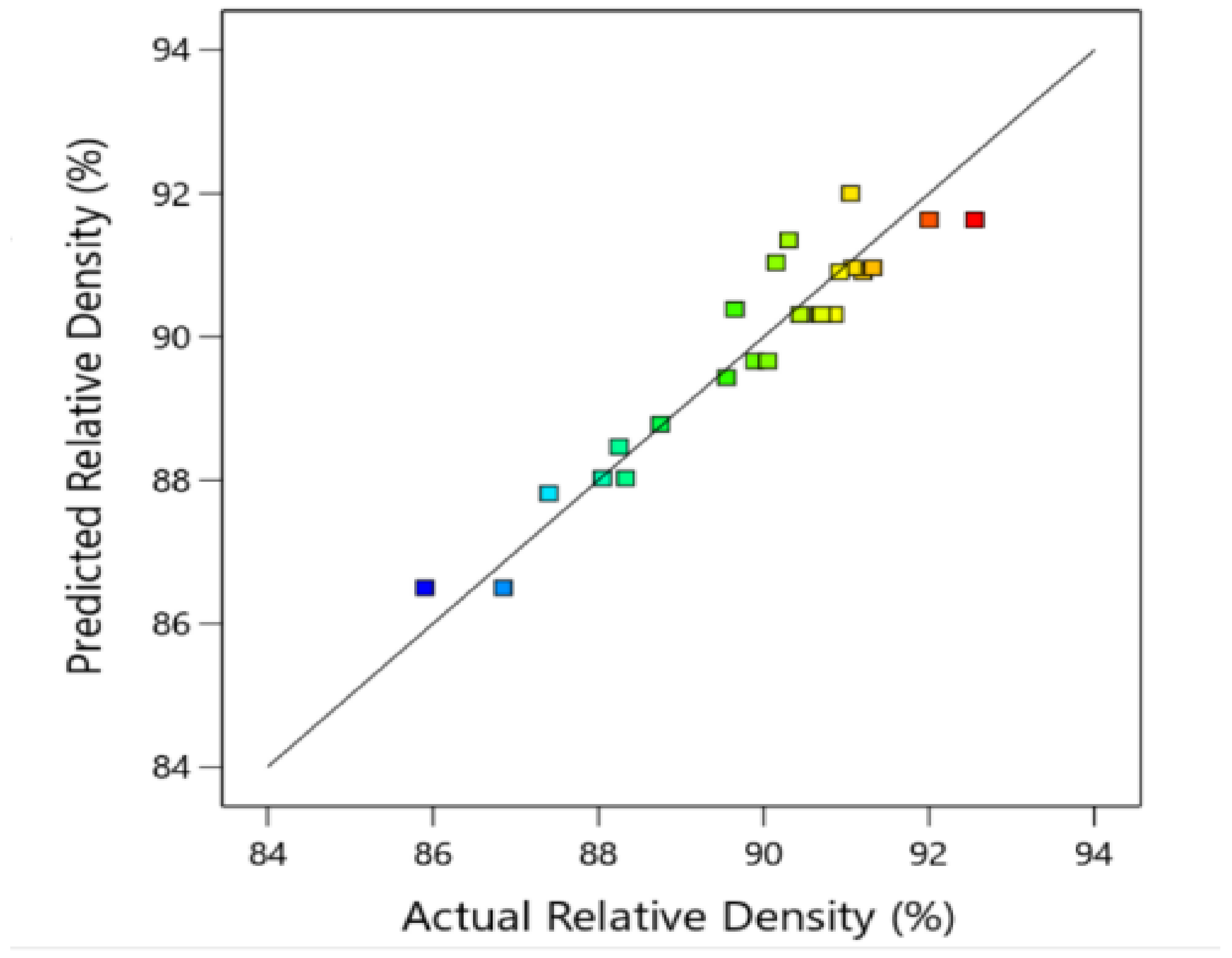
3.1.1. Machine Learning Prediction Models of RD
3.1.2. Regression Models and 3D Plots of RD
3.1.3. Optimization of RD
3.2. Hardness Distribution
3.2.1. Machine Learning Prediction Models of Hardness Distribution
3.2.2. Regression Models and 3D Plots of Hardness Distribution
3.2.3. Optimization of Hardness
3.3. Compression Properties
3.3.1. Machine Learning Prediction Models of Compression Distribution
3.3.2. Regression Models and 3D Plots of Compression Distribution
3.3.3. Optimization Results
4. Conclusions
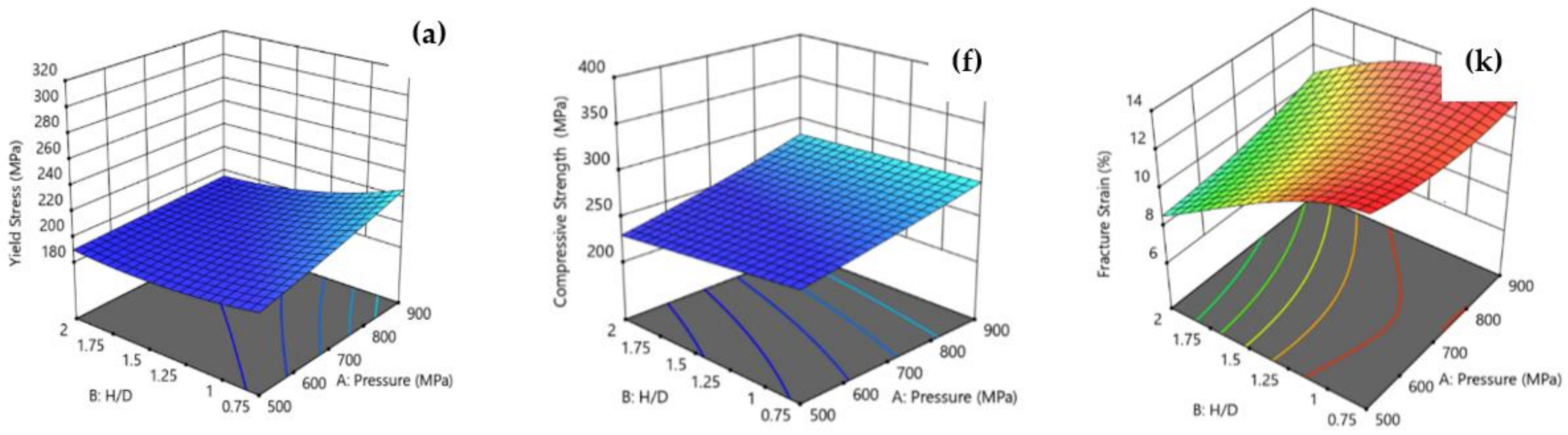
- The maximum RD obtained experimentally reached a value of 92.55% when the pressure was set at 700 MPa and the H/D was 1.25 for the Al-4Cu discs with no Al2O3;
- The RSM optimization findings confirm the maximum value of 92.791% and led the optimal AMC conditions to be a pressure = 893.89 MPa, H/D = 0.854, and Al2O3% = 0.031%;
- The outcomes of the RSM optimization performed on the hardness gave a maximum value of 121.199 Hv and led the optimal AMC conditions to be a pressure = 875.087 MPa, H/D = 0.87, and Al2O3% = 9.845%;
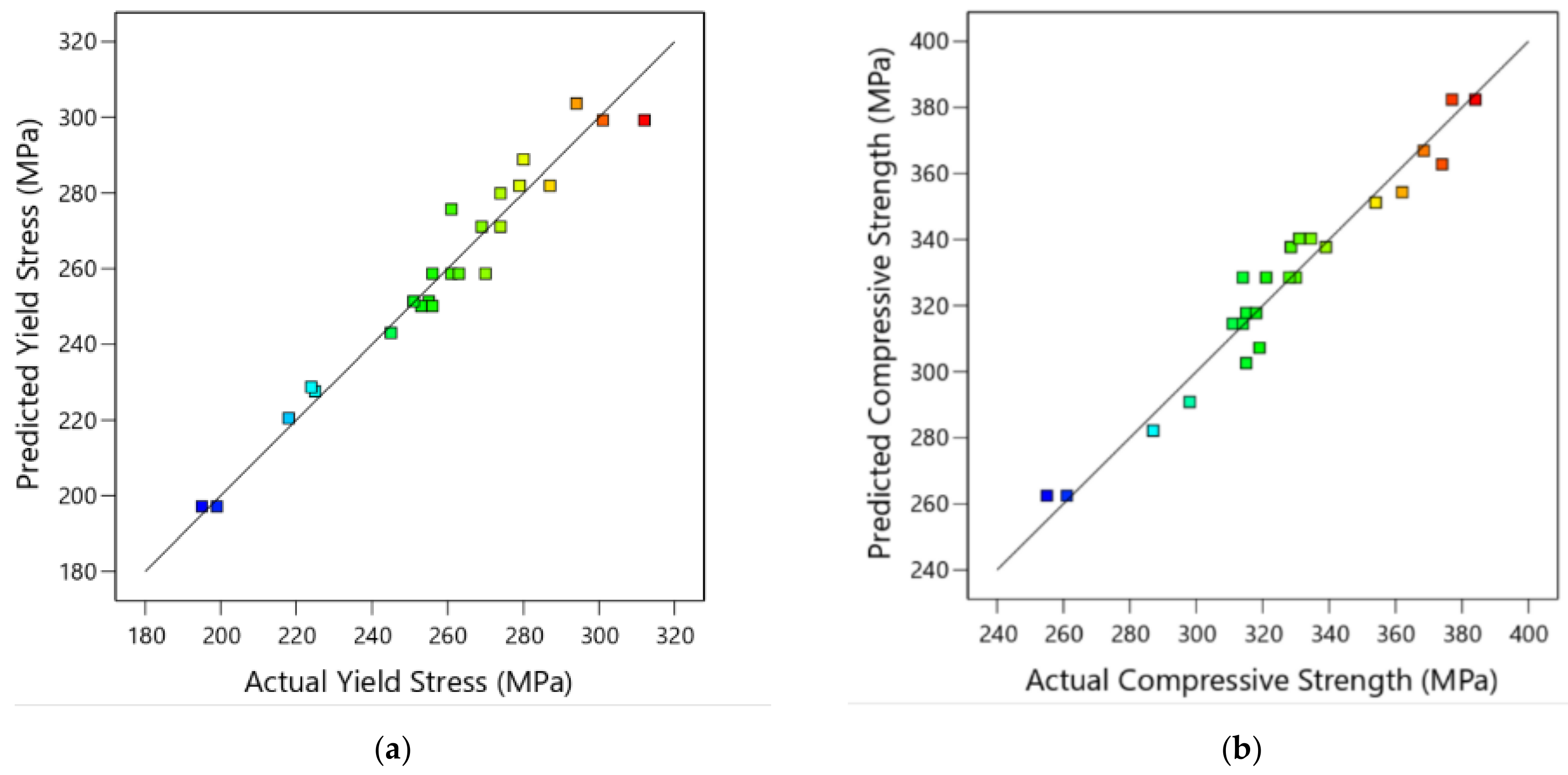
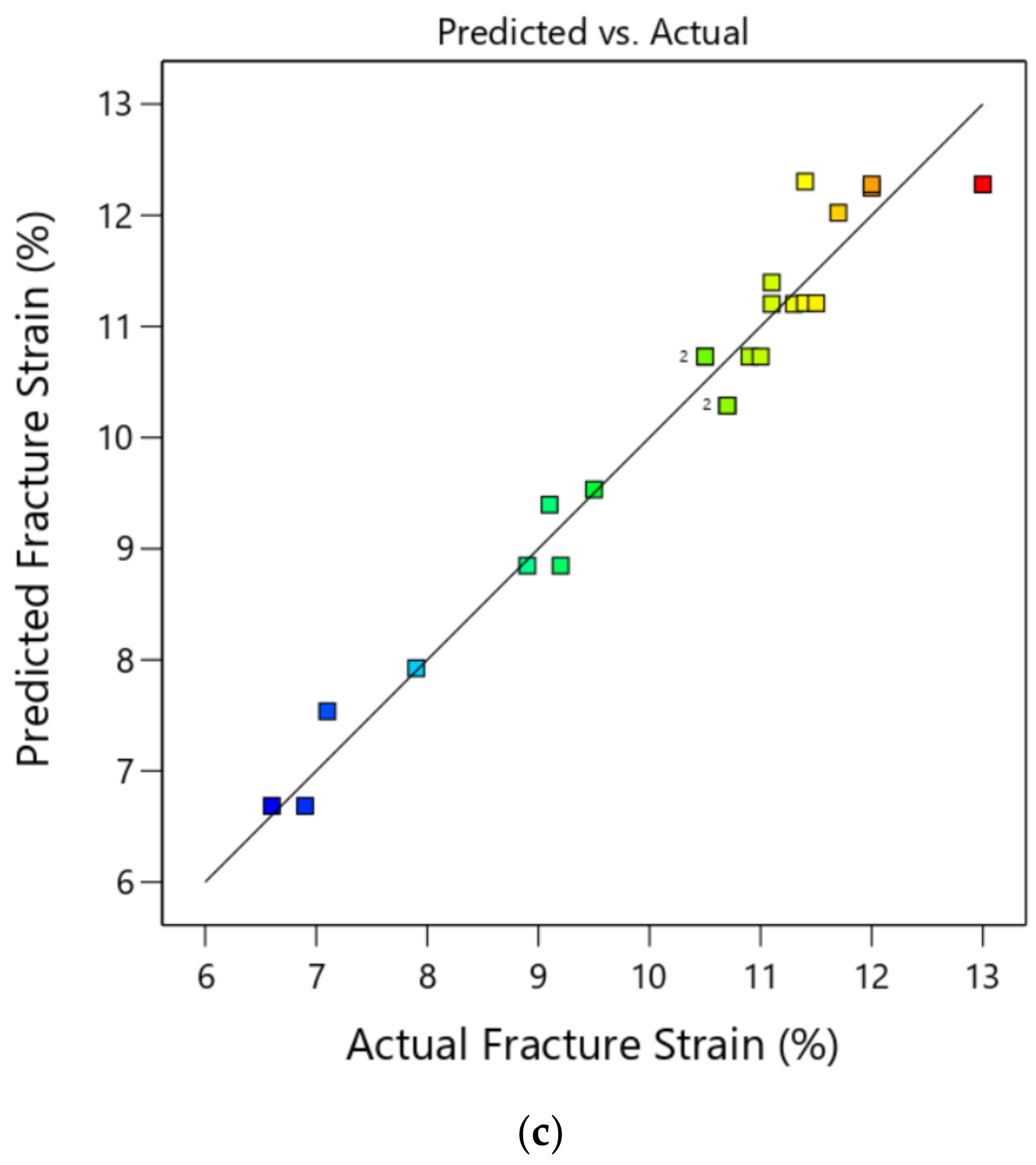
- The best yield strength obtained experimentally had a value of 312 MPa at 10% Al2O3, 700 MPa, and a 1.25 H/D, whereas the best compression strength obtained experimentally had a value of 384 MPa at 10% Al2O3, 700 MPa, and a 1.25 H/D. Moreover, the maximum fracture strain obtained experimentally had a value of 13 at 700 MPa, a 1.25 H/D, and 0% Al2O3;
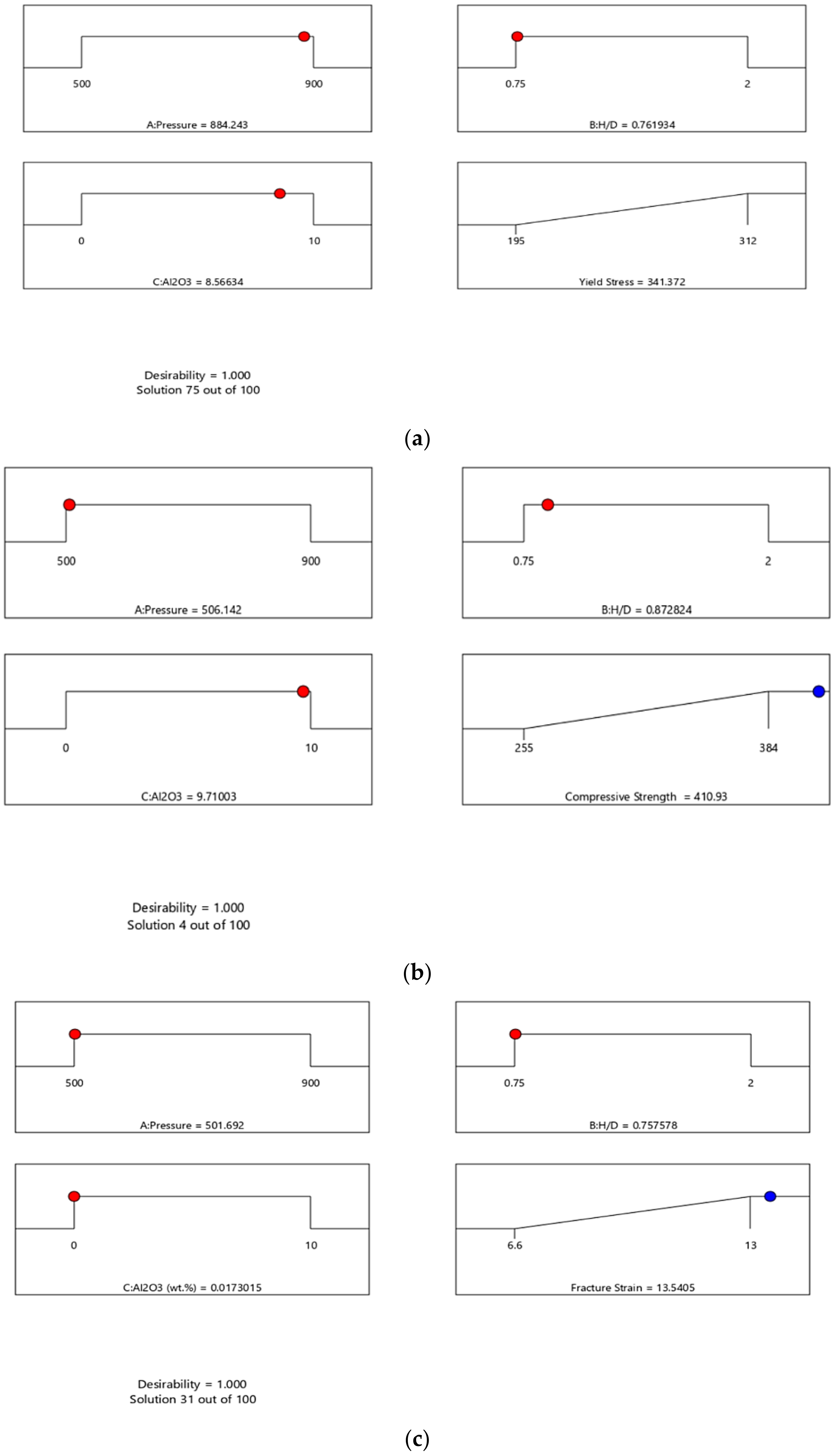
- The outcomes of the RSM optimization performed on the yield strength gave a maximum value of 341.372 MPa and led the optimal AMC conditions to be a pressure = 884.2 MPa, H/D = 0.762, and Al2O3% = 8.57%;
- The RSM optimization findings show a maximum value of the compressive strength of 410.93 MPa, which led the optimal AMC conditions to be a pressure = 506.142 MPa, H/D = 0.873, and Al2O3% = 9.71%;
- The outcomes of the RSM optimization performed on the fracture strain gave a maximum of 13.54 and led the optimal AMC conditions to be a pressure = 501.692 MPa, H/D = 0.757, and Al2O3% = 0.017%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Exp. No. | Hardness Hv | Yield Stress σy | Compressive Strength σuc | Fracture Strain εf | RD (%) |
|---|---|---|---|---|---|
| 1 | 69.5 | 225 | 315 | 11.7 | 90.15 |
| 2 | 64 | 218 | 287 | 12 | 89.65 |
| 3 | 68 | 224 | 298 | 11.4 | 90.30 |
| 4 | 72.5 | 245 | 319 | 11.1 | 91.05 |
| 5 | 74 | 256 | 314 | 10.5 | 90.44 |
| 6 | 77.5 | 261 | 330 | 10.9 | 90.67 |
| 7 | 88.5 | 274 | 362 | 9.1 | 88.25 |
| 8 | 84 | 261 | 354 | 9.5 | 87.40 |
| 9 | 91 | 280 | 368.5 | 7.9 | 88.75 |
| 10 | 99 | 294 | 374 | 7.1 | 89.55 |
| 11 | 79 | 270 | 328 | 11 | 90.85 |
| 12 | 77 | 263 | 321 | 10.5 | 90.70 |
| 13 | 69 | 255 | 311 | 11.3 | 88.05 |
| 14 | 82 | 279 | 339 | 8.9 | 91.20 |
| 15 | 86 | 274 | 334.5 | 10.7 | 91.08 |
| 16 | 66 | 253 | 315 | 11.4 | 89.89 |
| 17 | 105.5 | 301 | 377 | 6.9 | 85.90 |
| 18 | 59 | 195 | 255 | 12 | 92.00 |
| 19 | 69 | 251 | 314 | 11.1 | 88.33 |
| 20 | 80.5 | 287 | 328.5 | 9.2 | 90.92 |
| 21 | 84 | 269 | 331 | 10.7 | 91.32 |
| 22 | 68 | 256 | 318 | 11.5 | 90.05 |
| 23 | 108 | 312 | 384 | 6.6 | 86.85 |
| 24 | 57.5 | 199 | 261 | 13 | 92.55 |
References
- Rajan, K. Materials informatics. Mater. Today 2005, 8, 38–45. [Google Scholar] [CrossRef]
- Goulding, A.N.; Leung, J.F.W.; Neu, R.W. Communicating Materials Systems Knowledge through Processing-Structure-Properties-Performance (PSPP) Maps; Georgia Institute of Technology: Atlanta, GA, USA, 2018. [Google Scholar]
- Koli, D.K.; Agnihotri, G.; Purohit, R. A Review on Properties, Behaviour and Processing Methods for Al- Nano Al2O3 Composites. Procedia Mater. Sci. 2014, 6, 567–589. [Google Scholar] [CrossRef]
- Gireesh, C.H.; Prasad, K.D.; Ramji, K.; Vinay, P. Mechanical Characterization of Aluminium Metal Matrix Composite Reinforced with Aloe vera powder. Mater. Today Proc. 2018, 5, 3289–3297. [Google Scholar] [CrossRef]
- Miracle, D. Metal matrix composites—From science to technological significance. Compos. Sci. Technol. 2005, 65, 2526–2540. [Google Scholar] [CrossRef]
- Kai, X.; Li, Z.; Fan, G.; Guo, Q.; Tan, Z.; Zhang, W.; Su, Y.; Lu, W.; Moon, W.-J.; Zhang, D. Strong and ductile particulate reinforced ultrafine-grained metallic composites fabricated by flake powder metallurgy. Scr. Mater. 2013, 68, 555–558. [Google Scholar] [CrossRef]
- Asgharzadeh, H.; Sedigh, M. Synthesis and mechanical properties of Al matrix composites reinforced with few-layer graphene and graphene oxide. J. Alloy. Compd. 2017, 728, 47–62. [Google Scholar] [CrossRef]
- Nassef, A.; El-Garaihy, W.H.; El-Hadek, M. Mechanical and Corrosion Behavior of Al-Zn-Cr Family Alloys. Metals 2017, 7, 171. [Google Scholar] [CrossRef]
- Nassef, A.; El-Garaihy, W.H.; El-Hadek, M. Characteristics of Cold and Hot Pressed Iron Aluminum Powder Metallurgical Alloys. Metals 2017, 7, 170. [Google Scholar] [CrossRef]
- El-Garaihy, W.; El Rassoul, E.-S.A.; Al Ateyah, A.; Alaskari, A.M.; Oraby, S. Data Manipulation Approach and Parameters Interrelationships of the High-Pressure Torsion for AA6061-15%SiCp Composite. SAE Int. J. Mater. Manuf. 2018, 11, 167–182. [Google Scholar] [CrossRef]
- Aljohani, T.A.; Alawad, M.O.; Elkatatny, S.; Alateyah, A.I.; Bin Rubayan, M.T.; Alhajji, M.A.; AlBeladi, M.I.; Khoshnaw, F.; El-Garaihy, W.H. Electrochemical Behavior of SiC-Coated AA2014 Alloy through Plasma Electrolytic Oxidation. Materials 2022, 15, 3724. [Google Scholar] [CrossRef]
- Seleman, M.M.E.; Ahmed, M.M.Z.; Ataya, S.; Mohamed, M. El-Sayed Seleman, Mohamed, M.Z.; Ahmed, S.A. Microstructure and Mechanical Properties of Hot Extruded 6016 Aluminum Alloy/Graphite Composites. J. Mater. Sci. Technol. 2018, 34, 1580–1591. [Google Scholar] [CrossRef]
- Kaykılarlı, C.; Küçükelyas, B.; Akçamlı, N.; Uzunsoy, D.; Cansever, N. Processing and Characterization of Al-4Cu Matrix Composites Reinforced with Few Layered Graphene. Trans. Indian Inst. Met. 2022, 75, 2379–2388. [Google Scholar] [CrossRef]
- Gökçe, A.; Findik, F.; Kurt, A.O. Effects of Sintering Temperature and Time on the Properties of Al-Cu PM Alloy. Pract. Metallogr. 2017, 54, 533–551. [Google Scholar] [CrossRef]
- El-Katatny, S.M.; Nassef, A.E.; El-Domiaty, A.; El-Garaihy, W.H. Fundamental analysis of cold die compaction of reinforced aluminum powder. Int. J. Eng. Tech. Res. 2015, 3, 180–184. [Google Scholar]
- Wolla, D.W.; Davidson, M.J.; Khanra, A. Studies on the formability of powder metallurgical aluminum–copper composite. Mater. Des. 2014, 59, 151–159. [Google Scholar] [CrossRef]
- Seleman, M.M.E.-S.; Ataya, S.; Ahmed, M.M.Z.; Hassan, A.M.M.; Latief, F.H.; Hajlaoui, K.; El-Nikhaily, A.E.; Habba, M.I.A. The Additive Manufacturing of Aluminum Matrix Nano Al2O3 Composites Produced via Friction Stir Deposition Using Different Initial Material Conditions. Materials 2022, 15, 2926. [Google Scholar] [CrossRef]
- Kumar, A.; Gautam, R.K.; Tyagi, R. Dry sliding wear characteristics of in situ synthesized Al-TiC composites. Compos. Interfaces 2016, 23, 469–480. [Google Scholar] [CrossRef]
- Seydibeyoglu, M.O.; Dispinar, D.; Aybarc, U. Aluminum Metal Matrix Composites with SiC, Al2O3 and Graphene—Review. Arch. Foundry Eng. 2018, 18, 5–10. [Google Scholar]
- Rohatgi, P.K.; Kumar, P.A.; Chelliah, N.M.; Rajan, T.P.D. Solidification Processing of Cast Metal Matrix Composites Over the Last 50 Years and Opportunities for the Future. JOM 2020, 72, 2912–2926. [Google Scholar] [CrossRef]
- Ae, N. Application of Response Surface Methodology in Optimizing the Cold Compaction Parameters of Al-4Cu-xAl2O3 Composites. Adv. Metall. Mater. Eng. 2019, 2, 71–80. [Google Scholar]
- Butler, K.T.; Davies, D.W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine learning for molecular and materials science. Nature 2018, 559, 547–555. [Google Scholar] [CrossRef] [PubMed]
- Mahmoud, S.M.A.S.; Faraji, G.; Baghani, M.; Hashemi, M.S.; Sheidaei, A.; Baniassadi, M. Design of Refractory Alloys for Desired Thermal Conductivity via AI-Assisted In-Silico Microstructure Realization. Materials 2023, 16, 1088. [Google Scholar] [CrossRef] [PubMed]
- Kordijazi, A.; Zhao, T.; Zhang, J.; Alrfou, K.; Rohatgi, P. A Review of Application of Machine Learning in Design, Synthesis, and Characterization of Metal Matrix Composites: Current Status and Emerging Applications. JOM 2021, 73, 2060–2074. [Google Scholar] [CrossRef]
- Shen, C.; Wang, C.; Wei, X.; Li, Y.; van der Zwaag, S.; Xu, W. Physical metallurgy-guided machine learning and artificial intelligent design of ultrahigh-strength stainless steel. Acta Mater. 2019, 179, 201–214. [Google Scholar] [CrossRef]
- Stricker, M.; Yin, B.; Mak, E.; Curtin, W.A. Machine learning for metallurgy II. A neural-network potential for magnesium. Phys. Rev. Mater. 2020, 4, 103602. [Google Scholar] [CrossRef]
- Shaban, M.; Alateyah, A.I.; Alsharekh, M.F.; Alawad, M.O.; BaQais, A.; Kamel, M.; Alsunaydih, F.N.; El-Garaihy, W.H.; Salem, H.G. Influence of ECAP Parameters on the Structural, Electrochemical and Mechanical Behavior of ZK30: A Combination of Experimental and Machine Learning Approaches. J. Manuf. Mater. Process. 2023, 7, 52. [Google Scholar] [CrossRef]
- Shaban, M.; Alsharekh, M.F.; Alsunaydih, F.N.; Alateyah, A.I.; Alawad, M.O.; BaQais, A.; Kamel, M.; Nassef, A.; El-Hadek, M.A.; El-Garaihy, W.H. Investigation of the Effect of ECAP Parameters on Hardness, Tensile Properties, Impact Toughness, and Electrical Conductivity of Pure Cu through Machine Learning Predictive Models. Materials 2022, 15, 9032. [Google Scholar] [CrossRef]
- Marchand, D.; Curtin, W.A. Machine learning for metallurgy IV: A neural network potential for Al-Cu-Mg and Al-Cu-Mg-Zn. Phys. Rev. Mater. 2022, 6, 053803. [Google Scholar] [CrossRef]
- Kamal, T.; Gouthama; Upadhyaya, A. Machine Learning Based Sintered Density Prediction of Bronze Processed by Powder Metallurgy Route. Met. Mater. Int. 2022, 29, 1761–1774. [Google Scholar] [CrossRef]
- Harsha, N.; Raju, K.S.R.; Ramana, V.V.; Reddy, V. Fabrication and prediction of tensile strength of Al-Al2O3 nano composites. Mater. Today Proc. 2019, 18, 2197–2200. [Google Scholar] [CrossRef]
- Banerjee, T.; Dey, S.; Sekhar, A.P.; Datta, S.; Das, D. Design of Alumina Reinforced Aluminium Alloy Composites with Improved Tribo-Mechanical Properties: A Machine Learning Approach. Trans. Indian Inst. Met. 2020, 73, 3059–3069. [Google Scholar] [CrossRef]
- Jokhio, M.H.; Panhwer, M.I.; Unar, M.A. Modeling Mechanical Properties of Aluminum Composite Produced Using Stir Casting Method. arXiv 2016, arXiv:1605.09691. [Google Scholar] [CrossRef]
- Adithiyaa, T.; Chandramohan, D.; Sathish, T. Optimal prediction of process parameters by GWO-KNN in stirring-squeeze casting of AA2219 reinforced metal matrix composites. Mater. Today Proc. 2019, 21, 1000–1007. [Google Scholar] [CrossRef]
- Shabani, M.O.; Mazahery, A. Artificial Intelligence in numerical modeling of nano sized ceramic particulates reinforced metal matrix composites. Appl. Math. Model. 2012, 36, 5455–5465. [Google Scholar] [CrossRef]
- Razli, P.; Povezav, N.U.N.; Izdelavi, P.M.I.E. The performance of various artificial neurons interconnections in the modelling and experimental manufacturing of the composites. Mater. Tehnol. 2012, 46, 109–113. [Google Scholar]
- Natrayan, L.; Kumar, M.S. An integrated artificial neural network and Taguchi approach to optimize the squeeze cast process parameters of AA6061/Al2O3/SiC/Gr hybrid composites prepared by novel encapsulation feeding technique. Mater. Today Commun. 2020, 25, 101586. [Google Scholar] [CrossRef]
- Altinkok, N.; Koker, R. Neural network approach to prediction of bending strength and hardening behaviour of particulate reinforced (Al–Si–Mg)-aluminium matrix composites. Mater. Des. 2004, 25, 595–602. [Google Scholar] [CrossRef]
- Koker, R.; Altinkok, N.; Demir, A. Neural network based prediction of mechanical properties of particulate reinforced metal matrix composites using various training algorithms. Mater. Des. 2007, 28, 616–627. [Google Scholar] [CrossRef]
- Ghaedi, M.; Azad, F.N.; Dashtian, K.; Hajati, S.; Goudarzi, A.; Soylak, M. Central composite design and genetic algorithm applied for the optimization of ultrasonic-assisted removal of malachite green by ZnO Nanorod-loaded activated carbon. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2016, 167, 157–164. [Google Scholar] [CrossRef] [PubMed]
- Alateyah, A.I.; El-Garaihy, W.H.; Alawad, M.O.; El Sanabary, S.; Elkatatny, S.; Dahish, H.A.; Kouta, H. The Effect of ECAP Processing Conditions on Microstructural Evolution and Mechanical Properties of Pure Magnesium—Experimental, Mathematical Empirical and Response Surface Approach. Materials 2022, 15, 5312. [Google Scholar] [CrossRef]
- Alawad, M.O.; Alateyah, A.I.; El-Garaihy, W.H.; BaQais, A.; Elkatatny, S.; Kouta, H.; Kamel, M.; El-Sanabary, S. Optimizing the ECAP Parameters of Biodegradable Mg-Zn-Zr Alloy Based on Experimental, Mathematical Empirical, and Response Surface Methodology. Materials 2022, 15, 7719. [Google Scholar] [CrossRef] [PubMed]
- Albaijan, I.; Ahmed, M.M.Z.; Seleman, M.M.E.-S.; Touileb, K.; Habba, M.I.A.; Fouad, R.A. Optimization of Bobbin Tool Friction Stir Processing Parameters of AA1050 Using Response Surface Methodology. Materials 2022, 15, 6886. [Google Scholar] [CrossRef] [PubMed]
- El-Garaihy, W.H.; Alaskari, A.M.; Ameshaiei, E.A.; Oraby, S.E. On the effect of HPT processing conditions on relative density, mechanical properties and microstructural evolution of hot compacted AA6061– mathematical empirical and response surface approach. Adv. Mater. Lett. 2017, 8, 620–628. [Google Scholar] [CrossRef]
- Alateyah, A.I.; El-Shenawy, M.; Nassef, A.; El-Hadek, M.; Ahmed, M.M.Z.; Kouta, H.; El Sanabary, S.; El-Garaihy, W.H. Optimizing the ECAP processing parameters of pure Cu through experimental, finite element, and response surface approaches. Rev. Adv. Mater. Sci. 2023, 62, 20220297. [Google Scholar] [CrossRef]
- El-Garaihy, W.H.; Oraby, S.E.; Rassoul, E.-S.M.A.; Salem, H.G. On the Effect of SiC Content and Processing Temperature on Relative Density and Hardness of Hot Compacted Aluminum AA6061 Composite—Mathematical Empirical and Response Surface Approach. J. Mater. Sci. Res. 2015, 4, p1. [Google Scholar] [CrossRef]
- Santhosh, A.J.; Tura, A.D.; Jiregna, I.T.; Gemechu, W.F.; Ashok, N.; Ponnusamy, M. Optimization of CNC turning parameters using face centred CCD approach in RSM and ANN-genetic algorithm for AISI 4340 alloy steel. Results Eng. 2021, 11, 100251. [Google Scholar] [CrossRef]
- Dadrasi, A.; Fooladpanjeh, S.; Gharahbagh, A.A. Interactions between HA/GO/epoxy resin nanocomposites: Optimization, modeling and mechanical performance using central composite design and genetic algorithm. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 63. [Google Scholar] [CrossRef]
- Nassef, A.E.; Alateyah, A.; El-Hadek, M.A.; El-Garaihy, W.H. Mechanical behavior and fracture surface characterization of liquid-phase sintered Cu-Sn powder alloys. Adv. Mater. Lett. 2017, 8, 717–722. [Google Scholar] [CrossRef]
- Alam, M.A.; Hamdan, H.Y.; Azeem, M.; Hussain, P.B.; bin Salit, M.S.; Khan, R.; Arif, S.; Ansari, A.H. Modelling and optimisation of hardness behaviour of sintered Al/SiC composites using RSM and ANN: A comparative study. J. Mater. Res. Technol. 2020, 9, 14036–14050. [Google Scholar] [CrossRef]
- Devaneyan, S.P.; Ganesh, R.; Senthilvelan, T. On the Mechanical Properties of Hybrid Aluminium 7075 Matrix Composite Material Reinforced with SiC and TiC Produced by Powder Metallurgy Method. Indian J. Mater. Sci. 2017, 2017, 3067257. [Google Scholar] [CrossRef]
- Dubey, V.; Sharma, A.K.; Pimenov, D.Y. Prediction of Surface Roughness Using Machine Learning Approach in MQL Turning of AISI 304 Steel by Varying Nanoparticle Size in the Cutting Fluid. Lubricants 2022, 10, 81. [Google Scholar] [CrossRef]
- Behbahani, R.; Sarvestani, H.Y.; Fatehi, E.; Kiyani, E.; Ashrafi, B.; Karttunen, M.; Rahmat, M. Machine learning-driven process of alumina ceramics laser machining. Phys. Scr. 2023, 98, 015834. [Google Scholar] [CrossRef]
- Kurdi, F.T.; Amakhchan, W.; Gharineiat, Z. Random Forest Machine Learning Technique for Automatic Vegetation Detection and Modelling in LiDAR Data. Int. J. Environ. Sci. Nat. Resour. 2021, 28, 556234. [Google Scholar] [CrossRef]
- Kouta, H.; Elsanabary, S.; Elhadek, M.; Elkaseer, A. FE Simulation of Inertia Friction Welding of Similar PVC-PVC and PA6-PA6 Hollow Cylinders for Process Optimization FE Simulation of Inertia Friction Welding of Similar PVC-PVC and PA6- PA6 Hollow Cylinders for Process Optimization. Sylwan 2020, 6, 407–428. [Google Scholar]
- Elattar, Y.M.; Mahdy, M.A.; Sonbol, H.A. Prediction of Abrasive Water Jet Cutting Parameters Using Artificial Neural Network. In The International Conference on Applied Mechanics and Mechanical Engineering, Proceedings of the 18th International Conference on Applied Mechanics and Mechanical Engineering, Cairo, Egypt, 3–5 April 2018; Military Technical College: Cairo, Egypt, 2018; Volume 18, pp. 1–14. [Google Scholar] [CrossRef]
- Djavanroodi, F.; Omranpour, B.; Sedighi, M. Artificial Neural Network Modeling of ECAP Process. Mater. Manuf. Process. 2013, 28, 276–281. [Google Scholar] [CrossRef]
- Hazir, E.; Ozcan, T. Response Surface Methodology Integrated with Desirability Function and Genetic Algorithm Approach for the Optimization of CNC Machining Parameters. Arab. J. Sci. Eng. 2018, 44, 2795–2809. [Google Scholar] [CrossRef]
- Choudhury, A.; Nanda, J.; Das, S.N. The effect of compaction pressure, sintering time, and temperature on the characterization of an aluminum/alumina composite with rising alumina proportions. Curr. Chem. Lett. 2023, 12, 305–316. [Google Scholar] [CrossRef]
- Mohanavel, V.; Ravichandran, M. Influence of AlN particles on microstructure, mechanical and tribological behaviour in AA6351 aluminum alloy. Mater. Res. Express 2019, 6, 106557. [Google Scholar] [CrossRef]

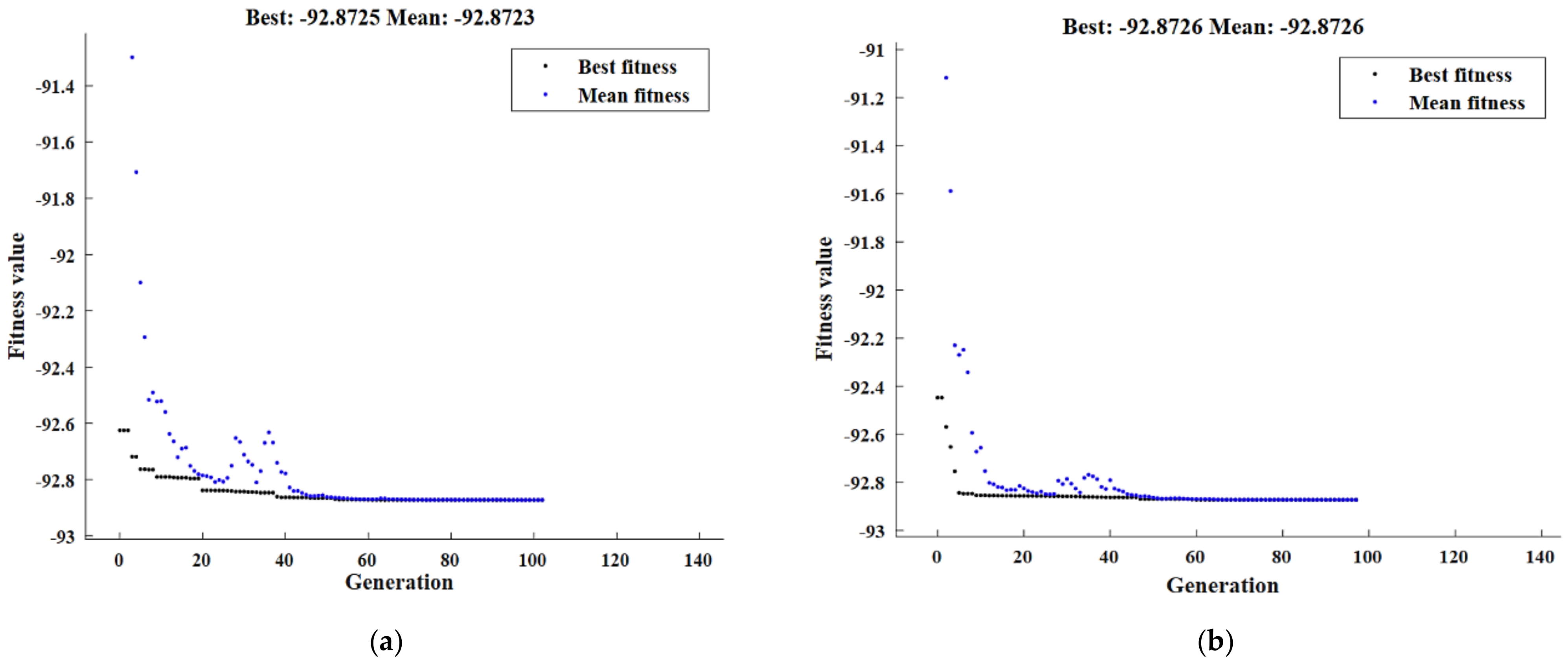
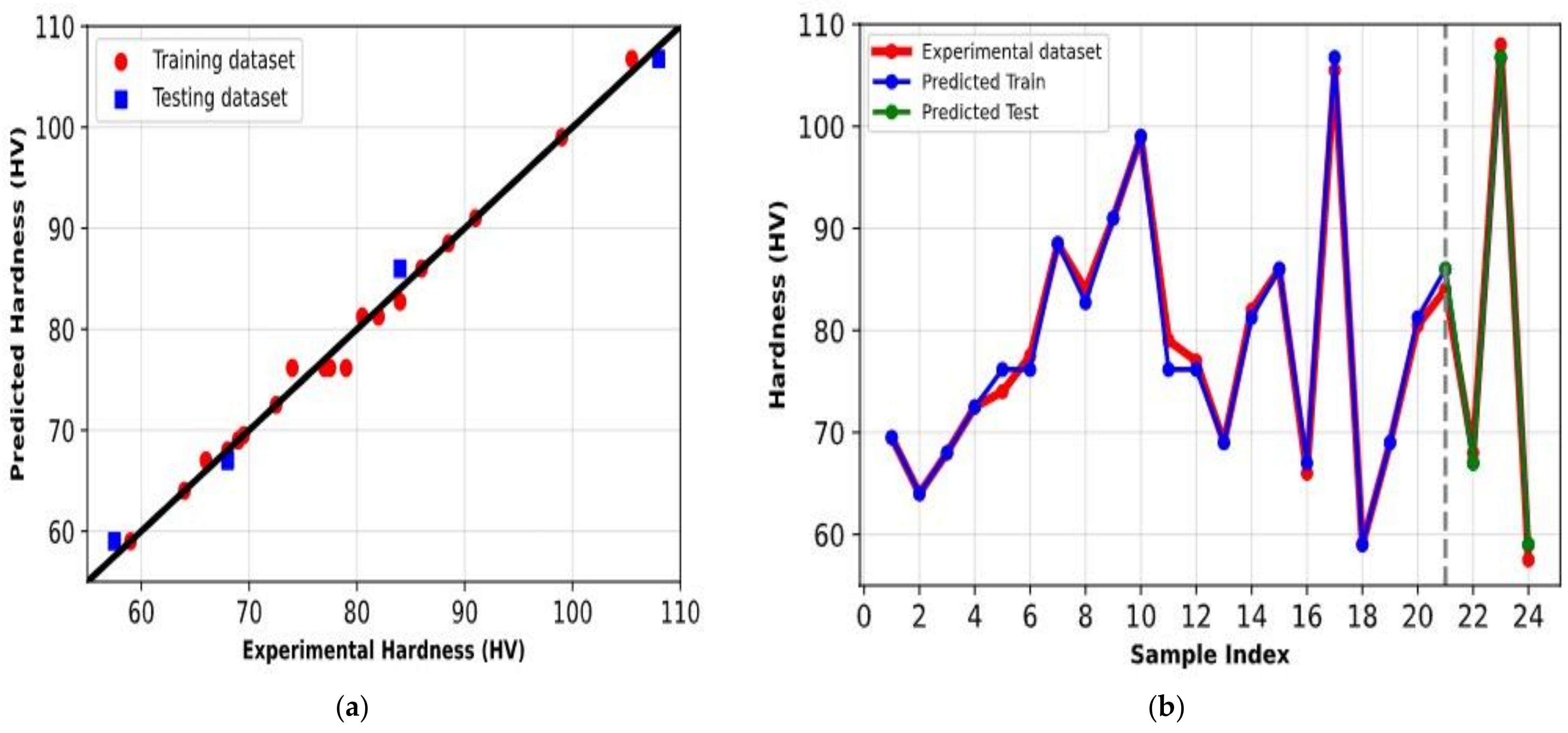
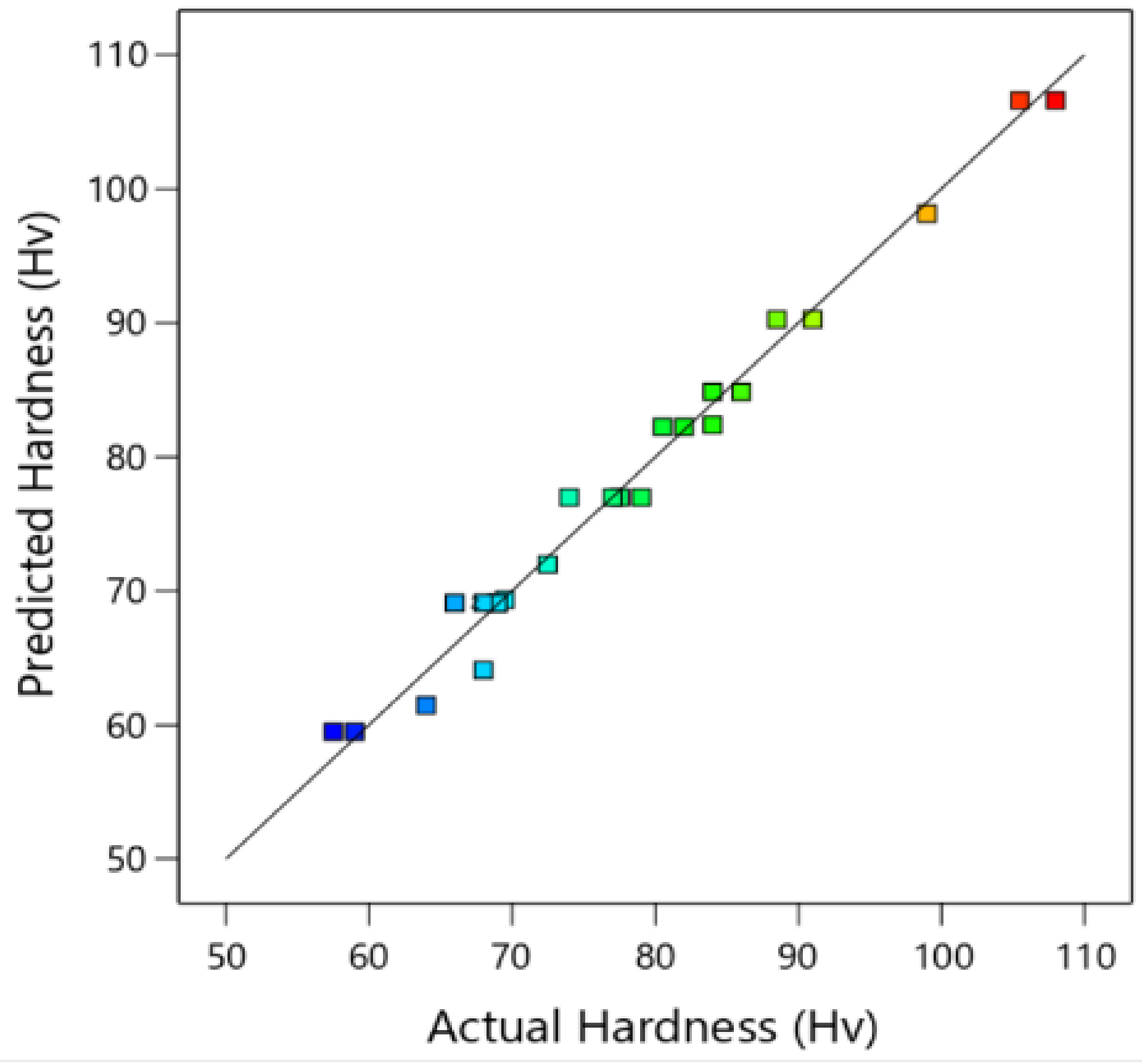

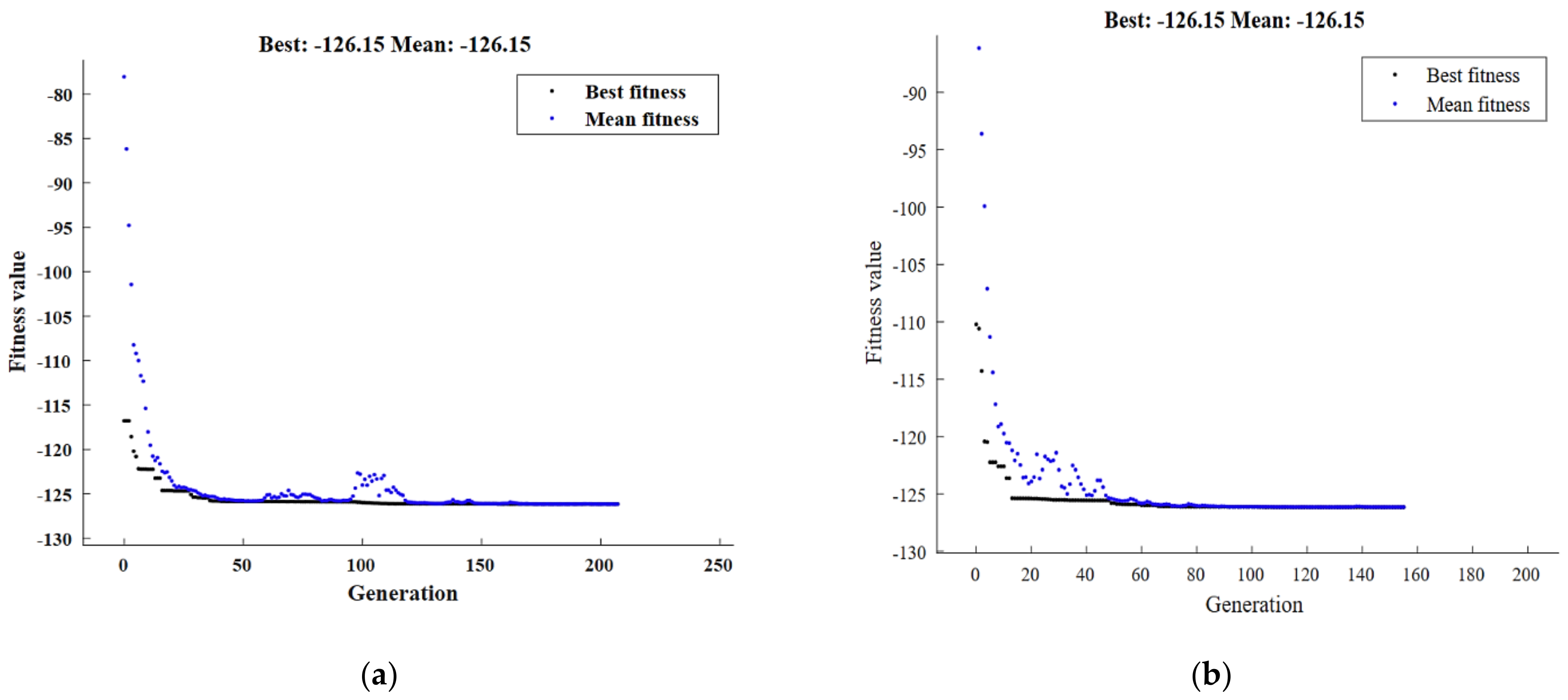
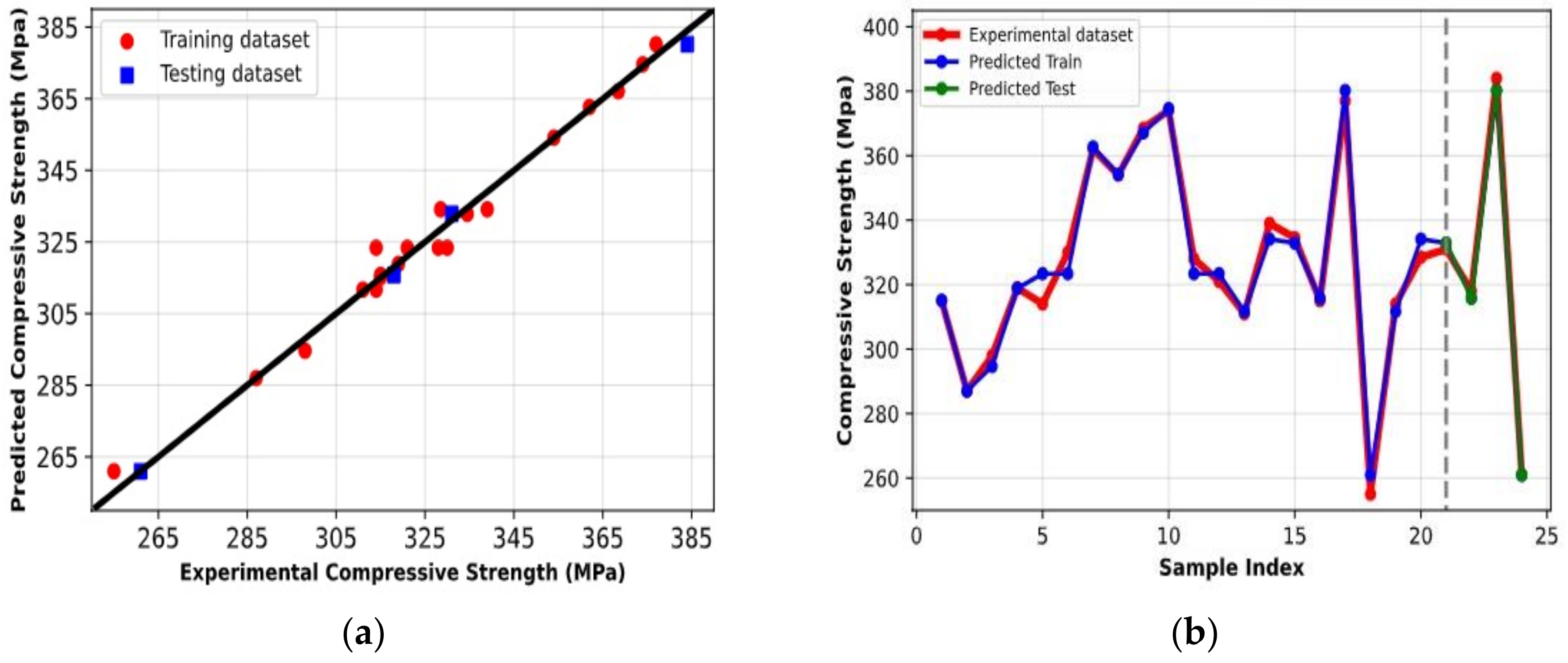
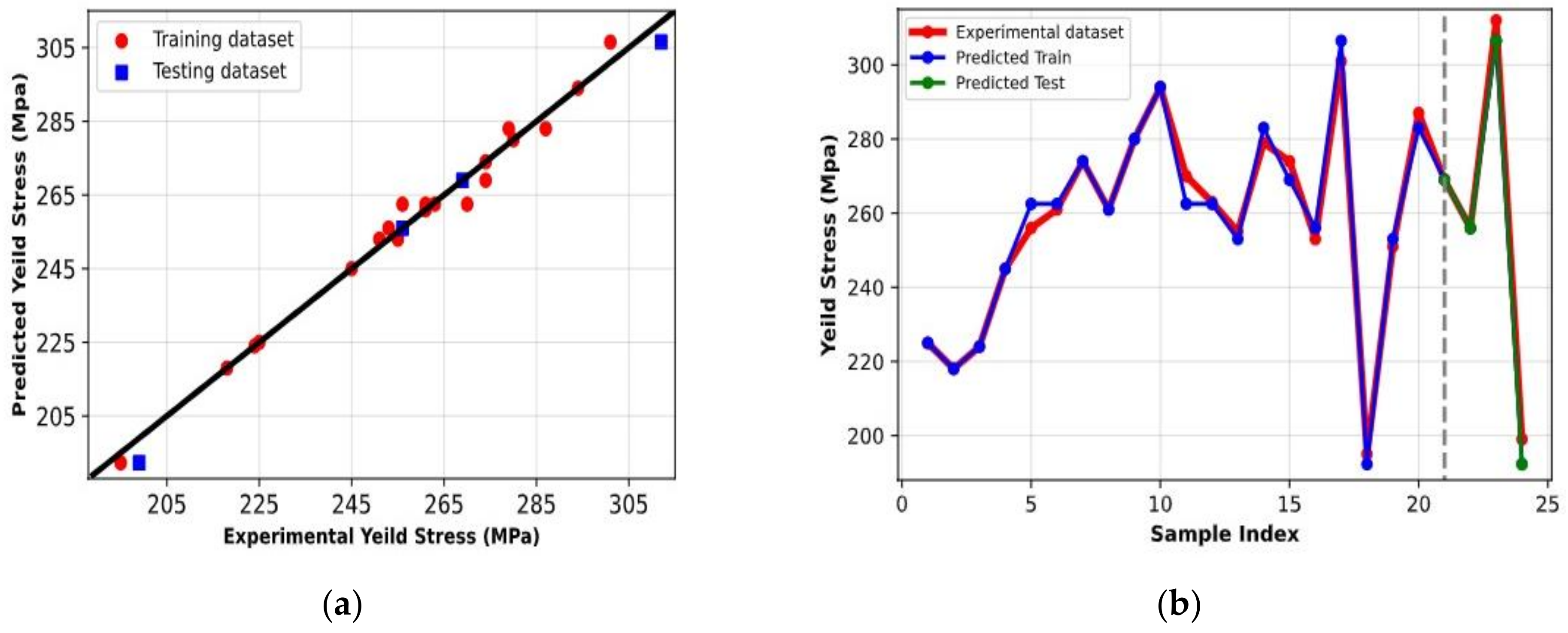

| Exp. No. | Al2O3 (wt. %) | H/D | Pressure (MPa) | Remark |
|---|---|---|---|---|
| 1 | 2.5 | 1.5 | 800 | Front-facing corners |
| 2 | 2.5 | 1.5 | 600 | |
| 3 | 2.5 | 1.0 | 600 | |
| 4 | 2.5 | 1.0 | 800 | |
| 5 | 5.0 | 1.25 | 700 | Repeated center |
| 6 | 5.0 | 1.25 | 700 | |
| 7 | 7.5 | 1.5 | 800 | Back-facing corners |
| 8 | 7.5 | 1.5 | 600 | |
| 9 | 7.5 | 1.0 | 600 | |
| 10 | 7.5 | 1.0 | 800 | |
| 11 | 5.0 | 1.25 | 700 | Repeated center |
| 12 | 5.0 | 1.25 | 700 | |
| 13 | 5.0 | 2.0 | 700 | Augmented experiments |
| 14 | 5.0 | 0.75 | 700 | |
| 15 | 5.0 | 1.25 | 900 | |
| 16 | 5.0 | 1.25 | 500 | |
| 17 | 10.0 | 1.25 | 700 | |
| 18 | 0.0 | 1.25 | 700 | |
| 19 | 5.0 | 2.0 | 700 | Repeated augmented experiments |
| 20 | 5.0 | 0.75 | 700 | |
| 21 | 5.0 | 1.25 | 900 | |
| 22 | 5.0 | 1.25 | 500 | |
| 23 | 10.0 | 1.25 | 700 | |
| 24 | 0.0 | 1.25 | 700 |
| Response | F-Value | Model Significant (p < 0.05) | Adeq Precision (Ratio > 4) | R2 | Adjusted R2 | Predicted R2 |
|---|---|---|---|---|---|---|
| Relative density (RD%) | 78.25 | <0.0001 | 28.8251 | 0.9031 | 0.8915 | 0.8752 |
| Hardness (Hv) | 276.02 | <0.0001 | 56.9531 | 0.9849 | 0.9814 | 0.9755 |
| Yield strength (σy) | 184.74 | <0.0001 | 47.7030 | 0.9700 | 0.9647 | 0.9559 |
| Compression strength (σc) | 122.52 | <0.0001 | 39.3438 | 0.9554 | 0.9476 | 0.9352 |
| Fracture strain (εf) | 190.89 | <0.0001 | 44.7085 | 0.9784 | 0.9732 | 0.9639 |
| ML | Training Set | Testing Set | ||
|---|---|---|---|---|
| RMSE | R2 | RMSE | R2 | |
| Linear regression | 0.68 | 0.82 | 0.55 | 0.89 |
| Regression trees | 0.28 | 0.97 | 0.74 | 0.79 |
| Random forest regression | 0.5 | 0.91 | 0.73 | 0.81 |
| Gaussian process regression | 0.27 | 0.97 | 0.58 | 0.87 |
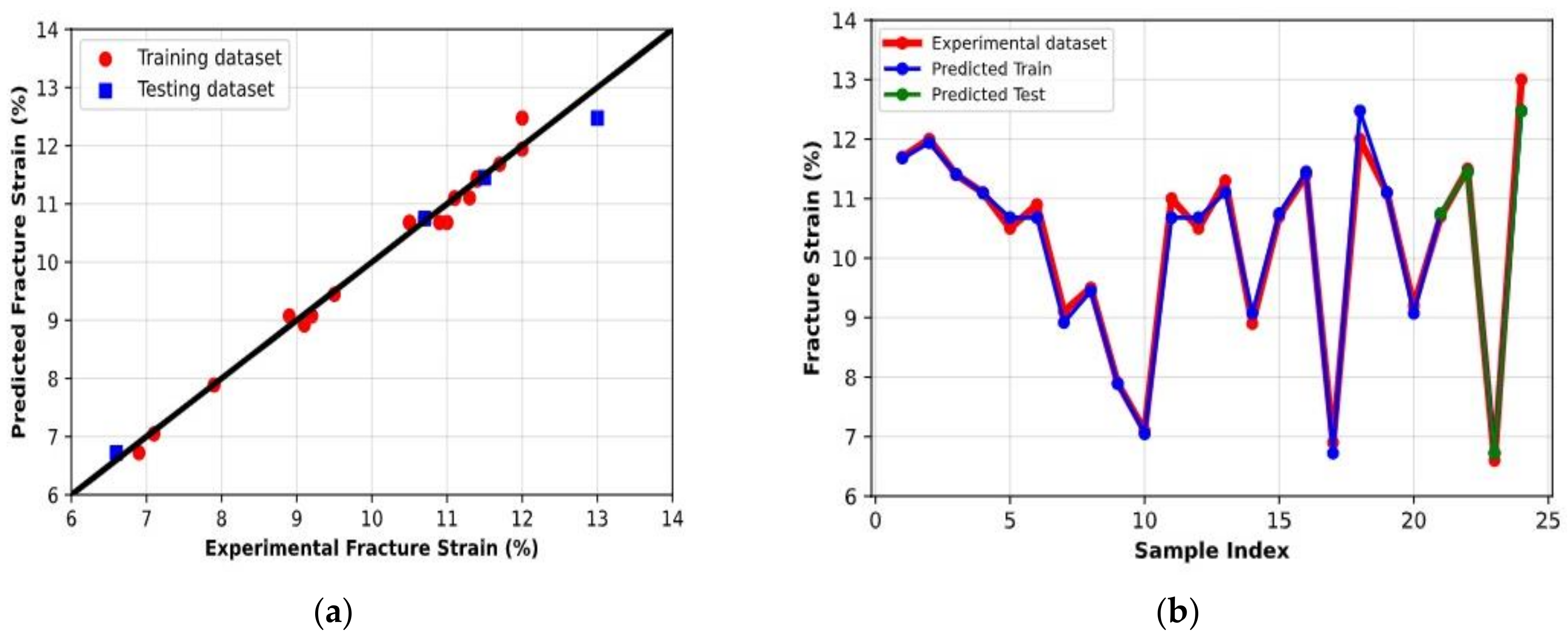
| Artificial neural networks | 0.19 | 0.98 | 0.24 | 1 |
| Input | RD% | ||||
|---|---|---|---|---|---|
| Pressure (MPa) | H/D | Al2O3 (wt. %) | Exp. | Predict | Error |
| 800 | 1.5 | 2.5 | 90.15 | 90.14973858 | 0.000261419 |
| 600 | 1.5 | 2.5 | 89.65 | 89.65010871 | −1.09 × 10−4 |
| 600 | 1 | 2.5 | 90.3 | 90.30285476 | −2.85 × 10−3 |
| 800 | 1 | 2.5 | 91.05 | 91.05233493 | −2.33 × 10−3 |
| 700 | 1.25 | 5 | 90.44 | 90.65393441 | −0.213934408 |
| 700 | 1.25 | 5 | 90.67 | 90.65393441 | 0.016065592 |
| 800 | 1.5 | 7.5 | 88.25 | 88.24640343 | 3.60 × 10−3 |
| 600 | 1.5 | 7.5 | 87.4 | 87.40036937 | −0.000369373 |
| 600 | 1 | 7.5 | 88.75 | 88.75127021 | −1.27 × 10−3 |
| 800 | 1 | 7.5 | 89.55 | 89.54729311 | 2.71 × 10−3 |
| 700 | 1.25 | 5 | 90.85 | 90.65393441 | 1.96 × 10−1 |
| 700 | 1.25 | 5 | 90.7 | 90.65393441 | 4.61 × 10−2 |
| 700 | 2 | 5 | 88.05 | 88.18914371 | −1.39 × 10−1 |
| 700 | 0.75 | 5 | 91.2 | 90.9179379 | 2.82 × 10−1 |
| 900 | 1.25 | 5 | 91.08 | 91.19658434 | −0.116584341 |
| 500 | 1.25 | 5 | 89.89 | 89.85855976 | 0.031440242 |
| 700 | 1.25 | 10 | 85.9 | 86.37184757 | −4.72 × 10−1 |
| 700 | 1.25 | 0 | 92 | 92.27624419 | −0.276244187 |
| 700 | 2 | 5 | 88.33 | 88.18914371 | 1.41 × 10−1 |
| 700 | 0.75 | 5 | 90.92 | 90.9179379 | 2.06 × 10−3 |
| 900 | 1.25 | 5 | 91.32 | 91.19658434 | 1.23 × 10−1 |
| 500 | 1.25 | 5 | 90.05 | 89.85855976 | 1.91 × 10−1 |
| 700 | 1.25 | 10 | 86.85 | 86.37184757 | 4.78 × 10−1 |
| 700 | 1.25 | 0 | 92.55 | 92.27624419 | 0.273755813 |
| ML | Training Set | Testing Set | ||
|---|---|---|---|---|
| RMSE | R2 | RMSE | R2 | |
| Linear regression | 2.81 | 0.95 | 2.21 | 0.93 |
| Regression trees | 1.12 | 0.99 | 2 | 0.94 |
| Random forest regression | 2.04 | 0.97 | 2.99 | 0.87 |
| Gaussian process regression | 1.13 | 0.99 | 2.15 | 0.95 |
| Artificial neural networks | 0.818 | 0.996 | 2.19 | 1 |
| Input | Hardness (HV) | ||||
|---|---|---|---|---|---|
| Pressure (MPa) | H/D | Al2O3 (wt. %) | Exp. | Predict | Error |
| 800 | 1.5 | 2.5 | 69.5 | 69.5 | 5.97 × 10−13 |
| 600 | 1.5 | 2.5 | 64 | 64 | −1.07 × 10−12 |
| 600 | 1 | 2.5 | 68 | 68 | 3.45 × 10−12 |
| 800 | 1 | 2.5 | 72.5 | 72.5 | −2.67 × 10−12 |
| 700 | 1.25 | 5 | 74 | 76.166667 | −2.166667 |
| 700 | 1.25 | 5 | 77.5 | 76.166667 | 1.3333333 |
| 800 | 1.5 | 7.5 | 88.5 | 88.5 | 7.82 × 10−13 |
| 600 | 1.5 | 7.5 | 84 | 82.725113 | 1.2748867 |
| 600 | 1 | 7.5 | 91 | 91 | 1.42 × 10−13 |
| 800 | 1 | 7.5 | 99 | 99 | −4.55 × 10−13 |
| 700 | 1.25 | 5 | 79 | 76.166667 | 2.8333333 |
| 700 | 1.25 | 5 | 77 | 76.166667 | 0.8333333 |
| 700 | 2 | 5 | 69 | 69 | 7.11 × 10−14 |
| 700 | 0.75 | 5 | 82 | 81.25 | 0.75 |
| 900 | 1.25 | 5 | 86 | 86 | 7.39 × 10−13 |
| 500 | 1.25 | 5 | 66 | 67 | −1 |
| 700 | 1.25 | 10 | 105.5 | 106.75 | −1.25 |
| 700 | 1.25 | 0 | 59 | 59 | 9.95 × 10−14 |
| 700 | 2 | 5 | 69 | 69 | 7.11 × 10−14 |
| 700 | 0.75 | 5 | 80.5 | 81.25 | −0.75 |
| 900 | 1.25 | 5 | 84 | 86 | −2 |
| 500 | 1.25 | 5 | 68 | 67 | 1 |
| 700 | 1.25 | 10 | 108 | 106.75 | 1.25 |
| 700 | 1.25 | 0 | 57.5 | 59 | −1.5 |
| Response | ML | Training Set | Testing Set | ||
|---|---|---|---|---|---|
| RMSE | R2 | RMSE | R2 | ||
| σy (MPa) | Linear regression | 8.27 | 0.918 | 5.14 | 0.91 |
| Regression trees | 3.87 | 0.98 | 6.8 | 0.83 | |
| Random forest regression | 5.69 | 0.96 | 9.01 | 0.71 | |
| Gaussian process regression | 5.63 | 0.96 | 14.44 | 0.80 | |
| Artificial neural networks | 3.17 | 0.98 | 5.19 | 0.99 | |
| σuc (MPa) | Linear regression | 7.51 | 0.95 | 3.04 | 0.99 |
| Regression trees | 4.21 | 0.98 | 7.72 | 0.96 | |
| Random forest regression | 5.97 | 0.97 | 12.11 | 0.91 | |
| Gaussian process regression | 3.52 | 0.98 | 4.36 | 0.98 | |
| Artificial neural networks | 3.58 | 0.98 | 4.55 | 0.98 | |
| εf (%) | Linear regression | 0.59 | 0.87 | 0.68 | 0.91 |
| Regression trees | 0.24 | 0.97 | 0.51 | 0.86 | |
| Random forest regression | 0.26 | 0.97 | 0.21 | 0.97 | |
| Gaussian process regression | 0.198 | 0.98 | 0.264 | 0.97 | |
| Artificial neural networks | 0.2 | 0.98 | 0.2 | 1 | |
| Input | Compressive Strength | Yield Strength | Fracture Strain | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pressure (MPa) | H/D | Al2O3 (wt. %) | Exp. | Predict | Error | Exp. | Predict | Error | Exp. | Predict | Error |
| 800 | 1.5 | 2.5 | 225 | 225.000061 | −6.17 × 10−5 | 315 | 315.14025 | −1.40 × 10−1 | 11.7 | 11.68187 | 1.81 × 10−2 |
| 600 | 1.5 | 2.5 | 218 | 218.000009 | −9.59 × 10−6 | 287 | 286.98075 | 1.92 × 10−2 | 12 | 11.93985 | 6.01 × 10−2 |
| 600 | 1 | 2.5 | 224 | 224.000018 | −1.82 × 10−5 | 298 | 294.62377 | 3.38 × 100 | 11.4 | 11.40852 | −8.52 × 10−3 |
| 800 | 1 | 2.5 | 245 | 244.999986 | 1.34 × 10−5 | 319 | 318.84562 | 1.54 × 10−1 | 11.1 | 11.09339 | 6.61 × 10−3 |
| 700 | 1.25 | 5 | 256 | 262.499990 | −6.499990521 | 314 | 323.39536 | −9.395361 | 10.5 | 10.67984 | −0.17984 |
| 700 | 1.25 | 5 | 261 | 262.499990 | −1.499990521 | 330 | 323.39536 | 6.6046387 | 10.9 | 10.67984 | 0.2201605 |
| 800 | 1.5 | 7.5 | 274 | 273.999999 | 9.57 × 10−7 | 362 | 362.70417 | −7.04 × 10−1 | 9.1 | 8.918651 | 1.81 × 10−1 |
| 600 | 1.5 | 7.5 | 261 | 261.000004 | −4.03203 × 10−6 | 354 | 354.13551 | −0.135514 | 9.5 | 9.444270 | 0.0557299 |
| 600 | 1 | 7.5 | 280 | 279.999997 | 2.54 × 10−6 | 368.5 | 367.07923 | 1.42 × 100 | 7.9 | 7.887332 | 1.27 × 10−2 |
| 800 | 1 | 7.5 | 294 | 294.000008 | −8.63 × 10−6 | 374 | 374.60069 | −6.01 × 10−1 | 7.1 | 7.047457 | 5.25 × 10−2 |
| 700 | 1.25 | 5 | 270 | 262.499990 | 7.50 × 100 | 328 | 323.39536 | 4.60 × 100 | 11 | 10.67984 | 3.20 × 10−1 |
| 700 | 1.25 | 5 | 263 | 262.499990 | 5.00 × 10−1 | 321 | 323.39536 | −2.40 × 100 | 10.5 | 10.67984 | −1.80 × 10−1 |
| 700 | 2 | 5 | 255 | 253.000037 | 2.00 × 100 | 311 | 311.69067 | −6.91 × 10−1 | 11.3 | 11.10294 | 1.97 × 10−1 |
| 700 | 0.75 | 5 | 279 | 282.999974 | −3.99997446 | 339 | 334.10906 | 4.8909386 | 8.9 | 9.073309 | −0.173309 |
| 900 | 1.25 | 5 | 274 | 268.999986 | 5.000013937 | 334.5 | 332.86319 | 1.6368112 | 10.7 | 10.74755 | −0.047559 |
| 500 | 1.25 | 5 | 253 | 255.999991 | −3.00 × 100 | 315 | 315.79756 | −7.98 × 10−1 | 11.4 | 11.45020 | −5.02 × 10−2 |
| 700 | 1.25 | 10 | 301 | 306.499993 | −5.49999346 | 377 | 380.21001 | −3.210014 | 6.9 | 6.722916 | 1.77 × 10−1 |
| 700 | 1.25 | 0 | 195 | 192.296478 | 2.70 × 100 | 255 | 260.97904 | −5.98 × 100 | 12 | 12.47473 | −4.75 × 10−1 |
| 700 | 2 | 5 | 251 | 253.000037 | −2.00 × 100 | 314 | 311.69067 | 2.31 × 100 | 11.1 | 11.10294 | −2.94 × 10−3 |
| 700 | 0.75 | 5 | 287 | 282.999974 | 4.00 × 100 | 328.5 | 334.10906 | −5.61 × 100 | 9.2 | 9.073309 | 1.27 × 10−1 |
| 900 | 1.25 | 5 | 269 | 268.999986 | 1.39 × 10−5 | 331 | 332.86319 | −1.86 × 100 | 10.7 | 10.74755 | −0.047559 |
| 500 | 1.25 | 5 | 256 | 255.999991 | 8.36 × 10−6 | 318 | 315.79756 | 2.20 × 100 | 11.5 | 11.45020 | 0.0497917 |
| 700 | 1.25 | 10 | 312 | 306.499993 | 5.50000654 | 384 | 380.21001 | 3.7899859 | 6.6 | 6.722916 | −1.23 × 10−1 |
| 700 | 1.25 | 0 | 199 | 192.296478 | 6.703521764 | 261 | 260.97904 | 0.020957 | 13 | 12.47473 | 0.5252705 |
| Response | DOE | RSM | GA | DOE-GA | |
|---|---|---|---|---|---|
| RD% | Value | 92.872 | 92.791 | 92.872 | 92.872 |
| Cond. | P = 900 MPa, H/D = 0.75, Al2O3 = 0% | P = 893.89 MPa, H/D = 0.854, Al2O3 = 0.031% | P = 900 MPa, H/D = 0.75, Al2O3 = 0% | P = 900 MPa, H/D = 0.75, Al2O3 = 0% | |
| Hv | Value | 126.27 | 121.199 | 126.15 | 126.15 |
| Cond. | P = 900 MPa, H/D= 0.75, Al2O3 = 10% | P = 875.087 MPa, H/D = 0.870, Al2O3 = 9.845% | P = 900 MPa, H/D = 0.75, Al2O3 = 10% | P = 900 MPa, H/D = 0.75, Al2O3 = 10% | |
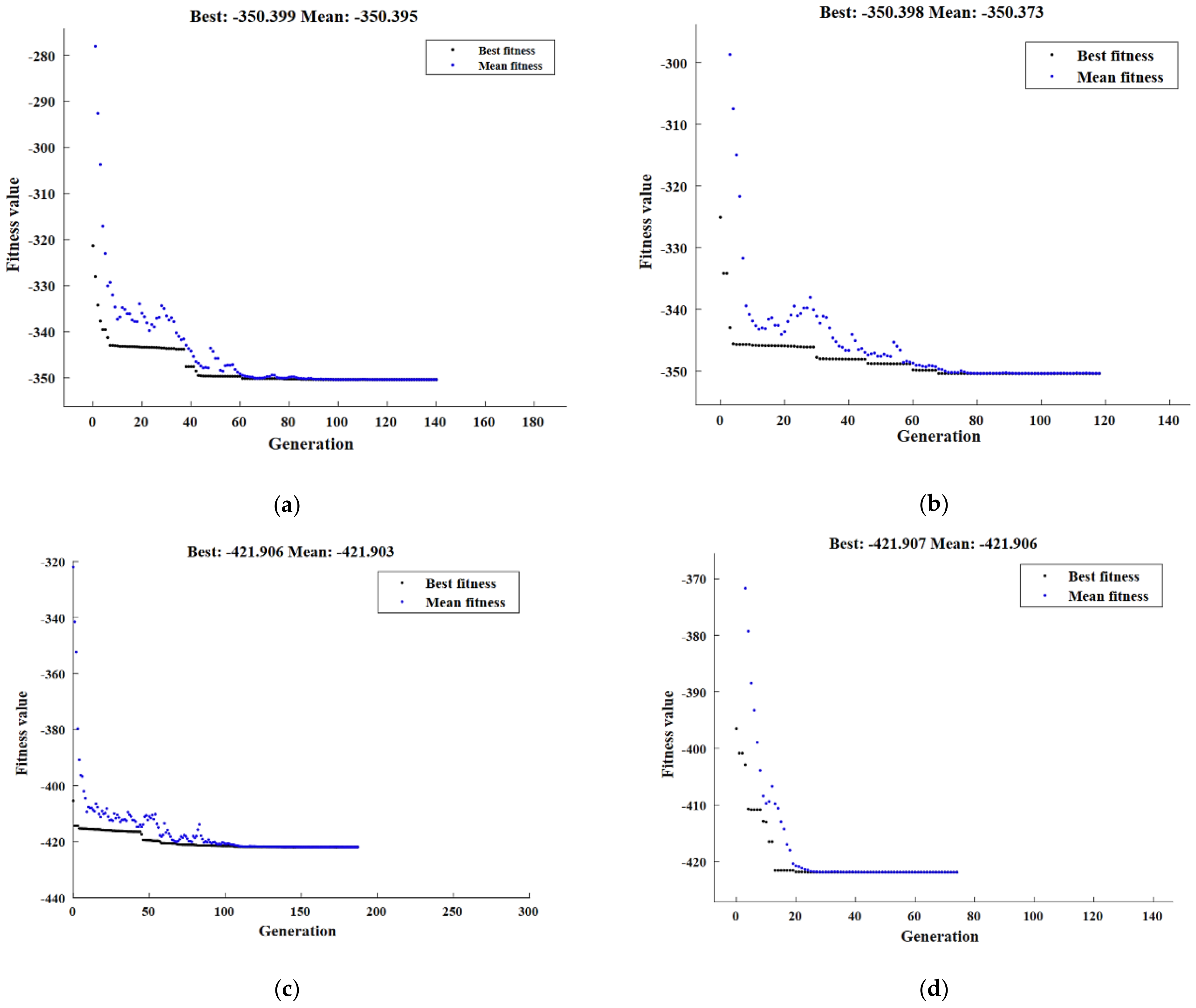
| σy (MPa) | Value | 312 | 341.372 | 350.399 | 350.398 |
| Cond. | P = 700 MPa, H/D = 1.25, Al2O3 = 10% | P = 884.243 MPa, H/D = 0.762, Al2O3 = 8.57% | P = 900 MPa, H/D = 0.75, Al2O3 = 10% | P = 900 MPa, H/D = 0.75, Al2O3 = 10% | |
| σuc (MPa) | Value | 384 | 410.93 | 421.906 | 421.906 |
| Cond. | P = 700 MPa, H/D = 1.25, Al2O3 = 10% | P = 506.142 MPa, H/D = 0.873, Al2O3 = 9.71% | P = 500 MPa, H/D = 0.75, Al2O3 = 10% | P = 500 MPa, H/D = 0.75, Al2O3 = 10% | |
| εf | Value | 13 | 13.54 | 13.0851 | 13.464 |
| Cond. | P = 700 MPa, H/D = 1.25, Al2O3 = 0% | P = 501.692 MPa, H/D = 0.757, Al2O3 = 0.017% | P = 501.12 MPa, H/D = 0.758, Al2O3 = 0% | P = 510 MPa, H/D = 0.75, Al2O3 = 0% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elkatatny, S.; Alsharekh, M.F.; Alateyah, A.I.; El-Sanabary, S.; Nassef, A.; Kamel, M.; Alawad, M.O.; BaQais, A.; El-Garaihy, W.H.; Kouta, H. Optimizing the Powder Metallurgy Parameters to Enhance the Mechanical Properties of Al-4Cu/xAl2O3 Composites Using Machine Learning and Response Surface Approaches. Appl. Sci. 2023, 13, 7483. https://doi.org/10.3390/app13137483
Elkatatny S, Alsharekh MF, Alateyah AI, El-Sanabary S, Nassef A, Kamel M, Alawad MO, BaQais A, El-Garaihy WH, Kouta H. Optimizing the Powder Metallurgy Parameters to Enhance the Mechanical Properties of Al-4Cu/xAl2O3 Composites Using Machine Learning and Response Surface Approaches. Applied Sciences. 2023; 13(13):7483. https://doi.org/10.3390/app13137483
Chicago/Turabian StyleElkatatny, Sally, Mohammed F. Alsharekh, Abdulrahman I. Alateyah, Samar El-Sanabary, Ahmed Nassef, Mokhtar Kamel, Majed O. Alawad, Amal BaQais, Waleed H. El-Garaihy, and Hanan Kouta. 2023. "Optimizing the Powder Metallurgy Parameters to Enhance the Mechanical Properties of Al-4Cu/xAl2O3 Composites Using Machine Learning and Response Surface Approaches" Applied Sciences 13, no. 13: 7483. https://doi.org/10.3390/app13137483
APA StyleElkatatny, S., Alsharekh, M. F., Alateyah, A. I., El-Sanabary, S., Nassef, A., Kamel, M., Alawad, M. O., BaQais, A., El-Garaihy, W. H., & Kouta, H. (2023). Optimizing the Powder Metallurgy Parameters to Enhance the Mechanical Properties of Al-4Cu/xAl2O3 Composites Using Machine Learning and Response Surface Approaches. Applied Sciences, 13(13), 7483. https://doi.org/10.3390/app13137483







