Electromagnetic Field Variation of ELF Near-Region Excited by HED in a Homogeneous Half-Space Model

Abstract

Great attention has been paid to the propagation of electromagnetic (EM) waves across the sea surface due to its important applications. Most of the previous research, however, focuses on the half-space model illustrating the deep sea environment. In this paper, EM field distribution in the extremely low frequency (ELF) near-region under horizontal electric dipole (HED) excitation in homogeneous half-space seawater is analyzed based on the general expression of the Sommerfeld integral using the quasistatic approximation method. The focus is on deriving complete and effective solutions in air and seawater regions under the cylindrical coordinates for the EM near-field, which is generated by an HED in a shallow sea. The resulting formulas can be given by a few summands in closed form as the well-known Fourier–Bessel integrals. The analytical approximate expression of ELF Sommerfeld EM field integral excited by the HED in the homogeneous half-space seawater is deduced under the condition that the propagation distance ρ satisfies kρ << 1. To this end, the EM field distribution in the range close to the HED antenna in seawater is simulated, the results have shown that the minimum attenuation value of the vertical electric component E_z is about 15 dB, and that of the radical magnetic components H_φ is about 30 dB, and these values are found to be of greatest potential for the near-field region propagation among the electric and magnetic components. Finally, the correctness of the proposed method is verified by comparison with Pan’s approximation method and Margetis’s exact expression approximation method, which demonstrated the correctness of the proposed method.

1. Introduction

Due to the high salinity and complex temperature and current distribution characteristics of seawater, its conductivity and dielectric constant are higher than those of air. The higher the conductivity of water, the greater the attenuation of EM waves. Therefore, the propagation characteristics of EM waves in seawater are considerably different from those in air. Experiments have shown that the amplitude and phase characteristics of ELF (3–30 Hz) EM waves are stable when they propagate in seawater, with small propagation loss and strong seawater penetration ability. Therefore, ELF EM waves have broad application prospects in geological exploration, submarine exploration, seismic detection, submarine communication, and other forms of geophysical exploration [1,2,3,4,5,6]. Many scholars have conducted in-depth studies on EM fields generated by low-frequency HED located in seawater or soil. In the representative monograph written by A. Banos [7], a complete analytical solution of the EM field excited by a dipole in half-space is given. In the decades that followed, R. W. P. King [8] described in detail the lateral EM waves generated by the excitation of horizontal and vertical electric dipoles (VEDs) in two-layer and three-layer media. It is worth mentioning that the lateral wave term of his solution can be expressed as an approximate expression containing a Fresnel integral. Several years later, Margetis derived the exact solution expression of an EM field excited by electric dipoles at the interface of half-space [9]. However, the transmitting point and receiving point can only be on the ground; off the ground is not accurate. Figure 1 demonstrates the EM wave propagation model in the half-space model in the two-layer medium in King’s monograph, in which L is a lateral wave, L₁ is a direct wave, and L₂ is a reflected wave.

Generally speaking, the long-term focus of EM research has been on the far-field characteristics of traditional problems such as EM propagation, radiation, and scattering, while the attention and research on the near-field characteristics are still relatively weak [10,11,12]. Sommerfeld was the first to give the approximate integral expression of EM field for electric dipoles in homogeneous half-space (hereinafter referred to as the Sommerfeld integral) [13], but this expression is difficult to solve by simple numerical integration. The key reason is that the Fourier–Bessel expression in the Sommerfeld integral has non-integrable terms at kρ → 0.

To solve this problem, D. Margetis [14] gave the exact near-field expression of the fundamental oscillator in half-space under the condition of kρ >> 1 by assuming that k_2/k₁ (k₂ and k₁ represent the wave number in seawater and air, respectively) tends to infinity. However, the half-space model of “air–seawater” cannot satisfy the condition of |k₂/k₁| << 1. Therefore, the exact formula is not suitable for solving the ELF EM field of the “air–seawater” half-space model. The quasistatic approximate method was first proposed by Wait [15], but it uses Laplace and Poisson equations to calculate the field in the air, so it cannot be applied to the near-field in half-space under the condition of k₂ << k₁. In recent years, this problem was also revisited by W. Y. Pan and K. Li [16], who addressed the ELF near-field wave propagation for the application of the marine controlled-source electromagnetics method as an extension of the above work. The computational scheme is developed from the approximated formulas in the book [8] by retaining fundamental terms. This motivates us to employ Maclaurin’s expansion near the poles of integrands from the Fourier–Bessel representations. H. L. Xu [17] proposed an approximate quasistatic approximation method for solving the “sea–rock” half-space, but the ELF near-field distribution in the deep-sea half-space was obtained using a simplified Sommerfeld integral in the paper, which was not applicable to the “air–seawater” half-space environment.

In addition, with the rapid development of computer technology and computational EM methods, efficient numerical methods have been developed for solving far-field problems with arbitrary source distribution. However, the calculation of the low-frequency near-field has always been a difficult problem to solve. For example, the method of moment (MOM) [18,19,20] has a singularity in the calculation of the near-field, and it is difficult to deal with it. The finite element method (FEM) [21,22,23] and finite difference time domain (FDTD) [24,25,26] have errors caused by boundary truncation; the former may have pseudo-solutions, and the latter is troubled by the difficulty of accurately fitting the surface boundary. In addition, numerical methods may even have problems such as “low-frequency crash” when the frequency is in the very low ranges. Therefore, in view of the above problems, we still have to use the regression analytic method to calculate the EM field propagation in the near-field region of ELF.

For ELF, the wavelength can be compared with the circumference of the Earth. For example, when the working frequency of ELF is 10 Hz, the wavelength is close to three-quarters of the circumference of the Earth. Thus, when the field and source points are in close proximity, it can be regarded as a near-field propagation problem. The propagation environment can be assumed as an idealized model, i.e., a homogeneous half-space, and the interface as a homogeneous plane. In this study, the EM field distribution in the ELF near-field region excited by an HED in homogeneous half-space seawater is studied based on the Sommerfeld integral. The expression is then simplified using an approximate method under the condition that the propagation distance k₀ρ << 1 (k₀ is the wave number in air and ρ is the propagation distance) in the near-field region. Then, the analytical approximate expression and spatial distribution of the EM field components in the near-field region are derived via simulation. Finally, we compare the quasistatic approximate calculation results with Pan’s approximation method and Margetis’s exact expression approximation method to verify the effectiveness of the proposed method.

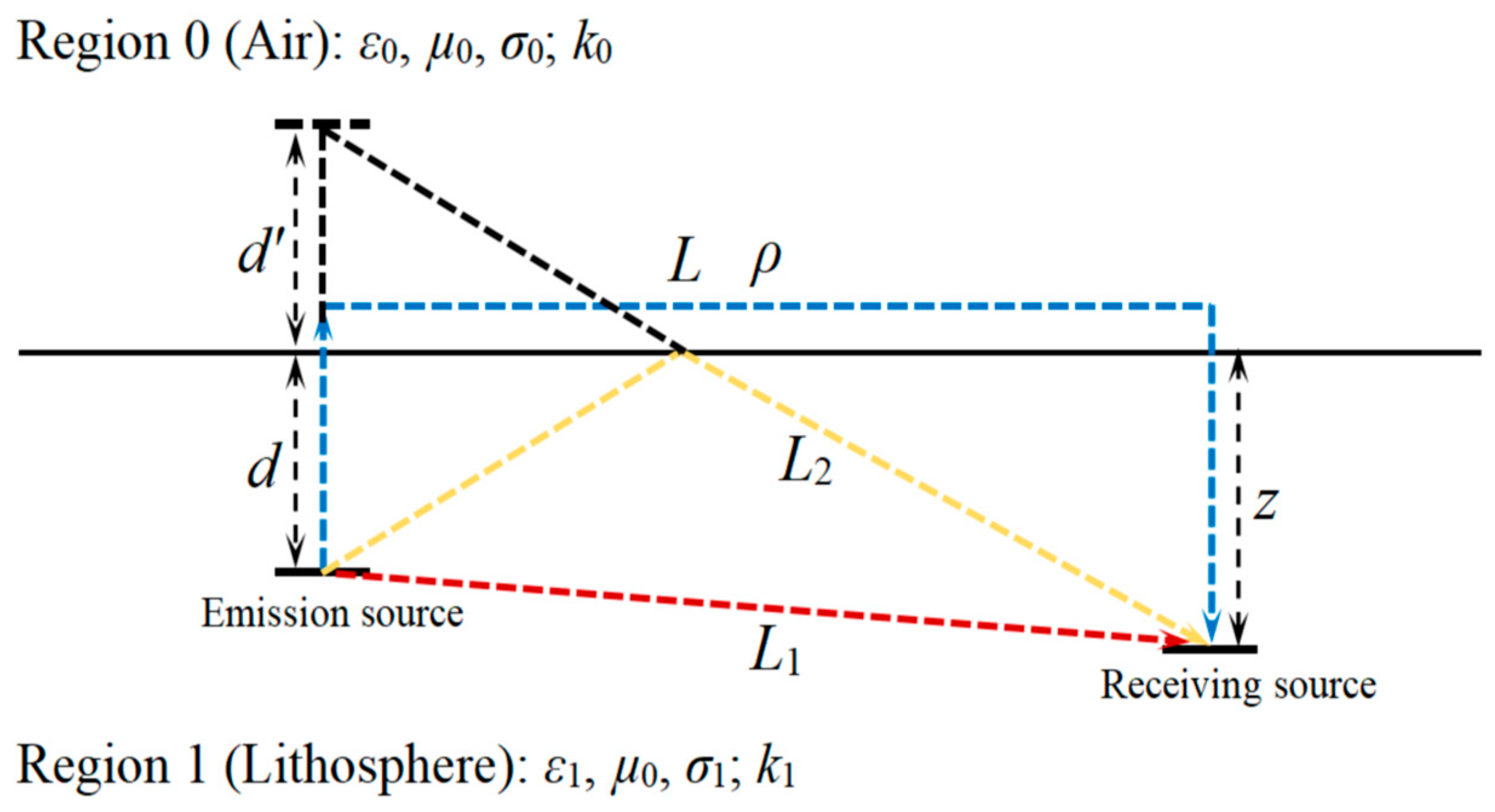
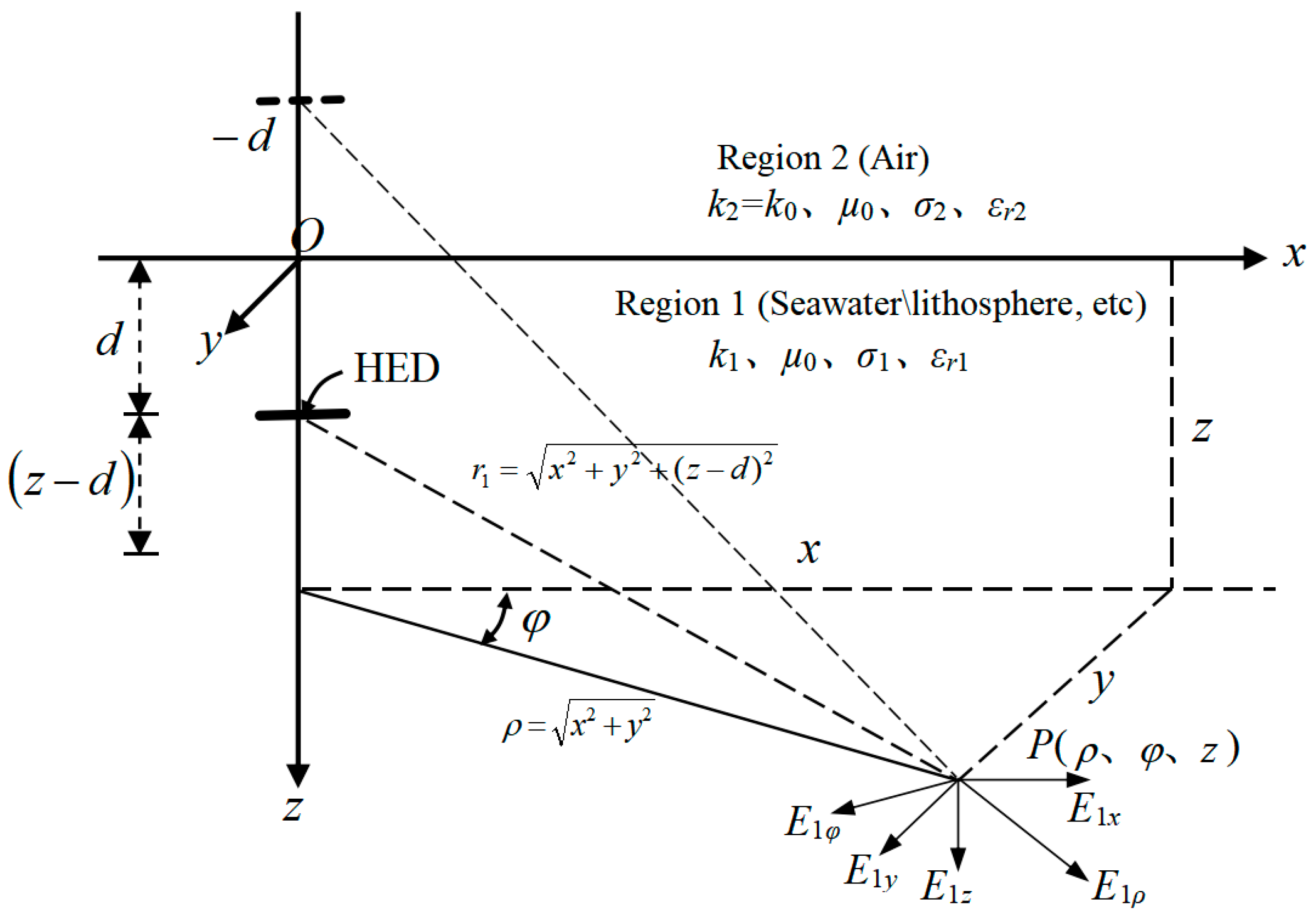
2. Propagation Model of ELF Near-Field Region Excited by HED

The EM field model in the near-field region of ELF excited by an HED in an unbounded, homogeneous half-space medium is shown in Figure 2. The homogeneous half-space medium model can be an air–seawater or air–lithosphere model. This paper focuses on the air–seawater medium. The sea surface was taken as the z = 0 plane; the sea region and air region were marked as regions 1 and 2, respectively.

Assuming that the HED antenna is located in the positive direction of the z-axis, parallel to the x-axis direction, the distance from the xoy plane, i.e., the sea level, is set as d meters; the electric moment is Idl; and the distance from the observation point P to the sea level is z meters. In a cylindrical coordinate system, the coordinates of the observation point P can be expressed as P(ρ, φ, z). The components of each electromagnetic field at point P are shown in Figure 2. Region 1 (z ≥ 0) was filled with seawater. µ₀, σ₁, and ε_r1 are the permeability, conductivity, and relative dielectric constant, respectively, and the wave number can be expressed as $k_1=\sqrt{{\epsilon }_{r1}}\omega /c$, where ω is the angular frequency and c is the speed of light. Region 2 (z ≤ 0) is an air medium with a permeability, conductivity, relative permittivity, and wave number of μ₀, σ₂, ε_r2 = 1, and k₂ = k₀ = ω/c, respectively. ρ is the propagation distance between the projection point of the electric dipole source and the observation point P, and r₁ is the geometric distance between the electric dipole source point and the observation point P in seawater. For low-frequency electric dipole excitation, which varies with the time harmonic factor e^−jωt, the integral expression of the EM field generated in region 1 (z ≥ 0) is given in A. N. Sommerfeld’s work [13] and will not be repeated here. The approximate analytical method is used to simplify the Sommerfeld integral of the ELF near-field region EM fields in homogeneous half-space seawater and derive its approximate analytical expression for the EM fields.

3. Analytical Approximate Expression of the Field Component

3.1. Quasistatic Approximate Propagation Conditions

Under the condition that the propagation distance satisfies k₂ρ << 1, the Fourier–Bessel function integral in the expression of the ELF electromagnetic field at or near the boundary of the two layers of media has discrete terms. The distribution of divergent poles is shown in Figure 3.

In order to evaluate the half-space Sommerfeld integral using the complex function method, the integrand must be divided into single-valued branches; that is, several slits must be made in the complex plane of λ, and the multivalued functions must be specified clearly and reasonably. For this reason, we take the radical function γ₁ = (k₁² − λ²)^1/2 as an example and first analyze its amplitude change on the complex plane; if k₁ = β₁ + jα₁, λ = ξ + jη, then

$${\gamma }_1=\sqrt{({\beta }_1^2-{\alpha }_1^2)-\left({\xi }^2-{\eta }^2\right)+2j({\alpha }_1{\beta }_1-\xi \eta )}$$

(1)

On the isoaxial hyperbola ξη = α₁β₁, the amplitude angle of γ₁ in Equation (1) is divided into three parts, as shown in Figure 3c: the amplitude angle of γ₁ near the virtual axis is 0, the amplitude angle of γ₁ on the dotted line is π/2, and the amplitude angle of γ₁ away from the virtual axis is π. If two symmetric slits are made over the entire λ complex plane, then γ₁ in the λ complex plane is singly analytic.

Under the same condition, these integrals diverge in the traditional sense. For example, the multivalued function D(λ) = k₁²γ₂ + k₂²γ₁ included in the Sommerfeld integral has four zeros on the Riemann surface. γ₁ is the propagation parameter in the seawater medium of region 1, and γ₂ is the propagation parameter in the air medium of region 2. Therefore, two sets of symmetrical slits are created on the λ complex plane, as shown in Figure 3a. Here, slits parallel to the imaginary axis were used to simplify the calculation. According to the loop integral theory of the complex variable function [27], the integral path along the real axis of the Sommerfeld integral can be converted into an integral along the slits C₁ and C₂.

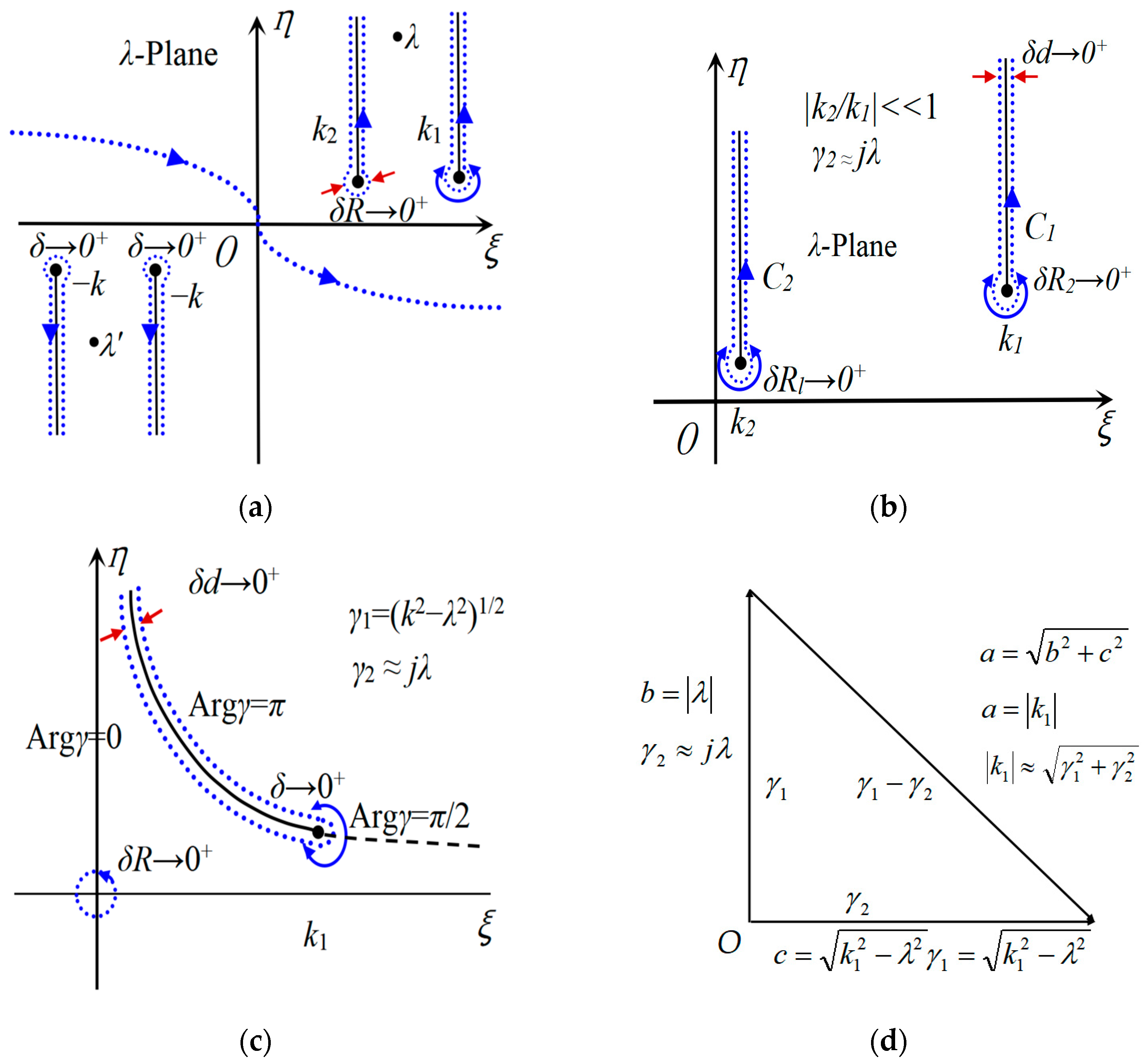
3.1.1. Approximation of the Propagation Parameter γ₂

Air and seawater have different electric parameters in the “air–seawater” homogeneous half-space model; therefore, the ELF near-field EM fields of the HED near the interface of the two media conforms to the quasistatic assumption: ω → 0, k₂ρ << 1, k₂ << k₁. Based on this assumption, the simplified root function can be approximated as follows:

$${\gamma }_2=\sqrt{k_2^2-{\lambda }^2}=\underset{\omega \to 0}{\lim }\sqrt{{(\frac{{\epsilon }_{r2}^{1/2}}{c}\omega )}^2-{\lambda }^2}\approx j\lambda$$

(2)

where ω is the angular frequency, λ is the wavelength, and j is an imaginary unit.

3.1.2. Approximation When |k₂| << |k₁|

Considering that the wave number k₂ of the air medium is considerably lower than that of the seawater medium k₁, i.e., |k₂| << |k₁|, the corresponding |k₂²γ₁|/|k₁²γ₂| approaches zero and the higher-order term can be ignored:

$$\left|\frac{k_2^2{\gamma }_1}{k_1^2{\gamma }_2}\right|\approx \frac{\left|k_2^2\right|}{\left|k_1^2\right|}\frac{\left|\sqrt{k_1^2-{\lambda }^2}\right|}{\left|j\lambda \right|}\approx \left|\frac{k_2}{k_1}\right|\left|\sqrt{{\left|\frac{k_2}{\lambda }\right|}^2-1}\right|<<1$$

(3)

According to the aforementioned assumptions, the integration path in Figure 3b can replace the original integration path in Figure 3a; the wave number k₂ is very close to the origin of the coordinate system. Figure 3c shows the geometric diagram of γ₁.

3.1.3. Approximation d << ρ and z << ρ

Referring to (1), under the quasistatic assumption, the slot position of the Sommerfeld integral fulcrum k₂ is close to the zero point of the imaginary axis. Because the ELF near-field conditions in seawater meet the relationship equations d << ρ and z << ρ, the multivalue function of the Sommerfeld integral in seawater can be approximated as follows:

$$\frac{k_1^2{\gamma }_2-k_2^2{\gamma }_1}{k_1^2{\gamma }_2+k_2^2{\gamma }_1}=\frac{1-k_2^2{\gamma }_1/k_1^1{\gamma }_2}{1+k_2^2{\gamma }_1/k_1^1{\gamma }_2}\approx 1$$

(4)

Substituting the Equations (2)~(4) into the Sommerfeld integral expressions, the Sommerfeld integral expression of each electromagnetic field component at any observation point P in the homogeneous seawater medium can be simplified to

$$E_{1\rho }=-\frac{\omega {\mu }_{0}Idl}{4\pi k_1^2}\cos \varphi \left[k_1^2{F}_1(k_1,d_0)-\frac{1}{2}{F}_2(k_1,d_0)\right.\left.+\frac{1}{2}{G}_4(k_1,d_1)-\frac{k_1^2}{2}{H}_1(d_1)\right]$$

(5)

$$E_{1\varphi }=\frac{\omega {\mu }_{0}Idl}{4\pi k_1^2}\sin \varphi \left[k_1^2{F}_1(k_1,d_0)-\frac{1}{2}{F}_2(k_1,d_0)\right.\left.+\frac{1}{2}{G}_5(k_1,d_1)-\frac{k_1^2}{2}{H}_2(d_1)\right]$$

(6)

$$E_{1z}=\frac{j\omega {\mu }_{0}Idl}{4\pi k_1^2}\cos \varphi \left[\pm F_3(k_1,d_0)+G_1(k_1,d_1)\right]$$

(7)

$$B_{1\rho }=-\frac{{\mu }_{0}Idl}{4\pi }\sin \varphi \left[\pm F_4(k_1,d_0)+\frac{1}{2}{G}_2(k_1,d_1)-\frac{1}{2}{H}_3(d_1)\right]$$

(8)

$$B_{1\varphi }=-\frac{{\mu }_{0}Idl}{4\pi }\cos \varphi \left[\pm F_4(k_1,d_0)+\frac{1}{2}{G}_3(k_1,d_1)-\frac{1}{2}{H}_4(d_1)\right]$$

(9)

$$B_{1z}=\frac{j{\mu }_{0}Idl}{4\pi }\sin \varphi \left[F_5(k_1,d_0)-H_5(d_1)\right]$$

(10)

where F₁ (k₁, d₀)~F₅ (k₁, d₀) represents the direct wave from the field source point (0, 0, d) to any near-field observation point P(ρ, φ, z) in the lower half-space, G₁ (k₁, d₁)~G₅ (k₁, d₁) represents the reflected wave from the field source image point (0, 0, −d) to any near-field observation point (ρ, φ, z) in the lower half-space, and H₁ (d₁)~H₅ (d₁) represents the side wave affected by the interface of the two media. φ is azimuth coordinates. r₀ is the geometric distance from the source point to the receiving point of the seawater medium, r₁ is the geometric distance from the image point of the field source to the receiving point of the air medium, d₀ is the vertical height between the source and receiving points of the electric dipole in the seawater medium, and d₁ is the vertical height between the image point of the field source and receiving point of the air medium. r₀, r₁ and d₀, d₁ are defined as follows:

$$d_0=\left|z-d\right|,d_1=z+d$$

(11)

$$r_0=\sqrt{d_0^2+{\rho }^2},r_1=\sqrt{d_1^2+{\rho }^2}$$

(12)

3.2. Bessel Integral Solution

The integral expressions of each field component from Equation (5)~(10) can be reduced to infinite integrals containing Bessel functions. The expressions of direct and reflected waves can be obtained by strictly solving the corresponding integral. According to the general solution of the integral formula given by King, the analytical expressions of the integrals F₁ (k₁, d₀)~F₅ (k₁, d₀), G₁ (k₁, d₁)~G₅ (k₁, d₁) can be obtained [8], and we have given the detailed solution in the Appendix A. Therefore, we only need to find the solution of the integral formulas H₁ (d₁)~H₅ (d₁) to obtain the final expression of the electromagnetic field.

As the integral formulas H₁ (d₁)~H₅ (d₁) of the side wave component contain a slow decay oscillation function, which cannot be directly obtained analytically, we use the approximate method for asymptotic estimation. H₁ (d₁)~H₅ (d₁) are expressed as follows [13]:

$$H_1(d_1)={\displaystyle {\int }_0^{\infty }\left\{\frac{{\gamma }_2-{\gamma }_1}{{\gamma }_2+{\gamma }_1}[J_0(\lambda \rho )+J_2(\lambda \rho )]\right\}}{\gamma }_1^{-1}{e}^{j{\gamma }_1{d}_1}\lambda d\lambda$$

(13)

$$H_2(d_1)={\displaystyle {\int }_0^{\infty }\left\{\frac{{\gamma }_2-{\gamma }_1}{{\gamma }_2+{\gamma }_1}[J_0(\lambda \rho )-J_2(\lambda \rho )]\right\}}{\gamma }_1^{-1}{e}^{j{\gamma }_1{d}_1}\lambda d\lambda$$

(14)

$$H_3(d_1)={\displaystyle {\int }_0^{\infty }\left\{\frac{{\gamma }_2-{\gamma }_1}{{\gamma }_2+{\gamma }_1}[J_0(\lambda \rho )-J_2(\lambda \rho )]\right\}}{e}^{j{\gamma }_1\left(z+d_1\right)}\lambda d\lambda$$

(15)

$$H_4(d_1)={\displaystyle {\int }_0^{\infty }\left\{\frac{{\gamma }_2-{\gamma }_1}{{\gamma }_2+{\gamma }_1}[J_0(\lambda \rho )+J_2(\lambda \rho )]\right\}}{e}^{j{\gamma }_1\left(z+d_1\right)}\lambda d\lambda$$

(16)

$$H_5(d_1)={\displaystyle {\int }_0^{\infty }\frac{{\gamma }_2-{\gamma }_1}{{\gamma }_2+{\gamma }_1}}{J}_1(\lambda \rho )e^{j{\gamma }_1{d}_1}{\gamma }_1^{-1}{\lambda }^{2}d\lambda$$

(17)

where J_n (λρ), n = 0, 1, 2, is the expression of the n-order Bessel function.

In Equations (13)~(17), the integrand function contains the multivalued function term A(λ) = (γ₂ − γ₁)/(γ₂ + γ₁). As it is known from the form text that the intermediate variable γ₁ can be expressed by γ₁ ≈ jλ, the absolute values for γ₁, γ₂, and k₁ are approximately defined by a triangular relationship, as shown in Figure 3d. According to the quasistatic approximation (2),

$$0<\left|{\gamma }_2-{\gamma }_1\right|\approx \left|-j\lambda -\sqrt{k_1^2-{\lambda }^2}\right|<\sqrt{{\lambda }^2+k_1^2-{\lambda }^2}=\left|k_1\right|$$

(18)

Based on Equation (18), the absolute value of vector γ₂ − γ₁ is proportional to the absolute value of vector k₁, which can be deduced as follows:

$$\left|{\gamma }_2-{\gamma }_1-k_1\right|d_1\approx \left|j\lambda -\sqrt{k_1^2-{\lambda }^2-k_1}\right|d_1\approx \xi \left|k_1{d}_1\right|<<1$$

(19)

where |ξ|≤1. Therefore, for infinitely small imaginary numbers [17],

$$j\left({\gamma }_2-{\gamma }_1-k_1\right)d_1\approx e^{j({\gamma }_2-{\gamma }_1-k_1)d_1}-1$$

(20)

In addition, the McLaughlin expansion of the function $e^{j({\gamma }_2-{\gamma }_1-k_1)d_m}$ is reserved for the first two orders:

$$e^{j({\gamma }_2-{\gamma }_1-k_1)d_1}\approx 1+j({\gamma }_2-{\gamma }_1-k_1)d_1-\frac{{(({\gamma }_2-{\gamma }_1-k_1)d_1)}^2}{2!},-\infty <0<\infty$$

(21)

Therefore,

$${({\gamma }_2-{\gamma }_1)}^2=\frac{2}{d_1^2}-\frac{2e^{j({\gamma }_2-{\gamma }_1-k_1)d_1}}{d_1^2}+\frac{2j({\gamma }_2-{\gamma }_1-k_1)d_1}{d_1^2}-k_1^2+2k_1({\gamma }_2-{\gamma }_1)$$

(22)

Substituting Equations (20) into (22), and simplifying Equation (22) further, we obtain the following:

$${({\gamma }_2-{\gamma }_1)}^2\approx 2j{k}_1\frac{e^{j({\gamma }_2-{\gamma }_1-k_1)d_1}-1}{d_1}+k_1^2$$

(23)

Combining the multivalued function A(λ) = (γ₂ − γ₁)/(γ₂ + γ₁) and Equation (23), we obtain the following:

$$A(\lambda )=\frac{{\gamma }_2-{\gamma }_1}{{\gamma }_2+{\gamma }_1}=\frac{{({\gamma }_2-{\gamma }_1)}^2}{k_2^2-k_1^2}\approx 2j{k}_1\frac{e^{j({\gamma }_2-{\gamma }_1-k_1)d_1}-1}{(k_2^2-k_1^2)d_1}+\frac{k_1^2}{k_2^2-k_1^2}$$

(24)

According to the property of the Bessel function, H₁ (d₁)~H₅ (d₁) along the real axis can be converted into the integral of slits C₁ and C₂ in Figure 3b, and the approximate expressions of H₁ (d₁)~H₅ (d₁) can be obtained as follows:

$$H_1(d_1)={\displaystyle {\int }_0^{\infty }\frac{{\left({\gamma }_2-{\gamma }_1\right)}^2}{k_2^2-k_1^2}}\left[J_0\left(\lambda \rho \right)+J_2\left(\lambda \rho \right)\right]{\gamma }_1^{-1}{e}^{j{\gamma }_1{d}_1}\lambda d\lambda \approx \frac{2}{\left(k_2^2-k_1^2\right)d_1{\rho }^2}\left[\left(-2j+k_1{d}_1\right)\left(e^{j{k}_1{d}_1}-e^{j{k}_1{r}_1}\right)+2j\left(e^{j{k}_2{d}_1}-e^{j{k}_1{r}_1}\right)\right]$$

(25)

$$H_2(d_1)={\displaystyle {\int }_0^{\infty }\frac{{\left({\gamma }_2-{\gamma }_1\right)}^2}{k_2^2-k_1^2}}\left[J_0\left(\lambda \rho \right)-J_2\left(\lambda \rho \right)\right]{\gamma }_1^{-1}{e}^{j{\gamma }_1{d}_1}\lambda d\lambda \approx \frac{2}{\left(k_2^2-k_1^2\right)d_1}\left\{\frac{2j{k}_1}{k_2}\left[\frac{e^{j{k}_2{d}_1}}{{\rho }^2}+\left(\frac{j{k}_2}{r_1}-\frac{1}{{\rho }^2}\right)e^{j{k}_2{r}_1}\right]\right.\left.-\left(2j-k_1{d}_1\right)\left[\frac{e^{j{k}_2{d}_1}}{{\rho }^2}+\left(\frac{j{k}_2}{r_1}-\frac{1}{{\rho }^2}\right)e^{j{k}_1{r}_1}\right]\right\}$$

(26)

$$H_3(d_1)={\displaystyle {\int }_0^{\infty }\frac{{\left({\gamma }_2-{\gamma }_1\right)}^2}{k_2^2-k_1^2}}\left[J_0\left(\lambda \rho \right)-J_2\left(\lambda \rho \right)\right]e^{j{\gamma }_1\left(z+d_1\right)}\lambda d\lambda \approx \frac{2k_1}{\left(k_2^2-k_1^2\right)d_1}\left\{\begin{array}{l}\left(2j-k_1{d}_1\right)\left[\frac{e^{j{k}_1{d}_1}}{{\rho }^2}+\frac{d_1{e}^{j{k}_1{r}_1}}{r_1}\left(\frac{j{k}_1}{r_1}-\frac{1}{r_1^2}-\frac{1}{{\rho }^2}\right)\right]\\ -2j\left[\frac{e^{j{k}_2{d}_1}}{{\rho }^2}+\frac{d_1{e}^{j{k}_2{r}_1}}{r_1}\left(\frac{j{k}_2}{r_1}-\frac{1}{r_1^2}-\frac{1}{{\rho }^2}\right)\right]\end{array}\right\}$$

(27)

$$H_4(d_1)={\displaystyle {\int }_0^{\infty }\frac{{\left({\gamma }_2-{\gamma }_1\right)}^2}{k_2^2-k_1^2}}\left[J_0\left(\lambda \rho \right)+J_2\left(\lambda \rho \right)\right]e^{j{\gamma }_1\left(z+d_1\right)}\lambda d\lambda \approx \frac{2k_1}{\left(k_2^2-k_1^2\right)d_1}\left\{\left(-2j+k_1{d}_1\right)\left(\frac{e^{j{k}_1{d}_1}}{{\rho }^2}-\frac{d_1{e}^{j{k}_1{r}_1}}{r_1{\rho }^2}\right)\right.\left.+2j\left(\frac{e^{j{k}_2{d}_1}}{{\rho }^2}-\frac{d_1{e}^{j{k}_2{r}_1}}{r_1{\rho }^2}\right)\right\}$$

(28)

$$H_5(d_1)={\displaystyle {\int }_0^{\infty }\frac{{\left({\gamma }_2-{\gamma }_1\right)}^2}{k_2^2-k_1^2}}{J}_1\left(\lambda \rho \right){\gamma }_1^{-1}{e}^{j{\gamma }_1{d}_1}{\lambda }^{2}d\lambda \approx \frac{k_1\rho }{\left(k_2^2-k_1^2\right)d_1}\left\{-2k_2{e}^{j{k}_2{r}_1}\left(\frac{j}{r_1^2}-\frac{1}{k_2{r}_1^3}\right)\right.\left.-e^{j{k}_1{r}_1}\left(j{k}_1^2{d}_1+2k_1\right)\left(\frac{j}{r_1^2}-\frac{1}{k_1{r}_1^3}\right)\right\}$$

(29)

3.3. Simplification of Field Component Expression

Let the electric moment be Idl = 1 A‧m; substituting Equations (25) to (29) into (5) to (10), respectively, we obtain the approximate expression of each EM field component. Taking the EM field components E_z as an example, this paper gives the process of simplifying the near-field approximate expression of the vertical magnetic field component. For k₂ρ << 1, the expressions of E_z can be given as follows:

$${E^{\prime }}_{1z}^{}=\frac{j\omega {\mu }_0\rho }{4\pi k_1}\cos \varphi \left[\mp \frac{d_0}{r_0}\left(\frac{k_1}{r_0^2}+\frac{3j}{r_0^3}-\frac{3}{k_1{r}_0^4}\right)e^{j{k}_1{r}_0}-\frac{d_1}{r_1}\left(\frac{k_1}{r_1^2}+\frac{3j}{r_1^3}-\frac{3}{k_1{r}_1^4}\right)e^{j{k}_1{r}_1}\right]$$

(30)

In the equation number, “+” is taken when z ≥ d, and “−” is taken when 0 ≤ z ≤ d. According to the quasistatic assumption, the distance relationship between the field source point and observation point is ρ >> d, ρ >> z, and r₀ ≈ r₁ ≈ ρ. Therefore, the approximate expression of the vertical EM field components E_z satisfying the quasistatic assumption can be obtained as follows:

$${E^{\prime }}_{1z}^{}=\frac{j\omega {\mu }_0\rho }{4\pi k_1}\cos \varphi \left(\frac{k_1}{{\rho }^2}+\frac{3j}{{\rho }^3}-\frac{3}{k_1{\rho }^4}\right)e^{j{k}_1\rho }\left(\mp d_0-d_1\right)$$

(31)

The second approximation of $e^{j{k}_1\rho }$ was expanded using McLaughlin’s progressive formula. In the process of simplification, the attenuation rate of EM waves in air was considerably less than that in seawater; thus, it meets the requirements of Im(k₂) << Im(k₁). The quasistatic approximate expression can be further simplified as follows:

$${E^{\prime }}_{1z}^{}=\frac{j\omega {\mu }_0}{4\pi k_1}\cos \varphi \left(\frac{k_1}{2{\rho }^2}+\frac{j{k}_1^2}{2\rho }\right)\left(\mp d_0+d_1\right)$$

(32)

In the same way, the near-field approximate expressions of the EM field components in the remaining “air–seawater” half-space can be obtained.

4. Spatial Distribution of EM Field Intensity in the Near-Field Region

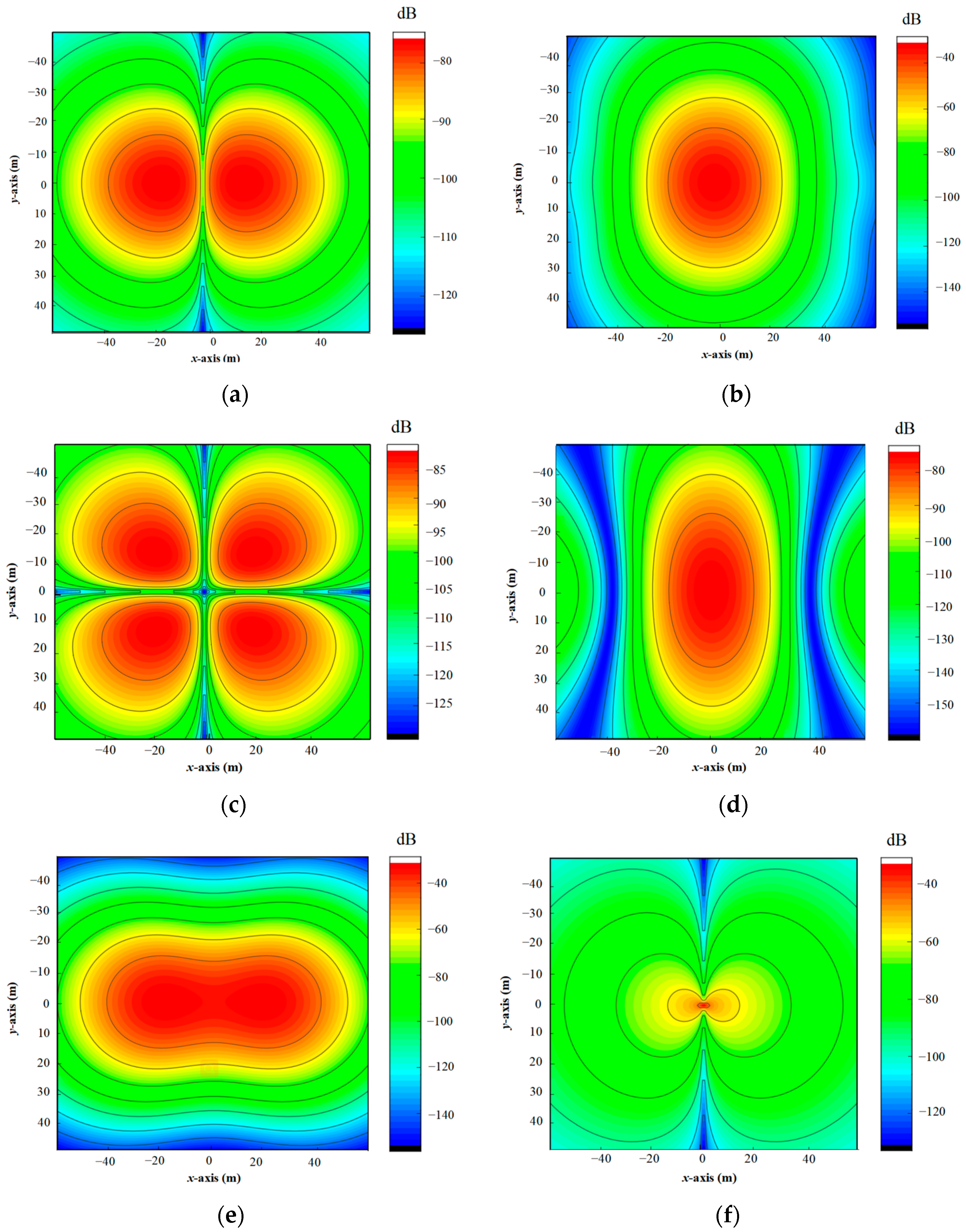
4.1. Spatial Distribution of EM Field Intensity

To further study the ELF near-field distribution of the HED antenna in seawater, we selected the model shown in Figure 2 and used the algorithm to evaluate the distribution of the EM field intensity of the observation plane on the square grid 100 m × 100 m at the plane of z = 1 m.

Assuming that the distance from the horizontal antenna to the sea surface is d = 10 m, the electric moment is Idl = 1A‧m, φ = π/4, the working frequency is 10 Hz, the propagation distance is ρ = 5000 m, and the height from the observation point to the sea surface is z = 1 m; μ₀ and ε₀ are the permeability and dielectric constant in a vacuum, respectively. The conductivity and relative permittivity of seawater are σ₁ = 4 S/m and ε₁ = 80, respectively. The EM field components changed with the height of the observation point. In the model shown in Figure 2, the coordinate origin is taken as the center, and a square area with a length and width of 100 m is obtained at the plane of z = 1 m. The amplitude distributions of each field component were simulated using Delphi software and are shown in Figure 4.

In the model shown in Figure 2, an HED antenna with a working frequency of 10 Hz is placed underwater at 1 m away from the sea surface. A voltage source is fed at the center point of the antenna. It is considered that the HED antenna is excited by an equal amplitude and phase source in order to analyze the law of field distribution in the underwater HED antenna. The radius of the thin wire is 2 cm. The wavelength of an EM wave at 10 Hz in seawater is approximately equal to 0.5 m for seawater conductivity equal to 4 S/m, and it is about 3 × 10⁷ m in air.

The results for electric fields are shown in Figure 4a–c, which include four color intensity plots for the three electric field components and the magnitude of the electric field. E_ρ exhibits maximum field intensity along the x-axis, and minimum field intensity along the y-axis, while E_z clearly shows that the shape and polarized direction for the HED antenna are placed along the y-axis; E_φ demonstrates that there is a strong electric field intensity in the y-axis direction and the fastest attenuation in the x-axis direction. In addition, the vertical electric component E_z is much stronger than E_ρ and E_φ for near-field region distance propagation in any direction, and the minimum attenuation is 15 dB. At the same time, we should also focus on the electric field strength in the x-axis direction of E_ρ and the y-axis direction of E_φ. Similar plots for magnetic fields are shown in Figure 4d–f. Figure 4d,e show the field distribution in air; the field distributions of H_ρ and H_φ at 10 Hz are drawn on the z = 1 m plane above the air–sea interface. It can be seen that H_ρ and H_φ have an obvious attenuation mutation point at 40 m, which may be caused by changes in the interface between air and seawater. Meanwhile, we can see that H_φ receives the strongest magnetic field strength in the x-axis direction, the decay rate is the slowest, and the lowest attenuation value is 30 dB, so we should pay attention to the magnetic field strength in this direction. Figure 4f shows that the maximum field intensity of H_z is along the x-axis, and the minimum field intensity is along the y-axis, while the radical magnetic component H_z is a little stronger than H_ρ and H_φ for near-field region distance in any direction, and the attenuation speed is relatively stable, and the minimum attenuation rate is maintained at 40 dB, which is suitable for near-field region distance propagation.

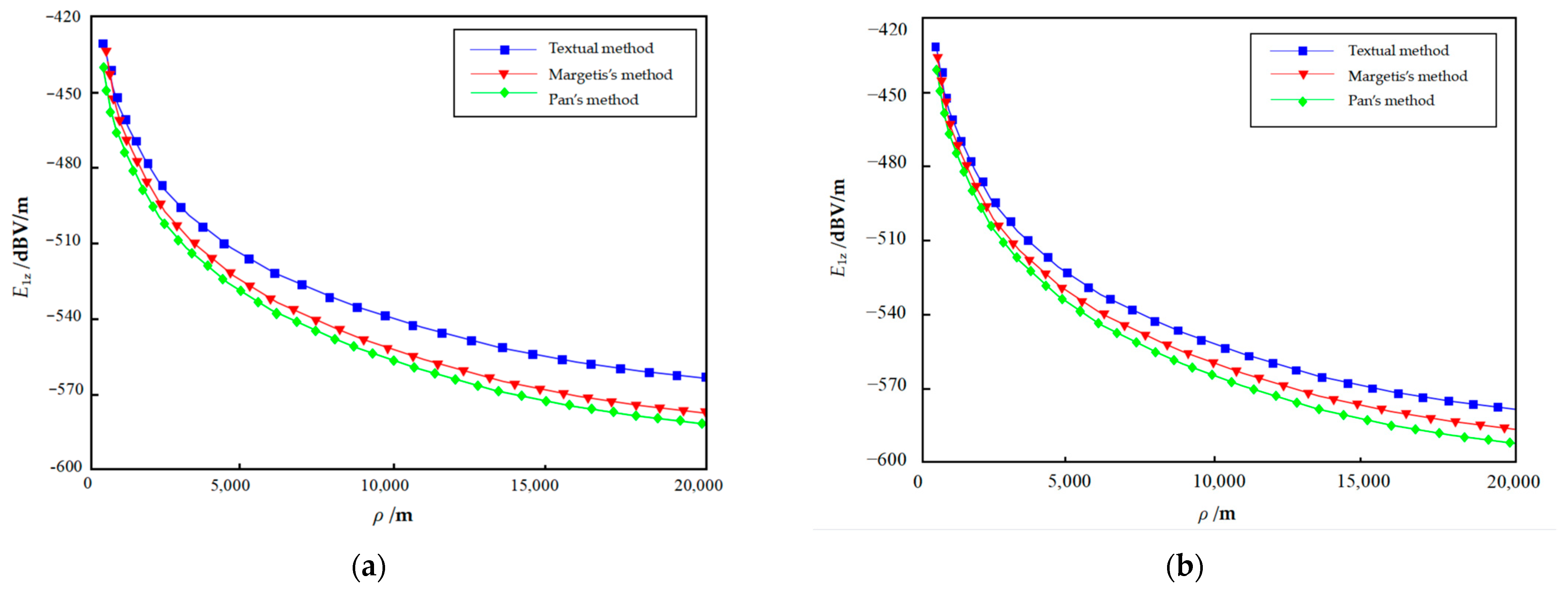
4.2. Comparative Validation Analysis

In order to verify the effectiveness of the method presented in this paper, Pan’s approximation [27] and Margetis’s exact expression [9] are respectively obtained by MacClaurin’s progressive simplification, and the obtained results are compared with the method presented in this paper. If both the field and source points are in seawater, the seawater and air conductivity are σ₁ = 4 S/m and σ₂ = 1.8 × 10⁻⁴ S/m, respectively, and the relative dielectric constants are ε_r1 = 80 and ε_r2 = 1, respectively. When calculated at 3 Hz and 30 Hz, the electric field component in the ρ direction changes with the distance, as shown in Figure 5.

As can be seen from Figure 5, the electric field components in the ρ direction obtained by different methods decrease with the increase in radial distance, and the variation trend is basically consistent. When the frequency is the same, the amplitude of E_1ρ obtained by Pan approximation decreases the most with distance, while the amplitude of E_1ρ obtained by Margetis’s exact expression is in the middle of the two approximation methods, and the amplitude obtained by this method decreases at the slowest rate, which also verifies that the method proposed in this paper has a good accuracy in calculating the electric field component in the near-field region. It can be seen from Figure 5 that at the same site, the E_1ρ amplitude decreases with the increase in operating frequency, and the amplitude decreases greatly in the ELF band high-frequency band. When the horizontal distance is less than 5000 m, the E_1ρ amplitude decreases significantly with the increase in the horizontal distance, and when the horizontal distance is greater than 5000 m, the decline trend tends to be gentle. As shown in Figure 5a, when the electric field component E_1ρ is operating at 3 Hz, the field strength decreases with the increase in the horizontal distance in the direction of ρ. If the horizontal distance is greater than 10 km, the seawater has little influence on the E_1ρ amplitude of the field point when it is higher than 500 m.

5. Conclusions

In this research, we employed the “air–seawater” homogeneous half-space model to obtain EM field integral expression in ELF near-field region under HED antenna excitation based on the general expression of the Sommerfeld integral using the quasistatic approximation method. The EM field distribution of an underwater dipole was simulated to calculate the field distribution in shallow seawater. After the calculation, the EM field distribution law in the vicinity of the HED antenna in seawater was analyzed. The simulated results show different attenuations with distance for each component. The vertical electric component E_z and radical magnetic components H_φ are found to be of the greatest potential for long-distance propagation among the electric and magnetic components, respectively. Finally, we verified the correctness of the proposed method by comparing it with Pan’s approximation method and Margetis’s exact expression approximation method, exhibiting the great potential of the proposed method for various kinds of applications in shallow sea environments. The proposed method could be also applied to the excitation of vertical and horizontal magnetic dipoles (VMDs/HMDs) and vertical electric dipoles (VEDs).