Method for Simulation Modeling of Integrated Multi-Energy Systems Based on the Concept of an Energy Hub

Abstract

The concept of multi-energy systems (MES) is widely applied in various areas of energy supply. This approach makes it possible to analyze the distribution of energy flows and their mutual influence both for local facilities and for power supply systems. At the same time, currently, promising systems for analysis, forecast, and control of the behavior of energy facilities are those that employ innovative methods, for example, different technologies of mathematical modeling. Their successful application requires a methodological approach to build mathematical models of integrated energy systems relying on simulation modeling. The approach proposed in this paper is based on the concept of an energy hub. It has been tested on a simulation model for two energy supply channels for a fragment of a real-world energy facility. The presented methodological approach to create mathematical models of integrated energy systems is based on simulation. This approach offers broad prospects for expanding the capabilities in the design and operation of integrated multi-energy systems.

1. Introduction

In recent years, energy systems have undergone substantial changes caused by a host of factors. These are a widespread use of renewable energy resources and energy storage devices, and the presence of active adaptive elements allowing control of branched energy systems in real time. Thus, power systems are nowadays multi-layered and complexly integrated engineering objects. A ramified information structure in the stages of energy generation, transmission, and use made it necessary to use new approaches to control and optimize these systems. This circumstance, in turn, has brought about fundamentally new issues, which can be resolved only within the framework of the fourth industrial revolution.

The above factors have led to the development and creation of principally new technical and information systems that are mathematical models. Currently, this approach is being implemented independently in each energy industry.

However, there are some energy objects for which the possibility of a quick and economically feasible transformation of various types of energy carriers into each other is essential. Research in this area is conducted based on the multi-energy systems (MES) concept, which relies on the energy hub concept [1].

Traditionally, various channels of energy (heat, gas, electricity) supply are considered independently of each other. At the process level, this affects various approaches to collect process information (data transfer protocols, forms of information storage, data analysis and presentation). Data on various channels are poorly integrated with each other (different data rates, sampling times). The level of analysis involves various mathematical descriptions of objects and various approaches to model such objects. A similar approach is currently being observed in the development of mathematical models in various energy supply applications. Various structural models are built for power, heat, and gas supply systems. For example, this approach cannot be used to create digital twins of multi-energy systems [2,3,4].

A distinctive feature of multi-energy systems is the need to consider various energy flows jointly, given their mutual influence. Traditionally, a methodological approach and mathematical tools for the joint use of various energy flows are considered in terms of their capability to convert one type of energy into another and in terms of their storage systems. The mathematical description of such models traditionally consists of their representation in a matrix notation. Such a mathematical description imposes significant restrictions on taking into account the performance characteristics of technical devices that are part of the energy hub. It should be noted that the characteristics of these devices have a non-linear dependence on the load.

At the same time, in recent years, methods of simulation modeling of various technological objects have been widely used. Some authors view this approach as one of the promising areas for the creation of mathematical models [5,6].

It is worth noting that the main issue facing the widespread adoption of the MES concept in practice is the absence of a modeling technique for the analysis of the structure and behavior of an object in all energy supply channels [7].

The paper presents a methodological approach to create mathematical models of integrated energy systems based on simulation modeling. The model rests on the energy hub concept. The novelty of this approach is the combination of the principles of simulation modeling and the concept of an energy hub, which makes it possible to take into account the nonlinearity of the change in characteristics depending on the loads. Also, the novelty of the approach is the use of a universal system of units of measurement for all technical parameters. The proposed approach offers broad prospects for expanding the design and operation capabilities for integrated multi-energy systems.

The structure of the article is as follows. In Section 1, the problem statement is given and the novelty of the research is described. In Section 2 of the article, the scope of the developed approach to model the concept of a multi-energy hub is considered. Section 3 provides traditional mathematical descriptions of multi-energy systems. On this basis, the principles of implementation of the simulation model are presented. Section 4 considers the construction of a simulation model for three channels of energy supply and presents a simulation model. The simulation results are given. In Section 5, conclusions are formulated.

2. Materials and Methods

Modern technological structures are complex multifactorial systems. The presence of active adaptive components, which allow all energy fields, including energy systems, to be controlled in real time, sets completely new objectives for control systems.

For the time being, the generally accepted control principles for energy objects are the creation of a mathematical models. This approach is grounded on the basic principles of the fourth industrial revolution (Industrial 4.0) and the model-based systems engineering. A mathematical model is a virtual copy of an object that faithfully reproduces and sets the structure, state, and behavior of this object in real time [8].

The main functions performed by the mathematical models include the following functions [9]:

• Collecting and processing the information that accurately reflects the state of an object in real time;
• Predicting the behavior of an object both in regular and emergency situations;
• Generating adequate control actions on the object.
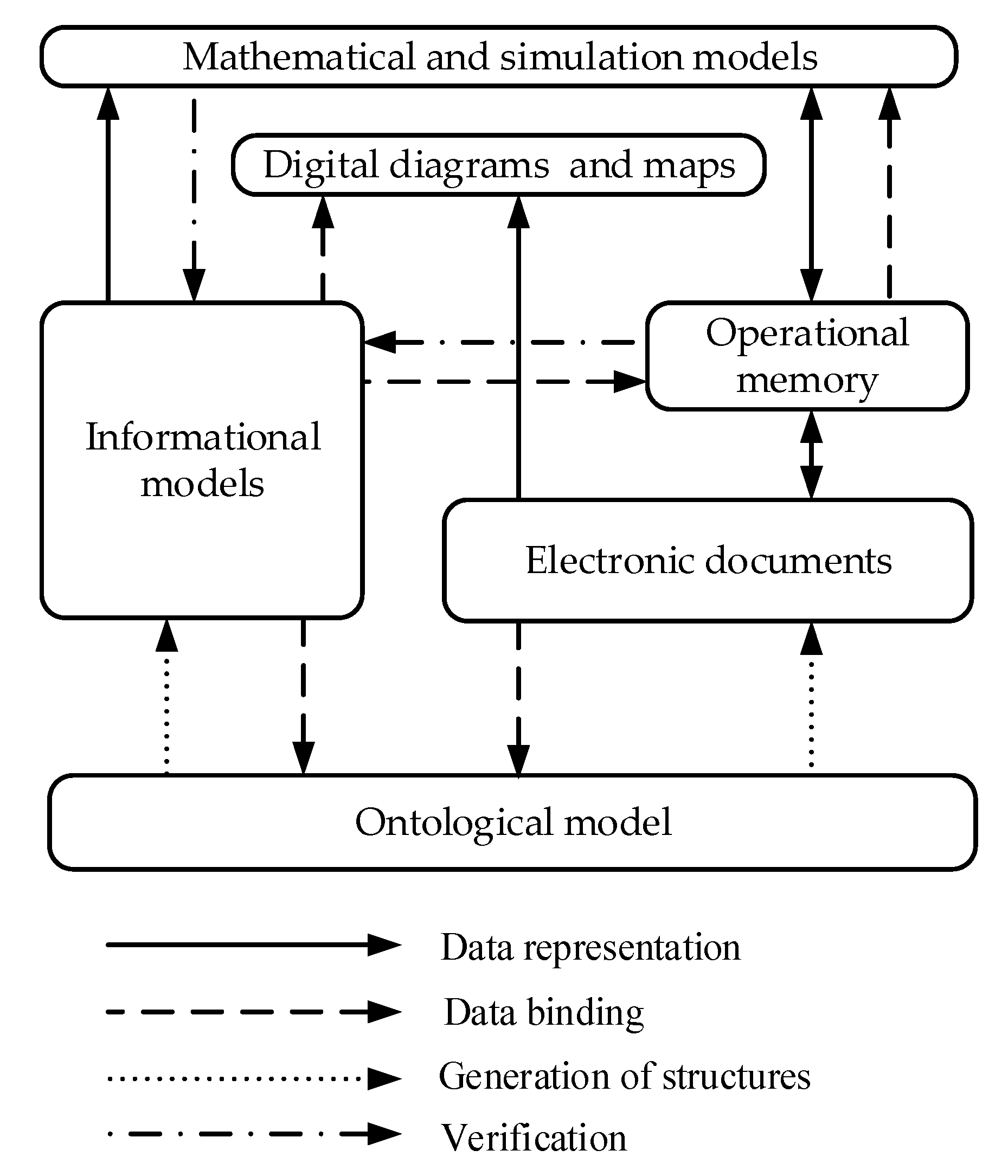
• The main components of the mathematical models of a technical object are listed below:
• Ontological models;
• Digital diagrams and maps;
• Electronic documentation;
• Information models;
• Real-time information;
• Mathematical and simulation models.

Figure 1 presents a structural diagram of the interaction of mathematical model components proposed in [10].

The individual components of the mathematical models’ infrastructure, when developed and operated, interact both with each other and with the data sources.

Individual components of the mathematical models are developed and refined even in the design stage of the real physical object. In the initial stage, a decisive role is played by mathematical or simulation models capable of predicting the behavior of the original, virtually working out its behavior in various conditions, and conducting a multi-criteria estimation.

Different levels of the internal structure of the mathematical models can be implemented in practice by different digital platforms. This study does not intend to examine in detail the entire internal structure of the mathematical models. A central problem solved by the mathematical models is the one related to the optimization of the functioning of a real-world technological object. This problem cannot be solved without a fairly simple, but at the same time effective mathematical or simulation model.

A distinctive feature of the mathematical models’ concept in the energy industries is that mathematical or simulation models are developed and verified using the existing generating and network structures. This feature enables us to use two different approaches to create simulation models:

• Models of physical processes that involve solving the systems of differential equations numerically;
• Models based on multilayer neural networks.

Both of these approaches have their advantages and disadvantages. The first approach had appeared long before the concept of mathematical models. Its undoubted merit is the well-developed methodological apparatus for modeling. Its use, however, is limited if it is impossible to obtain a rigorous mathematical description of the technical object.

The second approach can find approximations of unknown dependencies by training on an array of known data. This model can predict the behavior of a physical object when the description of its laws is very complex or completely indefinite. This approach, however, is only possible if there is a good training sample. It should also be noted that the forecasting accuracy will be rather low in emergencies because their observation history is small.

The choice of an approach will depend solely on the characteristics of the existing infrastructure, specific features of energy processes, their speed, and the ability of the information structure to transmit and process large amounts of data in real time. The above factors are decisive when choosing a methodology for creating a mathematical model in various energy industries.

3. Results

The contemporary structure of energy supply is a complex multifactorial system. Its distinctive feature is the presence of various generation systems and, hence, diverse energy flows: electrical, heat, gas, and others [11,12]. At the same time, along with traditional generation systems (electric and thermal power plants), there is wide use of renewable sources and storage systems in all energy supply channels [13,14,15]. There are also systems developed and widely used to quickly and economically convert various types of energy into each other: gas turbine plants, electric heating boilers, and others [16,17,18].

The above factors set a whole host of totally new objectives for the modern energy sector, which are related to the reliability, quality, and choice of the most economically feasible methods of energy production and transmission through various channels.

Thus, it became necessary to consider various energy systems, given their mutual influence on each other. The development of this area brought about the concepts of multi-energy system and energy hub.

The authors of [19] address the main principles of the energy hub concept. The relevance of this approach was substantiated by an analysis of existing energy systems and prospects for the development of future ones. The study revealed the need to address both conventional energy sources and intensive development of various non-conventional ones in the energy system planning and expansion strategy. The principal technical possibilities for the implementation of this concept are considered. The authors laid the methodological foundations for the mathematical description of multi-energy systems [20]. This approach is based on the following representation of the energy hub (Figure 2).

Where n is the number of ports. Each port consists of k nodes (k is the number of considered energy carriers). Each port is defined by the power vector $\overrightarrow{P}$. Then, the power vector for three types of energy carriers (electrical, chemical, thermal) can be represented as

$$\overrightarrow{P}=\left(\begin{array}{c}\begin{array}{c}{P}_{el}\\ P_{ch}\end{array}\\ P_{th}\end{array}\right),$$

(1)

where P_el, P_ch, _and P_th are powers through the channel of electrical, chemical, and thermal energy, respectively. The relation between two nodes can be determined through the transmission ratio ${ŋ}_{\alpha \beta }$:

$$P_{\beta }={ŋ}_{\alpha \beta }{P}_{\alpha },$$

(2)

where P_α and P_β are the input and output energy, respectively.

In turn,

$$P_{\alpha }=k_{\beta \alpha }{P}_{\beta },$$

(3)

where k_βα is the feedback coefficient, and α and β are indices of arbitrary energy channels.

The relation between two nodes can be determined through the transmission ratio c_αβ:

$$C_{\alpha \beta }={\displaystyle \sum }_P{ŋ}_{\alpha \beta }^{\left(P\right)}{\mathsf{\nu }}_{\alpha \beta }^{\left(P\right)},$$

(4)

where ${\mathsf{\nu }}_{\alpha \beta }^{\left(P\right)}$ is the dispatch factor.

Equations for an arbitrary number of channels can have the form

$${\overrightarrow{P}}_j={\overrightarrow{C}}_{ij}{\overrightarrow{P}}_i;$$

(5)

$${\overrightarrow{P}}_i={\overrightarrow{D}}_{ij}{\overrightarrow{P}}_j,$$

(6)

where ${\overrightarrow{P}}_j,$ ${\overrightarrow{P}}_i$ are power vectors, ${\overrightarrow{C}}_{ij}, {\overrightarrow{D}}_{ij}$ are the transmission ratio and feedback coefficients.

Later, M. Geidl and G. Andersson in [21,22,23,24] developed and refined the main points of this concept.

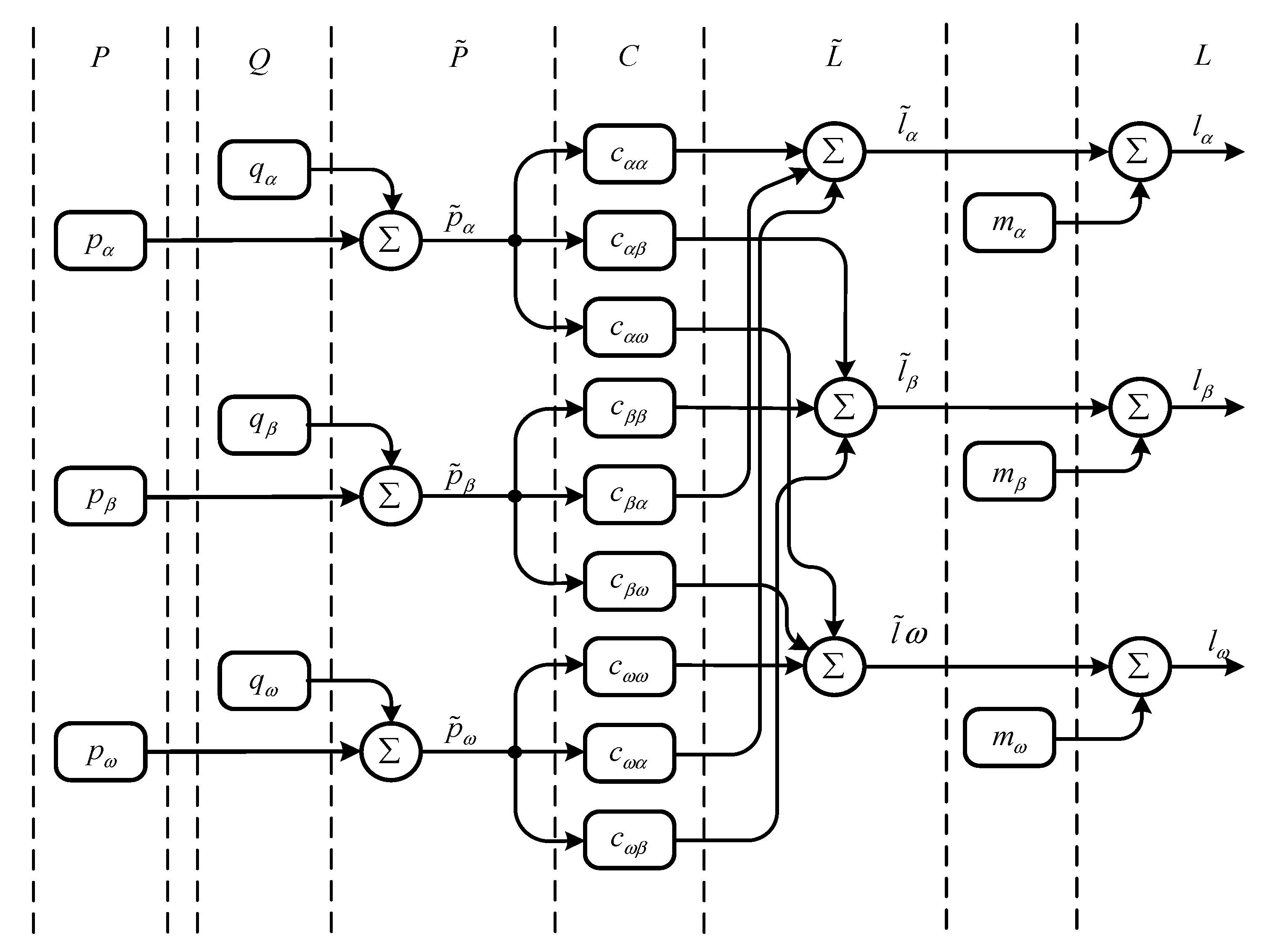
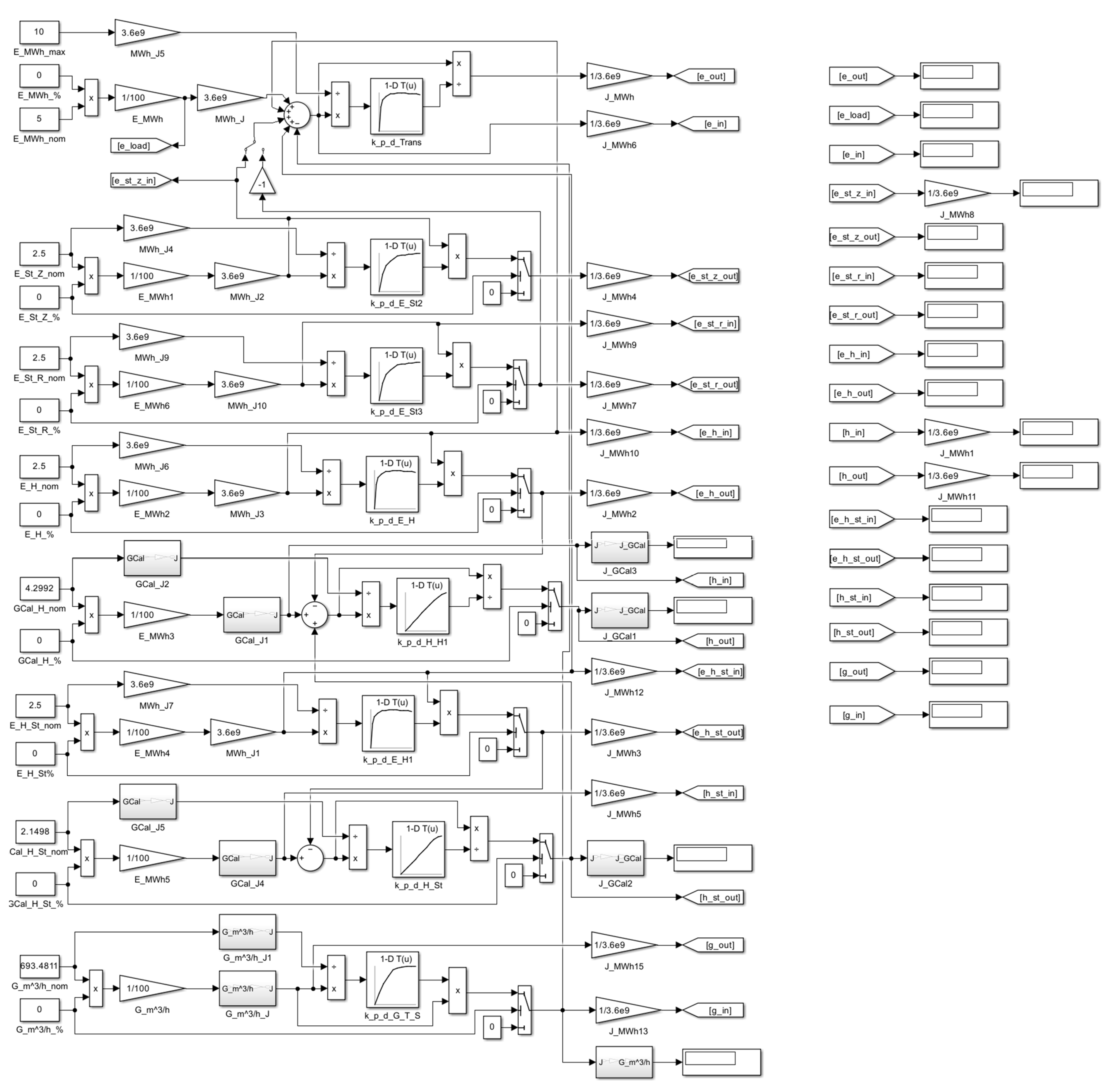
An energy hub is defined as an interface between energy sources, consumers, and the transmission infrastructure. The energy hub contains the following basic components:

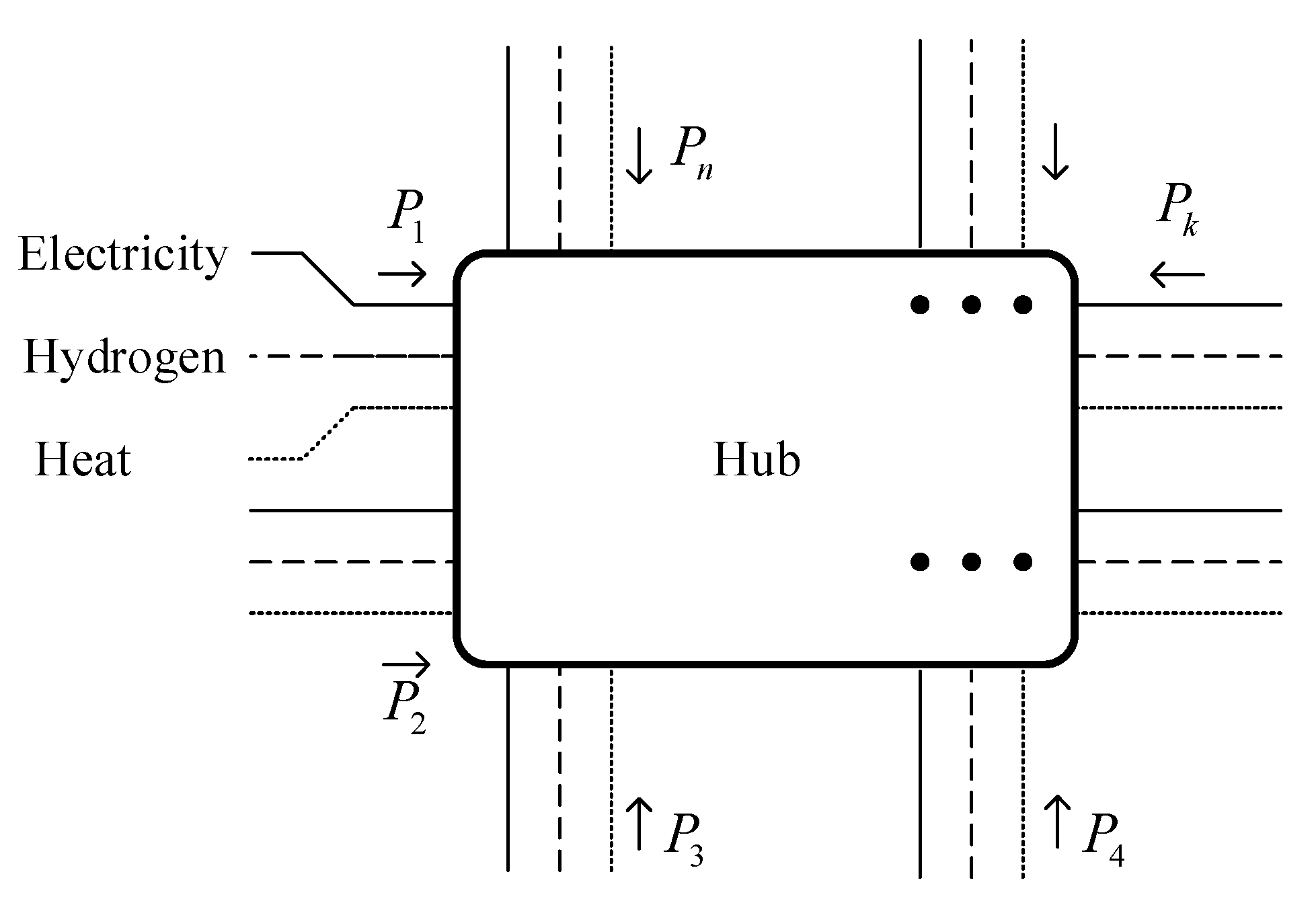
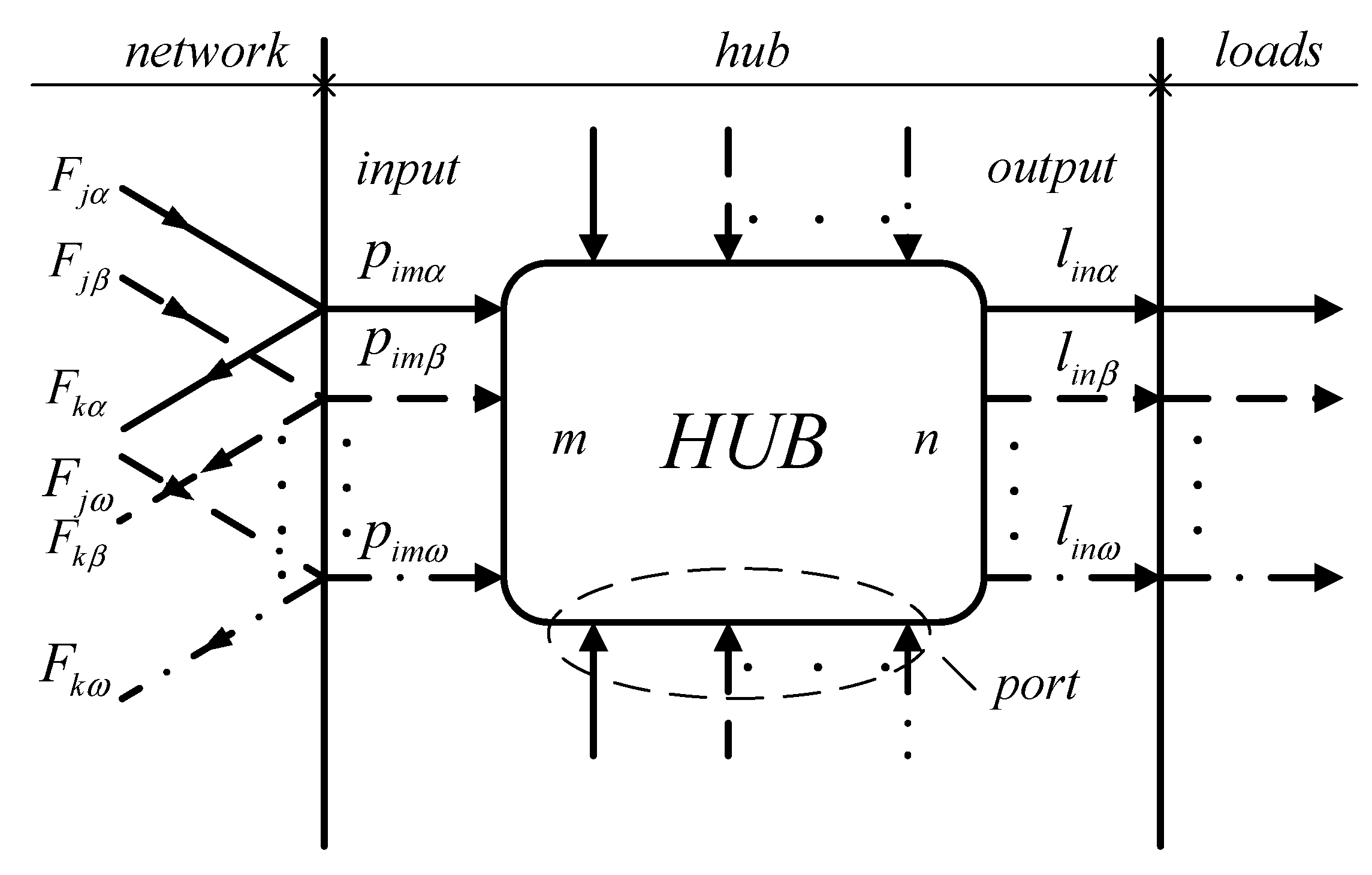
• Input and output;
• Converters of various types of energy into each other;
• Energy storage systems.
• The study of multi-energy systems was conducted under the following assumptions:
• The system is in a steady state;
• The energy flow has the direction from input to output;
• Energy flows are characterized only by energy indices.

A flow diagram of an energy hub with ports is shown in Figure 3.

The mathematical description of the energy hub, which relates the input and output flows through various energy channels in a matrix, is shown below:

$$\underset{output\hspace{0.17em}{L}_{in}}{\underbrace{\left|\begin{array}{c}{l}_{in\alpha }\\ ⋮\\ l_{in\omega }\end{array}\right|}}=\underset{C_{imn}}{\underbrace{\left|\begin{array}{ccc}{c}_{\alpha \alpha }& \cdots & c_{\omega \alpha }\\ ⋮& \ddots & ⋮\\ c_{\alpha \omega }& \cdots & c_{\omega \omega }\end{array}\right|}}\underset{input\hspace{0.17em}{P}_{im}}{\underbrace{\left|\begin{array}{c}{p}_{im\alpha 1}\\ ⋮\\ p_{im\omega }\end{array}\right|}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}$$

(7)

where C_imn is a direct transformation matrix.

The direct transformation matrix determines the internal relations between the energy hub and the factors of converting one type of energy to another. The system of Equation (7) allows obtaining the amount of energy for each of the input channels required to provide the energy load curves of the consumer [25].

In the case of solving the inverse problem, a matrix of inverse transformations is introduced:

$$\underset{input\hspace{0.17em}{P}_{im}}{\underbrace{\left|\begin{array}{c}{p}_{im\alpha }\\ ⋮\\ p_{im\omega }\end{array}\right|}}=\underset{D_{inm}}{\underbrace{\left|\begin{array}{ccc}{d}_{\alpha \alpha }& \cdots & d_{\omega \alpha }\\ ⋮& \ddots & ⋮\\ d_{\alpha \omega }& \cdots & d_{\omega }\end{array}\right|}}\underset{output\hspace{0.17em}{L}_{in}}{\underbrace{\left|\begin{array}{c}{l}_{im\alpha 1}\\ ⋮\\ l_{im\omega }\end{array}\right|}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}$$

(8)

The relationship between the coefficients of the inverse and direct transformation has an unambiguous form:

$$d_{\beta \alpha }=\left\{\begin{array}{c}{c}_{\alpha \beta }^{-1} if c_{\alpha \beta }\ne 0\\ 0 else \end{array}\right.$$

(9)

Equations (7) and (8) describe the energy transfer port → port. In the case of n output ports, the energy for each input channel is determined as follows:

$$P_{im}={\displaystyle \sum }_{n=1}^N{D}_{inm}{L}_{in}$$

(10)

This mathematical description of the energy hub does not include parameters to factor in energy flows for the case of energy storage devices.

In 2007, M. Geidel [26] identified the application areas for the energy hub concept. These included the ones listed below:

• Power plants with cogeneration and trigeneration [27];
• Large industrial entities employing various types of energy carriers in their technological process;
• Large office and administrative buildings;
• Limited geographic areas;
• Islanded energy systems.

It is worth noting that the study presented in [28] investigated mostly multi-energy systems under the following assumptions:

• All transient processes are damped, the system is in a steady state, and all values remain practically constant;
• Losses are taken into account only for the energy hub elements;
• Energy flows are directed from input to output;
• Power flows through converting devices are characterized only by energy and efficiency.

Based on the above mathematical description of the energy hub, the redistribution of energy flows was considered given the energy storage systems.

Figure 4 shows an energy storage device as a simplified model [29].

The energy storage device is assumed to consist of the internal idealized storage unit and an external interface. The steady-state values of the input and output power are related to each other by the following relationship:

$${\tilde{q}}_{\alpha }=e_{\alpha }{q}_{\alpha }.$$

(11)

Given the direction of the energy flow (charge, discharge), we determine the coefficient $e_{\alpha }$ as

$$d_{\beta \alpha }=\left\{\begin{array}{c}{e}_{\alpha }^{+} if q_{\alpha }\ge 0 \left(charging/standby\right)\\ \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$e_{\alpha }^{-} $}\right. 0 else \left(discharging\right) \end{array}\right.$$

(12)

In general, an energy hub can contain an arbitrary number of energy storage devices. They can also be connected at both the input and the output of various energy supply channels. The flow diagram for one of the energy supply channels is shown in Figure 5.

In the case of energy accumulation at the input and energy supply from the storage device at the output, the equations of input and output energy flow and a converter of one energy type into another will be

$${\tilde{p}}_{\alpha }=p_{\alpha }-q_{\alpha };$$

(13)

$${\tilde{l}}_{\beta }=l_{\beta }+m_{\beta }.$$

(14)

Given all inputs and outputs of the converter of one energy type into another, the vector of input and output will be

$$\breve{L}=C\breve{P}.$$

(15)

Based on Equations (7) and (8), we can write

$$L+M=C\left[P-Q\right].$$

(16)

The concept of an equivalent vector of energy flow of a storage device $M^{eq}$ is introduced to factor in storage devices; then, the vector of energy flows at the energy hub output is

$$L=C\left[P-Q\right]-M=CP-M^{eq}.$$

(17)

In turn,

$$M^{eq}=CQ+M.$$

(18)

The matrix form, given coefficient $\dot{E}$, is

$$\underset{M^{eq}}{\underbrace{\left|\begin{array}{c}{m}_{\alpha }^{eq}\\ m_{\beta }^{eq}\\ ⋮\\ m_{\omega }^{eq}\end{array}\right|}}=\underset{S}{\underbrace{\left|\begin{array}{cccc}{s}_{\alpha \alpha }& s_{\beta \alpha }& \cdots & s_{\omega \alpha }\\ s_{\alpha \beta }& s_{\beta \beta }& \cdots & s_{\omega \beta }\\ ⋮& ⋮& \ddots & ⋮\\ s_{\alpha \omega }& s_{\beta \omega }& \cdots & s_{\omega \omega }\end{array}\right|}}\hspace{0.17em}\hspace{0.17em}\underset{\dot{E}}{\underbrace{\left|\begin{array}{c}{\dot{e}}_{\alpha }\\ {\dot{e}}_{\beta }\\ ⋮\\ {\dot{e}}_{\omega }\end{array}\right|}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}$$

(19)

The matrix of the energy hub outputs, with the storage devices taken into account, is

$$L=CP-S\dot{E}=\left[C-S\right]\left|\begin{array}{c}P\\ \dot{E}\end{array}\right|.$$

(20)

This mathematical description is the basis for studying the operating conditions of the energy hub. As a result, we have systems of linear algebraic equations with constant coefficients. This description is optimal for investigating the energy hub to optimize its functioning depending on the objective function.

At present, there is no specific implementation of mathematical models. Even within the framework of one technical object, different channels are monitored using different software implementations [30,31]. The monitoring data are stored in different databases and are not related to each other by time stamps. This circumstance does not allow accumulating information, that is, for example, using complex neural networks as control systems.

Hence, the conclusion that the major issue of the widespread use of MES is the absence of simulation modeling systems enabling an analysis of the structure and behavior of an object in the design stage.

At the same time, the approach that has recently become widespread in studying the operating conditions of energy objects suggests the use of simulation models. The data obtained from modeling are the basis for solving optimization problems or for designing various analysis and control systems (big data, digital shadow, forecasting, and control systems based on the use of neural networks) [32]. In [33], two possible approaches to model multi-energy systems are considered. These are an integrated approach with all elements of a multi-energy system modeled on a single software platform and an approach that involves harmonizing simulation models of individual elements with the aid of a single program module that matches the inputs and outputs of separate modules with each other. Moreover, the individual components have their dedicated models, which are characteristic of various energy supply channels [34].

The process of developing approaches to model multi-energy systems should take account of some fundamental factors, one of which is the application area of the concept. In [35,36,37], the applicability boundaries are determined in terms of the geographical location of the objects:

• Power plants with cogeneration and trigeneration;
• Large industrial enterprises that employ various types of energy carriers in their technological process;
• Large office and administrative buildings;
• Limited geographic areas;
• Isolated (islanded) energy systems.
• This classification can be roughly divided into two large groups:
• Local objects that use various types of energy carriers in their technological process of energy supply and that are part of a larger energy supply system;
• Local energy systems (islanded energy systems), including sources, transmission systems, and receivers of various types of energy carriers [38].

The approach proposed in [30,31] is most suitable for modeling the first group. It can be conventionally called the modeling of a local hub. Its software implementation rests on an integrated approach. The systems of simulation modeling of an energy hub should factor in the following points:

• Features of signal transmission in the simulation system;
• Restrictions imposed on the use of standard modules;
• Various units of measurement for different energy supply channels;
• Feasibility of technical implementation of the systems for storage and conversion of one type of energy into another;
• Algorithms for describing nonlinear elements of transmission and conversion systems;
• Simplicity, clarity, and ability to change simulation parameters under direct control;
• The possibility of using the obtained algorithms for creating a model to study the functioning of the energy hub, depending on the objective functions;
• The possibility of using the resulting model as a control object to explore the applicability of various control algorithms.
• Specific features of signal propagation in simulation systems.

Figure 6 shows a block diagram of a multi-energy system according to the following equation:

$$\underset{P}{\underbrace{\left|\begin{array}{c}{p}_{\alpha }\\ p_{\beta }\\ p_{\omega }\end{array}\right|}}-\underset{Q}{\underbrace{\left|\begin{array}{c}{q}_{\alpha }\\ q_{\beta }\\ q_{\omega }\end{array}\right|}}=\underset{\tilde{P}}{\underbrace{\left|\begin{array}{c}{\tilde{p}}_{\alpha }\\ {\tilde{p}}_{\beta }\\ {\tilde{p}}_{\omega }\end{array}\right|}};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\underset{\tilde{L}}{\underbrace{\left|\begin{array}{c}{\tilde{l}}_{\alpha }\\ {\tilde{l}}_{\beta }\\ {\tilde{l}}_{\omega }\end{array}\right|}}=\underset{C}{\underbrace{\left|\begin{array}{ccc}{c}_{\alpha \alpha }& c_{\beta \alpha }& c_{\omega \alpha }\\ c_{\alpha \beta }& c_{\beta \beta }& c_{\omega \beta }\\ c_{\alpha \omega }& c_{\beta \omega }& c_{\omega \omega }\end{array}\right|}}\underset{\tilde{P}}{\underbrace{\left|\begin{array}{c}{\tilde{p}}_{\alpha }\\ {\tilde{p}}_{\beta }\\ {\tilde{p}}_{\omega }\end{array}\right|}};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\underset{\tilde{L}}{\underbrace{\left|\begin{array}{c}{\tilde{l}}_{\alpha }\\ {\tilde{l}}_{\beta }\\ {\tilde{l}}_{\omega }\end{array}\right|}}-\underset{M}{\underbrace{\left|\begin{array}{c}{m}_{\alpha }\\ m_{\beta }\\ m_{\omega }\end{array}\right|}}=\underset{L}{\underbrace{\left|\begin{array}{c}{l}_{\alpha }\\ l_{\beta }\\ l_{\omega }\end{array}\right|}}$$

(21)

The parameters given for this equation are the consumer load curves for three channels. It is necessary to determine the amount of energy received from the network for each energy supply channel. The downside of this system of equations is that in this case, it does not consider the feasibility of the technical implementation of energy storage devices and the possibility of converting one type of energy into another.

We will consider a simulation modeling system to model energy storage devices and transitions of one type of energy to another in multi-energy systems. It is necessary to follow the general principles of studying multi-energy systems. The basic ones are that all transient processes fade and the system is in a steady state.

Modern versions of the simulation modeling system have an extensive library of standard modules for modeling various technical systems, including those of electric power, hydraulics, and pneumatics. It is, however, worth noting that these modules are intended primarily for the study of transient processes. Their mathematical description usually contains a system of differential equations. Such an approach for the research of various steady-state conditions seems to be redundant. Moreover, when investigating the mutual influence of different energy flows on each other, the time constants of the modules can be neglected.

Transient processes in power supply systems last 5–7 supply voltage periods (the time required to produce a complete cycle of waveforms), while transients in heat supply systems can reach tens of minutes. Thus, it is advisable to use simplified modeling methods. If transient processes must be considered, the simulation model can be expanded with the modules from specialized libraries.

As an example, we will consider a multi-energy system for the three most common types of energy carriers: electricity, heat, and natural gas. To simplify the internal structure of the energy hub model, it is necessary to arrange modules that convert different units of measurement to a single unit at the input and output of the hub. We assume J (W) as such a basic measurement unit.

The analysis carried out by the authors shows that the various mathematical descriptions of a multi-energy hub are based on the basic assumptions given above.

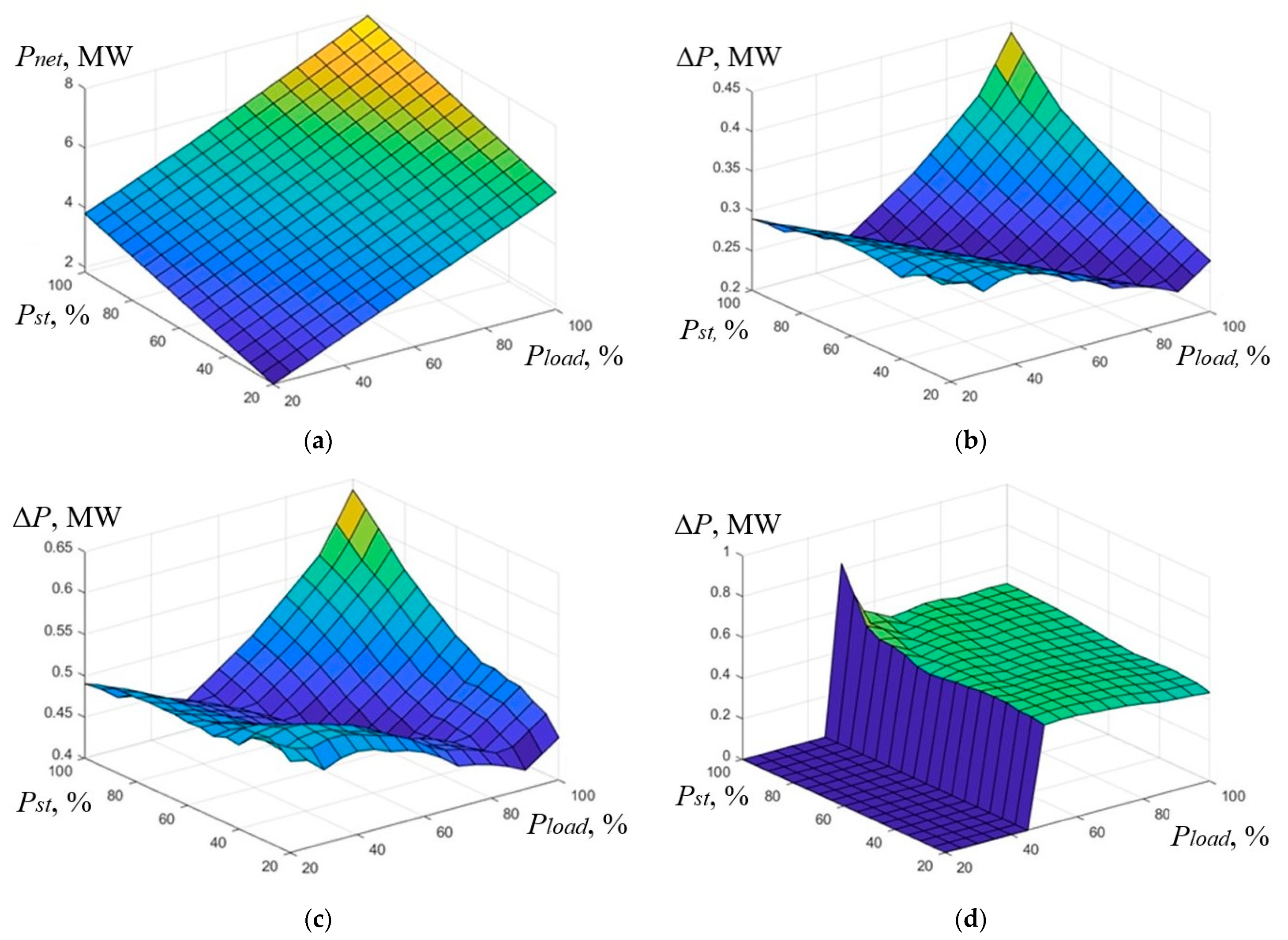
4. Discussion

When creating simplified models of the energy hub components, we need to consider the technical structure of the system and, based on the data obtained, determine the necessary and sufficient parameters of the model elements depending on the objective function implemented by the simulation model. The generally accepted assumptions suggest that the energy hub consists of converters, storage devices, and energy transmission systems [39,40].

Energy conversion systems are represented by the following systems, devices, and structure:

• Systems that change the characteristics of an energy channel without converting one type of energy into another (transformers, heat exchangers);
• Systems that convert one type of energy into another, i.e., energy conversion systems: electric heating devices, gas turbines, and others.
• Energy storage systems are as follows:
• Electric energy storage devices (electrochemical, pneumatic, pumped, and kinetic);
• Thermal energy storage devices (tanks and others);
• Gas storage facilities.
• Energy transmission systems include the following points:
• Power transmission lines;
• Heat networks;
• Gas supply structure.

When modeling a real-world multi-energy system, one should consider the feasibility of its technical implementation and the need to factor in its structure in the simulation model [2]. The flow diagram of the simulation model can be represented as shown in Figure 7.

Figure 7 shows a flow diagram for the three most common energy supply channels. This approach, however, can be employed to simulate the systems containing an arbitrary number of energy supply channels.

The specific implementation of this flow diagram depends on the software implementation of the simulation systems. Thus, the simulation model of a multi-energy system that implements the integrated approach can be represented as follows (Figure 8).

The models designed based on the above principles include the following models:

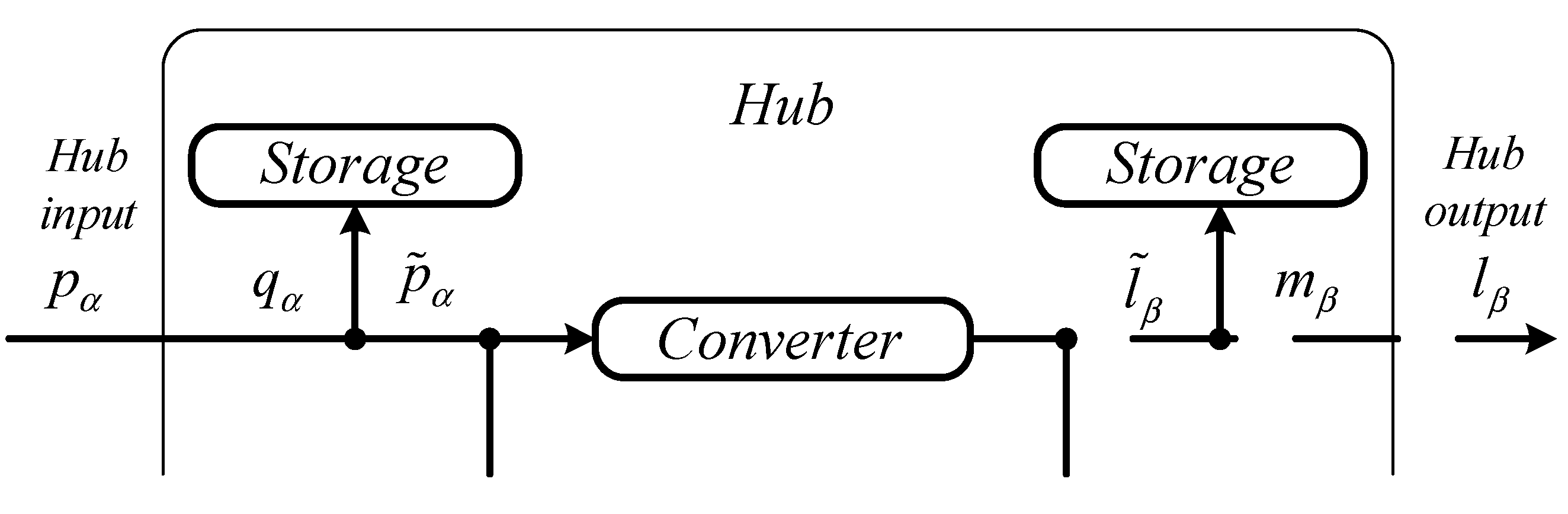
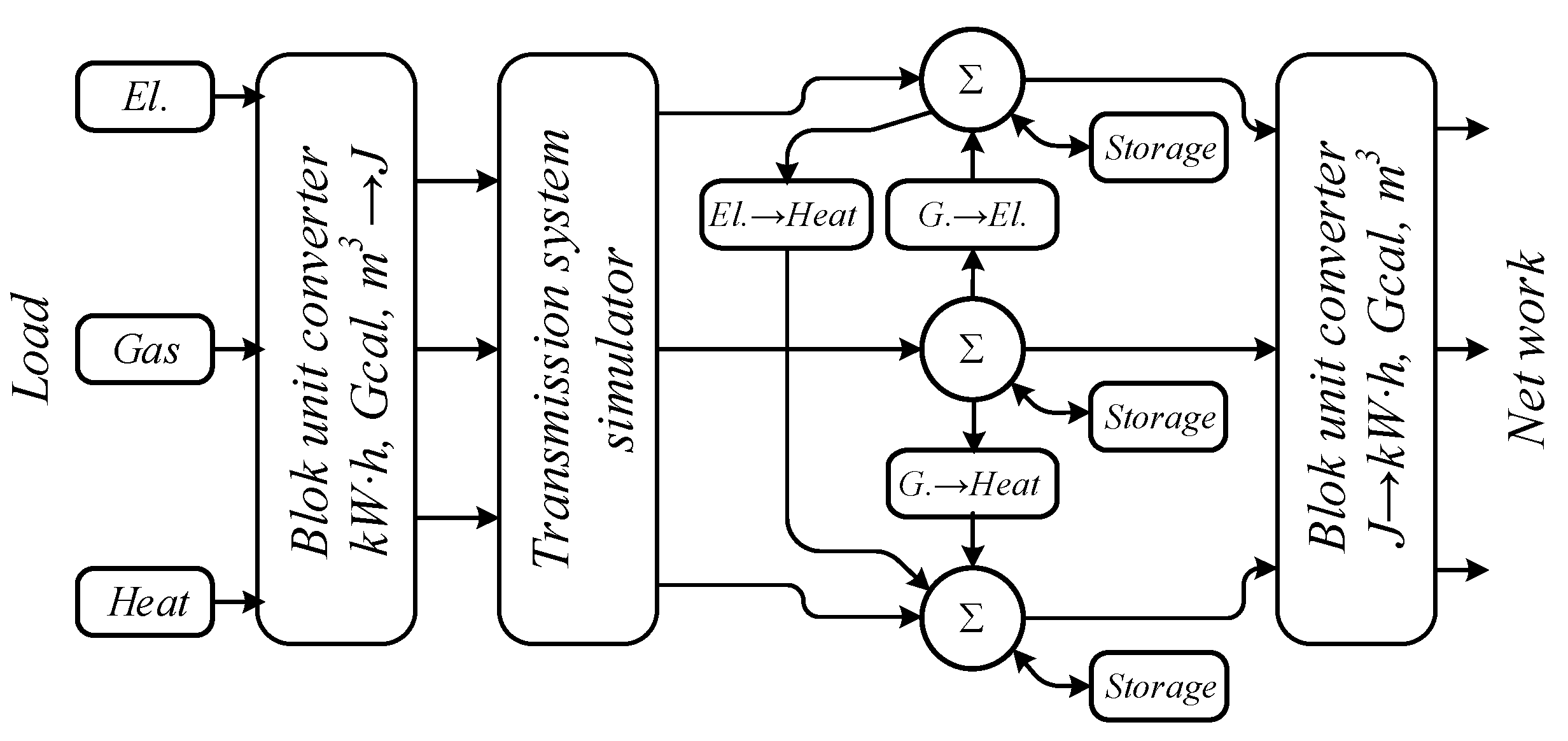
• A simulation model of a multi-energy system for two energy (electrical and thermal) supply channels;
• A model of converters of electrical energy into thermal energy;
• A model of the electrical and thermal energy storage systems.

The simulation model considers the joint operation of the energy supply system for all channels, given their mutual influence. When building a model, the objective function is to determine the energy losses in all the main components of the energy hub. The developed model makes it possible to study the mutual influence of various energy supply channels on each other, to determine the energy losses in all the main elements of the energy supply system under various operating conditions, and factor in the functioning of the storage systems when accumulating and supplying energy.

The computational experiment involved examining the operating conditions of the electrical energy storage device in the charge and discharge modes with the consumer load varying in a wide range and determining the total energy and energy losses at the power supply channel input. The simulation results for charging and discharging the energy storage device are shown in Figure 9.

The analysis of the obtained results makes it possible to estimate the region of minimum energy losses in the components of the energy hub for various operating conditions in the power supply channel and storage systems. The non-linearity of changes in losses is due to the non-linearity of the efficiency of devices depending on the load.

The non-linearity of the obtained characteristics is explained by the curve of the change in the efficiency of the transformer along the power supply channel and the characteristics of the charge and discharge of the energy storage.

Relying on this approach, one can determine the system parameters in a wide range of load changes (this study examined the levels of and relationships between changes in energy losses in the components of the energy supply system and the operating modes of the energy storage system).

5. Conclusions

A unified approach is proposed to build simulation models of multi-energy systems in various simulation systems.

The research into the mathematical description of multi-energy systems provided methodological approaches developed to construct simulation models of multi-energy systems. The use of these approaches enables the construction of simulation models in various simulation systems.

The computational experiment indicates the performance of this approach. The objective function of the study during the computational experiment was the assessment of the magnitude of energy losses in the main components of the energy hub. The presented graphical results of simulation allow visual evaluation of the minima of energy losses under various operating conditions of the power supply system for two channels: power supply and heat supply.

In the future, with a sufficient amount of data obtained for a real-world physical object, verification and refinement of the simulation model will be carried out. There are also plans to create a database that can be used to devise and test various approaches for the development of control systems for multi-energy systems, depending on the various objective functions of the study.