Assessment of AC Corrosion Probability in Buried Pipelines with a FEM-Assisted Stochastic Approach
Abstract
1. Introduction
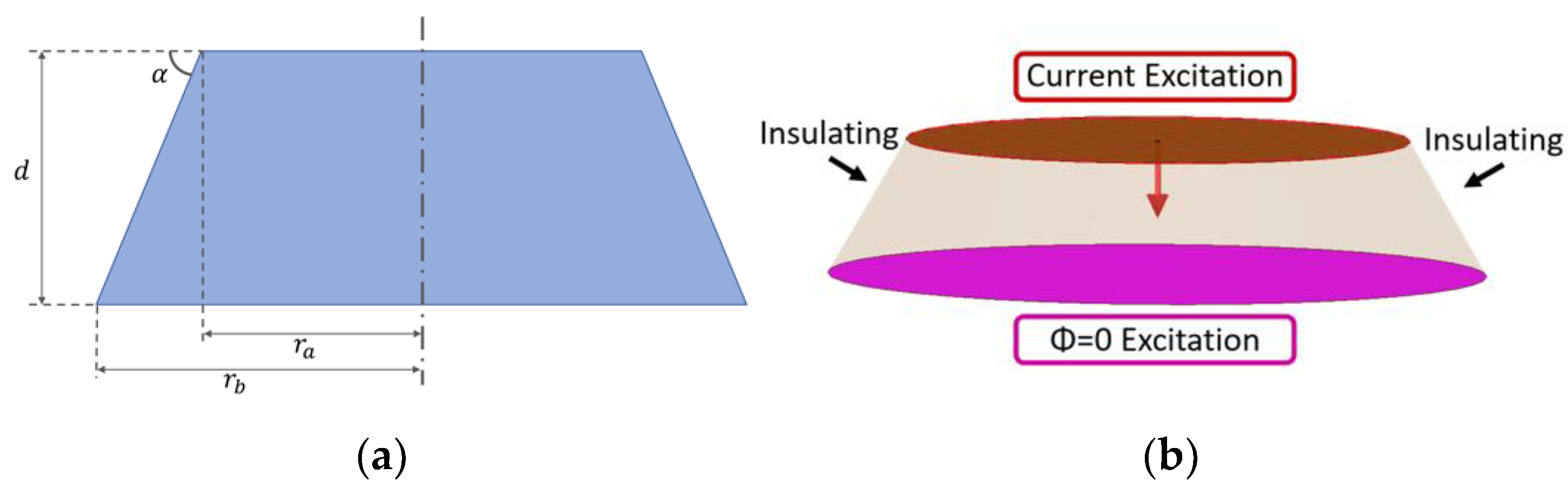
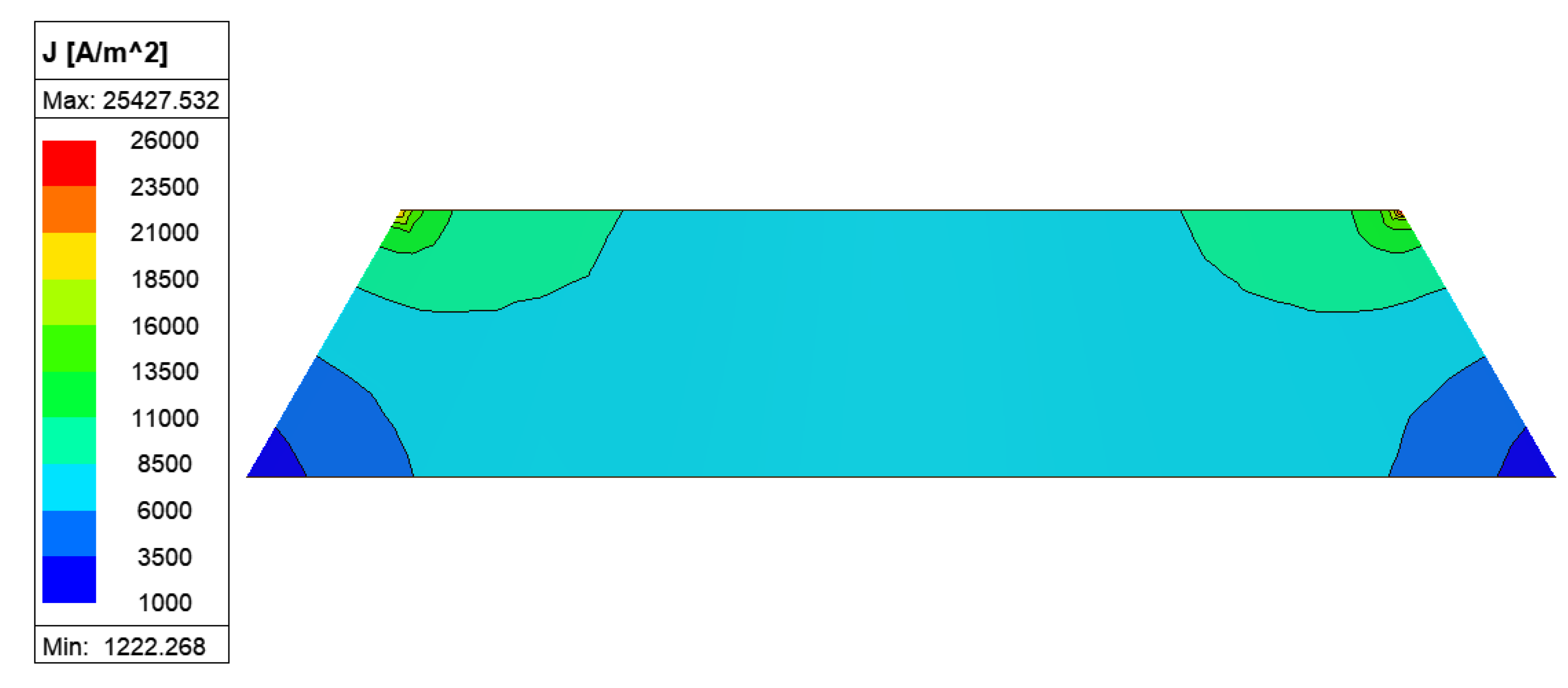
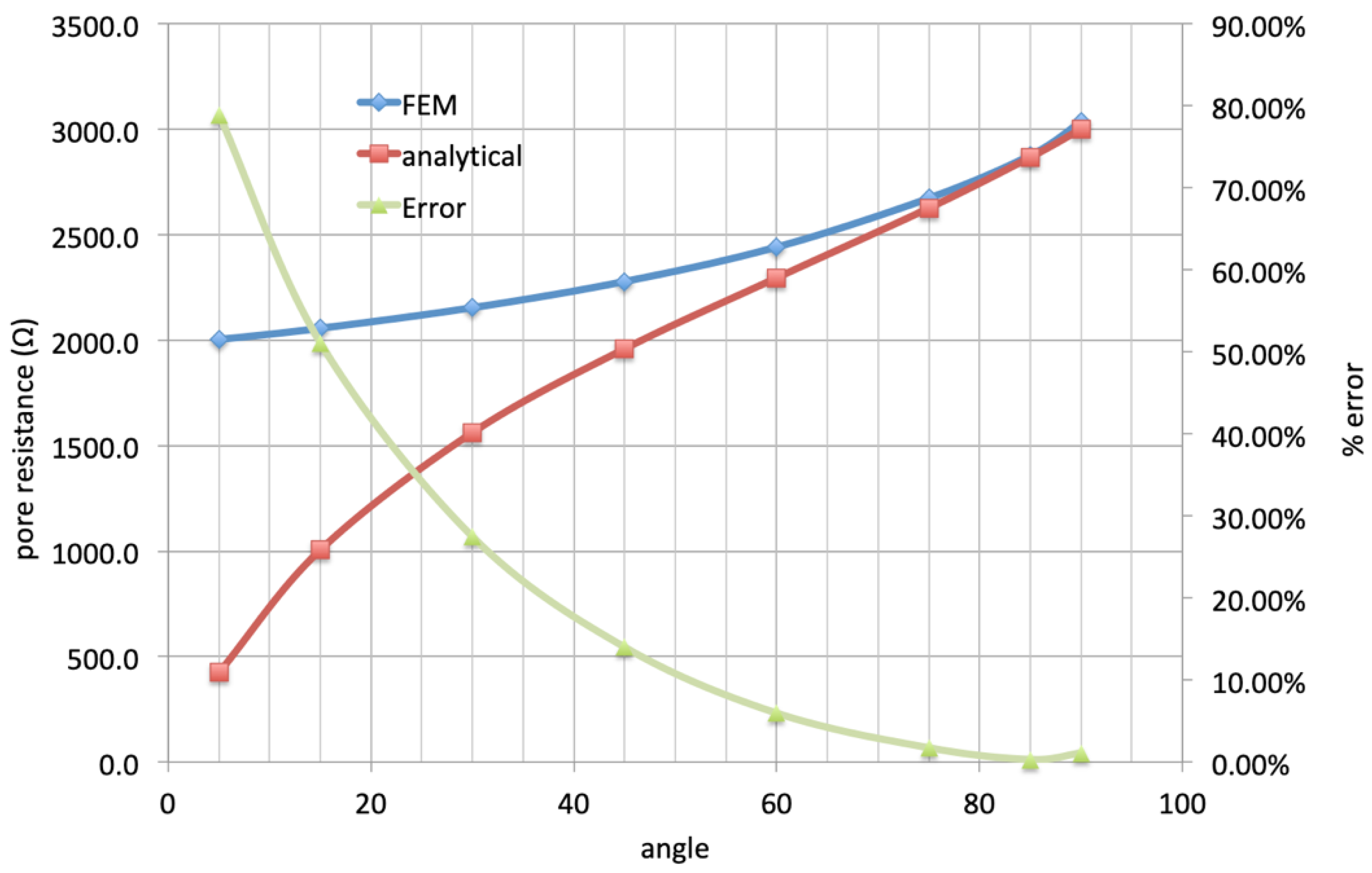
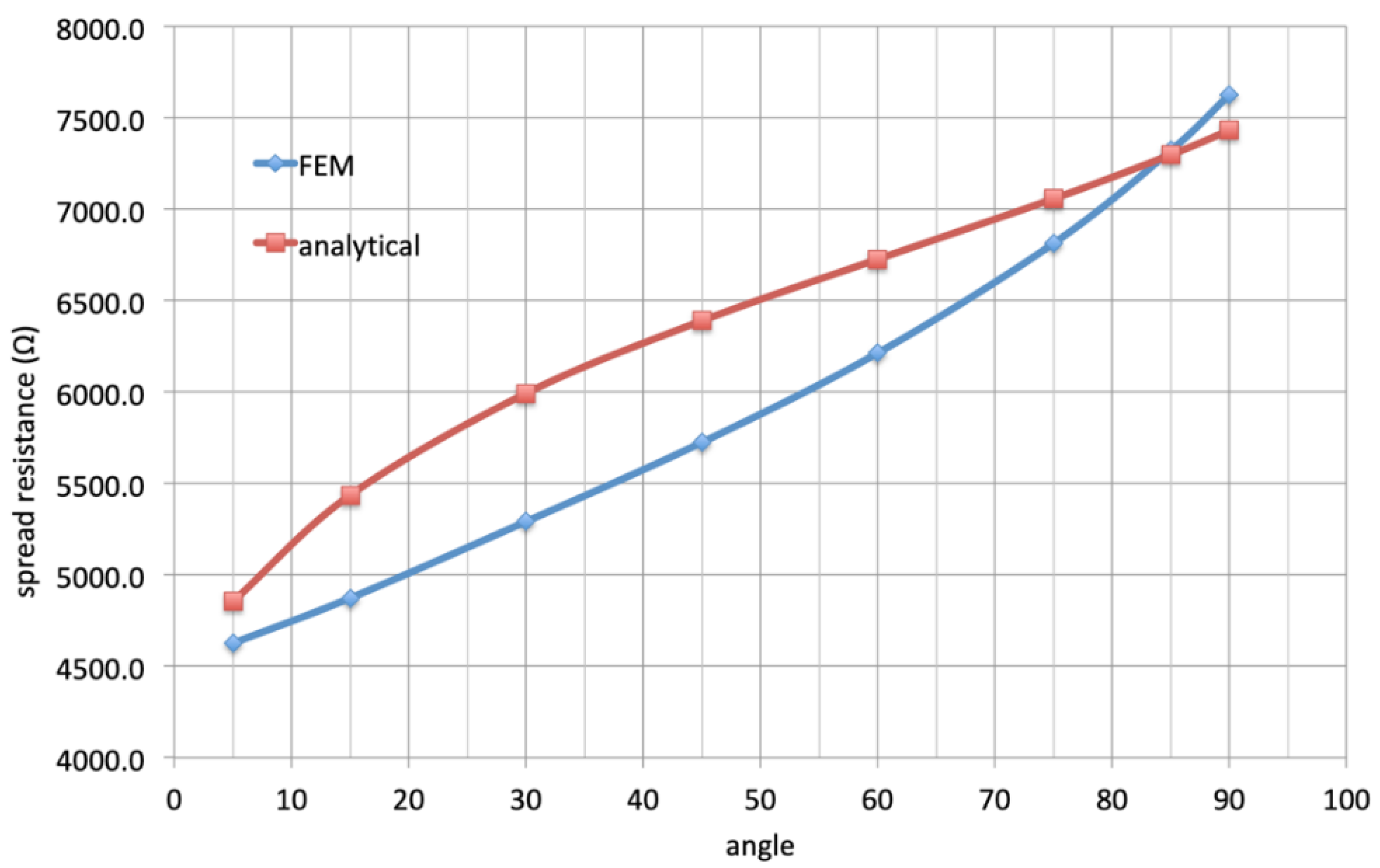
2. Finite Element Analysis of the Spread Resistance of a Coating Defect
3. Probabilistic Evaluation of the Leakage Current Density through a Holiday in the Coating
- If V is the value of the induced voltage in a specific point along the pipeline due to the electromagnetic influence produced by nearby High Voltage power lines or electrified railway lines.
- If, at the same point, a holiday in the pipeline insulating coating is present.
3.1. Relationships among Induced Voltage, Current Density and Holiday Area
3.2. Probability Distribution of the Holidays Area
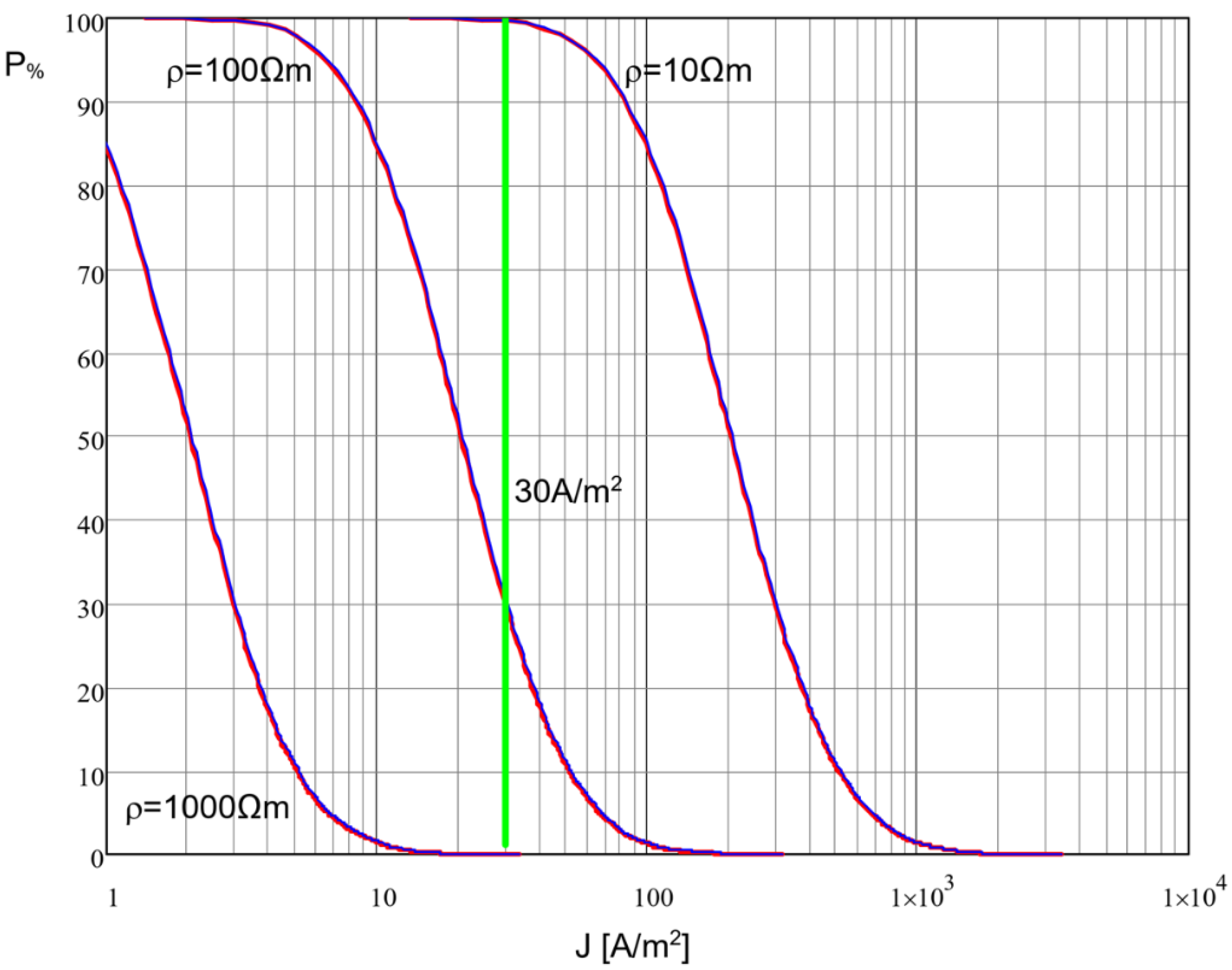
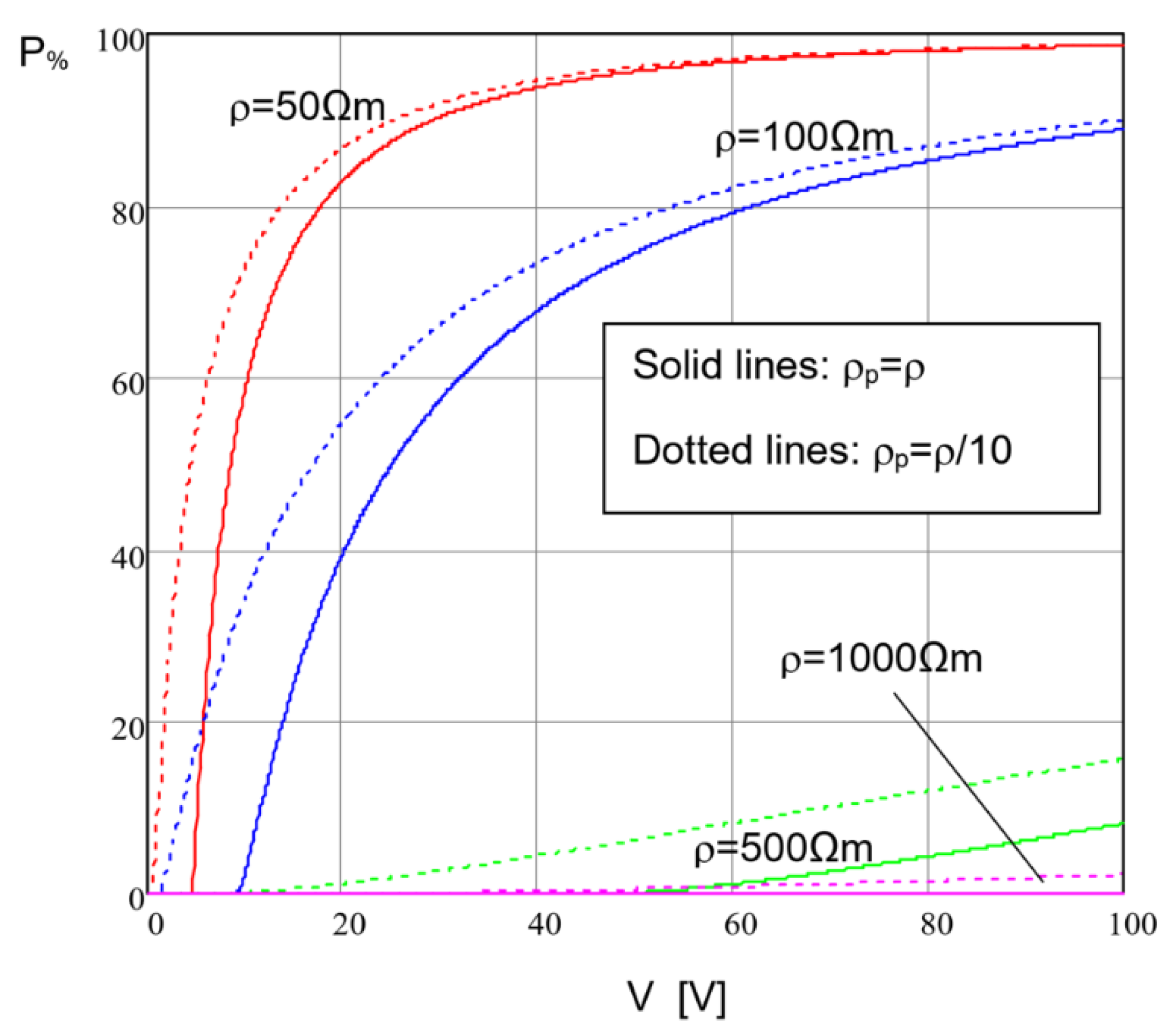
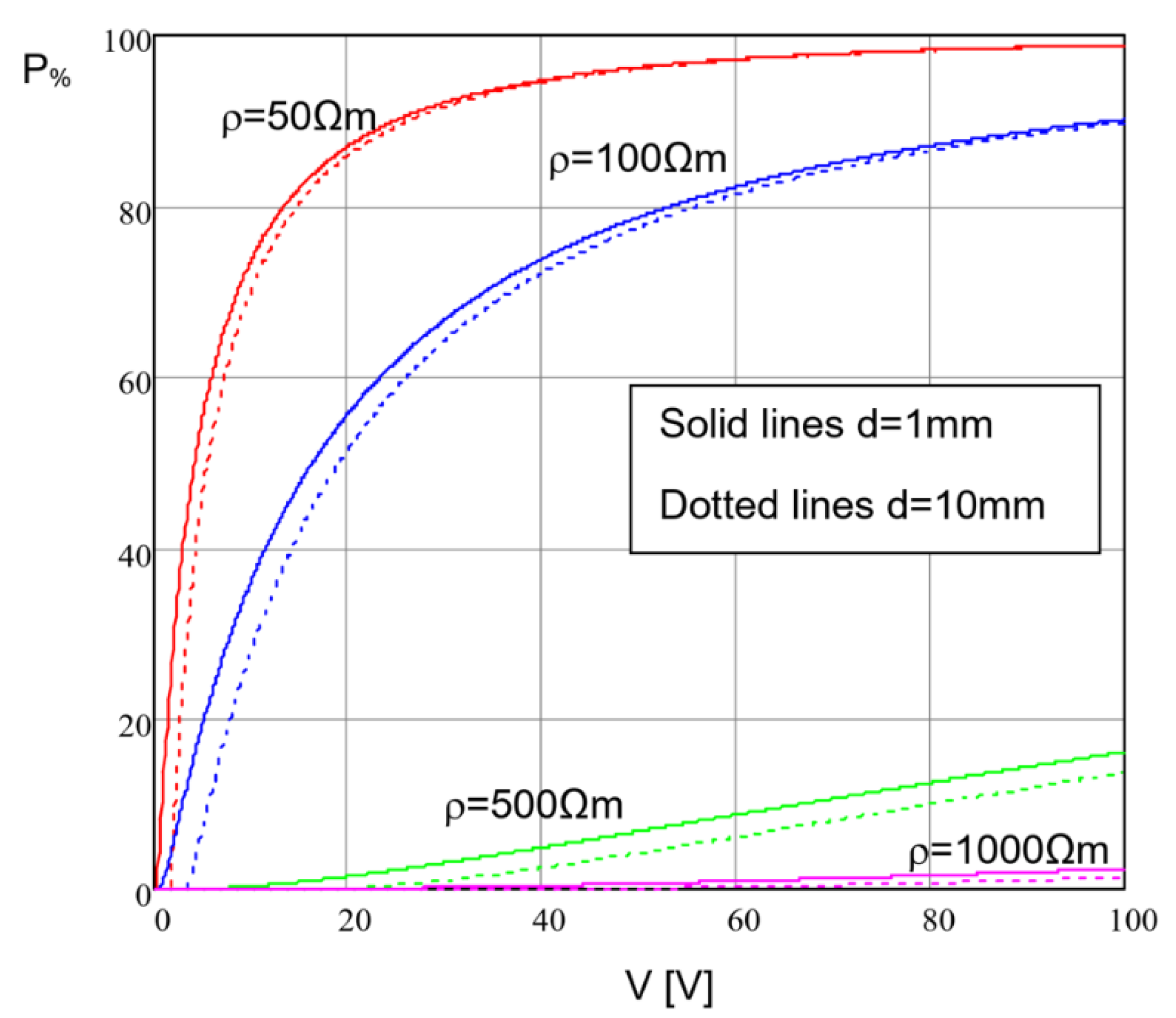
3.3. Probability of Exceeding the Limit Value Jlim
3.4. Influence of the Main Parameters
- (1)
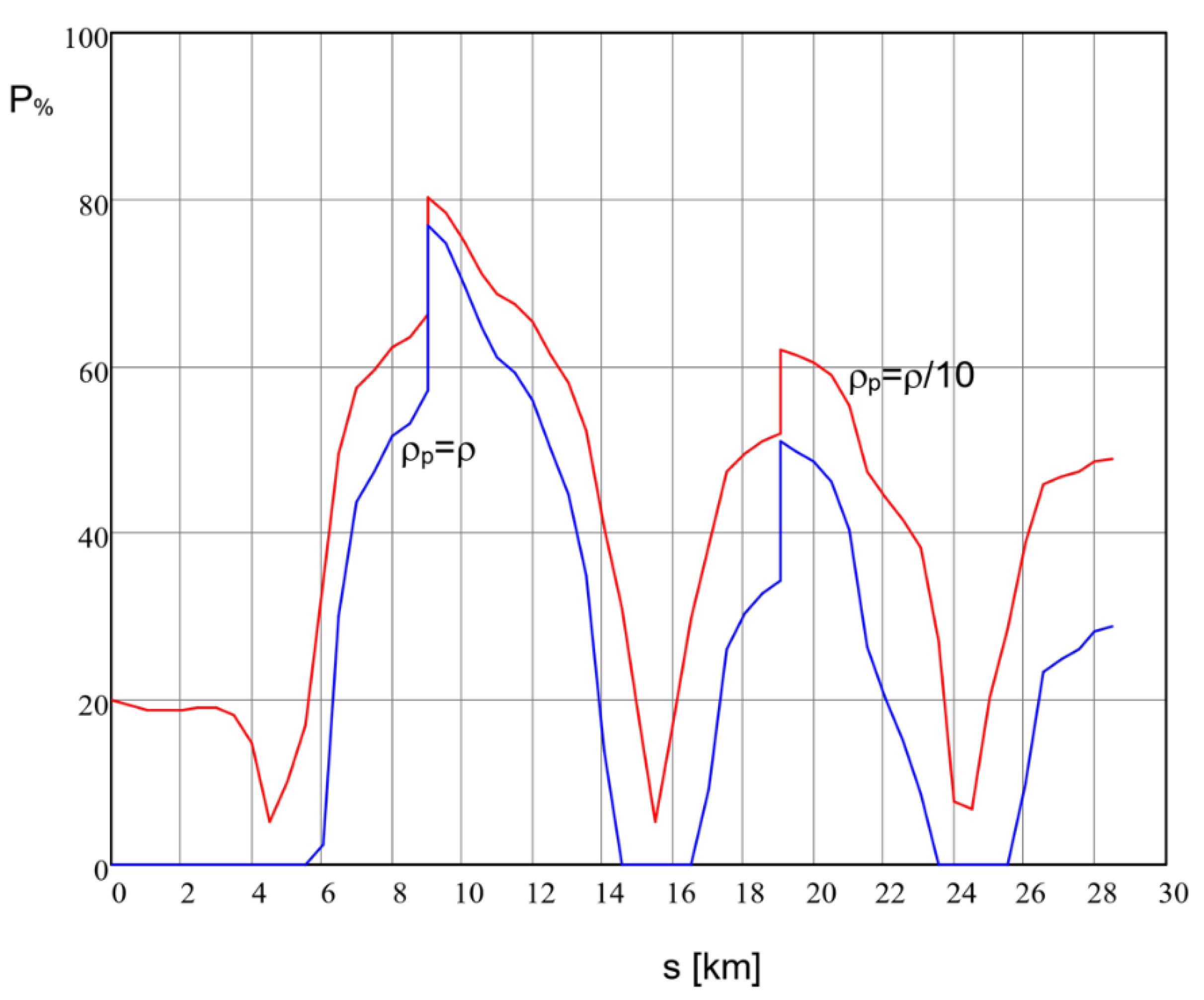
- The resistivity of the material inside the pore is equal to the soil resistivity, i.e.,: ;
- (2)
- The resistivity is one order of magnitude smaller than i.e., . This hypothesis is suggested by some results based on field measurements and described in [38].
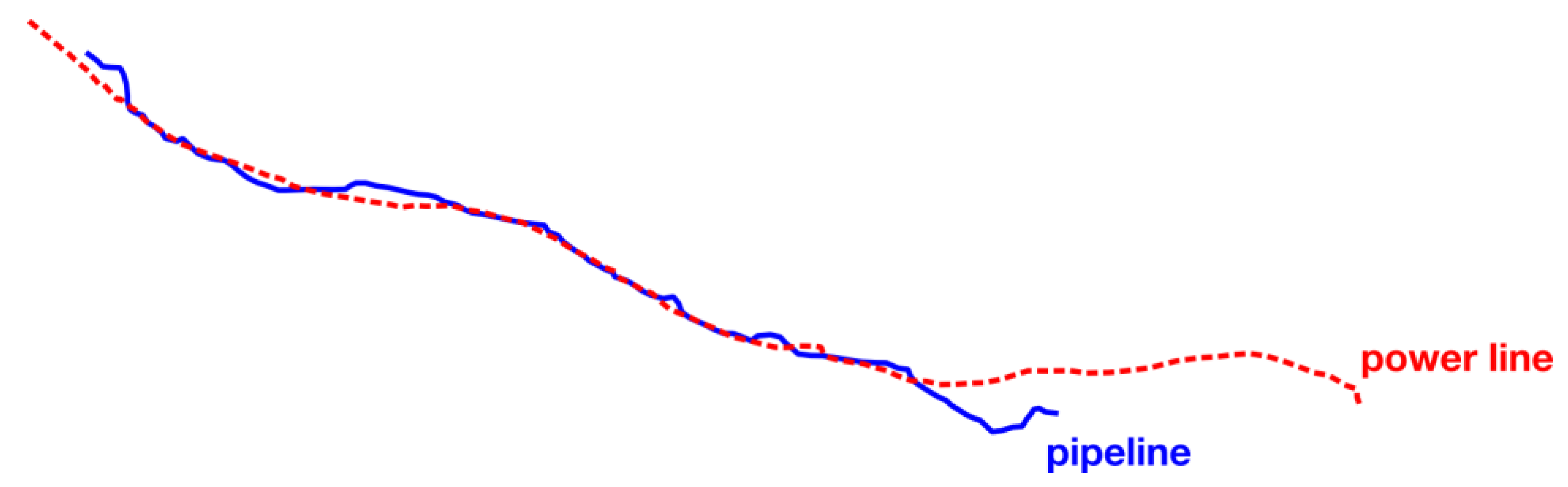
3.5. Example of Application to a Real Case of 50 Hz Interference
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A
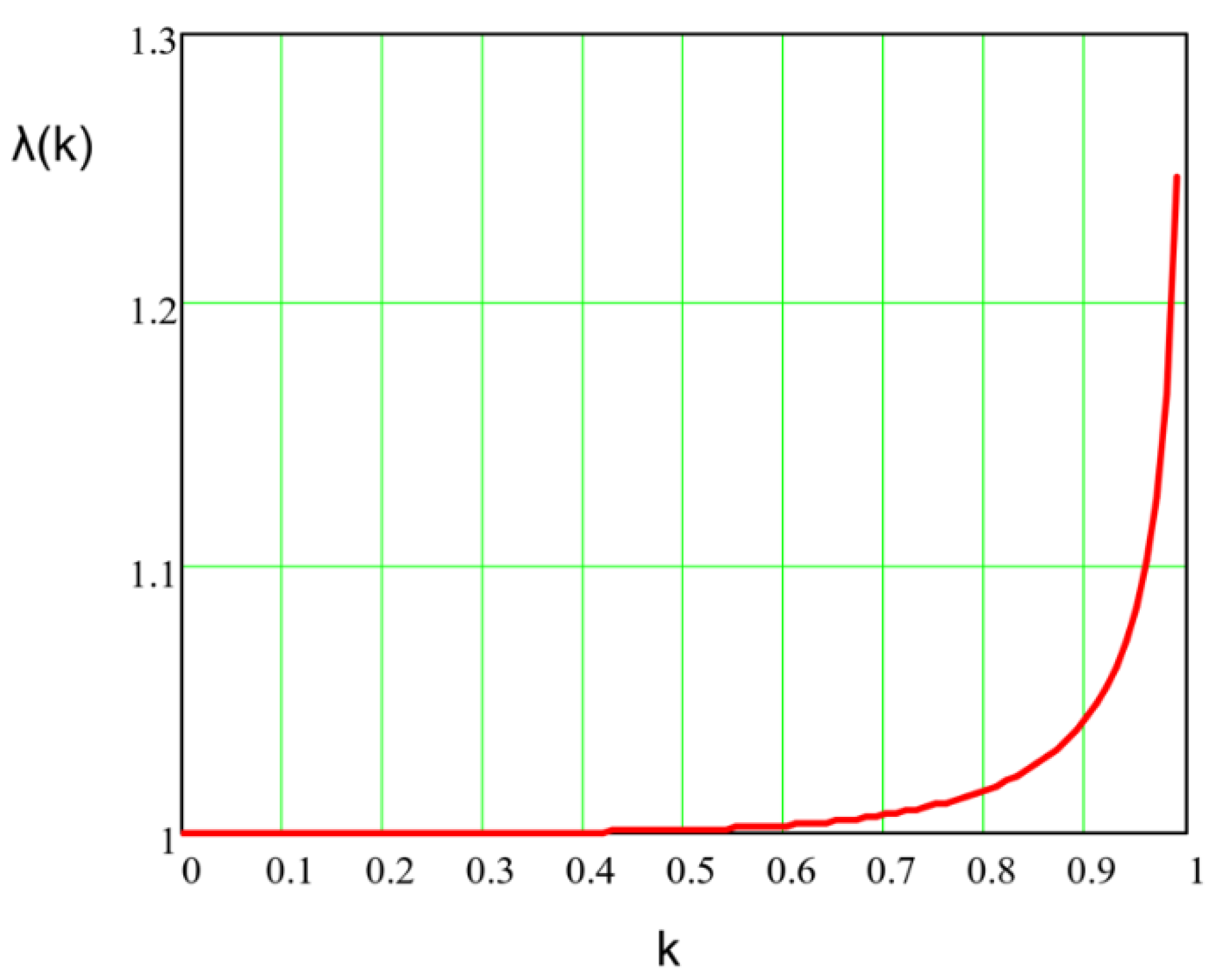
- The holiday area with log-normal distribution given by (9);
- The ellipse eccentricity k with uniform distribution inside the interval [0, 1).
References
- Taflove, A.; Dabkowski, J. Prediction Method for Buried Pipeline Voltages Due to 60 Hz AC Inductive Coupling Part I-Analysis. IEEE Trans. Power Appar. Syst. 1979, PAS-98, 780–787. [Google Scholar] [CrossRef]
- Al-Gabalawy, M.A.; Mostafa, M.A.; Hamza, A.S.; Hussien, S.A. Modeling of the KOH-Polarization Cells for Mitigating the Induced AC Voltage in the Metallic Pipelines. Heliyon 2020, 6, e03417. [Google Scholar] [CrossRef]
- Chen, M.; Liu, S.; Zhu, J.; Xie, C.; Tian, H.; Li, J. Effects and Characteristics of AC Interference on Parallel Underground Pipelines Caused by an AC Electrified Railway. Energies 2018, 11, 2255. [Google Scholar] [CrossRef]
- Charalambous, C.A.; Demetriou, A.; Lazari, A.L.; Nikolaidis, A.I. Effects of Electromagnetic Interference on Underground Pipelines Caused by the Operation of High Voltage AC Traction Systems: The Impact of Harmonics. IEEE Trans. Power Deliv. 2018, 33, 2664–2672. [Google Scholar] [CrossRef]
- Cigré Working Group 36.02. Guide on the Influence of High Voltage AC Power Systems on Metallic Pipelines; CIGRE: Paris, France, 1995; p. 135. [Google Scholar]
- Brenna, A.; Beretta, S.; Ormellese, M. AC Corrosion of Carbon Steel under Cathodic Protection Condition: Assessment, Criteria and Mechanism. A Review. Materials 2020, 13, 2158. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Zhang, H.; Karady, G.G. Transient Analysis of Inductive Induced Voltage between Power Line and Nearby Pipeline. Int. J. Electr. Power Energy Syst. 2017, 84, 47–54. [Google Scholar] [CrossRef]
- Muresan, A.; Papadopoulos, T.A.; Czumbil, L.; Chrysochos, A.I.; Farkas, T.; Chioran, D. Numerical Modeling Assessment of Electromagnetic Interference Between Power Lines and Metallic Pipelines: A Case Study. In Proceedings of the 2021 9th International Conference on Modern Power Systems (MPS), Cluj-Napoca, Romania, 16–17 June 2021; pp. 1–6. [Google Scholar]
- Moraes, C.M.; de Matos, G.H.S.; Martins-Britto, A.G.; Silva, K.M.; Lopes, F.V. Total AC Interferences Between a Power Line Subject to a Single-Phase Fault and a Nearby Pipeline with Multilayered Soil. IEEE Trans. Electromagn. Compat. 2023, 65, 1–10. [Google Scholar] [CrossRef]
- Cigré Working Group C4. 2.02. AC Corrosion on Metallic Pipelines Due to Interference from AC Power Lines—Phenomenon, Modelling and Countermeasures; CIGRE: Paris, France, 2006. [Google Scholar]
- Ametani, A.; Paolone, M.; Yamamoto, K.; Haddad, A.M.; He, J.; Ishii, M.; Judendorfer, T.; Jung-Wook, W.; Keri, A.J.F.; Nucci, C.A.; et al. Guideline for Numerical Electromagnetic Analysis Method. CIGRE Tech. Broch. 543 2013, 1, 1–106. [Google Scholar]
- Lucca, G. Different Approaches in Calculating AC Inductive Interference from Power Lines on Pipelines. IET Sci. Meas. Technol. 2018, 12, 802–806. [Google Scholar] [CrossRef]
- Andolfato, R.; Bernardi, L.; Fellin, L. Aerial and Grounding System Analysis by the Shifting Complex Images Method. IEEE Trans. Power Deliv. 2000, 15, 1001–1009. [Google Scholar] [CrossRef]
- Steele, C.W. Numerical Computation of Electric and Magnetic Fields; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Micu, D.; Christoforidis, G.; Czumbil, L. AC Interference on Pipelines Due to Double Circuit Power Lines: A Detailed Study. Electr. Power Syst. Res. 2013, 103, 1–8. [Google Scholar] [CrossRef]
- Christoforidis, G.; Labridis, D.; Dokopoulos, P. A Hybrid Method for Calculating the Inductive Interference Caused by Faulted Power Lines to Nearby Buried Pipelines. IEEE Trans. Power Deliv. 2005, 20, 1465–1473. [Google Scholar] [CrossRef]
- Christoforidis, G.; Labridis, D.; Dokopoulos, P. Inductive Interference on Pipelines Buried in Multilayer Soil Due to Magnetic Fields from Nearby Faulted Power Lines. IEEE Trans. Electromagn. Compat. 2005, 47, 254–262. [Google Scholar] [CrossRef]
- Cristofolini, A.; Popoli, A.; Sandrolini, L. Numerical modelling of interference from AC Power Lines on buried metallic pipelines in presence of mitigation wires. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–6. [Google Scholar]
- Popoli, A.; Sandrolini, L.; Cristofolini, A. Finite element analysis of mitigation measures for AC interference on buried pipelines. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Genova, Italy, 11–14 June 2019; pp. 1–5. [Google Scholar]
- Popoli, A.; Sandrolini, L.; Cristofolini, A. A Quasi-3D Approach for the Assessment of Induced AC Interference on Buried Metallic Pipelines. Int. J. Electr. Power Energy Syst. 2019, 106, 538–545. [Google Scholar] [CrossRef]
- Popoli, A.; Sandrolini, L.; Cristofolini, A. Inductive Coupling on Metallic Pipelines: Effects of a Nonuniform Soil Resistivity along a Pipeline-Power Line Corridor. Electr. Power Syst. Res. 2020, 189, 106621. [Google Scholar] [CrossRef]
- Munteanu, C.; Mates, G.; Purcar, M.; Topa, V.; Pop, I.T.; Grindei, L.; Racasan, A. Electromagnetic Field Model for the Numerical Computation of Voltages Induced on Buried Pipelines by High Voltage Overhead Power Lines. Eur. Phys. J. Appl. Phys. 2012, 58, 30902. [Google Scholar] [CrossRef]
- Schoonjans, B.; Deconinck, J. Calculation of HVAC Inductive Coupling Using a Generalized BEM for Helmholtz Equations in Unbounded Regions. Int. J. Electr. Power Energy Syst. 2017, 84, 242–251. [Google Scholar] [CrossRef]
- Dawalibi, F.P.; Donoso, F. Integrated Analysis Software for Grounding, EMF, and EMI. IEEE Comput. Appl. Power 1993, 6, 19–24. [Google Scholar] [CrossRef]
- Dawalibi, F.P.; Southey, R.D. Analysis of Electrical Interference from Power Lines to Gas Pipelines. I. Computation Methods. IEEE Trans. Power Deliv. 1989, 4, 1840–1846. [Google Scholar] [CrossRef]
- Haynes, G.J.; Manning, T.; Baete, C.; Barton, L. Variances in pipeline AC interference computational modeling. In Proceedings of the Corrosion Conference and Expo 2019, 24–28 March 2019; NACE International: Nashville, TN, USA, 2019; Volume 2019. [Google Scholar]
- Baete, C.; Haynes, G.; Marmillo, J. Unmasking AC Threats on Petrochemical Pipelines. In CORROSION 2021; OnePetro: Richardson, TX, USA, 2021; p. D121S049R011. [Google Scholar]
- Dinzi, R.; Hutauruk, Y.; Siregar, Y.; Mubarakah, N.; Sinulingga, E.P. Optimization design of grounding system substation with multilayer soil model. In Proceedings of the 2022 6th International Conference on Electrical, Telecommunication and Computer Engineering (ELTICOM), Medan, Indonesia, 22–23 November 2022; pp. 85–91. [Google Scholar]
- Turri, R.; Andolfato, R.; Cuccarollo, D. A Numerical Simulation Tool for Cathodic Protection and Electromagnetic Interference Analysis. In Proceedings of the NACE Milano Italia Section–Conference & Expo 2016 A European Event for the Corrosion Prevention of Oil&Gas Industry, Genoa, Italy, 29–31 May 2016; Volume 17. [Google Scholar]
- Lucca, G. AC Corrosion on Pipelines: Influence of the Surface Layer Soil Resistivity in Evaluating the Current Density by a Probabilistic Approach. Prog. Electromagn. Res. M 2019, 79, 175–186. [Google Scholar] [CrossRef]
- Djogo, G.; Salama, M.M.A. Calculation of Inductive Coupling from Power Lines to Multiple Pipelines and Buried Conductors. Electr. Power Syst. Res. 1997, 41, 75–84. [Google Scholar] [CrossRef]
- Paul, C.R. Analysis of Multiconductor Transmission Lines; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- ITU-T. Directives concerning the protection of telecommunication lines against harmful effects from electric power and electrified railway lines. In Capacitive, Inductive and Conductive Coupling: Physical Theory and Calculation Methods; ITU-T: Geneva, Switzerland, 1989; Volume 3. [Google Scholar]
- Ruehli, A.; Antonini, G.; Jiang, L. Circuit Oriented Electromagnetic Modeling Using the PEEC Techniques; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- EN 15280; Evaluation of a.c. Corrosion Likelihood of Buried Pipelines Applicable to Cathodically Protected Pipelines. CEN: Brussels, Belgium, 2013.
- Nielsen, L.V.; Petersen, M.B.; Bortels, L.; Parlongue, J. Effect of Coating Defect Size, Coating Defect Geometry, and Cathodic Polarization on Spread Resistance: Consequences in Relation to AC Corrosion Monitoring; CeoCor: Bruges, Belgium, 2010; pp. 1–14. [Google Scholar]
- ANSYS. Maxwell Release 2022 R2, 275 Technology Drive; ANSYS: Canonsburg, PA, USA, 2022. [Google Scholar]
- Di Biase, L. CEOCOR: AC Corrosion on Cathodically Protected Pipelines—Guidelines for Risk Assessment and Mitigation Measures, Annex N. 2: Corrosion Due to Alternating Current on Metallic Buried Pipelines: Background and Perspectives, CeoCor, 2001.
- Lucca, G.; Di Biase, L.; Moro, M. AC Corrosion on Buried Pipelines: A Probabilistic Approach. In Proceedings of the 6th CEOCOR 6th International Congress, Giardini Naxos, Italia, 13–16 May 2003. [Google Scholar]
- Boersma, J.; Danick, E. On the Solution of an Integral Equation Arising in Potential Problems for Circular and Elliptic Disks. SIAM J. Appl. Math. 1993, 53, 931–941. [Google Scholar] [CrossRef]





| Paper | Applied Methodology | Physical Quantities Evaluated | Type of Calculation |
|---|---|---|---|
| Taflove and Dabkowski, 1979 [1] Dawalibi and Southey, 1989 [25] Djogo and Salama, 1997 [31] | Equivalent Transmission Line Circuit a | Induced voltage | Deterministic |
| Christoforidis et al., 2005 [16,17] | 2D FEM + Circuit theory | Induced voltage Induced current | Deterministic |
| Micu et al., 2013 [15] | 2D FEM + Circuit theory | Induced voltage | Deterministic |
| Wu et al., 2017 [7] | Equivalent Transmission Line Circuit (time domain) | Induced voltage Induced current | Deterministic |
| Cristofolini et al., 2018 [18] Popoli et al., 2019 [19] | 2D FEM | Induced voltage Induced current | Deterministic |
| Lucca, 2019 [30] | Equivalent Transmission Line Circuit | Current density | Probabilistic |
| Popoli et al., 2019 [20] Popoli et al., 2020 [21] | 2D FEM + Circuit theory (Quasi-3D method) | Induced voltage Induced current | Deterministic |
| Muresan et al., 2021 [8] | Equivalent Transmission Line Circuit (EMTP-RV), PEEC b (XGSLab) | Induced voltage | Deterministic |
| Moraes et al., 2023 [9] | Equivalent Transmission Line Circuit (EMTP) | Induced voltage Induced current | Deterministic |
| This work | Equivalent Transmission Line Circuit | Current density | Probabilistic |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lucca, G.; Sandrolini, L.; Popoli, A.; Simonazzi, M.; Cristofolini, A. Assessment of AC Corrosion Probability in Buried Pipelines with a FEM-Assisted Stochastic Approach. Appl. Sci. 2023, 13, 7669. https://doi.org/10.3390/app13137669
Lucca G, Sandrolini L, Popoli A, Simonazzi M, Cristofolini A. Assessment of AC Corrosion Probability in Buried Pipelines with a FEM-Assisted Stochastic Approach. Applied Sciences. 2023; 13(13):7669. https://doi.org/10.3390/app13137669
Chicago/Turabian StyleLucca, Giovanni, Leonardo Sandrolini, Arturo Popoli, Mattia Simonazzi, and Andrea Cristofolini. 2023. "Assessment of AC Corrosion Probability in Buried Pipelines with a FEM-Assisted Stochastic Approach" Applied Sciences 13, no. 13: 7669. https://doi.org/10.3390/app13137669
APA StyleLucca, G., Sandrolini, L., Popoli, A., Simonazzi, M., & Cristofolini, A. (2023). Assessment of AC Corrosion Probability in Buried Pipelines with a FEM-Assisted Stochastic Approach. Applied Sciences, 13(13), 7669. https://doi.org/10.3390/app13137669










