Influence of Spherical Caverns on the Failure Characteristics of Neighboring Tunnels under True Triaxial Conditions: Insights from an Experimental Test and Discrete Element Simulation
Abstract
:1. Introduction
2. Test Design
2.1. Material Selection and Property
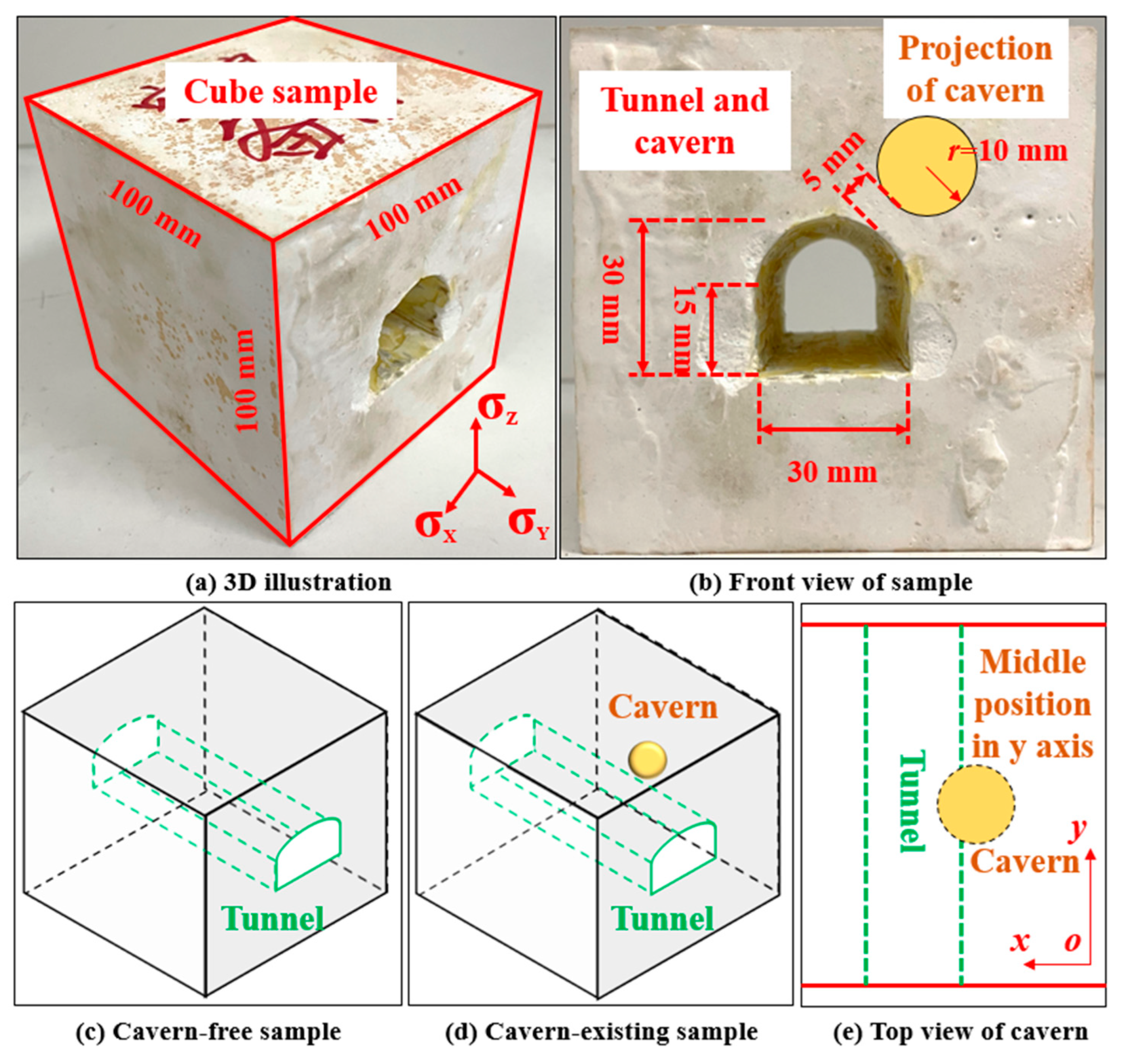
2.2. Controlled Samples’ Design
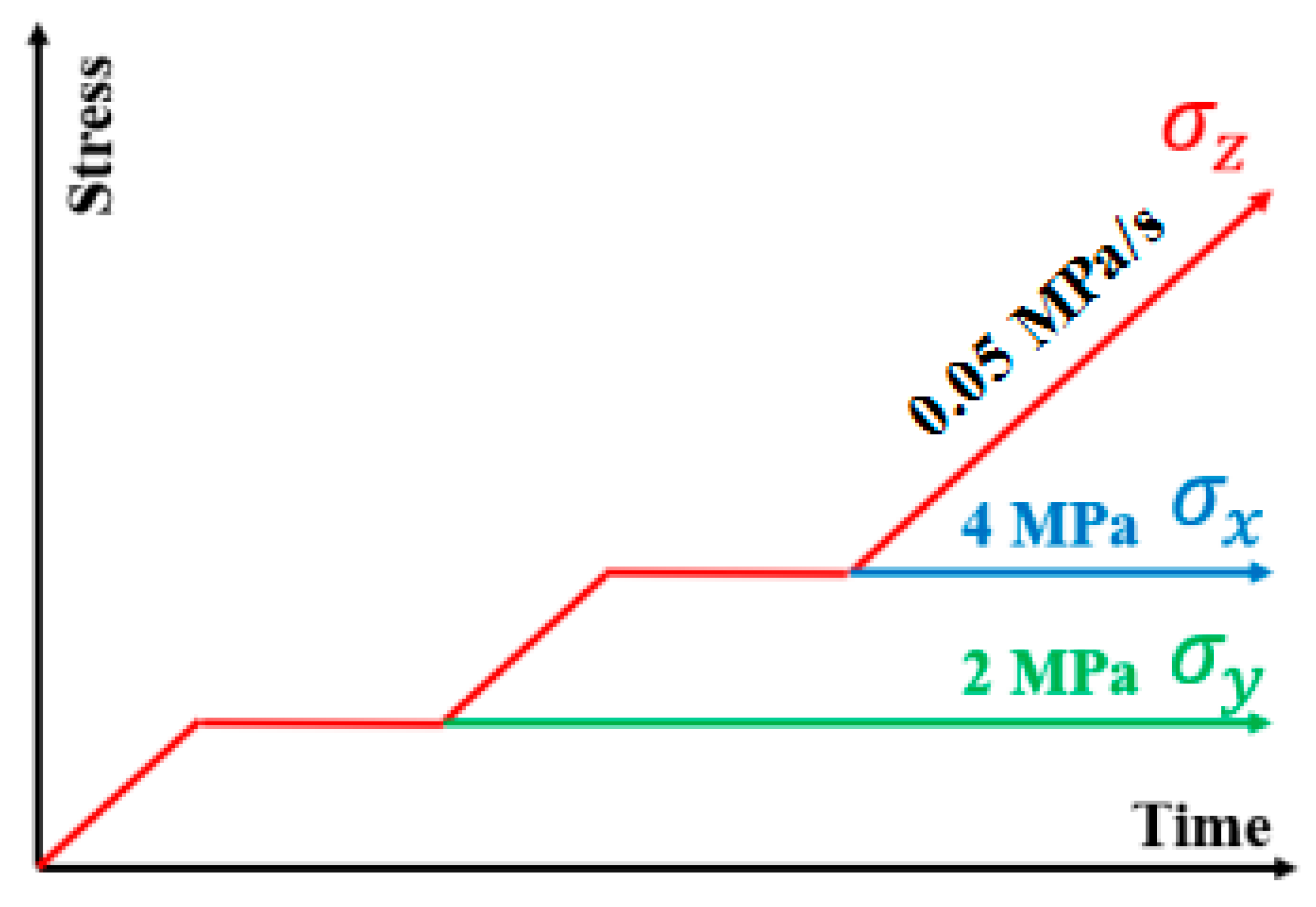
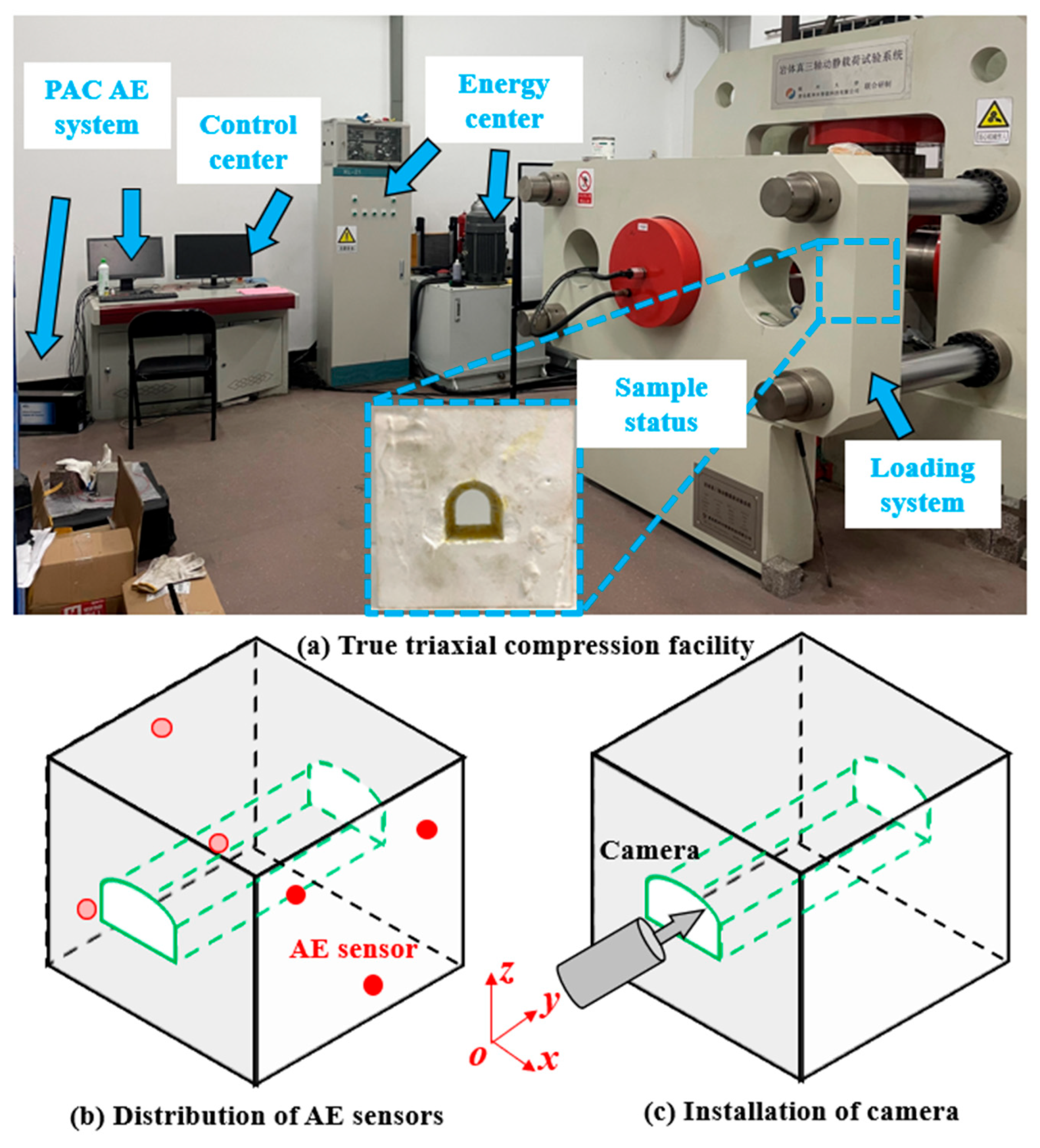
2.3. True Triaxial Compression Test and Monitoring Facilities
3. Test Results
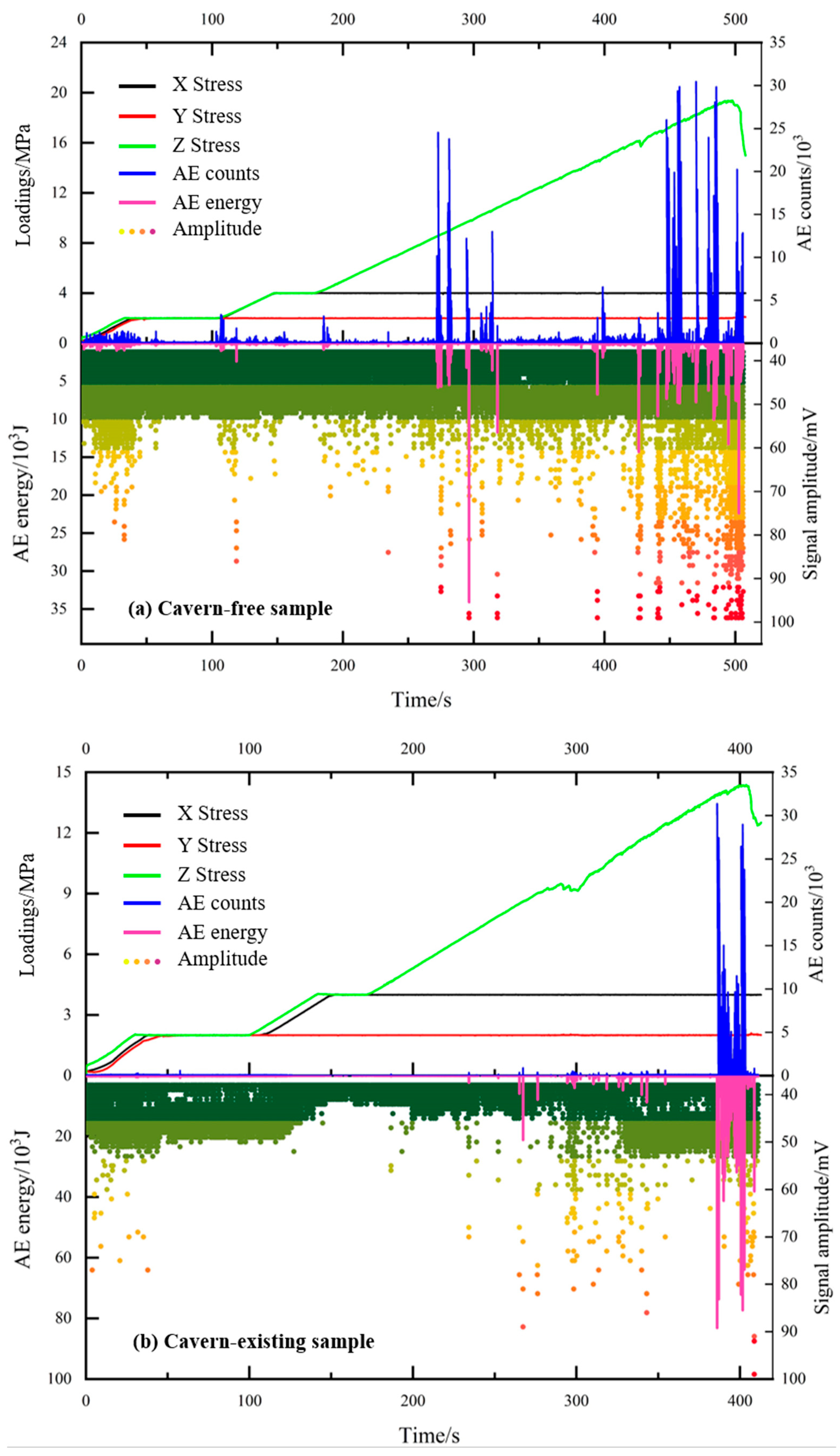
3.1. Mechanical Characteristics and Acoustic Response
3.2. Development of Secondary Cracks on the Tunnel-Surrounding Rock
3.3. Splitting Failure of the Tunnel-Surrounding Rock
4. Numerical Simulation
4.1. Numerical Model and the Related Parameters
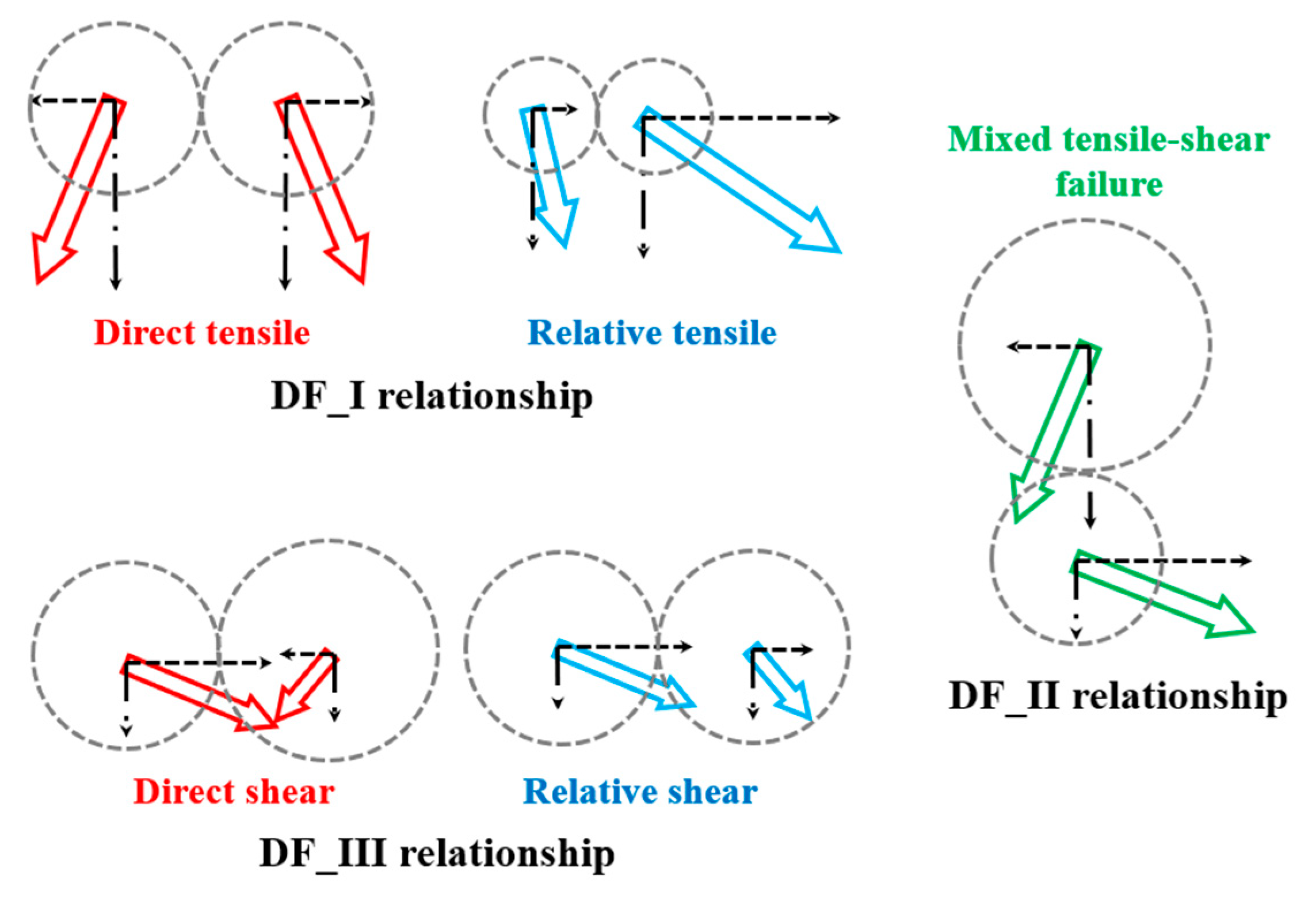
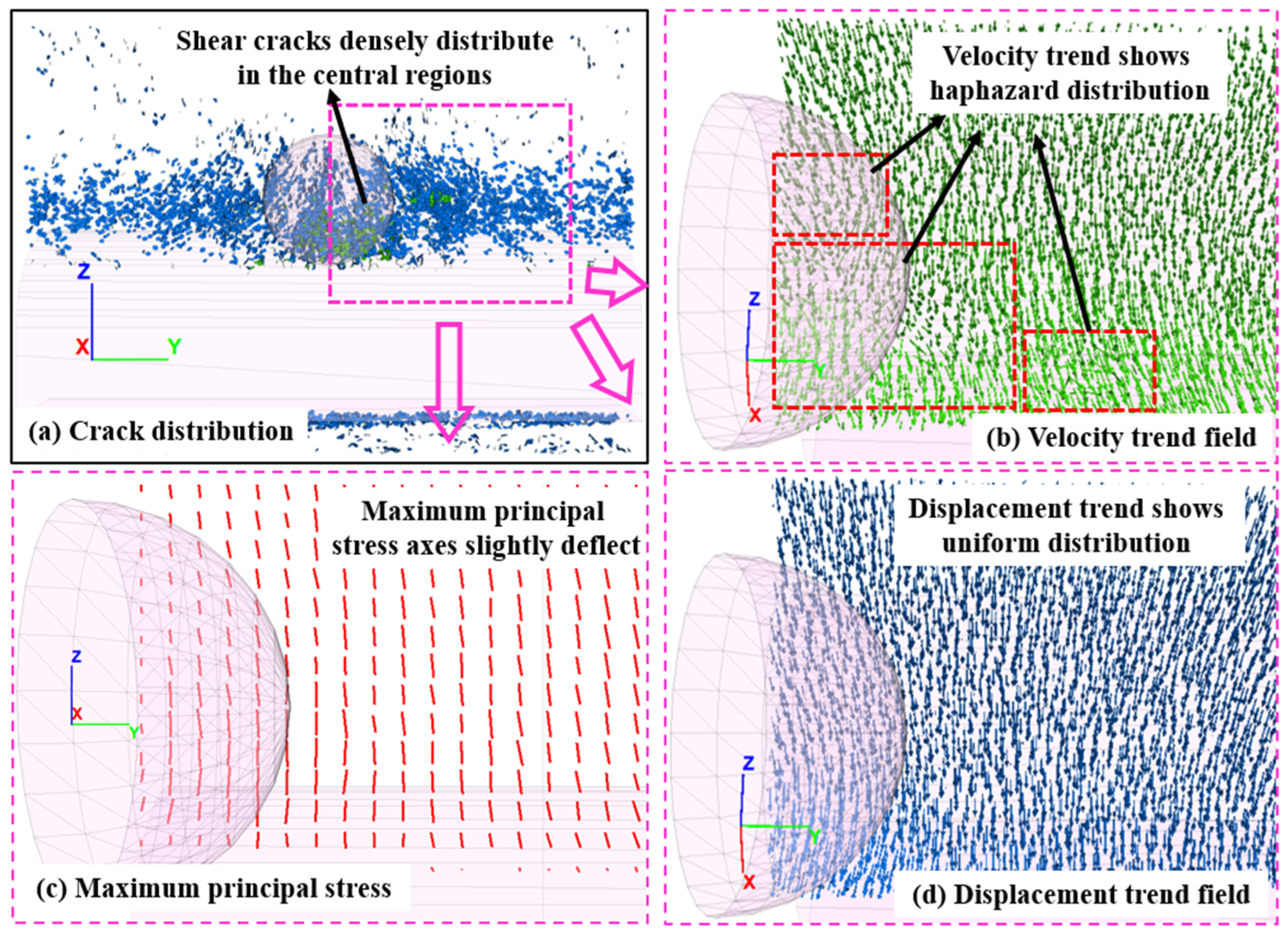
4.2. Cracking Mechanism Analysis
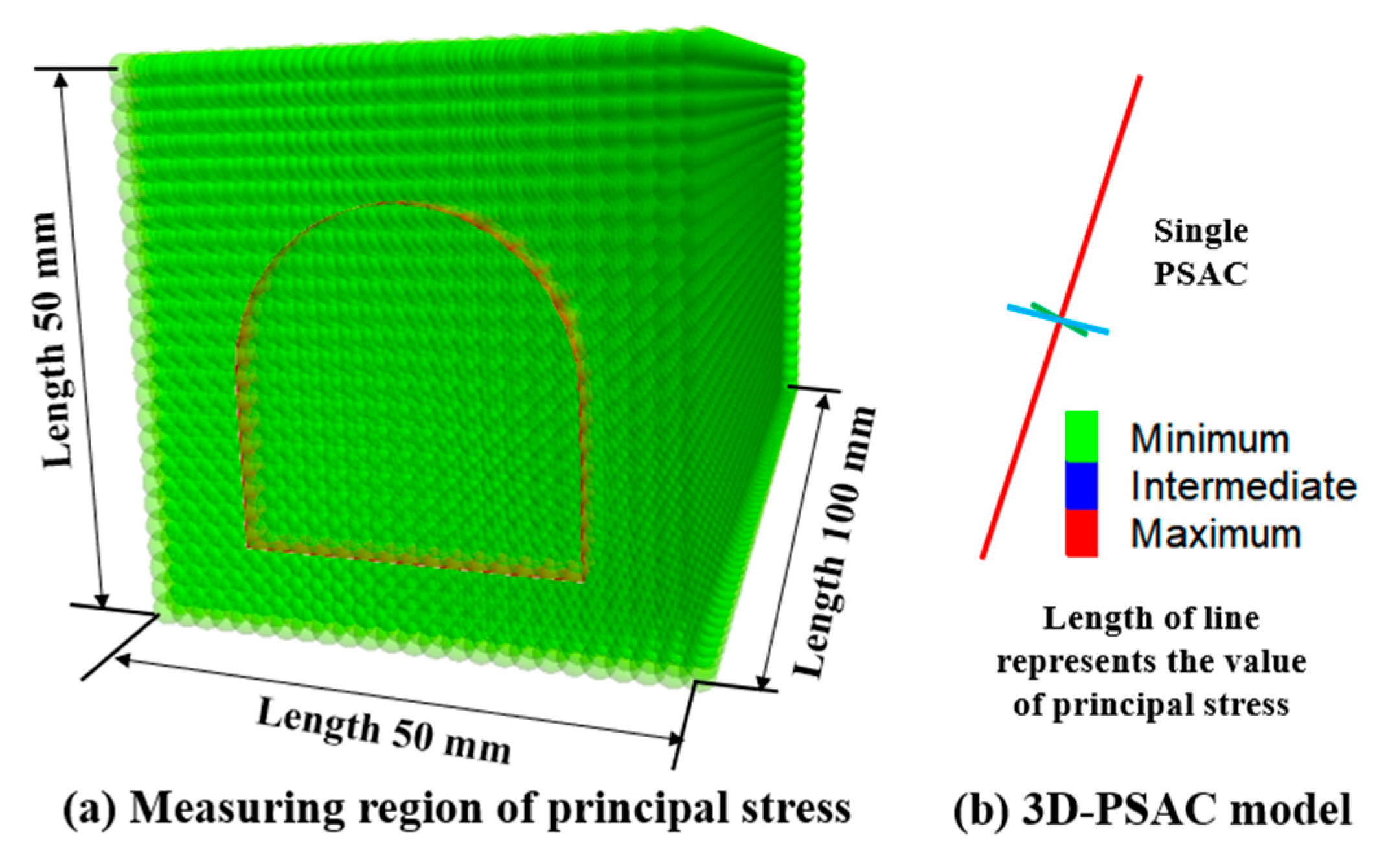
4.3. Estimation of the Stress Field
4.4. Numerical Results and Discussions
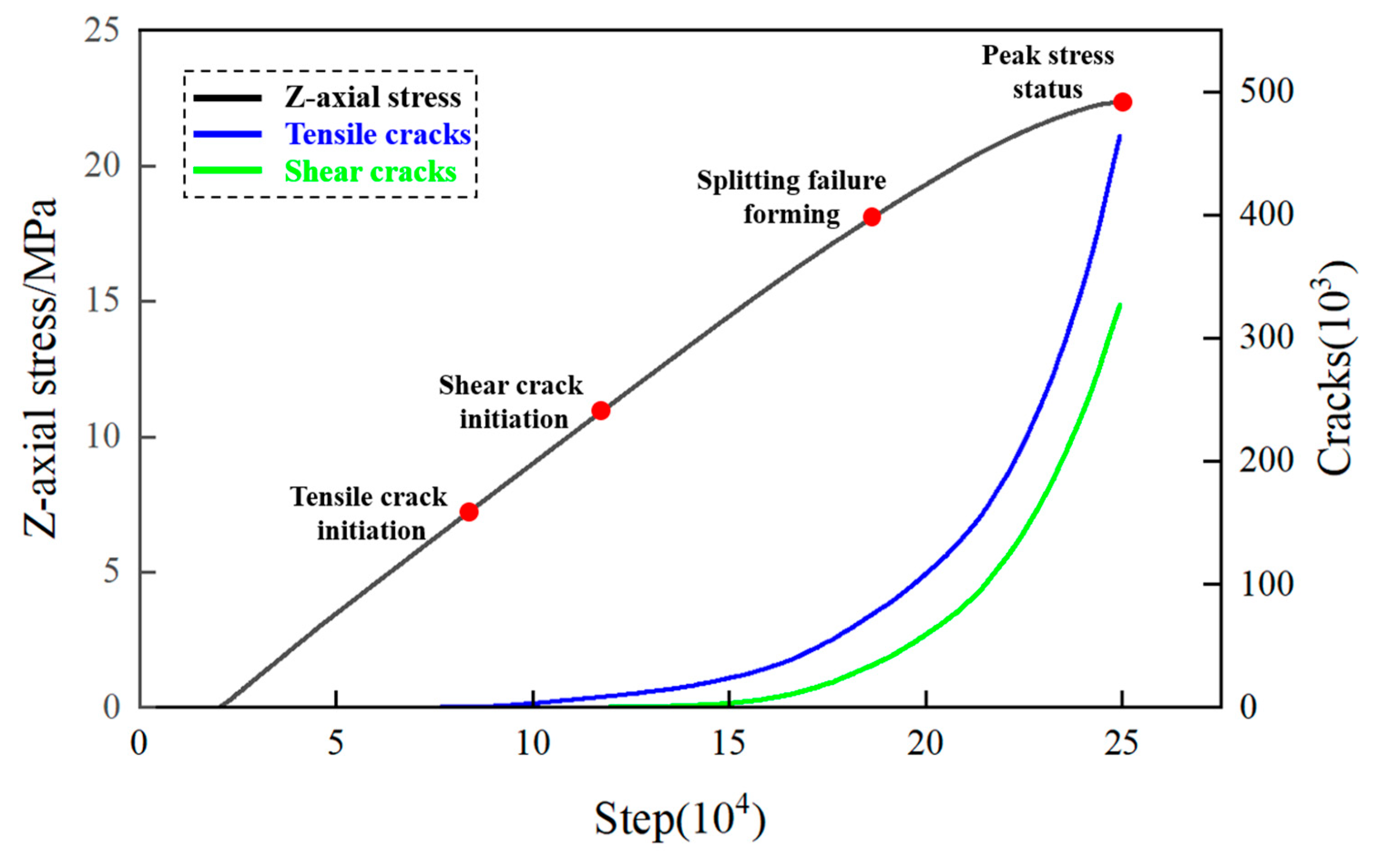
4.4.1. Cavern-Free Sample
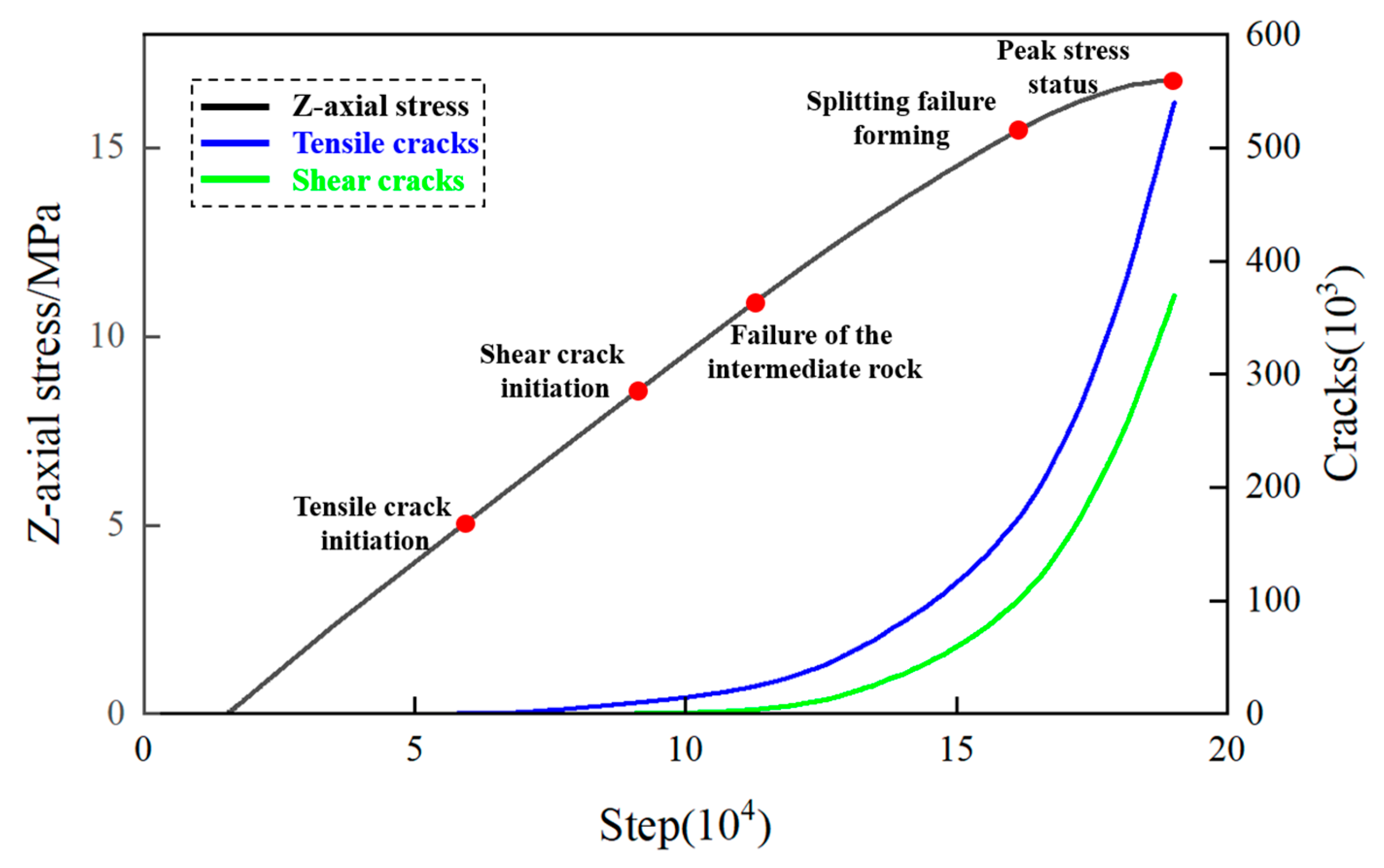
4.4.2. Cavern-Existing Sample
4.4.3. Influence of the True 3D Prefabricated Cavern
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- He, M.; Cheng, T.; Qiao, Y.; Li, H. A review of rockburst: Experiments, theories, and simulations. J. Rock Mech. Geotech. Eng. 2023, 15, 1312–1353. [Google Scholar] [CrossRef]
- Li, B.; Gao, P.; Cao, Y.; Gong, W.; Zhang, S.; Zhang, J. Damage and Failure Characteristics of Surrounding Rock in Deep Circular Cavern under Cyclic Dynamic Load: A True Triaxial Experiment Investigation. Minerals 2022, 12, 134. [Google Scholar] [CrossRef]
- Luo, Y. Influence of water on mechanical behavior of surrounding rock in hard-rock tunnels: An experimental simulation. Eng. Geol. 2020, 277, 105816. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, G.-Y.; Ma, S.-W. Failure behavior of horseshoe-shaped tunnel in hard rock under high stress: Phenomenon and mechanisms. Trans. Nonferrous Met. Soc. China 2022, 32, 639–656. [Google Scholar] [CrossRef]
- Qiu, W.; Ai, X.; Zheng, Y. First application of mechanized method using earth pressure balance TBM with large horseshoe-shaped cross section to loess mountain tunnel: A case study of Baicheng tunnel. Tunn. Undergr. Space Technol. 2022, 126, 104547. [Google Scholar] [CrossRef]
- Gong, F.Q.; Luo, Y.; Liu, D.Q. Simulation tests on spalling failure in deep straight-wall-top-arch tunnels. Chin. J. Geotech. Eng. 2019, 41, 1091–1100. [Google Scholar] [CrossRef]
- Gong, F.-Q.; Luo, Y.; Li, X.-B.; Si, X.-F.; Tao, M. Experimental simulation investigation on rockburst induced by spalling failure in deep circular tunnels. Tunn. Undergr. Space Technol. 2018, 81, 413–427. [Google Scholar] [CrossRef]
- Si, X.; Peng, K.; Luo, S. Experimental Investigation on the Influence of Depth on Rockburst Characteristics in Circular Tunnels. Sensors 2022, 22, 3679. [Google Scholar] [CrossRef]
- Zhang, L.; Chao, W.; Liu, Z.; Cong, Y.; Wang, Z. Crack propagation characteristics during progressive failure of circular tunnels and the early warning thereof based on multi-sensor data fusion. Géoméch. Geophys. Geo-Energy Geo-Resour. 2022, 8, 172. [Google Scholar] [CrossRef]
- Li, D.; Xiao, P.; Han, Z.; Zhu, Q. Mechanical and failure properties of rocks with a cavity under coupled static and dynamic loads. Eng. Fract. Mech. 2018, 225, 106195. [Google Scholar] [CrossRef]
- Luo, Y.; Gong, F.; Liu, D.; Wang, S.; Si, X. Experimental simulation analysis of the process and failure characteristics of spalling in D-shaped tunnels under true-triaxial loading conditions. Tunn. Undergr. Space Technol. 2019, 90, 42–61. [Google Scholar] [CrossRef]
- Gong, F.; Wu, W.; Ren, L. Rockburst process and strength-weakening effect of the high-stress circular tunnel under internal unloading. J. Rock Mech. Geotech. Eng. 2023, 15, 864–885. [Google Scholar] [CrossRef]
- Zhang, X.-P.; Liu, Q.; Wu, S.; Tang, X. Crack coalescence between two non-parallel flaws in rock-like material under uniaxial compression. Eng. Geol. 2015, 199, 74–90. [Google Scholar] [CrossRef]
- Zhang, X.-P.; Wong, L.N.Y. Displacement field analysis for cracking processes in bonded-particle model. Bull. Eng. Geol. Environ. 2013, 73, 13–21. [Google Scholar] [CrossRef]
- Li, B.-X.; Yu, S.; Zhu, W.-S.; Yang, L.; Cai, W.-B.; Xue, Y.-G.; Li, Y. The crack coalescence mode and physical field evolutionary characteristics of a brittle material containing two 3-D parallel embedded flaws. Theor. Appl. Fract. Mech. 2020, 110, 102836. [Google Scholar] [CrossRef]
- Aliabadian, Z.; Sharafisafa, M.; Tahmasebinia, F.; Shen, L. Experimental and numerical investigations on crack development in 3D printed rock-like specimens with pre-existing flaws. Eng. Fract. Mech. 2020, 241, 107396. [Google Scholar] [CrossRef]
- Sharafisafa, M.; Aliabadian, Z.; Tahmasebinia, F.; Shen, L. A comparative study on the crack development in rock-like specimens containing unfilled and filled flaws. Eng. Fract. Mech. 2020, 241, 107405. [Google Scholar] [CrossRef]
- Fan, W.; Yang, H.; Jiang, X.; Cao, P. Experimental and numerical investigation on crack mechanism of folded flawed rock-like material under uniaxial compression. Eng. Geol. 2021, 291, 106210. [Google Scholar] [CrossRef]
- Huang, S.; Yao, N.; Ye, Y.; Cui, X. Strength and Failure Characteristics of Rocklike Material Containing a Large-Opening Crack under Uniaxial Compression: Experimental and Numerical Studies. Int. J. Géoméch. 2019, 19, 4019098. [Google Scholar] [CrossRef]
- Xia, K.; Ren, R.; Liu, F. Numerical analysis of mechanical behavior of stratified rocks containing a single flaw by utilizing the particle flow code. Eng. Anal. Bound. Elem. 2022, 137, 91–104. [Google Scholar] [CrossRef]
- Yan, Z.; Dai, F.; Liu, Y.; Li, A.; Du, H. Numerical assessment of the rate-dependent cracking behaviours of single-flawed rocks in split Hopkinson pressure bar tests. Eng. Fract. Mech. 2021, 247, 107656. [Google Scholar] [CrossRef]
- You, W.; Dai, F.; Liu, Y. Experimental and numerical investigation on the mechanical responses and cracking mechanism of 3D confined single-flawed rocks under dynamic loading. J. Rock Mech. Geotech. Eng. 2022, 14, 477–493. [Google Scholar] [CrossRef]
- Liu, B.; Zhou, Y.; Gao, Y.-T.; Xu, C. Experimental and numerical study on crack development characteristics between two cavities in rock-like material under uniaxial compression. Theor. Appl. Fract. Mech. 2020, 109, 102755. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Yin, P.-F.; Zhang, Y.-C.; Chen, M.; Zhou, X.-P.; Jing, H.-W.; Zhang, Q.-Y. Failure behavior and crack evolution mechanism of a non-persistent jointed rock mass containing a circular hole. Int. J. Rock Mech. Min. Sci. 2019, 114, 101–121. [Google Scholar] [CrossRef]
- Zhao, Y.; Gao, Y.; Wu, S.; Chen, L.; Zhang, C. Experimental and numerical study of failure characteristics of brittle rocks with single internal 3D open-type flaw. Acta Geotech. 2021, 16, 3087–3113. [Google Scholar] [CrossRef]
- Zhao, Y.; Gao, Y.; Wu, S. Influence of different concealment conditions of parallel double flaws on mechanical properties and failure characteristics of brittle rock under uniaxial compression. Theor. Appl. Fract. Mech. 2020, 109, 102751. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, X.; Zhou, L.; Berto, F. Progressive failure of brittle rocks with non-isometric flaws: Insights from acousto-optic-mechanical (AOM) data. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 1787–1802. [Google Scholar] [CrossRef]
- Zhou, X.-P.; Zhang, J.-Z.; Berto, F. Fracture Analysis in Brittle Sandstone by Digital Imaging and AE Techniques: Role of Flaw Length Ratio. J. Mater. Civ. Eng. 2020, 32, 04020085. [Google Scholar] [CrossRef]
- Alitalesh, M.; Yazdani, M.; Fakhimi, A.; Naeimabadi, M. Effect of loading direction on interaction of two pre-existing open and closed flaws in a rock-like brittle material. Undergr. Space 2019, 5, 242–257. [Google Scholar] [CrossRef]
- Wu, S.; Xu, X. A Study of Three Intrinsic Problems of the Classic Discrete Element Method Using Flat-Joint Model. Rock Mech. Rock Eng. 2015, 49, 1813–1830. [Google Scholar] [CrossRef]
- Wang, P.; Yin, Z.-Y.; Wang, Z.-Y. Micromechanical Investigation of Particle-Size Effect of Granular Materials in Biaxial Test with the Role of Particle Breakage. J. Eng. Mech. 2022, 148, 04021133. [Google Scholar] [CrossRef]
- Zhang, S.; Ma, X. How Does In Situ Stress Rotate Within a Fault Zone? Insights From Explicit Modeling of the Frictional, Fractured Rock Mass. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022348. [Google Scholar] [CrossRef]
- Zhou, X. Dynamic damage constitutive relation of mesoscopic heterogenous brittle rock under rotation of principal stress axes. Theor. Appl. Fract. Mech. 2010, 54, 110–116. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, C.; Qi, Q.; Wu, S. Rotation and deflection of 3D principal stress axes induced by a prefabricated single flaw in sandstone: A numerical investigation based on DEM. Theor. Appl. Fract. Mech. 2022, 120, 103430. [Google Scholar] [CrossRef]
- Yin, Z.-Y.; Wang, P.; Zhang, F. Effect of particle shape on the progressive failure of shield tunnel face in granular soils by coupled FDM-DEM method. Tunn. Undergr. Space Technol. 2020, 100, 103394. [Google Scholar] [CrossRef]
- Nguyen, H.B.K.; Rahman, M.M.; Fourie, A.B. Effect of Particle Shape on Constitutive Relation: DEM Study. J. Geotech. Geoenviron. Eng. 2020, 146, 04020058. [Google Scholar] [CrossRef]







| Paremeters Name | Notes |
|---|---|
| Chemical composition of gypsum powder | a-CaSO4-1/2H2O |
| Mesh number | 2000 |
| Initial setting period/min | ≥3.0 |
| Final setting period/min | ≤30.0 |
| 2 h strength/MPa | 4.0 |
| Uniaxial compressive strength/MPa | 26.63 |
| Tensile strength/MPa | 1.13 |
| Elastic modulus/GPa | 17.19 |
| Micro-Parameters | Value |
|---|---|
| 1.66 | |
| Minimum grain diameter | 1.0 |
| 0.3 | |
| 0.0 | |
| 0.9 | |
| 0.1 | |
| 1 | |
| 3 | |
| (GPa) | 12.8 |
| 1.0 | |
| (MPa) | (1.2, 0.1) |
| (MPa) | (16.5, 1.5) |
| Macro-parameters of the ISRM sample (real/numerical model) | Value |
| Uniaxial compressive strength (UCS)/MPa | 26.63/26.58 |
| Elastic modulus (EM)/GPa | 17.19/17.15 |
| Tensile strength (TS)/MPa | 1.13/1.12 |
| Related properties of the cubic model | Value |
| Length of cubic model/mm | 100 |
| Total particle number | 1,098,824 |
| Interval between each saving file/steps | 5000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; She, X.; Zhao, Y. Influence of Spherical Caverns on the Failure Characteristics of Neighboring Tunnels under True Triaxial Conditions: Insights from an Experimental Test and Discrete Element Simulation. Appl. Sci. 2023, 13, 7688. https://doi.org/10.3390/app13137688
Chen C, She X, Zhao Y. Influence of Spherical Caverns on the Failure Characteristics of Neighboring Tunnels under True Triaxial Conditions: Insights from an Experimental Test and Discrete Element Simulation. Applied Sciences. 2023; 13(13):7688. https://doi.org/10.3390/app13137688
Chicago/Turabian StyleChen, Congcong, Xianwei She, and Yusong Zhao. 2023. "Influence of Spherical Caverns on the Failure Characteristics of Neighboring Tunnels under True Triaxial Conditions: Insights from an Experimental Test and Discrete Element Simulation" Applied Sciences 13, no. 13: 7688. https://doi.org/10.3390/app13137688
APA StyleChen, C., She, X., & Zhao, Y. (2023). Influence of Spherical Caverns on the Failure Characteristics of Neighboring Tunnels under True Triaxial Conditions: Insights from an Experimental Test and Discrete Element Simulation. Applied Sciences, 13(13), 7688. https://doi.org/10.3390/app13137688





