Balanced Foot Dorsiflexion Requires a Coordinated Activity of the Tibialis Anterior and the Extensor Digitorum Longus: A Musculoskeletal Modelling Study
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
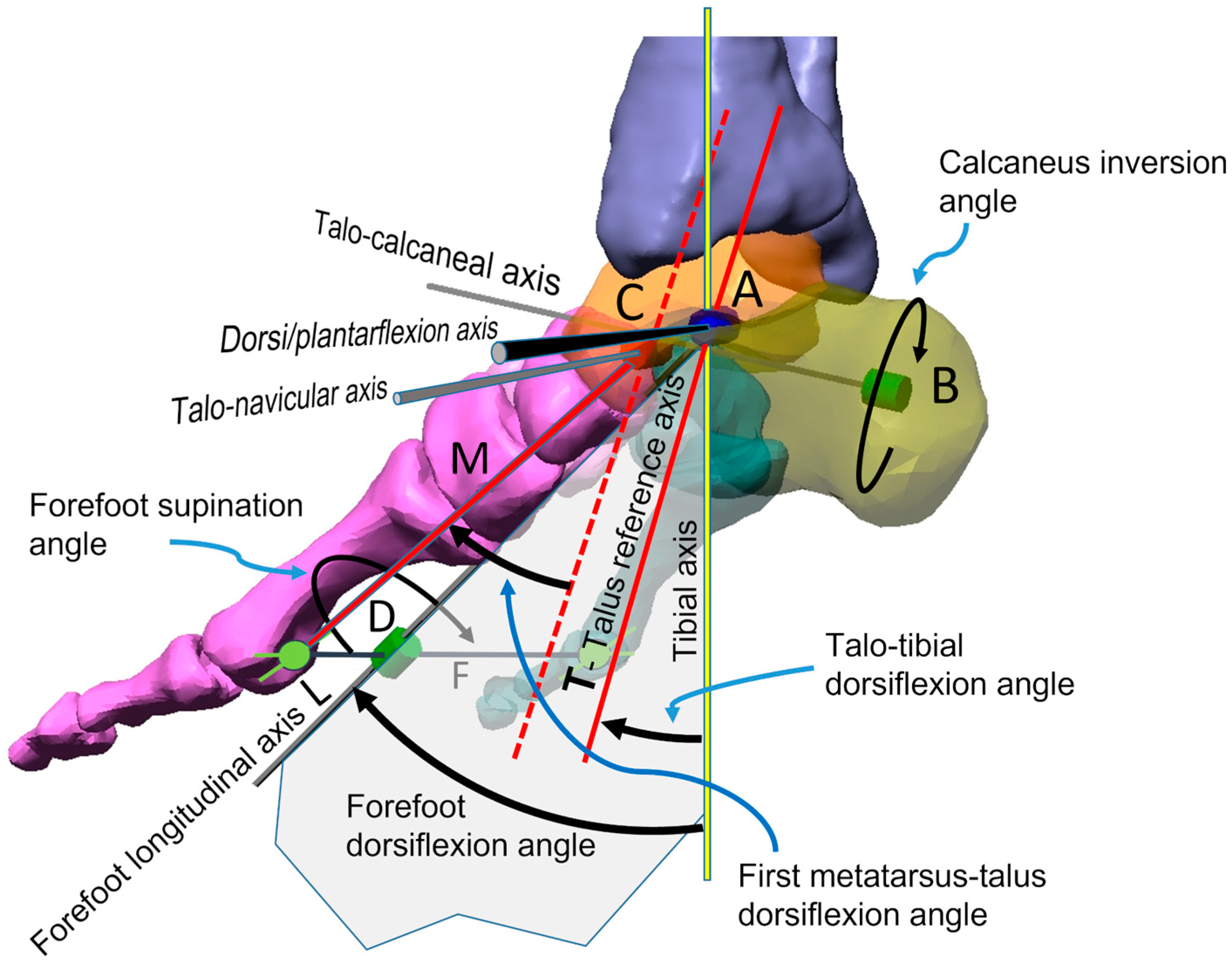
2.1. Foot Angles Definition
- The forefoot dorsiflexion/plantarflexion angle and forefoot supination/pronation angle. A mediolateral axis, fixed to the distal tibia and passing through the centre of curvature of the tibial trochlea, was adopted as the dorsi/plantarflexion axis (see revolute joint A in Figure 2). A bar (labelled L in Figure 2), representing the longitudinal axis of the foot, was connected to revolute joint A, while the other extremity of the bar was connected to the forefoot. Since the bar could only move in a plane perpendicular to the dorsi/plantarflexion axis, the connection with the forefoot was defined as follows: a transverse bar labelled F was connected to the first and fifth metatarsal heads through constraints that allowed medial–lateral and distal–proximal translations and all the three pertaining rotations. These were named the ‘sphere on plane’ constraints. The transverse bar F was then connected to bar L by a revolute joint (labelled D in Figure 2) which was oriented on the longitudinal axis of the foot. In this way, the pronation/supination and other movements out of the sagittal plane were not constrained by our measuring system. The rotation of bar L about the dorsi/plantarflexion axis was measured by revolute joint A, and was defined as the ‘forefoot dorsiflexion’ angle. The rotation of transverse bar F about the longitudinal axis of the foot was measured by revolute joint D, and was named the ‘forefoot supination’ angle.
- Talotibial rotation angle. A bar labelled T was hinged to revolute joint A and connected to the talus through a ‘sphere on plane’ constraint (see above). Bar T acts as a reference axis for the talus. Revolute joint A provided us with the talotibial rotation angle.
- First metatarsus–talus rotation angle. A mediolateral axis passes through the centre of the talonavicular joint (talonavicular axis). Revolute joint C (see Figure 2) was designed to measure the dorsi/plantarflexion angle of the first metatarsal bone in relation to the reference axis of the talus (parallel to bar T). A bar (labelled M in Figure 2) was hinged to revolute joint C and connected to the first metatarsal bone by a sphere on plane constraint. The angle measured by revolute joint C was named the ‘first metatarsus–talus’ rotation angle.
- Calcaneus inversion/eversion angle. The axis of rotation of the talocalcaneal joint, the Henke axis [34], was identified as an axis passing through the superior part of the talus and the lateral tuberosity of the calcaneus. When the foot was on the ground, the talocalcaneal axis was oriented at 42° over the horizontal plane and 16° medially about the longitudinal foot axis. The corresponding revolute joint (labelled B in Figure 2) was fixed to the talus and provided us with the relative rotation of the calcaneus about the talus (the calcaneus inversion/eversion angle).
2.2. Foot Unloading
2.3. Simulated Muscle Contractions in Normal Conditions
2.4. Simulated Muscle Contractions in Stroke-Like Conditions
3. Results
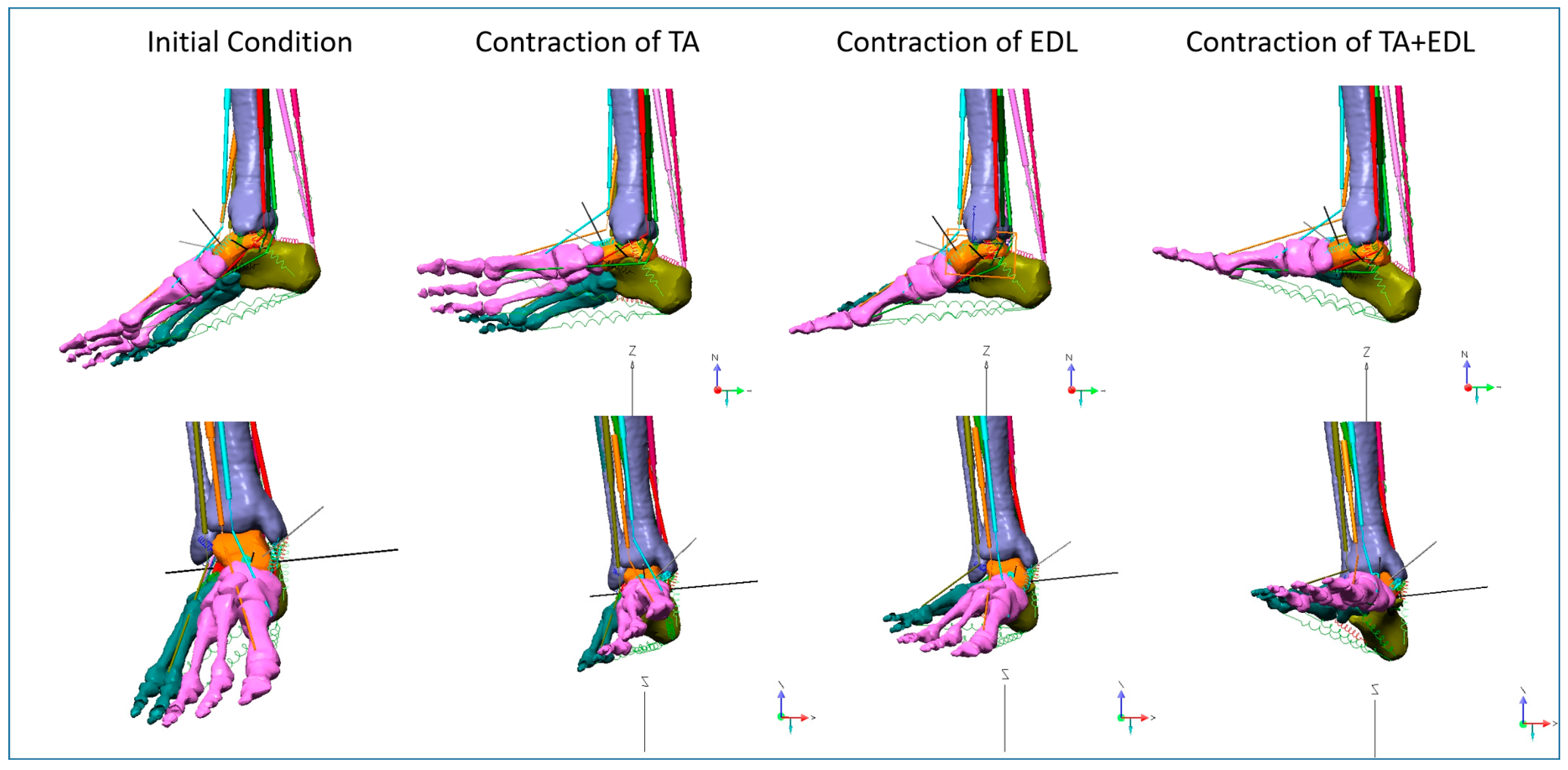
3.1. Initial Model Condition
3.2. Maximum Muscle Shortening
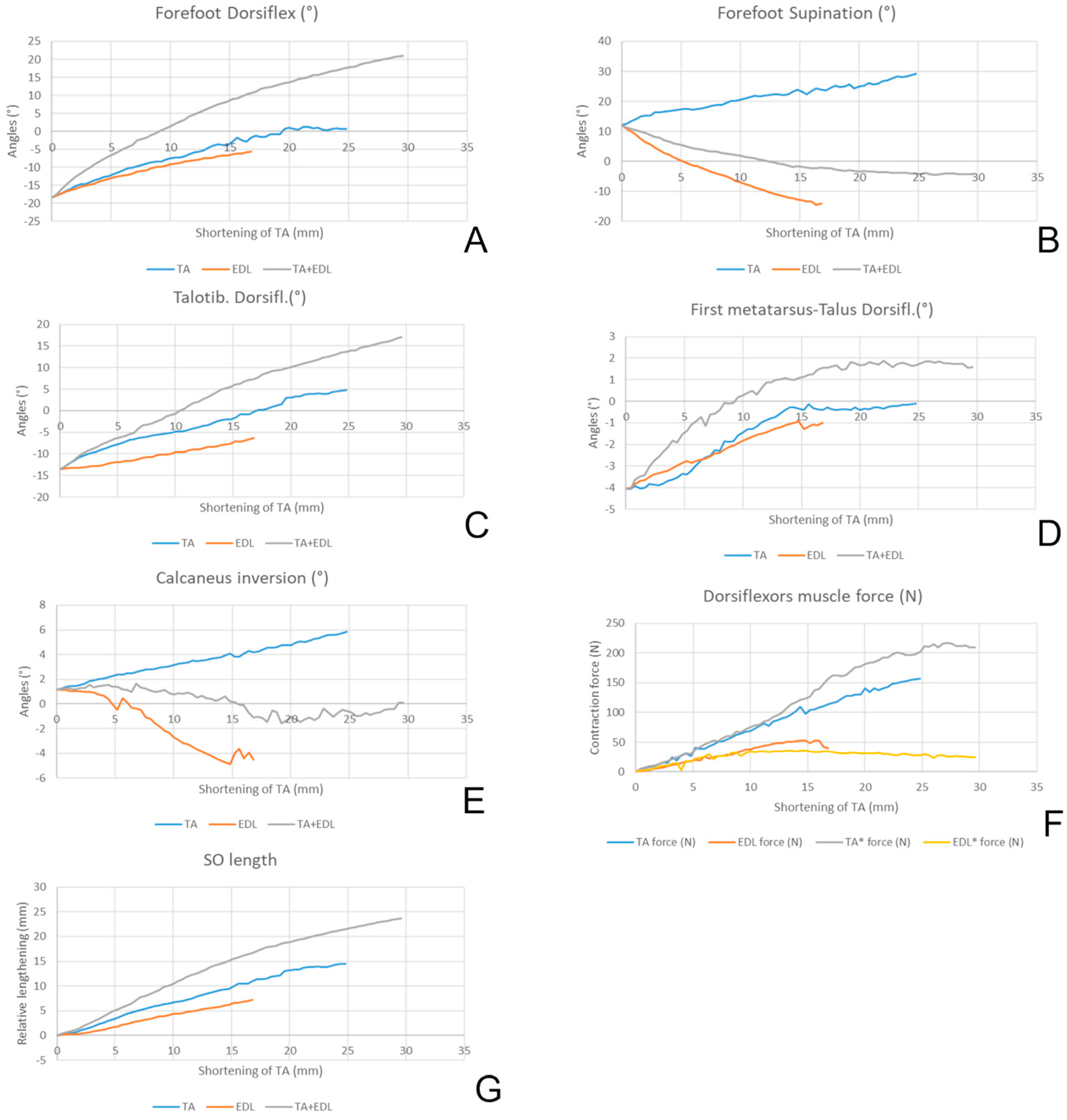
3.3. Effect of TA, EDL and TA + EDL Contraction on Dorsiflexion
- -
- Foot dorsiflexion produced by the TA was progressively limited as far as the SO was constrained to shorter excursions. After that limit, the effect of the TA contractions switched from dorsiflexion to plantarflexion (panel A);
- -
- Forefoot supination increased more rapidly as soon as the SO length achieved its limit (panel B);
- -
- Talus dorsiflexion about the tibia was stopped while the first metatarsus increased in dorsiflexion (panels C and D);
- -
- The calcaneus inversion increased more rapidly (panel E);
- -
- The force of the TA increased considerably as long as the SO lengthening was reduced.
- -
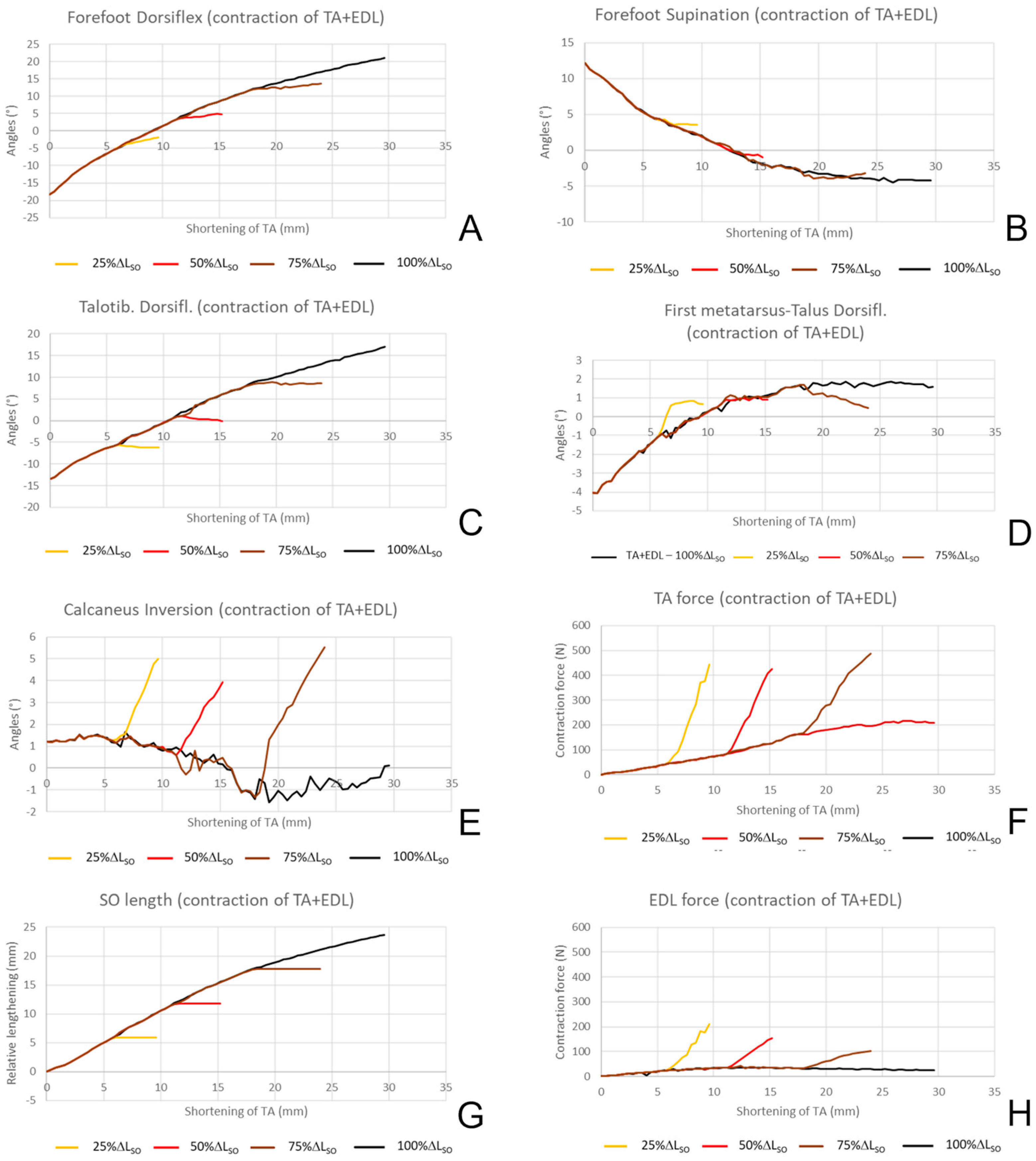
- Foot dorsiflexion slows down and comes to a stop as the limitation of the SO lengthening progresses (panel A);
- -
- Forefoot pronation and the talotibial dorsiflexion stop at different angles in correspondence with the SO lengthening limitation (panels B and C);
- -
- Dorsiflexion of the first metatarsus is affected differently at the beginning of the movement (SO lengthening limited at 25%) than at the end (SO lengthening capped at 75%). In the former case, dorsiflexion increased; in the latter, dorsiflexion lessened (panel D);
- -
- The calcaneus undergoes a sharp inversion as soon as the SO lengthening stops (panel E);
- -
- The contraction force of both the TA and EDL abruptly increases when SO lengthening is halted (panels F and H).
4. Discussion
4.1. Modelling and Validation
4.2. Clinical Implications
4.3. Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Inzitari, D.; Carlucci, G. Italian Stroke Guidelines (SPREAD): Evidence and clinical practice. Neurol. Sci. 2006, 27, s225–s227. [Google Scholar] [CrossRef] [PubMed]
- Lim, K.B.; Kim, J.-A. Activity of Daily Living and Motor Evoked Potentials in the Subacute Stroke Patients. Ann. Rehabil. Med. 2013, 37, 82–87. [Google Scholar] [CrossRef] [PubMed]
- Moura Rde, C.; Fukujima, M.M.; Aguiar, A.S.; Fontes, S.V.; Dauar, R.F.; Prado, G.F. Predictive factors for spasticity among ischemic stroke patients. Arq. Neuropsiquiatr. 2009, 67, 1029–1036. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lundström, E.; Smits, A.; Terént, A.; Borg, J. Time-course and determinants of spasticity during the first six months following first-ever stroke. J. Rehabil. Med. 2010, 42, 296–301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Urban, P.P.; Wolf, T.; Uebele, M.; Marx, J.J.; Vogt, T.; Stoeter, P.; Bauermann, T.; Weibrich, C.; Vucurevic, G.D.; Schneider, A.; et al. Occurence and Clinical Predictors of Spasticity after Ischemic Stroke. Stroke 2010, 41, 2016–2020. [Google Scholar] [CrossRef] [Green Version]
- Wissel, J.; Schelosky, L.D.; Scott, J.; Christe, W.; Faiss, J.H.; Mueller, J. Early development of spasticity following stroke: A prospective, observational trial. J. Neurol. 2010, 257, 1067–1072. [Google Scholar] [CrossRef] [Green Version]
- Ryu, J.S.; Lee, J.W.; Lee, S.I.; Chun, M.H. Factors Predictive of Spasticity and Their Effects on Motor Recovery and Functional Outcomes in Stroke Patients. Top. Stroke Rehabil. 2010, 17, 380–388. [Google Scholar] [CrossRef]
- de Haart, M.; Geurts, A.C.; Huidekoper, S.C.; Fasotti, L.; van Limbeek, J. Recovery of standing balance in postacute stroke patients: A rehabilitation cohort study11No commercial party having a direct financial interest in the results of the research supporting this article has or will confer a benefit upon the authors(s) or upon any organization with which the author(s) is/are associated. Arch. Phys. Med. Rehabil. 2004, 85, 886–895. [Google Scholar] [CrossRef]
- Keenan, M.A.; Perry, J.; Jordan, C. Factors affecting balance and ambulation following stroke. Clin. Orthop. Relat. Res. 1984, 182, 165–171. [Google Scholar] [CrossRef]
- Edwards, P.; Hsu, J. SPLATT Combined with Tendo Achilles Lengthening for Spastic Equinovarus in Adults: Results and Predictors of Surgical Outcome. Foot Ankle 1993, 14, 335–338. [Google Scholar] [CrossRef]
- Lawrence, S.J.; Botte, M.J. Management of the Adult, Spastic, Equinovarus Foot Deformity. Foot Ankle Int. 1994, 15, 340–346. [Google Scholar] [CrossRef] [PubMed]
- Hebela, N.; Keenan, M. Neuro-orthopedic management of the dysfunctional extremity in upper motor neuron syndromes. Eur. J. Phys. Rehabil. Med. 2004, 40, 145. [Google Scholar]
- Giannotti, E.; Merlo, A.; Zerbinati, P.; Prati, P.; Masiero, S.; Mazzoli, D. Safety and long-term effects on gait of hemiplegic patients in equinovarus foot deformity surgical correction followed by immediate rehabilitation: A prospective observational study. Eur. J. Phys. Rehabil. Med. 2019, 55, 169–175. [Google Scholar] [CrossRef]
- Gage, J. Gait analysis. An essential tool in the treatment of cerebral palsy. Clin. Orthop. Relat. Res. 1993, 288, 126–134. [Google Scholar] [CrossRef]
- Vogt, J.C.; Bach, G.; Cantini, B.; Perrin, S. Split anterior tibial tendon transfer for varus equinus spastic foot deformity: Initial clinical findings correlate with functional results: A series of 132 operated feet. Foot Ankle Surg. 2011, 17, 178–181. [Google Scholar] [CrossRef] [PubMed]
- King, B.W.; Ruta, D.J.; Irwin, T.A. Spastic foot and ankle deformities: Evaluation and treatment. Foot Ankle Clin. 2014, 19, 97–111. [Google Scholar] [CrossRef]
- Freire, B.; Abou, L.; Dias, C.P. Equinovarus foot in stroke survivors with spasticity: A narrative review of muscle–tendon morphology and force production adaptation. Int. J. Ther. Rehabil. 2020, 27, 1–8. [Google Scholar] [CrossRef]
- Kamath, A.F.; Pandya, N.K.; Namdari, S.; Hosalkar, H.S.; Keenan, M.A. Surgical Technique for the Correction of Adult Spastic Equinovarus Foot. Tech. Foot Ankle Surg. 2009, 8, 160–167. Available online: https://journals.lww.com/techfootankle/Fulltext/2009/12000/Surgical_Technique_for_the_Correction_of_Adult.3.aspx (accessed on 1 February 2023). [CrossRef]
- Limpaphayom, N.; Chantarasongsuk, B.; Osateerakun, P.; Prasongchin, P. The split anterior tibialis tendon transfer procedure for spastic equinovarus foot in children with cerebral palsy: Results and factors associated with a failed outcome. Int. Orthop. 2015, 39, 1593–1598. [Google Scholar] [CrossRef]
- Keenan, M.A. The Management of Spastic Equinovarus Deformity Following Stroke and Head Injury. Foot Ankle Clin. 2011, 16, 499–514. [Google Scholar] [CrossRef]
- Perry, J. The Use of Gait Analysis for Surgical Recommendations in Traumatic Brain Injury. J. Head Trauma Rehabil. 1999, 14, 116–135. Available online: https://journals.lww.com/headtraumarehab/Fulltext/1999/04000/The_Use_of_Gait_Analysis_for_Surgical.3.aspx (accessed on 1 February 2023). [CrossRef]
- Waters, R.L.; Perry, J.; Garland, D. Surgical correction of gait abnormalities following stroke. Clin. Orthop. Relat. Res. 1978, 131, 54–63. [Google Scholar] [CrossRef]
- Duchenne, G.B. Physiology of Motion; J.B. Lippincott Company: Philadelphia, PA, USA, 1949. [Google Scholar]
- Reynard, F.; Dériaz, O.; Bergeau, J. Foot varus in stroke patients: Muscular activity of extensor digitorum longus during the swing phase of gait. Foot 2009, 19, 69–74. [Google Scholar] [CrossRef] [PubMed]
- Deltombe, T.; Wautier, D.; Cloedt, P.; Fostier, M.; Gustin, T. Assessment and treatment of spastic equinovarus foot after stroke: Guidance from the Mont-Godinne interdisciplinary group. J. Rehabil. Med. 2017, 49, 461–468. [Google Scholar] [CrossRef] [Green Version]
- Campanini, I.; Cosma, M.; Manca, M.; Merlo, A. Added Value of Dynamic EMG in the Assessment of the Equinus and the Equinovarus Foot Deviation in Stroke Patients and Barriers Limiting Its Usage. Front. Neurol. 2020, 11, 583399. [Google Scholar] [CrossRef]
- Hosalkar, H.; Goebel, J.; Reddy, S.; Pandya, N.K.; Keenan, M.A. Fixation Techniques for Split Anterior Tibialis Transfer in Spastic Equinovarus Feet. Clin. Orthop. Relat. Res. 2008, 466, 2500–2506. [Google Scholar] [CrossRef] [Green Version]
- Frigo, C.A. Special Issue: Musculoskeletal Models in a Clinical Perspective. Appl. Sci. 2021, 11, 6250. [Google Scholar] [CrossRef]
- Killen, B.A.; Falisse, A.; De Groote, F.; Jonkers, I. In Silico-Enhanced Treatment and Rehabilitation Planning for Patients with Musculoskeletal Disorders: Can Musculoskeletal Modelling and Dynamic Simulations Really Impact Current Clinical Practice? Appl. Sci. 2020, 10, 7255. [Google Scholar] [CrossRef]
- Fregly, B.J. A Conceptual Blueprint for Making Neuromusculoskeletal Models Clinically Useful. Appl. Sci. 2021, 11, 2037. [Google Scholar] [CrossRef]
- Frigo, C.A.; Donno, L. The Effects of External Loads and Muscle Forces on the Knee Joint Ligaments during Walking: A Musculoskeletal Model Study. Appl. Sci. 2021, 11, 2356. [Google Scholar] [CrossRef]
- Tzanetis, P.; Marra, M.A.; Fluit, R.; Koopman, B.; Verdonschot, N. Biomechanical Consequences of Tibial Insert Thickness after Total Knee Arthroplasty: A Musculoskeletal Simulation Study. Appl. Sci. 2021, 11, 2423. [Google Scholar] [CrossRef]
- Valente, G.; Taddei, F.; Leardini, A.; Benedetti, M.G. Effects of Hip Abductor Strengthening on Musculoskeletal Loading in Hip Dysplasia Patients after Total Hip Replacement. Appl. Sci. 2021, 11, 2123. [Google Scholar] [CrossRef]
- Zographos, S.; Chaminade, B.; Hobatho, M.C.; Utheza, G. Experimental study of the subtalar joint axis: Preliminary investigation. Surg. Radiol. Anat. 2001, 22, 271–276. [Google Scholar] [CrossRef]
- Riener, R.; Edrich, T. Identification of passive elastic joint moments in the lower extremities. J. Biomech. 1999, 32, 539–544. [Google Scholar] [CrossRef]
- Trompetto, C.; Currà, A.; Puce, L.; Mori, L.; Serrati, C.; Fattapposta, F.; Abbruzzese, G.; Marinelli, L. Spastic dystonia in stroke subjects: Prevalence and features of the neglected phenomenon of the upper motor neuron syndrome. Clin. Neurophysiol. 2019, 130, 521–527. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gracies, J. Pathophysiology of spastic paresis. I: Paresis and soft tissue changes. Muscle Nerve Off. J. Am. Assoc. Electrodiagn. Med. 2005, 31, 535–551. [Google Scholar] [CrossRef]
- Gracies, J. Pathophysiology of spastic paresis. II: Emergence of muscle overactivity. Muscle Nerve Off. J. Am. Assoc. Electrodiagn. Med. 2005, 31, 552–571. [Google Scholar] [CrossRef]
- Mazzoli, D.; Giannotti, E.; Rambelli, C.; Zerbinati, P.; Galletti, M.; Mascioli, F.; Prati, P.; Merlo, A. Long-term effects on body functions, activity and participation of hemiplegic patients in equino varus foot deformity surgical correction followed by immediate rehabilitation. A prospective observational study. Top. Stroke Rehabil. 2019, 26, 518–522. [Google Scholar] [CrossRef]
- Perry, J.; Burnfield, J.M. Gait Analysis: Normal and Pathological Function, 2nd ed.; Slack: Thorofare, NJ, USA, 2010. [Google Scholar]
- Damiano, D.L.; Prosser, L.A.; Curatalo, L.A.; Alter, K.E. Muscle Plasticity and Ankle Control after Repetitive Use of a Functional Electrical Stimulation Device for Foot Drop in Cerebral Palsy. Neurorehabilit. Neural Repair 2012, 27, 200–207. [Google Scholar] [CrossRef]
- Weber, D.J.; Stein, R.B.; Chan, K.M.; Loeb, G.E.; Richmond, F.J.; Rolf, R.; James, K.; Chong, S.L.; Thompson, A.K.; Misiaszek, J. Functional electrical stimulation using microstimulators to correct foot drop: A case study. Can. J. Physiol. Pharmacol. 2004, 82, 784–792. [Google Scholar] [CrossRef]
- Giannotti, E.; Merlo, A.; Zerbinati, P.; Longhi, M.; Prati, P.; Masiero, S.; Mazzoli, D. Early rehabilitation treatment combined with equinovarus foot deformity surgical correction in stroke patients: Safety and changes in gait parameters. Eur. J. Phys. Rehabil. Med. 2015, 52, 296–303. [Google Scholar] [PubMed]
- Kendall, F.P.; McCreary, E.K. Muscles, Testing and Function; Williams & Wilkins: Philadelphia, PA, USA, 1983. [Google Scholar]
- Kapandji, I.A. The Physiology of the Joints; Churchill Livingstone: London, UK, 1987; Volume 2-Lower limb. [Google Scholar]
- Bavikatte, G.; Subramanian, G.; Ashford, S.; Allison, R.; Hicklin, D. Early identification, intervention and management of post-stroke spasticity: Expert consensus recommendations. J. Cent. Nerv. Syst. Dis. 2021, 13, 11795735211036576. [Google Scholar] [CrossRef] [PubMed]
- Miller, S.C.; Korff, T.; Waugh, C.; Fath, F.; Blazevich, A.J. Tibialis Anterior Moment Arm: Effects of Measurement Errors and Assumptions. Med. Sci. Sports Exerc. 2015, 47, 428–439. [Google Scholar] [CrossRef] [PubMed]
- Maganaris, C.N. Force–length characteristics of in vivo human skeletal muscle. Acta Physiol. Scand. 2001, 172, 279–285. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lenhardt, S.A.; McIntosh, K.C.; Gabriel, D.A. The surface EMG-force relationship during isometric dorsiflexion in males and females. Electromyogr. Clin. Neurophysiol. 2009, 49, 227. [Google Scholar]
- Friederich, J.A.; Brand, R.A. Muscle fiber architecture in the human lower limb. J. Biomech. 1990, 23, 91–95. [Google Scholar] [CrossRef]
- Campanini, I.; Bò, M.C.; Salsi, F.; Bassi, M.C.; Damiano, B.; Scaltriti, S.; Lusuardi, M.; Merlo, A. Physical therapy interventions for the correction of equinus foot deformity in post-stroke patients with triceps spasticity: A scoping review. Front. Neurol. 2022, 13, 1026850. [Google Scholar] [CrossRef] [PubMed]
- Blankevoort, L.; Huiskes, R. Ligament-Bone Interaction in a Three-Dimensional Model of the Knee. J. Biomech. Eng. 1991, 113, 263–26991. [Google Scholar] [CrossRef] [Green Version]
- Mkandawire, C.; Ledoux, W.; Sangeorzan, B.J.; Ching, R.P. Foot and ankle ligament morphometry. J. Rehabil. Res. Dev. 2005, 42, 809–820. [Google Scholar] [CrossRef]
- Cheung, J.T.-M.; Zhang, M.; An, K.-N. Effects of plantar fascia stiffness on the biomechanical responses of the ankle–foot complex. Clin. Biomech. 2004, 19, 839–846. [Google Scholar] [CrossRef]
- Siegler, S.; Block, J.; Schneck, C.D. The Mechanical Characteristics of the Collateral Ligaments of the Human Ankle Joint. Foot Ankle 1988, 8, 234–242. [Google Scholar] [CrossRef] [PubMed]
- Gefen, A. The in Vivo Elastic Properties of the Plantar Fascia during the Contact Phase of Walking. Foot Ankle Int. 2003, 24, 238–244. [Google Scholar] [CrossRef] [PubMed]
- Martelli, S.; Valente, G.; Viceconti, M.; Taddei, F. Sensitivity of a subject-specific musculoskeletal model to the uncertainties on the joint axes location. Comput. Methods Biomech. Biomed. Eng. 2014, 18, 1555–1563. [Google Scholar] [CrossRef] [PubMed] [Green Version]


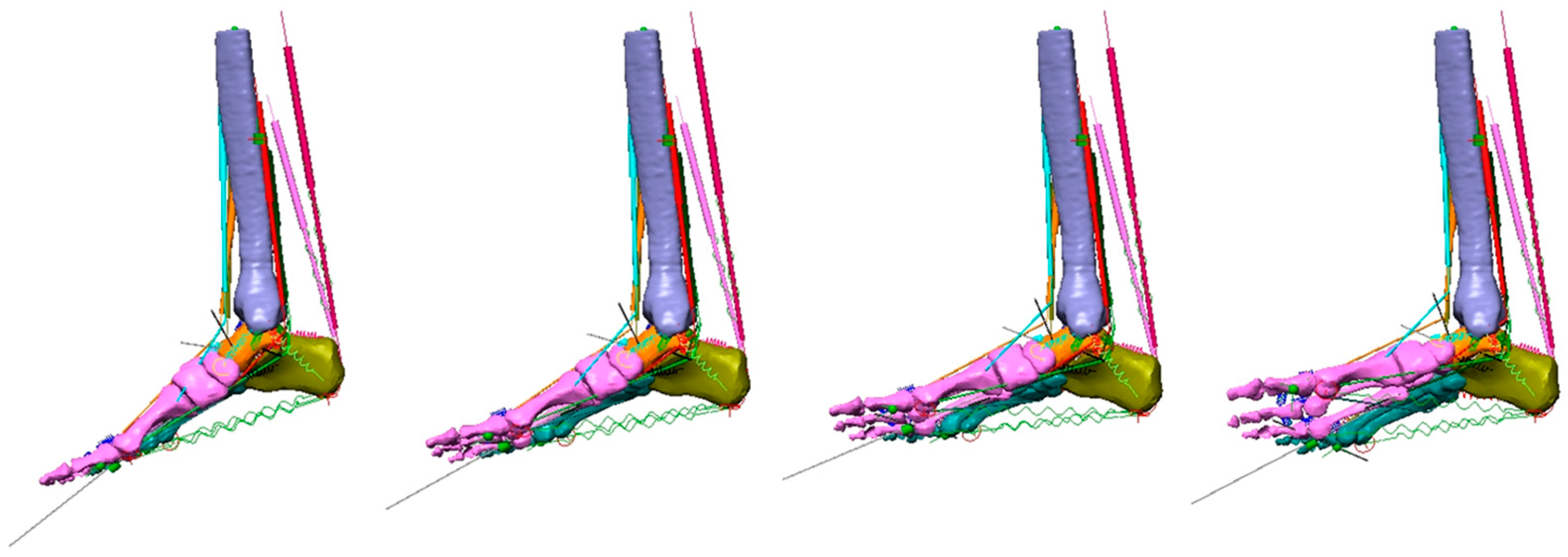
| Joint Rotation | Initial Condition | TA | EDL | TA + EDL |
|---|---|---|---|---|
| Forefoot dorsiflexion | −18° | 18° | 12° | 39° |
| Forefoot supination | 12° | 18° | −25 | 16° |
| Talotibial dorsiflexion | −13.5 | 18.5° | 6° | 30.5° |
| First metatarsus–talus dorsiflexion | −4° | 4° | 3° | 5.6° |
| Calcaneus inversion | 1.2° | 4.8° | −5.6° | −3° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frigo, C.A.; Merlo, A.; Brambilla, C.; Mazzoli, D. Balanced Foot Dorsiflexion Requires a Coordinated Activity of the Tibialis Anterior and the Extensor Digitorum Longus: A Musculoskeletal Modelling Study. Appl. Sci. 2023, 13, 7984. https://doi.org/10.3390/app13137984
Frigo CA, Merlo A, Brambilla C, Mazzoli D. Balanced Foot Dorsiflexion Requires a Coordinated Activity of the Tibialis Anterior and the Extensor Digitorum Longus: A Musculoskeletal Modelling Study. Applied Sciences. 2023; 13(13):7984. https://doi.org/10.3390/app13137984
Chicago/Turabian StyleFrigo, Carlo Albino, Andrea Merlo, Cristina Brambilla, and Davide Mazzoli. 2023. "Balanced Foot Dorsiflexion Requires a Coordinated Activity of the Tibialis Anterior and the Extensor Digitorum Longus: A Musculoskeletal Modelling Study" Applied Sciences 13, no. 13: 7984. https://doi.org/10.3390/app13137984
APA StyleFrigo, C. A., Merlo, A., Brambilla, C., & Mazzoli, D. (2023). Balanced Foot Dorsiflexion Requires a Coordinated Activity of the Tibialis Anterior and the Extensor Digitorum Longus: A Musculoskeletal Modelling Study. Applied Sciences, 13(13), 7984. https://doi.org/10.3390/app13137984






