Best Relay Selection Strategy in Cooperative Spectrum Sharing Framework with Mobile-Based End User
Abstract
:1. Introduction
- (1)
- The best relay selection strategy is exploited to enhance the performance of underlay cognitive relay networks deploying a mobile-based end user.
- (2)
- The outage probabilities of the proposed system model are obtained and investigated with the consideration of interference power constraints over mixed fading channels.
- (3)
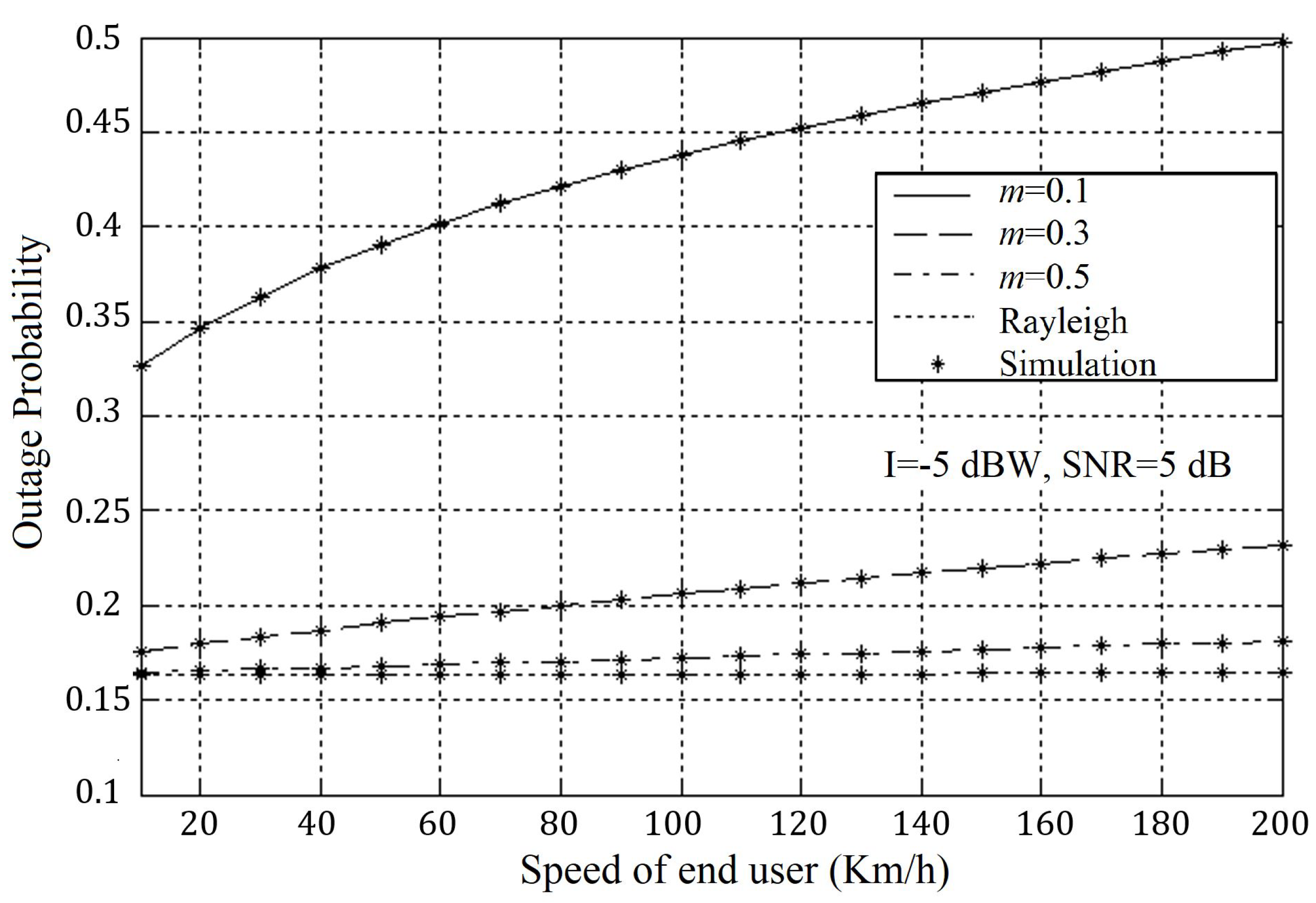
- The effect of various factors that could influence the system performance such as the number of relays, fading severity parameters, fading model, PU location, and mobile end user speed are investigated as well.
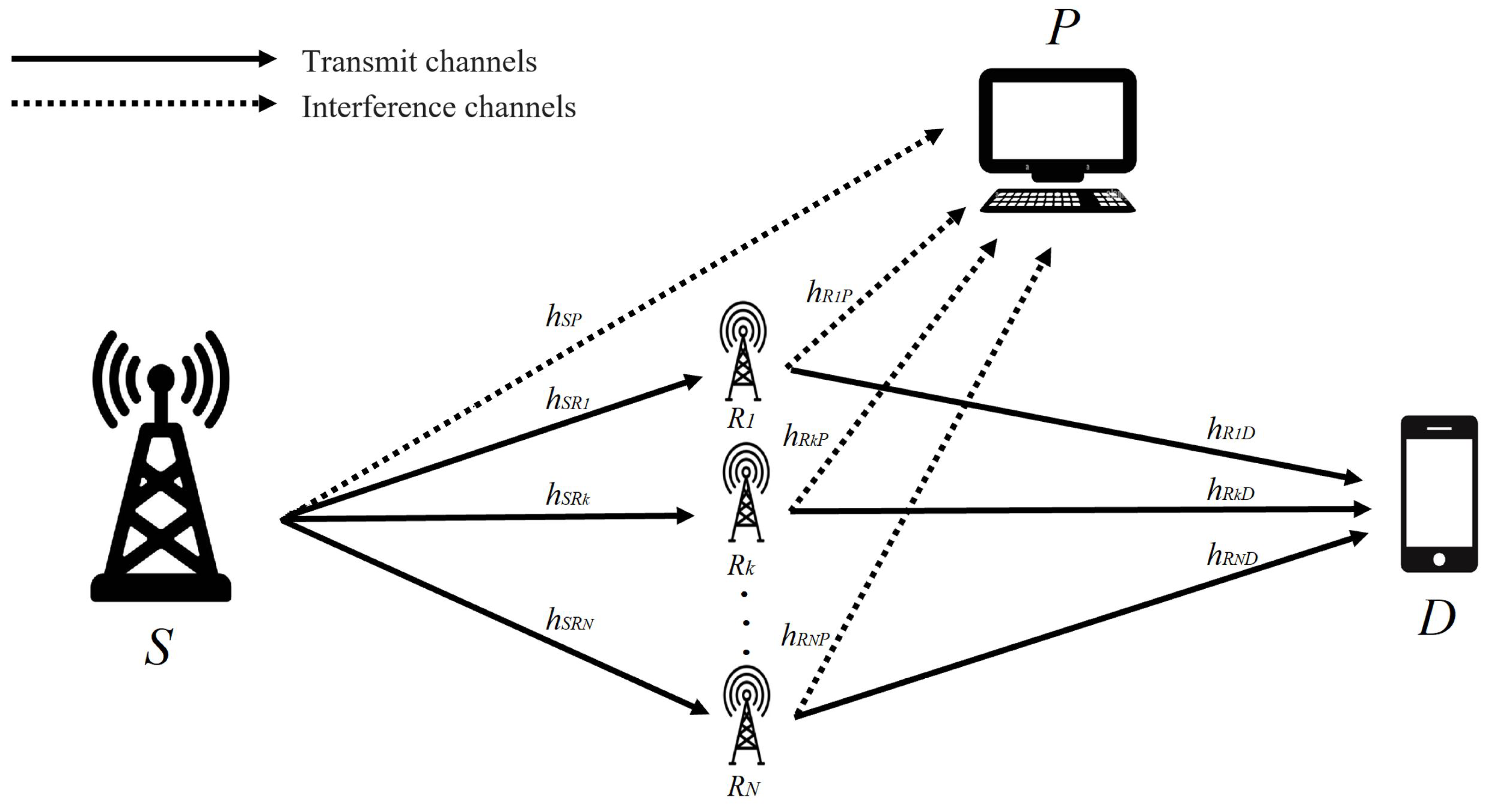
2. System Model
3. Performance Analysis
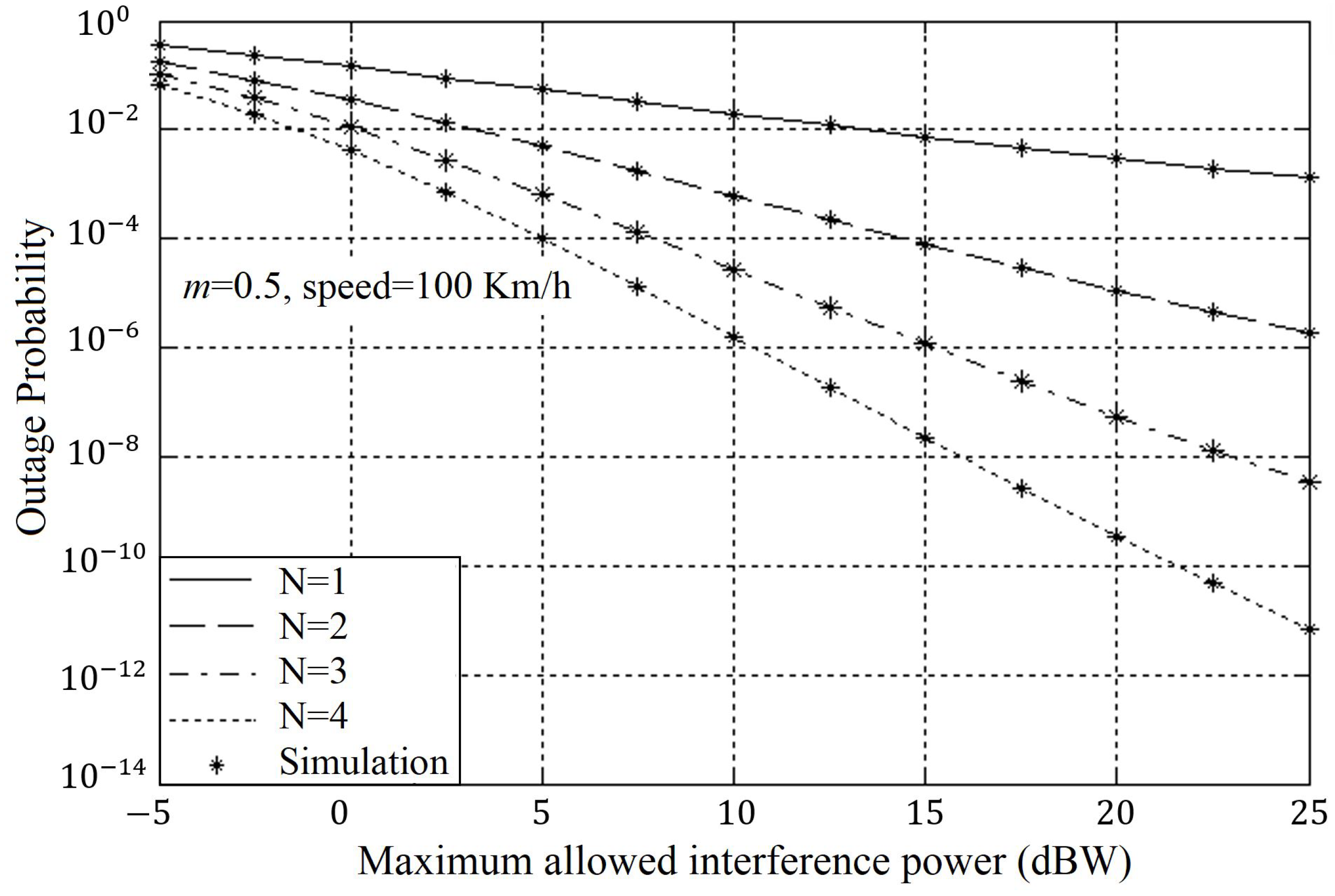
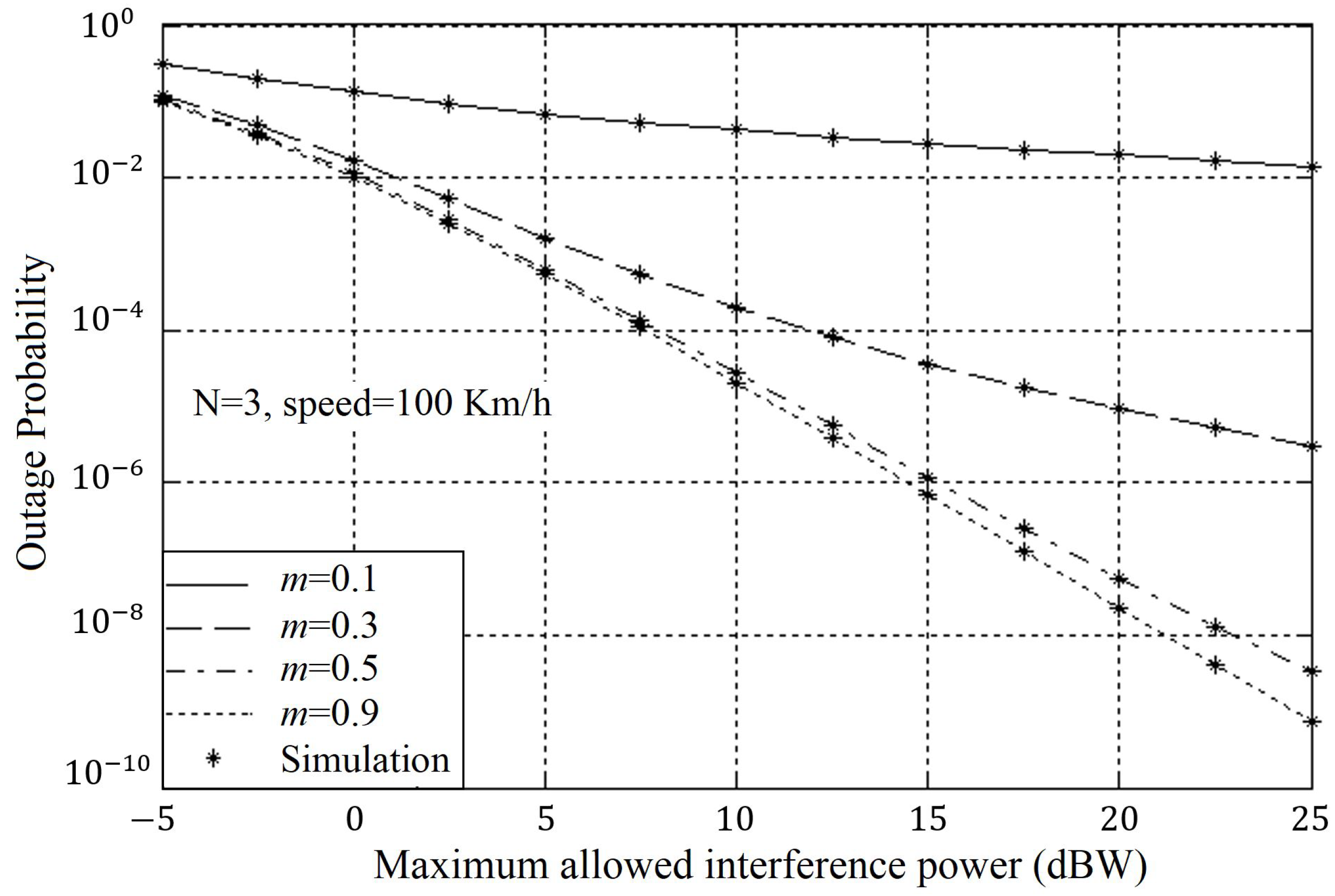
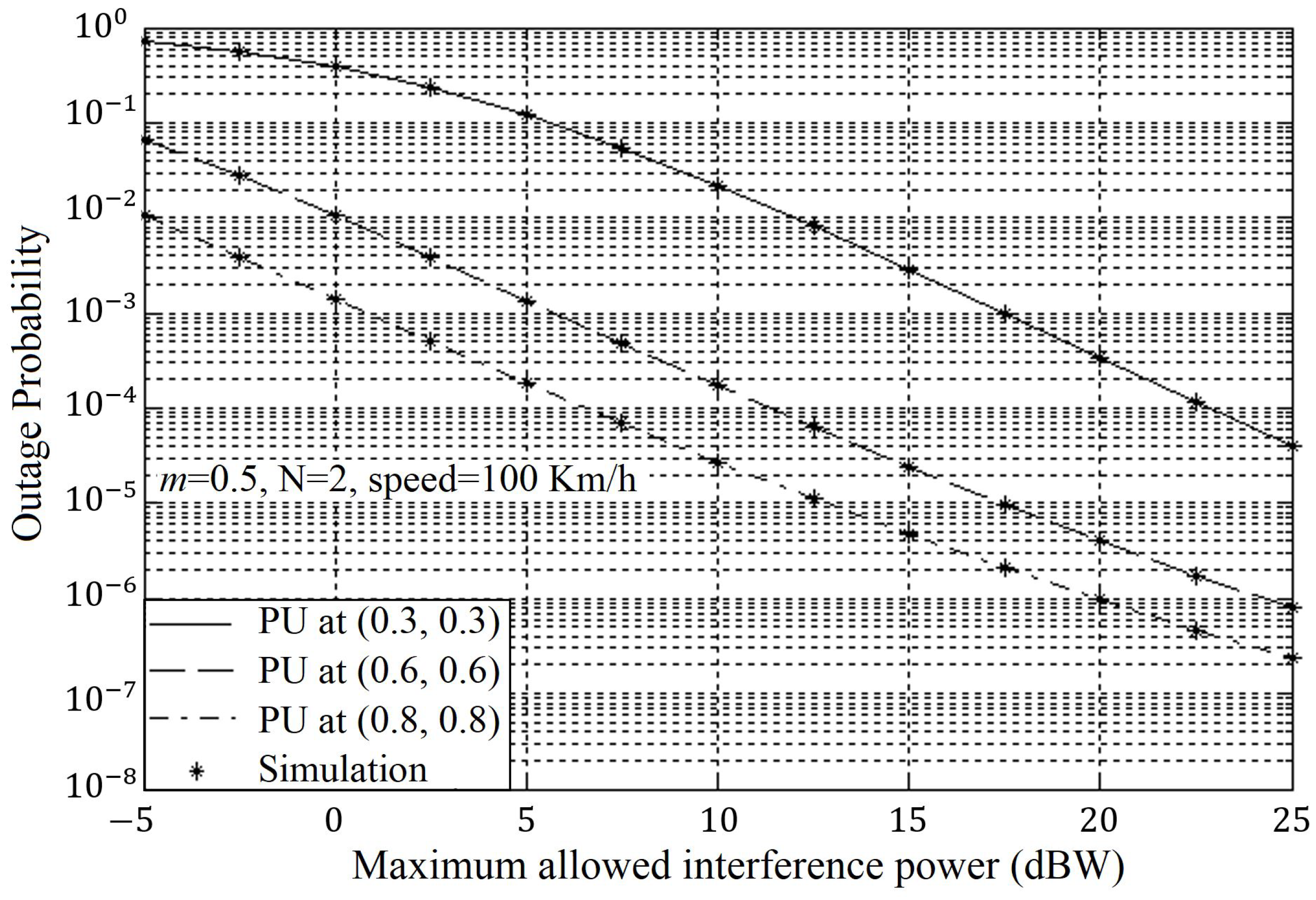
4. Results and Discussion
5. Conclusions
6. Limitations and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of F W ij (w)
Appendix B. Derivation of
Appendix C. Derivation of FγD(γ)
References
- Zikria, Y.B.; Kim, S.W.; Afzal, M.K.; Wang, H.; Rehmani, M.H. 5G mobile services and scenarios: Challenges and solutions. Sustainability 2018, 10, 3626. [Google Scholar]
- Imoize, A.L.; Adedeji, O.; Tandiya, N.; Shetty, S. 6G enabled smart infrastructure for sustainable society: Opportunities, challenges, and research roadmap. Sensors 2021, 21, 1709. [Google Scholar]
- Ibrahim, A.J.; Hassan, A.; Disina, A.H.; Pindar, Z.A. The Technologies of 5G: Opportunities Applications and Challenges. Int. J. Syst. Eng. 2021, 5, 59. [Google Scholar]
- Alhashimi, H.F.; Hindia, M.N.; Dimyati, K.; Hanafi, E.B.; Safie, N.; Qamar, F.; Azrin, K.; Nguyen, Q.N. A Survey on Resource Management for 6G Heterogeneous Networks: Current Research, Future Trends, and Challenges. Electronics 2023, 12, 647. [Google Scholar]
- Sylla, T.; Mendiboure, L.; Maaloul, S.; Aniss, H.; Chalouf, M.A.; Delbruel, S. Multi-Connectivity for 5G Networks and Beyond: A Survey. Sensors 2022, 22, 7591. [Google Scholar]
- Alhulayil, M.; López-Benítez, M. Novel LAA waiting and transmission time configuration methods for improved LTE-LAA/Wi-Fi coexistence over unlicensed bands. IEEE Access 2020, 8, 162373–162393. [Google Scholar]
- Patriciello, N.; Lagén, S.; Bojović, B.; Giupponi, L. NR-U and IEEE 802.11 Technologies Coexistence in Unlicensed mmWave Spectrum: Models and Evaluation. IEEE Access 2020, 8, 71254–71271. [Google Scholar]
- Alhulayil, M.; López-Benítez, M. Coexistence mechanisms for LTE and Wi-Fi networks over unlicensed frequency bands. In Proceedings of the 2018 11th International Symposium on Communication Systems, Networks & Digital Signal Processing (CSNDSP), Budapest, Hungary, 18–20 July 2018; pp. 1–6. [Google Scholar]
- Mehrnoush, M.; Sathya, V.; Roy, S.; Ghosh, M. Analytical Modeling of Wi-Fi and LTE-LAA Coexistence: Throughput and Impact of Energy Detection Threshold. IEEE/ACM Trans. Netw. 2018, 26, 1990–2003. [Google Scholar]
- Alhulayil, M.; López-Benítez, M. Static contention window method for improved LTE-LAA/Wi-Fi coexistence in unlicensed bands. In Proceedings of the 2019 International Conference on Wireless Networks and Mobile Communications (WINCOM), Fez, Morocco, 29 October–1 November 2019; pp. 1–6. [Google Scholar]
- Alhulayil, M.; López-Benítez, M. Dynamic contention window methods for improved coexistence between LTE and Wi-Fi in unlicensed bands. In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference Workshop (WCNCW), Marrakech, Morocco, 15–18 April 2019; pp. 1–6. [Google Scholar]
- Alhulayil, M.; López-Benítez, M. LTE/Wi-Fi coexistence in unlicensed bands based on dynamic transmission opportunity. In Proceedings of the 2020 IEEE Wireless Communications and Networking Conference Workshops (WCNCW), Seoul, Republic of Korea, 6–9 April 2020; pp. 1–6. [Google Scholar]
- Alhulayil, M.; López-Benítez, M. Methods for the allocation of almost blank subframes with fixed duty cycle for improved LTE-U/Wi-Fi coexistence. In Proceedings of the 2019 International Conference on Wireless Networks and Mobile Communications (WINCOM), Fez, Morocco, 29 October–1 November 2019; pp. 1–6. [Google Scholar]
- Rapetswa, K.; Cheng, L. Convergence of mobile broadband and broadcast services: A cognitive radio sensing and sharing perspective. Intell. Converg. Netw. 2020, 1, 99–114. [Google Scholar]
- Kumar, A.; Kumar, K. Multiple access schemes for cognitive radio networks: A survey. Phys. Commun. 2020, 38, 100953. [Google Scholar]
- Kulin, M.; Kazaz, T.; De Poorter, E.; Moerman, I. A Survey on Machine Learning-Based Performance Improvement of Wireless Networks: PHY, MAC and Network Layer. Electronics 2021, 10, 318. [Google Scholar]
- Singhal, C.; Rajesh, A. Review on cross-layer design for cognitive ad-hoc and sensor network. IET Commun. 2020, 14, 897–909. [Google Scholar]
- Jasim, M.A.; Shakhatreh, H.; Siasi, N.; Sawalmeh, A.H.; Aldalbahi, A.; Al-Fuqaha, A. A Survey on Spectrum Management for Unmanned Aerial Vehicles (UAVs). IEEE Access 2021, 10, 11443–11499. [Google Scholar]
- Lu, X.; Yan, S.; Yang, W.; Liu, C.; Ng, D.W.K. Short-Packet Covert Communication in Interweave Cognitive Radio Networks. IEEE Trans. Veh. Technol. 2022, 72, 2649–2654. [Google Scholar]
- Sharmila, A.; Dananjayan, P. Spectrum Sharing Techniques in Cognitive Radio Networks–A Survey. In Proceedings of the 2019 IEEE International Conference on System, Computation, Automation and Networking (ICSCAN), Pondicherry, India, 29–30 March 2019; pp. 1–4. [Google Scholar]
- Khan, F.; Filippou, M.C.; Sellathurai, M. Cooperative Communication Techniques for Spectrum Sharing. Spectr. Shar. Next Front. Wirel. Netw. 2020, 8, 147–167. [Google Scholar]
- Wen, X.; Ruan, Y.; Li, Y.; Zhang, R. Cognitive Region Design for Overlay Cognitive Satellite Terrestrial Networks. IEEE Commun. Lett. 2020, 25, 244–248. [Google Scholar]
- Salameh, H.B.; Abdel-Razeq, S.; Al-Obiedollah, H. Integration of Cognitive Radio Technology in NOMA-Based B5G Networks: State of the Art, Challenges, and Enabling Technologies. IEEE Access 2023, 11, 12949–12962. [Google Scholar]
- Aslam, M.M.; Du, L.; Zhang, X.; Chen, Y.; Ahmed, Z.; Qureshi, B. Sixth Generation (6G) Cognitive Radio Network (CRN) Application, Requirements, Security Issues, and Key Challenges. Wirel. Commun. Mob. Comput. 2021, 2021, 1331428. [Google Scholar]
- Bhattacharjee, S.; Acharya, T.; Bhattacharya, U. Cognitive radio based spectrum sharing models for multicasting in 5G cellular networks: A survey. Comput. Netw. 2022, 208, 108870. [Google Scholar]
- Hlayel, M.; Hayajneh, A.M.; Al-Mistarihi, M.F.; Shurman, M.; Darabkh, K.A. Closed-form expression of bit error rate in dual-hop dual-branch mixed relaying cooperative networks with best-path selection over Rayleigh fading channels. In Proceedings of the 2014 IEEE 11th International Multi-Conference on Systems, Signals & Devices (SSD14), Barcelona, Spain, 11–14 February 2014; pp. 1–4. [Google Scholar]
- Tian, C.; Qian, Z.; Wang, X.; Hu, L. Analysis of Joint Relay Selection and Resource Allocation Scheme for Relay-Aided D2D Communication Networks. IEEE Access 2019, 7, 142715–142725. [Google Scholar]
- Al-Mistarihi, M.F.; Harb, M.M.; Darabkh, K.A.; Aqel, A.S. On the performance analysis of dual hop relaying systems using differential amplify-and-forward along with post-detection selection combining techniques over Nakagami-m fading channels. Trans. Emerg. Telecommun. Technol. 2020, 31, e4065. [Google Scholar]
- Mohaisen, R.; Al-Mistarihi, M.F.; Darabkh, K.A. Outage Probability Evaluation for Relay-Based DF Cooperative Diversity Systems with Multipath Fading Channels and Non-Identical Interferers. In Proceedings of the 2020 5th IEEE International Conference on Recent Advances and Innovations in Engineering (ICRAIE), Jaipur, India, 1–3 December 2020; pp. 1–5. [Google Scholar]
- Mohaisen, R.; Al-Mistarihi, M.F.; Darabkh, K.A. Bit-Error Rate Analysis of Relay-Based DF Cooperative Diversity Systems Considering Multipath Fading Channels Along with Non-Identical Interferers. In Proceedings of the 2020 7th NAFOSTED Conference on Information and Computer Science (NICS), Ho Chi Minh City, Vietnam, 26–27 November 2020; pp. 393–398. [Google Scholar]
- Al-Mistarihi, M.F.; Mohaisen, R.; Sharaqa, A.; Shurman, M.M.; Darabkh, K.A. Performance evaluation of multiuser diversity in multiuser two-hop cooperative multi-relay wireless networks using maximal ratio combining over Rayleigh fading channels. Int. J. Commun. Syst. 2015, 28, 71–90. [Google Scholar]
- Rathika, M.; Sivakumar, P. Machine learning-optimized relay selection method for mitigating interference in next generation communication networks. Wirel. Netw. 2023, 29, 1969–1981. [Google Scholar]
- Tweneboah-Koduah, S.; Affum, E.A.; Agyemang-Prempeh Agyekum, K.; Ajagbe, S.A.; Adigun, M.O. Performance of Cooperative Relay NOMA with Large Antenna Transmitters. Electronics 2022, 11, 3482. [Google Scholar]
- Al-Mistarihi, M.F.; Aqel, A.S.; Darabkh, K.A. BER Analysis in Dual Hop Differential Amplify-and-Forward Relaying Systems with Selection Combining Using M-ary Phase-Shift Keying over Nakagami-m Fading Channels. In Proceedings of the 19th International Conference on Next Generation Wired/Wireless Advanced Networks and Systems Co-Located with the 12th International Conference on Internet of Things and Smart Spaces (NEW2AN/ruSMART 2019), St. Petersburg, Russia, 26–28 August 2019; Springer LNCS: Berlin/Heidelberg, Germany, 2019; pp. 688–699. [Google Scholar]
- Bhattacharyya, S.; Kumar, P.; Sharma, S.; Darshi, S.; Almohammedi, A.A. A Hybrid-Combine-and-Forward Relaying Scheme for Network Coded Cooperative Systems. In Proceedings of the 2021 IEEE International Conference on Advanced Networks and Telecommunications Systems (ANTS), Hyderabad, India, 13–16 December 2021; pp. 426–431. [Google Scholar]
- Gupta, R.; Gupta, J. Future generation communications with game strategies: A comprehensive survey. Comput. Commun. 2022, 192, 1–32. [Google Scholar]
- Tashman, D.H.; Hamouda, W. An Overview and Future Directions on Physical-Layer Security for Cognitive Radio Networks. IEEE Netw. 2020, 35, 205–211. [Google Scholar]
- Sharma, N.; Kumar, K. Resource allocation trends for ultra dense networks in 5G and beyond networks: A classification and comprehensive survey. Phys. Commun. 2021, 48, 101415. [Google Scholar]
- Agrawal, S.K.; Samant, A.; Yadav, S.K. Spectrum sensing in cognitive radio networks and metacognition for dynamic spectrum sharing between radar and communication system: A review. Phys. Commun. 2022, 52, 101673. [Google Scholar]
- Chopra, K.; Bose, R.; Joshi, A. Secrecy Performance of Threshold-Based Cognitive Relay Network With Diversity Combining. J. Commun. Netw. 2018, 20, 383–395. [Google Scholar]
- Pham, M.N. On the secrecy outage probability and performance trade-off of the multi-hop cognitive relay networks. Telecommun. Syst. 2020, 73, 349–358. [Google Scholar]
- Kandelusy, O.M.; Kirsch, N.J. Cognitive Multi-User Multi-Relay Network: A Decentralized Scheduling Technique. IEEE Trans. Cogn. Commun. Netw. 2020, 7, 609–623. [Google Scholar]
- Al-Mistarihi, M.F.; Mohaisen, R.; Darabkh, K.A. BER analysis in relay-based DF cooperative diversity systems over Rayleigh fading channels with non-identical interferers near the destination. In Proceedings of the 2019 International Conference on Advanced Communication Technologies and Networking (CommNet), Rabat, Morocco, 12–14 April 2019; pp. 1–5. [Google Scholar]
- Al-Mistarihi, M.F.; Mohaisen, R.; Darabkh, K.A. Performance of relay-based decode-and-forward cooperative diversity systems over Rayleigh fading channels with non-identical interferers. IET Commun. 2019, 13, 3135–3144. [Google Scholar]
- Al-Mistarihi, M.F.; Mohaisen, R.; Darabkh, K.A. Closed-form expression for BER in relay-based df cooperative diversity systems over Nakagami-m fading channels with non-identical interferers. In Proceedings of the Internet of Things, Smart Spaces, and Next Generation Networks and Systems: 19th International Conference, NEW2AN 2019, and 12th Conference, ruSMART 2019, St. Petersburg, Russia, 26–28 August 2019; pp. 700–709. [Google Scholar]
- Al-Mistarihi, M.F.; Mohaisen, R.; Darabkh, K.A. Performance evaluation of decode and forward cooperative diversity systems over Nakagami-m fading channels with non-identical interferers. Int. J. Electr. Comput. Eng. (IJECE) 2020, 10, 5316–5328. [Google Scholar]
- Ravindran Unnithan Jalaja, R.; Velmurugan, P.G.S.; Thiruvengadam, S.J. Performance Analysis of Energy Efficient Spatial Modulation in Bidirectional Cooperative Cognitive Radio System with Eavesdropper. Wirel. Pers. Commun. 2022, 125, 101–118. [Google Scholar]
- Linh, N.T.Y.; Tu, N.H.; Son, P.N.; Bao, V.N.Q. Dual-hop relaying networks for short-packet URLLCs: Performance analysis and optimization. J. Commun. Netw. 2022, 24, 408–418. [Google Scholar]
- Sultan, K. Best Relay Selection Schemes for NOMA Based Cognitive Relay Networks in Underlay Spectrum Sharing. IEEE Access 2020, 8, 190160–190172. [Google Scholar]
- Al-Mistarihi, M.F.; Sharaqa, A.; Mohaisen, R.; Abu-Alnadi, O.; Abu-Seba, H. Performance analysis of multiuser diversity in multiuser two-hop amplify and forward cooperative multi-relay wireless networks. In Proceedings of the 2012 35th International Convention MIPRO, Opatija, Croatia, 21–25 May 2012; pp. 647–651. [Google Scholar]
- Aswathi, V.; Babu, A.V. Optimal power allocation for non-orthogonal multiple access enabled full-duplex underlay cognitive relay networks under partial relay selection. Trans. Emerg. Telecommun. Technol. 2022, 33, e4569. [Google Scholar]
- Wu, Y.; Qian, L.P.; Mao, H.; Yang, X.; Zhou, H.; Shen, X. Optimal Power Allocation and Scheduling for Non-Orthogonal Multiple Access Relay-Assisted Networks. IEEE Trans. Mob. Comput. 2018, 17, 2591–2606. [Google Scholar]
- Yang, Q.; Zhu, L.; Xie, M.; Zhu, M.; Zhao, H. Performance Analysis in Multi-Relay DF Cognitive Relay Networks under Nakagami–m fading channels. In Proceedings of the 2020 IEEE Computing, Communications and IoT Applications (ComComAp), Beijing, China, 20–22 December 2020; pp. 1–6. [Google Scholar]
- Velmurugan, P.G.S.; Thiruvengadam, S.J.; Kumaravelu, V.B.; Rajendran, S.; Parameswaran, R.; Imoize, A.L. Performance Analysis of Full Duplex Bidirectional Machine Type Communication System Using IRS with Discrete Phase Shifter. Appl. Sci. 2023, 13, 7128. [Google Scholar]
- Shurman, M.; Al-Mistarihi, M.F.; Alhulayil, M. Outage probability of dual-hop amplify-and-forward cognitive relay networks under interference power constraints over Nakagami-m fading channels. In Proceedings of the 2015 38th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 25–29 May 2015; pp. 516–520. [Google Scholar]
- Alhulayil, M.; Al-Mistarihi, M.F.; Shurman, M. Outage probability of amplify-and-forward underlay cognitive relay networks with selection diversity over Nakagami-m fading channels. In Proceedings of the 2015 38th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 25–29 May 2015; pp. 521–525. [Google Scholar]
- Shurman, M.M.; Al-Mistarihi, M.F.; Alhulayil, M.M. Performance analysis of amplify-and-forward cognitive relay networks with interference power constraints over Nakagami-m fading channels. IET Commun. 2016, 10, 594–605. [Google Scholar]
- Alhulayil, M.; Al-Mistarihi, M.F.; Shurman, M.M. Performance Analysis of Dual-Hop AF Cognitive Relay Networks with Best Selection and Interference Constraints. Electronics 2022, 12, 124. [Google Scholar]
- Watterson, C.; Juroshek, J.; Bensema, W. Experimental confirmation of an HF channel model. IEEE Trans. Commun. Technol. 1970, 18, 792–803. [Google Scholar]
- Nakagami, M. The m-distribution: A general formula of intensity distribution of rapid fading. In Statistical Methods of Radio Wave Propagation; Hoffman, W.C., Ed.; Pergamon: Oxford, UK, 1960. [Google Scholar]
- Yip, K.W.; Ng, T.S. A simulation model for Nakagami-m fading channels, m < 1. IEEE Trans. Commun. 2000, 48, 214–221. [Google Scholar]
- Subotic, V.; Primak, S.L. A new vector channel simulator for sub rayleigh fading. In Proceedings of the 7th European Conference on Wireless Technology, Amsterdam, The Netherlands, 11–12 October 2004; pp. 49–52. [Google Scholar]
- Gradshteyn, I.; Ryzhik, I. Tables of Integrals, Series and Products, 7th ed.; Academic Press: Burlington, MA, USA; Elsevier: London, UK, 2007. [Google Scholar]
- Hasna, M.O.; Alouini, M.S. Outage Probability of Multihop Transmission Over Nakagami Fading Channels. IEEE Commun. Lett. 2003, 7, 216–218. [Google Scholar]
- Liu, T.; Song, L.; Li, Y.; Huo, Q.; Jiao, B. Performance analysis of hybrid relay selection in cooperative wireless systems. IEEE Trans. Commun. 2012, 60, 779–788. [Google Scholar]
- Neumeier, S.; Walelgne, E.A.; Bajpai, V.; Ott, J.; Facchi, C. Measuring the Feasibility of Teleoperated Driving in Mobile Networks. In Proceedings of the 2019 Network Traffic Measurement and Analysis Conference (TMA), Paris, France, 19–21 June 2019; pp. 113–120. [Google Scholar]
- Duy, T.T.; Alexandropoulos, G.C.; Tung, V.T.; Son, V.N.; Duong, T.Q. Outage performance of cognitive cooperative networks with relay selection over double-Rayleigh fading channels. IET Commun. 2016, 10, 57–64. [Google Scholar]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1994; Volume 2. [Google Scholar]
- Subotic, V.; Primak, S. BER analysis of equalized OFDM systems in Nakagami, m < 1 fading. Wirel. Pers. Commun. 2007, 40, 281–290. [Google Scholar]
- Ahmad, I.; Habibi, D. A novel mobile WiMAX solution for higher throughput. In Proceedings of the 2008 16th IEEE International Conference on Networks, New Delhi, India, 12–14 December 2008; pp. 1–5. [Google Scholar]
| Parameter | Values |
|---|---|
| Nakagami-m fading parameter (m) | 0.1, 0.3, 0.5, 0.9 |
| Rayleigh fading parameter (, , ) | 1, 1, 1 |
| Number of relays (N) | 1, 2, 3, 4 |
| Path loss exponent () | 4 |
| Variance of the AWGN term at () | −10 dBW |
| Interference power constraint (I) | −5 dBW |
| SNR | 5 dBW |
| Speed of the SU D | 100 Km/h |
| Threshold for the outage () | 1 dBW |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahem, L.N.; Al-Mistarihi, M.F.; Khodeir, M.A.; Alhulayil, M.; Darabkh, K.A. Best Relay Selection Strategy in Cooperative Spectrum Sharing Framework with Mobile-Based End User. Appl. Sci. 2023, 13, 8127. https://doi.org/10.3390/app13148127
Ibrahem LN, Al-Mistarihi MF, Khodeir MA, Alhulayil M, Darabkh KA. Best Relay Selection Strategy in Cooperative Spectrum Sharing Framework with Mobile-Based End User. Applied Sciences. 2023; 13(14):8127. https://doi.org/10.3390/app13148127
Chicago/Turabian StyleIbrahem, Lama N., Mamoun F. Al-Mistarihi, Mahmoud A. Khodeir, Moawiah Alhulayil, and Khalid A. Darabkh. 2023. "Best Relay Selection Strategy in Cooperative Spectrum Sharing Framework with Mobile-Based End User" Applied Sciences 13, no. 14: 8127. https://doi.org/10.3390/app13148127
APA StyleIbrahem, L. N., Al-Mistarihi, M. F., Khodeir, M. A., Alhulayil, M., & Darabkh, K. A. (2023). Best Relay Selection Strategy in Cooperative Spectrum Sharing Framework with Mobile-Based End User. Applied Sciences, 13(14), 8127. https://doi.org/10.3390/app13148127





