Finite Element Analysis (FEA) of the Stress and Strain Distribution in Cone-Morse Implant–Abutment Connection Implants Placed Equicrestally and Subcrestally
Abstract
:1. Introduction
2. Materials and Methods
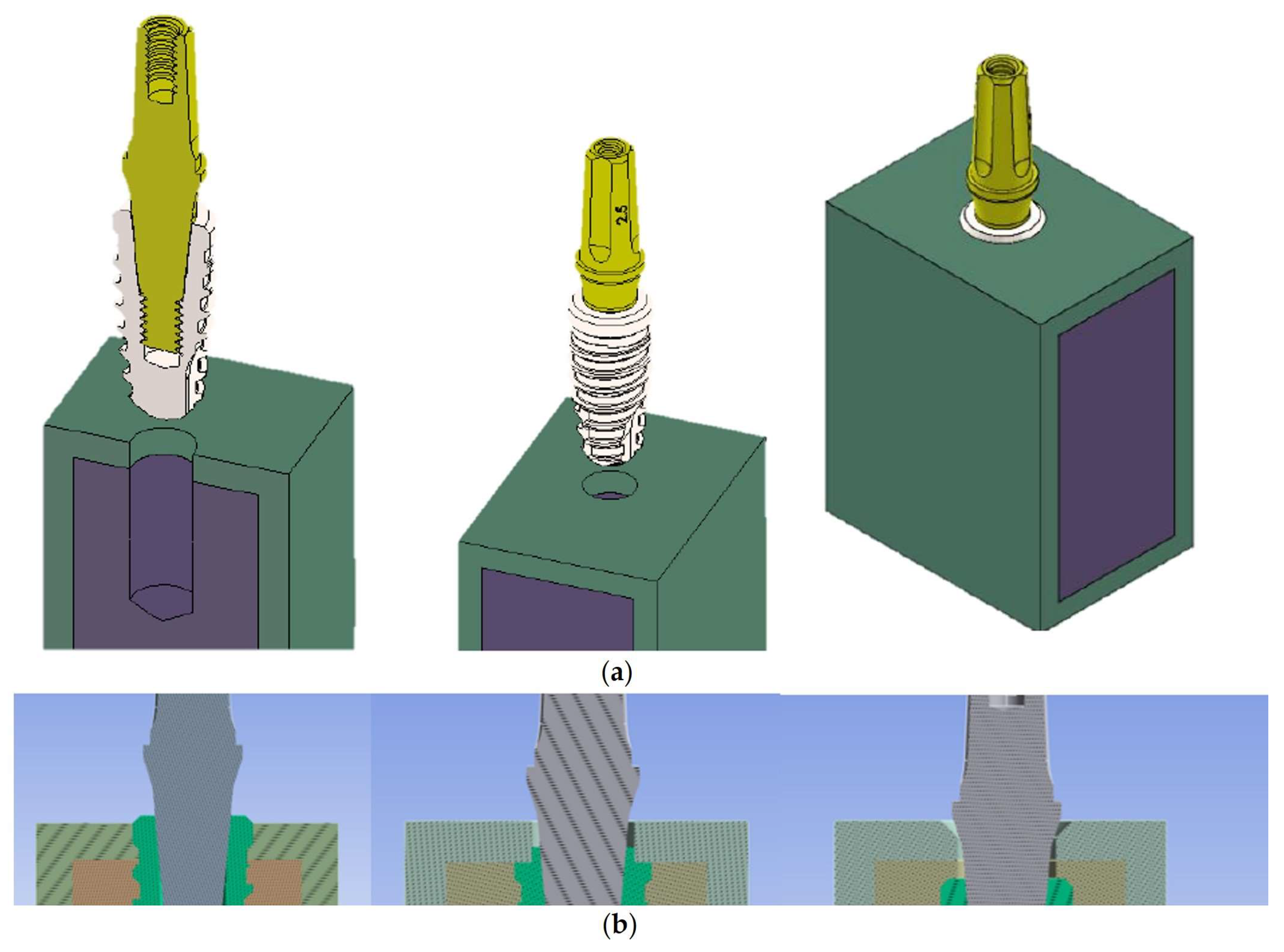
2.1. Modelling
2.2. Loads
2.3. Finite Element Method (FEM)
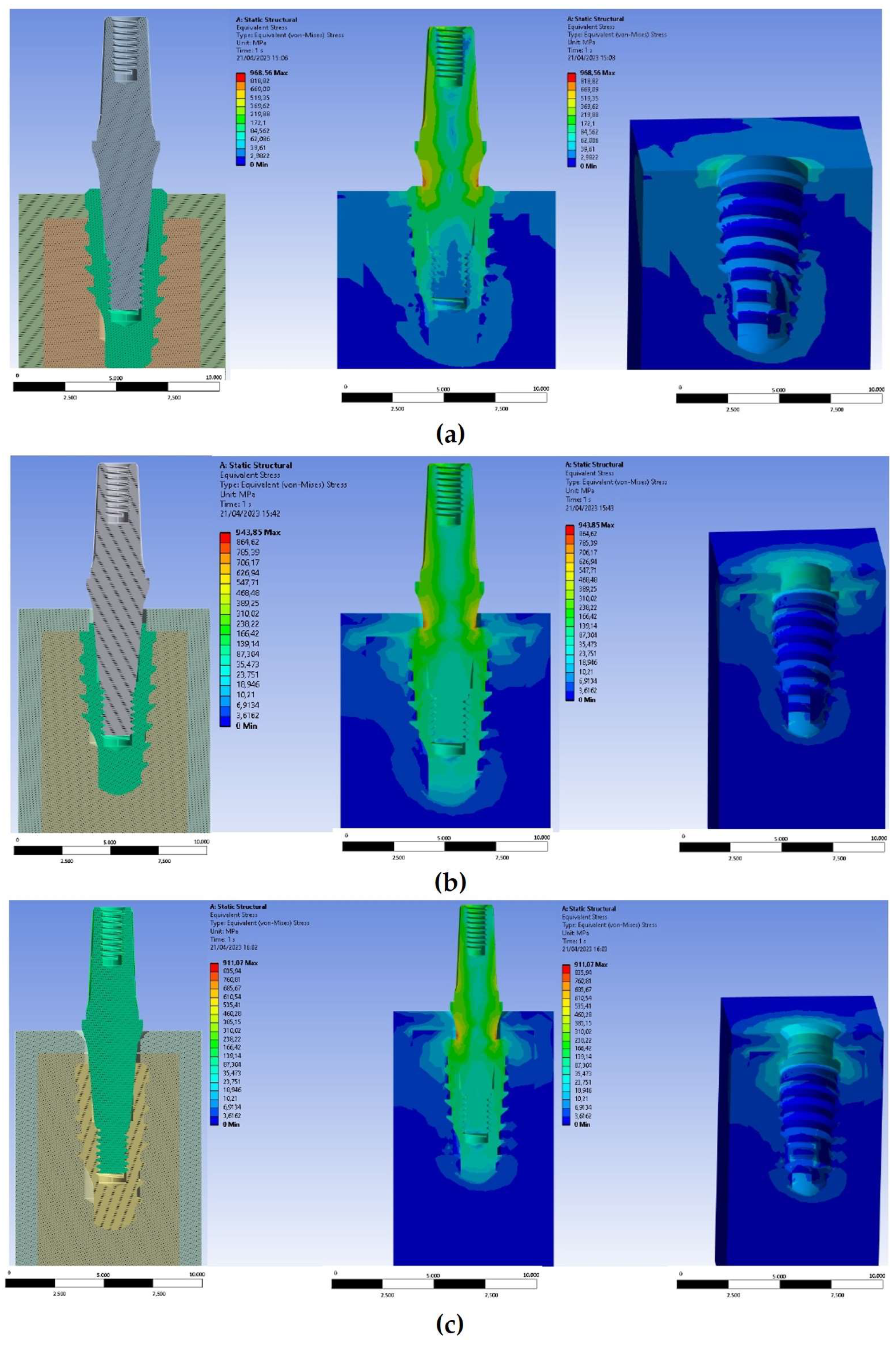
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kohen, J.; Matalon, S.; Block, J.; Ormianer, Z. Effect of implant insertion and loading protocol on long-term stability and crestal bone loss: A comparative study. J. Prosthet. Dent. 2016, 6, 697–702. [Google Scholar] [CrossRef] [PubMed]
- Fontanella, C.G.; Carniel, E.L.; Parpaiola, A.; Toia, M.; Natali, A.N. Interaction Phenomena between Dental Implants and Bone Tissue in Case of Misfit: A Pilot Study. Appl. Sci. 2023, 13, 6004. [Google Scholar] [CrossRef]
- Roccuzzo, M.; Roccuzzo, A.; Ramanuskaite, A. Papilla height in relation to the distance between bone crest and interproximal contact point at single-tooth implants: A systematic review. Clin. Oral Implant. Res. 2018, 29 (Suppl. 15), 50–61. [Google Scholar] [CrossRef] [PubMed]
- Froum, S.J.; Cho, S.C.; Florio, S.; Misch, C.M. Use of Narrow-Diameter Implants in Treatment of Severely Atrophic Maxillary Anterior Region With Implant-Supported Fixed Restorations. Compend. Contin. Educ. Dent. 2016, 37, 334–339. [Google Scholar] [PubMed]
- Valles, C.; Rodriguez-Ciurana, X.; Muñoz, F.; Permuy, M.; López-Alonso, H.; Nart, J. Influence of implant neck surface and placement depth on crestal bone changes and soft tissue dimensions around platform-switched implants: A histologic study in dogs. J. Clin. Periodontol. 2018, 7, 869–883. [Google Scholar] [CrossRef]
- Massoumi, F.; Taheri, M.; Mohammadi, A.; Amelirad, O. Evaluation of the Effect of Buccolingual and Apicocoronal Positions of Dental Implants on Stress and Strain in Alveolar Bone by Finite Element Analysis. J. Dent. Tehran. 2018, 15, 10–19. [Google Scholar]
- Cruz, R.S.; Lemos, C.A.A.; de Luna Gomes, J.M.; Fernandes, E.; Oliveira, H.F.; Pellizzer, E.P.; Verri, F.R. Clinical comparison between crestal and subcrestal dental implants: A systematic review and meta-analysis. J. Prosthet. Dent. 2022, 3, 408–417. [Google Scholar] [CrossRef]
- Barros, R.R.; Novaes, A.B., Jr.; Muglia, V.A.; Iezzi, G.; Piattelli, A. Influence of interimplant distances and placement depth on peri-implant bone remodeling of adjacent and immediately loaded Morse cone connection implants: A histomorphometric study in dogs. Clin. Oral Implant. Res. 2010, 4, 371–378. [Google Scholar] [CrossRef]
- Assenza, B.; Tripodi, D.; Scarano, A.; Perrotti, V.; Piattelli, A.; Iezzi, G.; D’Ercole, S. Bacterial leakage in implants with different implant-abutment connections: An in vitro study. J. Periodontol. 2012, 4, 491–497. [Google Scholar] [CrossRef]
- D’Ercole, S.; Tripodi, D.; Marzo, G.; Bernardi, S.; Continenza, M.A.; Piattelli, A.; Iaculli, F.; Mummolo, S. Microleakage of bacteria in different implant-abutment assemblies: An in vitro study. J. Appl. Biomater. Funct. Mater. 2015, 2, 174–180. [Google Scholar] [CrossRef]
- Tripodi, D.; D’Ercole, S.; Iaculli, F.; Piattelli, A.; Perrotti, V.; Iezzi, G. Degree of bacterial microleakage at the implant-abutment junction in Cone Morse tapered implants under loaded and unloaded conditions. J. Appl. Biomater. Funct. Mater. 2015, 4, 367–371. [Google Scholar] [CrossRef]
- Castro, D.S.; Araujo, M.A.; Benfatti, C.A.; dos Reis Pereira de Araujo, C.; Piattelli, A.; Perrotti, V.; Iezzi, G. Comparative histological and histomorphometrical evaluation of marginal bone resorption around external hexagon and Morse cone implants: An experimental study in dogs. Implant. Dent. 2014, 3, 270–276. [Google Scholar] [CrossRef]
- Degidi, M.; Iezzi, G.; Scarano, A.; Piattelli, A. Immediately loaded titanium implant with a tissue-stabilizing/maintaining design (‘beyond platform switch’) retrieved from man after 4 weeks: A histological and histomorphometrical evaluation. A case report. Clin. Oral Implant. Res. 2008, 3, 276–282. [Google Scholar] [CrossRef]
- Degidi, M.; Perrotti, V.; Shibli, J.A.; Novaes, A.B.; Piattelli, A.; Iezzi, G. Equicrestal and subcrestal dental implants: A histologic and histomorphometric evaluation of nine retrieved human implants. J. Periodontol. 2011, 5, 708–715. [Google Scholar] [CrossRef]
- Degidi, M.; Nardi, D.; Daprile, G.; Piattelli, A. Nonremoval of immediate abutments in cases involving subcrestally placed post-extractive tapered single implants: A randomized controlled clinical study. Clin. Implant. Dent. Relat. Res. 2014, 6, 794–805. [Google Scholar] [CrossRef]
- Chu, C.M.; Huang, H.L.; Hsu, J.T.; Fuh, L.J. Influences of internal tapered abutment designs on bone stresses around a dental implant: Three-dimensional finite element method with statistical evaluation. J. Periodontol. 2012, 1, 111–118. [Google Scholar] [CrossRef]
- Ferraro-Bezerra, M.; Rodrigues Carvalho, F.S.; Nogueira Cunto, G.M.; Duarte Carneiro, B.G.; de Barros Silva, P.G. Does subcrestal position affect insertion torque of different implant designs at different bone densities? An In Vitro Model Study. Int. J. Oral Maxillofac. Implant. 2021, 3, 460–467. [Google Scholar] [CrossRef]
- Valles, C.; Rodríguez-Ciurana, X.; Clementini, M.; Baglivo, M.; Paniagua, B.; Nart, J. Influence of subcrestal implant placement compared with equicrestal position on the peri-implant hard and soft tissues around platform-switched implants: A systematic review and meta-analysis. Clin. Oral Investig. 2018, 2, 555–570. [Google Scholar] [CrossRef]
- Salles Sotto-Maior, B.; de Andrade Lima, C.; Mendes Senna, P.; de Villa Camargos, G.; Del Bel Cury, A.A. Biomechanical evaluation of subcrestal dental implants with different bone anchorages. Braz. Oral Res. 2014, 28, S1806-83242014000100235. [Google Scholar] [CrossRef]
- Saleh, M.H.A.; Ravidà, A.; Suárez-López Del Amo, F.; Lin, G.H.; Asa’ad, F.; Wang, H.L. The effect of implant-abutment junction position on crestal bone loss: A systematic review and meta-analysis. Clin. Implant. Dent. Relat. Res. 2018, 4, 617–633. [Google Scholar] [CrossRef]
- Kumar, V.; Arya, G.; Singh, P.; Chauhan, P. A meta analysis for evaluation of marginal bone level changes at dental implants. Natl. J. Maxillofac. Surg. 2021, 12, 13–16. [Google Scholar] [CrossRef] [PubMed]
- Nagarajan, B.; Murthy, V.; Livingstone, D.; Surendra, M.P.; Jayaraman, S. Evaluation of crestal bone loss around implants placed at equicrestal and subcrestal levels before loading: A prospective clinical study. J. Clin. Diagn. Res. 2015, 12, ZC47–ZC50. [Google Scholar] [CrossRef] [PubMed]
- Sargolzaie, N.; Zarch, H.H.; Arab, H.; Koohestani, T.; Ramandi, M.F. Marginal bone loss around crestal or subcrestal dental implants: Prospective clinical study. J. Korean Assoc. Oral Maxillofac. Surg. 2022, 3, 159–166. [Google Scholar] [CrossRef]
- Palacios-Garzón, N.; Velasco-Ortega, E.; López-López, J. Bone loss in implants placed at subcrestal and crestal level: A systematic review and meta-analysis. Materials 2019, 1, 154. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palacios-Garzón, N.; Mauri-Obradors, E.; Ayuso-Montero, R.; Velasco-Ortega, E.; Anglada-Cantarell, J.M.; López-López, J. Marginal bone loss in internal conical connection implants placed at the crestal and subcrestal levels before prosthetic loading: A randomized clinical study. Materials 2022, 10, 3729. [Google Scholar] [CrossRef]
- Pessoa, R.S.; Sousa, R.M.; Pereira, L.M.; Neves, F.D.; Bezerra, F.J.; Jaecques, S.V.; Sloten, J.V.; Quirynen, M.; Teughels, W.; Spin-Neto, R. Bone remodeling around implants with External Hexagon and Morse-Taper connections: A randomized, controlled, split-mouth, clinical trial. Clin. Implant. Dent. Relat. Res. 2017, 1, 97–110. [Google Scholar] [CrossRef] [Green Version]
- Gatti, C.; Gatti, F.; Silvestri, M.; Mintrone, F.; Rossi, R.; Tridondani, G.; Piacentini, G.; Borrelli, P. A prospective multicenter study on radiographic crestal bone changes around dental implants placed at crestal or subcrestal level: One-year findings. Int. J. Oral Maxillofac. Implant. 2018, 4, 913–918. [Google Scholar] [CrossRef]
- Ercoli, C.; Jammal, G.; Buyers, M.; Tsigarida, A.A.; Chochlidakis, K.M.; Feng, C.; Caton, J. Influence of apico-coronal implant placement on post-surgical crestal bone loss in humans. J. Periodontol. 2017, 8, 762–770. [Google Scholar] [CrossRef]
- Chatterjee, P.; Shashikala, R.; Navneetham, A. comparative study of the crestal vs subcrestal placement of dental implants via radiographic and clinical evaluation. J. Contemp. Dent. Pract. 2022, 6, 623–627. [Google Scholar]
- Fetner, M.; Fetner, A.; Koutouzis, T.; Clozza, E.; Tovar, N.; Sarendranath, A.; Coelho, P.G.; Neiva, K.; Janal, M.N.; Neiva, R. The effects of subcrestal implant placement on crestal bone levels and bone-to-abutment contact: A microcomputed tomographic and histologic study in dogs. Int. J. Oral Maxillofac. Implant. 2015, 5, 1068–1075. [Google Scholar] [CrossRef] [Green Version]
- Huang, B.; Meng, H.; Zhu, W.; Witek, L.; Tovar, N.; Coelho, P.G. Influence of placement depth on bone remodeling around tapered internal connection implants: A histologic study in dogs. Clin. Oral Implant. Res. 2015, 8, 942–949. [Google Scholar] [CrossRef] [PubMed]
- Jain, S.; Mattoo, K.; Khalid, I.; Baig, F.A.H.; Kota, M.Z.; Ishfaq, M.; Ibrahim, M.; Hassan, S. A study of 42 partially edentulous patients with single-crown restorations and implants to compare bone loss between crestal and subcrestal endosseous implant placement. Med. Sci. Monit. 2023, 29, 939225. [Google Scholar] [CrossRef] [PubMed]
- Kang, N.; Wu, Y.Y.; Gong, P.; Yue, L.; Ou, G.M. A study of force distribution of loading stresses on implant-bone interface on short implant length using 3-dimensional finite element analysis. Oral Surg. Oral Med. Oral Pathol. Oral Radiol. 2014, 5, 519–523. [Google Scholar] [CrossRef]
- Ellendula, Y.; Sekar, A.C.; Nalla, S.; Basany, R.B.; Sailasri, K.; Thandu, A. Biomechanical evaluation of stress distribution in equicrestal and sub-crestally placed, platform-switched Morse taper dental implants in D3 bone: Finite Element Analysis. Cureus 2022, 4, 24591. [Google Scholar] [CrossRef] [PubMed]
- Sesha, M.R.; Sunduram, T.; Eid Abdelmagyd, H.A. Biomechanical evaluation of stress distribution in subcrestal placed platform-switched short dental implants in D4 bone: In vitro Finite Element Model study. J. Pharm. Bioallied. Sci. 2020, 12, S134–S139. [Google Scholar] [CrossRef] [PubMed]
- Santonocito, D.; Nicita, F.; Risitano, G. A parametric study on a dental implant geometry influence on bone remodelling through a numerical algorithm. Prosthesis 2021, 2, 157–172. [Google Scholar] [CrossRef]
- Rismanchian, M.; Askari, N.; Shafiei, S. The effect of placement depth of platform-switched implants on periimplant cortical bone stress: A 3-dimensional finite element analysis. Implant. Dent. 2013, 22, 165–169. [Google Scholar] [CrossRef]
- Li, R.; Wu, Z.; Chen, S.; Li, X.; Wan, Q.; Xie, G.; Pei, X. Biomechanical behavior analysis of four types of short implants with different placement depths using the finite element method. J. Prosthet. Dent. 2023, 3, e1–e447. [Google Scholar] [CrossRef]
- Macedo, J.P.; Pereira, J.; Faria, J.; Souza, J.C.M.; Alves, J.L.; López-López, J.; Henriques, B. Finite element analysis of peri-implant bone volume affected by stresses around Morse taper implants: Effects of implant positioning to the bone crest. Comput. Methods Biomech. Biomed. Engin. 2018, 12, 655–662. [Google Scholar] [CrossRef]
- Macedo, J.P.; Pereira, J.; Faria, J.; Pereira, C.A.; Alves, J.L.; Henriques, B.; Souza, J.C.M.; López-López, J. Finite Element Analysis of stress extent at peri-implant bone surrounding external hexagon or Morse taper implants. J. Mech. Behav. Biomed. Mater. 2017, 71, 441–447. [Google Scholar] [CrossRef] [Green Version]
- Cruz, R.S.; Fernandes E Oliveira, H.F.; Araújo Lemos, C.A.; de Souza Batista, V.E.; da Silva, R.C.; Verri, F.R. Biomechanical influence of narrow-diameter implants placed at the crestal and subcrestal level in the maxillary anterior region. A 3D finite element analysis. J. Prosthodont. 2023, in press. [Google Scholar] [CrossRef]
- Baggi, L.; Di Girolamo, M.; Vairo, G.; Sannino, G. Comparative evaluation of osseointegrated dental implants based on platform-switching concept: Influence of diameter, length, thread shape, and in-bone positioning depth on stress-based performance. Comput. Math. Methods Med. 2013, 2013, 250929. [Google Scholar] [CrossRef]
- Weng, D.; Nagata, M.J.; Bell, M.; Bosco, A.F.; de Melo, L.G.; Richter, E.J. Influence of microgap location and configuration on the periimplant bone morphology in submerged implants. An experimental study in dogs. Clin. Oral Implant. Res. 2008, 11, 1141–1147. [Google Scholar] [CrossRef]
- Weng, D.; Nagata, M.J.; Bell, M.; de Melo, L.G.; Bosco, A.F. Influence of microgap location and configuration on peri-implant bone morphology in nonsubmerged implants: An experimental study in dogs. Int. J. Oral Maxillofac. Implant. 2010, 3, 540–547. [Google Scholar]
- Weng, D.; Nagata, M.J.; Leite, C.M.; de Melo, L.G.; Bosco, A.F. Influence of microgap location and configuration on radiographic bone loss in nonsubmerged implants: An experimental study in dogs. Int. J. Prosthodont. 2011, 5, 445–452. [Google Scholar]
- Weng, D.; Nagata, M.J.; Bosco, A.F.; de Melo, L.G. Influence of microgap location and configuration on radiographic bone loss around submerged implants: An experimental study in dogs. Int. J. Oral Maxillofac. Implant. 2011, 5, 941–946. [Google Scholar]
- Pontes, A.E.F.; Ribeiro, F.S.; Iezzi, G.; Pires, J.R.; Zuza, E.P.; Piattelli, A.; Marcantonio, E., Jr. Bone-Implant Contact around Crestal and Subcrestal Dental Implants Submitted to Immediate and Conventional Loading. Sci. World J. 2014, 2014, 606947. [Google Scholar] [CrossRef] [Green Version]
- Shamami, D.Z.; Karimi, A.; Beigzadeh, B.; Haghpanahi, M.; Navidbakhsh, M. A 3D Finite Element Study for Stress Analysis in Bone Tissue Around Single Implants with Different Materials and Various Bone Qualities. J. Biomater. Tissue Eng. 2014, 8, 632–637. [Google Scholar] [CrossRef]
- Shirazi, H.A.; Ayatollahi, M.; Karimi, A.; Navidbakhsh, M. A comparative finite element analysis of two types of axial and radial functionally graded dental implants with titanium one around implant-bone interface. Sci. Eng. Compos. Mater. 2016, 5, 747–754. [Google Scholar] [CrossRef] [Green Version]
- Dos Santos, M.V.; Elias, C.N.; Lima, J.H.C. The effects of superficial roughness and design on the primary stability of dental implants. Clin. Implant. Dent. Relat. Res. 2011, 3, 215–223. [Google Scholar] [CrossRef]
- Tribst, J.P.M.; de Morais, D.C.; de Matos, J.D.M.; da Rocha Scalzer Lopes, G.; de Oliveira Dal Piva, A.M.; Borges, A.L.S.; Bottino, M.A.; Lanzotti, A.; Martorelli, M.; Ausiello, P. Influence of Framework Material and Posterior Implant Angulation in Full-Arch All-on-4 Implant-Supported Prosthesis Stress Concentration. Dent. J. 2022, 1, 12. [Google Scholar] [CrossRef] [PubMed]





| Material | Young’s Modulus (GPa) | Poisson’s Ratio |
|---|---|---|
| Cortical bone | 13.7 | 0.30 |
| Cancellous bone | 0.3 | 0.30 |
| Titanium | 117 | 0.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Pietro, N.; Ceddia, M.; Romasco, T.; De Bortoli Junior, N.; Mello, B.F.; Tumedei, M.; Specchiulli, A.; Piattelli, A.; Trentadue, B. Finite Element Analysis (FEA) of the Stress and Strain Distribution in Cone-Morse Implant–Abutment Connection Implants Placed Equicrestally and Subcrestally. Appl. Sci. 2023, 13, 8147. https://doi.org/10.3390/app13148147
Di Pietro N, Ceddia M, Romasco T, De Bortoli Junior N, Mello BF, Tumedei M, Specchiulli A, Piattelli A, Trentadue B. Finite Element Analysis (FEA) of the Stress and Strain Distribution in Cone-Morse Implant–Abutment Connection Implants Placed Equicrestally and Subcrestally. Applied Sciences. 2023; 13(14):8147. https://doi.org/10.3390/app13148147
Chicago/Turabian StyleDi Pietro, Natalia, Mario Ceddia, Tea Romasco, Nilton De Bortoli Junior, Bruno Freitas Mello, Margherita Tumedei, Alessandro Specchiulli, Adriano Piattelli, and Bartolomeo Trentadue. 2023. "Finite Element Analysis (FEA) of the Stress and Strain Distribution in Cone-Morse Implant–Abutment Connection Implants Placed Equicrestally and Subcrestally" Applied Sciences 13, no. 14: 8147. https://doi.org/10.3390/app13148147
APA StyleDi Pietro, N., Ceddia, M., Romasco, T., De Bortoli Junior, N., Mello, B. F., Tumedei, M., Specchiulli, A., Piattelli, A., & Trentadue, B. (2023). Finite Element Analysis (FEA) of the Stress and Strain Distribution in Cone-Morse Implant–Abutment Connection Implants Placed Equicrestally and Subcrestally. Applied Sciences, 13(14), 8147. https://doi.org/10.3390/app13148147










