Flaw Size Quantification for Cable Flaw Inspection System with Inductive Search Coil Sensor
Abstract
:1. Introduction
2. Methodology
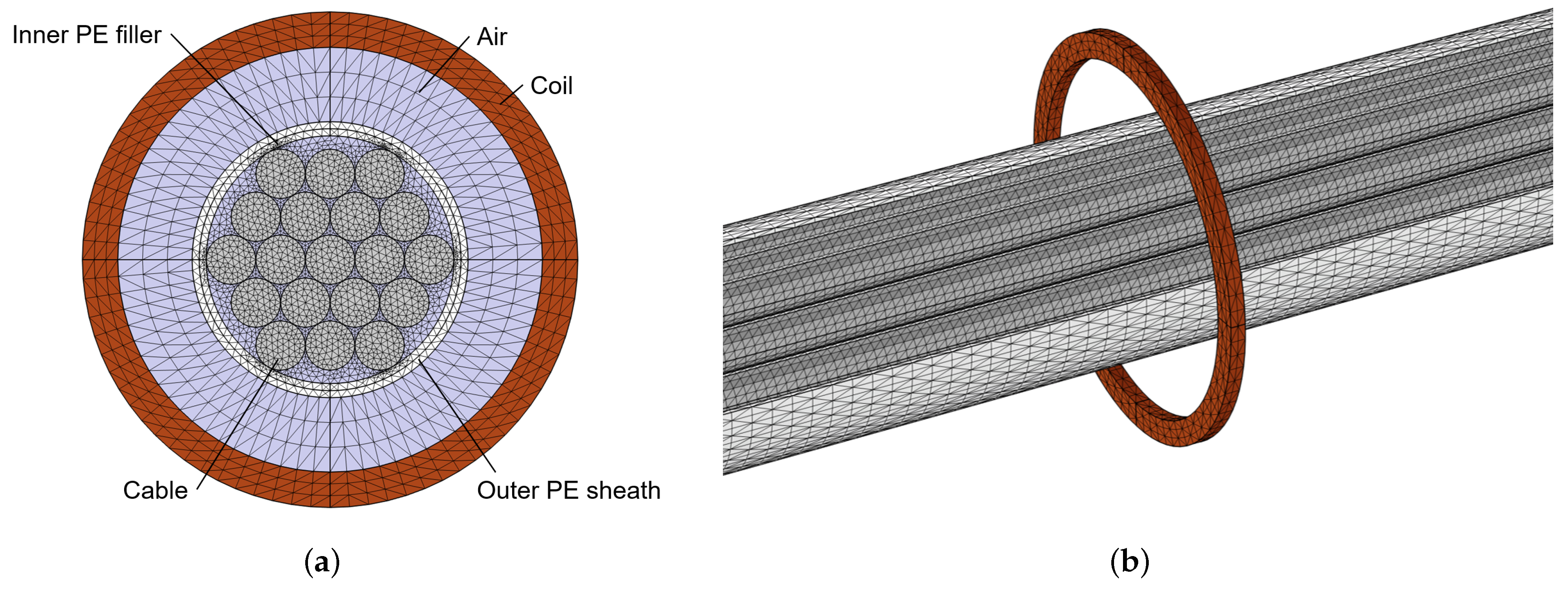
2.1. Model-Based Principle
2.2. Data Processing Procedure
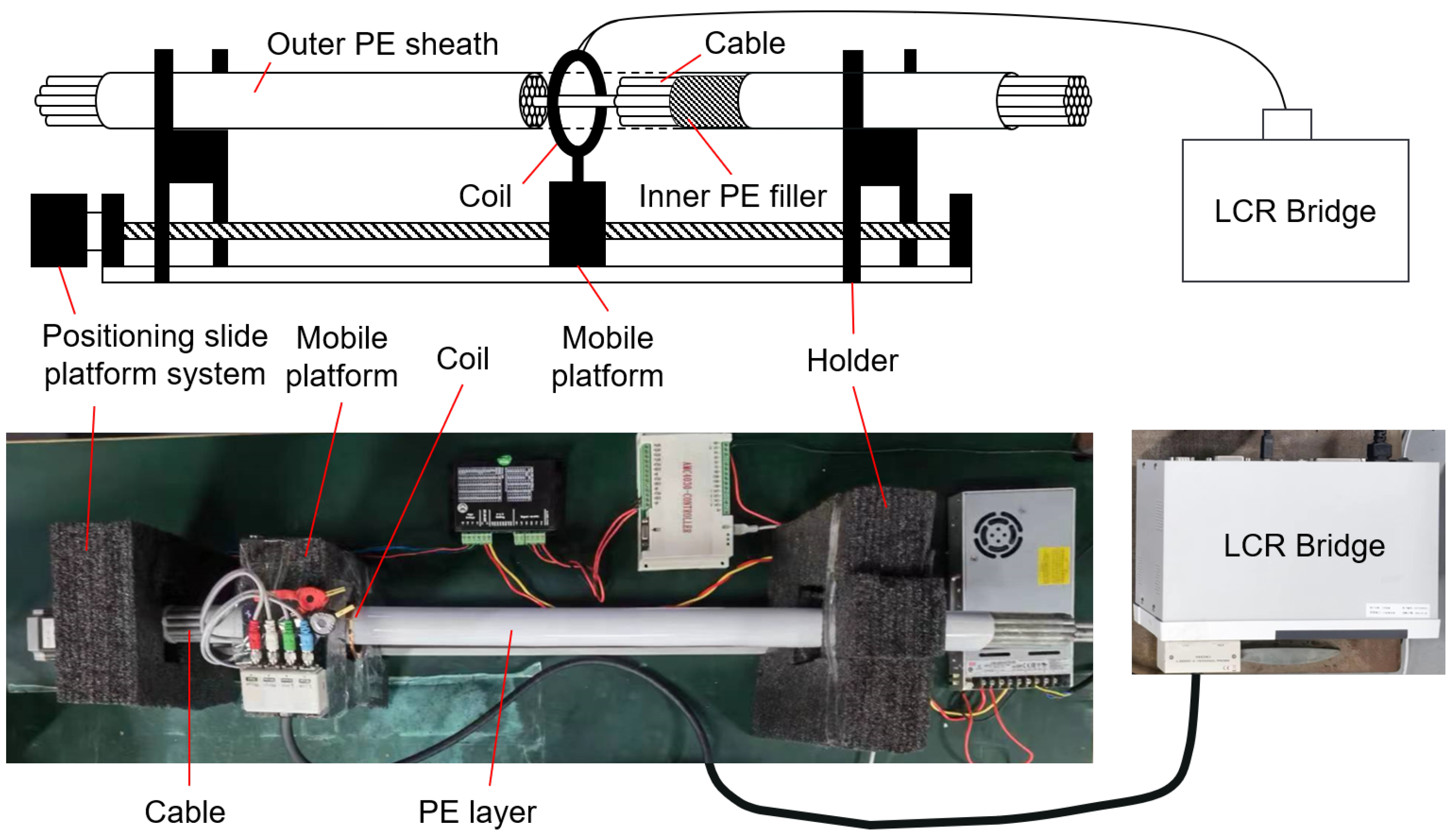
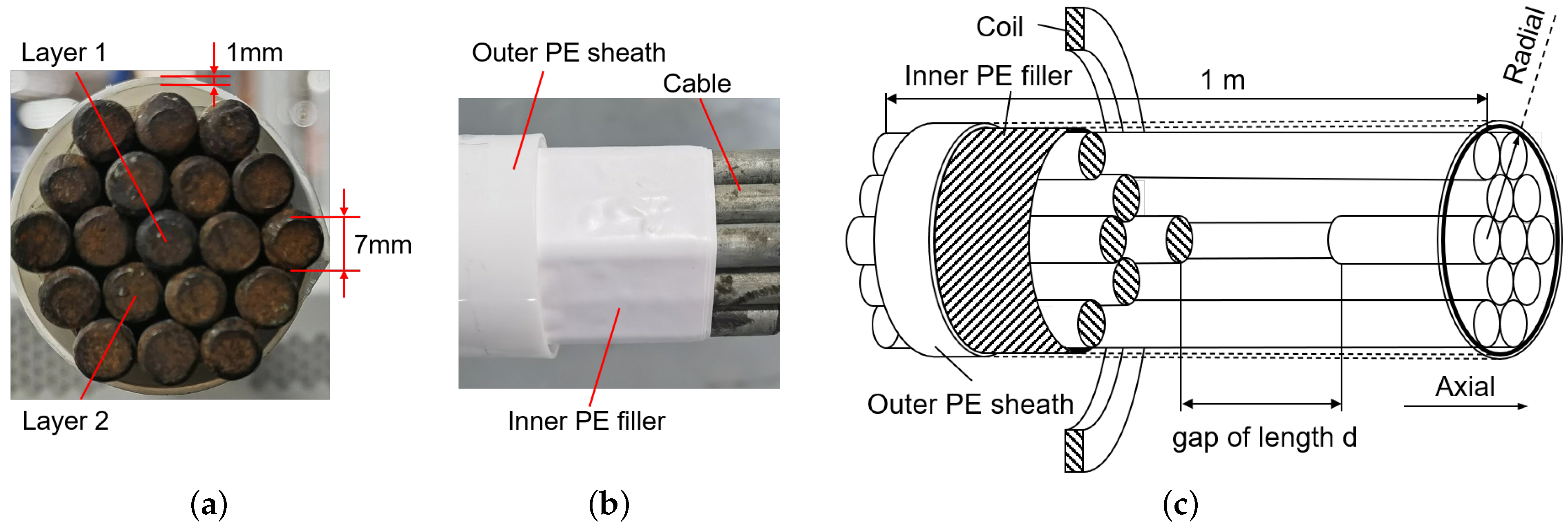
3. Experiment Setup
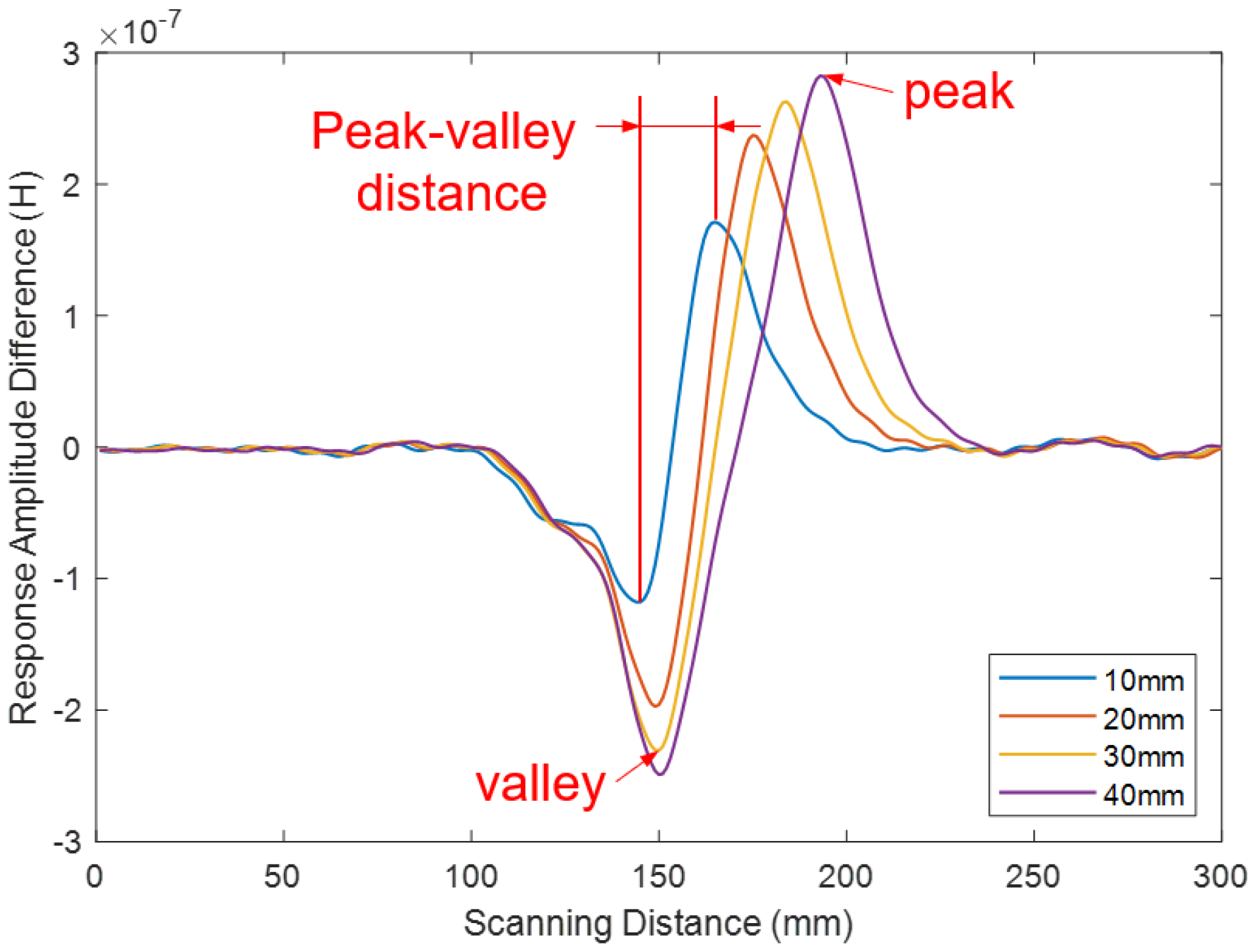
4. Experimental Result Analysis
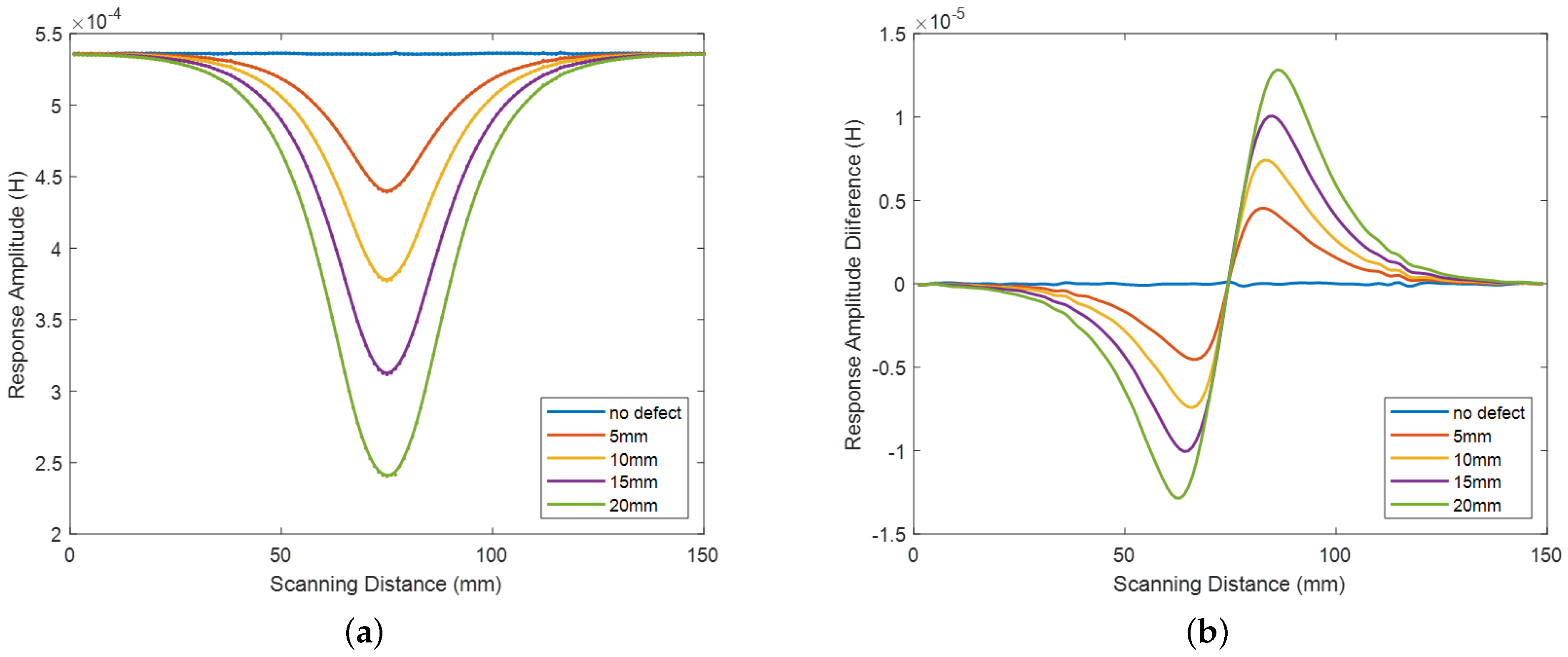
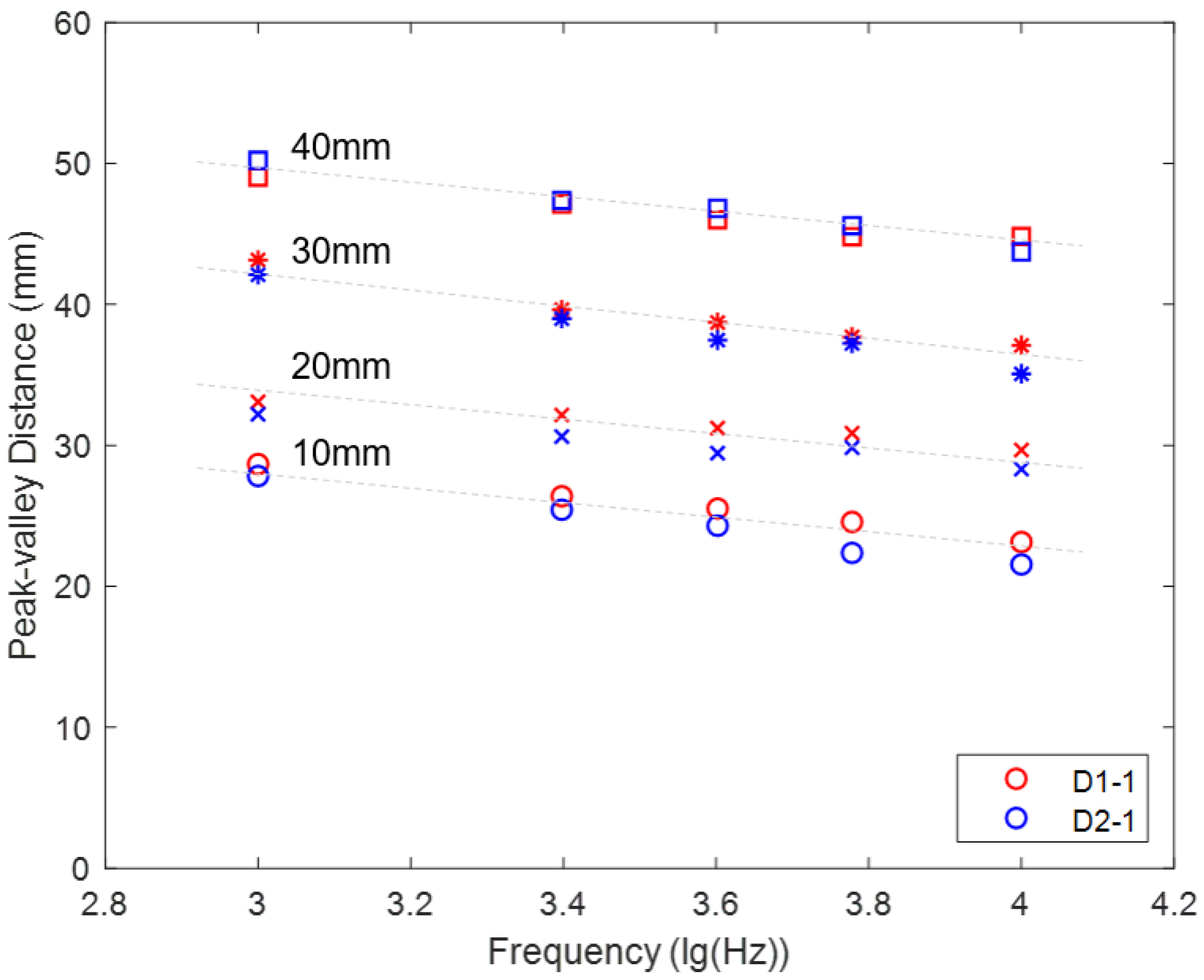
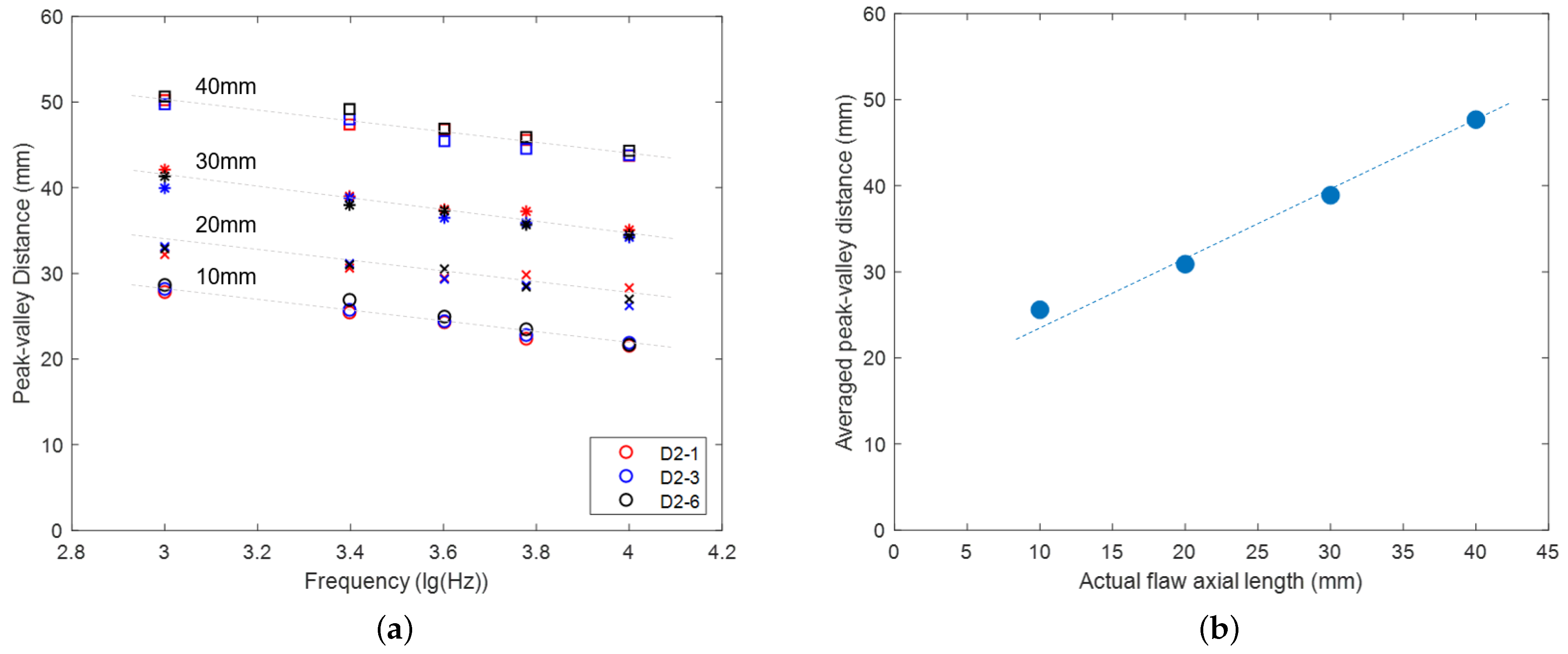
4.1. Analysis of Flaw Length Based on Flaw Position
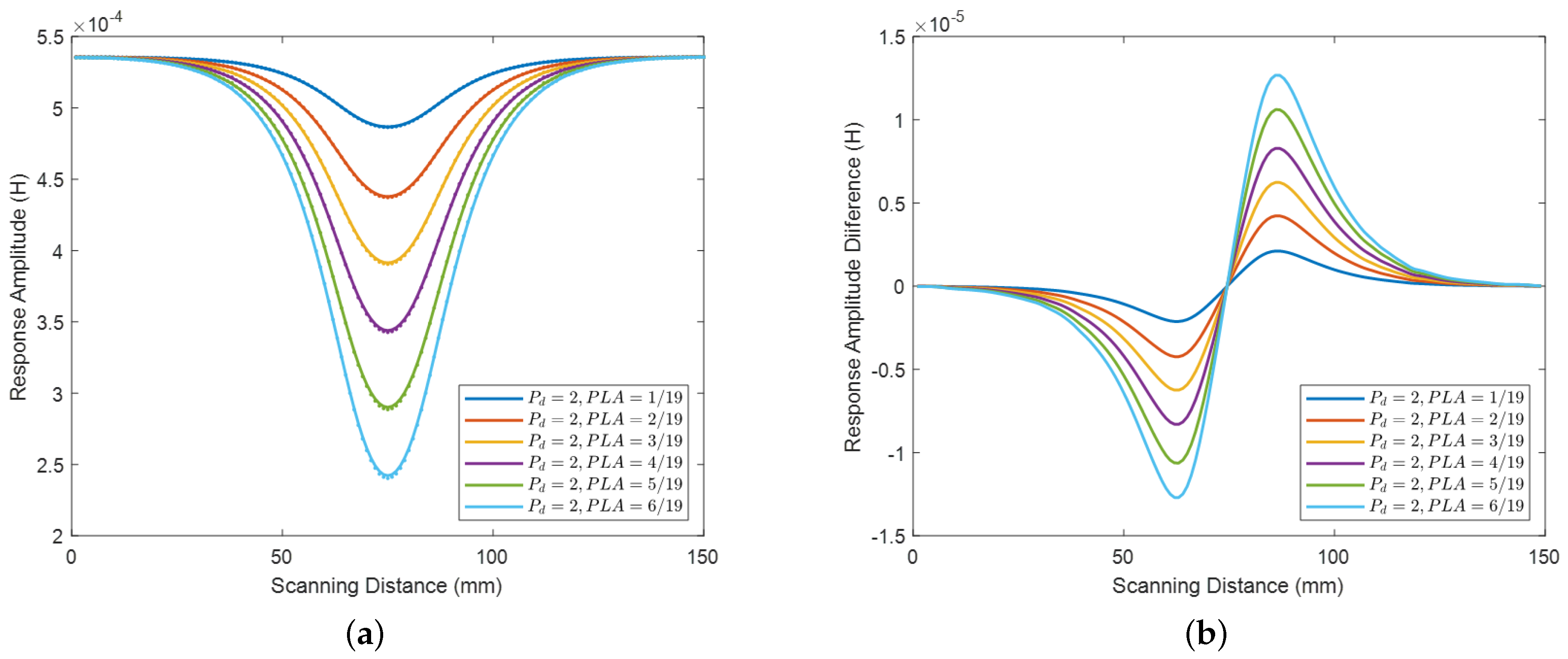
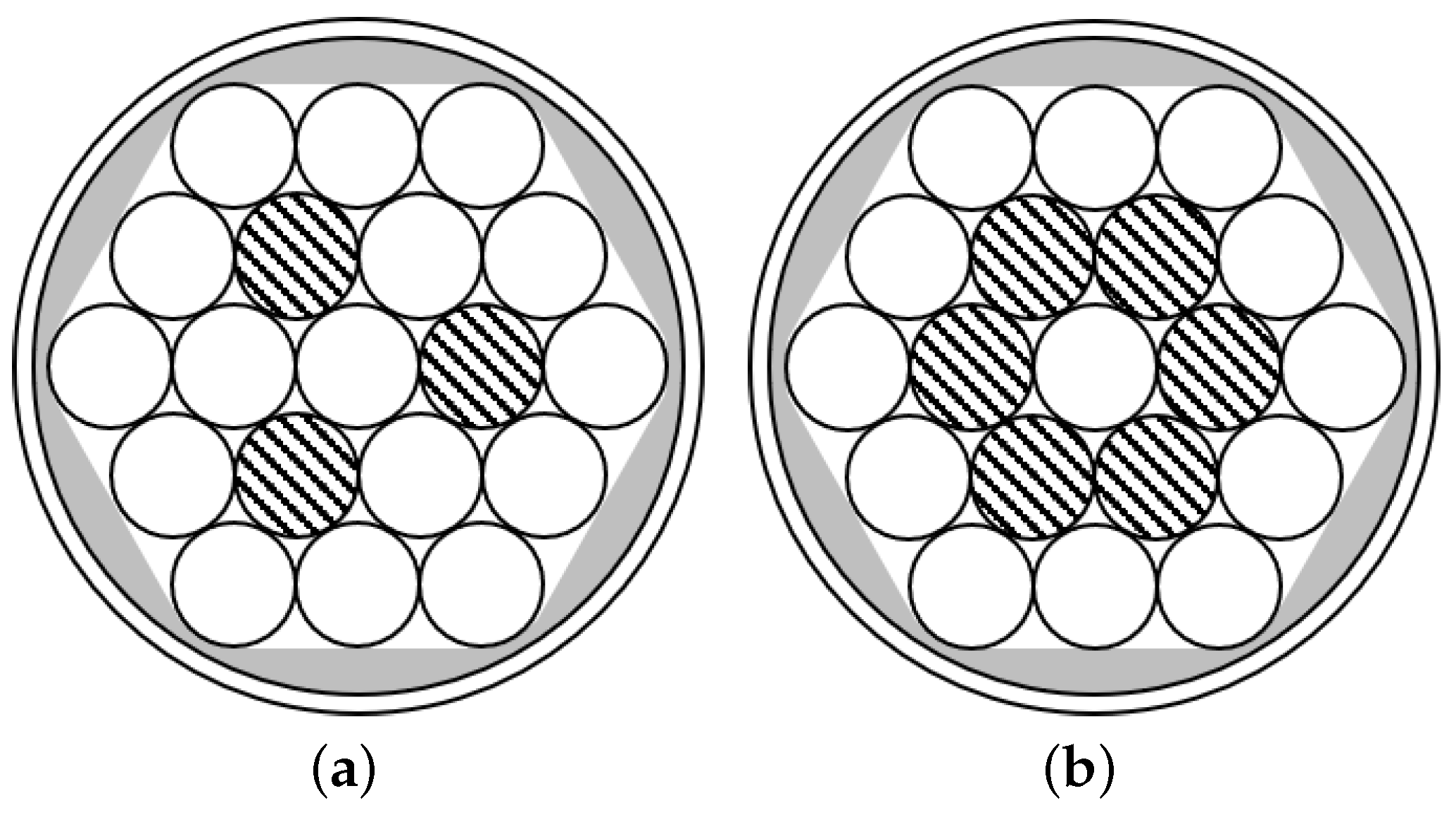
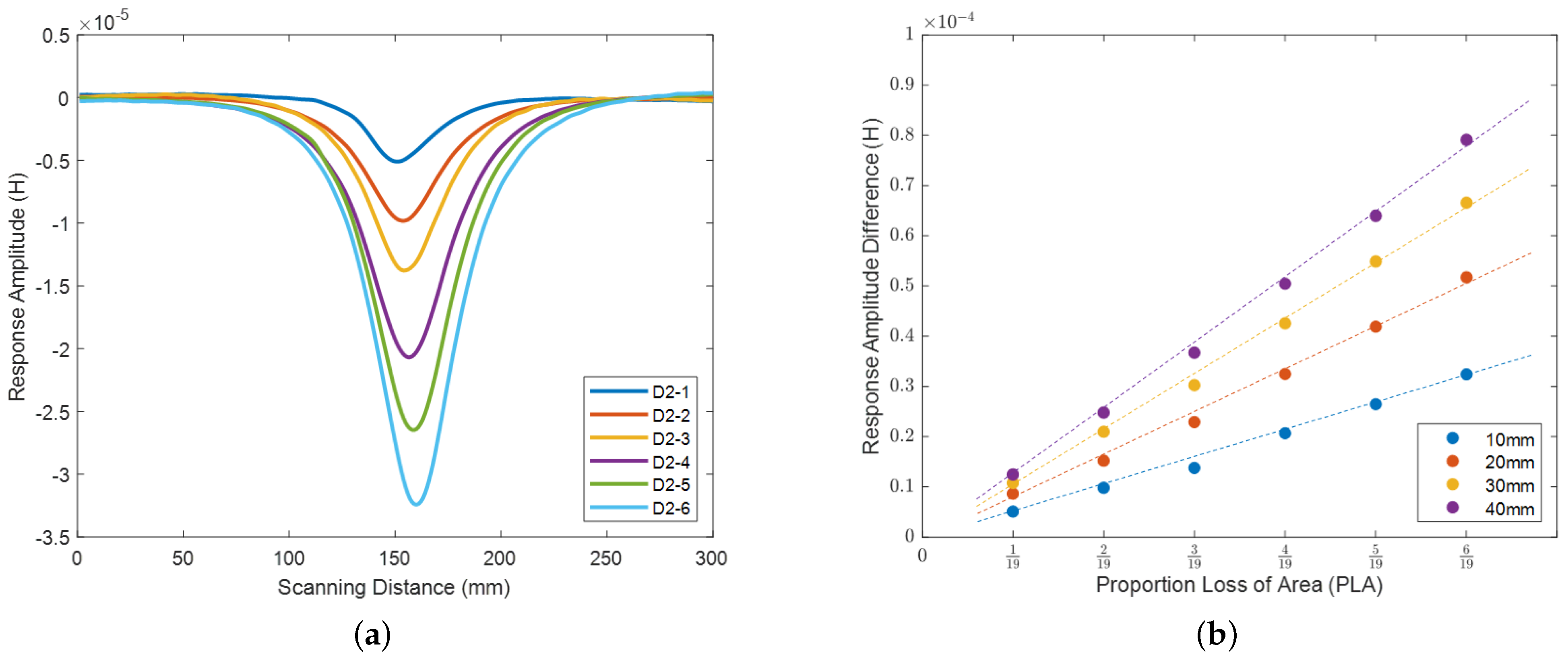
4.2. Analysis of Flaw Length Based on Flaw Cross-Sectional Area
4.3. Analysis of Response Amplitude Based on Flaw Position
4.4. Analysis of Response Amplitude Based on Flaw Cross-Section Area
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, Y.L. Making good use of structural health monitoring systems of long-span cable-supported bridges. J. Civ. Struct. Health Monit. 2018, 8, 477–497. [Google Scholar] [CrossRef]
- Farhangdoust, S.; Mehrabi, A. Health monitoring of closure joints in accelerated bridge construction: A review of non-destructive testing application. J. Adv. Concr. Technol. 2019, 17, 381–404. [Google Scholar] [CrossRef] [Green Version]
- Khedmatgozar Dolati, S.S.; Caluk, N.; Mehrabi, A.; Khedmatgozar Dolati, S.S. Non-Destructive Testing Applications for Steel Bridges. Appl. Sci. 2021, 11, 9757. [Google Scholar] [CrossRef]
- Dwivedi, S.K.; Vishwakarma, M.; Soni, A. Advances and researches on non destructive testing: A review. Mater. Today Proc. 2018, 5, 3690–3698. [Google Scholar] [CrossRef]
- Zolfaghari, A.; Kolahan, F. Reliability and sensitivity of visible liquid penetrant NDT for inspection of welded components. Mater. Test. 2017, 59, 290–294. [Google Scholar] [CrossRef]
- Manikandan, K.; Sivagurunathan, P.A.; Ananthan, S.; Moshi, A.A.M.; Bharathi, S.S. Study on the influence of temperature and vibration on indications of liquid penetrant testing of A516 low carbon steel. Mater. Today Proc. 2021, 39, 1559–1564. [Google Scholar] [CrossRef]
- Bado, M.F.; Casas, J.R. A review of recent distributed optical fiber sensors applications for civil engineering structural health monitoring. Sensors 2021, 21, 1818. [Google Scholar] [CrossRef]
- Sasy Chan, Y.W.; Wang, H.P.; Xiang, P. Optical Fiber Sensors for Monitoring Railway Infrastructures: A Review towards Smart Concept. Symmetry 2021, 13, 2251. [Google Scholar] [CrossRef]
- He, J.; Zhou, Z.; Jinping, O. Optic fiber sensor-based smart bridge cable with functionality of self-sensing. Mech. Syst. Signal Process. 2013, 35, 84–94. [Google Scholar] [CrossRef]
- Zhang, C.; Ge, Y.; Hu, Z.; Zhou, K.; Ren, G.; Wang, X. Research on deflection monitoring for long span cantilever bridge based on optical fiber sensing. Opt. Fiber Technol. 2019, 53, 102035. [Google Scholar] [CrossRef]
- Oh, S.j.; Jung, M.j.; Lim, C.; Shin, S.c. Automatic detection of welding defects using faster R-CNN. Appl. Sci. 2020, 10, 8629. [Google Scholar] [CrossRef]
- Schaal, C.; Bischoff, S.; Gaul, L. Damage detection in multi-wire cables using guided ultrasonic waves. Struct. Health Monit. 2016, 15, 279–288. [Google Scholar] [CrossRef]
- Zhang, P.; Tang, Z.; Duan, Y.; Yun, C.B.; Lv, F. Ultrasonic guided wave approach incorporating SAFE for detecting wire breakage in bridge cable. Smart Struct. Syst. 2018, 22, 481–493. [Google Scholar]
- Hong, X.; Zhou, J.; He, Y. Damage detection of anchored region on the messenger cable based on matching pursuit algorithm. Mech. Syst. Signal Process. 2019, 130, 221–247. [Google Scholar] [CrossRef]
- Selim, H.; Delgado-Prieto, M.; Trull, J.; Pico, R.; Romeral, L.; Cojocaru, C. Defect reconstruction by non-destructive testing with laser induced ultrasonic detection. Ultrasonics 2020, 101, 106000. [Google Scholar] [CrossRef]
- Wang, X.; Niederleithinger, E.; Hindersmann, I. The installation of embedded ultrasonic transducers inside a bridge to monitor temperature and load influence using coda wave interferometry technique. Struct. Health Monit. 2022, 21, 913–927. [Google Scholar] [CrossRef]
- Zolfaghari, A.; Zolfaghari, A.; Kolahan, F. Reliability and sensitivity of magnetic particle nondestructive testing in detecting the surface cracks of welded components. Nondestruct. Test. Eval. 2018, 33, 290–300. [Google Scholar] [CrossRef]
- Tout, K.; Meguenani, A.; Urban, J.P.; Cudel, C. Automated vision system for magnetic particle inspection of crankshafts using convolutional neural networks. Int. J. Adv. Manuf. Technol. 2021, 112, 3307–3326. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, B.; Kang, Y.; Liu, B.; Wang, S.; Duan, Z. A Novel Thermography-Based Dry Magnetic Particle Testing Method. IEEE Trans. Instrum. Meas. 2022, 71, 9505309. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, C.; Li, R.; Cai, M.; Jia, G. Theory and application of magnetic flux leakage pipeline detection. Sensors 2015, 15, 31036–31055. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Luo, N.; Feng, G. Quantitative Study on MFL Signal of Pipeline Composite Defect Based on Improved Magnetic Charge Model. Sensors 2021, 21, 3412. [Google Scholar] [CrossRef]
- Oh, C.K.; Joh, C.; Lee, J.W.; Park, K.Y. Corrosion Detection in PSC Bridge Tendons Using Kernel PCA Denoising of Measured MFL Signals. Sensors 2020, 20, 5984. [Google Scholar] [CrossRef]
- Ni, Y.; Zhang, Q.; Xin, R. Magnetic flux detection and identification of bridge cable metal area loss damage. Measurement 2021, 167, 108443. [Google Scholar] [CrossRef]
- Ono, K. Review on structural health evaluation with acoustic emission. Appl. Sci. 2018, 8, 958. [Google Scholar] [CrossRef] [Green Version]
- Xin, H.; Cheng, L.; Diender, R.; Veljkovic, M. Fracture acoustic emission signals identification of stay cables in bridge engineering application using deep transfer learning and wavelet analysis. Adv. Bridge Eng. 2020, 1, 6. [Google Scholar] [CrossRef]
- Li, G.; Zhao, Z.; Li, Y.; Li, C.Y.; Lee, C.C. Preprocessing Acoustic Emission Signal of Broken Wires in Bridge Cables. Appl. Sci. 2022, 12, 6727. [Google Scholar] [CrossRef]
- Casas, J.R.; Moughty, J.J. Bridge damage detection based on vibration data: Past and new developments. Front. Built Environ. 2017, 3, 4. [Google Scholar] [CrossRef] [Green Version]
- Saidin, S.S.; Jamadin, A.; Abdul Kudus, S.; Mohd Amin, N.; Anuar, M.A. An overview: The application of vibration-based techniques in bridge structural health monitoring. Int. J. Concr. Struct. Mater. 2022, 16, 69. [Google Scholar] [CrossRef]
- Zarbaf, S.E.H.A.M.; Norouzi, M.; Allemang, R.; Hunt, V.; Helmicki, A.; Venkatesh, C. Vibration-based cable condition assessment: A novel application of neural networks. Eng. Struct. 2018, 177, 291–305. [Google Scholar] [CrossRef]
- Machorro-Lopez, J.M.; Valtierra-Rodriguez, M.; Amezquita-Sanchez, J.P.; Carrion-Viramontes, F.J.; Quintana-Rodriguez, J.A. A shannon entropy-based methodology to detect and locate cables loss in a cable-stayed bridge. Int. J. Appl. Mech. 2021, 13, 2150063. [Google Scholar] [CrossRef]
- Peng, Z.; Li, J.; Hao, H. Long-term condition monitoring of cables for in-service cable-stayed bridges using matched vehicle-induced cable tension ratios. Smart Struct. Syst 2022, 29, 167–179. [Google Scholar]
- Yanez-Borjas, J.J.; Machorro-Lopez, J.M.; Camarena-Martinez, D.; Valtierra-Rodriguez, M.; Amezquita-Sanchez, J.P.; Carrion-Viramontes, F.J.; Quintana-Rodriguez, J.A. A new damage index based on statistical features, PCA, and Mahalanobis distance for detecting and locating cables loss in a cable-stayed bridge. Int. J. Struct. Stab. Dyn. 2021, 21, 2150127. [Google Scholar] [CrossRef]
- Ren, J.; Zhang, B.; Zhu, X.; Li, S. Damaged cable identification in cable-stayed bridge from bridge deck strain measurements using support vector machine. Adv. Struct. Eng. 2022, 25, 754–771. [Google Scholar] [CrossRef]
- Van Bladel, J.G. Electromagnetic Fields; John Wiley & Sons: Hoboken, NJ, USA, 2007; Volume 19. [Google Scholar]
- Guru, B.S.; Hiziroglu, H.R. Electromagnetic Field Theory Fundamentals; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]






| Parameter | Values |
|---|---|
| Flaw axial length | 10 mm, 20 mm, 30 mm, 40 mm |
| Excitation frequency | 1000 & 2500 & 4000 & 6000 & 10,000 Hz |
| Layer NO. | , |
| Flaw cross-sectional area | {1/19, 2/19,..., j/19} PLA |
| Axial Length (mm) | Averaged Amplitude under (H) | Averaged Amplitude under (H) | Amplitude Difference (H) | Proportion of Difference |
|---|---|---|---|---|
| 10 | 4.342 | 4.828 | 0.486 ± 0.075 | 10.1 ± 1.5% |
| 20 | 8.094 | 8.466 | 0.372 ± 0.093 | 4.4 ± 1.1% |
| 30 | 9.850 | 10.554 | 0.704 ± 0.103 | 6.7 ± 1.0% |
| 40 | 11.519 | 12.525 | 1.006 ± 0.039 | 8.0 ± 0.3% |
| Flaw Position | Excitation Frequency | Flaw Length | Flaw Cross-Sectional Area |
|---|---|---|---|
| 2500 Hz | 10ߝ40 mm | 1/19 to 6/19 PLA on Layer 2 |
| Methodology | Advantages | Limitations | Reference |
|---|---|---|---|
| Dye Penetrant (DP) testing | Simple method for detecting shallow cracks | Costly for assessing quality at multiple locations | [5,6] |
| Optical Fiber Sensing | Stable and precise for cable force monitoring | Complex detection process and high sensitivity | [7,8,9,10] |
| Radio-graphic Testing (RT) | Capable for internal structure examination | Costly and potential health risks due to radiation exposure | [11] |
| Ultrasonic Testing (UT) | Quick detection of defects with strong penetration ability | Poor intuitiveness of detection results | [12,13,14,15,16] |
| Magnetic Particle Testing (MT) | Analysis of magnetic flux leakage for surface or near-surface flaws | Shallow depth measurement capabilities | [17,18,19] |
| Magnetic Flux Leakage (MFL) | Highly effective and easy to achieve quantitative testing | Sensitivity to lift-off height and excitation intensity | [20,21,22,23] |
| Acoustic Emission (AE) testing | Monitoring of cable force and vibration frequency during dynamic processes | Decreased accuracy with increasing distance | [24,25,26] |
| Vibration-based method | Remote sensing | Complex data analysis | [27,28,29,30,31,32,33] |
| The proposed method | Less data processing, real-time responsiveness, and lightweight for robots to carry | Applied to small-sized cables currently |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Z.; Zhao, M.; Ding, N.; Qian, H. Flaw Size Quantification for Cable Flaw Inspection System with Inductive Search Coil Sensor. Appl. Sci. 2023, 13, 8414. https://doi.org/10.3390/app13148414
Fang Z, Zhao M, Ding N, Qian H. Flaw Size Quantification for Cable Flaw Inspection System with Inductive Search Coil Sensor. Applied Sciences. 2023; 13(14):8414. https://doi.org/10.3390/app13148414
Chicago/Turabian StyleFang, Zehao, Min Zhao, Ning Ding, and Huihuan Qian. 2023. "Flaw Size Quantification for Cable Flaw Inspection System with Inductive Search Coil Sensor" Applied Sciences 13, no. 14: 8414. https://doi.org/10.3390/app13148414
APA StyleFang, Z., Zhao, M., Ding, N., & Qian, H. (2023). Flaw Size Quantification for Cable Flaw Inspection System with Inductive Search Coil Sensor. Applied Sciences, 13(14), 8414. https://doi.org/10.3390/app13148414






