Novel Faulted-Section Location Method for Active Distribution Networks of New-Type Power Systems

Abstract

This paper puts forward a fault location method combining the improved matrix algorithm and the genetic tabu algorithm based on multi-source information in view of the limitation of existing fault location methods in active distribution networks, such as long-time consumption, low accuracy, and low tolerance performance. Firstly, the fault region location method is proposed to simplify the active distribution network model and reduce the matrix calculation dimension. Secondly, the improved matrix algorithm is proposed to locate the fault section, and a positioning result verification method is proposed to improve the tolerance performance. Finally, the genetic tabu algorithm is proposed to optimize suspicious fault sections when the verification is incorrect and obtain the positioning result. The simulation results show that the fault location method proposed in this paper locates faster and performs better in both accuracy and tolerance in different fault conditions than others.

1. Introduction

Many countries are accelerating the construction of new-type power systems. With the development of distribution network technology and the establishment of the “dual carbon” target [1], distributed generation (DG) has been widely used due to its characteristics of low energy consumption, cleanliness, and flexibility [2]. Distributed power generation is characterized by randomness, intermittency, vulnerability to environmental impacts, and small reserves [3]. With the access of DG to the distribution network, the uncertainty of the power flow direction leads to an increased risk of power grid failure [4]. Investigating fault location methods with better performance is significant in improving the safety and stability of distribution network operations [5].

After a fault occurs in the active distribution network, fast and accurate fault location is a prerequisite for ensuring the reliability of the power supply [6]. The active distribution network is a multi-power system whose structure is more complex. The uncertainty of distributed power generation directly impacts the current, loss, voltage distribution, and short-circuit level of the entire line. The voltage of each point, such as the section switch and the circuit breaker, will increase significantly. With the access of DG, the problem of reverse power flow will be caused, which leads to the unsatisfactory effect of traditional fault location methods. Therefore, the fault location problem of the active distribution network is an important issue in the research of smart grids [7].

In the context of the automation upgrades of distribution network equipment, many fault location methods based on feeder terminal unit (FTU) upload information have been proposed. There are direct and indirect methods for fault location [8]. The direct method mainly includes the matrix algorithm [9], and the indirect method primarily consists of the particle swarm optimization algorithm [10], immune algorithm [11], ant colony algorithm [12], and other intelligent algorithms.

The principle of the matrix algorithm is to obtain the fault judgment matrix by matrix calculation to locate the fault sections [13]. Reference [14] adopts a specific correction method for different location results. However, this correction method can only adapt to one-third of cases of the error fault information. In Reference [15], a method combining a matrix algorithm and an optimization algorithm is proposed. However, the “minimum set” cannot contain all suspected fault sections. Reference [16] proposes a fault location matrix algorithm based on voltage magnitude comparison, determining the fault sections by comparing the voltage magnitudes at both ends of the suspected fault sections.

Based on the “minimum set” theory, the intelligent algorithm calculates the fault sections that best explain the fault information by solving the fitness function [17]. Reference [18] proposes to evaluate population individuals by calculating antibody affinity. However, the evaluation has to be realized between individuals in each generation, which seriously affects the convergence speed. Reference [19] proposes adaptive crossover and mutation probabilities, adjusted nonlinearly according to the Sigmoid function. However, the parameter setting of this method is complicated. Reference [20] is applied to fault location in the internet of things (IoT) power distribution. The improved unmanned aerial vehicle (UAV) model and particle swarm optimization algorithm are used for fault location, improving the operational efficiency and adaptability of the algorithm.

In summary, the following limitations exist in the research of active distribution network fault location methods: (1) With the increase in distribution network scale and the access of a large number of DGs, the existing fault location methods will find it hard to meet the requirements of fault location accuracy and rapidity. (2) The intelligent algorithm generally has the limitations of premature convergence, making it difficult to search for the correct fault sections. (3) When multiple elements of fault information are incorrect, fault location methods have the problem of balancing positioning speed and accuracy. In response to the above shortcomings, this paper advances a fault section location method of the active distribution network based on multi-source information. The main contents of this paper are as follows:

• The fault region location algorithm is proposed to ensure that the fault region contains all possible faulted sections, simplifying the fault system and reducing the matrix calculation dimension.
• An improved matrix algorithm using a non-square matrix form of computation is proposed to adapt to the access of multiple DGs. The algorithm can accurately locate single and multiple faults in non-T-connected sections.
• A verification method suitable for the improved matrix algorithm positioning results is proposed to improve the tolerance performance.
• A fault hypothesis and fitness function are proposed based on the FTU uploading equipment status and protection action information. Moreover, the genetic tabu algorithm is proposed to locate the fault section by optimization calculation. The method can accurately locate single and multiple faults when the fault information is incorrect.
• The remainder of this paper is arranged as follows. Section 2 proposes the construction of the node status list and topology search method for suspicious fault regions. Section 3 analyzes the deficiencies of the traditional matrix algorithm and proposes an improved matrix algorithm. Section 3.3 proposes a verification method suitable for the improved matrix algorithm. Section 4 proposes a genetic tabu algorithm to quickly and accurately achieve fault location using equipment status and protection action information. Section 5 builds an IEEE-34 node active distribution network model based on the PSCAD platform and implements the proposed algorithm using Python software. Different fault conditions are simulated to test the proposed algorithm and compared with other fault location methods.

2. Fault Region Location

This paper puts forward a fault region location method to reduce the fault location model. Firstly, the fault information needed for fault location is introduced. Secondly, the construction method of the node status list is proposed. Finally, a topology search method for suspicious fault regions and a method to obtain the fault regions are proposed.

2.1. Fault Information and Status Definition

The fault location method needs protection action and equipment status information. The protection action information is obtained through the FTU. The protection action region is between the action switch and the next-level protection switch. The FTU and the internal measuring point of DG upload the equipment status information. The positive direction is the system power pointing to each switch node or DG. The following definitions distinguish the fault current direction:

$$\mathrm{Status}=\left\{\begin{array}{l}1,\mathrm{Switch}\mathrm{alarms}\mathrm{and}\mathrm{positive}\mathrm{fault}\mathrm{current}\mathrm{flows}\hfill \\ 0,\mathrm{Switch}\mathrm{does}\mathrm{not}\mathrm{send}\mathrm{an}\mathrm{alarm}\hfill \\ -1,\mathrm{Switch}\mathrm{alarms}\mathrm{and}\mathrm{reverse}\mathrm{fault}\mathrm{current}\mathrm{flows}\hfill \end{array}\right.$$

(1)

2.2. Node Status List

The system shown in Figure 1 contains eight switching nodes from S₁ to S₈ and six feeder sections from L₁ to L₆. Here are the steps to create a node status list:

(1)

Number each FTU and the internal measuring point of DG according to the positive direction.

Table 1. List of the numbering results.

Node Number	Equipment	Node Number	Equipment
1	FTU1	5	FTU5
2	FTU2	6	FTU6
3	FTU3	7	DG1
4	FTU4	8	DG2

shows the numbering results for the system in Figure 1.

(2)

The node status list consists of five parts: node number, upstream node number, downstream node number, equipment status information, and whether the node is a DG internal measuring point. The node status list of Figure 1 is shown in

Table 2. Node status list.

Node	Upstream Node	Downstream Node	Equipment Status	DG	Node	Upstream Node	Downstream Node	Equipment Status	DG
1	0	2	0	0	5	4	0	0	0
2	1	3, 4	0	0	6	4	7	0	0
3	2	8	0	0	7	6	0	0	1
4	2	5, 6	0	0	8	3	0	0	1

.

2.3. Fault Region Location Method

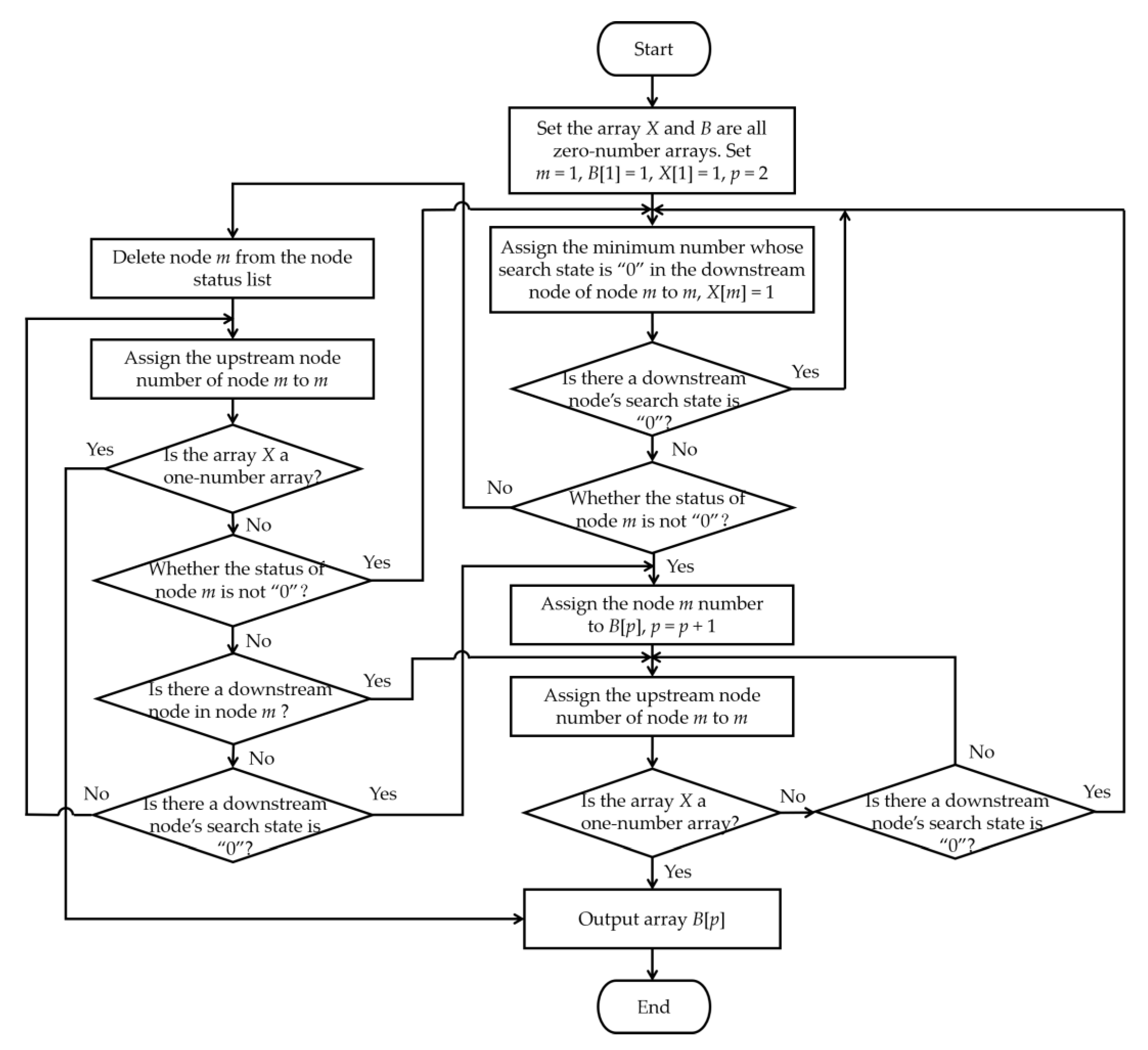
The suspicious fault region is the connected region where all boundary nodes have alarm information. A suspicious fault region location algorithm is proposed to obtain the boundary nodes, which uses the idea of depth-first traversal in the tree search method.

The algorithm sets two variables and arrays: m, p, X, B. Variable m represents the node number of the temporary detection. Variable p is the auxiliary iteration parameter. Array X marks the node search state. Array B records boundary nodes. The procedure is explained in detail in the following steps, and the flow chart is shown in Figure 2.

• Set the initial value of m as 1; the arrays X and B are all zero-number arrays; the initial node B[1] = 1, X[1] = 1, p = 2;
• Assign the search state as “0” in the downstream node of node m to m, set X[m] = 1;
• If node m has a downstream node, go back to step 2; otherwise, check whether the equipment status information of node m is not “0”. If it is not “0”, set B[p] = m, p = p + 1, then go to step 6; otherwise, delete node m from the node status list and go to step 4;
• Assign the upstream node number of node m to m, and check whether the array X is a one-number array. If not, run the next step; otherwise, go to step 8;
• Check whether a downstream node search status as “0” exists on node m. If it exists, go back to step 2; otherwise, check whether node m has a downstream node. If not, check whether the equipment status information of node m is not “0”. If it is not “0”, set B[p] = m, p = p + 1, go to step 6; otherwise, go back to step 4. If it exists, go to step 6;
• Assign the upstream node number of node m to m, and check whether the array X is a one-number array. If not, run the next step; otherwise, go to step 8;
• Check whether a downstream node whose search status as “0” exists on node m. If not, go back to step 6; otherwise, go back to step 2;
• Terminate the program, output the array B, and obtain the boundary nodes.

The suspicious fault region is determined through the boundary nodes in array B. The protection action information obtains the protection action region. Check whether the suspicious fault region contains the protection action region. If it does, the suspicious fault region is the fault region; otherwise, the node farthest away from the system power in the protection action region is regarded as a boundary node. The fault region is determined together with the boundary nodes in array B. The fault node status list is generated from the fault region.

3. Improved Matrix Algorithm

This section introduces the calculation principle of the traditional matrix algorithm, proposes an improved matrix algorithm that can adapt to the access of DG, and presents a verification method to improve tolerance performance.

3.1. Traditional Matrix Algorithm

Firstly, the principle of the traditional matrix algorithm for the open-loop state is introduced. The number of switch nodes S_j and feeder sections L_i is equal and assumed as m_l. The correlation matrix D′ is defined as follows:

$$D^{\prime }=\begin{array}{c}\stackrel{{{\displaystyle S}}_1\hspace{0.17em}\hspace{0.17em}{{\displaystyle S}}_2\hspace{0.17em}\hspace{0.17em}\cdots \hspace{0.17em}\hspace{0.17em}{{\displaystyle S}}_{{{\displaystyle m}}_l}}{\left[\begin{array}{ccccc}& & & & \\ & & & & \\ & & & & \\ & & & & \end{array}\right]}\begin{array}{c}{{\displaystyle L}}_1\\ {{\displaystyle L}}_2\\ ⋮\\ {{\displaystyle L}}_{{{\displaystyle m}}_l}\end{array}\end{array}$$

(2)

$${D^{\prime }}_{ij}=\left\{\begin{array}{l}1,\mathrm{When}\mathrm{section}i\mathrm{fail},\mathrm{switch}\mathrm{node}j\mathrm{sends}\mathrm{an}\mathrm{alarm}\hfill \\ 0,\mathrm{When}\mathrm{section}i\mathrm{fail},\mathrm{switch}\mathrm{node}j\mathrm{does}\mathrm{not}\mathrm{send}\mathrm{an}\mathrm{alarm}\hfill \end{array}\right.$$

(3)

The elements of the 1 × m_l feeder section status matrix L′ are defined as follows:

$$l_i=\left\{\begin{array}{l}1,\mathrm{Feeder}\mathrm{section}{L}_i\mathrm{is}\mathrm{faulty}\hfill \\ 0,\mathrm{Feeder}\mathrm{section}{L}_i\mathrm{is}\mathrm{not}\mathrm{faulty}\hfill \end{array}\right.$$

(4)

The elements of the 1 × m_l fault information matrix I′ are defined as follows:

$$I_j=\left\{\begin{array}{l}1,\mathrm{Switch}\mathrm{node}{S}_j\mathrm{sends}\mathrm{an}\mathrm{alarm}\hfill \\ 0,\mathrm{Switch}\mathrm{node}{S}_j\mathrm{doesn}’\mathrm{t}\mathrm{send}\mathrm{an}\mathrm{alarm}\hfill \end{array}\right.$$

(5)

Define the following logical operation. Matrix K and matrix M are two matrices of the same dimension:

$$K=\left|M\right|$$

(6)

$$K_{ij}=\left\{\begin{array}{c}1,M_{ij}>0\\ 0,M_{ij}\le 0\end{array}\right.$$

(7)

From the definition of the correlation matrix D′, the following relationship can be calculated for radial distribution networks:

$$I^{\prime }=\left|L^{\prime }{D}^{\prime }\right|$$

(8)

After simplification, we can obtain the equation for calculating the matrix L′:

$$L^{\prime }=\left|I^{\prime }{D^{\prime }}^{-1}\right|$$

(9)

The fault section is the section in which the calculation result of “1” in matrix L′.

Secondly, the calculation principle for the closed-loop state is introduced. The algorithm adopts the method of separate analysis and superposition judgment. When analyzing one of the power supplies, set the positive direction as the power supply pointing to each node. Open the interface circuit breakers of other power supplies. The results of individual power supply are calculated separately, and the sets of fault sections are F₁, F₂, …, and F_i. The set of fault sections F of the entire active distribution networks is:

$$F=F_1\cup F_2\cup \cdots \cup F_i$$

(10)

3.2. Improved Matrix Algorithm

An improved matrix algorithm is proposed to address the shortcomings of the traditional matrix algorithm, considering the internal measuring point of DG so that the number of switch nodes is greater than the feeder sections. The algorithm is computed in a non-square matrix form. Assuming the number of switch nodes S_i is m_s and feeder sections L_j is m_l. The network description matrix D is defined as follows:

$$D^{\prime }=\begin{array}{c}\stackrel{{{\displaystyle L}}_1\hspace{0.17em}\hspace{0.17em}{{\displaystyle L}}_2\hspace{0.17em}\hspace{0.17em}\cdots \hspace{0.17em}\hspace{0.17em}{{\displaystyle L}}_{{{\displaystyle m}}_l}}{\left[\begin{array}{ccccc}& & & & \\ & & & & \\ & & & & \\ & & & & \end{array}\right]}\begin{array}{c}{{\displaystyle S}}_1\\ {{\displaystyle S}}_2\\ ⋮\\ {{\displaystyle S}}_{{{\displaystyle m}}_s}\end{array}\end{array}$$

(11)

$$D_{ij}=\left\{\begin{array}{l}1,\mathrm{Node}i\mathrm{connected}\mathrm{to}\mathrm{section}j,\mathrm{positive}\mathrm{direction}\mathrm{towards}\mathrm{section}j\hfill \\ 0,\mathrm{Node}i\mathrm{is}\mathrm{not}\mathrm{connected}\mathrm{to}\mathrm{section}j\hfill \\ -1,\mathrm{Node}i\mathrm{connected}\mathrm{to}\mathrm{section}j,\mathrm{positive}\mathrm{direction}\mathrm{reverses}\mathrm{section}j\hfill \end{array}\right.$$

(12)

The elements of the 1 × m_s fault information matrix I are defined as follows:

$$I_i=\left\{\begin{array}{l}1,\mathrm{Node}i\mathrm{alarms}\mathrm{in}\mathrm{the}\mathrm{positive}\mathrm{direction}\hfill \\ 0,\mathrm{Node}i\mathrm{does}\mathrm{not}\mathrm{send}\mathrm{an}\mathrm{alarm}\hfill \\ -1,\mathrm{Node}i\mathrm{alarms}\mathrm{in}\mathrm{the}\mathrm{opposite}\mathrm{direction}\hfill \end{array}\right.$$

(13)

A 1 × m_l matrix represents the fault judgment matrix L:

$$L=\left[l_1,l_2,l_3,\cdots ,l_{m_l}\right]$$

(14)

The physical meaning is the number of nodes in which the fault current flows into the feeder section minus nodes in which the fault current flows out of the feeder section.

According to the definition of matrix D, taking l₁ as an example, the following arithmetic relations exist for radial active distribution networks:

$$l_1=\left\{I_1·D\left(1,1\right)+I_2·D\left(2,1\right)+\cdots +I_{m_s}·D\left(S_{m_s},1\right)\right\}=\left\{I{\left[D\left(1,1\right)D\left(2,1\right)\cdots D\left(S_{m_s},1\right)\right]}^T\right\}$$

(15)

This relationship is further extended to the entire active distribution network. To attain the calculation equation of the fault judgment matrix L:

$$L=ID$$

(16)

According to the physical meaning of matrix L, the fault criterion is as follows:

$$\mathrm{Fault}\mathrm{criterion}\left\{\begin{array}{l}{l}_i>1,\mathrm{Section}\mathrm{is}\mathrm{faulty}\\ l_i=1,\mathrm{Non}\mathrm{T}\mathrm{section}\mathrm{fault}\mathrm{or}\mathrm{T}\mathrm{connected}\mathrm{section}\mathrm{single}\mathrm{fault}\\ l_i<1,\mathrm{Section}\mathrm{is}\mathrm{not}\mathrm{faulty}\end{array}\right.$$

(17)

When the result of “1” appears in a specific section, check whether the section is a T-connected section. If not, the section is considered faulty; otherwise, check whether other sections are faulty. If there are faults in other sections, we assume that the T-connected section does not faulty; otherwise, the T-connected section is faulty.

3.3. Improved Matrix Algorithm Verification

The improved matrix algorithm cannot accurately locate multiple faults with T-connected sections. This section proposes a verification method based on the traditional matrix algorithm and superposition principle. According to I′ = |L′D′|, the matrix I* can be derived from the matrix L′ and the matrix D′. Determine whether the calculated matrix I* is the same as the matrix I brought by equipment status information. If they are the same, the positioning result is correct. Otherwise, further fault location is performed in the next section. Each positioning result of the improved matrix algorithm is verified. The calculation steps of the verification method are as follows:

(1)

Write the feeder section status matrix L′ according to the positioning result.

(2)

When analyzing one of the power supplies, the correlation matrix D′ considering the causality between the faulted section and the alarm of the switch, has the same structure as the matrix shown in Equation (2). Matrix D′ is defined as follows:

$$D_{ij}^{\prime }=\left\{\begin{array}{l}1,\mathrm{When}\mathrm{section}i\mathrm{fail},\mathrm{node}j\mathrm{alarms}\mathrm{in}\mathrm{the}\mathrm{positive}\mathrm{direction}\hfill \\ 0,\mathrm{When}\mathrm{section}i\mathrm{fail},\mathrm{node}j\mathrm{does}\mathrm{not}\mathrm{send}\mathrm{an}\mathrm{alarm}\hfill \\ -1,\mathrm{When}\mathrm{section}i\mathrm{fail},\mathrm{node}j\mathrm{alarms}\mathrm{in}\mathrm{the}\mathrm{opposite}\mathrm{direction}\hfill \end{array}\right.$$

(18)

When analyzing one of the power supplies, the nodes nearest to the other power supplies are regarded as disconnected. Delete the rows corresponding to the disconnected nodes in the network description matrix D to attain the network description matrix D_i in the square matrix form. When describing the same system, the network description matrix and the correlation matrix contain the same line topology. Through calculation, we find that the two matrices of the same system are inverse matrices to each other. Therefore, the correlation matrix of the system can be calculated using the following equation:

$$D_i^{\prime }=D_i^{-1}$$

(19)

Each power supply is analyzed separately to obtain m_s − m_l + 1 correlation matrices D_i′.

(3)

Define the following logical operation. Matrix K and matrix M are two matrices of the same dimension:

$$K=\Vert M\Vert$$

(20)

$$K_{ij}=\left\{\begin{array}{l}1,M_{ij}>0\hfill \\ 0,M_{ij}=0\hfill \\ -1,M_{ij}<0\hfill \end{array}\right.$$

(21)

Same as the traditional matrix algorithm principle, using the equation:

$$I_i=L^{\prime }{D}_i^{\prime }$$

(22)

to obtain m_s − m_l + 1 fault information matrix I_i.

(4)

Each matrix I_i must be supplemented with “0” at the nodes it does not contain to obtain a matrix I_i* of 1 × m_s. Then, through the equation:

$$I^{*}=I_1^{*}+I_2^{*}+\mathrm{\dots }+I_{m_S-m_l+1}^{*}$$

(23)

obtain the fault information matrix I*. Determine whether the matrix I* and the matrix I obtained from the equipment status information are the same.

The flow chart of the verification is shown in Figure 3.

3.4. Improved Matrix Algorithm Analysis

The improved matrix algorithm cannot accurately deal with multiple faults with T-connected sections. Specifically, it includes the following two cases:

(1)

As shown in Figure 4, multiple faults with the T-connected section occur in (i), and a single fault occurs in (ii). In the two cases, the equipment status information of the S₁, S₂, and S₃ nodes is the same, which is 1, −1, and 1. In matrix L, the results of these sections are all 1. According to the fault criterion, the T-connected section of l_i = 1 is not faulty when other fault sections are present. Therefore, the algorithm cannot accurately locate whether the T-connection section of l_i = 1 is faulty in the case of multiple faults.

(2)

As shown in Figure 5, multiple faults with the T-connected section occur in (i), and a single fault occurs in (ii). In the two cases, the equipment status information of the S₁, S₂, and S₃ nodes is the same, which is 1, 1, and 0. In matrix L, the results of these sections are all 0. According to the fault criterion, the T-connected section of l_i = 0 is not faulty. Therefore, the algorithm cannot accurately locate whether the T-connected section of l_i = 0 is faulty in the case of multiple faults.

In summary, the improved matrix algorithm can accurately locate single and multiple faults in non-T-connected sections without error fault information. However, it cannot accurately judge whether the T-connected sections of l_i = 1 and l_i = 0 have failed under multiple faults.

4. Genetic Tabu Algorithm

This paper proposes a genetic tabu algorithm (GTA) to locate the fault section further. This section defines the fault hypothesis and the fitness function, derives the equation for calculating the expected status of fault information, and introduces the calculation principle and parameter selection of the genetic tabu algorithm.

4.1. Fault Hypothesis

The calculated fault sections, the T-connected sections with l_i = 1 and l_i = 0, and the sections inside the protection action region are used as the suspicious fault sections. The three factors, “different combinations of suspicious fault sections fail”, “protection of misoperation or rejection”, and “error equipment status information”, are taken as a fault hypothesis. Suppose there are m_l suspicious fault sections. There are m_e protections and m_s nodes in the fault region. The basic form of the fault hypothesis is as follows:

$$H=\left[L,O,R,A\right]$$

(24)

(1)

$L=\left[l_1,l_2,\mathrm{\dots },l_{m_l}\right]$, and the control variable is set as l_i, depending on whether section i is faulty. l_i = 0 means section i is not faulty; l_i = 1 indicates section i is faulty.

(2)

$O=\left[o_1,o_2,\mathrm{\dots },o_{m_e}\right]$, and the control variable is set as o_i, depending on whether protection i has a misoperation. o_i = 0 indicates that protection i does not have a misoperation; o_i = 1 shows protection i has a misoperation.

(3)

$R=\left[r_1,r_2,\mathrm{\dots },r_{m_e}\right]$, and the control variable is set as r_i, depending on whether protection i has a rejection. r_i = 0 indicates that protection i does not have a rejection; r_i = 1 indicates that protection i has a rejection.

(4)

$A=\left[A_{1,1},A_{1,2},A_{2,1},A_{2,2},\mathrm{\dots },A_{m_s,1},A_{m_s,2}\right]$, and the control variable is set as A_i,1, A_i,2, depending on whether there is error equipment status information for node i. The error results are represented by A_i,1, A_i,2 shown in

Table 3. Equipment status information error situation.

Equipment Status Information	Error Factor Ai,1	Error Factor Ai,2	Upload Information
1	0	1	0
	1	0	−1
0	0	1	1
	1	0	−1
−1	0	1	0
	1	0	1

.

4.2. Fitness Function

A fitness function reflects the difference between the expected and actual status of the protection action and equipment status information. The fitness function F(H) can provide feedback on the rationality of the fault hypothesis. The smaller the F(H) is, the higher the reliability of the fault hypothesis. F(H) is shown as follows:

$$minF\left(H\right)=w_1\sum _{i=1}^{m_e}\left|e_i-e_i^{\prime }\left(H\right)\right|+w_2\sum _{j=1}^{m_s}\left|I_j-I_j^{\prime }\left(H\right)\right|+w_3\left\{\sum _{p=1}^{m_l}{l}_p+\sum _{i=1}^{m_e}\left(o_i+r_i\right)+\sum _{j=1}^{m_s}\sum _{k=1}^2{A}_{j,k}\right\}$$

(25)

F(H) consists of two parts. The first part is the alarm difference index. This part reflects the difference between the expected and actual status of the fault information:

$$w_1\sum _{i=1}^{m_e}\left|e_i-e_i^{\prime }\left(H\right)\right|+w_2\sum _{j=1}^{m_s}\left|I_j-I_j^{\prime }\left(H\right)\right|$$

(26)

(1)

e_i is the actual status of protection i. e_i = 0 indicates that the protection is inactive. e_i = 1 indicates that it is active. I_j is the actual equipment status information of node j.

(2)

e_i′(H) and I_j′(H) represent the expected protection action status of protection i, and the expected equipment status information of node j, and are calculated according to the H.

(3)

|e_i − e_i′(H)| is the difference between the expected and actual status of protection action information of protection i. |I_j − I_j′(H)| is the difference between the expected and actual status of equipment status information of node j.

The second part of the fitness function is the fault hypothesis minimization index:

$$w_3\left\{\sum _{p=1}^{m_l}{l}_p+\sum _{i=1}^{m_e}\left(o_i+r_i\right)+\sum _{j=1}^{m_s}\sum _{k=1}^2{A}_{j,k}\right\}$$

(27)

This component shows that, when the alarm difference index is the same, the lower the total number of fault sections, misoperations, and rejection protections, and nodes with error equipment status information, the higher the reliability of the fault hypothesis.

To select the case where the alarm discrepancy index is the smallest, set w₁ > w₃, w₂ > w₃. According to the actual reliability of the relay, protection must be more than 99%, and the probability of misoperation and rejection can be selected as 0.1%. According to the statistics of the long-term operation of the active distribution system, the probability of error equipment status information can be selected as 1%. When the probabilities of false protection action and error equipment status information are the same, the alarm discrepancy index calculated from the protection action information is the same as the equipment status information. We can obtain the following equation:

$${0.01}^{w_1}={0.001}^{w_2}$$

(28)

w₁ = 1.5w₂ is calculated. Therefore, w₁ = 150, w₂ = 100, and w₃ = 1 can be selected. The loss function and cost function of the optimization process are defined. The loss function is used to evaluate the difference between the predicted and true values of the model, which refers to the error of a sample. The cost function is defined on the entire training set, which refers to the average of all sample errors. Since the fault location is optimized according to the difference between the expected and actual status of the fault information, this paper uses the loss function as an absolute value to construct the cost function. The calculation equation of the loss function L(H) and the cost function c(H) are:

$$L(H)=\left|e_i-e_i^{\prime }\left(H\right)\right|+\left|I_j-I_j^{\prime }\left(H\right)\right|$$

(29)

$$c(H)=\frac{1}{m_e+m_s}\left(\sum _{i=1}^{m_e}\left|e_i-e_i^{\prime }\left(H\right)\right|+\sum _{j=1}^{m_s}\left|I_j-I_j^{\prime }\left(H\right)\right|\right)$$

(30)

4.3. Expected Protection Action Status

This section derives the calculation equation of the expected protection action status $f_{e_i}\left(H\right)$ during normal operation, and the expected protection action status e_i′(H), which considers the protection of incorrect action.

4.3.1. Expected Protection Action Status When Incorrect Action Is Not Considered

At present, the majority of relay protection in the distribution system still adopts overcurrent protection. On this basis, the protection action expected status is discussed.

(1)

Main protection

Set e_i is the main protection of section L_j, and its action logic is that when section L_j of protection e_i fails (l_j = 1), the protection e_i should act.

$$f_{e_i}\left(H\right)=l_j$$

(31)

(2)

Backup protection

Set e_i is the remote backup protection of section L_j, and e_x is the main protection of section L_j. The section in the remote backup protection region of protection e_i is represented by Y(e_i). When there is a section L_j fault (l_j = 1) in Y(e_i), and its main protection e_x refuses to operate (r_x = 1), the protection e_i should act.

$$f_{e_i}\left(H\right)=\sum _{l_j\in Y\left(e_i\right)}{l}_j·r_x$$

(32)

4.3.2. Expected Protection Action Status Considering Incorrect Action

As shown in

Table 4. Expected protection action status.

${\mathit{f}}_{{\mathit{e}}_{\mathit{i}}}\left(\mathit{H}\right)$	oi	ri	ei′(H)	Explanation
1	0	0	1	Protection should act and receive protection action information
1	0	1	0	Protection should act, but due to the rejection of the protection, we will not receive protection action information
0	0	0	0	Protection should not act and will not receive protection action information
0	1	0	1	Protection should not act, but due to the misoperation of the protection, we will receive protection action information

, by combining $f_{e_i}\left(H\right)$ with the misoperation variable o_i and the rejection variable r_i, we can attain the expected protection action status e_i′(H).

According to Table 4, the calculation equation of e_i′(H) can be obtained:

$$e_i^{\prime }\left(H\right)=\overline{o_i}·\overline{r_i}·f_{e_i}\left(H\right)+o_i·\overline{r_i}·\overline{f_{e_i}\left(H\right)}$$

(33)

4.4. Equipment Expected Status Information

This section derives the calculation equation of the equipment expected status information $I_j^{*}\left(H\right)$ when it is normal, and the equipment expected status information $I_j^{\prime }\left(H\right)$, which considers the hypothesis of “error equipment status information”.

4.4.1. Equipment Expected Status Information without Considering Error Information

Introducing the switching function, which establishes a conversion from the fault section to the equipment status information. The switching function is defined as:

$$I_{ju}^{*}\left(H\right)=\left\{{\displaystyle \prod }_u^{M^{\prime }}\left[K_u\left(1-{\displaystyle \prod }_{j,s_u}{l}_{j,s_u}\right)\right]\right\}{\displaystyle \prod }_{j,d}^N{l}_{j,d}$$

(34)

$$I_{jd}^{*}\left(H\right)=\left\{{\displaystyle \prod }_d^{N^{\prime }}\left[K_d\left(1-{\displaystyle \prod }_{j,s_d}{l}_{j,s_d}\right)\right]\right\}{\displaystyle \prod }_{j,u}^M{l}_{j,u}$$

(35)

$$I_j^{*}\left(H\right)=I_{ju}^{*}\left(H\right)-I_{jd}^{*}\left(H\right)$$

(36)

The physical meaning of each element is as follows: $I_j^{*}\left(H\right)$ is the switching function of the node j, which is “1” when there is a positive alarm, “−1” when there is a reverse alarm, and “0” when there is no alarm; $I_{ju}^{*}\left(H\right)$ and $I_{jd}^{*}\left(H\right)$, respectively, represent the upstream and downstream switching functions of node j; $l_{j,s_u}$ and $l_{j,s_d}$, respectively, represent the status of the section between the node j to the upstream power supply s_u and the downstream power supply s_d; s_u and s_d include the main power supply and DG; M’ and N’ are the number of upstream and downstream power supplies, respectively; l_j,u and l_j,d, respectively, represent the status of all upstream and downstream sections of node j; M and N are the number of all sections in the upstream and downstream, respectively; “$\prod$” represents the logical “or” operation; K_u and K_d are the upstream and downstream power supply coefficients, respectively, and the power supply access is “1”; otherwise, it is “0”.

4.4.2. Equipment Expected Status Information Considering Error Information

As shown in Table 3, by combining $I_j^{\prime }\left(H\right)$ with the error factor A_j,k and the $I_j^{*}\left(H\right)$, we can attain the calculation equation of the $I_j^{\prime }\left(H\right)$. The calculation equation is as follows:

$$I_j^{\prime }\left(H\right)=\left\{\begin{array}{l}\overline{A_{j,1}}·A_{j,2}-A_{j,1}·\overline{A_{j,2}},I_j^{*}=0\hfill \\ \overline{A_{j,1}}\overline{·A_{j,2}}-A_{j,1}·\overline{A_{j,2}},I_j^{*}=1\hfill \\ A_{j,1}·\overline{A_{j,2}}-\overline{A_{j,1}}·\overline{A_{j,2}},I_j^{*}=-1\hfill \end{array}\right.$$

(37)

4.5. Genetic Tabu Algorithm

This section introduces the genetic tabu algorithm (GTA) overall design, calculation principle, and parameter selection. The genetic algorithm (GA) and tabu search (TS) are two commonly used algorithms for the fault location of the active distribution network. Among them, the core idea of the GA is “Natural selection, survival of the fittest”. The algorithm optimizes by simulating the evolutionary theory in nature and has strong robustness and flexibility. However, the search granularity of the GA is coarse, and it is prone to premature convergence or non-convergence. Based on the neighborhood search algorithm, TS introduces a tabu table to limit the optimal local solution. Hence, it is easier to achieve the global optimum, and the search accuracy is higher. However, due to the low search efficiency of neighborhood search on large-scale problems, this algorithm takes more time to deal with the fault location problem of the distribution network.

4.5.1. Genetic Tabu Algorithm Overall Design

A genetic tabu algorithm suitable for fault location of the large-scale active distribution network is proposed by combining the high search efficiency of the GA and the high search accuracy of TS to complete the optimization calculation together so that the algorithm can improve the accuracy based on ensuring the calculation speed and meet the requirements of power supply reliability of distribution network.

Firstly, according to the practical problem of fault location in the active distribution network, the genetic coding rules of the GA are designed. The suspicious fault section is encoded as a one-dimensional matrix. The value of each element in the matrix represents whether the section is faulty, where “1” represents that the section is faulty, and “0” represents that the section is not faulty. The individual in the GA is represented as such a binary gene string. In this design, once the fault section is detected, it will cause a rapid decrease in the fitness function’s value. The GA can retain this dominant gene, thus avoiding the repeated search of the algorithm, which greatly improves the optimization efficiency. At the same time, individuals can accurately reflect the fault situation.

Secondly, the natural selection rules are designed according to the idea of TS. In natural selection, the top 50% of fitness of the current population individuals are selected as the parent generation. Then, one individual gene is selected for the mutation to generate a neighborhood. The mutated individuals are also added to the parent generation to obtain the parent population of the same size. This natural selection rule corresponds to the actual fault location. The fault situation represented by individual neighborhoods is close to the current fault situation. In addition, to ensure the running speed of the algorithm, several individuals with the highest fitness in the child generation are updated into the tabu table after natural selection to prevent the algorithm from repeatedly searching and falling into the local optimum.

Then, the initial population is generated by the greedy algorithm. Considering that the probability of single faults is higher than that of multiple faults, the initial population preferentially generates all individuals of single faults. Then, it fills the initial population with a random method. On the one hand, it can quickly screen out the dominant individuals with smaller fitness function values in the initial population. On the other hand, it can also avoid the phenomenon that the algorithm converges too late or does not converge, thus accelerating the convergence speed of the algorithm.

Finally, according to the designed natural selection rules and genetic algorithm, the iteration is carried out to attain the fault section location result.

The GTA can accurately locate various complex fault conditions. Section 5 uses the IEEE-34 node system to simulate and verify the algorithm’s performance. However, simulation experiments need to be carried out in larger-scale systems to make the algorithm more mature and adapt to the operation mode of large-scale systems.

4.5.2. Genetic Tabu Algorithm Implementation Process

The flowchart of fault location using the genetic tabu algorithm is shown in Figure 6.

The implementation process of the genetic tabu algorithm is as follows:

• Read the original data such as network node parameters, protection action and equipment status information, and set the population size, and the crossover and mutation rate, and encode according to the designed rules;
• Generate the initial population according to the greedy algorithm;
• According to the fitness function, the fitness of individuals in the population is calculated, respectively. Check whether the genetic algorithm termination condition is met. If the condition is not met, go to Step 4; otherwise, go to Step 8;
• The individuals are cross-calculated according to the crossover rate;
• Calculate the mutation of individuals according to the mutation rate;
• Natural selection is carried out to generate new populations;
• Record N individuals with the highest fitness to the tabu table according to the contempt criterion, and go back to Step 3;
• Stop the operation and output the positioning result.

4.5.3. Genetic Tabu Algorithm Parameter Selection

Analyze and select the six parameters involved in the GTA. The population size G is the number of individuals the algorithm searches at once. The population size selects 1% of the total size of H to balance the search range of the algorithm iteration and the total number of iterations, G = 1%2^x. The population dimension D is the gene length of each individual. The gene length of the individual is equal to the number of feeder sections. The crossover rate P₁ is the probability of individual crossover in one iteration process. According to the operation experience of the genetic algorithm, the crossover rate P₁ = 80% is selected. The mutation rate P₂ is the probability of individual variation during an iteration. Since the process of natural selection includes mutation calculation, this paper selects a lower mutation rate, P₂ = 5%. N is the number of individuals recorded in the tabu table after each iteration, and the tabu length L is the length of the tabu table. To balance the convergence speed and avoid a repeated search, N is selected as 1% of the population size, N = 1%G; L is selected to be updated once in five iterations, L = 5N. The values of the above six parameters will be set according to the system model in Section 5.

5. Simulation Analysis

Based on the PSCAD platform, this section builds an IEEE-34 node active distribution network model, as shown in Figure 7. The system contains thirty-four switching nodes from S₁ to S₃₄ and thirty-two feeder sections from L₁ to L₃₂. Python software programs the fault region location algorithm, improved matrix algorithm and verification, and GTA. The performance of the proposed algorithms is tested by simulating single faults, multiple faults in non-T-connected sections, multiple faults with T-connected sections, and faults with fault information errors.

Considering factors such as power supply reliability, investment, management, and maintenance workload, the number of distribution line sections should not exceed three, which means that a maximum of two switches are installed between two pieces of protection equipment. Therefore, the protection installation position in the system is shown in Figure 7. The system comprises 15 pieces of protection equipment, 32 feeder sections, and 34 switching nodes.

Table 5. Node number corresponding to the protection.

Protection	Corresponding Node Number	Protection	Corresponding Node Number
e1	1	e9	19
e2	4	e10	21
e3	5	e11	22
e4	8	e12	24
e5	10	e13	25
e6	14	e14	29
e7	15	e15	30
e8	18

shows the node number corresponding to each protection.

Table 6. The IEEE-34 node active distribution network node status list.

Node	Upstream Node	Downstream Node	Equipment Status	DG	Node	Upstream Node	Downstream Node	Equipment Status	DG
1	0	2	0	0	18	17	0	0	0
2	1	3	0	0	19	17	20	0	0
3	2	4	0	0	20	19	21, 22	0	0
4	3	5, 6	0	0	21	20	34	0	0
5	4	0	0	0	22	20	23, 24	0	0
6	4	7	0	0	23	22	0	0	0
7	6	8	0	0	24	22	25, 28	0	0
8	7	9	0	0	25	24	26	0	0
9	8	10, 13	0	0	26	25	27	0	0
10	9	11	0	0	27	26	33	0	0
11	10	12	0	0	28	24	29	0	0
12	11	0	0	0	29	28	30, 32	0	0
13	9	14, 15	0	0	30	29	31	0	0
14	13	0	0	0	31	30	0	0	0
15	13	16	0	0	32	29	0	0	0
16	15	17	0	0	33	27	0	0	1
17	16	18, 19	0	0	34	21	0	0	1

shows the system node status list.

When the IEEE-34 node active distribution network has complex faults, such as multiple faults with fault information errors, the maximum number of suspicious fault sections is about 15, and the fault hypothesis contains about 30,000 cases. According to the parameter selection rules in Section 4.5.3, the specific data of the parameters of the genetic tabu algorithm are set. The population size G is set to 1% of the total size of the fault hypothesis, G = 300. The population dimension D is the number of feeder sections in the system shown in Figure 7, D = 32. The crossover rate P₁ = 80%, and the mutation rate P₂ = 5%. N is selected as 1% of the population size, N = 3. The tabu length L is selected to be updated once in five iterations, L = 15.

5.1. Test Case 1: Single Fault

A single fault is simulated in the active distribution network shown in Figure 7, assuming that L₂₄ is faulty. The master station receives the protection e₁₂ action information, and the protection action region includes sections L₂₄ and L₂₈. The equipment status information is I = [1 1 1 1 0 1 1 1 1 0 0 0 1 0 1 1 1 0 1 1 −1 1 0 1 −1 −1 −1 0 0 0 0 0 −1 −1]. Firstly, the suspicious fault region is located, and the boundary nodes are S₁, S₃₃, and S₃₄. Secondly, it is judged that the suspicious fault region does not contain the entire protection action region. Therefore, node S₂₈ farthest from the power supply in the protection action region is the boundary node. Finally, the fault region is obtained according to all boundary nodes, including 23 switching nodes and 21 feeder sections.

The schematic diagram of the fault region is shown in Figure 8. The fault node status list is shown in

Table 7. Fault node status list of a single fault in the IEEE-34 node active distribution network.

Node	Upstream Node	Downstream Node	Equipment Status	DG	Node	Upstream Node	Downstream Node	Equipment Status	DG
1	0	2	1	0	19	17	20	1	0
2	1	3	1	0	20	19	21, 22	1	0
3	2	4	1	0	21	20	34	−1	0
4	3	6	1	0	22	20	24	1	0
6	4	7	1	0	24	22	25, 28	1	0
7	6	8	1	0	25	24	26	−1	0
8	7	9	1	0	26	25	27	−1	0
9	8	13	1	0	27	26	33	−1	0
13	9	15	1	0	28	27	0	0	0
15	13	16	1	0	33	27	0	−1	1
16	15	17	1	0	34	21	0	−1	1
17	16	19	1	0

.

The matrix I = [1 1 1 1 1 1 1 1 1 1 1 1 1 1 −1 1 1 −1 −1 −1 0 −1 −1]. According to L = ID, obtain the matrix L = [0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 2 0 0 0 0]. l₂₄ = 2 illustrates that this section is faulty. Where the T-connected section l₂₀ = 1, search for the other fault section, or this is judged as a non-fault section. The location result is L₂₄. Calculate the matrix I when the power S, DG1, and DG2 are supplied separately: IS* = [1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 0 0 0 0 0], I_DG1* = [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 −1 −1 −1 0 −1 0], I_DG2* = [0 0 0 0 0 0 0 0 0 0 0 0 0 0 −1 1 1 0 0 0 0 0 −1]. The matrix I* = [1 1 1 1 1 1 1 1 1 1 1 1 1 1 −1 1 1 −1 −1 −1 0 −1 −1]. Because I* = I, verify that the positioning result is correct. The results of multiple simulation experiments on single faults in

Table 8. The results of single fault simulation experiments.

Fault Section	Boundary Nodes	Location Result	Correct or Not
L8	S1, S33, S34	L8	correct
L19	S1, S33, S34	L19	correct
L11	S1, S12, S33, S34	L11	correct
L26	S1, S33, S34	L26	correct
L32	S1, S32, S33, S34	L32	correct

show that the improved matrix algorithm can accurately locate single faults.

5.2. Test Case 2: Multiple Faults in Non-T-Connected Sections

The calculation process of multiple faults in non-T-connected sections by the improved matrix algorithm is similar to that in the previous section and will not be repeated here. Multiple simulation experiments are carried out for multiple faults location in non-T-connected sections. The results in

Table 9. The results of multiple faults in non-T-connected section simulation experiments.

Fault Sections	Boundary Nodes	Location Result	Correct or Not
L8, L28	S1, S28, S33, S34	L8, L28	correct
L14, L19	S1, S14, S33, S34	L14, L19	correct
L6, L11, L30	S1, S12, S31, S33, S34	L6, L11, L30	correct
L5, L15, L26	S1, S5, S33, S34	L5, L15, L26	correct
L7, L16, L25, L32	S1, S32, S33, S34	L7, L16, L25, L32	correct

show that the improved matrix algorithm can accurately locate multiple faults in non-T-connected sections.

5.3. Test Case 3: Multiple Faults with T-Connected Sections

Multiple faults with T-connected sections are simulated in the distribution network shown in Figure 7, assuming that L₉, L₁₁, and L₂₈ are faulty. This involves attaining the protection e₄, e₅, and e₁₂ action information and the equipment status information I = [1 1 1 1 0 1 1 1 1 1 1 0 −1 0 −1 −1 −1 0 −1 −1 −1 0 0 0 −1 −1 −1 1 0 0 0 0 −1 −1]. The boundary nodes are S₁, S₁₂, S₂₈, S₃₃, and S₃₄. The matrix I = [1 1 1 1 1 1 1 1 1 1 0 −1 −1 −1 −1 −1 −1 −1 0 0 −1 −1 −1 1 −1 −1].

The improved matrix calculation is carried out to obtain the matrix L = [0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1]. Non-T-connected sections l₁₁ = 1 and l₂₈ = 1 illustrate that the two sections are fault sections. For the T-connected section l₉ = 1, search for the other fault sections; otherwise, it is judged as a non-fault section. The fault section location result is L₁₁ and L₂₈. I* = [1 1 1 1 1 1 1 1 1 1 0 −1 −1 −1 −1 −1 −1 −1 1 1 −1 −1 −1 1 −1 −1]. Because I* ≠ I, the positioning result is wrong. The suspicious fault sections are: L₄, L₈, L₉, L₁₀, L₁₁, L₁₂, L₁₃, L₁₇, L₂₀, L₂₂, L₂₄, and L₂₈. According to the operation rules of the GTA, the optimization process is shown in Figure 9.

According to the calculation, the fault sections are L₉, L₁₁, and L₂₈, and the fitness function value is 3. Multiple simulation experiments are carried out on multiple faults with T-connected sections. The results in

Table 10. The results of multiple faults with T-connected section simulation experiments.

Fault Sections	Improved Matrix Calculation	Verification Result	Suspicious Fault Sections	Genetic Tabu Algorithm	Correct or Not
L4, L6	L6	unsuccess	L4, L6, L7, L9, L13, L15, L16, L17, L20, L22, L24	L4, L6	correct
L9, L30	L9, L30	success	——	——	correct
L8, L17, L26	L8, L26	unsuccess	L4, L8, L9, L13, L15, L16, L17, L22, L24, L25, L26, L27	L8, L17, L26	correct
L13, L18, L28	L13, L18, L28	success	——	——	correct
L13, L14, L22, L29	L14, L22, L29	unsuccess	L4, L8, L9, L13, L14, L17, L22, L23, L29, L32	L13, L14, L22, L29	correct
L5, L18, L20, L24	L5, L18, L20	unsuccess	L5, L9, L13, L18, L19, L20, L22, L24, L28	L5, L18, L20, L24	correct

show that GTA can accurately locate multiple faults with T-connected sections.

5.4. Test Case 4: Fault Information Error Condition

Multiple faults with fault information errors are simulated in the active distribution network shown in Figure 7. Suppose that L₉ and L₁₈ are faulty, and the fault information I₄ is wrong to change from 1 to 0 and I₂₄ from −1 to 1. Attain the protection e₄ and e₈ action information. The boundary nodes are S₁, S₁₈, S₃₃, and S₃₄. The matrix I = [1 1 1 0 1 1 1 1 −1 −1 −1 −1 1 −1 −1 −1 −1 1 −1 −1 −1 −1 −1]. Obtain the matrix L = [0 0 1 −1 0 0 0 2 0 0 0 −1 1 0 1 0 −2 2 0 0 0]. l₉ = 2, l₂₄ = 2, and non-T-connected sections l₃ = 1 and l₁₈ = 1 illustrate that the four sections are faulty; where T-connected section l₂₀ = 1, search for other fault sections, otherwise it is judged as a non-fault section. The fault location result is L₃, L₉, L₁₈, and L₂₄. The matrix I* = [1 1 1 −1 −1 −1 −1 −1 −1 −1 −1 −1 1 −1 −1 0 1 1 0 0 0 −1 −1]. Because I* ≠ I, the positioning result is wrong. The suspicious fault sections are L₃, L₈, L₉, L₁₃, L₁₈, L₂₀, and L₂₄.

The optimization process is shown in Figure 10. According to the calculation, the fault sections are L₉ and L₁₈, the fitness function value is 4, and the error fault information values I₄ and I₂₄ are detected. Multiple simulation experiments are carried out on faults with fault information errors. The results in

Table 11. Multiple faults with fault information error simulation experiments.

Fault Sections	Error Fault Information	Suspicious Fault Sections	Genetic Tabu Algorithm	Fitness Function	Correct or Not
L8	I16: −1→1	L4, L8, L9, L13, L16, L17, L20, L22, L24	L8	2	correct
L20	e4: 0→1	L4, L8, L9, L13, L17, L20, L22, L24	L20	2	correct
L10, L16	I4: 1→0, I24: −1→0	L3, L10, L11, L12, L13, L15, L16, L17, L20, L24	L10, L16	4	correct
L17, L28	e7: 1→0, I8: 1→−1 I18: 0→1	L4, L7, L9, L13, L17, L18, L20, L22, L24, L28	L17, L28	5	correct
L3, L14, L24	I8: −1→1, I17: −1→1 I22: 1→0	L1, L2, L3, L4, L8, L9, L14, L17, L20, L24, L28	L3, L14, L24	6	correct
L9, L18, L30	I11: 0→1, I18: 1→0 e15: 1→0	L4, L8, L9, L11, L13, L17, L18, L20, L24, L29, L30, L31	L9, L18, L30	6	correct

show that the GTA has high tolerance performance.

In summary, the proposed algorithm can accurately locate various fault conditions. The algorithm proposed in this paper fully combines the advantages of the fast calculation speed of the improved matrix algorithm and the high tolerance performance of the GTA. The improved matrix algorithm is used to reduce the dimension of the optimization of the GTA, and the GTA is used to solve the problem that the improved matrix algorithm cannot accurately locate multiple faults with T-connected sections and faults with fault information errors. The simulation results show that the positioning algorithm can correctly locate the fault section in complex fault conditions with higher accuracy and solve the problem of fault information errors with better tolerance performance. The accuracy, tolerance performance, and rapidity of the location algorithm will be further verified by a large number of comparative experiments in the next section.

5.5. Algorithm Comparison

The four algorithms of the immune algorithm (IA), improved quantum genetic algorithm (IQGA), improved genetic algorithm (IGA), and GTA are compared and analyzed from four aspects: algorithm complexity, average positioning accuracy, average convergence algebra, and average execution time, to test the performance of the GTA.

The calculation complexity of the four algorithms is analyzed. Since this paper uses the fault region location and the improved matrix algorithm to perform two dimensionality-reduction operations, the fault hypothesis contains up to 2¹⁵ cases or about thirty-thousand cases when performing the GTA. When assuming IA, IQGA, and IGA, calculations are performed in the smallest range of fault regions, and the fault hypothesis contains at least 2²² or about four million cases. Moreover, the computational gap between the algorithms increases exponentially with the expansion of the active distribution network model. Therefore, from the perspective of calculation, the GTA is the simplest.

The conditions of single faults, multiple faults, and faults with fault information errors are simulated. The results of the algorithms are shown in

Table 12. Comparison of results of algorithms for single fault location.

Algorithm	Computational Complexity	Average Convergence Algebra	Average Positioning Accuracy/%	Average Execution Time/s
IA	222	74	70.3	3.747
IQGA	222	28	93.5	2.485
IGA	222	42	56.5	2.953
GTA	215	20	99.1	1.666

,

Table 13. Comparison of results of algorithms for multiple fault location.

Algorithm	Computational Complexity	Average Convergence Algebra	Average Positioning Accuracy/%	Average Execution Time/s
IA	222	79	68.2	3.809
IQGA	222	33	91.8	2.358
IGA	222	43	55.7	2.986
GTA	215	20	96.3	1.689

and

Table 14. Comparison of results of algorithms for faults with fault information error location.

Algorithm	Computational Complexity	Average Convergence Algebra	Average Positioning Accuracy/%	Average Execution Time/s
IA	222	87	68.1	3.822
IQGA	222	25	90.3	2.668
IGA	222	58	53.3	3.102
GTA	215	20	94.2	1.783

.

The average positioning accuracy of the GTA is the highest, and it can still be maintained above 94% in the most complex fault conditions. Under the cooperation of the GA and the TA, the GTA has a fast convergence speed and strong search ability. The GTA can iterate to the optimal value within 20 generations, and the average execution time is kept within 2 s. IQGA converges to the optimal solution of about 25 generations in the case of simple faults and about 35 generations in the case of complex faults, and the convergence speed is significantly slower. IQGA has good accuracy and execution time.

Since the antibody and antigen in IA are encoded as binary codes, the intimacy calculation between each qubit in each population generation should be realized, which seriously affects the convergence speed. The simulation results show that the IA has slow convergence speed, low positioning accuracy, and long execution time. The iterative results of IGA are random, the iterative process is unstable, and it may not converge to the optimal value correctly. The positioning accuracy is the lowest, and the convergence speed is slow. In summary, compared with other algorithms, the GTA has simpler calculation, higher location accuracy, faster convergence speed, and shorter execution time, which is more suitable for fault section location of active distribution networks.

6. Conclusions

A fault section location algorithm combining the improved matrix algorithm and the GTA is proposed. The algorithm uses protection action and equipment status information, and can locate fault sections more efficiently. Firstly, considering the frequent changes in the topology of the active distribution network, a method for constructing the node status list is proposed. According to the idea of depth-first traversal in the tree search method, a topology search method for suspicious fault regions is proposed. The fault regions are obtained by combining the protection action regions to ensure they contain all possible fault sections. This algorithm can streamline the fault system and reduce the matrix calculation dimension.

Secondly, an improved matrix algorithm is proposed to adapt to the access of DG, which is computed in a non-square matrix form. It can accurately locate single faults and multiple faults in non-T-connected sections. However, due to the limitations of the matrix calculation, the algorithm cannot accurately determine whether the T-connected sections of l_i = 1 and l_i = 0 are faulty in multiple faults. Therefore, based on the traditional matrix algorithm and superposition principle, this section proposes a verification method to improve tolerance performance. The GTA locates the fault sections when the verification is incorrect. Taking advantage of the fast calculation speed of the matrix can reduce the dimension of GTA optimization.

Thirdly, the GTA is proposed to solve the problems that the improved matrix algorithm cannot accurately locate the multiple faults with T-connected sections and faults with fault information errors. A fault hypothesis based on equipment status and protection action information is proposed; a fitness function is constructed to reflect the difference between the actual and expected status of the fault information; the calculation equation of the expected status of the fault information is derived; the genetic coding rules, natural selection rules, greedy algorithm, and parameter selection are introduced. The GTA is used to find the fault hypothesis that reasonably explains received fault information, and the fault section location results are obtained. By comparing the optimization results with the fault information obtained by monitoring, error fault information can be obtained, which is convenient for the staff to maintain.

Finally, the proposed algorithm is simulated in various fault conditions in the IEEE-34 node active distribution network. According to the experimental results, the proposed algorithm can accurately locate single faults, multiple faults, and faults with fault information errors. According to the comparative simulation results of the proposed algorithm and the other three intelligent optimization algorithms, the proposed algorithm has the highest average positioning accuracy, faster convergence speed, shorter execution time, and simpler calculation, which is more suitable for fault section location of active distribution networks. The next step will focus on determining the specific branch of the T-connected section fault and the accurate fault location.