A Study on the Movement Characteristics of Fuel in the Fuel Tank during the Maneuvering Process
Abstract
1. Introduction
2. Research Object and Numerical Method
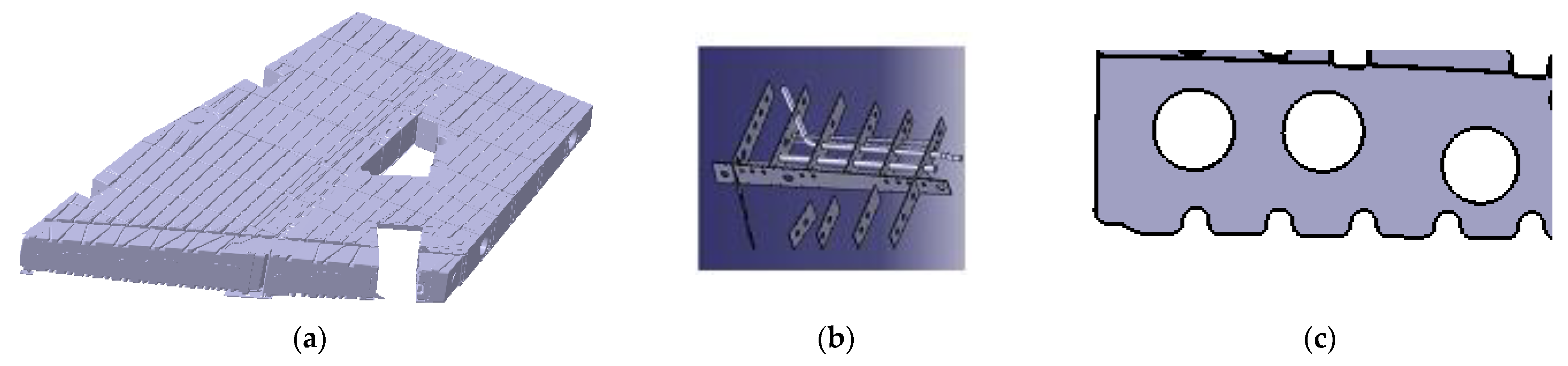
2.1. Research Object
2.2. Numerical Calculation Method and Validation
2.3. Boundary Conditions
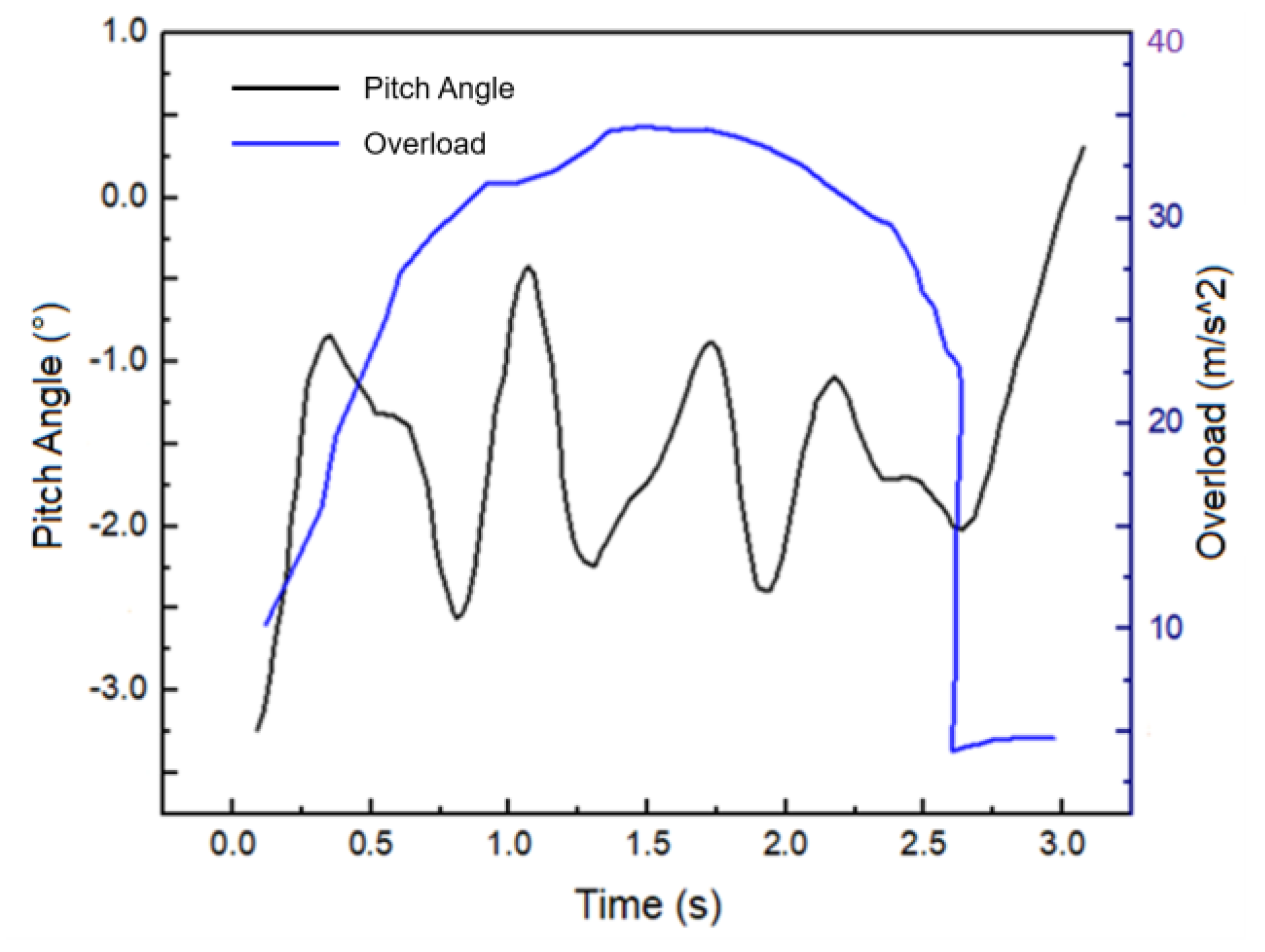
2.4. External Excitation
3. Results and Analysis
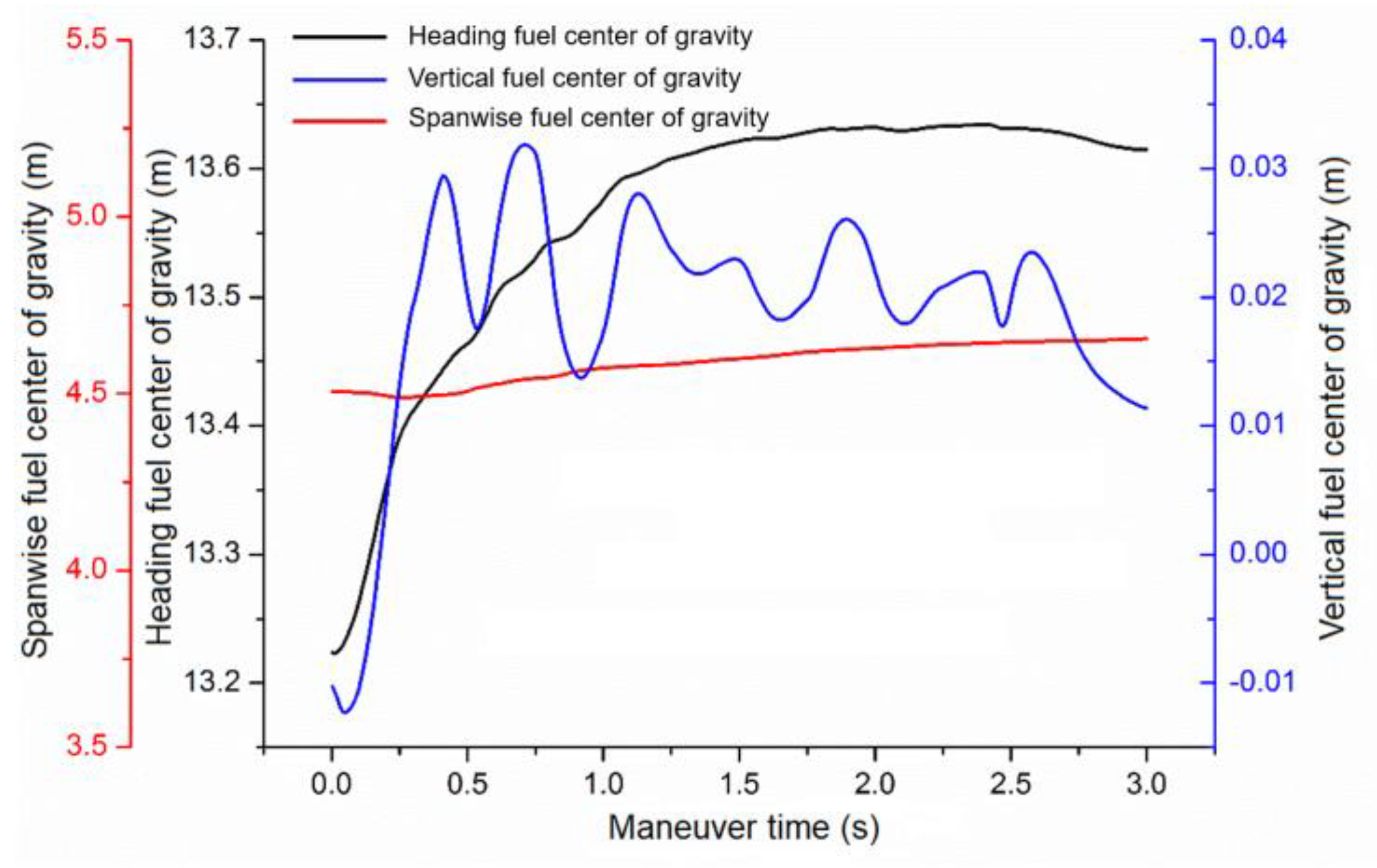
3.1. Fuel Center of Gravity Variation
3.2. Free Liquid Level Analysis
3.3. Analysis of Fuel Impact Force
3.4. Analysis of Fuel Velocity Field Characteristics
4. Conclusions
- (1)
- Compared to other studies related to the free surface of fluids, the object of this paper is not an idealized and simplified model, but an aircraft wing fuel tank model that encompasses all structural elements. The fuel tank structure considered here includes not only the surrounding walls but also internal transverse frames, longitudinal walls, and flow holes. These structures are carefully designed according to the fuel tank design standards. The presented results reflect the comprehensive damping effect of the fuel tank structure on fuel motion, thereby providing a more realistic representation of the fuel’s movement characteristics during aircraft maneuvering.
- (2)
- Compared with our previous work [22], the flow characteristics of fuel in a flat tank are different from those of an approximate cube tank, and the size and shape of the movement space of the fuel have a significant influence on the movement of the free liquid level.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zienkiewicz, O.C.; Taylor, R.L.; Nithiarasu, P. The Finite Element Method for Fluid Dynamics, 7th ed.; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Moukalled, F.; Mangani, L.; Darwish, M. The Finite Volume Method in Computational Fluid Dynamics: An Advanced Introduction with OpenFOAM and matlab. In Fluid Mechanics and Its Applications, 1st ed.; Springer: New York, NY, USA, 2015; Volume 113. [Google Scholar]
- Cruchaga, M.; Battaglia, L.; Storti, M.; D’Elia, J. Numerical modeling and experimental validation of free surface flow problems, Arch. Comput. Methods Eng. 2016, 23, 139–169. [Google Scholar] [CrossRef]
- Eswaran, M.; Saha, U.; Maity, D. Effect of baffles on a partially filled cubic tank: Numerical simulation and experimental validation. Comput. Struct. 2009, 87, 198–205. [Google Scholar] [CrossRef]
- Yuan, C.; Wang, P.; Jin, X. Dynamic analysis of flexible container under wind actions by ALE finite-element method. J. Wind Eng. Ind. Aerod. 2010, 98, 881–887. [Google Scholar] [CrossRef]
- Akyildiz, H.; Unal, N.E. Sloshing in a three-dimensional rectangular tank: Numerical simulation and experimental validation. Ocean Eng. 2006, 33, 2135–2149. [Google Scholar] [CrossRef]
- Akyildiz, H.; Unal, E. Experimental investigation of pressure distribution on a rectangular tank due to the liquid sloshing. Ocean Eng. 2005, 32, 1503–1516. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to testing of the fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to no-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–398. [Google Scholar] [CrossRef]
- Yang, X.F.; Peng, S.L.; Liu, M.B. A new kernel function for SPH with applications to free surface flows. Appl. Math. Model. 2014, 38, 3822–3833. [Google Scholar] [CrossRef]
- Feng, D.L.; Liu, M.B.; Li, H.Q.; Liu, G.R. Smoothed particle hydrodynamics modeling of linear shaped charge with jet formation and penetration effects. Comput. Fluids 2013, 86, 77–85. [Google Scholar] [CrossRef]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Colagrossi, A.; Antuono, M.; Le Touzé, D. Theoretical considerations on the free-surface role in the smoothed-particle-hydrodynamics model. Phys. Rev. E 2009, 79, 056701. [Google Scholar] [CrossRef] [PubMed]
- Celebi, M.S.; Akyildiz, H. Nonlinear modeling of liquid sloshing in a moving rectangular tank. Ocean Eng. 2002, 29, 1527–1553. [Google Scholar] [CrossRef]
- Liu, M.-B.; Zong, Z.; Chang, J.-Z. Developments and applications of smoothed particle hydrodynamics. Adv. Mech. 2011, 41, 217–234. [Google Scholar]
- Onate, E.; Idelsohn, S.; Zienkiewicz, O.; Taylor, R. A finite point method in computational mechanics: Applications to convective transport and fluid flow. Int. J. Numer. Methods Eng. 1996, 39, 3839–3866. [Google Scholar] [CrossRef]
- Wang, L.; Xie, H.; Zhang, L. Analysis of fuel sloshing in UAV launching process. Aeronaut. Sci. Technol. 2016, 27, 36–40. (In Chinese) [Google Scholar]
- Yang, S.L.; Chen, X.F.; Du, F.X. Coupling Dynamics Analysis of Aircraft Fuel Tank Sloshing Fluid and Solid under Maneuvering Behavior. J. Aeronaut. 2019, 40, 13. [Google Scholar]
- Yang, R. Research of Fuel Sloshing in Aircraft Integral Tanks by the ALE Finite Element Method. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2016. (In Chinese). [Google Scholar]
- Yuan, X.F. Research of Fuel Sloshing in Aircraft Wing Tank Based on VOF Method and Sloshing Suppression. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2016. (In Chinese). [Google Scholar]
- Liu, G.; Lin, Y.; Guan, G. Experimental study of sloshing pattern on LNG independent C type tank. J. Dalian Univ. Technol. 2017, 57, 467–475. (In Chinese) [Google Scholar]
- Li, Z.H.; Wang, Y.M.; Liu, J.; Tong, X.L.; Zhao, Y. Characteristics of Fuel Flowing and Sloshing in Crossing Multi-compartments Tank. Acta Aeronaut. Astronaut. Sin. 2021, 42, 525818. (In Chinese) [Google Scholar]

| Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| X(m) | 12.6 | 13.3 | 12.8 | 12.5 | 12.8 | 12.5 | 13.1 | 13.2 |
| Y(m) | 3.7 | 4.8 | 4.8 | 4.3 | 4.0 | 3.8 | 3.6 | 3.9 |
| Z(m) | 0.1 | 0.08 | 0.08 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Sensor | Characteristics |
|---|---|
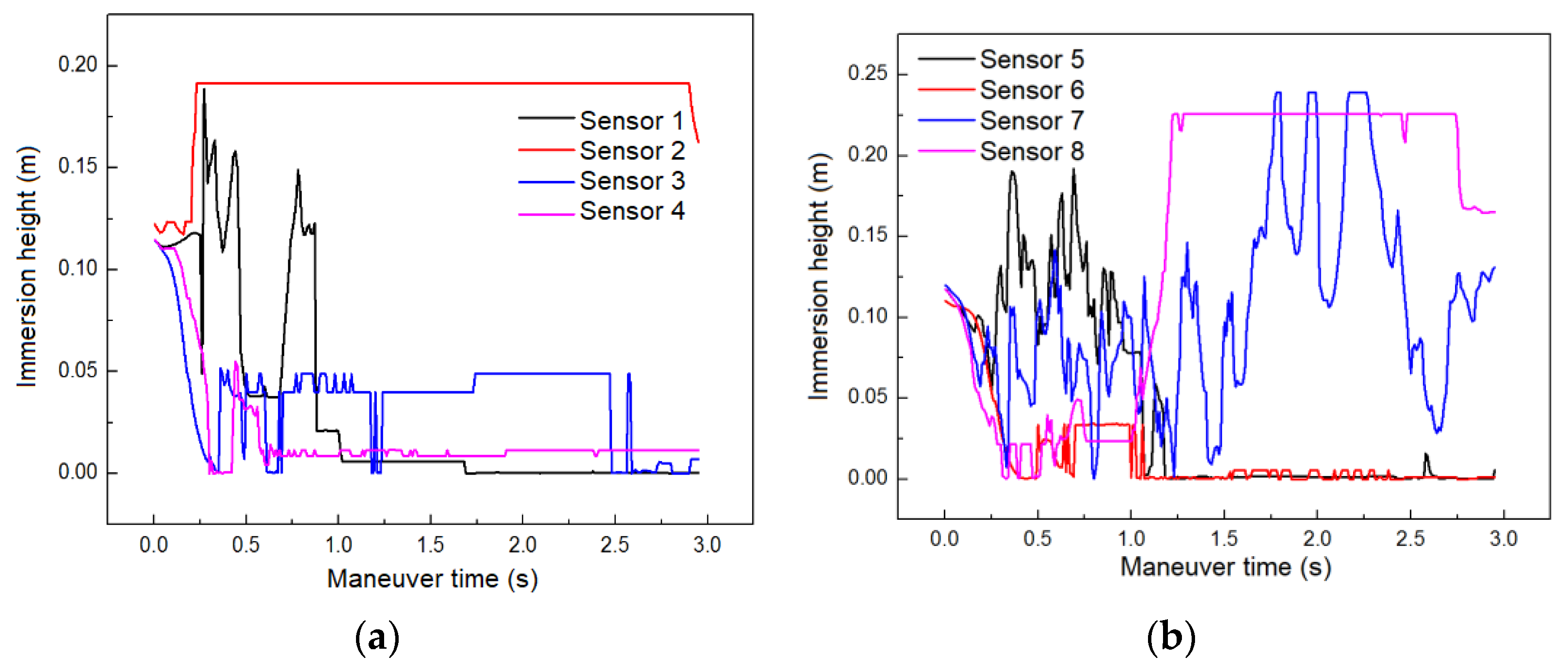
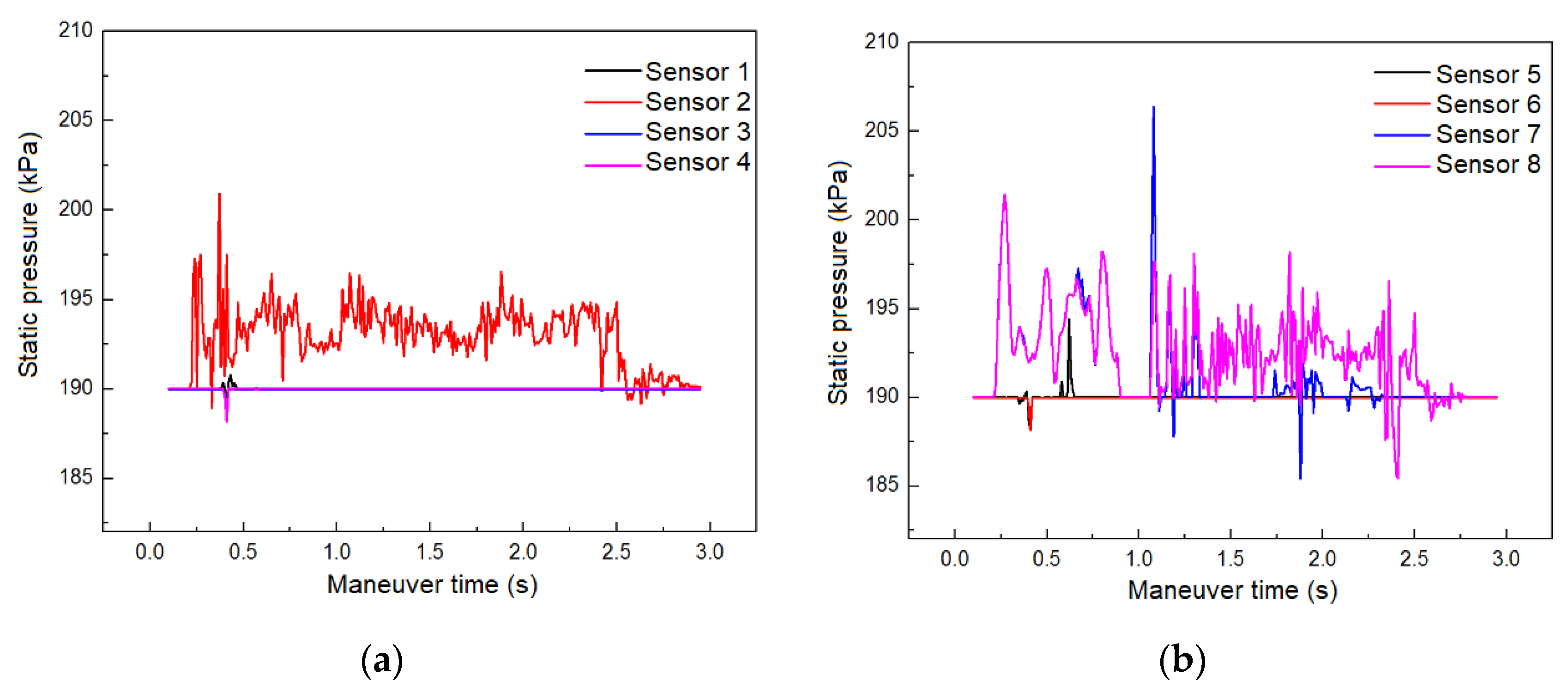
| Sensor 1 | The immersion height of Sensor 1 fluctuates in a “double-peak” pattern, and eventually approaches zero, indicating that there is no fuel present at this location in the later stage of the maneuver |
| Sensor 2 | Within the first 0.3 s of the maneuver, the immersion height of Sensor 2 rapidly increases to its maximum position, and then remains at a stable high level, indicating that the fuel at this location occupies the entire region between the bottom and top of the tank |
| Sensors 3, 4, and 6 | The immersion heights of Sensors 3, 4, and 6 are mostly below 0.05 m, indicating that there is little or no fuel at these three measurement locations during the maneuver. |
| Sensor 5 | The trend of the immersion height of Sensor 5 is similar to that of Sensor 1. |
| Sensor 7 | The free liquid level at this location has rapidly and complexly changing characteristics. Within the first 1.5 s of the maneuver, the free liquid level oscillates through approximately six peaks/valleys with an average height of 0.07 m. In the latter 1.5 s of the maneuver, the liquid level gradually decreases after experiencing three high-level oscillations of peaks/valleys, with the liquid level reaching a maximum of 0.23 m and a minimum of 0.02 m during the oscillation process. |
| Sensor 8 | The immersion height of Sensor 8 remains below 0.05 m in the early stage of the maneuver, and rapidly increases to and stabilizes at 0.22 m at t = 1.1 s, indicating that this location has been rapidly filled with fuel. |
| Time | Fuel Motion Characteristics |
|---|---|
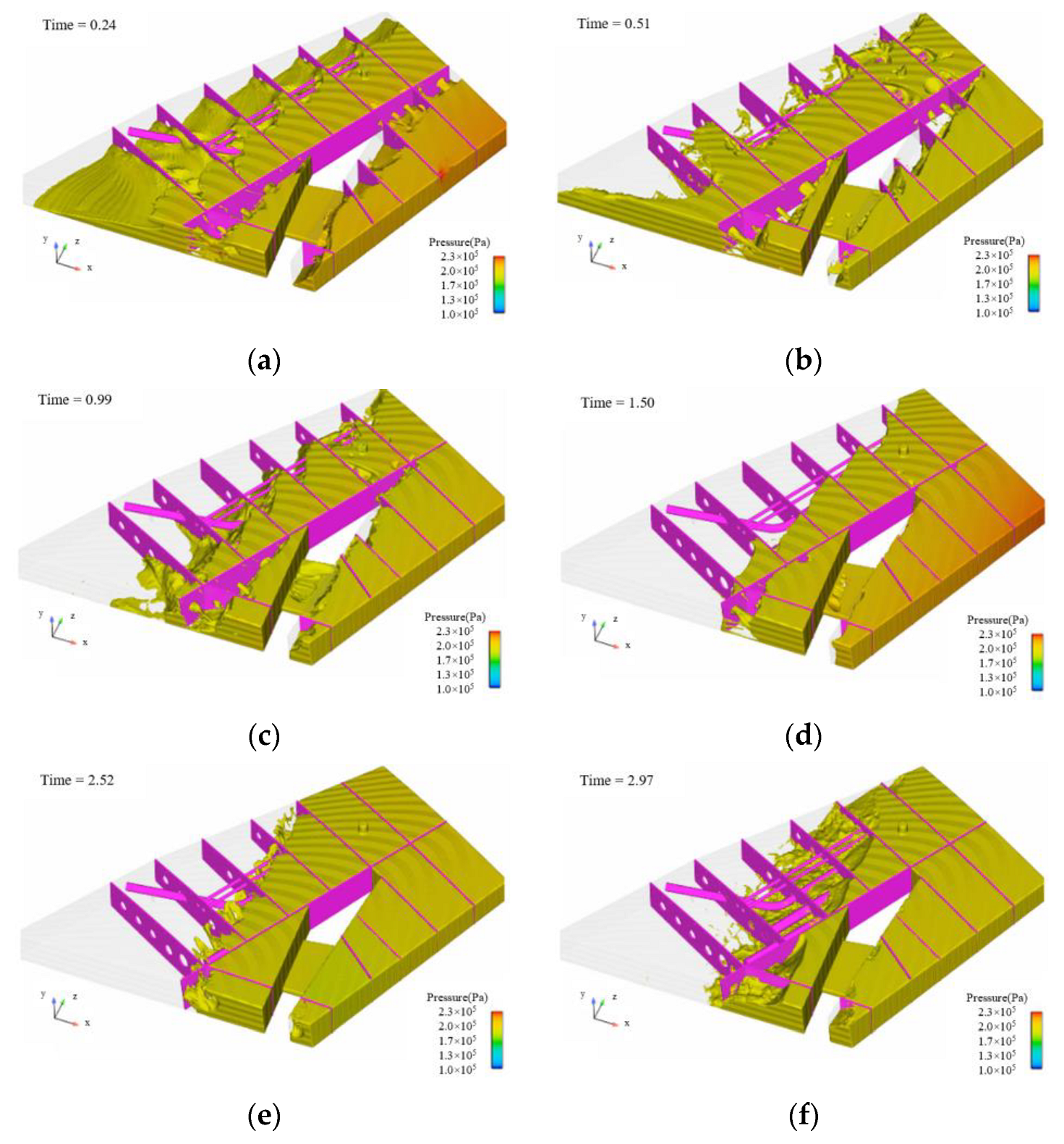
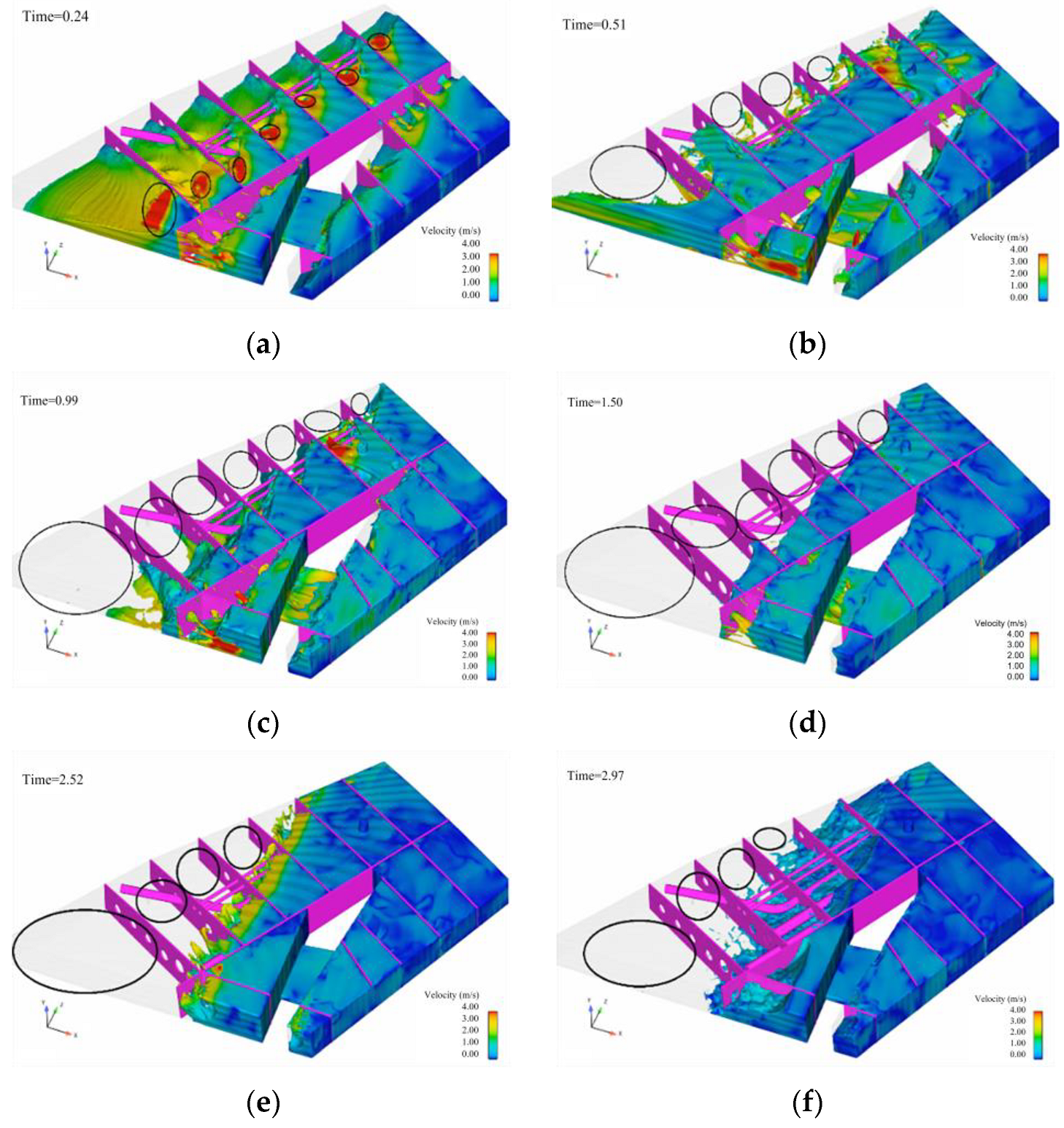
| t = 0.24 s | The fuel surface is shaking and tilting towards one side. |
| t = 0.51 s | The free surface phenomenon becomes more complex, with significant surface fragmentation; the fuel at the circular marker inside the compartment moves backward and fills the tail, forming an fuel-free zone. |
| t = 0.99 s | The fuel-free zone expands, and almost all the fuel in the front moves backward. |
| t ≥ 1.5 s | The fuel free surface exhibits significant fragmentation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Ruan, C.; Lu, S.; Li, Z. A Study on the Movement Characteristics of Fuel in the Fuel Tank during the Maneuvering Process. Appl. Sci. 2023, 13, 8636. https://doi.org/10.3390/app13158636
Wang Y, Ruan C, Lu S, Li Z. A Study on the Movement Characteristics of Fuel in the Fuel Tank during the Maneuvering Process. Applied Sciences. 2023; 13(15):8636. https://doi.org/10.3390/app13158636
Chicago/Turabian StyleWang, Yameng, Chenran Ruan, Song Lu, and Zhenghong Li. 2023. "A Study on the Movement Characteristics of Fuel in the Fuel Tank during the Maneuvering Process" Applied Sciences 13, no. 15: 8636. https://doi.org/10.3390/app13158636
APA StyleWang, Y., Ruan, C., Lu, S., & Li, Z. (2023). A Study on the Movement Characteristics of Fuel in the Fuel Tank during the Maneuvering Process. Applied Sciences, 13(15), 8636. https://doi.org/10.3390/app13158636








