Features of the Application of Coherent Noise Suppression Methods in the Digital Holography of Particles

Abstract

The paper studies the influence of coherent noises on the quality of images of particles reconstructed from digital holograms. Standard indicators (for example, signal-to-noise ratio) and such indicators as the boundary contrast and boundary intensity jump previously proposed by the authors are used to quantify the image quality. With the use of these parameters, for examples of some known methods of suppressing coherent noises in a holographic image (eliminating the mutual influence of virtual and real images in in-line holography, and time averaging), the features and ranges of applicability of such correction were determined. It was shown that the use of the complex field amplitude reconstruction method based on the Gerchberg–Saxton algorithm and the spatial-frequency method improves the quality of determining the particle image boundary (by boundary intensity jump) starting from the distance between a hologram and a particle, which is about twice the Rayleigh distance. In physical experiments with model particles, averaging methods were studied to suppress non-stationary coherent noises (speckles). It was also shown that averaging over three digital holograms or over three holographic images is sufficient to provide a quality of particle image boundary suitable for particle recognition. In the case of multiple scattering, when it is necessary to impose a limit on the working volume length (depth of scene) of the holographic camera, the paper provides estimates that allow selecting the optimal working volume length. The estimates were made using the example of a submersible digital holographic camera for plankton studies.

1. Introduction

Digital optical holography of particles [1,2,3] is one of the methods for the noninvasive study of particles of different origins in different media. The principle of holographic recording makes it possible to register information on all particles of the studied medium volume per exposure and further analyze their reconstructed holographic images. An in-line holographic scheme is typically used to study particles when the radiation scattered on the particles represents a subject wave and the radiation that passed without scattering is a reference wave. A hologram is an interference pattern of these waves recorded on any carrier (photoemulsion, charge-coupled device (CCD), or complementary metal-oxide semiconductor (CMOS) matrix). The interference pattern for registration must be stable during exposure, which is ensured by a short pulse of coherent radiation.

At the same time, this may cause undesirable effects associated with the coherence of radiation—coherent noises in the reconstructed image related to the parameters of the medium with the analyzed particles, as well as to the twin-image effect of the studied particle [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]. The latter appears due to the fact that the reconstruction of a real particle image from a hologram by illuminating it with a coherent wave (or numerical modeling of lighting in digital holography) leads to the simultaneous reconstruction of the virtual image of this particle. The interference of waves corresponding to these images deteriorates the quality of the reconstructed image and reduces the accuracy of its focusing and classification. There are special difficulties in studying particle images when this effect is observed for several closely spaced particles.

Two known methods of suppressing the twin-image effect are considered as examples in the article: a complex field amplitude reconstruction method based on the Gerchberg–Saxton algorithm and a spatial-frequency method having a different physical and algorithmic basis. The main task of the study of these methods is to determine whether the boundary conditions for their use depend on their physical basis or, to a greater extent, are determined by the features of the quality indicators of the particle holographic image. This implies the use of the previously proposed quantitative indicators of the quality of particle images (boundary contrast and boundary intensity jump), which are compared and applied in the article along with other existing methods (mean square error (MSE), signal-to-noise ratio (SNR) or peak signal-to-noise ratio (PSNR), dispersion of image intensity, distinctive ability).

Another source of coherent noise is the cross-interference of waves scattered on particles and the turbulence of the medium. This noise also reduces the quality of particle images and makes it difficult to recognize them.

Here, to reduce this noise, a well-known method—averaging—is also considered. The paper also studies whether the number of averages required to achieve the quality of images of particles reconstructed from a hologram sufficient for their recognition by the distinguishability parameter depends on the averaging method. The averaging method means the averaging of holograms, the averaging of reconstructed holographic images, the multispectral recording of a hologram, or multispectral image reconstruction.

This paper considers some practical issues related to the use of well-known methods for suppressing the above-mentioned coherent noises, their efficiency, and their limits of applicability. There may be no conditions or possibilities for complete suppression in a real holographic experiment.

For example, for non-stationary noise and non-stationary objects, as well as for strong noise characterized by multiple scattering, which may occur in natural experiments due to turbidity or turbulence of the medium, under conditions of in-line holography, there is no opportunity to form a sufficient sample (number of averages); therefore, the article studies the question of determining the permissible depth of the scene.

The experimental results were obtained both in laboratory conditions with model particles and in real media when plankton were studied with the use of a submersible digital holographic camera (DHC—digital holographic camera) [22]. The obtained results, estimates, and conditions are applicable to the holography of particles of any nature and in any media (gas, liquid, and solid). They are used in this study for the DHC technology designed for the holographic study of plankton and other marine particles [22].

2. Methods and Equipment

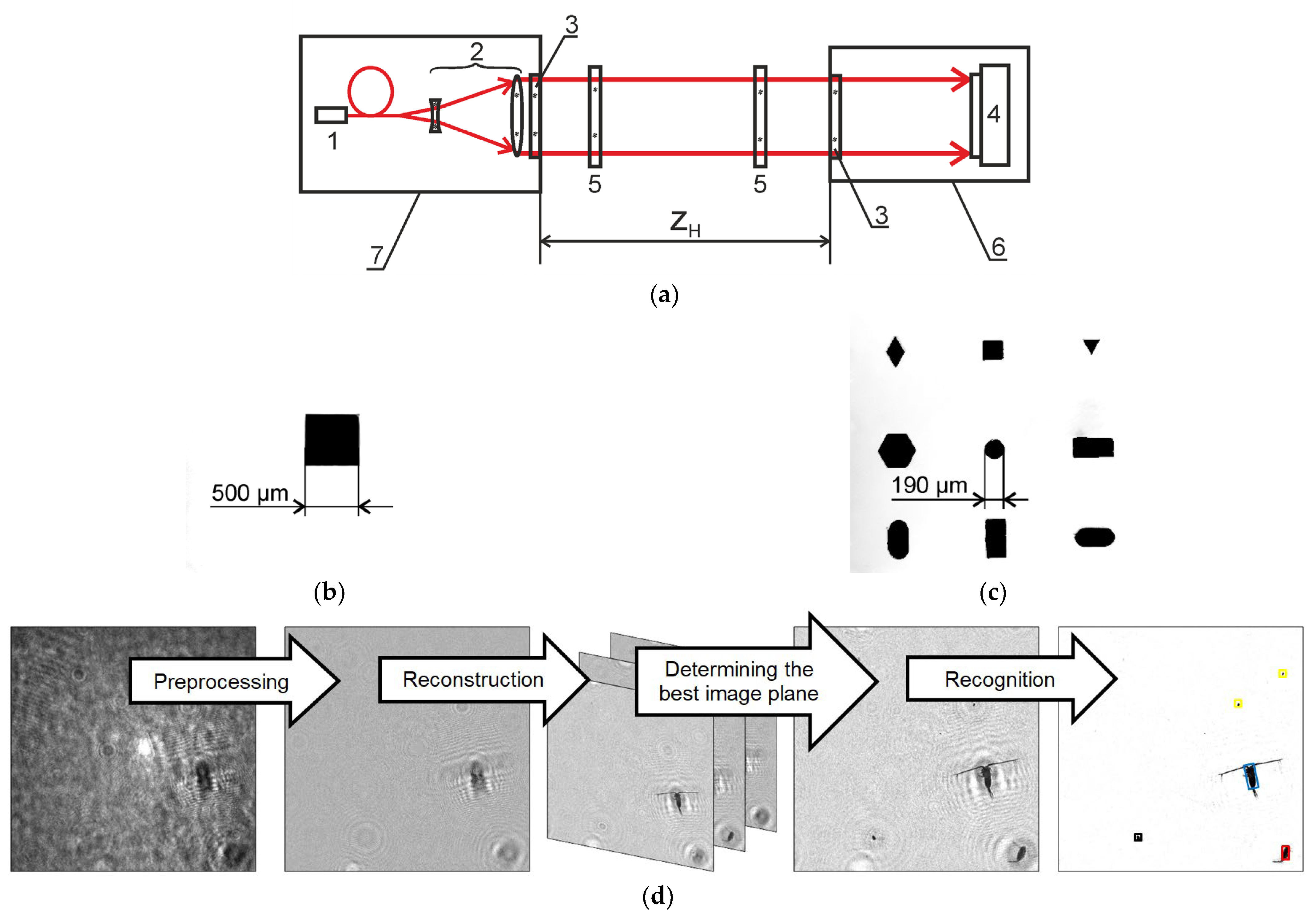
2.1. Digital Holographic Camera

DHC is designed to measure dispersed particles using the principles of digital holography according to the in-line scheme [22,23] (Gabor scheme); Figure 1. Note that this scheme does not impose high requirements for the coherence of radiation during hologram recording, since the path difference between the object wave (radiation scattered on particles) and the reference wave (radiation passed without scattering) is quite small. Therefore, we use a laser diode as a source of radiation. The DHC registers a digital hologram of the entire volume of the medium with studied particles per exposure (laser diode pulse). The particle images are reconstructed numerically from a preprocessed digital hologram by calculating the diffraction integral [1,2,3], and further processing of holographic images [23,24], including determining the best image plane of the particle, allows detecting the spatial distribution of particles (three-dimensional coordinates of each particle), size, shape, speed, and direction of movement of each particle, and ensuring their recognition [24,25] (Figure 1d). In other words, the DHC technology, which is digital hologram recording, reconstruction of particle images from it, and processing of holographic images, makes it possible to create a virtual 3D image of the volume with test particles.

Model particles are used for physical modeling in laboratory experiments and for calibration in field conditions. They represent opaque figures of regular shape (Figure 1b,c) placed by a photolithographic method on a 2.65 mm thick glass plate fixed in a metal frame (together we will call them the caliber, since in real experiments they are used to calibrate the DHC on magnification). The DHC design assumes that the calibers are placed in four positions [23], but for the purposes of this study, only two end positions were chosen—near the portholes (Figure 1a).

Figure 2 shows one of the modifications of the DHC with a folded in-line scheme using prisms to reduce the size of the DHC while maintaining the length of the studied volume (depth of scene). The length of the studied volume is the total distance between the surfaces of optical parts bordering water ((3) and (6)). The length of the test volume and thus the volume itself are changed by replacing the calibrated control rods (8). The design provides for the installation of four calibers (7) on the path of a laser beam in the working volume to perform calibration at magnification. The main parts of the DHC are the illuminating (9) and recording (10) modules connected by a synchronization line, located in two strong deep-sea cases with portholes (3) and connectors. The lighting module is designed to position a laser (1) and an optical system to form the optical radiation beam (2). The recording module includes an optical system to receive optical radiation (5), as well as a CMOS camera (4) and a control system for operating modes (synchronization). The modules are optically connected via the mirror-prism system (6) that provides registration information about up to 0.75 l of the studied volume (marked red) per exposure.

2.2. Holographic Particle Image Quality Indicators

To assess the influence of distortions considered in this study (non-stationary coherent noises and the twin-image effect) on the image quality of a particle reconstructed from a digital hologram, it is necessary to use quantitative indicators of the particle image quality. The most common parameters used for this are MSE [26], SNR or PSNR [27], and image intensity dispersion σ [28]. These parameters are applicable when the reference image is used, and in this case, they allow comparing the noisy test image with the reference image (without noise).

In a holographic study of real particles under natural conditions, for example, plankton and other marine particles, it is impossible to compare the reconstructed image with the reference image. Moreover, the accurate determination of the size and shape of the particle based on its holographic image [24,25], as well as its recognition, require a clear definition of the image boundary, which, in turn, requires accurate digital focusing, i.e., to determine the value z at which the image is of the highest quality (sharp). To assess the digital focusing quality of reconstructed particle images, we will use the quality indicators of the particle image reconstructed from the digital hologram—boundary contrast K and boundary intensity jump P at the boundary of the particle image [29]. For this purpose, let us define areas with much smaller width than the particle size along the boundary of the reconstructed image of the particle from the external (background) and internal sides of the particle image. The boundary contrast and boundary intensity jump characterize the quality of boundary detection: $K=\frac{\langle I_{\mathrm{int}.}\rangle }{\langle I_{\mathrm{ext}.}\rangle }$—boundary contrast and $\mathsf{\Delta }I=\frac{\langle I_{\mathrm{int}.}\rangle -\langle I_{\mathrm{ext}.}\rangle }{I_{\mathrm{av}}}$—boundary intensity jump, where $\langle I_{\mathrm{int}.}\rangle =\frac{{{\displaystyle \sum }}_{i=1}^n{I}_i}{n}$—average intensity of the internal area; $\langle I_{\mathrm{ext}.}\rangle =\frac{{{\displaystyle \sum }}_{i=1}^m{I}_i}{m}$—average intensity of the external area; $I_i$—intensity of i pixel; n, m—number of pixels of the internal and external areas, respectively; and $I_{\mathrm{av}}$—average image intensity.

To assess the possibility of recognizing the shape of a particle (for flat model particles with known parameters), the study uses the distinctive ability ${\delta }_s=\frac{\left| s_{im}-s\right|}{s}$ over the area and ${\delta }_l=\frac{\left| l_{im}-l\right|}{l}$ over the length of the boundary, where $l_{im}$—length of the boundary of the particle holographic image, $s_{im}$—area of the particle holographic image, $l$—length of the boundary of the model particle itself, and $s$—its area [23]. We will use the distinctive ability indicators in laboratory experiments with flat model particles with known geometric parameters.

3. Methods for Suppressing the Twin-Image Effect

Let us consider the in-line scheme (Figure 3) to record a hologram of a certain particle that is illuminated by a flat wave with unit amplitude for simplicity. The amplitude transmission in a particle plane $\left({\mathrm{x}}_0,{\mathrm{y}}_0\right)$:

$$\mathrm{T}\left({\mathrm{x}}_0,{\mathrm{y}}_0\right)=1-\mathrm{a}\left({\mathrm{x}}_0,{\mathrm{y}}_0\right),$$

(1)

where $\mathrm{a}\left({\mathrm{x}}_0,{\mathrm{y}}_0\right)$—function describing a particle (amplitude absorption of a particle) [2]. Note that the amplitude transmission $1-\mathrm{a}\left({\mathrm{x}}_0,{\mathrm{y}}_0\right)$ under illumination with a flat wave with unit amplitude up to a constant is equal to the complex amplitude of the field in the plane $\left({\mathrm{x}}_0,{\mathrm{y}}_0\right)$ directly behind the particle.

A CCD or CMOS camera is placed in the interference region of the reference and object waves, in the recording plane of the digital hologram $\left({\mathrm{x}}_1,{\mathrm{y}}_1\right)$. The complex amplitude of the field in the recording plane $\left({\mathrm{x}}_1,{\mathrm{y}}_1\right)$ can be represented by a diffraction integral:

$$\begin{gathered} \mathrm{U}\left({\mathrm{x}}_1,{\mathrm{y}}_1,\mathrm{z}\right)=\underset{\infty }{\overset{\infty }{{\displaystyle \iint }}}\mathrm{T}\left({\mathrm{x}}_0,{\mathrm{y}}_0\right)\frac{\exp \left(\mathrm{ikz}\right)}{\mathrm{i}\mathsf{\lambda }\mathrm{z}}·\exp \left(\frac{\mathrm{ik}}{2\mathrm{z}}\left[{\left({\mathrm{x}}_1-{\mathrm{x}}_0\right)}^2+{\left({\mathrm{y}}_1-{\mathrm{y}}_0\right)}^2\right]\right){\mathrm{dx}}_0{\mathrm{dy}}_0 \\ =\exp \left(\mathrm{ikz}\right){{\displaystyle \iint }}_{\infty }^{\infty }\mathrm{T}\left({\mathrm{x}}_0,{\mathrm{y}}_0\right){\mathrm{h}}_{\mathrm{z}}\left({\mathrm{x}}_1-{\mathrm{x}}_0,{\mathrm{y}}_1-{\mathrm{y}}_0\right){\mathrm{dx}}_0{\mathrm{dy}}_0=\exp \left(\mathrm{ikz}\right)\left(\mathrm{T}\otimes {\mathrm{h}}_{\mathrm{z}}\left(\mathrm{x},\mathrm{y}\right)\right), \end{gathered}$$

(2)

where z—distance from the particle plane to the recording plane, $\mathrm{k}=\frac{2\mathsf{\pi }}{\mathsf{\lambda }}$—wave number, λ—wavelength of the illuminating radiation, ${\mathrm{h}}_{\mathrm{z}}\left(\mathrm{x},\mathrm{y}\right)=\frac{1}{\mathrm{i}\mathsf{\lambda }\mathrm{z}}·\exp \left(\frac{\mathrm{ik}}{2\mathrm{z}}\left({\mathrm{x}}^2+{\mathrm{y}}^2\right)\right)$—convolution kernel (Fresnel function), and ⊗ denotes the convolution itself.

The intensity distribution recorded by the CCD camera is ${\mathrm{I}}_{\mathrm{H}}\left({\mathrm{x}}_1,{\mathrm{y}}_1\right)=\mathrm{U}\left({\mathrm{x}}_1,{\mathrm{y}}_1,\mathrm{z}\right)·{\mathrm{U}}^{*}\left({\mathrm{x}}_1,{\mathrm{y}}_1,\mathrm{z}\right).$

A particle image is reconstructed numerically from a digital hologram using the diffraction integral:

$$\mathrm{U}\left({\mathrm{x}}_2,{\mathrm{y}}_2,\mathrm{z}\right)={{\displaystyle \iint }}_{\infty }^{\infty }\mathrm{t}\left({\mathrm{x}}_1,{\mathrm{y}}_1\right)\frac{\exp \left(\mathrm{ikz}\right)}{\mathrm{i}\mathsf{\lambda }\mathrm{z}}·\exp \left(\frac{\mathrm{ik}}{2\mathrm{z}}\left[{\left({\mathrm{x}}_2-{\mathrm{x}}_1\right)}^2+{\left({\mathrm{y}}_2-{\mathrm{y}}_1\right)}^2\right]\right){\mathrm{dx}}_1{\mathrm{dy}}_1.$$

(3)

Here, $\mathrm{t}\left({\mathrm{x}}_1,{\mathrm{y}}_1\right)$ is the amplitude transmission of a hologram, which, in the case of ideal hologram recording, is equal, up to a constant, to the recorded intensity ${\mathrm{I}}_{\mathrm{H}}\left({\mathrm{x}}_1,{\mathrm{y}}_1\right)$, and when the hologram is illuminated with a plane wave with unit amplitude, it equals, up to a constant, to the complex amplitude of the reconstructed wave immediately behind the hologram in the plane $\left({\mathrm{x}}_1,{\mathrm{y}}_1\right)$. In digital holography, the hologram illumination and image reconstruction are modeled numerically.

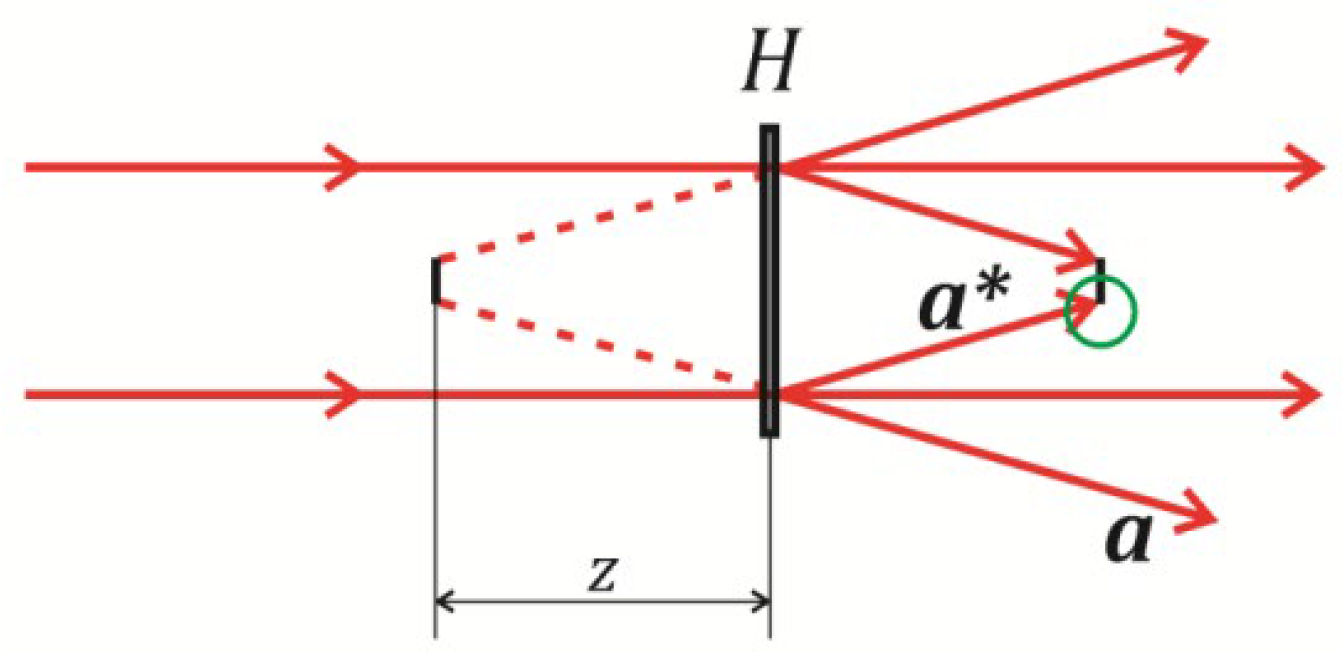
In both optical and digital holography, a reconstructed wave in a plane located at a distance z from the hologram represents an overlapping of two coherent waves (Figure 3): a wave that is a complex conjugate object wave and forms a real image of a particle, and a wave that propagates from a virtual image located at a distance 2z from the real image. The result of this interaction is a system of fringes overlapping a sharp image of a particle (Figure 4)—the so-called twin-image effect.

The influence of this effect on the visually determined image quality of the particle under certain conditions of the hologram recording is insignificant, but it may result in noticeable distortions in the intensity distribution near the particle image boundary (Figure 4a,b) and, thus, degrade the reliability of automatic recognition. This is especially noticeable in reconstructed images of one or more closely spaced adjacent particles (Figure 4c). In this case, it is necessary to apply one of the methods [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21] for suppressing the twin-image effect. This paper considers, as examples, a complex field amplitude reconstruction method based on the Gerchberg–Saxton algorithm [30] and a spatial-frequency method to identify the features, range of applicability, and efficiency of suppressing the twin-image effect.

3.1. Complex Field Amplitude Reconstruction Method Based on the Gerchberg–Saxton Algorithm

The complex field amplitude reconstruction method based on the Gerchberg–Saxton algorithm, which is the iterative calculation of the complex field amplitude (instead of the registered intensity distribution) in the recording plane of the digital hologram, has various implementations and is described in many studies, for example, [14,15,16,17]. This study considers the case when the intensity distributions ${\mathrm{I}}_1\left(\mathrm{x},\mathrm{y}\right)$ and ${\mathrm{I}}_2\left(\mathrm{x},\mathrm{y}\right)$ of two digital holograms are recorded at distances ${\mathrm{z}}_1$ and ${\mathrm{z}}_2$ from the particle (Figure 5) [15].

Prior to the iteration, it is assumed that the complex field amplitude in the plane of the first hologram ${\mathrm{U}}_1\left(\mathrm{x},\mathrm{y},{\mathrm{z}}_1\right)=\sqrt{{\mathrm{I}}_1\left(\mathrm{x},\mathrm{y}\right)}$, i.e., the phase of the complex field amplitude, equals 0.

At the first stage of the iteration algorithm, knowing the distribution ${\mathrm{U}}_1\left(\mathrm{x},\mathrm{y},{\mathrm{z}}_1\right)$ in the plane ${\mathrm{z}}_1$, the complex amplitude of the field ${\mathrm{U}}_{{\mathrm{z}}_2}\left(\mathrm{x},\mathrm{y},\mathrm{d}\right)$ is calculated using a diffraction integral after its propagation from the plane at a distance ${\mathrm{z}}_1$ into the plane at a distance ${\mathrm{z}}_2$:

$${\mathrm{U}}_{{\mathrm{z}}_1\to {\mathrm{z}}_2}\left(\mathrm{x},\mathrm{y},\mathrm{d}\right)=\exp \left(\mathrm{ikd}\right){\mathrm{U}}_{{\mathrm{z}}_1}\left(\mathrm{x},\mathrm{y},{\mathrm{z}}_1\right)\otimes {\mathrm{h}}_{\mathrm{d}}\left(\mathrm{x},\mathrm{y}\right)=\left|{\mathrm{U}}_{{\mathrm{z}}_2}\left(\mathrm{x},\mathrm{y},\mathrm{d}\right)\right|\exp \left({\mathrm{i}\mathsf{\phi }}_2\left(\mathrm{x},\mathrm{y}\right)\right)$$

(4)

where ${\mathsf{\phi }}_2\left(\mathrm{x},\mathrm{y}\right)$—phase of the complex field amplitude in the plane ${\mathrm{z}}_2$ and $\mathrm{d}={\mathrm{z}}_2-{\mathrm{z}}_1$.

At the second stage, we calculate the module of the complex field amplitude in the plane at a distance ${\mathrm{z}}_2$ as the square root of the intensity recorded in this plane $\left|{\mathrm{U}}_{{\mathrm{z}}_2}\left(\mathrm{x},\mathrm{y},\mathrm{d}\right)\right|=\sqrt{{\mathrm{I}}_2\left(\mathrm{x},\mathrm{y}\right)}$, and use the phase from the result of the previous calculation (Formula (4)):

$${\mathrm{U}}_{{\mathrm{z}}_2}\left(\mathrm{x},\mathrm{y},{\mathrm{z}}_2\right)=\sqrt{{\mathrm{I}}_2\left(\mathrm{x},\mathrm{y}\right)}\exp \left({\mathrm{i}\mathsf{\phi }}_2\left(\mathrm{x},\mathrm{y}\right)\right).$$

(5)

At the third stage, knowing the complex amplitude of the field ${\mathrm{U}}_{{\mathrm{z}}_2}\left(\mathrm{x},\mathrm{y},{\mathrm{z}}_2\right)$ (Formula (5)), similar to the first stage, we calculate the complex amplitude of the field ${\mathrm{U}}_{{\mathrm{z}}_1}\left(\mathrm{x},\mathrm{y},-\mathrm{d}\right)$ after its propagation from the plane at a distance ${\mathrm{z}}_2$ into the plane at a distance ${\mathrm{z}}_1$:

$${\mathrm{U}}_{{\mathrm{z}}_2\to {\mathrm{z}}_1}\left(\mathrm{x},\mathrm{y},-\mathrm{d}\right)=\exp \left(-\mathrm{ikd}\right){\mathrm{U}}_{{\mathrm{z}}_2}\left(\mathrm{x},\mathrm{y},{\mathrm{z}}_1\right)\otimes {\mathrm{h}}_{-\mathrm{d}}\left(\mathrm{x},\mathrm{y}\right)=\left|{\mathrm{U}}_{{\mathrm{z}}_1}\left(\mathrm{x},\mathrm{y},-\mathrm{d}\right)\right|\exp \left({\mathrm{i}\mathsf{\phi }}_1\left(\mathrm{x},\mathrm{y}\right)\right).$$

(6)

At the fourth stage, using the module of the complex field amplitude in the plane at a distance ${\mathrm{z}}_1$ calculated as $\left|{\mathrm{U}}_{{\mathrm{z}}_1}\left(\mathrm{x},\mathrm{y},\mathrm{d}\right)\right|=\sqrt{{\mathrm{I}}_1\left(\mathrm{x},\mathrm{y}\right)}$, and the phase ${\mathsf{\phi }}_1\left(\mathrm{x},\mathrm{y}\right)$ from the Formula (6), we obtain

$${\mathrm{U}}_{{\mathrm{z}}_1}\left(\mathrm{x},\mathrm{y},{\mathrm{z}}_1\right)=\sqrt{{\mathrm{I}}_1\left(\mathrm{x},\mathrm{y}\right)}\exp \left({\mathrm{i}\mathsf{\phi }}_1\left(\mathrm{x},\mathrm{y}\right)\right).$$

(7)

As a result of one iteration consisting of four stages, we obtain complex amplitudes of the fields ${\mathrm{U}}_{{\mathrm{z}}_1}\left(\mathrm{x},\mathrm{y},{\mathrm{z}}_1\right)$ and ${\mathrm{U}}_{{\mathrm{z}}_2}\left(\mathrm{x},\mathrm{y},{\mathrm{z}}_2\right)$ instead of the intensity distributions ${\mathrm{I}}_1\left(\mathrm{x},\mathrm{y}\right)$ and ${\mathrm{I}}_2\left(\mathrm{x},\mathrm{y}\right)$ of recorded digital holograms. Knowing the complex field amplitude in the recording plane, we can calculate the particle transmittance $\left(1-\mathrm{a}\left(\mathrm{x},\mathrm{y}\right)\right)$:

$$\begin{gathered} \exp \left(-{\mathrm{ikz}}_2\right){\mathrm{U}}_{{\mathrm{z}}_2}\left(\mathrm{x},\mathrm{y},{\mathrm{z}}_2\right)\otimes {\mathrm{h}}_{-{\mathrm{z}}_2}\left(\mathrm{x},\mathrm{y}\right)=\exp \left(-{\mathrm{ikz}}_2\right)\exp \left({\mathrm{ikz}}_2\right)\left({\mathrm{T}}^{\prime }\left(\mathrm{x},\mathrm{y}\right)\otimes {\mathrm{h}}_{{\mathrm{z}}_2}\left(\mathrm{x},\mathrm{y}\right)\right)\otimes {\mathrm{h}}_{-{\mathrm{z}}_2}\left(\mathrm{x},\mathrm{y}\right) \\ ={\mathrm{T}}^{\prime }\left(\mathrm{x},\mathrm{y}\right)\otimes \left({\mathrm{h}}_{{\mathrm{z}}_2}\left(\mathrm{x},\mathrm{y}\right)\otimes {\mathrm{h}}_{-{\mathrm{z}}_2}\left(\mathrm{x},\mathrm{y}\right)\right)={\mathrm{T}}^{\prime }\left(\mathrm{x},\mathrm{y}\right)\otimes \mathsf{\delta }\left(\mathrm{x},\mathrm{y}\right)={\mathrm{T}}^{\prime }\left(\mathrm{x},\mathrm{y}\right)=1-{\mathrm{a}}^{\prime }\left(\mathrm{x},\mathrm{y}\right). \end{gathered}$$

(8)

In this case, the influence of the virtual image on the real image of a particle will decrease with each subsequent iteration, and ${\mathrm{a}}^{\prime }\left(\mathrm{x},\mathrm{y}\right)$ will tend to $\mathrm{a}\left(\mathrm{x},\mathrm{y}\right)$.

3.2. Spatial-Frequency Method

The diffraction integral (3) can be presented as a convolution of two functions, and up to the constant $\exp \left(ikz\right)$, the complex field amplitude reconstructed from the digital hologram at a distance z from the hologram plane will take the following form:

$$\begin{gathered} U\left(x_2,y_2,z\right)=\underset{-\infty }{\overset{\infty }{{\displaystyle \iint }}}{I}_H\left(x_2,y_2\right)·\frac{\exp \left(ikz\right)}{i\lambda z}·\exp \left\{\frac{ik}{2z}\left[{\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2\right]\right\}d{x}_{1}d{y}_1 \\ =\exp \left(ikz\right)·I_H\left(x_2,y_2\right)\otimes h_z\left(x_2,y_2\right)=\left(-a^{*}\otimes h_z^{*}-a\otimes h_z\right)\otimes h_z\left(x_2,y_2\right) \end{gathered}$$

(9)

The Fresnel convolution has the following properties [31,32]:

• $h_z\left(x,y\right)\otimes h_z^{*}\left(x,y\right)=h_z\left(x,y\right)\otimes h_{-z}\left(x,y\right)=\delta \left(x,y\right)$ ($\delta$—Dirac delta function);
• $h_{z_1}\left(x,y\right)\otimes h_{z_2}\left(x,y\right)=h_{z_1+z_2}\left(x,y\right)$.

Let us use these properties to convert (9) to the following form [31,32]:

$$U\left(x_2,y_2,z\right)=-a^{*}\left(x_2,y_2\right)-a\left(x_2,y_2\right)\otimes h_{z2}\left(x_2,y_2\right)$$

(10)

In case of an opaque particle, the complex field amplitude in the plane of the real image of a particle is as follows:

$$\mathrm{U}\left({\mathrm{x}}_2,{\mathrm{y}}_2,\mathrm{z}\right)=-\mathrm{a}\left({\mathrm{x}}_2,{\mathrm{y}}_2\right)-\mathrm{a}\left({\mathrm{x}}_2,{\mathrm{y}}_2\right)\otimes {\mathrm{h}}_{2\mathrm{z}}\left({\mathrm{x}}_2,{\mathrm{y}}_2\right)=-\mathrm{a}\left({\mathrm{x}}_2,{\mathrm{y}}_2\right)\otimes \left(\delta +{\mathrm{h}}_{2\mathrm{z}}\left({\mathrm{x}}_2,{\mathrm{y}}_2\right)\right),$$

(11)

where $\delta$—Dirac delta function and $a\left(x,y\right)=\left\{\begin{array}{c}1, if \left(x,y\right)\in particle\\ 0, if \left(x,y\right)\notin particle\end{array}\right.$—real function.

According to the convolution theorem, the Fourier image of the convolution of two functions is equal to the product of their Fourier images:

$${\mathcal{F}}^{+}\left(\mathrm{U}\left({\mathrm{x}}_2,{\mathrm{y}}_2,\mathrm{z}\right)\right)={\mathcal{F}}^{+}\left(-\mathrm{a}\left({\mathrm{x}}_2,{\mathrm{y}}_2\right)\right){\mathcal{F}}^{+}\left(\delta +{\mathrm{h}}_{2\mathrm{z}}\left({\mathrm{x}}_2,{\mathrm{y}}_2\right)\right).$$

(12)

If we multiply this expression by the inverse value ${\mathcal{F}}^{+}\left(\delta +{\mathrm{h}}_{2\mathrm{z}}\left({\mathrm{x}}_2,{\mathrm{y}}_2\right)\right)$, we obtain the Fourier image of the complex amplitude of the field corresponding to the real particle image:

$${\mathcal{F}}^{+}\left(-\mathrm{a}\left({\mathrm{x}}_2,{\mathrm{y}}_2\right)\right){\mathcal{F}}^{+}\left(\delta +{\mathrm{h}}_{2\mathrm{z}}\left(x_2,y_2\right)\right)·\frac{1}{{\mathcal{F}}^{+}\left(\delta +{\mathrm{h}}_{2\mathrm{z}}\left({\mathrm{x}}_2,{\mathrm{y}}_2\right)\right)}=-{\mathcal{F}}^{+}\left(\mathrm{a}\left({\mathrm{x}}_2,{\mathrm{y}}_2\right)\right).$$

(13)

It is now quite easy to obtain a field distribution by applying the inverse Fourier transform:

$${\mathcal{F}}^{-}\left({\mathcal{F}}^{+}\left(\mathrm{a}\left({\mathrm{x}}_2,{\mathrm{y}}_2\right)\right)\right)=\mathrm{a}\left({\mathrm{x}}_2,{\mathrm{y}}_2\right).$$

(14)

Thus, an image free from the twin-image effect is formed in the plane of a particle image reconstructed from a digital hologram as a result of the interaction of the Fourier image of the complex field amplitude with the filter, the transmission of which is determined by the relation [31]:

$$F\left(u,v\right)=\frac{1}{{\mathcal{F}}^{+}\left(\delta +{\mathrm{h}}_{2\mathrm{z}}\left(\mathrm{x},\mathrm{y}\right)\right)}=\frac{1}{1+exp\left[2i\pi \lambda z\left(u^2+v^2\right)\right]}.$$

(15)

where u,v—spatial frequencies.

4. Results and Discussion

4.1. Suppression of the Twin-Image Effect

4.1.1. Digital Filtering

A numerical holography experiment was performed according to the in-line scheme of two model opaque square particles with a side of 89.7 µm, located in one plane on a transparent homogeneous background. The numerical reconstruction of particle images from the modeled digital hologram (Figure 6a) shows a band pattern in particle images associated with the twin-image effect. After digital filtering using a filter described in Section 3.2 (Formula (15)) [12], we can see that the mutual influence of the real and virtual images has significantly decreased (Figure 6b).

It should be noted that the twin-image effect in general and especially for closely spaced adjacent particles affects the energy distribution in the image regions used to determine K and ΔI (Section 2.2) and, thus, the accuracy of determining the best image plane of a particle, which is determined by K and ΔI maximum values. In field experiments, the position of the best image plane is taken as the longitudinal coordinate of a particle, therefore, the accuracy of its determination plays a key role in the study of the particle dynamics in space.

For the described experiment, Figure 7 shows the depsendence of the determination error of the best image plane $\Delta =\left|\mathrm{z}-{\mathrm{z}}_{\mathrm{P}}\right|$ of one of the square particles on the distance between the centers of mass of images of adjacent particles (Figure 6), where $\mathrm{z}$—distance from particles to the recording plane, ${\mathrm{z}}_{\mathrm{P}}$—distance from the plane of the digital hologram to the best image plane determined by the maximum boundary intensity jump $\mathsf{\Delta }\mathrm{I}$.

The figure shows that digital filtering of a virtual image at small distances between particles reduces the determination error of the best image plane approximately twice and then reduces it to zero. The oscillating nature of the best image plane error is explained by the influence of interference bands caused by the twin-image effect on the quality indicators used to determine the best image plane. This demonstrates the need to suppress a twin image in digital particle holography measurement systems, as well as to determine the boundary conditions for the relevant algorithms.

4.1.2. Boundary Condition for the Gerchberg–Saxton Method

In this work, the Gerchberg–Saxton method was used in the reconstruction of holographic images of experimentally recorded digital holograms of a circular opaque model particle with a diameter of d = 124.2 µm (Figure 8a) located at a distance z from the hologram recording plane. The size of digital holograms: 2048 × 2048 pixels; pixel size: 3.45 × 3.45 μm; wavelength: λ = 0.66 μm.

The results of this iteration are shown in Figure 8 for a circular model particle. Note that, despite the large number of iterations, it is not possible to completely eliminate the twin-image effect.

Let us define ${\mathrm{z}}_{\mathrm{R}}$ as the minimum distance at which the quality indicator of the particle image boundary after applying the method increases compared to the quality indicator of the particle image boundary before applying this method.

Calculations of the dependence of the quality indicators of the reconstructed images of this model particle with a diameter d = 124.2 µm on the position of the particle $z$ (Figure 9) showed that under the given experimental conditions this position is $z=z_R=$50 ± 4 mm, while the boundary intensity jump ΔI almost doubles (increases by 1.9 ± 0.2 times).

Further, $z_R$ values for model particles of different diameters (Figure 10, points) under the same conditions were experimentally determined. Since we know the parameters of a model particle, PSNR was used as the quality indicator in these experiments. It was found that $z_R$ depends on the size of the studied particles and the wavelength of the recording radiation, while the empirical dependence is described well by the formula $z_R=\frac{2d^2}{\lambda }$ (solid line in Figure 10).

4.1.3. Boundary Condition for the Spatial-Frequency Method

The experiments on the digital hologram recording for the spatial-frequency method were conducted for model opaque circle particles with a diameter of 89.7 μm and 133.2 μm. Figure 11 shows the dependencies PSNR, K, and ΔI on the distance between the particle and the recording plane (Figure 11a,c—for a particle with a diameter of 89.7 μm, Figure 11b,d—for a particle with a diameter of 133.2 μm), which confirm that the use of this filtering improves the quality of the particle image boundary according to a boundary intensity jump by at least 1.7 times if the same condition as in Section 4.1.2 is satisfied: $z_R\ge \frac{2d^2}{\lambda }$.

4.1.4. Discussion of Results in Section 4.1

Although the complex field amplitude reconstruction method based on the Gerchberg–Saxton algorithm and the spatial-frequency method have a different physical and algorithmic basis, the results show that the conditions under which their application significantly improves the quality of determination of the particle image boundary coincide: $z_R\ge \frac{2d^2}{\lambda }$. Here, d for a particle of arbitrary shape is the particle’s circumscribed diameter. This suggests that this condition does not depend on the implemented algorithm but is related to the holographic image quality of the used particle, which is based on determining the sharpness of the image boundary (boundary contrast or boundary intensity jump).

The fact that $z_R$ is about twice the Rayleigh distance $\frac{d^2}{\lambda }$ defining the conditional boundary between Fresnel and Fraunhofer diffraction [33,34,35] can be explained as follows.

This is explained by the distribution of the wave field corresponding to the virtual and real images in the boundary region of the real particle image, which is marked with a green circle in Figure 3. Figure 12 shows the results of numerical calculations of the diffraction pattern using Formula (2) on an opaque circular disk in the boundary region for different distances $\mathrm{z}$.

The above diagrams show that when $\mathrm{z}$ varies from the Rayleigh distance $\frac{{\mathrm{z}}_{\mathrm{R}}}{2}$ to the Rayleigh double distance ${\mathrm{z}}_{\mathrm{R}}$, there is an intersection of the first dark fringe of the diffraction pattern from the virtual image and the external area identified along the boundary of the real particle image to determine the quality indicators used. This affects the quality indicators K and ΔI, leads to errors in determining their values and, as a result, errors in determining the best image plane. With $\mathrm{z}>{\mathrm{z}}_{\mathrm{R}}$, these contributions are opposite: the Poisson light spot of the diffraction pattern from the virtual image increases the average intensity of the internal area highlighted along the boundary of the particle image, and the first minimum of the diffraction pattern does not actually change the average intensity of the external one. With $\mathrm{z}={\mathrm{z}}_{\mathrm{R}}$, the contribution of the virtual image to the average intensity of the internal and external areas identified along the boundary of the particle image is almost the same, and the effect on the boundary contrast is maximized. Further, this situation is maintained, but the intensity of the diffraction pattern fringes from the virtual image is substantially reduced by diffraction divergence, so the effect on the boundary contrast is also reduced. Hence, this causes the error in determining the best image plane at $\mathrm{z}>{\mathrm{z}}_{\mathrm{R}}$.

Thus, the distance ${\mathrm{z}}_{\mathrm{R}}$ determines the minimum distance to the studied particle, at which the twin image is most suppressed.

Figure 13 shows a holographic image of a particle obtained by a submersible DHC (Figure 2) during a natural field experiment [36].

4.2. Coherent Noises Associated with the Impact of Medium Inhomogeneities during Hologram Recording

In particle holography, it is assumed that when a hologram of the volume of the medium with particles is recorded, its holographic image is reconstructed layer-by-layer, the best image planes of the particles are determined, and the geometric parameters of the particles (size, shape, position in space) are analyzed. The optical properties of the particles (transmittance, refractive index) differ from the parameters of the medium, and the medium itself is optically homogeneous. In real media, the degree of optical homogeneity may be low, which may occur in the case of sea or lake water and make it difficult to use a submersible DHC to study plankton and other particles [23,36].

The optical inhomogeneity of the medium with studied particles may be caused by the inclusions of other phases of a substance (microbubbles in water, surface defects, suspensions of microparticles of a different nature; Figure 14a), as well as variations in the refractive index of the medium caused by disturbances of optical constants (turbulence from propellers, thermohaline currents, upwelling, temperature gradients, etc.; Figure 14b).

Thus, there are noises in the image of a particle reconstructed from a hologram associated with the influence of medium inhomogeneities (wave aberrations and phase shifts caused by them) during hologram recording by a coherent radiation source. Such noises may be stationary if the cause does not change over time, but they are most often non-stationary.

There are several situations that require the suppression of such noises:

• Non-stationary noises and a stationary object.

  -

  Averaging using a multispectral radiation source at the stage of digital hologram recording [5,6];

  -

  Averaging using a multispectral radiation source at the stage of particle image reconstruction from a digital hologram [37,38];

  -

  Averaging over several digital holograms [12];

  -

  Averaging over several reconstructed holographic images [4,39].

• Non-stationary noises and a moving object: limits on the geometry of the holographic experiment.

Despite the difference in the physical principles of generating such noises, they are united by the random nature of a phase shift, so the methods of suppression can be the same and based on the generation of random changes in the phases of interfering waves, followed by averaging the resulting intensity distributions. Therefore, this section considers approaches and some practical issues to improve the image using the example of averaging holograms and holographic images, as well as determining a reasonable number of averaging scenarios to achieve the desired image quality. Besides, the paper presents the averaging results for a non-stationary object with a justification of the limits on the geometry of the holographic experiment.

4.2.1. Averaging over Several Digital Holograms

The averaging over several digital holograms was performed by recording the holograms of stationary model particles (Figure 1) placed in water containing a suspension of smaller scattering particles—hydrosol or small-scale turbulence. In total, 70 holograms were recorded at different time intervals, with further averaging. The obtained results (Figure 15) showed that starting from the averaging of three digital holograms, the boundary intensity jump ΔI of the reconstructed images of model particles does not change within the error limit and exceeds the threshold value of the criteria for acceptable quality of particle images [29] (ΔI = 0.25 in Figure 15). For boundary contrast K, such a condition [29] is already fulfilled during the averaging of two digital holograms (K = 2 in Figure 15). The averaging of three digital holograms makes it possible to improve the quality of reconstructed images of model particles compared to reconstructed images obtained without hologram averaging: K increased by 1.6 times and ΔI increased by 1.7 times. These estimates are consistent with the theoretical estimate of the coherent noise reduction by $\sqrt{N}$ times [38,40,41], where N is the number of statistically averaged independent digital holograms.

The results of the study of the dependence of quality indicators on the number of averaged images of particles reconstructed from digital holograms also showed that the averaging over three digital holograms is sufficient to achieve the given quality indicators of the particle image boundary. Such averaging is possible for a stationary object and can be used to form a reference “zero” frame, which is used to eliminate photometric inhomogeneities in the reconstructed holographic image.

In a real dynamic situation, a multispectral source with a laser diode fiber multiplexer can be used for the same purpose. We conducted an experiment to record three digital holograms of a model particle at wavelengths of 668.7 nm, 640.9 nm, and 660.2 nm.

The averaging was performed over two or three reconstructed images of the model particle. Figure 16 shows the dependencies of quality indicators on the number of averaged images of a model object. As in the previous case, the averaging of three digital holograms improves the quality of the reconstructed holographic image of a particle by at least 1.7 times in terms of the distinctive ability and the boundary intensity jump.

Moreover, in the considered case of digital holography, this averaging can be performed at the stage of hologram reconstruction by modeling a polychromatic source, which makes the technical implementation much easier.

4.2.2. Non-Stationary Object

In the case of multiple scattering on fine inclusions of the medium, both the object and the reference waves may be so distorted that the averaging methods will be ineffective. A laboratory experiment using a digital holographic camera was conducted to assess the impact of the extension of the scattering medium and its turbidity on the image quality of a particle reconstructed from a digital hologram. The DHC design provides for a discrete variation of the length of the test volume. The length of the test volume ($z_H$ in Figure 1) may equal 51 mm, 202 mm, 349.4 mm, or 498.6 mm. In laboratory conditions, we simulated water with different turbidities, into which the DHC was placed, by adding pure tap water to turbid lake water (dense microalgae hydrosol). The water turbidity was measured using the 2100P Turbidimeter for six samples: 7.48 nephelometric turbidity units (NTU), 6.60 NTU, 5.46 NTU, 4.65 NTU, 2.03 NTU, 0.53 NTU, and 0.1 NTU. The maximum turbidity corresponded to lake weedy water, while the minimum corresponded to water from the water line.

A model particle of a caliber (Figure 1b) located near the illuminating laser (Figure 1a) was used as an object of holography in all experiments. Digital holograms of this opaque model particle of a square shape with a size of 500 × 500 μm were recorded for different sizes of the test volume and different turbidities of the medium. The dependencies of the particle distinctive ability on the length of the test volume were obtained for different turbidities of the water with model particles at the hologram recording stage. Considering that the shape of a square particle is recognized at a distinctive ability of not more than 0.2 [23], the dependence of the length of the studied volume on the medium turbidity according to the distinctive ability of 0.2 was obtained (Figure 17). The graph in Figure 17 allows optimizing the length of the registered medium volume (depth of the holographic scene) depending on turbidity.

In the graph in Figure 17, $z_H{}_{max}$—maximum possible length of the working volume ensuring the specified distinctive ability in clean water (turbidity—0.1 NTU), $z_H{}_{min}$—minimum length of the working volume ensuring the specified distinctive ability in turbid lake water (turbidity—7.5 NTU). The dependence shown in the figure is asymptotic both with respect to the length of the working volume and turbidity. Extreme turbidity is determined in relation to the minimum $z_H{}_{min}=50$ mm and maximum $z_H{}_{max}=500$ mm lengths of the working volume.

4.2.3. Discussion of Results in Section 4.2

The averaging methods discussed in the section show that when averaging over a small number of frames, it is possible to achieve a noticeable improvement in the quality of the image reconstructed from a hologram. At the same time, the method of averaging is not that critical here: over digital holograms or reconstructed images of particles. The physical reason for limiting the correction possibilities in the case of Gabor holography is the inability to achieve large phase shifts when forming a sample for averaging, as is carried out in the case of non-in-line holography [39]. However, the use of several correction methods can improve the reliability of particle recognition from holographic images.

The limitations on the length of the volume registered by the holographic camera make it possible to achieve a larger effect. Figure 18 shows holographic images of the caliber model particle in the extreme position at the illuminating module porthole (the most unfavorable point) at different lengths of the studied volume (in a marine experiment, the length of the studied volume of a submersible DHC was successively reduced to increase the distinctive ability of the DHC in turbid seawater). The obtained results made it possible to choose the length of the studied volume (494 mm) with an acceptable quality of the reconstructed image (Figure 18c,d).

However, in this case, it is necessary to be prepared to significantly reduce the recording volume and, as a result, the sampling of particles for analysis. Thus, the adaptation of the DHC to the in situ conditions of Lake Baikal to eliminate turbulent flows led to the fact that this volume was 0.02 L instead of the nominal 0.5 L [42].

5. Conclusions

The paper presents the results of applying the methods for suppressing coherent noises in the reconstructed particle image related to the scattering parameters of the medium with the studied particles, as well as to the twin-image effect of the investigated particle. Addressing the research questions formulated in the introduction, the authors come to the following practical conclusions.

On the examples of the method of complex field amplitude reconstruction based on the Gerchberg–Saxton algorithm and a spatial-frequency method, it was shown that the methods for suppressing the twin-image effect of a particle image reconstructed from an in-line hologram improve the quality of the particle image boundary detection according to a boundary intensity jump by at least 1.7 times if the condition $z\ge \frac{2d^2}{\lambda }$ is satisfied, where z is the distance from the particle to the hologram registration plane, d is the particle circumscribed diameter, and λ is the wavelength. Thus, the expression $z=\frac{2d^2}{\lambda }$ is a distance condition for the effective use of appropriate algorithms and should be taken into account in the design features of the DHC and other holographic cameras used to record the in-line holograms of particles.

The methods based on the averaging of digital holograms or images of particles reconstructed from digital holograms are considered to suppress non-stationary coherent noises associated with the heterogeneity of the medium and the studied particles. The study of the dependence of the quality indicators of the reconstructed images of particles on the number of averaging showed that averaging over at least three digital holograms is sufficient to achieve the quality of the particle image boundary suitable for particle recognition. At the same time, the method of averaging is not that critical here: over three digital holograms or images of particles.

The multiple scattering conditions require a limit on the length of the studied medium volume (DHC holographic depth of scene). This limit depends on turbidity and may vary within the limits of not more than 500 mm for clean water and 50 mm for turbid water.