Evaluation of Mechanical Performance of a New Disc Spring-Cable Counter Pressure Shock Absorber
Abstract
1. Introduction
2. Design of the DSCCP Shock Absorber
2.1. Design Principle
2.2. Key Parameter Calculation and Design Process
2.2.1. Axial Bearing Capacity
2.2.2. Vertical Stiffness
2.2.3. Deformation Energy
2.2.4. Design Process
- (1)
- The outer and inner diameters D and d are selected and determined based on the space situation of the disc spring. Generally speaking, C = D/d = 1.7~2.5. The reason is that poor space utilization may be caused if D is too large; and difficult installation of the internal cable may be caused if d is too small.
- (2)
- Designing the ratio between the free height h0 and thickness t based on the self-deformation characteristics of the disc spring. The ratio is suggested to be h0/t < 0.5 if a linear relationship is required between bearing capacity and deformation, which is the common choice. The ratio is suggested to be 0.5 < h0/t < if zero stiffness characteristic is required.
- (3)
- Choosing a stacking and pairing method to form the disc spring group, which is then used to determine the deformation and bearing capacity of each disc spring. The number i of paired disc spring group can be calculated according to the total vertical deformation.
- (4)
- Verifying the stress σOM of the disc spring at the OM point, as shown in Figure 3, which should be less than the ultimate stress of the material. Besides, the stresses at points II and III should also be checked to meet the design requirements.
- (5)
- Selecting the pre-compression deformation f2 and then calculating the initial stiffness. Usually, f2 = 0.15~0.2h0.
- (6)
- Calculating the bearing capacity of the steel cable based on the pre-compression deformation of disc spring, which is then used to select suitable steel cable.
3. Numerical Simulation and Modal Validation
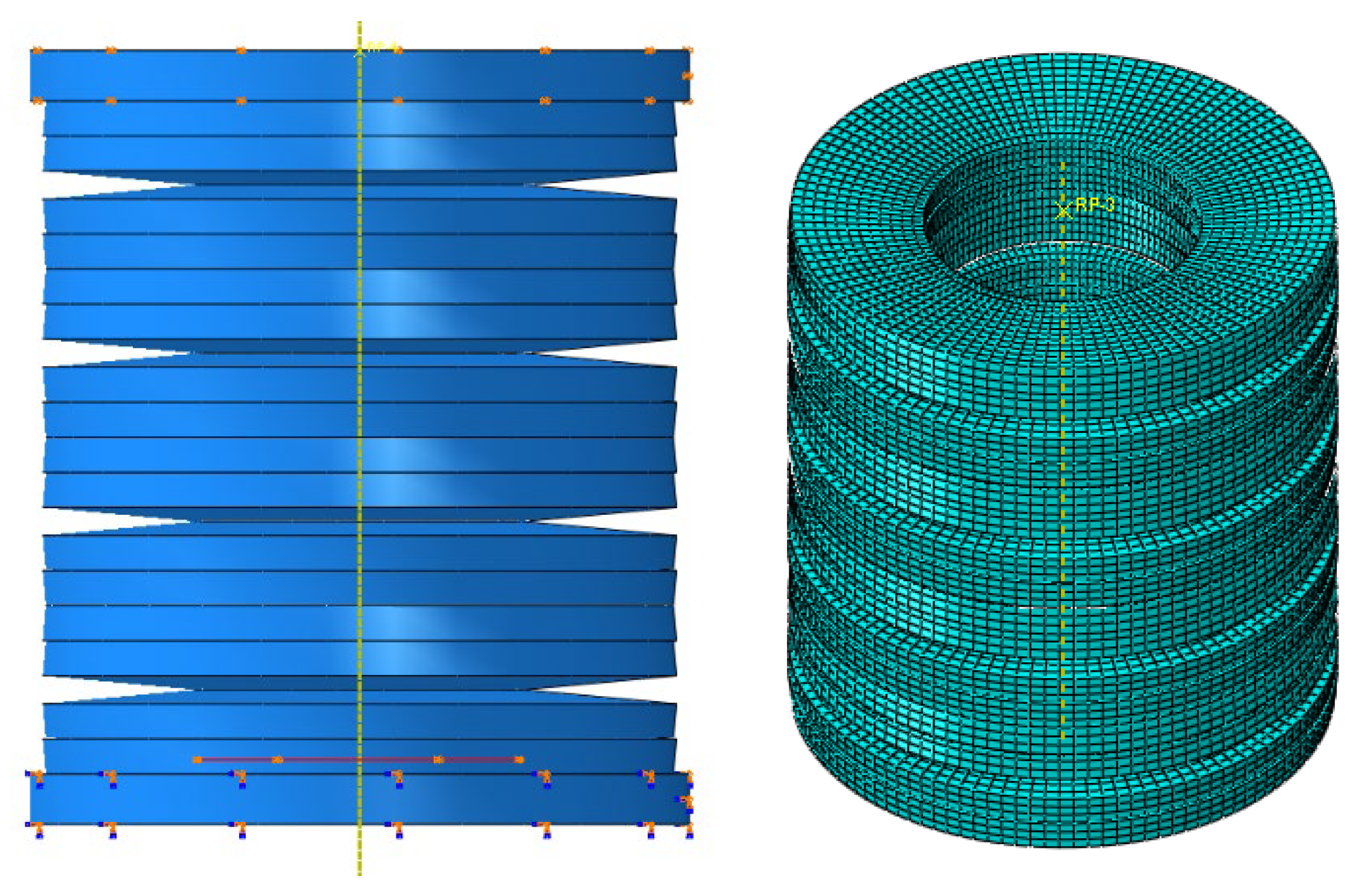
3.1. Model Establishment
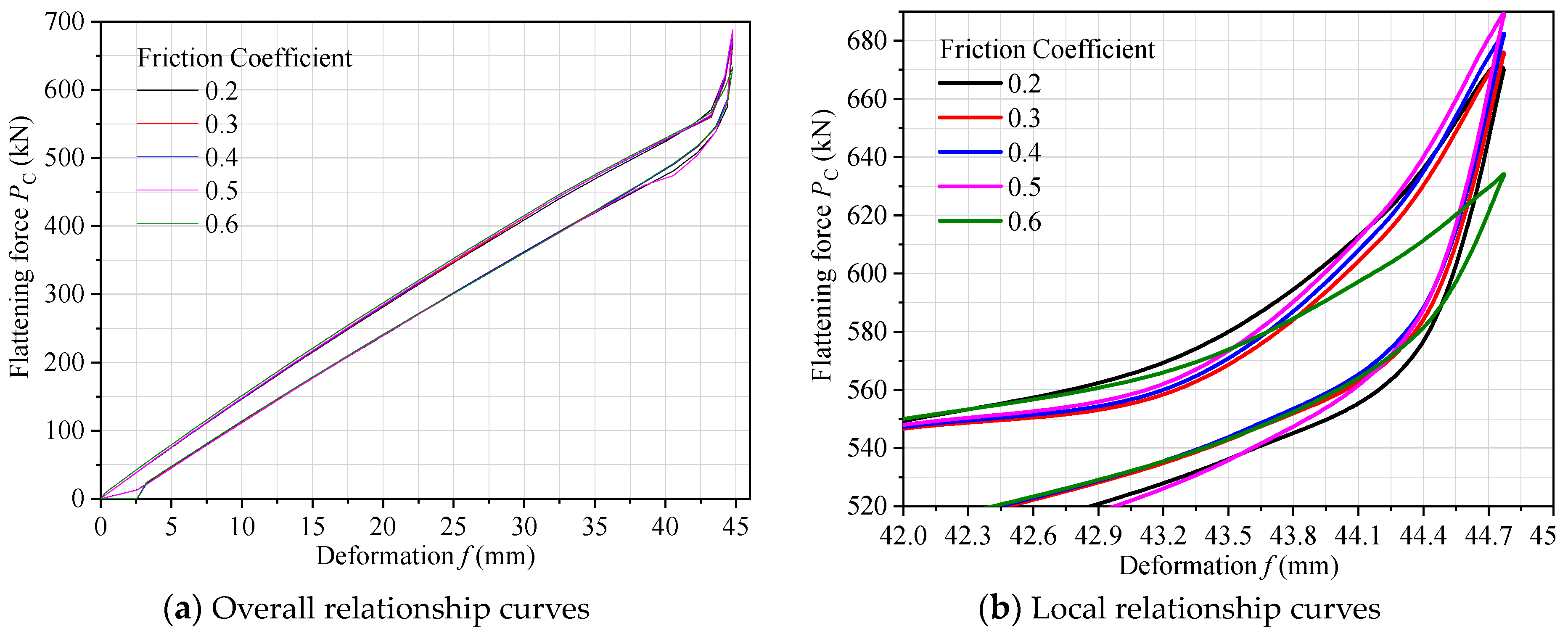
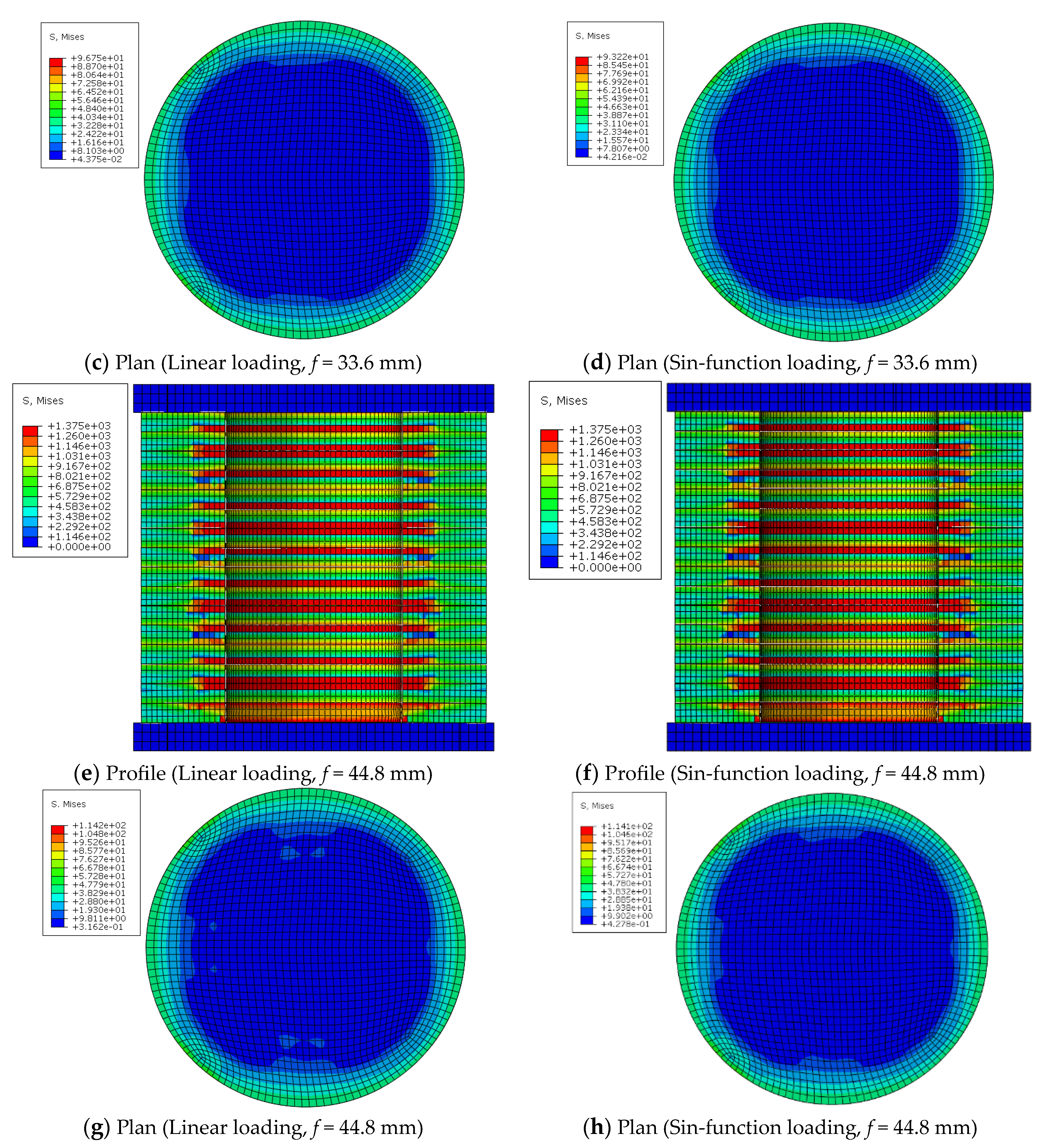
3.2. Analysis of Friction Coefficient μ2
3.3. Model Validation
4. Mechanical Property Test
4.1. Design and Production of Test Prototype
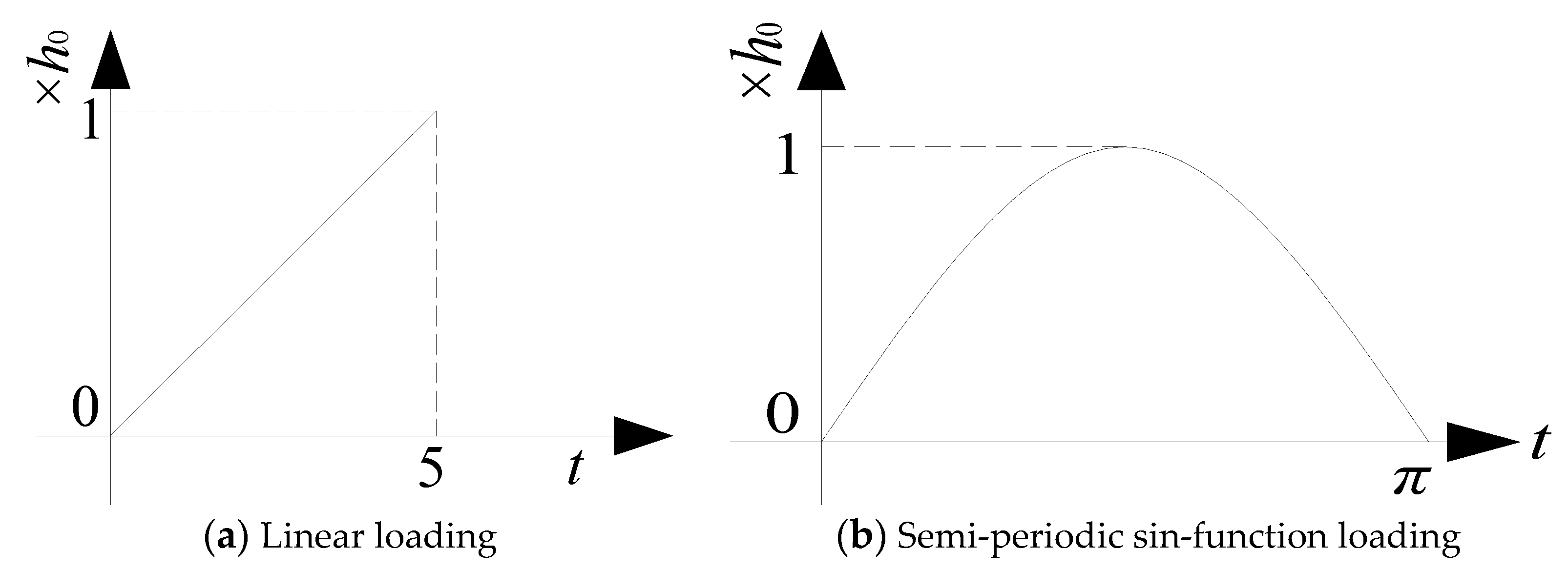
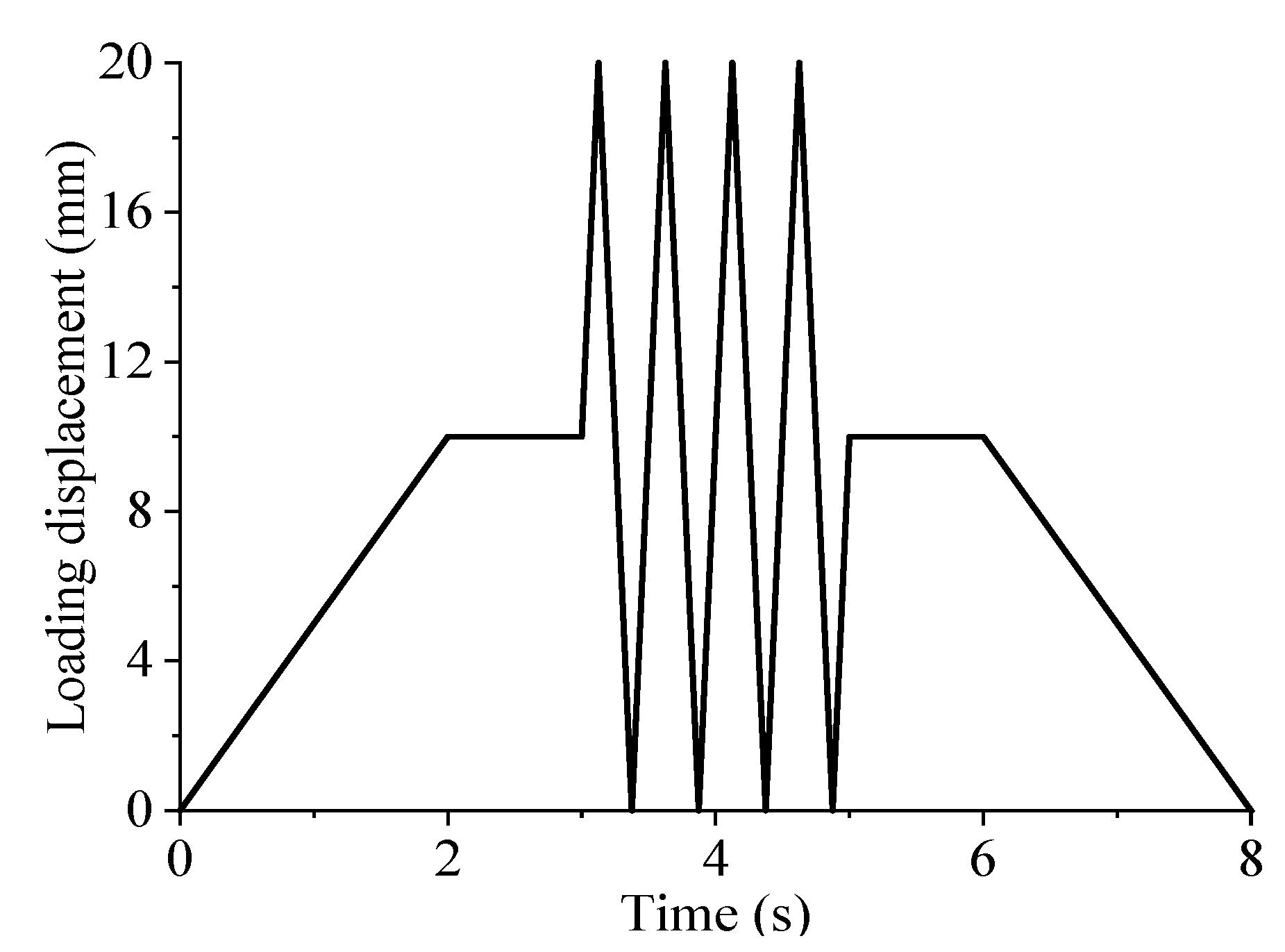
4.2. Test Loading Scheme Design
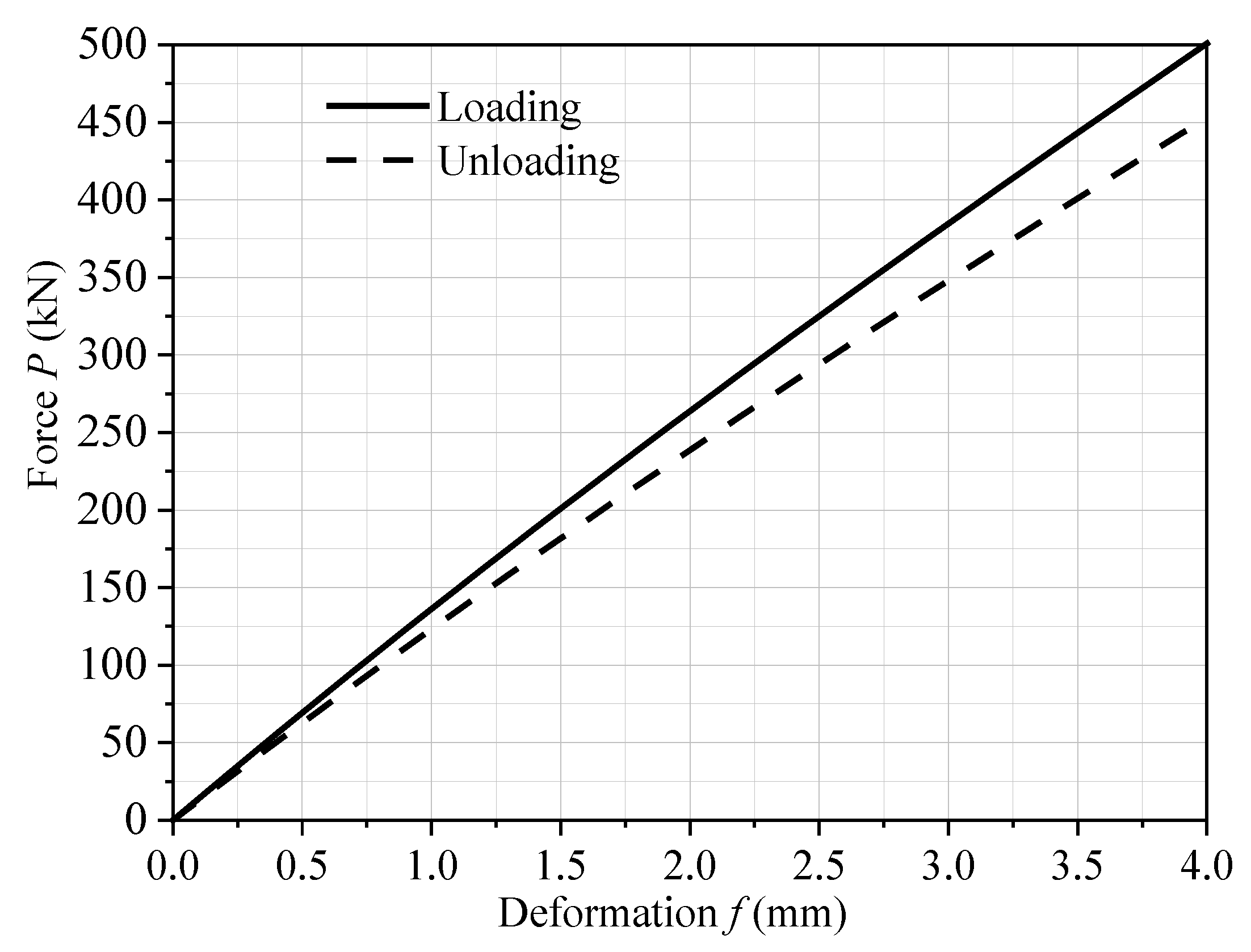
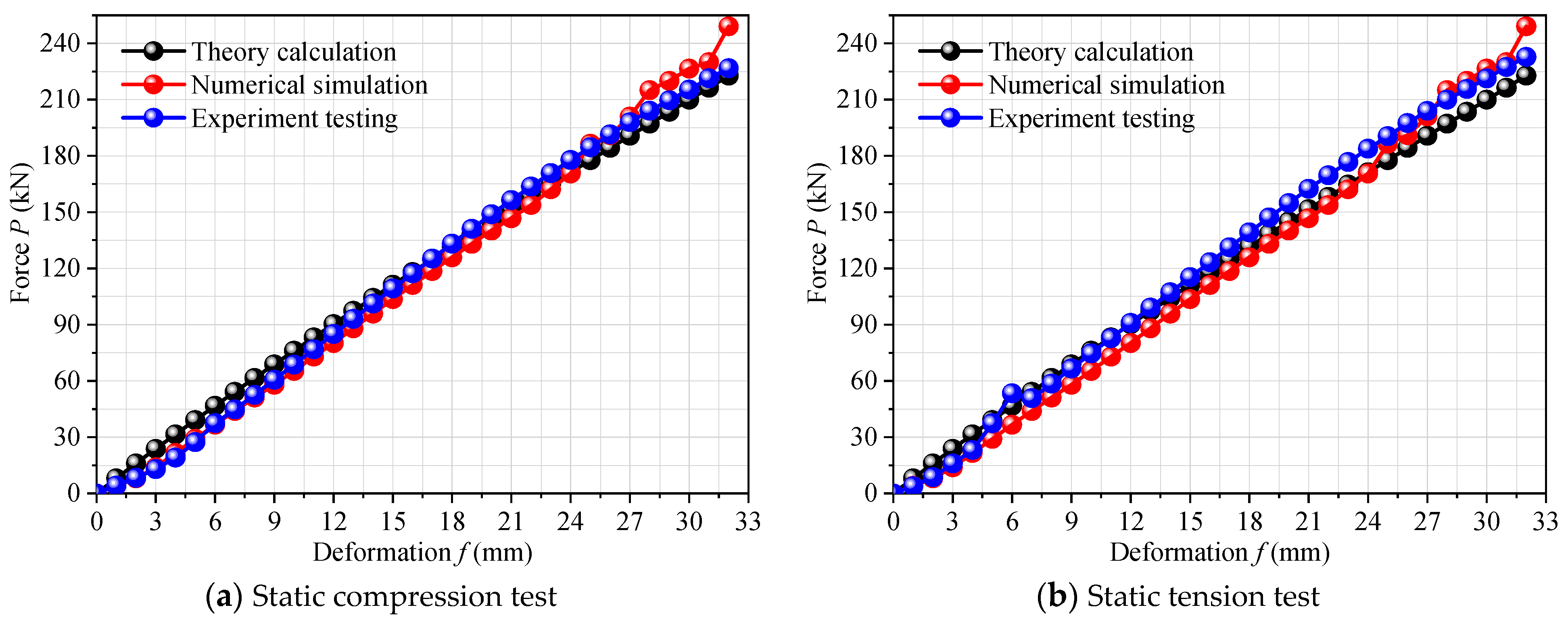
4.3. Static Test Results
4.4. Dynamic Test Results
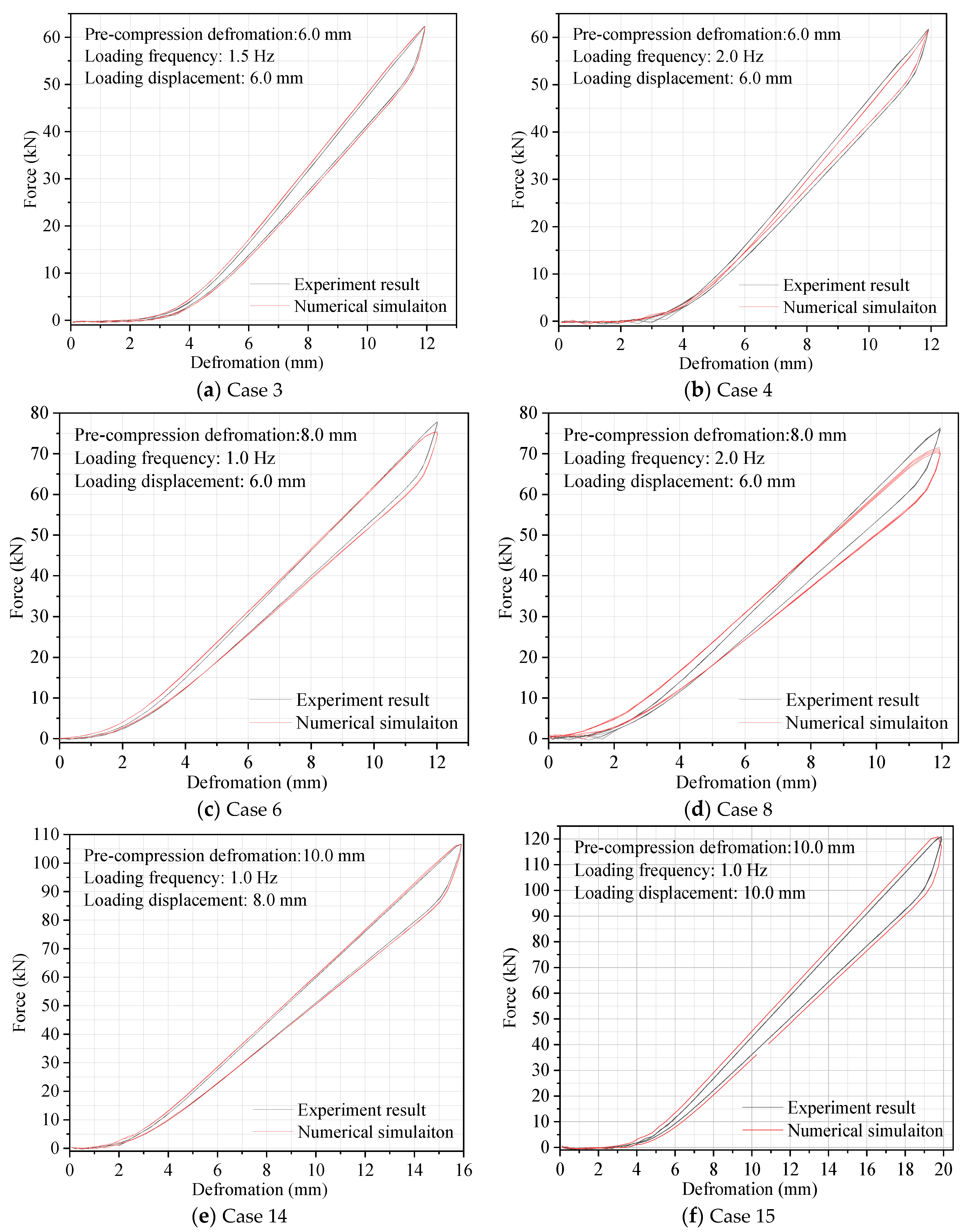
4.4.1. Test Result
4.4.2. Result Discussion
5. Conclusions
- (1)
- A new vertical disc spring-cable counter pressure (DSCCP) shock absorber was proposed and validated, which has a function such that the disc spring group is always in a compression working state and causes energy dissipation, regardless of whether it is in tension or compression motion.
- (2)
- The friction coefficients between disc springs, and between the disc spring and cover plate, are suggested to be 0.005 and 0.3, respectively, to achieve the best agreement between numerical and theoretical results for the mechanical performance of the DSCCP shock absorber. For example, the errors of the flattening force of the DSCCP shock absorber between simulation and theory are only 4.58% under linear static loading, and 4.14% under sin-function static loading.
- (3)
- Under static loading, the bearing capacity of the DSCCP shock absorber shows a linear relationship with the loading displacement. The static compression and tensile results show consistent agreement with theory, simulation and experiment. Under the condition of ultimate tensile deformation, the errors between the experimental results and the theoretical and numerical results are only 4.47% and 6.56%, respectively.
- (4)
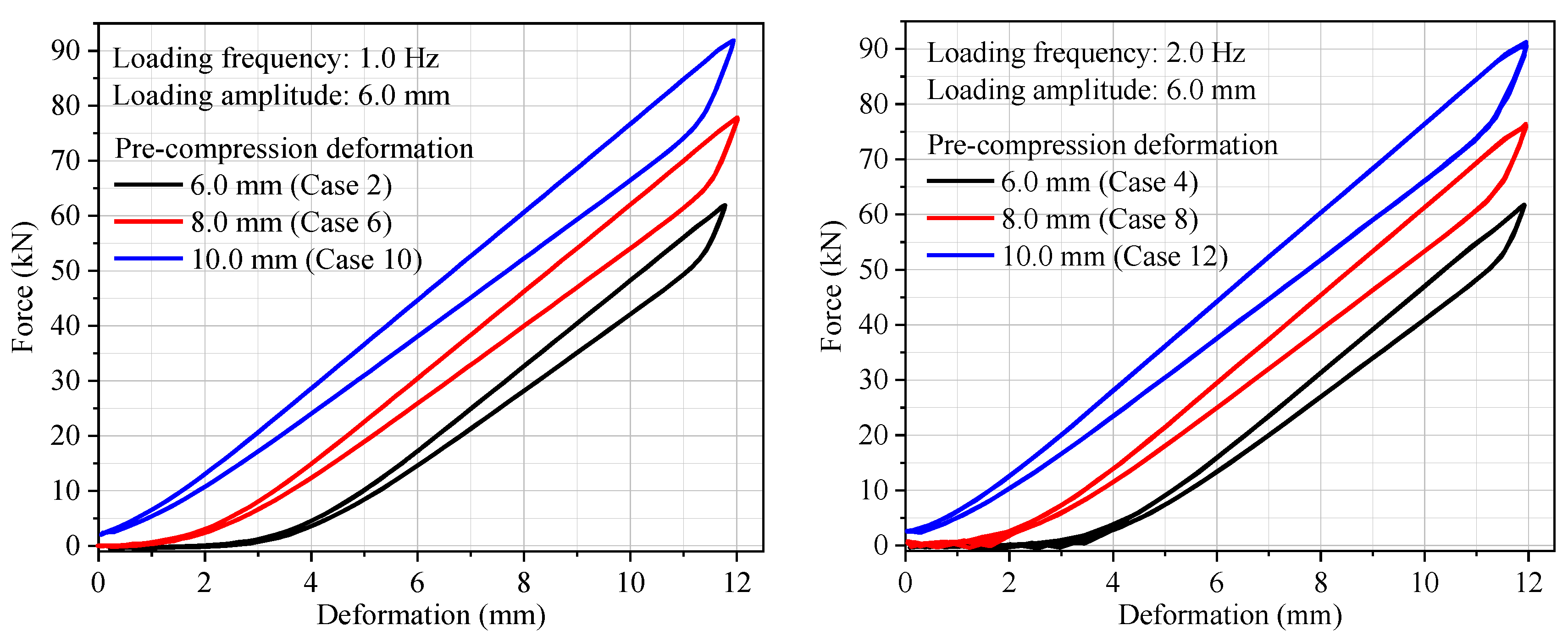
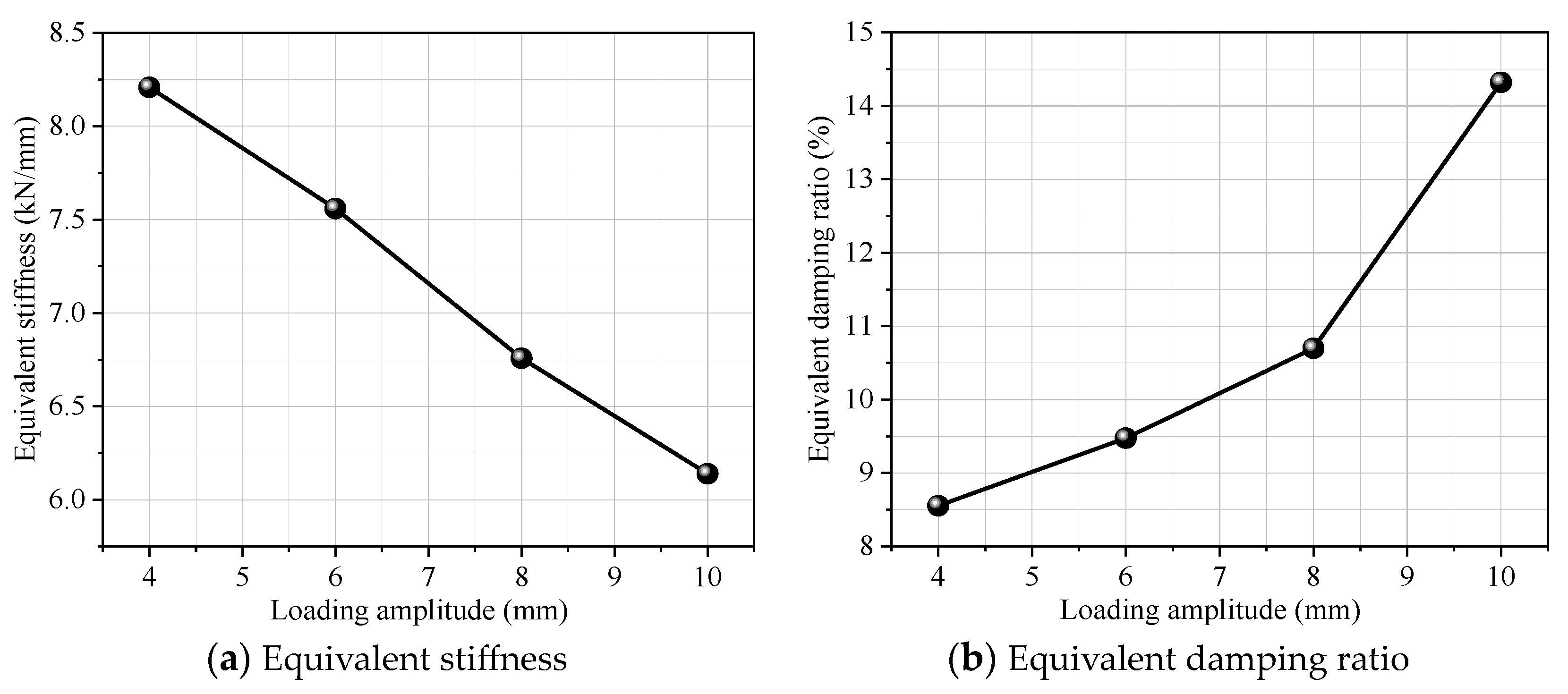
- Under dynamic loading, the bearing capacity of the DSCCP shock absorber first shows a trend of slow growth, then rapid growth with the increase of loading displacement. The energy dissipation capacity of the shock absorber shows an increase with the increase of loading displacement. The minimum equivalent damping ratio of all the dynamic test cases is 7% (case 3), and the maximum is up to 15.3% (case 9).
- (5)
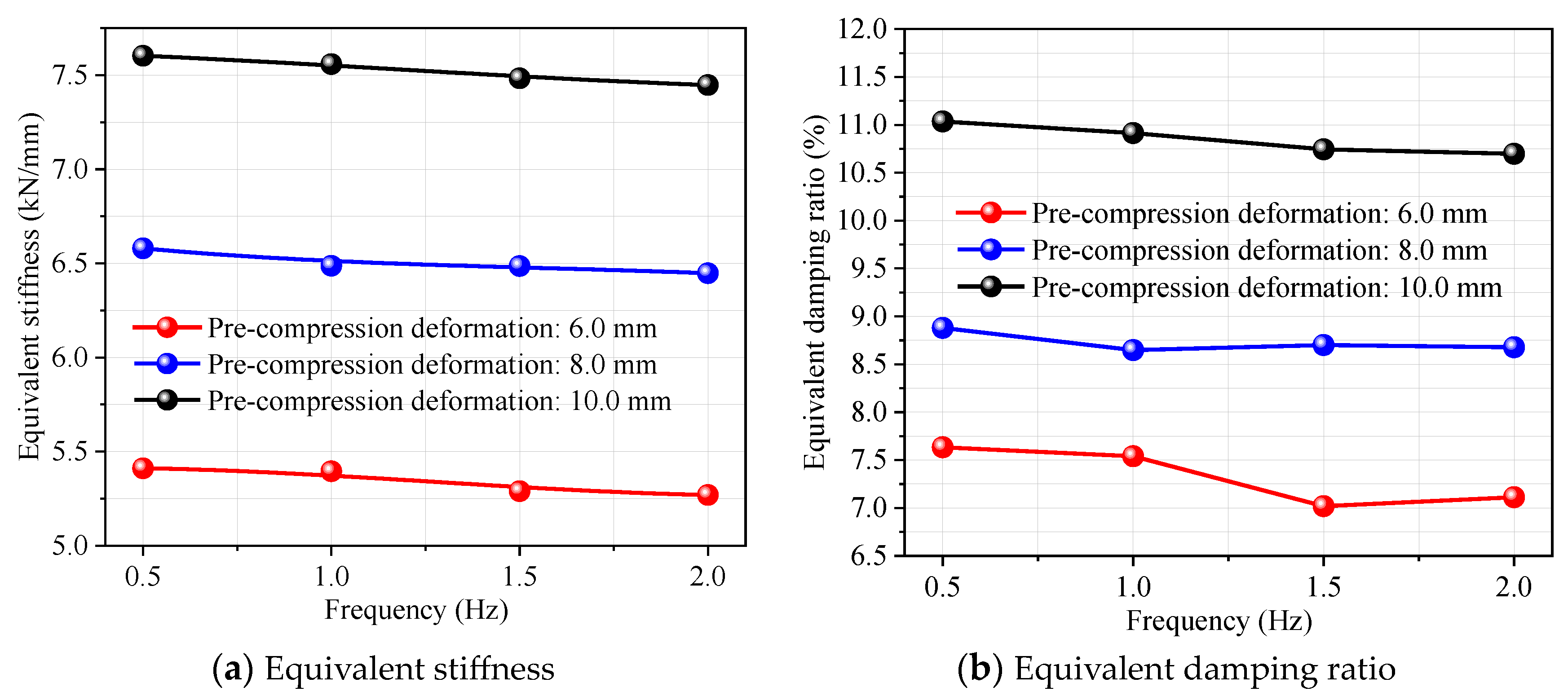
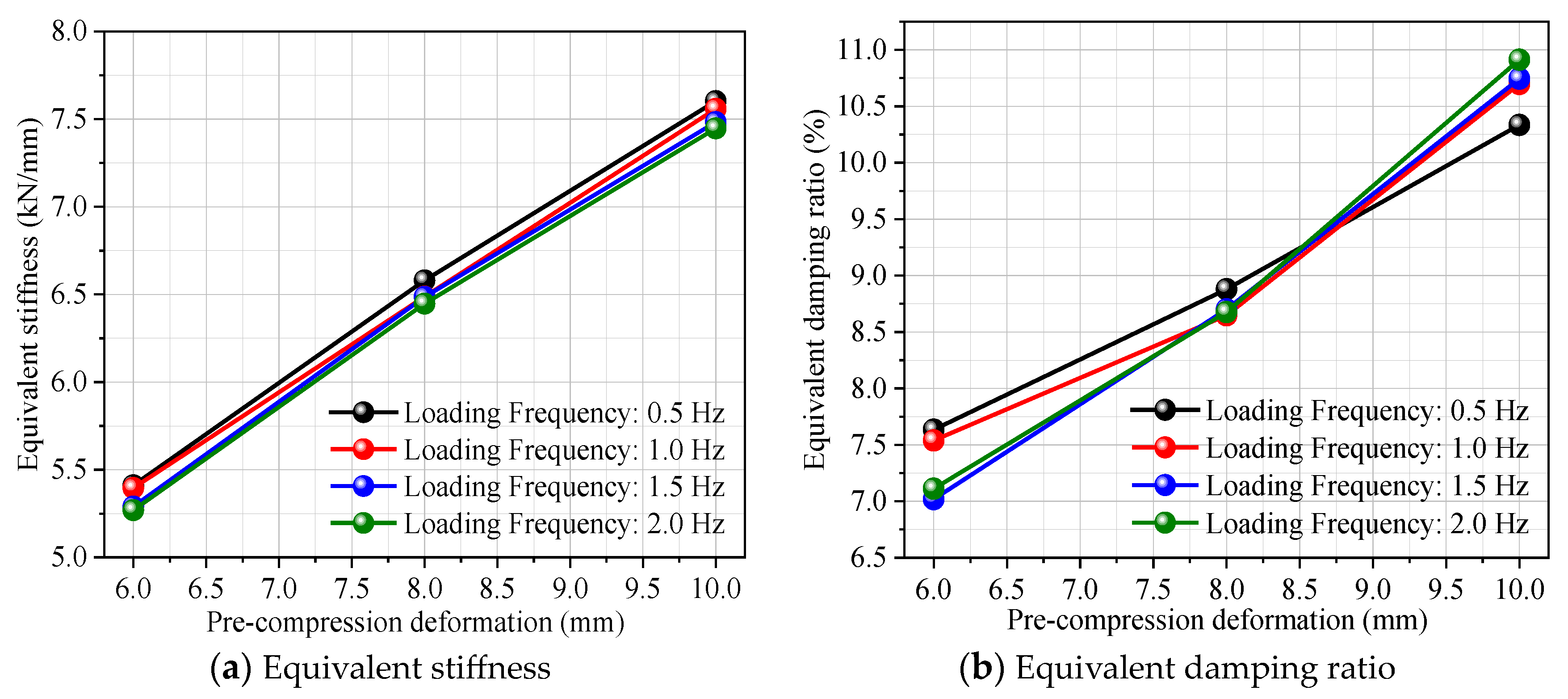
- Under the same pre-compression deformation conditions, the equivalent stiffness and equivalent damping ratio of the shock absorber slowly decrease with the loading frequency, with a maximum decrease of only 2.59%. Under the same loading frequency, the equivalent stiffness and equivalent damping ratio of the shock absorber exhibit a linear and significantly increasing trend with pre-compression deformation. Under the same loading frequency and pre-compression deformation conditions, the equivalent stiffness of the shock absorber decreases continuously with the increase of loading frequency, but the equivalent damping ratio increases continuously with the loading frequency.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Sun, Y.B.; Cao, T.J.; Xiao, Y. Full-scale steel column tests under simulated horizontal and vertical earthquake loadings. J. Constr. Steel Res. 2016, 163, 105767. [Google Scholar] [CrossRef]
- Ruiz-García, J. Examination of the vertical earthquake ground motion component during the September 19, 2017 (Mw = 7.1) earthquake in Mexico City. Soil Dyn. Earthq. Eng. 2018, 110, 13–17. [Google Scholar] [CrossRef]
- Quin, H. Dynamic stress drop and rupture dynamics of the October 15, 1979 Imperial Valley, California, earthquake. Tectonophysics 1990, 175, 93–117. [Google Scholar] [CrossRef]
- Trifunac, M.D.; Todorovska, M.I. Duration of strong ground motion during Northridge, California, earthquake of January 17, 1994. Soil Dyn. Earthq. Eng. 2012, 38, 119–127. [Google Scholar] [CrossRef]
- Chen, L.Y. Dynamical Response of High-Rise Structure under the Vertical Seismic Action; Xi’an University of Architecture and Technology: Xi’an, China, 2007. [Google Scholar]
- Yin, Q.; Hu, Q.G.; Li, P. The near-field seismic vertical and horizontal response spectra and design spectra. Ind. Constr. 2013, 43, 57–60. [Google Scholar]
- Cui, X.L. The Isolation Performance Study of a New Three-Dimensional Seismic Isolation Pier; Hunan University: Changsha, China, 2016. [Google Scholar]
- Hason, M.M.; Hanoon, A.N.; Abdulhameed, A.A. Particle swarm optimization technique based prediction of peak ground acceleration of Iraq’s tectonic regions. J. King Saud Univ.-Eng. Sci. 2021; in press. [Google Scholar] [CrossRef]
- Xin, Y.Y. Importance of the vertical seismic effect. In Proceedings of the The Second Academic Symposium on Earthquake Prevention and Disaster Reduction Engineering, Kunming, China, 3–5 December 2005. [Google Scholar]
- Li, X.Y.; Xue, S.D. Mechanism and Devices for 3-dimensional seismic isolation Bearing in Vertical Direetion. J. Beijing Univ. Technol. 2008, 34, 1043–1047. [Google Scholar]
- Han, J.P.; Zhou, W. Preliminary investigation on characteristics of vertical ground motion during Wenchuan earthquake. Eng. Mech. 2012, 29, 211–219. [Google Scholar]
- Zhou, W. Analysis on Seismic Performance of Reinforced Concrete Frame Structure including Vertical Ground Motion Based on Wenchuan Earthquake; Lanzhou University of Technology: Lanzhou, China, 2011. [Google Scholar]
- Elagamal, A.; He, L. Vertical Earthquake Ground motion records: An overview. J. Earthq. Eng. 2012, 8, 663–697. [Google Scholar] [CrossRef]
- Wu, D.; Tan, P. Research on vertical strong ground motion simulation of Fukuoka earthquake. J. Guangzhou Univ. 2013, 12, 40–43. [Google Scholar]
- Dang, Y.; Huo, K.C. Vertical earthquake response of multi-storey isolated buildings. J. Earthq. Eng. Eng. 2010, 30, 139–145. [Google Scholar]
- He, Z.J.; Ding, J.M.; Lu, T.T. Vertical earthquake action analysis for mega frame-core tube structure of the Shanghai Tower. J. Build. Struct. 2014, 35, 27–33. [Google Scholar]
- Li, Y. Research on Seismic Behavior of Piers Considering Vertical Earthquake Force; Chang’an University: Xi’an, China, 2015. [Google Scholar]
- Castiglioni, C.A.; Kanyılmaz, A. Vertical Seismic Isolation of Ancient Statues Displayed in Base Isolated Museum Buildings. In Proceedings of the XIV European Conference on Earthquake Engineering, Ohrid, North Macedonia, 30 August–3 September 2010. [Google Scholar]
- Zhou, Z.G.; Sun, C.X. Seismic response analysis of Fukushima nuclear power plants under the 2011 Great Eastern Japan Earthquake. J. Earthq. Eng. Eng. Vib. 2016, 1, 8–15. [Google Scholar]
- Ma, L.; Shi, Q.; Wang, B.; Tao, Y.; Wang, P. Research on design and numerical simulation of self-centering prefabricated RC beam-column joint with pre-pressed disc spring devices. Soil Dyn. Earthq. Eng. 2023, 166, 107762. [Google Scholar] [CrossRef]
- Chou, C.C.; Chung, P.T. Development of cross-anchored dual-core self-centering braces for seismic resistance. J. Constr. Steel Res. 2014, 101, 19–32. [Google Scholar] [CrossRef]
- Xiao, F. Design of New Type Three-Dimensional Seismic Isolation Device and Application Study in Ancient Timber Structure; Guangzhou University: Guangzhou, China, 2018. [Google Scholar]
- Almen, J.O.; Laszlo, A. The uniform-section disk spring. Trans. Am. Soc. Mech. Eng. 1936, 58, 305–314. [Google Scholar] [CrossRef]
- Zheng, L.J. Study on Theoretical Analysis and Numerical Simulation of the Load in Conical Disk Springs. Mach. Des. Manuf. Eng. 2002, 31, 12–13. [Google Scholar]
- Zhang, T.S. Discuss on Assumptions of the Almen-Laszlo Equation for Diaphragm Spring. Automob. Technol. 2003, 12, 12–14. [Google Scholar]
- Ozaki, S.; Tsuda, K.; Tominaga, J. Analyses of static and dynamic behavior of coned disk springs: Effects of friction boundaries. Thin-Walled Struct. 2012, 59, 132–143. [Google Scholar] [CrossRef]
- Sun, L.M.; Wang, X.B.; Shi, L. Research on stiffness of combination disk spring. J. Zhengzhou Univ. 2007, 28, 120–123, 127. [Google Scholar]
- Fawazi, N.; Lee, J.Y. An improved load-displacement prediction for a coned disc spring using the energy method. ARPN J. Eng. Appl. Sci. 2016, 11, 833–836. [Google Scholar]
- Xu, L.H.; Fan, X.W.; Li, Z.X. Development and experimental verification of a prepressed spring self-centering energy dis-sipation brace. Eng. Struct. 2016, 127, 49–61. [Google Scholar] [CrossRef]
- Noureldin, M.; Memon, S.A.; Gharagoz, M.; Kim, J. Performance-based seismic retrofit of RC structures using concentric braced frames equipped with friction dampers and disc springs. Eng. Struct. 2021, 243, 112555. [Google Scholar] [CrossRef]
- Dong, H.H.; Du, X.L.; Han, Q.; Hao, H.; Bi, K.M.; Wang, X.Q. Performance of an innovative self-centering buckling restrained brace for mitigating seismic responses, of bridge structures with double column piers. Eng. Struct. 2017, 148, 47–62. [Google Scholar] [CrossRef]
- Fan, X.W.; Xu, L.H.; Li, Z.X. Seismic performance evaluation of steel frames with pre-pressed spring self-centering braces. J. Constr. Steel Res. 2019, 162, 105761. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.; Waters, T. Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic. J. Sound Vib. 2007, 301, 678–689. [Google Scholar] [CrossRef]
- Kovacic, I.; Brennan, M.J.; Waters, T.P. A study of a nonlinear vibration isolator with a quasi-zero stiffness characteristic. J. Sound Vib. 2008, 315, 700–711. [Google Scholar] [CrossRef]
- João, G.; Luís, G.; Seyedsajjad, H.; Rita, M.; João, G.F. The Design of a Structural Hy-per-Resisting Element for Life-Threatening Earthquake Risk (SHELTER) for Building Collapse Scenarios: The Safety Chairs. Appl. Sci. 2022, 12, 4103. [Google Scholar]
- Wang, X.B. A Study on the Mechanical Properties of Disc Springs; Zhengzhou University: Zhengzhou, China, 2007. [Google Scholar]
- Cai, Y. Test Research of Disc Spring Vertical Isolation Device; Guangzhou University: Guangzhou, China, 2012. [Google Scholar]








| D (mm) | d (mm) | t (mm) | h0 (mm) | H0 (mm) | F = 0.75h0 | ||
|---|---|---|---|---|---|---|---|
| f (mm) | F (kN) | σII/σIII (N/mm2) | |||||
| 250 | 127 | 14 | 5.6 | 19.6 | 4.2 | 249 | 1220 |
| Loading Type | μ1 | μ2 | Maximum Deformation | Numerical Simulation I (kN) | Theoretical Calculation II (kN) | Error |(I − II)/I| × 100% |
|---|---|---|---|---|---|---|
| Linear loading | 0.005 | 0.2 | 44.8 mm | 727 | 647 | 11.01% |
| 0.3 | 44.8 mm | 678 | 647 | 4.58% | ||
| 0.4 | 44.8 mm | 685 | 647 | 5.48% | ||
| 0.5 | 44.8 mm | 732 | 647 | 11.60% | ||
| 0.6 | 44.8 mm | 736 | 647 | 12.05% | ||
| Sin-function loading | 0.005 | 0.2 | 44.8 mm | 670 | 647 | 3.33% |
| 0.3 | 44.8 mm | 675 | 647 | 4.14% | ||
| 0.4 | 44.8 mm | 681 | 647 | 5.04% | ||
| 0.5 | 44.8 mm | 688 | 647 | 5.97% | ||
| 0.6 | 44.8 mm | 696 | 647 | 7.51% |
| Loading Type | μ1 | μ2 | Maximum Deformation | Numerical Simulation/I | Theoretical Calculation/II | Error |(I − II)/I| × 100% |
|---|---|---|---|---|---|---|
| Linear loading | 0.005 | 0.3 | 44.8 mm | 643,225 N | 647,028 N | 0.59% |
| Sin-function loading | 0.005 | 0.3 | 44.8 mm | 635,456 N | 647,028 N | 1.82% |
| Outer Diameter D (mm) | Inner Diameter d (mm) | Thickness t (mm) | Free Height h0 (mm) | Total Height H0 (mm) | Deformation f = 0.75h0 | ||
|---|---|---|---|---|---|---|---|
| f (mm) | F (kN) | σII or σIIIc (N/mm2) | |||||
| 140 | 72 | 8 | 3.2 | 11.2 | 2.4 | 75.3 | 1280 |
| Case | Pre-Compression Deformation/mm | Loading Frequency/Hz | Loading Amplitude/mm |
|---|---|---|---|
| 1~4 | 6.0 | 0.5/1.0/1.5/2.0 | 6.0 |
| 5~8 | 8.0 | 0.5/1.0/1.5/2.0 | 6.0 |
| 9~12 | 10.0 | 0.5/1.0/1.5/2.0 | 6.0 |
| 13~15 | 10.0 | 1.0 | 4.0/8.0/10.0 |
| Loading | Items | Theory | Simulation | Test | Error IV = (I − III)/I × 100% | Error V=(II − III)/II × 100% |
|---|---|---|---|---|---|---|
| Static compression test | f = 0.75h0 | 24 mm | 24 mm | 24 mm | 0 | 0 |
| P (0.75h0) | 171 kN | 171 kN | 178 kN | −3.82% | −4.21% | |
| f = h0 | 32 mm | 32 mm | 32 mm | 0 | 0 | |
| P (h0) | 223 kN | 249 kN | 227 kN | −1.77% | 8.97% | |
| Static tension test | f = 0.75h0 | 24 mm | 24 mm | 24 mm | 0 | 0 |
| P (0.75h0) | 171 kN | 171 kN | 183 kN | −7.32% | −7.73% | |
| f = h0 | 32 mm | 32 mm | 32 mm | 0 | 0 | |
| P (h0) | 223 kN | 249 kN | 232 kN | −4.47% | 6.56% |
| Case | Frequency (Hz) | Equivalent Stiffness (kN/mm) | Error (I − II)/I × 100% | Equivalent Damping Ratio | Error (III − IV)/III × 100% | ||
|---|---|---|---|---|---|---|---|
| Test/I | Simulation/II | Test/III | Simulation/IV | ||||
| 1 | 0.5 | 5.41 | 5.11 | 5.55% | 0.076 | 0.075 | 1.32% |
| 2 | 1 | 5.4 | 5.36 | 0.74% | 0.075 | 0.077 | −2.67% |
| 3 | 1.5 | 5.29 | 5.29 | 0.00% | 0.07 | 0.075 | −7.14% |
| 4 | 2 | 5.27 | 5.27 | 0.00% | 0.071 | 0.078 | −9.86% |
| 5 | 0.5 | 6.58 | 6.55 | 0.46% | 0.089 | 0.086 | 3.37% |
| 6 | 1 | 6.49 | 6.28 | 3.24% | 0.086 | 0.091 | −5.81% |
| 7 | 1.5 | 6.49 | 6.11 | 5.86% | 0.087 | 0.09 | −3.45% |
| 8 | 2 | 6.45 | 6.01 | 6.82% | 0.087 | 0.091 | −4.60% |
| 9 | 0.5 | 7.6 | 7.63 | −0.39% | 0.153 | 0.158 | −3.27% |
| 10 | 1 | 7.56 | 7.39 | 2.25% | 0.107 | 0.1 | 6.54% |
| 11 | 1.5 | 7.48 | 7.21 | 3.61% | 0.107 | 0.101 | 5.61% |
| 12 | 2 | 7.45 | 7.19 | 3.49% | 0.109 | 0.108 | 0.92% |
| 13 | 1 | 8.21 | 8.07 | 1.71% | 0.086 | 0.078 | 9.30% |
| 14 | 1 | 6.76 | 6.75 | 0.15% | 0.107 | 0.112 | −4.67% |
| 15 | 1 | 6.14 | 6.12 | 0.33% | 0.143 | 0.134 | 6.29% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wu, X.; Ji, S.; Xiao, F.; Wang, D. Evaluation of Mechanical Performance of a New Disc Spring-Cable Counter Pressure Shock Absorber. Appl. Sci. 2023, 13, 8718. https://doi.org/10.3390/app13158718
Wang Y, Wu X, Ji S, Xiao F, Wang D. Evaluation of Mechanical Performance of a New Disc Spring-Cable Counter Pressure Shock Absorber. Applied Sciences. 2023; 13(15):8718. https://doi.org/10.3390/app13158718
Chicago/Turabian StyleWang, Yanfeng, Xiaohui Wu, Shaofeng Ji, Faping Xiao, and Dayang Wang. 2023. "Evaluation of Mechanical Performance of a New Disc Spring-Cable Counter Pressure Shock Absorber" Applied Sciences 13, no. 15: 8718. https://doi.org/10.3390/app13158718
APA StyleWang, Y., Wu, X., Ji, S., Xiao, F., & Wang, D. (2023). Evaluation of Mechanical Performance of a New Disc Spring-Cable Counter Pressure Shock Absorber. Applied Sciences, 13(15), 8718. https://doi.org/10.3390/app13158718





