Study on the Yield Behavior of Closed-Cell Foams under Multiaxial Loads Based on Different Yield Definitions
Abstract
:1. Introduction
2. Methodology
2.1. The Finite Element Model
2.2. Mechanical Properties of Bulk Materials
2.3. Basic Loading Conditions
2.4. The Macro Normal Stresses and Strain
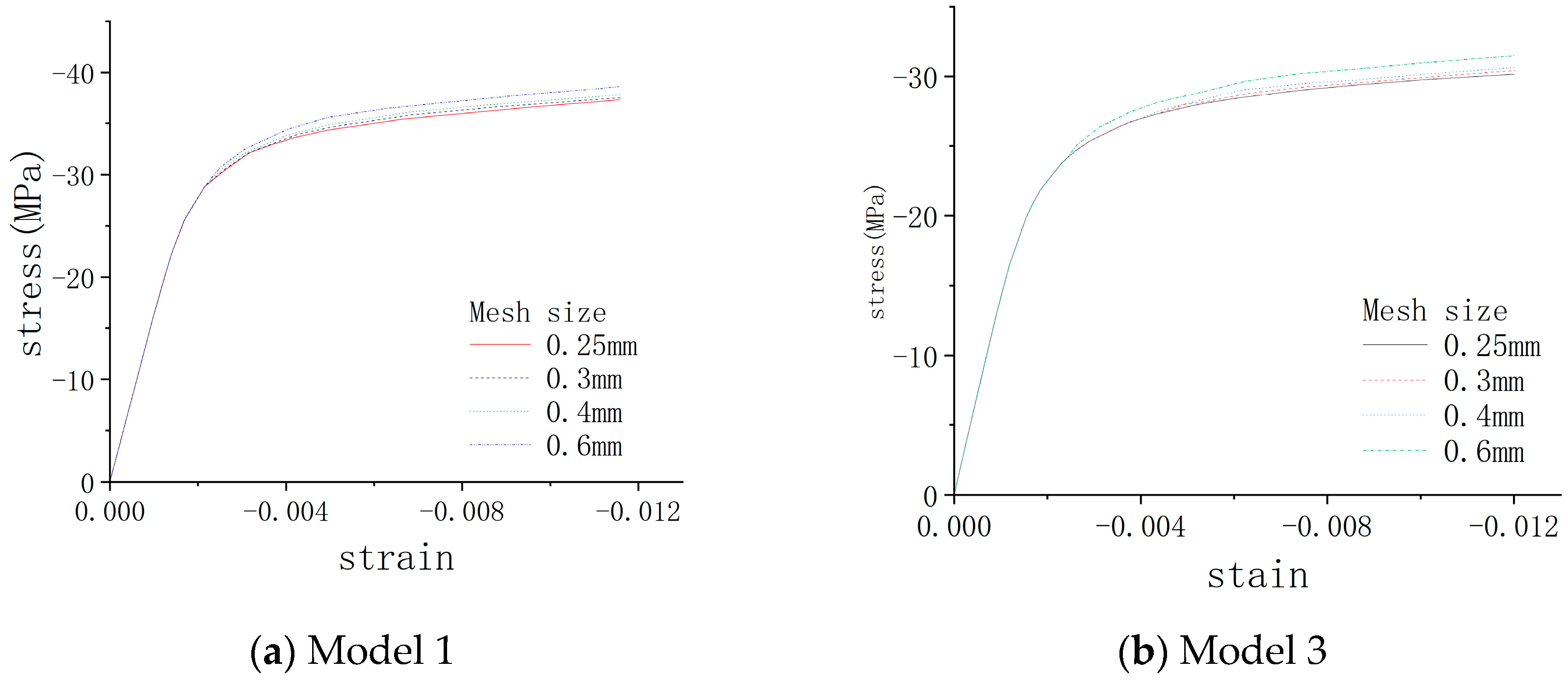
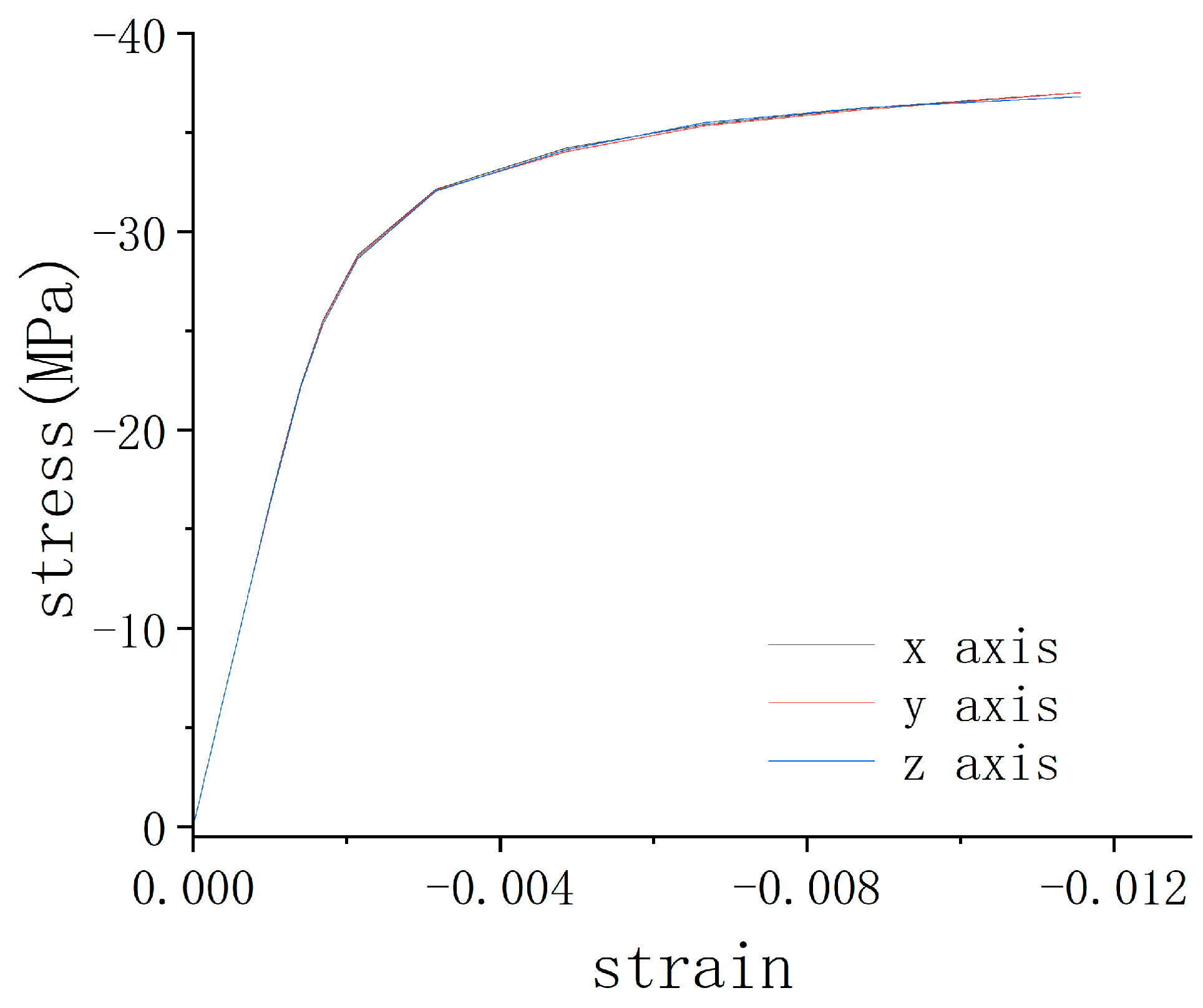
2.5. Mesh Convergence Analysis
2.6. Multiaxial Loading Conditions
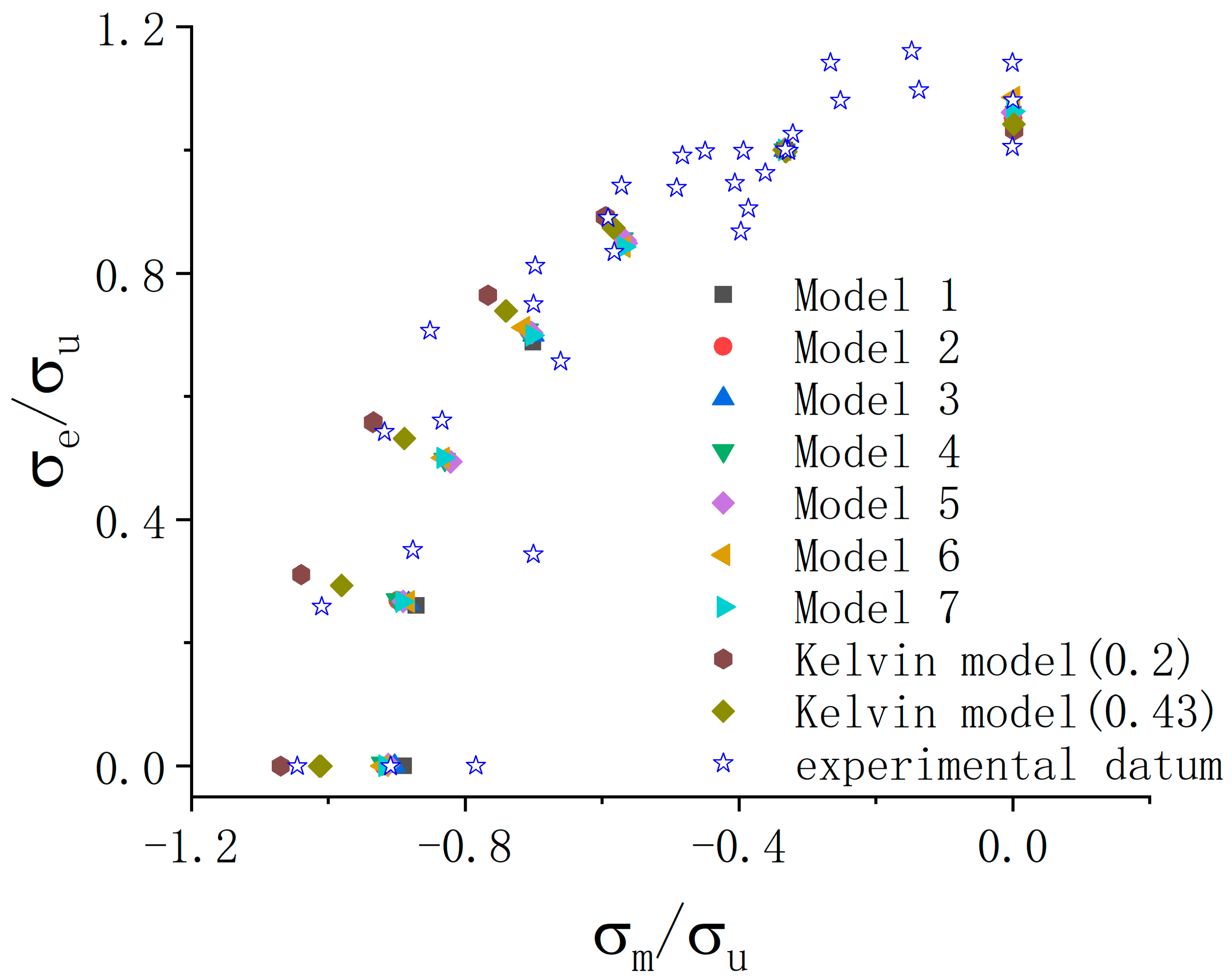
3. Results and Discussion
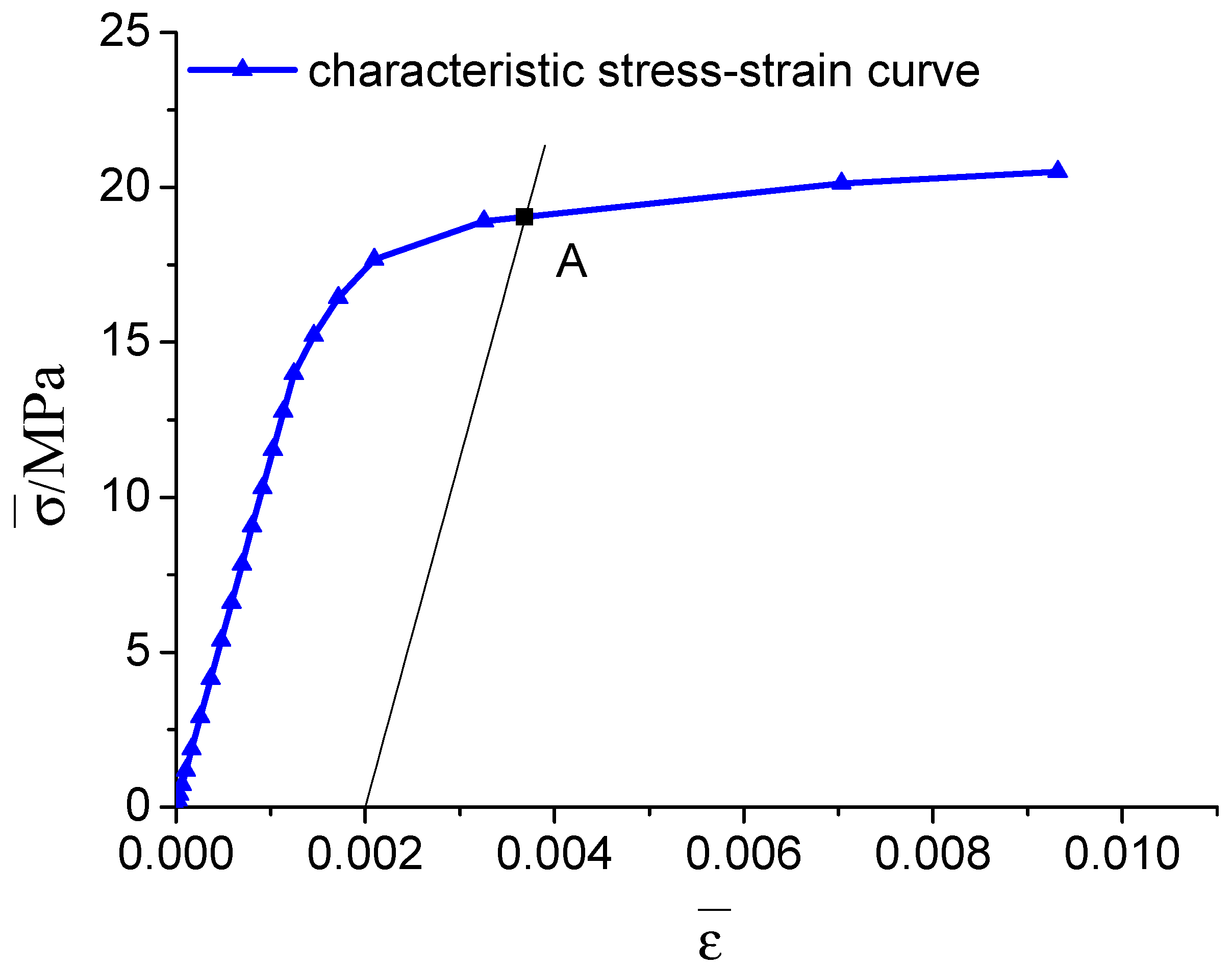
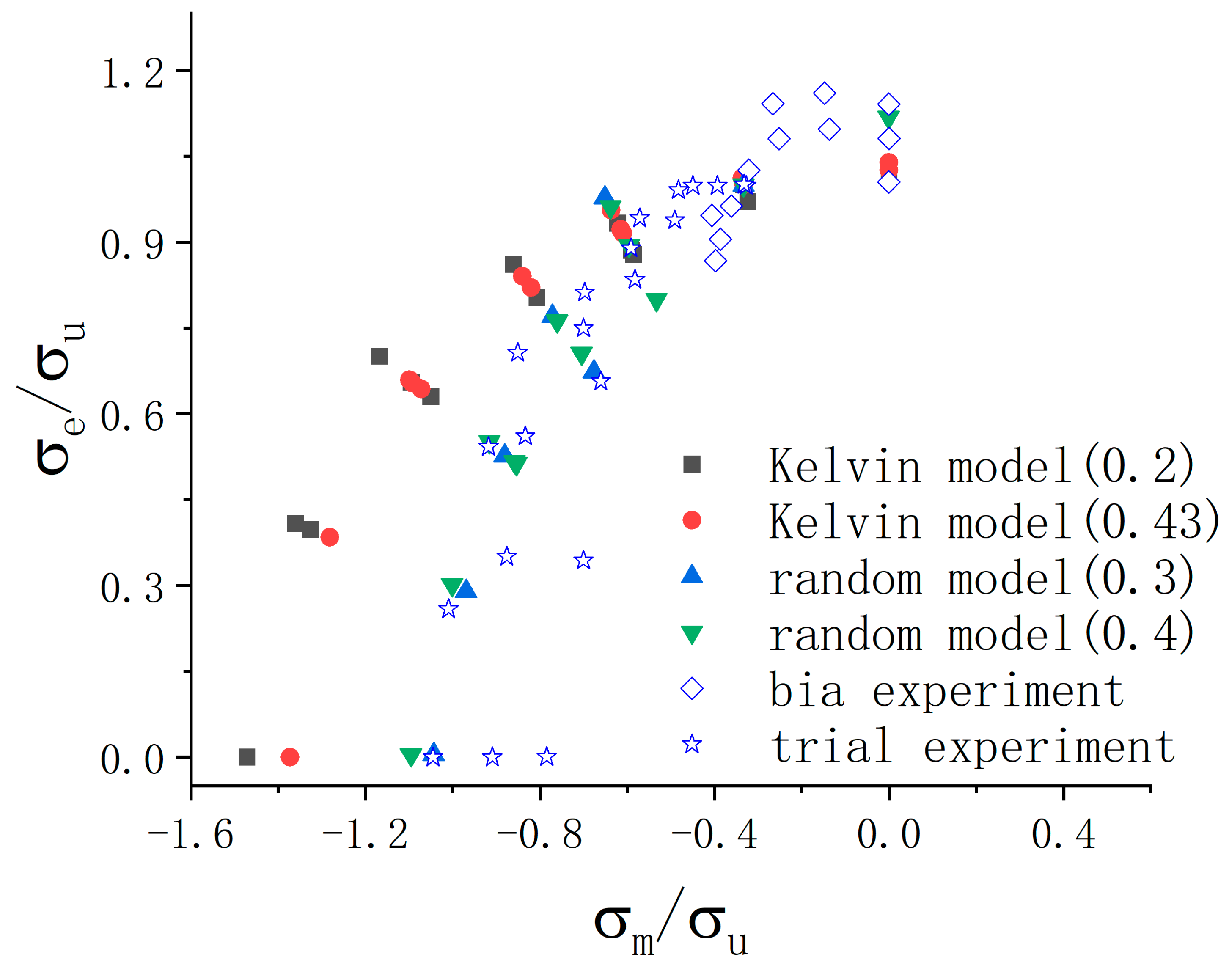
3.1. Yield Points Defined by 0.2% offset of the Characteristic Plastic Strain
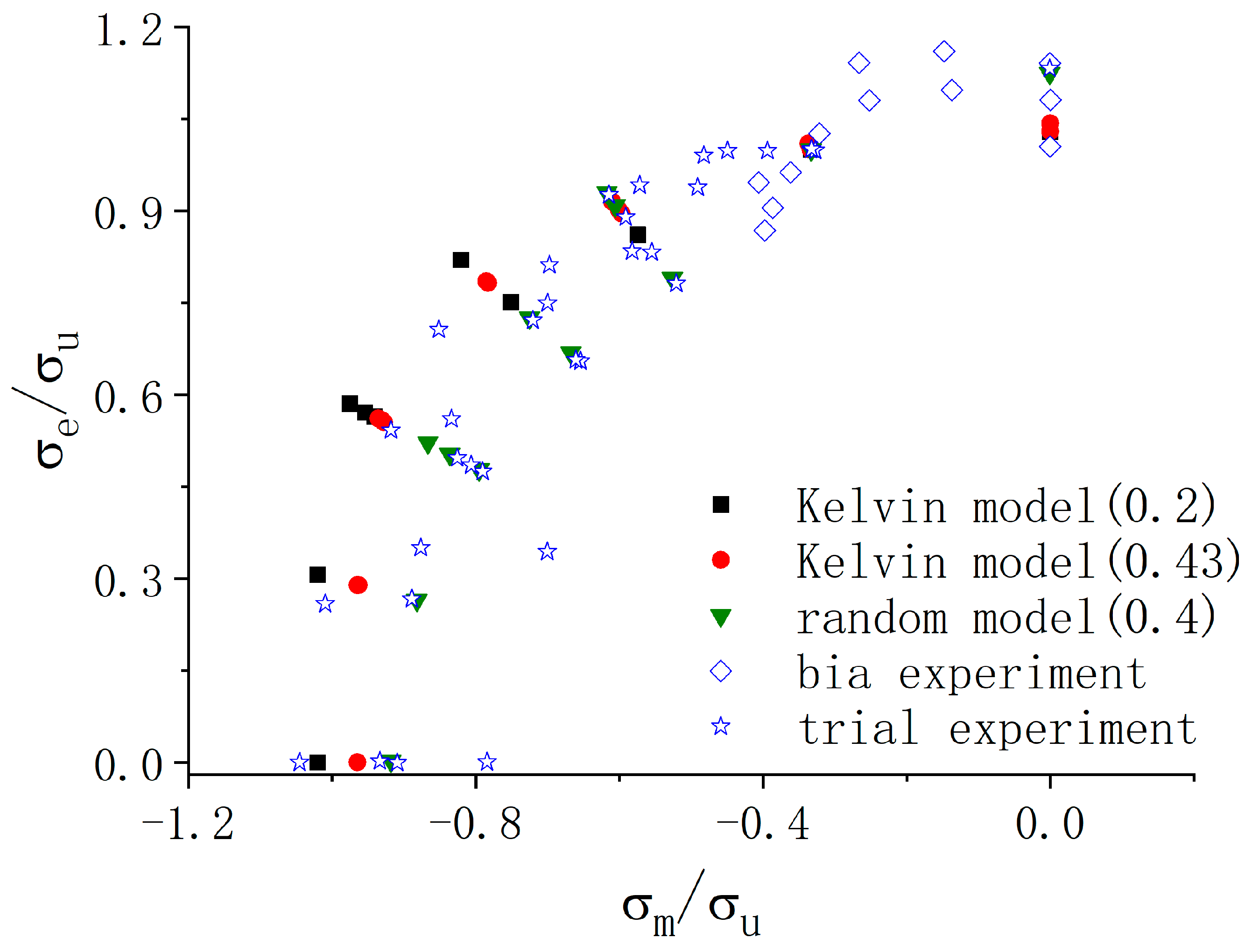
3.2. Yield Points Defined by the Critical Plastic Dissipation Energy
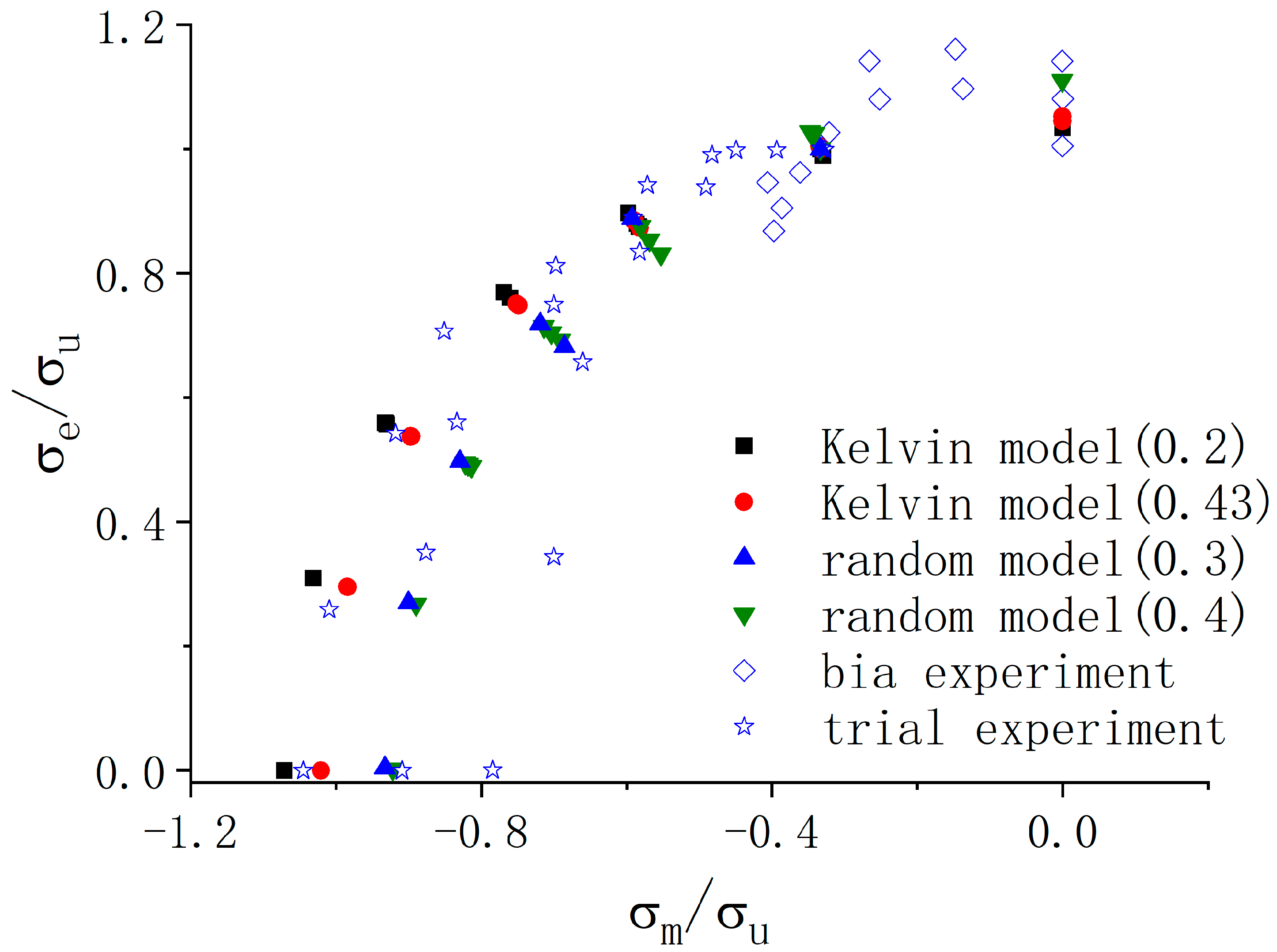
3.3. Yield Points Defined by the Critical Plastic Dissipation Energy at the Microscopic Scale
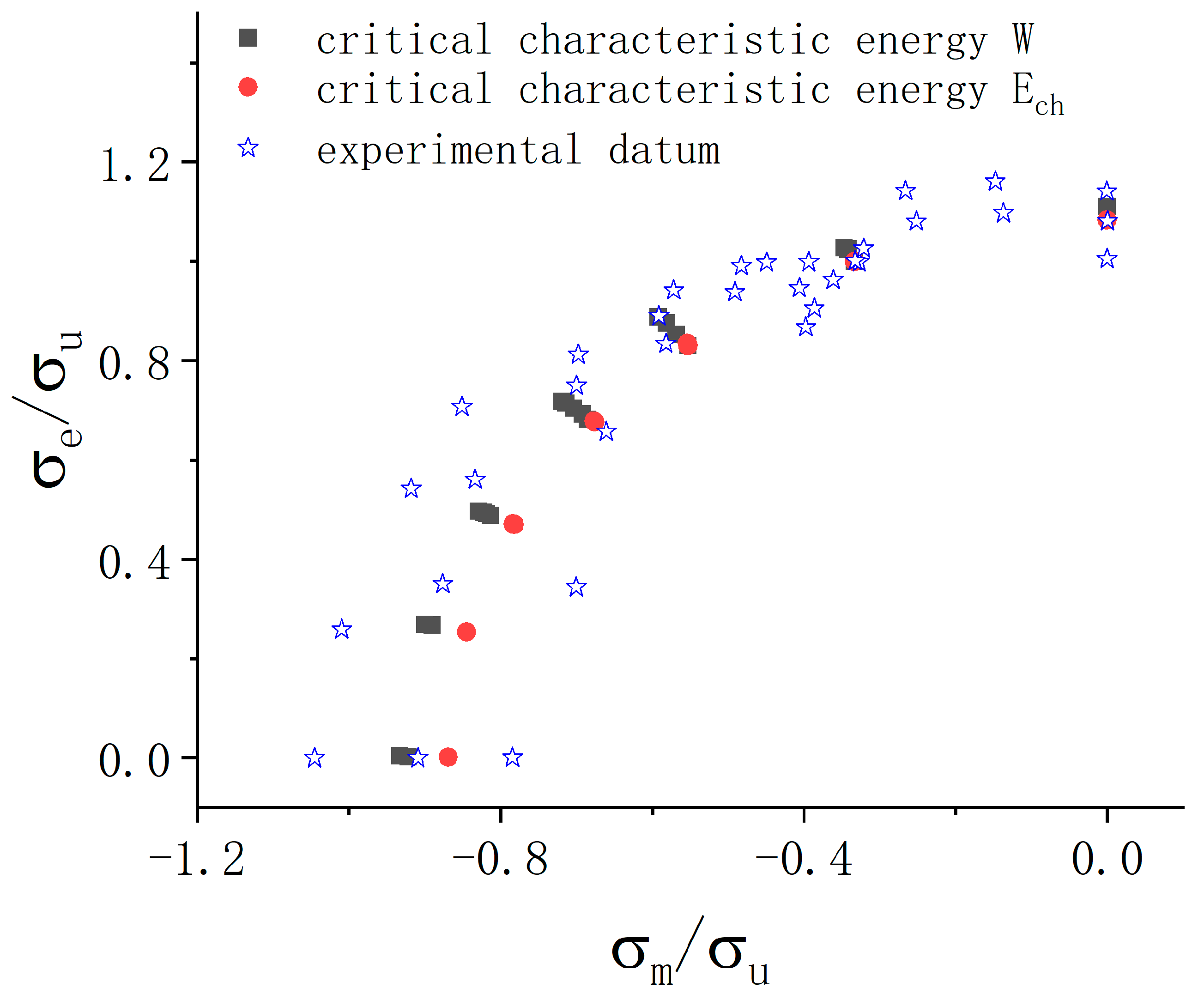
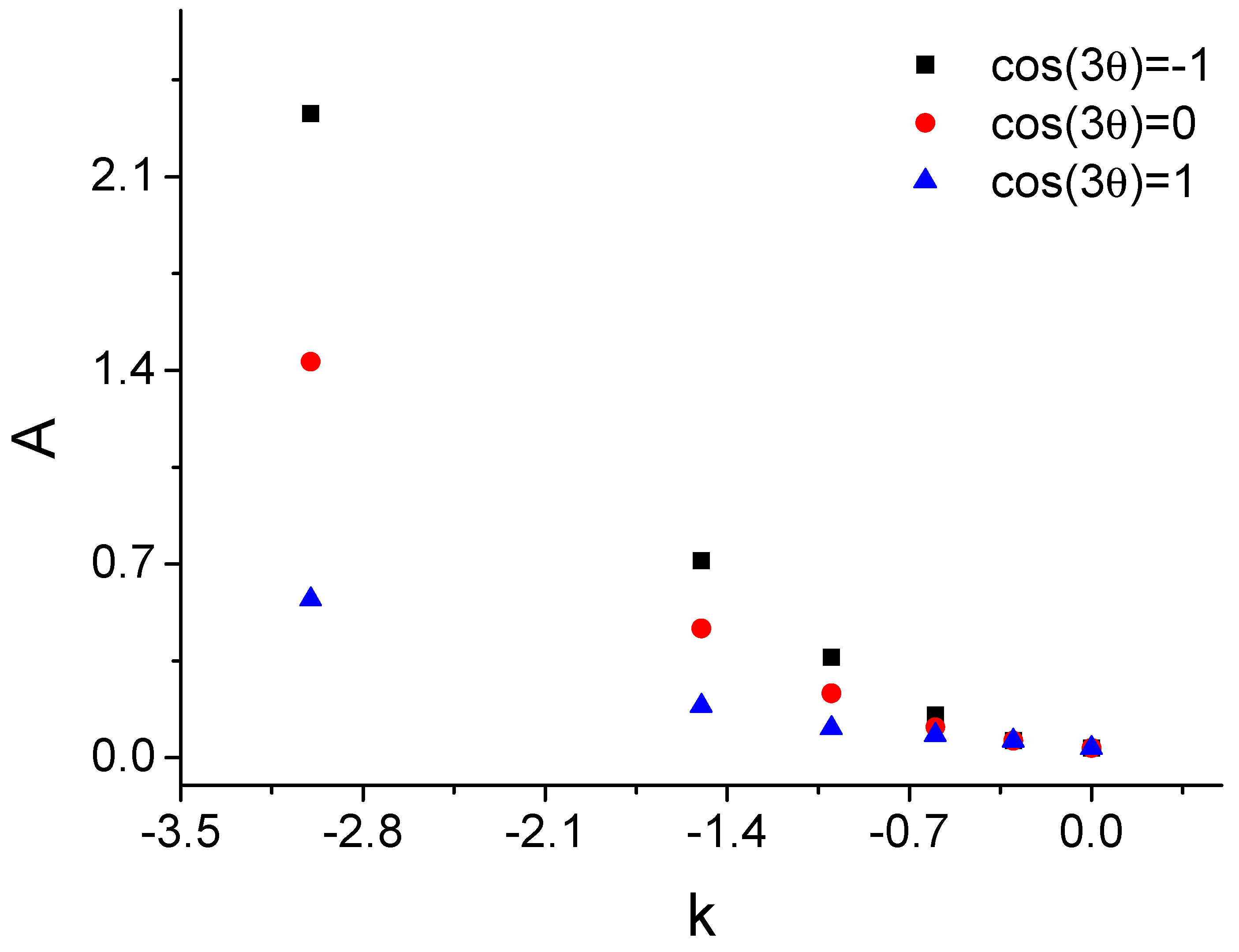
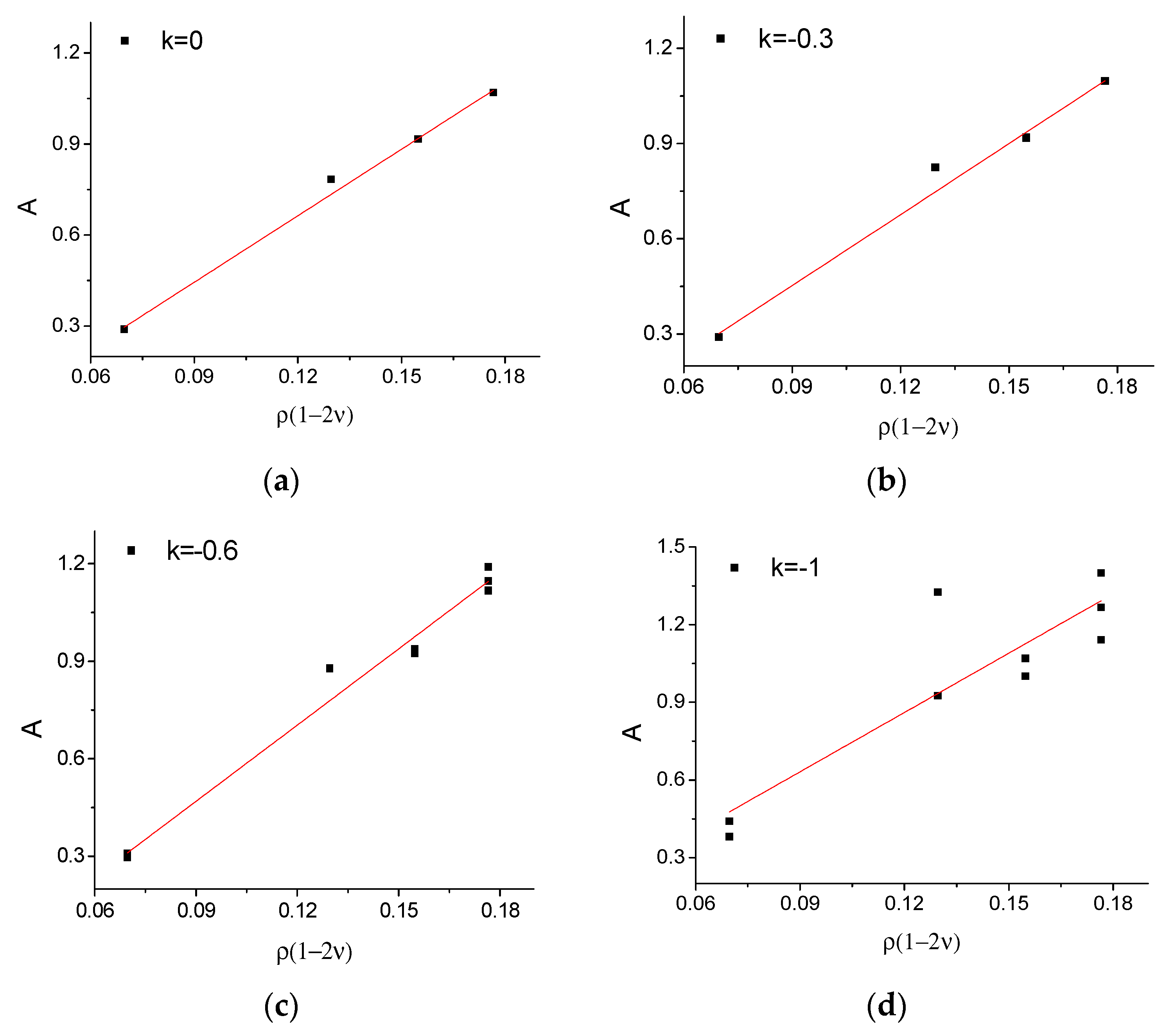
3.4. Yield Points Defined by the Critical Characteristic Energy
3.5. Yield Points Defined by the Critical Characteristic Energy
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Doyoyo, M.; Wierzbicki, T. Experimental studies on the yield behavior of ductile and brittle aluminum foams. Int. J. Plast. 2003, 19, 1195–1214. [Google Scholar] [CrossRef]
- Mohr, D.; Doyoyo, M. A new method for the biaxial testing of cellular solids. Exp. Mech. 2003, 43, 173–182. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, Z.; Zhao, L.; Shu, X. Loading rate effect on yield surface of aluminum alloy foams. Mat. Sci. Eng. A 2012, 543, 193–199. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, Z.; Zhao, L.; Shu, X. Uniaxial and biaxial failure behaviors of aluminum alloy foams. Compos. Part B Eng. 2014, 61, 340–349. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A. Isotropic constitutive models for metallic foams. J. Mech. Phys. Solids 2000, 48, 1253–1283. [Google Scholar] [CrossRef] [Green Version]
- Deshpande, V.S.; Fleck, N.A. Multi-axial yield behaviour of polymer foams. Acta Mater. 2001, 49, 1859–1866. [Google Scholar] [CrossRef]
- Gioux, G.; Mccormack, T.M.; Gibson, L.J. Failure of aluminum foams under multiaxial loads. Int. J. Mech Sci. 2000, 42, 1097–1117. [Google Scholar] [CrossRef]
- Sridhar, I.; Fleck, N.A. The multiaxial yield behaviour of an aluminium alloy foam. J. Mater. Sci. 2005, 40, 4005–4008. [Google Scholar] [CrossRef]
- Bailly, N.; Petit, Y.; Desrosier, J.M.; Laperriere, O.; Langlois, S.; Wagnac, E. Strain Rate Dependent Behavior of Vinyl Nitrile Helmet Foam in Compression and Combined Compression and Shear. Appl. Sci. 2020, 10, 8286. [Google Scholar] [CrossRef]
- Ruan, D.; Lu, G.; Ong, L.S.; Wang, B. Triaxial compression of aluminium foams. Compos. Sci. Technol. 2007, 67, 1218–1234. [Google Scholar] [CrossRef]
- Peroni, L.; Avalle, M.; Peroni, M. The mechanical behaviour of aluminium foam structures in different loading conditions. Int. J. Impact. Eng. 2008, 35, 644–658. [Google Scholar] [CrossRef]
- Combaz, E.; Bacciarini, C.; Charvet, R.; Dufour, W.; Dauphin, F.; Mortensen, A. Yield surface of polyurethane and aluminium replicated foam. Acta Mater. 2010, 58, 5168–5183. [Google Scholar] [CrossRef]
- Combaz, E.; Bacciarini, C.; Charvet, R.; Dufour, W.; Dauphin, F.; Mortensen, A. Multiaxial yield behaviour of Al replicated foam. J. Mech. Phys. Solids 2011, 59, 1777–1793. [Google Scholar] [CrossRef]
- Ayyagari, R.S.; Vural, M. Multiaxial yield surface of transversely isotropic foams: Part I modeling. J. Mech. Phys. Solids 2015, 74, 49–67. [Google Scholar] [CrossRef]
- Shafiq, M.; Ayyagari, R.S.; Ehaab, M.; Vural, M. Multiaxial yield surface of transversely isotropic foams: Part II Experimental. J. Mech. Phys. Solids 2015, 76, 224–736. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F.; Zhang, J.; Triantafillou, T.C. Failure surfaces for cellular materials under multiaxial loads—I. Modelling. Int. J. Mech. Sci. 1989, 31, 635–663. [Google Scholar] [CrossRef]
- Miller, R.E. A continuum plasticity model for the constitutive and indentation behaviour of foamed metals. Int. J. Mech Sci. 2000, 42, 729–754. [Google Scholar] [CrossRef]
- Vengatachalam, B.; Poh, L.H.; Liu, Z.S.; Qin, Q.H.; Swaddiwudhipong, S. Initial yield behaviour of closed-cell aluminium foams in biaxial loading. Int. J. Mech. Sci. 2021, 191, 106063. [Google Scholar] [CrossRef]
- Mills, N.J. Deformation mechanisms and the yield surface of low-density, closed-cell polymer foams. J. Mater. Sci. 2010, 45, 5831–5843. [Google Scholar] [CrossRef]
- Nammi, S.K.; Myler, P.; Edwards, G. Finite element analysis of closed-cell aluminium foam under quasi-static loading. Mater. Design 2010, 31, 712–722. [Google Scholar] [CrossRef]
- Ye, W.; Barbier, C.; Zhu, W.; Combescure, A.; Baillis, D. Macroscopic multiaxial yield and failure surfaces for light closed-cell foams. Int. J. Solids Struct. 2015, 69–70, 60–70. [Google Scholar] [CrossRef]
- Chen, Y.; Das, R.; Battley, M.; Xu, Z. Compressive and shear strengths of the ductile closed-cell Kelvin and Weaire-Phelan foams along the lattice direction [100]. Thin-Wall. Struct. 2018, 132, 237–249. [Google Scholar] [CrossRef]
- Kader, M.A.; Islam, M.A.; Saadatfar, M.; Hazell, P.J.; Brown, A.D.; Ahmed, S.; Escobedo, J.P. Macro and micro collapse mechanisms of closed-cell aluminium foams during quasi-static compression. Mater. Des. 2017, 118, 11–21. [Google Scholar] [CrossRef]
- Wang, E.D.; Sun, G.; Zheng, G.Y.; Li, Q. Characterization of initial and subsequent yield behaviors of closed-cell aluminum foams under multiaxial loadings. Compos. Part B Eng. 2020, 202, 108247. [Google Scholar] [CrossRef]
- Wang, E.D.; Sun, G.; Zheng, G.Y.; Li, Q. On multiaxial failure behavior of closed-cell aluminum foams under medium strain rates. Thin-Wall. Struct. 2021, 160, 107278. [Google Scholar] [CrossRef]
- Luo, G.; Xue, P.; Sun, S. Investigations on the yield behavior of metal foam under multiaxial loadings by an imaged-based mesoscopic model. Int. J. Mech. Sci. 2018, 142, 153–162. [Google Scholar] [CrossRef]
- Zhang, J.L.; Lu, Z.X. Numerical modeling of the compression process of elastic open-cell foams. Chin. J. Aeronaut. 2007, 20, 215–222. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Qiao, D.; Tang, L.; Liu, Z.; Liu, Y.; Jiang, Z.; Zhou, L. Global topology of yield surfaces of metallic foams in principal-stress space and principal-strain space studied by experiments and numerical simulations. Int. J. Mech. Sci. 2017, 134, 562–575. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, L.; Liu, Z.; Jiang, Z.; Liu, Y.; Wu, Y. Yield properties of closed-cell aluminum foam under triaxial loadings by a 3D Voronoi model. Mech. Mater. 2017, 104, 73–84. [Google Scholar] [CrossRef]
- Vengatachalam, B.; Poh, L.H.; Liu, Z.S.; Qin, Q.H.; Swaddiwudhipong, S. Three dimensional modelling of closed-cell aluminium foams with predictive macroscopic behaviour. Mech. Mater. 2019, 136, 103067. [Google Scholar] [CrossRef]
- Hu, Y.; Fang, Q.Z.; Qian, J. Effect of cell structure on the uniaxial compression properties of closed-cell foam materials. Mater. Today Commun. 2021, 26, 102–104. [Google Scholar] [CrossRef]
- Hu, Y.; Fang, Q.Z.; Sha, B.L.; Zhao, M.D. Effect of the large cells on the fatigue properties of closed-cell aluminum alloy foam. Compos. Struct. 2018, 200, 59–68. [Google Scholar] [CrossRef]
- Hu, Y.; Fang, Q.Z.; Yu, H.M.; Hu, Q.W. Numerical simulation on thermal properties of closed-cell metal foams with different cell size distributions and cell shapes. Mater. Today Commun. 2020, 24, 100968. [Google Scholar] [CrossRef]
- Veyhl, C.; Fiedler, T.; Herzig, T. Thermal Conductivity Computations of Sintered Hollow Sphere Structures. Metals 2012, 2, 113–121. [Google Scholar] [CrossRef] [Green Version]
- Fiedler, T.; Löffler, R.; Bernthaler, T.; Winkler, R.; Belova, I.V.; Murch, G.E.; Öchsner, A. Numerical analyses of the thermal conductivity of random hollow sphere structures. Mater. Lett. 2009, 63, 1125–1127. [Google Scholar] [CrossRef]
- Su, Y.; Li, Z.; Gong, X.; Ouyang, Q.; Guo, Q.; Guo, C. Structural modeling and mechanical behavior of Metal-Porous-Polymer-Composites (MPPCs) with different polymer volume fractions. Compos. Struct. 2016, 153, 673–681. [Google Scholar] [CrossRef]
- Serban, D.-A.; Negru, R.; Filipescu, H.; Marşavina, L. Investigations on the influence of the triaxial state of stress on the failure of polyurethane rigid foams. Contin. Mech. Thermodyn. 2020, 35, 905–918. [Google Scholar] [CrossRef]
- Chen, C.; Lu, T.J. A phenomenological framework of constitutive modelling for incompressible and compressible elasto-plastic solids. Int. J. Solids Struct. 2000, 37, 7769–7786. [Google Scholar] [CrossRef]
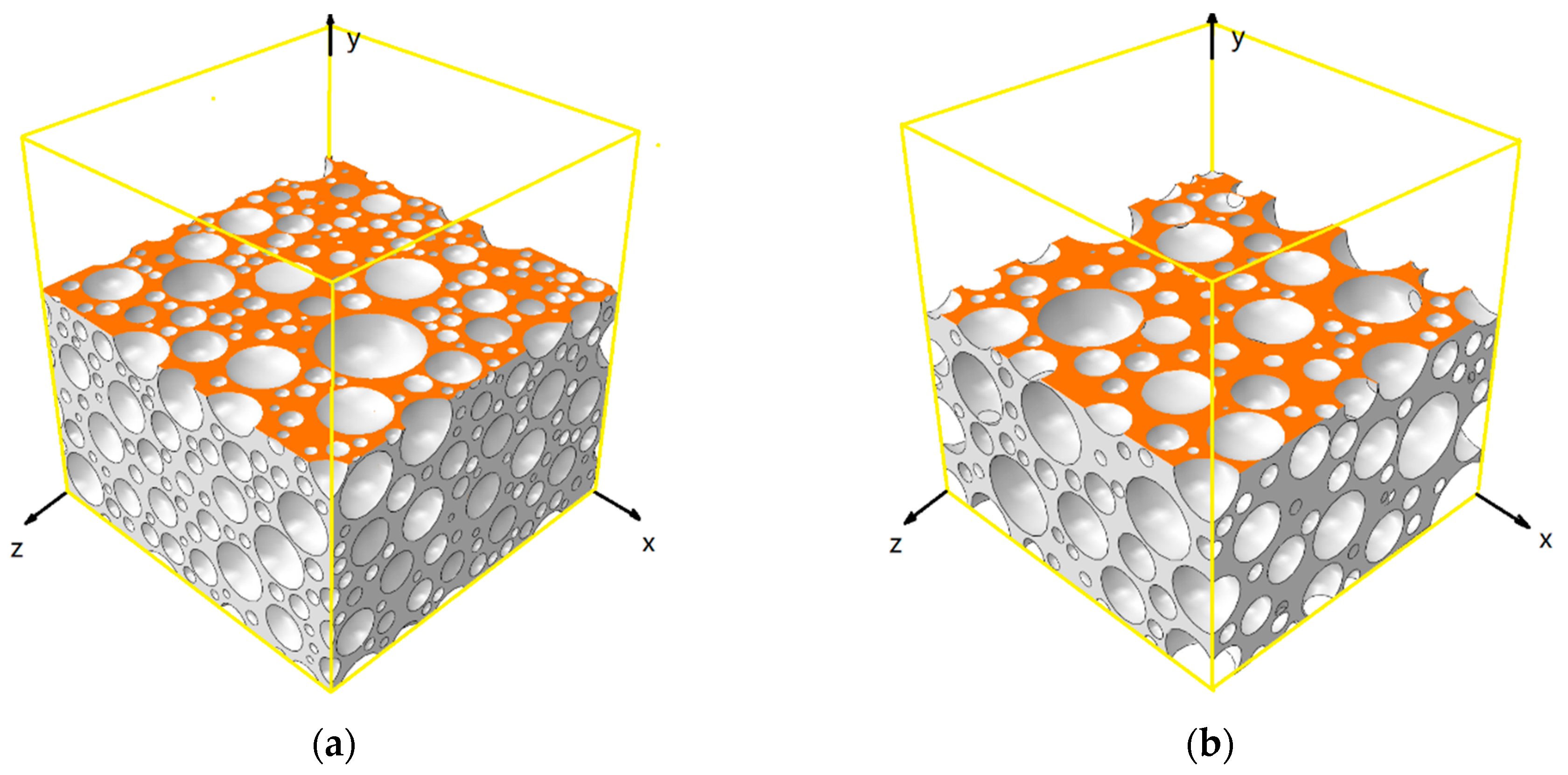
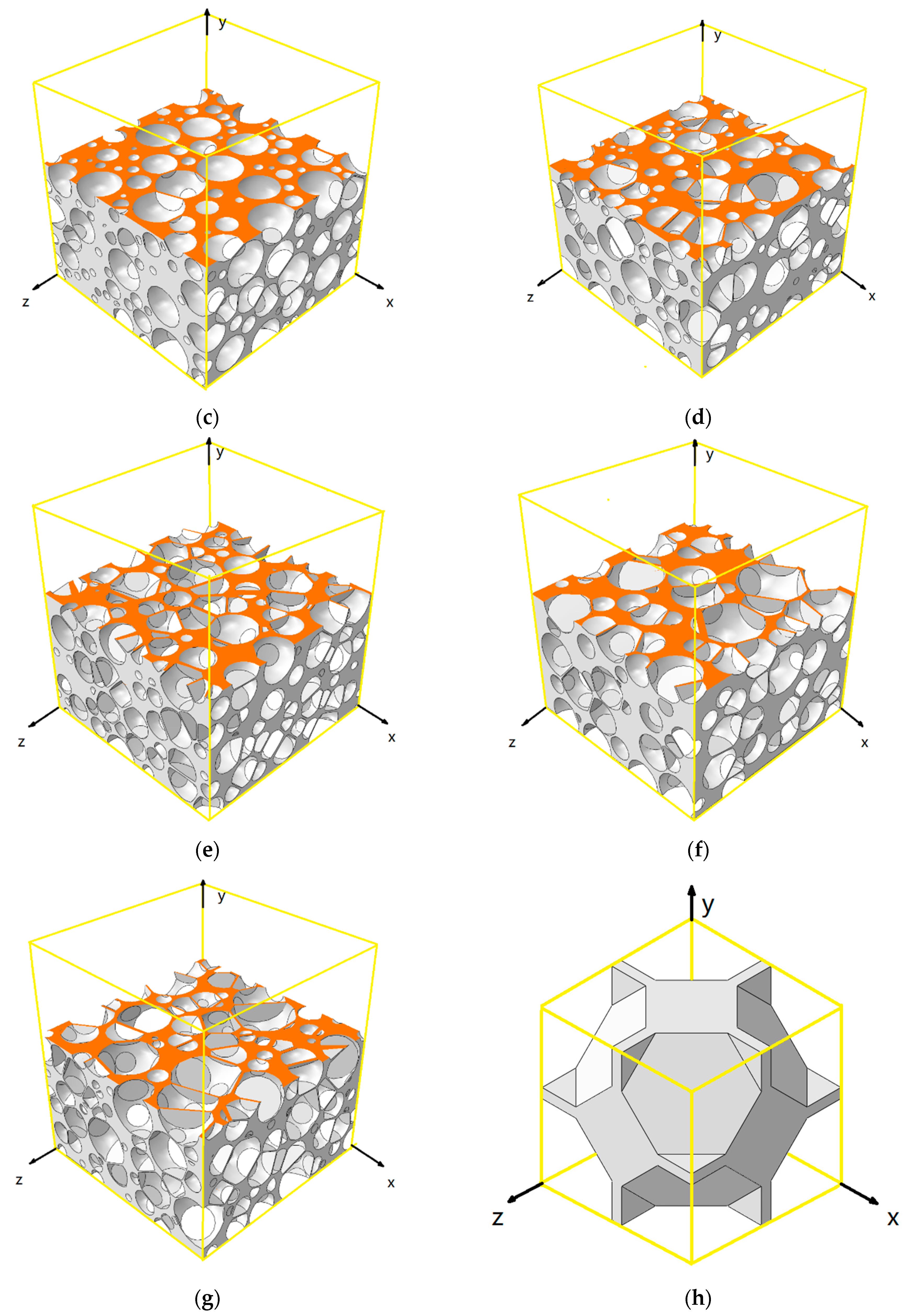


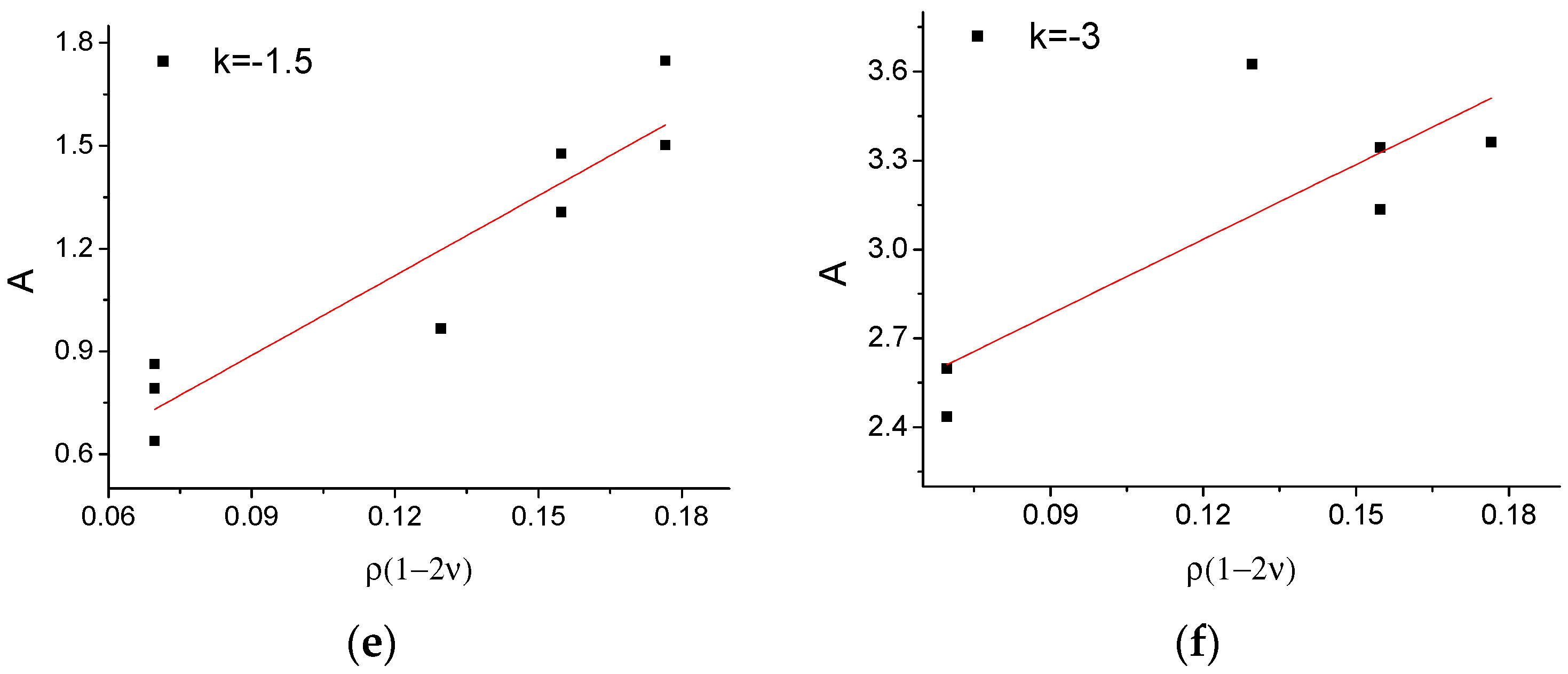
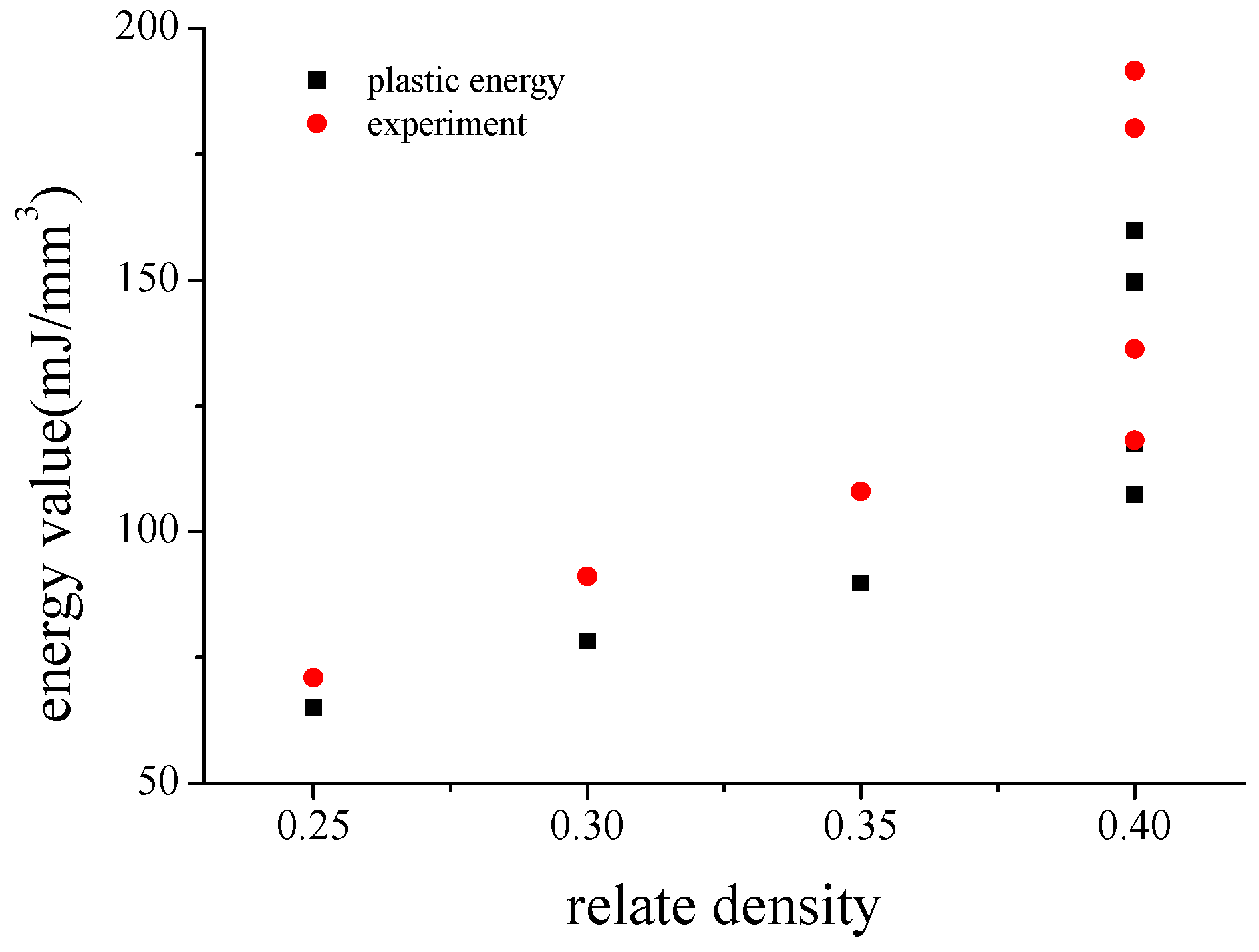

| Number | Relative Density | ||
|---|---|---|---|
| 1 | 0.4 | 3.11 | 0 |
| 2 | 0.4 | 3.79 | 0 |
| 3 | 0.4 | 3.3 | 0.026 |
| 4 | 0.4 | 3.29 | 0.06 |
| 5 | 0.35 | 3.41 | 0.088 |
| 6 | 0.3 | 3.68 | 0.101 |
| 7 | 0.25 | 3.71 | 0.102 |
| Material Parameter | Value |
|---|---|
| Elasticity modulus E/MPa | 72,400 |
| Poisson’s ratio | 0.33 |
| /MPa | 77.8 |
| /MPa | 140 |
| Model Number | Number of Element | |||
|---|---|---|---|---|
| Size 0.6 mm | Size 0.4 mm | Size 0.3 mm | Size 0.25 mm | |
| 1 | 121,478 | 305,784 | 585,765 | 867,593 |
| 3 | 104,871 | 259,658 | 457,528 | 862,369 |
| 1 | 1. | −2 | −1 | |
| 2 | −1 | −1 | 1 | |
| 0 | 0 | −1 | −3 | −1 |
| 1 | −1.366 | −3.732 | −3 | 0 |
| 1 | −2 | −2 | −3 | 1 |
| 1 | 1 | −4 | −1.5 | −1 |
| −0.134 | −1 | −1.8661 | −1.5 | 0 |
| 0 | −1 | −1 | −1.5 | 1 |
| −1 | −1 | −2.5 | −1 | −1 |
| −1 | −2.367 | −3.733 | −1 | 0 |
| −1 | −4 | −4 | −1 | 1 |
| −4 | −4 | −7 | −0.6 | −1 |
| −1.9364 | −3 | −4 | −0.6 | 0.0534 |
| −1 | −2 | −2 | −0.6 | 1 |
| −3 | −3 | −4 | −0.3 | −1 |
| −1 | −1.375 | −1.375 | −0.3 | 1 |
| −1 | −1 | −1 | 0 |
| Related Density | Plastic Dissipation Energy Per Unit Volume (×10−3 mJ/mm3) | |||||||
|---|---|---|---|---|---|---|---|---|
| Kelvin | Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | Model 6 | Model 7 | |
| 0.43 | 60.6 | |||||||
| 0.2 | 22.8 | |||||||
| 0.4 | 57.3 | 48.1 | 39.7 | 31.5 | ||||
| 0.35 | 21.4 | |||||||
| 0.3 | 20.1 | |||||||
| 0.25 | 15.7 | |||||||
| W (J/mm3) | ||||
|---|---|---|---|---|
| 0 | 0 | −1 | 0.03833 | 0.03373 |
| 1 | −1.366 | −3.732 | 0.03833 | 0.03537 |
| 1 | −2 | −2 | 0.03833 | 0.03742 |
| −1 | −1 | −4 | 0.03833 | 0.03381 |
| −0.134 | −1 | −1.8661 | 0.03833 | 0.03714 |
| 0 | −1 | −1 | 0.03833 | 0.0355 |
| −1 | −1 | −2.5 | 0.03833 | 0.03517 |
| −1 | −2.367 | −3.733 | 0.03833 | 0.03734 |
| −1 | −4 | −4 | 0.03833 | 0.0363 |
| −4 | −4 | −7 | 0.03833 | 0.03643 |
| −1.9364 | −3 | −4 | 0.03833 | 0.03726 |
| −1 | −2 | −2 | 0.03833 | 0.03689 |
| −3 | −3 | −4 | 0.03833 | 0.03742 |
| −1 | −1 | −1 | 0.03833 | 0.03776 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Fang, Q.; Qian, J.; Hu, Y. Study on the Yield Behavior of Closed-Cell Foams under Multiaxial Loads Based on Different Yield Definitions. Appl. Sci. 2023, 13, 8732. https://doi.org/10.3390/app13158732
Yu H, Fang Q, Qian J, Hu Y. Study on the Yield Behavior of Closed-Cell Foams under Multiaxial Loads Based on Different Yield Definitions. Applied Sciences. 2023; 13(15):8732. https://doi.org/10.3390/app13158732
Chicago/Turabian StyleYu, Huimin, Qinzhi Fang, Jiong Qian, and Yang Hu. 2023. "Study on the Yield Behavior of Closed-Cell Foams under Multiaxial Loads Based on Different Yield Definitions" Applied Sciences 13, no. 15: 8732. https://doi.org/10.3390/app13158732




