Heavy-Duty Use and Charging of Power Tool Battery Packs: A Simulation-Based Study to Improve Cooling Strategies
Abstract
:Featured Application
Abstract
1. Introduction
- (1)
- They must be powerful, as the comparatively small battery has to provide a lot of energy in a short time, especially when the tools are in use. This generates a lot of heat for a short time, which needs to be dissipated by the cooling system.
- (2)
- They must help achieve the shortest possible charging time. The duration of the charging process is determined on the one hand by the charging current (fast charging). In power tools, however, it is precisely the excessively high temperature at the start of the charging process that restricts charging. Charging cannot be started immediately as the battery pack has to cool down first, and thus, the charging process is significantly prolonged by this cool-down time. A charging process that is as short as possible and thus the short downtime of the devices are of great interest to the user.
- (3)
- They must be lightweight and take up very little space. Portability and user-friendliness can only be achieved this way [2].
- (4)
- They must be maintenance-free and have user-independent control of both the cooling system and the battery management system, as well as their interaction. It is essential that the control system is as simple and independent as possible, as the units are intended for end users.
- (5)
- (6)
- They must promote the long battery life of the pack. This is important in order to maximize user acceptance, but also in terms of resource conservation and sustainability. This can be achieved through a cooling system which keeps the pack at the most comfortable temperature range for the cells [5].
2. Methods
2.1. Battery Cell Model
2.2. Material Properties and Heat Transfer Model
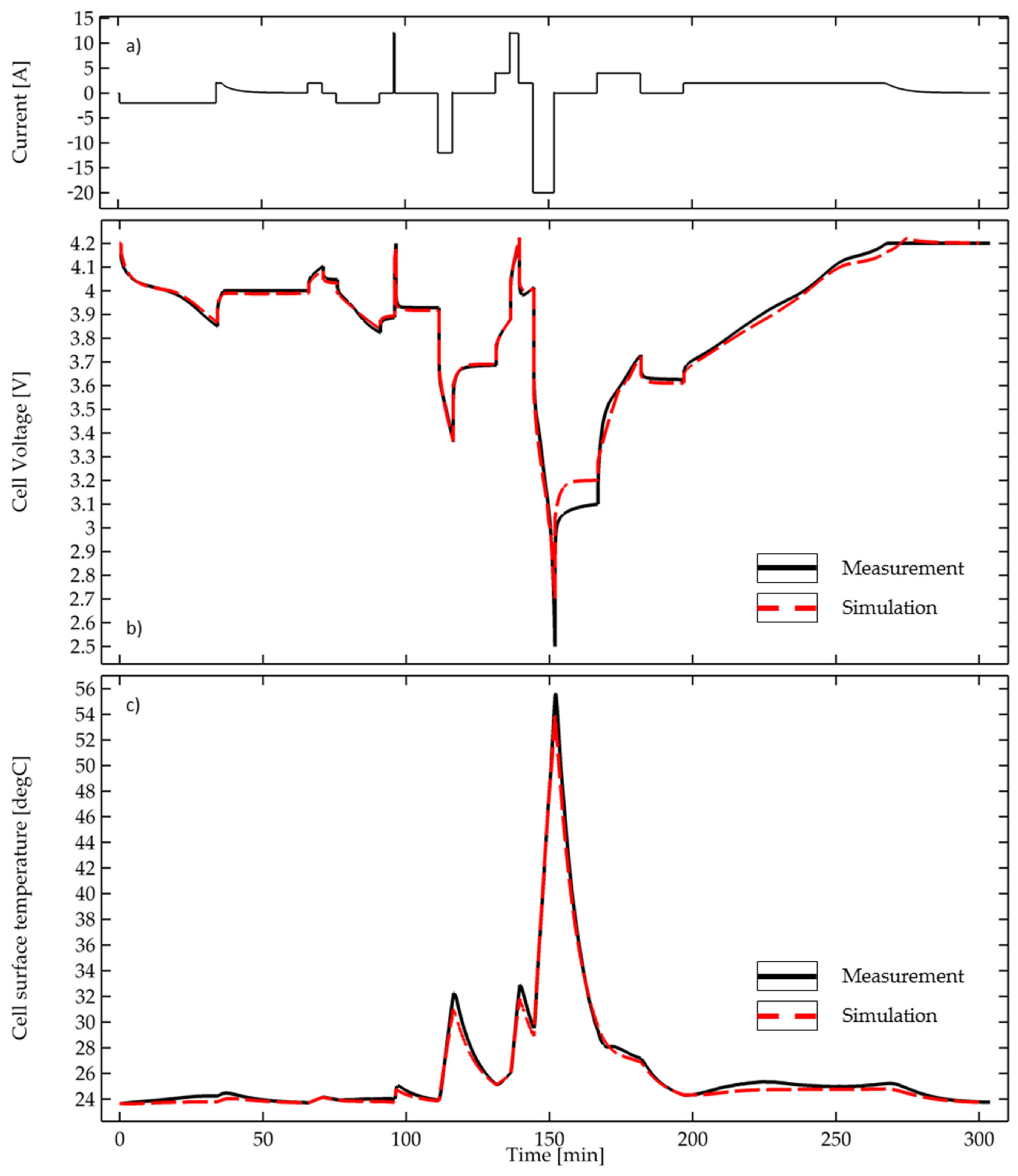
3. Results and Discussion
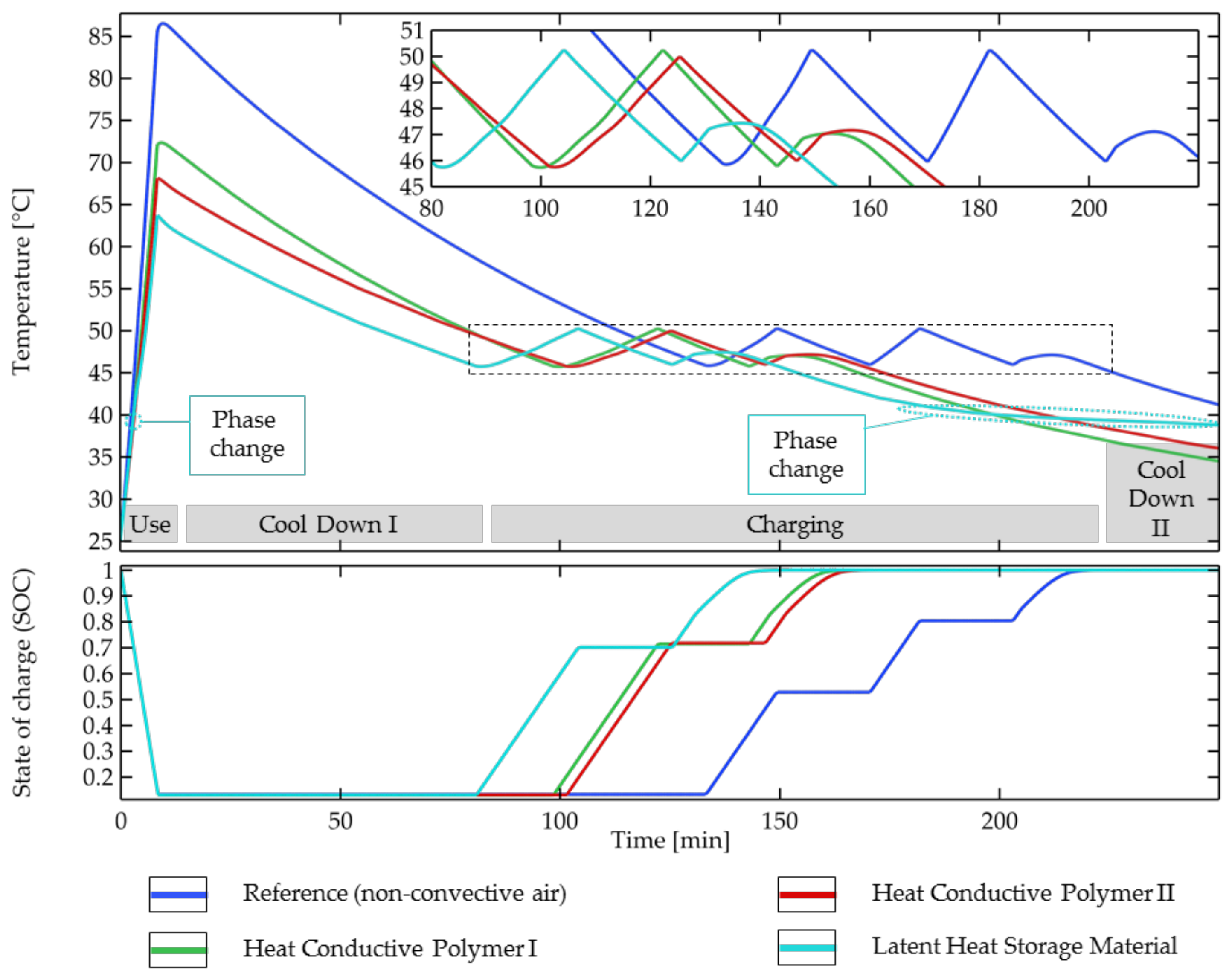
3.1. Influence of Cooling Material on the Pack Performance during Use/Charge Cycle (Material Sweep Study)
3.1.1. Use and Cool-Down Phase I
3.1.2. Charging and Cool-Down Phase II
3.1.3. Summary (Material Sweep)
3.2. Temperature Homogeneity in the Battery Pack
3.3. Influence of Ambient Conditions—Surrounding Temperature and Ventilation (Parameter Sweep Study)
3.3.1. Influence of Ambient Temperature
3.3.2. Influence of Air Movement Around the Pack
3.3.3. Summary (Parameter Sweep)
4. Conclusions
- Due to its ability to quickly absorb high amounts of thermal energy, the latent heat storage material performs best during the use phase (discharging) followed by heat-conductive polymer II with a high heat capacity. The maximum temperature is reduced up to 26% and is for all the solid cooling materials below the maximum temperature of 80 °C allowed for discharging by the cell manufacturer.
- For the length of the whole cycle until the battery was fully charged (A–C), a shortening of 32% was reached using the latent heat storage material (25% was reached without a phase change using heat-conductive polymer I).
- The ability to cool down quickly is of high importance for the total length of the cycle, as cooling down comprises up to 56% (till fully charged) and up to 86% (till reaching 26 °C after charging) of the total cycle time. High thermal conductivity and a low heat capacity are beneficial for short cool-down phases. Compared to the reference, a shortening of the cool-down phase I of 42% (28% without a phase change) was achieved with the solid cooling materials.
- For the charging phase, all the investigated materials fail to transfer away or absorb enough heat to prevent reaching the stop temperature and have to interrupt the charging at least once to cool down back to the start temperature. Comparable total charging times are reached for all the solid materials, which have to be interrupted once for cooling during charging, while the reference has to be interrupted two times. Compared to the reference scenario (the non-convective air), a shortening of the charging up to 23% was achieved using the solid cooling materials. The influence of the differences in the materials properties of the solid cooling materials on the length of the step is only minor. Less often reaching the “stop temperature” during charging proved to be very important for short charging times. Fitting the start and stop temperatures or a temperature-adapted charging protocol, in which the charging current automatically lowers when the cell temperature is close to the “stop temperature” (CC-CT charging), might help shorten charging under different conditions.
- The temperature homogeneity in the battery pack is significantly lower for the reference than for that of the investigated solid cooling materials. Heat-conductive polymer I showed the lowest total cell temperature differences, and therefore most likely the cell aging will differ the least.
- By performing a parameter variation study, the strong influence of the ambient temperature and convection coefficient was demonstrated. It is advised to carefully evaluate future use conditions of power tools when designing power tool cooling systems. Active cooling (e.g., by a fan in the cooling unit) or cooling fins might enhance the heat transfer from the pack surface and thus help to reduce the length of the cool-down phases significantly.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Input Parameters for the Cell Model and the Thermal Model
- OCV
- Cell Capacity
- Temperature Derivative of Open Circuit Voltage (dE/dT)
- Voltage Losses
- Cell Thermal Material Properties
| Input Parameter 1 | Unit | Measurement | Literature | Optimization in Comsol | Value Used in Cell Model |
|---|---|---|---|---|---|
| Cell capacity | Ah | 4.1 | 4.07 | 4.07 | |
| Ohmic overpotential at 1 C | mV | 55 2/77.6 3 | 54.4 [49] | 72.71 | 72 |
| Charge exchange current | - | - | 1 [48], 5.5 [50] | 2.4 | 2.4 |
| Diffusion time constant R2/C2 | mV/C | 1000 | 31.775/101.84 | 31.7/101 | |
| Density (cell) | kg/m3 | 2887 4 | 2000/ 2615.7 [51]/ 2560 [52]/ 2453 [53] | - | 2887 |
| Heat capacity (cell) | J/kgK | 952 4 | 1060 [54]/ 1605 [51]/ 1000 [52]/ 1009 [53] | 1185.9 | 1256.7 |
| Thermal conductivity (cell) | W/mK | 0.87 4 | 3 [51]/1 [52]/ 1 [53] | 0.86436 | 0.87 |
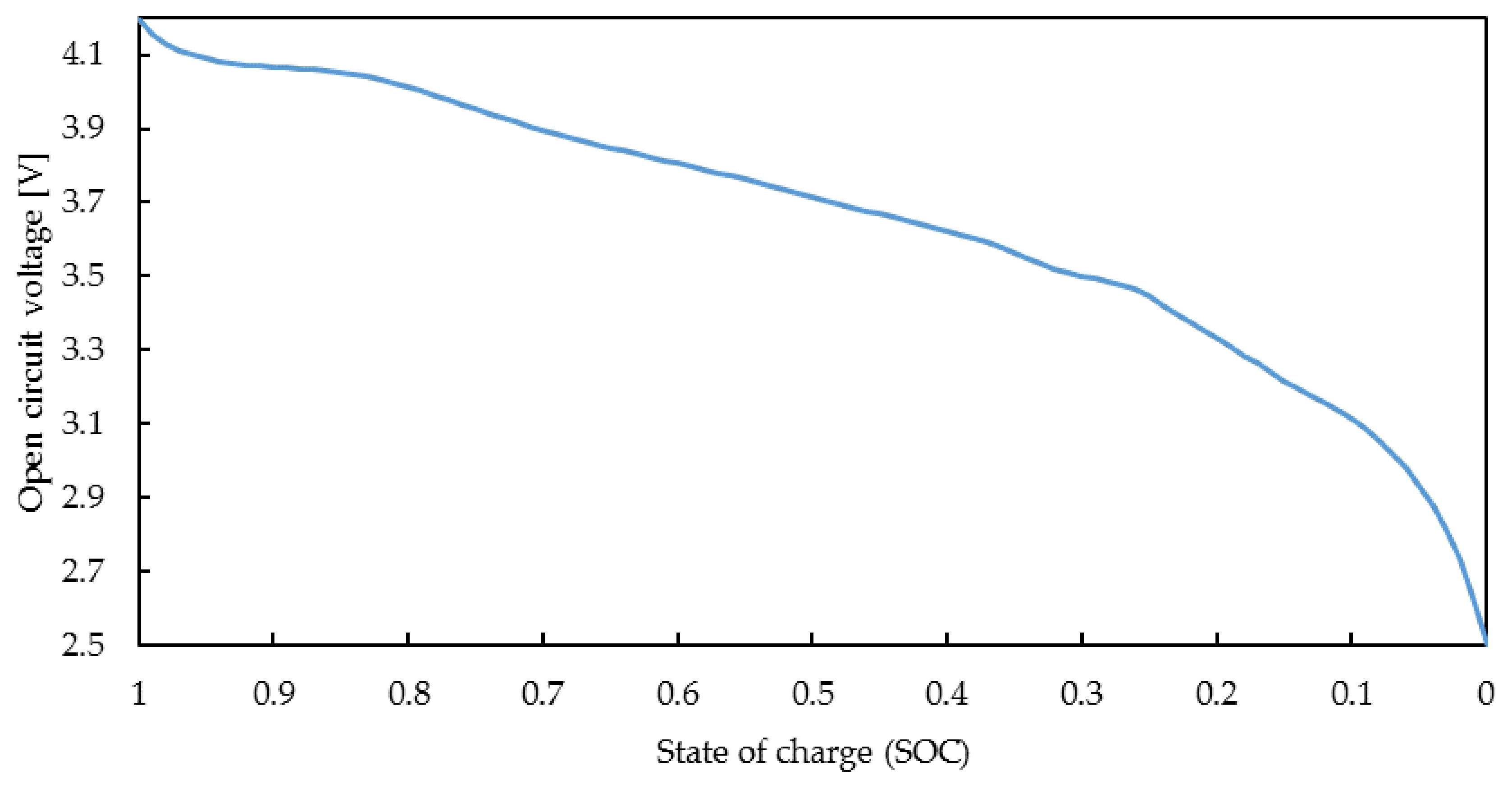
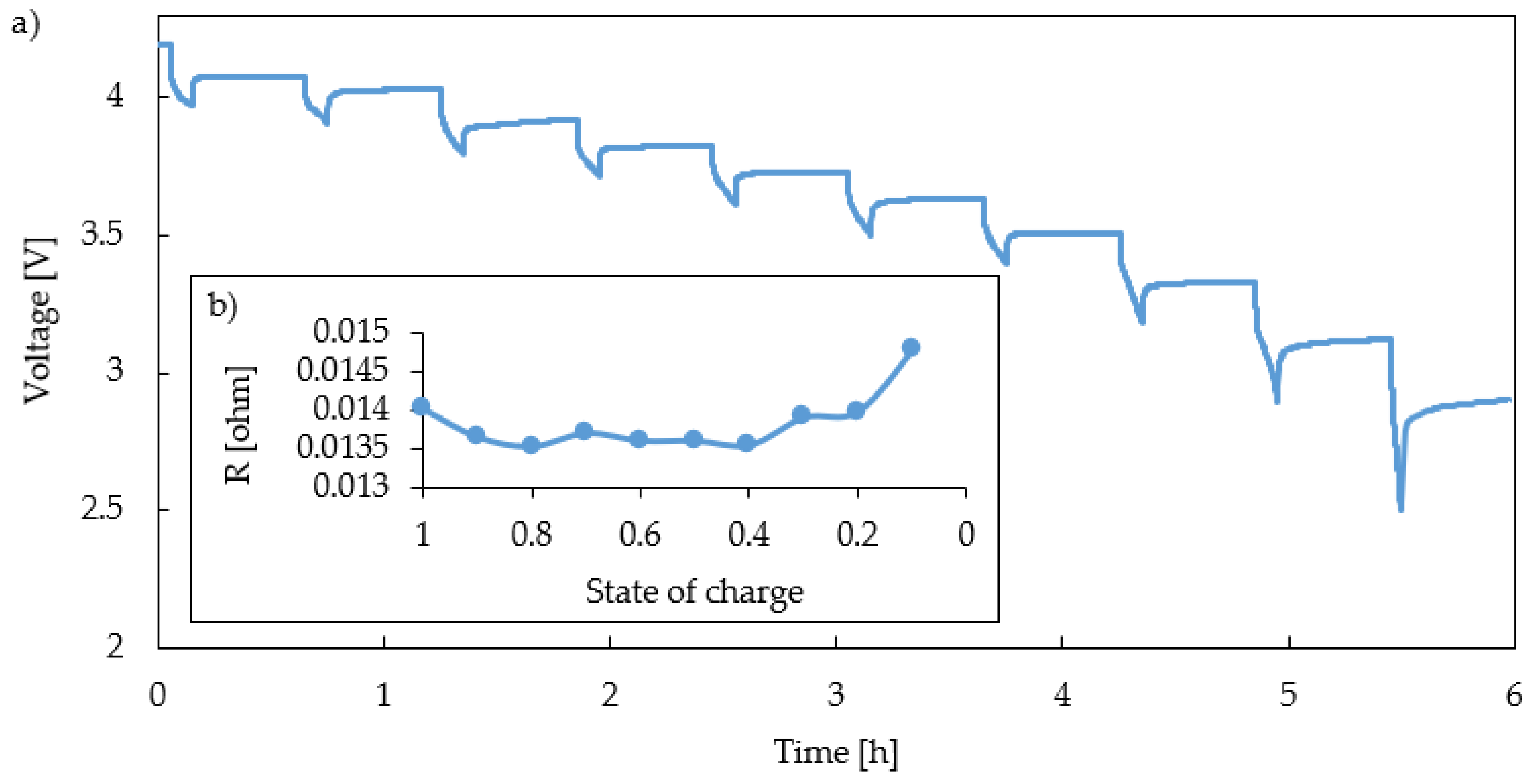
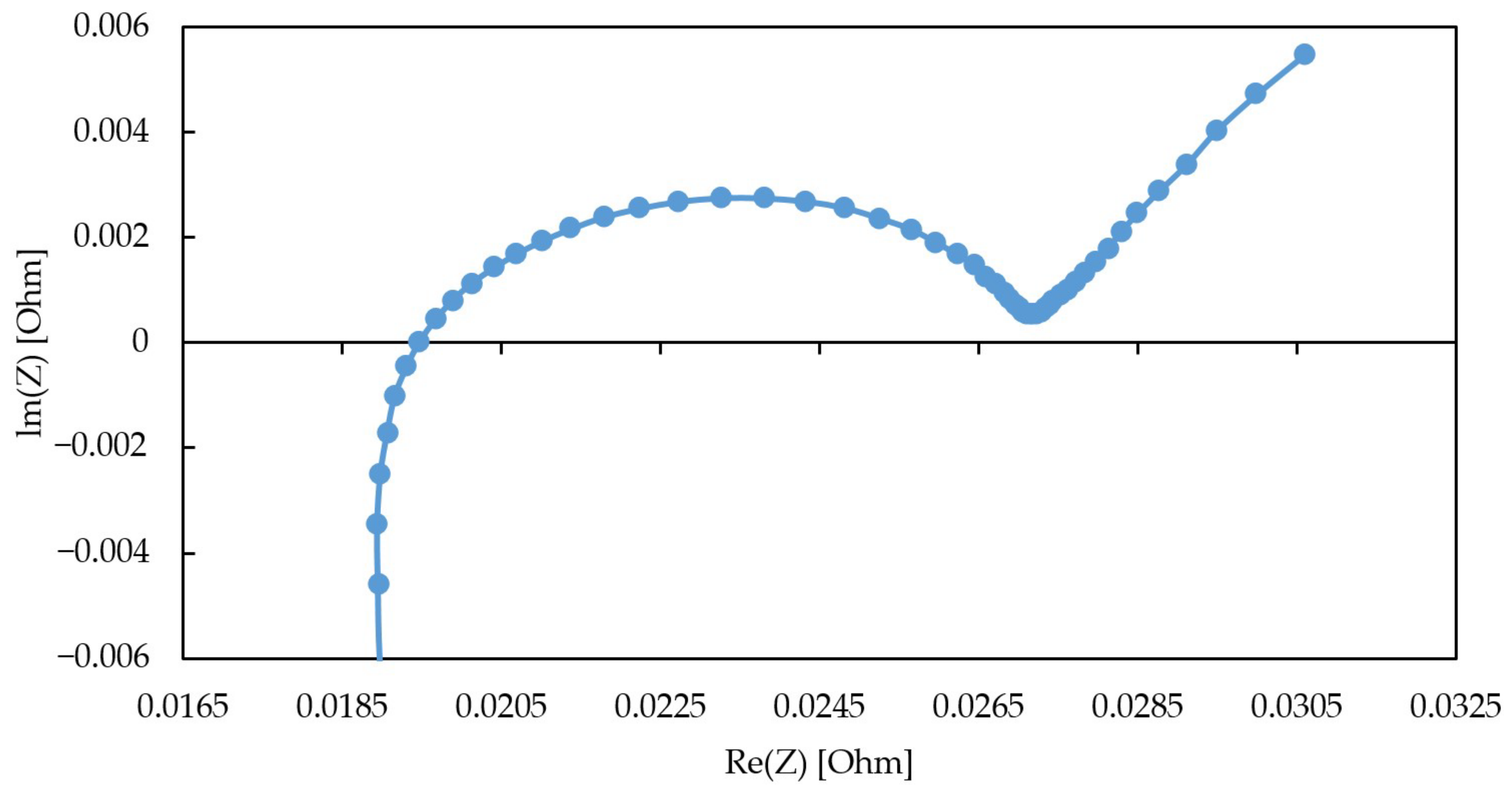
| Battery Model | |
|---|---|
| cell type | Samsung INR 21700 40T |
| number of cells | 20 |
| initial state of charge (SOC) | 1 |
| discharge current/cell (use phase) | 25 A |
| charging current/cell | 5 A |
| thermal model | |
| initial temperature of cells and cooling system | 25 °C |
| convection boundary condition at the cooling system surface | |
| convection coefficient | 5 W/m2 K |
| temperature | 25 °C |
Appendix B. Simulation Equations
| Formula | |
|---|---|
| Battery simulation: | Comsol lumped battery model |
| Battery cell voltage | |
| Open circuit voltage | |
| Ohmic voltage loss | |
| Activation overpotential voltage loss | |
| Concentration overpotential voltage loss | for x = 1 (particle surface) |
| Electrochemical heat sources | |
| Heat transfer model: | Comsol heat transfer in solids |
| Heat transfer in solids equation | |
| Convective heat flux |
References
- Mills, A.; Al-Hallaj, S. Simulation of passive thermal management system for lithium-ion battery packs. J. Power Sources 2005, 141, 307–315. [Google Scholar] [CrossRef]
- Pandur, Z.; Šušnjar, M.; Bačić, M. Battery Technology. Croat. J. For. Eng. 2021, 42, 135–148. [Google Scholar] [CrossRef]
- Weydanz, W. Encyclopedia of Electrochemical Power Sources—Power Tools: Batteries; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Vetter, J.; Novák, P.; Wagner, M.R.; Veit, C.; Möller, K.-C.; Besenhard, J.O.; Winter, M.; Wohlfahrt-Mehrens, M.; Vogler, C.; Hammouche, A. Ageing mechanisms in lithium-ion batteries. J. Power Sources 2005, 147, 269–281. [Google Scholar] [CrossRef]
- Waldmann, T.; Wilka, M.; Kasper, M.; Fleischhammer, M.; Wohlfahrt-Mehrens, M. Temperature dependent ageing mechanisms in Lithium-ion batteries—A Post-Mortem study. J. Power Sources 2014, 262, 129–135. [Google Scholar] [CrossRef]
- Kang, J.; Rizzoni, G. Study of relationship between temperature and thermal energy, operating conditions as well as environmental factors in large-scale lithium-ion batteries. Int. J. Energy Res. 2014, 38, 1994–2002. [Google Scholar] [CrossRef]
- Zadeh, P.G.; Gholamalizadeh, E.; Wang, Y.; Chung, J.D. Electrochemical modeling of a thermal management system for cylindrical lithium-ion battery pack considering battery capacity fade. Case Stud. Therm. Eng. 2022, 32, 101878. [Google Scholar] [CrossRef]
- Khan, M.R.; Swierczynski, M.J.; Kær, S.K. Towards an ultimate battery thermal management system—A review. Batteries 2017, 3, 9. [Google Scholar] [CrossRef]
- Zadeh, P.G.; Gholamalizadeh, E.; Wang, Y.; Chung, J.D. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: Challenges and recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- Khan, M.R.; Swierczynski, M.J.; Kær, S.K. Towards a Smarter Battery Management System for Electric Vehicle Applications: A Critical Review of Lithium-Ion Battery State of Charge Estimation. Energies 2019, 12, 446. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.; Hussain, A.; Mohamed, A. State of charge and state of health diagnosis of batteries with voltage-controlled models. J. Power Sources 2022, 544, 231828. [Google Scholar] [CrossRef]
- Ali, M.U.; Zafar, A.; Nengroo, S.H.; Hussain, S.; Alvi, M.J.; Kim, H.-J. Nonlinear extension of battery constrained predictive charging control with transmission of Jacobian matrix. Int. J. Electr. Power Energy Syst. 2023, 146, 108762. [Google Scholar] [CrossRef]
- Braun, J.A.; Behmann, R.; Schmider, D.; Bessler, W.G. Analysis and Synthesis of Architectures for Automotive Battery Management Systems. Appl. Sci. 2022, 12, 10756. [Google Scholar] [CrossRef]
- Thakur, A.K.; Ahmed, M.S.; Kang, H.; Prabakaran, R.; Said, Z.; Rahman, S.; Sathyamurthy, R.; Kim, J.; Hwang, J.-Y. Critical Review on Internal and External Battery Thermal Management Systems for Fast Charging Applications. Adv. Energy Mater. 2013, 13, 2202944. [Google Scholar] [CrossRef]
- Pesaran, A.A. Battery thermal management in EV and HEVs—Issues and solutions. Battery Man 2001, 43, 34–49. [Google Scholar]
- Khateeb, S.A.; Amiruddin, S.; Farid, M.; Selman, J.R.; Al-Hallaj, S. Thermal management of Li-ion battery with phase change material for electric scooters—Experimental validation. J. Power Sources 2005, 142, 345–353. [Google Scholar] [CrossRef]
- Patel, J.R.; Rathod, M.K. Recent developments in the passive and hybrid thermal management techniques of lithium-ion batteries. J. Power Sources 2020, 480, 228820. [Google Scholar] [CrossRef]
- Yamanaka, T.; Kihara, D.; Takagishi, Y.; Yamaue, T. Multi-physics equivalent circuit models for a cooling system of a lithium ion battery pack. Batteries 2020, 6, 44. [Google Scholar] [CrossRef]
- Lazrak, A.; Fourmigué, J.-F.; Robin, J.-F. An innovative practical battery thermal management system based on phase change materials: Numerical and experimental investigations. Appl. Therm. Eng. 2018, 128, 20–32. [Google Scholar] [CrossRef]
- Park, H. A design of air flow configuration for cooling lithium ion battery in hybrid electric vehicles. J. Power Sources 2013, 239, 30–36. [Google Scholar] [CrossRef]
- Yu, K.; Yang, X.; Cheng, Y.; Li, C. Thermal analysis and two-directional air flow thermal management for lithium-ion battery pack. J. Power Sources 2014, 270, 193–200. [Google Scholar] [CrossRef]
- Rao, Z.; Qian, Z.; Kuang, Y.; Li, Y. Thermal performance of liquid cooling based thermal management system for cylindrical lithium-ion battery module with variable contact surface. Appl. Therm. Eng. 2017, 123, 1514–1522. [Google Scholar] [CrossRef]
- Chen, D.; Jiang, J.; Kim, G.-H.; Yang, C. Comparison of different cooling methods for lithium ion battery cells. Appl. Therm. Eng. 2016, 94, 846–854. [Google Scholar] [CrossRef]
- Zhao, G.; Wang, X.; Negnevitsky, M.; Li, C. An up-to-date review on the design improvement and optimization of the liquid-cooling battery thermal management system for electric vehicles. Appl. Therm. Eng. 2023, 219, 119626. [Google Scholar] [CrossRef]
- Khateeb, S.A.; Farid, M.M.; Selman, J.R.; Al-Hallaj, S. Design and simulation of a lithium-ion battery with a phase change material thermal management system for an electric scooter. J. Power Sources 2004, 128, 292–307. [Google Scholar] [CrossRef]
- Septiadi, W.N.; Alim, M.; Adi, M.N.P. The application of battery thermal management system based on heat pipes and phase change materials in the electric bike. J. Energy Storage 2022, 56, 106014. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Z.; Jia, L.; Yang, L. Paraffin and paraffin/aluminum foam composite phase change material heat storage experimental study based on thermal management of Li-ion battery. Appl. Therm. Eng. 2015, 78, 428–436. [Google Scholar] [CrossRef]
- Kizilel, R.; Lateef, A.; Sabbah, R.; Farid, M.M.; Selman, J.R.; Al-Hallaj, S. Passive control of temperature excursion and uniformity in high-energy Li-ion battery packs at high current and ambient temperature. J. Power Sources 2008, 183, 370–375. [Google Scholar] [CrossRef]
- Kizilel, R.; Sabbah, R.; Selman, J.R.; Al-Hallaj, S. An alternative cooling system to enhance the safety of Li-ion battery packs. J. Power Sources 2009, 194, 1105–1112. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, S.; Wang, G.; Weng, J.; Ouyang, D.; Wu, X.; Zhao, L.; Wang, J. Experimental Analysis on the Thermal Management of Lithium-Ion Batteries Based on Phase Change Materials. Appl. Sci. 2020, 10, 7354. [Google Scholar] [CrossRef]
- Goud, V.M.; Satyanarayana, G.; Ramesh, J.; Pathanjali, G.A.; Ruben Sudhakar, D. An experimental investigation and hybrid neural network modelling of thermal management of lithium-ion batteries using a non-paraffinic organic phase change material, Myristyl alcohol. J. Energy Storage 2023, 72, 108395. [Google Scholar] [CrossRef]
- Boomstra, M.W.; van Asseldonk, M.; Geurts, B.J.; Nazarychev, V.M.; Lyulin, A.V. Effects of branching and polydispersity on thermal conductivity of paraffin waxes. Int. J. Heat Mass Transf. 2022, 195, 123192. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Min, H.; Li, H.; Li, Q. Performance investigation of a passive battery thermal management system applied with phase change material. J. Energy Storage 2021, 35, 102279. [Google Scholar] [CrossRef]
- Luo, J.; Zou, D.; Wang, Y.; Wang, S.; Huang, L. Battery thermal management systems (BTMs) based on phase change material (PCM): A comprehensive review. Chem. Eng. J. 2022, 430, 132741. [Google Scholar] [CrossRef]
- Talele, V.; Patil, M.S.; Panchal, S.; Fraser, R.; Fowler, M.; Gunti, S.R. Novel metallic separator coupled composite phase change material passive thermal design for large format prismatic battery pack. J. Energy Storage 2023, 58, 106336. [Google Scholar] [CrossRef]
- Tang, A.; Chen, W.; Shao, X.; Jin, Y.; Li, J.; Xia, D. Experimental investigation of aluminum nitride/carbon fiber-modified composite phase change materials for battery thermal management. Int. J. Energy Res. 2022, 46, 12737–12757. [Google Scholar] [CrossRef]
- Samimi, F.; Babapoor, A.; Azizi, M.; Karimi, G. Thermal management analysis of a Li-ion battery cell using phase change material loaded with carbon fibers. Energy 2016, 96, 355–371. [Google Scholar] [CrossRef]
- Zhao, Y.; Jin, L.; Zou, B.; Qiao, G.; Zhang, T.; Cong, L.; Jiang, F.; Li, C.; Huang, Y.; Ding, Y. Expanded graphite—Paraffin composite phase change materials: Effect of particle size on the composite structure and properties. Appl. Therm. Eng. 2020, 171, 115015. [Google Scholar] [CrossRef]
- Goli, P.; Legedza, S.; Dhar, A.; Salgado, R.; Renteria, J.; Balandin, A.A. Graphene-enhanced hybrid phase change materials for thermal management of Li-ion batteries. J. Power Sources 2014, 248, 37–43. [Google Scholar] [CrossRef]
- Zhang, K.; Han, B.; Yu, X. Electrically conductive carbon nanofiber/paraffin wax composites for electric thermal storage. Energy Convers. Manag. 2012, 64, 62–67. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, C.-F.; Zhou, J.-G.; Xiong, X.; Wang, Y.-P. Thermal performance of battery thermal management system using fins to enhance the combination of thermoelectric Cooler and phase change Material. Appl. Energy 2022, 322, 119503. [Google Scholar] [CrossRef]
- Choudhari, V.G.; Dhoble, A.S.; Panchal, S. Numerical analysis of different fin structures in phase change material module for battery thermal management system and its optimization. Int. J. Heat Mass Transf. 2020, 163, 120434. [Google Scholar] [CrossRef]
- Sun, Z.; Guo, Y.; Zhang, C.; Whitehouse, J.; Zhou, Q.; Xu, H.; Wang, C. Experimental study of battery passive thermal management system using copper foam-based phase change materials. Int. J. Thermofluids 2023, 17, 100255. [Google Scholar] [CrossRef]
- Zheng, Y.; Shi, Y.; Huang, Y. Optimisation with adiabatic interlayers for liquid-dominated cooling system on fast charging battery packs. Appl. Therm. Eng. 2019, 147, 636–646. [Google Scholar] [CrossRef]
- Ranjbaran, Y.S.; Shojaeefard, M.H.; Molaeimanesh, G.R. Thermal performance enhancement of a passive battery thermal management system based on phase change material using cold air passageways for lithium batteries. J. Energy Storage 2023, 68, 107744. [Google Scholar] [CrossRef]
- Shelkea, A.V.; Buston, J.E.; Gill, J.; Howard, D.; Williams, R.C.; Read, E.; Abaza, A.; Cooper, B.; Richards, P.; Wen, J.X. Combined numerical and experimental studies of 21700 lithium-ion battery thermal runaway induced by different thermal abuse. Int. J. Heat Mass Transf. 2022, 194, 123099. [Google Scholar] [CrossRef]
- Vogiatzis, D.; Schacht, H.-J.; Schmidt, S.; Kirchberger, R.; Arenz, M. Investigation on Transient Behavior and SoC Balancing of a Hybrid Powertrain Hand-Held Tool; SAE Technical Paper Series; SAE International400 Commonwealth Drive: Warrendale, PA, USA, 2022. [Google Scholar]
- COMSOL. COMSOL Multiphysics Reference Manual v. 5.4; COSMOL: Burlington, MA, USA, 2018. [Google Scholar]
- Quinn, J.B.; Waldmann, T.; Richter, K.; Kasper, M.; Wohlfahrt-Mehrens, M. Energy density of cylindrical Li-ion cells—A comparison of commercial 18650 to the 21700 cells. J. Electrochem. Soc. 2018, 165, A3284. [Google Scholar] [CrossRef]
- Ovejas, V.J.; Cuadras, A. State of charge dependency of the overvoltage generated in commercial Li-ion cells. J. Power Sources 2019, 418, 176–185. [Google Scholar] [CrossRef]
- Kang, T.; Park, S.; Lee, P.-Y.; Cho, I.-H.; Yoo, K.; Kim, J. Thermal Analysis of a Parallel-Configured Battery Pack (1S18P) Using 21700 Cells for a Battery-Powered Train. Electronics 2020, 9, 447. [Google Scholar] [CrossRef]
- Hosseini Moghaddam, S.M. Designing Battery Thermal Management Systems (BTMS) for Cylindrical Lithium-Ion Battery Modules Using CFD. Master’s Thesis, KTH School of Industrial Engineering and Management Energy Technology, Stockholm, Sweden, 2018. [Google Scholar]
- Kerler, M.; Lienkamp, M. COFAT 2015—A method to find a thermal optimum cell size. In Proceedings of the Conference on Future Automotive Technology, Munich, Germany, 3–4 May 2015. [Google Scholar]
- Faber, M.; RItz, S.; Börner, M.; Sauer, D.U. Technique to Determine the specific heat Capacity of Lithium-ion Battery cells. In Proceedings of the AABC Europe 2019, Strasbourg, France, 27–31 January 2019. [Google Scholar]
- Chen, S.C.; Wan, C.C.; Wang, Y.Y. Thermal analysis of lithium-ion batteries. J. Power Sources 2005, 140, 111–124. [Google Scholar] [CrossRef]



| Material | Density [kg/m3] | Specific Heat Capacity [J/kgK] | Volumetric Heat Capacity [J/m3 K] | Thermal Conductivity [W/mK] | Melting Point [°C] | Heat of Fusion [W/kg] |
|---|---|---|---|---|---|---|
| Reference (non-conv. air) | Comsol database “air” [48] | - | - | |||
| Heat-conductive polymer I | 1540 | 1470 | 2,263,800 | 2.2 | - | - |
| Heat-conductive polymer II | 980 | 3500 | 3,430,000 | 0.74 | - | - |
| Latent heat storage material | 1220 | 2100 | 2,562,000 | 0.4 | 39 1 | 70,000 1 |
| Material [min] ([%]) | Use (A) | Cool-Down Phase I (B) | Charge (C) | Cool-Down Phase II (D) | Total | |
|---|---|---|---|---|---|---|
| Reference (non conv. air) | 8.5 (2%) | 125 (23%) | 91.6 (17%) | 318.1 (59%) | 543 | |
| Heat-Conductive Polymer I | 8.5 (2%) | 90 (19%) | 70.8 (15%) | 303.9 (64%) | 473 | |
| Heat-Conductive Polymer II | 8.5 (2%) | 93.5 (18%) | 70.9 (14%) | 347.9 (67%) | 521 | |
| Latent Heat Storage Material | 8.5 (1%) | 72.5 (13%) | 71.2 (12%) | 427.7 (74%) | 580 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Königer, V.; Knoblauch, V. Heavy-Duty Use and Charging of Power Tool Battery Packs: A Simulation-Based Study to Improve Cooling Strategies. Appl. Sci. 2023, 13, 8848. https://doi.org/10.3390/app13158848
Königer V, Knoblauch V. Heavy-Duty Use and Charging of Power Tool Battery Packs: A Simulation-Based Study to Improve Cooling Strategies. Applied Sciences. 2023; 13(15):8848. https://doi.org/10.3390/app13158848
Chicago/Turabian StyleKöniger, Veit, and Volker Knoblauch. 2023. "Heavy-Duty Use and Charging of Power Tool Battery Packs: A Simulation-Based Study to Improve Cooling Strategies" Applied Sciences 13, no. 15: 8848. https://doi.org/10.3390/app13158848
APA StyleKöniger, V., & Knoblauch, V. (2023). Heavy-Duty Use and Charging of Power Tool Battery Packs: A Simulation-Based Study to Improve Cooling Strategies. Applied Sciences, 13(15), 8848. https://doi.org/10.3390/app13158848





