Grammar Correction for Multiple Errors in Chinese Based on Prompt Templates

Abstract

Grammar error correction (GEC) is a crucial task in the field of Natural Language Processing (NLP). Its objective is to automatically detect and rectify grammatical mistakes in sentences, which possesses immense application research value. Currently, mainstream grammar-correction methods primarily rely on sequence labeling and text generation, which are two kinds of end-to-end methods. These methods have shown exemplary performance in areas with low error density but often fail to deliver satisfactory results in high-error density situations where multiple errors exist in a single sentence. Consequently, these methods tend to overcorrect correct words, leading to a high rate of false positives. To address this issue, we researched the specific characteristics of the Chinese grammar error correction (CGEC) task in high-error density situations. We proposed a grammar-correction method based on prompt templates. Firstly, we proposed a strategy for constructing prompt templates suitable for CGEC. This strategy transforms the CGEC task into a masked fill-in-the-blank task compatible with the masked language model BERT. Secondly, we proposed a method for dynamically updating templates, which incorporates already corrected errors into the template through dynamic updates to improve the template quality. Moreover, we used the phonetic and graphical resemblance knowledge from the confusion set as guiding information. By combining this with BERT’s prediction results, the model can more accurately select the correct characters, significantly enhancing the accuracy of the model’s prediction correction results. Our methods were validated through experiments on a public grammar-correction dataset. The results indicate that our method achieves higher correction performance and lower false correction rates in high-error density scenarios.

1. Introduction

Grammar correction, an incredibly crucial application task, plays a role in education, official document processing, and many pre-processing stages of natural language processing tasks. While grammatical errors can occur in any language, this paper only focuses on the grammar-correction task in Chinese text. Influenced by Chinese text’s inherent characteristics and usage habits, Chinese grammar error correction (CGEC) errors show noticeable differences and diversity. Furthermore, for non-native speakers’ Chinese sentences, multiple types of errors often occur in a single sentence. Under such high-error density conditions, accurately detecting and correcting complex and diverse Chinese grammatical errors is a challenging task. The types of grammatical errors can be broadly divided into redundancy errors (R), missing errors (M), word order errors (W), and wrong word errors (S), based on their characteristics [1]. R-type errors refer to the existence of unnecessary or repetitive linguistic elements in a sentence, leading to verbosity or unnecessary repetition. M-type errors denote the absence of essential linguistic elements or structures in a sentence, causing the sentence to be incomplete or not fluent. W-type errors point to an incorrect word or phrase order in a sentence, resulting in grammar rules or unclear meaning violations. S-type errors signify the presence of misspelled words in a sentence, making the sentence inaccurate or hard to understand. For example,

Table 1. Types of Chinese Grammar Errors.

Correct Sentence	Redundancy Error (R)	Missing Error (M)	Word Order Error (W)	Wrong Word Error (S)
小猫捉一个老鼠	小猫捉一个老鼠鼠	小-捉一个老鼠	小猫一个捉老鼠	小帽捉一个老鼠
The cat catches a mouse	The cat catches a mouse mouse	The—catches a mouse	The cat a catches mouse	The hat catches a mouse

shows situations of these four types of errors in Chinese text.

Two essential methods are typically employed in solving the Chinese grammar error correction (CGEC) problem: sequence labeling and text generation. The sequence labeling approach first assigns labels to each character in the text, indicating whether it should be “added, deleted, modified, or retained”. Then, by learning the dependencies between the labels, they allocate corresponding labels to the characters and finally modify the text sequence according to the labels to obtain the correct text. The text generation approach, meanwhile, focuses on understanding the relationships between characters in the input text and employs generative language models to produce corrected text. However, due to the interference of erroneous characters, these methods often learn incorrect dependencies on the semantic information of erroneous characters, thus modifying correct characters into erroneous ones. Furthermore, when multiple errors exist in a single sentence, they overlook the consideration of information corrected from previous errors.

In response to the characteristics of Chinese text data in high-error-density domains and the problems with the above methods, this paper proposes a Chinese multi-error grammar-correction method based on a prompt template. This method follows a three-step framework: error detection, template construction, and prediction correction. Specifically, in the error-detection module, we have built a sequence labeling model for grammar error detection based on the pre-trained masked model MacBERT [2] (MLM as correction BERT) -BiLSTM-CRF architecture, to identify the positions and types of grammar errors in sentences. Then, in the prompt template construction module, we designed corresponding prompt template construction strategies according to the positions and types of grammar errors obtained. We use [MASK] to hide the information of erroneous characters in the prompt template and then use BERT’s masking prediction capability to predict the [MASK] position in the prompt template. At the same time, the information on corrected errors is dynamically updated in the prompt template during the masking prediction process. Finally, we have integrated BERT’s predictions with confusion sets to generate a more accurate final correction. These confusion sets include phonetically or visually similar characters; for instance, due to visual similarity, the characters ‘人’ and ‘入’ would be in the same confusion set. By considering these sets, we can enhance the precision of character generation In summary, the main contributions of this paper can be summarized as follows:

(1)

To solve the CGEC problem in high-error-density domains, a multi-error grammar-correction method based on a prompt template is proposed.

(2)

A grammar error-detection model based on MacBERT-BiLSTM-CRF is proposed, which uses MacBERT as an embedder to learn rich semantic representations, which ensures the dependency of long-text semantic information through the BiLSTM network, and outputs grammar error information through the dependency between tokens in the CRF.

(3)

A prompt template-construction strategy and a method for dynamically updating templates are proposed. This method transforms sentences with high error density into BERT-adaptable prompt templates based on the error-detection information of the text. It integrates the information of corrected errors into the template during the masking prediction process to improve the quality of the template.

(4)

Considering the utilization of error character information in sentences, by extracting the phonetically and visually similar candidate character set matching, the error character from the confusion set, and combining it with BERT’s prediction results, the model can more accurately select the correction character.

(5)

Experiments were conducted on public grammar-correction datasets, especially on datasets containing multiple errors, proving the effectiveness of the proposed method.

2. Related Work

This chapter primarily introduces two syntax-correction methods; namely, the current mainstream sequence labeling paradigm and text generation paradigm, and the exploration of relevant work using prompt learning and prompt templates.

2.1. Grammar-Correction Method Based on Sequence Labeling and Text Generation

Research on Chinese grammar error correction can be divided into two categories: methods based on sequence labeling and methods based on text generation. The fundamental idea of sequence labeling-based methods is to define corresponding ‘delete’, ‘retain’, ‘add’, and other operation tags according to error types like ‘redundant’, ‘correct’, ‘missing’, etc. These operation tags are then added to the text sequence. The model learns the dependencies between these operation tags and predicts the operation tag for each character in the text sequence, which is then used for grammar correction. This type of method was earlier proposed and applied in the field of English error correction. Awasthi et al. [3] used sequence labeling to implement text correction by first marking characters in the sequence with self-defined tags, then predicting the corresponding operation tags through an iterative process involving multiple rounds of prediction and refinement. However, this paper only provided simple definitions for operation tags. Later, Omelianchuk et al. [4]. refined the design of operation tags, defining 5000 tags, including ‘add’, ‘delete’, ‘modify’, ‘retain’, etc., and then using a pre-trained transformer and multi-round iterative sequence labeling to obtain the operation tags for the target sequence. Deng et al. [5] achieved text correction by combining a pre-trained transformer encoder and an editing space in the field of Chinese text correction. This editing space comprises 8772 tags, also known as the operation tag set, where each tag represents a specific editing action, such as adding, deleting, or modifying a character. Given the characteristics of Chinese text, some scholars have tried to integrate phonetically and graphically similar knowledge into the grammar-correction model. Li Jiacheng et al. [6] proposed a correction model integrating a pointer network with confusion set knowledge. While predicting word editing operations, the model also allows the pointer network to choose words from the confusion set incorporating phonetic and graphical similarity knowledge, thus improving correction results for substitution errors. However, sequence labeling methods, despite their fast inference speed and small dataset requirements, demand high-quality annotated data and are restricted by the size of the operation tag set, making it challenging to handle complex problems encountered in real-life applications.

Text-generation-based methods incorporate the concept of neural machine translation, translating original sentences directly into correct ones by learning the dependencies between each word in the input sequence. However, unlike translation tasks, both the input and target sequences of grammar-correction tasks are in the same language and share many identical characters. Therefore, characters can often be directly extracted from the input sequence to the target sequence during text generation. For this, Wang et al. [7] proposed a grammar-correction model that integrates a copy mechanism. Based on transformer architecture, this model predicts the character at the current position in the target sequence given the input sequence and uses a balancing factor to control whether to copy characters from the input sequence to the target generation sequence. Additionally, Wang et al. [8] proposed a grammar-correction model that combines a dynamic residual structure with the transformer model to capture semantic information, during target sequence generation, better. They also used corrupted text for data augmentation. Fu et al. [9] proposed a three-stage method for grammar correction. They first eliminated shallow errors like spelling or punctuation based on a pre-trained language model and a set of similar characters. Then, they built transformer models at the character and word levels to handle grammatical errors. Finally, they reordered the results from the previous two stages in the ensemble stage, selecting the optimal output. Text-generation methods only need to generate correct text based on the input sequence using the learned dependencies during the correction process, hence eliminating the need to define specific error types. However, this method needs to improve on issues of controllability and interpretability.

2.2. Prompt Learning and Prompt Templates

In recent years, with the emergence of various large-scale pre-training models, the research methodology is gradually transitioning from the traditional ‘pre-training + fine-tuning’ paradigm to the prompt-based ‘pre-training + prompting + prediction’ paradigm. The traditional ‘pre-training + fine-tuning’ paradigm involves training the model on a large dataset (pre-training) and optimizing it for a specific task (fine-tuning). It is usually necessary to set an objective function according to the specific downstream task and retrain the corresponding domain corpus to adjust the parameters of the pre-trained model to adapt to the downstream task. However, when it comes to using ultra-large-scale pre-trained models, such as the GPT-3 model [10] with 175 billion parameters, matching downstream tasks using the ‘pre-training + fine-tuning’ paradigm is often time-consuming and costly. Moreover, since the pre-trained model already performs well in its original domain, using fine-tuning for domain transfer is restricted by the original domain, which might damage its performance. Therefore, modifications to the pre-trained model are avoided in the ‘pre-training + prompting + prediction’ paradigm of prompt learning. Instead, prompt templates are constructed better to fit the downstream tasks with the pre-trained model. As research on prompt learning flourishes, the ‘pre-training + prompting + prediction’ paradigm is gradually evolving into the fourth paradigm in the field of natural language processing [11].

In prompt learning, the design of prompt templates mainly involves the position and quantity of prompts, which can be divided into manually designed and automatically learned methods. Manually designed prompt templates are based on human experience and professional knowledge in the field of natural language. Petroni et al. [12] designed corresponding cloze templates for each relation in the knowledge source by manual definition, exploring the facts and common knowledge contained in language models. Schick et al. [13] transformed input examples into cloze examples containing task description information, successfully combining task description with standard supervised learning. Manually designed prompt templates are intuitive and smooth, but highly depend on human language expertise and frequent trial-and-error, resulting in high costs for high-quality, prompt templates. Therefore, automatic learning of prompt templates has been explored, which can be divided into discrete and continuous types. Discrete prompts use unique discrete characters as prompts to generate prompt templates automatically. Ben-David et al. [14] proposed a domain-adaptive algorithm that trains models to generate unique domain-related features, which are then connected with the original input to form prompt templates. Continuous prompts construct soft prompt templates from a vector-embedding perspective and perform prompting directly in the model’s embedding space. Li et al. [15] froze model parameters while constructing task-specific continuous vector sequences as soft prompts by adding prefixes. Furthermore, many scholars combine these two methods to obtain higher quality prompt templates, such as Zhong et al. [16], who initially defined prompt templates using a discrete search method, then initiated virtual tokens according to the template and fine-tuned embeddings, for optimization. Han et al. [17] proposed a rule-based prompt-tuning method, which combines sub-templates manually designed into a complete prompt template, according to logical rules, and inserts virtual tokens with adjustable embeddings.

In this paper, a sequence labeling model is built to detect grammar errors in the text, and the text is accordingly constructed into a fill-in-the-blank form of prompt template based on error types. Simultaneously, the information of the corrected errors is dynamically updated into the prompt template, improving the quality of the prompt template and fully utilizing BERT’s masked prediction ability, enabling it to accurately predict the blanks in the prompt template.

3. Methodology

In this chapter, we will introduce the method proposed by us. Figure 1 illustrates the Chinese grammar-correction framework based on the prompt templates that we have proposed. The input is a sentence X = (x1, x2, …, xi) containing grammar errors, where x represents each character in the input text sequence, and i is the length of sentence X. The goal of the CGEC task is to correct all grammar errors in X and output the correct text sequence Y = (y1, y2, …, yi). It should be noted that, due to the specific nature of the CGEC task, the length of the output correct text sequence Y does not have to be the same as the length of the input erroneous text sequence X. In our model framework, the grammar-correction task is divided into two stages: error detection and error correction, focusing on four types of errors: W, R, S, and M. First, the MacBERT-BiLSTM-CRF sequence labeling model is used to obtain the error types and position information in the sentence. Then, based on different error types, prompt templates are generated and dynamically updated using multiple strategy mechanisms. Finally, the correct characters are obtained by combining the predictions from BERT with a confusion set. The following sections will provide a detailed description of each layer’s structure.

3.1. Error-Detection Layer

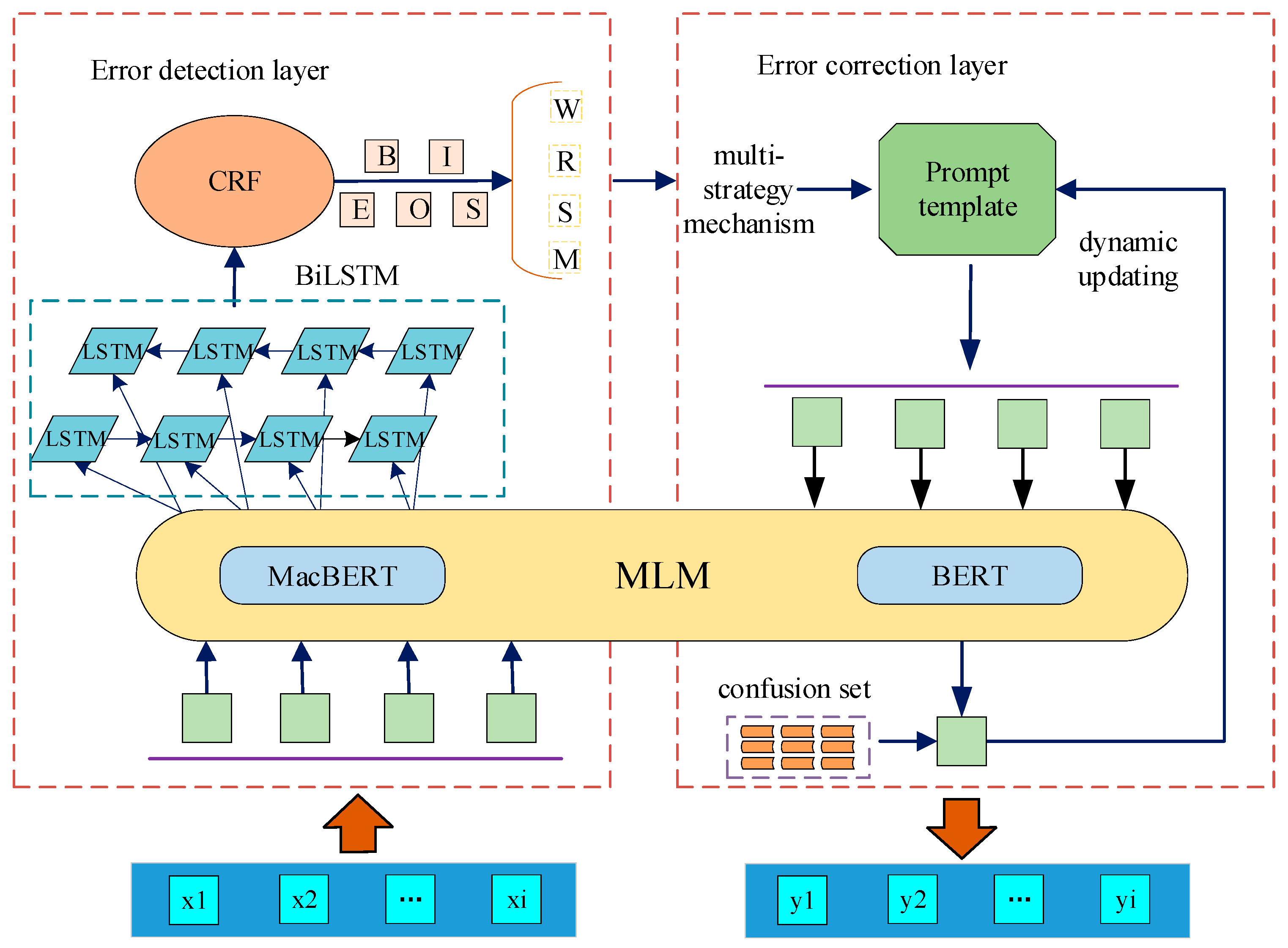
In the error-detection layer, we constructed the MacBERT-BiLSTM-CRF sequence labeling model to obtain information about the grammatical error types and positions in a sentence. The process is as follows: (1) Utilizing the pre-trained model MacBERT to capture the semantic relationships between characters in the input text and extract the semantic information within the text. (2) Encoding the output of MacBERT further in the BiLSTM to better capture the contextual features of the sequence. (3) Finally, utilizing the labeling dependency modeling capability of the CRF network, the prediction and decoding of labels are performed on the output of the BiLSTM, resulting in the final annotation results.

3.1.1. MacBERT Layer

In the process of detecting errors, we use MacBERT to convert the input text into vector representations. MacBERT is a pre-trained model optimized for Chinese language tasks. Through training on a large-scale Chinese corpus, it learns rich representations of the Chinese language. MacBERT is a variant of BERT, and its structure is similar to BERT, consisting of compositional embedding layers and multiple stacked transformer encoder layers. The embedding layer transforms the input text into a mathematical representation and includes token, positional, and segment embeddings. Token embedding converts each character of the input text into a fixed-dimensional word-embedding vector. Positional embedding captures the positional information within the input sequence, encoding the position of each word in the sequence. It is added after word embedding. Segment embedding is used to differentiate relationships between different sentences. Each word is marked as belonging to the first sentence (Segment A) or the second sentence (Segment B). The outputs of these three embedding layers are element-wise summed and passed as input to the transformer encoder layers.

However, unlike BERT, MacBERT improves the masking strategy used during pre-training. It discards the strategy of masking tokens with the whole word [MASK] and, instead, uses a similar word replacement for masking. When a masked word is not similar, a random word is selected for replacement. In this strategy, 15% of the characters in the input sentence are masked, 80% are replaced with similar words, 10% are replaced with random words, and the remaining 10% are kept unchanged. As shown in

Table 2. Comparison of Masking Strategies between BERT and MacBERT.

Pretrained Model	Original Sentence	Masked Sentence
BERT	小猫捉一个老鼠	小猫[MASK]一个老[MASK]
MacBERT	小猫捉一个老鼠	小猫桌一个老书

, in the masking strategy of BERT, masking the original sentence would result in “小猫[MASK]一个老[MASK]” (The cat [MASK] an [MASK]). In the masking strategy of MacBERT, masking the original sentence would result in “小猫桌一个老书” (The cat table an old book), where “桌” (table) and “书” (book) are similar characters corresponding to the characters “猫” (cat) and “鼠” (mouse) in the original sentence. This masking strategy reduces the gap between the pre-training and fine-tuning stages and makes MacBERT more suitable for the task of text error detection.

3.1.2. BiLSTM Layer

LSTM, as a particular type of recurrent neural network (RNN), addresses the two challenges encountered in handling extended textual information in traditional RNNs by introducing gate mechanisms to control information flow and retention. The first challenge is ‘gradient explosion’, where gradients (amounts used for optimizing the network) grow exponentially and disrupt the learning process. The second challenge is ‘long-term dependencies’, i.e., the difficulty of associating information that appeared earlier with the later parts of a long sequence [18]. It consists of three main gate controllers: the forget gate, input gate, and output gate, along with a memory cell state for information transmission within the network. The architecture of an LSTM unit is depicted in Figure 2, where we show the hidden state $h_t$ output at time step t. The forget gate $f_t$ combines the previous time step’s hidden state $h_{t-1}$ with the current input $x_t$ and passes it through a sigmoid activation function σ to determine which information to discard from the cell state. The input gate has two parts determining which new information should be stored in the cell state. The first part is a sigmoid layer, which decides which values to update, and the second part is a tanh layer, which generates a new candidate value vector $\tilde{c}$ that could be added to the state. The old cell state $c_{t-1}$ is then updated to obtain the new cell state $c_t$. Finally, the output gate determines which values to output. Specifically, it first applies a sigmoid layer to determine the output portion and then processes the state with a tanh function. The two are multiplied to obtain the final hidden state $h_t$.

The calculation formulas for each part of an LSTM unit are as follows, with the formula for the forget gate shown in Equation (1):

$$f_t=\sigma (W_f·[h_{t-1},x_t]+b_f)$$

(1)

In the equations, $W_f$ represents the weight matrix for the forget gate, $b_f$ is the bias term for the forget gate, $x_t$ is the input at the current time step, and $h_{t-1}$ is the previous hidden state.

The input gate consists of the activation value $i_t$ and the candidate value vector ${\tilde{c}}_t$, which are calculated as shown in Equations (2) and (3):

$$i_t=\sigma (W_t·[h_{t-1},x_t]+b_i)$$

(2)

$${\tilde{c}}_t=\tanh (W_c·[h_{t-1},x_t]+b_c)$$

(3)

In this case, $W_t$ represents the weight matrix for the input gate, $b_i$ is the bias term for the input gate, $W_c$ is the weight matrix for the candidate value vector, and $b_c$ is the bias term for the candidate value vector.

We can now obtain the updated cell state $c_t$, which is calculated as shown in Equation (4):

$$c_t=f_t\ast c_{t-1}+i_t\ast {\tilde{c}}_t$$

(4)

In the equations, $c_{t-1}$ represents the previous cell state, $f_t$ is the activation value of the forget gate, $i_t$ is the activation value of the input gate, and ${\tilde{c}}_t$ is the candidate value vector.

Finally, we obtain the hidden state $h_t$ through the output gate, which is calculated as shown in Equations (5) and (6):

$$o_t=\sigma (W_o·[h_{t-1},x_t]+b_o)$$

(5)

$$h_t=o_t\ast \tanh (c_t)$$

(6)

In the equations, $W_o$ represents the weight matrix for the output gate, $b_o$ is the bias term for the output gate, and $c_t$ is the current cell state.

The LSTM network composed of the aforementioned structure has achieved good results in addressing the issues of gradient explosion and long-term dependencies encountered in processing long textual information. However, it can only capture information in a sequential manner from either the forward or backward direction, thus being unable to consider the contextual information of an element in both preceding and succeeding contexts. On the other hand, BiLSTM can simultaneously consider the past and future contexts, allowing for better capture of bidirectional semantic dependencies. It consists of two LSTM units: a forward LSTM and a backward LSTM. At a given time point t, the forward LSTM receives the input X = (x1, x2, …, xt), while the backward LSTM receives the input X = (xT, x(T − 1), …, xt), where T is the total length of the input sequence. Therefore, for BiLSTM, the hidden state at each time point t is composed of the hidden states of both the forward and backward LSTMs, as shown in Equation (7):

$$y_t=f(h^{f_t},h^{l_t})$$

(7)

where $y_t$ represents the current hidden state of the BiLSTM, f is the function used to combine the two LSTMs, $h^{f_t}$ represents the hidden state of the forward LSTM, and $h^{l_t}$ represents the hidden state of the backward LSTM.

3.1.3. CRF Layer

The Conditional Random Field (CRF) network is a discriminative model used for sequence labeling tasks, primarily aimed at assigning labels to sequential data. In this study, because BiLSTM does not consider label information during the prediction process, the CRF network is employed to compensate for this deficiency, serving as a constraint to improve the accuracy of predicted labels. The objective of the CRF network is to learn a conditional probability P(Y|X), given the input X = (x1, x2, …, xn), which represents the probability of an output label sequence Y = (y1, y2, …, yn).

In the CRF network, given the input X, the label sequence scores for every possible output Y are typically computed based on two components: transition scores and emission scores. Transition scores consider the transitions between adjacent labels in the label sequence, while emission scores consider the matching degree between labels and corresponding input features at each position. The computation formula is shown in Equation (8):

$$Score\left(X, Y\right)={\displaystyle \sum _{i=1}^n{L}_{i,y_i}}+{\displaystyle \sum _{i=1}^n{k}_{y_{i-1},y_i}}$$

(8)

where $L_{i,y_i}$ represents the emission score, indicating the matching degree between the given input at position i and the label $y_i$. $k_{y_{i-1},y_i}$, which represents the transition score from label $y_{i-1}$ to label $y_i$.

Next, the scores of the label sequences are exponentiated, and the exponential sum of all possible label sequences is normalized to obtain the probabilities of the label sequences. The computation formula is shown in Equation (9):

$$p(Y|X)=\frac{e^{Score(X,Y)}}{{\displaystyle \sum _{\tilde{Y}\in Y_X}{e}^{Score(X,\tilde{Y})}}}$$

(9)

Finally, the Viterbi algorithm is used to obtain the label sequence $\overline{Y}$ with the highest probability. The computation formula is shown in Equation (10):

$$\overline{Y}=\arg \max Score(X,\tilde{Y})$$

(10)

In addition, when using the CRF network, it is necessary to add label constraints to avoid generating illegal sequences. In this study, the BIOES annotation scheme is employed to label four types of errors: redundancy (R), missing (M), disorder (W), and wrong word (S). Specifically, the errors are represented by the following prefixes: the prefix “B-” indicates the beginning of an error, “I-” is for the middle part, “E-” represents the end, “S-” is used for a single character error, and “O-” is for other situations. For example, the labels for redundancy (R) errors can include “B-R”, “I-R”, “E-R”, and so on.

3.2. Error-Correction Layer

This study employs the prompt-based learning approach which is employed in the error-correction layer. It combines multiple strategy mechanisms to construct prompt templates for the grammatical error information generated by the error-detection layer. The prompt templates are dynamically updated. Then, the BERT model is utilized to predict the missing parts in the templates. Finally, the missing parts are combined with a confusion set to obtain the final corrected characters.

3.2.1. Multiple Strategy Mechanism

In response to different error-detection results, this study first defines relatively simple strategies for constructing templates:

Redundancy: Based on the error position and count, the redundant parts are deleted and replaced with a placeholder [VAR] while maintaining the original sentence length.

Missing: [MASK] tags are added at the corresponding positions.

Disorder: The positions of the disordered words or characters are reversed according to the markers.

Wrong word: The incorrect characters are deleted, and the corresponding number of [MASK] tags is added.

However, when using the above strategies to construct prompt templates in scenarios with multiple errors, there is often an issue of accurately locating subsequent error positions due to changes in sentence length. For example, for the correct sentence “小猫捉一个老鼠” (The cat catches a mouse) and the erroneous sentence “小捉一个老鼠鼠” (Catch a mouse), the following two error information can be obtained: ① “2, M” (missing at position 2) and ② “7, R” (redundancy at position 7). Supposed prompt templates are constructed based on these error-detection results using multiple strategies. In that case, the first error is addressed by adding a [MASK] tag at the corresponding position, resulting in “小[MASK]捉一个老鼠鼠”. However, due to the change in sentence length, the subsequent positioning of the second error (② “7, R”) will be incorrect.

To address this issue, this study records the position information of each error when constructing the prompt templates. The index of the error position is then used to reposition the error when constructing the template. This ensures that subsequent error positions can still be correctly aligned with the adjusted sentence. By adopting this approach, even if the sentence length changes, the positions of the errors can still be accurately identified, and corresponding prompt templates can be constructed. The specific process of the multiple strategy mechanism is illustrated in Figure 3.

3.2.2. Result Prediction

This study utilizes BERT as the prompt model to predict the masked gaps in the constructed prompt templates. In this context, BERT can be thought of as a pre-trained problem solver: it is designed to understand and predict language. It works by paying attention to each word in a sentence and learning the meaning behind the words. During the pre-training phase, BERT focuses on two tasks: the Masked Language Model (MLM) and Next Sentence Prediction (NSP). The MLM involves predicting randomly masked input words, while NSP focuses on predicting whether one sentence is the following sentence of another.

In this study, the MLM task of BERT is primarily discussed. The key idea of MLM is to mask a certain proportion of words in the source text and have the model predict the masked words based on the remaining words in the given sentence. This helps to enhance the language modeling capability of the model and falls under the category of self-supervised learning. In BERT, MLM is used for deep bidirectional representation learning, as illustrated in Figure 4.

Figure 4 demonstrates the process of masking and predicting the sentence “The cat catches a mouse” in the MLM task of BERT. Firstly, a random selection of tokens in the sentence is masked. In Figure 4, the character “cat” is masked and represented by the [MASK] token. The masked sentence is then passed through the embedding layer, producing corresponding word vectors Wi and a particular vector Wm for the [MASK] token. Next, the word vectors are fed into the transformer layer, which utilizes the contextual semantics of the sentence to make probability predictions for the vector representation Fm of the masked token Wm. Finally, the softmax classifier computes the probability distribution of the tokens and determines the target word “cat”.

Therefore, the BERT model trained using MLM not only learns rich language representations but also possesses the ability to perform mask prediction. This paper transforms the grammar-correction task into an MLM task, utilizing the mask prediction approach.

The process of error correction, based on the constructed prompt templates, is as follows (Algorithm 1):

Algorithm 1: Grammar-Correction Error-Correction Process Based on Prompt Templates

Input: Prompt template T = (t1, [MASK], t3, …, tn)

Output: Corrected text L = (l1, l2, l3, …, ln)

begin: Create a list ‘masks’ of length 512;  // Used to mark the positions that need to be predicted while (‘MASK]’ in T) do     // Check if ‘[MASK]’ tag exists in the template T   Convert to word vectors through the embedding layer and input into BERT;   Use BERT to predict the first [MASK] tag in the template and obtain the prediction result Pt and its corresponding weight Htop;   Extract the set of characters corresponding to the masked erroneous character in the confusion set Confusion[];   Calculate the weight distribution of Confusion[], obtain the maximum weight Hmax and its cor-responding character Ct;   if (Htop > Hmax)     u = Pt;      // Set the BERT prediction result Pt as the correction result u    else     u = Ct;    // Set the character Ct from Confusion[] as the correction result u Update the template T with the correction result u at the corresponding position; end while end

4. Experiments

4.1. Experimental Data and Evaluation Metrics

The experiment in this article uses three standard error-correction datasets: Lang-8, HSK, and MuCGEC [19]. Among them, Lang-8 and HSK are training corpora, while MuCGEC is the testing corpus. In addition, an analysis was conducted on the proportion of sentences with varying numbers of errors in the MuCGEC corpus, with details as shown in

Table 3. Test Corpus Analysis Table.

Number of Errors per Sentence	Proportion of Sentences in Test Corpus
One	22%
Two	22%
Three	15%
Three or more	41%

. As can be seen from the table, sentences containing three or more errors account for more than half of the testing corpus, satisfying the testing experiment requirements under scenarios with multiple grammatical errors.

The experiment’s results are evaluated based on precision, recall, and the F0.5 score. These are used to assess the performance of the model. The formulae for calculating these metrics are as shown in Equations (11)–(13):

$$\mathrm{Precision}=\frac{{\displaystyle \sum _{s\in Source}\left|e(s)\cap g(s)\right|}}{{\displaystyle \sum _{s\in Source}\left|e(s)\right|}}$$

(11)

$$\mathrm{Recall}=\frac{{\displaystyle \sum _{s\in Source}\left|e(s)\cap g(s)\right|}}{{\displaystyle \sum _{s\in Source}\left|g(s)\right|}}$$

(12)

$$\mathrm{F}0.5=\frac{(1+{0.5}^2)\times \mathrm{precision}\times \mathrm{recall}}{{0.5}^2\times \mathrm{precision}+\mathrm{recall}}$$

(13)

In the equations, e(s) represents the model’s output prediction, and g(s) represents the standard answer for the original text.

4.2. Experimental Environment and Hyperparameter Settings

The experiment was conducted using the Python programming language and the TensorFlow deep learning framework. The hardware environment involved an NVIDIA TITAN V graphics card with 12G of VRAM. We used the pre-trained model hfl/MacBERT-large, consisting of 24 sublayers, a hidden dimension of 1024, 16 attention heads, and 324M parameters. We also used the pre-trained model Chinese-BERT-Base, which has 12 sublayers, a hidden dimension of 768, 12 attention heads, and a total of 110M parameters. The specific hyperparameter settings of the model are shown in

Table 4. Hyperparameter Settings.

Hyperparameters	Settings
Epoch	10
Batch Size	256
Max Sequence Length	256
Learning Rate	1 × 10−5
Dropout	0.1
Optimizer	Adam
Gradient Accumulation	128

.

Due to limited computing resources, supporting training with larger batch sizes is impossible. Therefore, in the experiment, the method of Gradient Accumulation was used. That is, during calculation, the gradient of each batch is first accumulated, and after accumulating for a certain number of times, the network parameters are updated, and the gradient is cleared.

4.3. Results and Analysis

In the experiment, five error-correction models were selected for comparison with the model proposed in this paper, focusing on error detection and correction on the testing corpus. The specific details of the compared models are as follows:

Model 1 [20]: iFLYTEK ZhiJian utilizes a BiLSTM-CRF model framework with CRF and introduces deep semantic features. It employs probability integration to fuse the outputs of multiple models and further optimizes the results by incorporating a template matcher.

Model 2: Baidu Intelligent Cloud Text Proofreading System identifies various types of errors, including incorrect words, characters, and punctuation in Chinese texts, and provides suggestions for correction.

Model 3 [4]: GECToR is a sequence labeling-based grammar-correction model that uses transformer as the base model. It employs token-level correction methods, such as insertion, deletion, and replacement, to handle different types of grammatical errors.

Model 4 [21]: Pycorrector (T5) is an open-source Chinese text proofreading tool available on GitHub. It fine-tunes the Langboat/mengzi-t5-base pre-trained model on the error-correction dataset.

Model 5 [22]: This model is based on a convolutional encoder–decoder architecture for grammar correction. It utilizes a multi-layer convolutional neural network as both the encoder and decoder, incorporating attention mechanisms and non-linear operations to capture language context and relationships for grammar error correction.

The results of the error detection and correction comparison experiments are shown in

Table 5. Comparison of Error-Detection Performance.

Model	Precision	Recall	F0.5
Model 1	69.62	9.99	31.73
Model 2	67.73	5.75	21.47
Model 3	33.11	25.46	31.23
Model 4	35.84	5.09	16.23
Model 5	12.82	4.81	9.62
Our Model	70.66	28.58	54.58

and

Table 6. Comparison of Error-Correction Performance.

Model	FN	Precision	Recall	F0.5
Model 1	3401	55.51	7.91	25.19
Model 2	3511	51.13	4.33	16.18
Model 3	3192	23.94	18.45	22.59
Model 4	3508	23.45	3.33	10.63
Model 5	3598	7.23	2.76	5.46
Our Model	3097	38.39	20.08	32.47

, respectively. Table 6 introduces false negatives (FNs) as the fourth evaluation metric to validate the proposed model’s effectiveness in reducing false correction rates. FN represents the number of instances where the model incorrectly identifies true positives as false negatives (incorrectly correcting correct words to incorrect words).

We carried out a comparison with existing methods on a consistent evaluation dataset, MuCGEC. As can be seen in Table 5, our MacBERT-BiLSTM-CRF-based model excels in error detection, significantly surpassing other models in the F0.5 score. This is mainly due to the model’s unique architecture that combines the strengths of MacBERT, BiLSTM, and CRF. MacBERT provides a comprehensive understanding of the context, while BiLSTM and CRF work in concert to capture and classify the complex grammar error patterns, thereby boosting the model’s precision. Table 6 further elucidates that our model not only excels in reducing the number of FNs, i.e., correctly identified words erroneously corrected, but also maintains a balance between precision and recall, as reflected in the highest F0.5 score. It shows that our model has effectively eliminated multiple errors in the sentences, thus eliminating the issue found in Model 1 and Model 2 of sacrificing recall to achieve higher precision. This is a critical aspect in real-world applications: identifying errors as accurately as possible and ensuring that no mistakes are overlooked.

To further analyze the impact of the number of grammatical errors on the model’s error-correction performance, this paper divided the MuCGEC grammar-correction dataset into four subsets based on the different numbers of errors per sentence: Mu_1, Mu_2, Mu_3, and Mu_4. The Mu_1 dataset contains sentences with one error, the Mu_2 dataset contains sentences with two errors, the Mu_3 dataset contains sentences with three errors, and the Mu_4 dataset contains sentences with four or more errors. Comparative experiments were conducted on these four datasets; the results are shown in Figure 5.

The following observations and conclusions were drawn by comparing the model in this paper and existing methods on four datasets with different error numbers:

(1)

The proposed model achieved the best performance in terms of F0.5 on all datasets, and its precision consistently remained relatively high compared to other models. However, some models had higher precision on specific datasets. However, the proposed model demonstrated an advantage in F0.5 scores when considering a recall. This indicates that the proposed model balanced identifying all errors (recall) and avoiding false positives (precision).

(2)

All models performed relatively well due to the higher occurrence of word-related errors in the Mu_3 dataset and word-related errors being relatively more straightforward to detect and correct than disorder-related or omission-related errors. Additionally, on the Mu_1, Mu_2, and Mu_4 datasets, as the number of errors increased, the performance of all models declined, mainly reflected in a decrease in recall. However, the proposed model exhibited a relatively minor decrease in recall, suggesting that it maintained relatively stable performance when handling more complex sentences with more errors.

(3)

Furthermore, the GECToR model, based on sequence labeling, showed good recall performance on the dataset, but lower precision. This is because it requires multiple editing operations to correct all errors in sentences with multiple errors. However, complex combinations of errors impose higher demands on the model regarding selecting editing operations and their order, leading to decreased precision. On the other hand, the proposed model achieved a better balance between the two, resulting in the highest F0.5 score.

(4)

The comparative experimental results show that our model demonstrates significant advantages in handling sentences with multiple errors, especially regarding the F0.5 score. Notably, for other models, as the number of errors in a sentence increases, the performance of the models tends to decrease. However, by employing a unique method of Chinese grammar error-correction prompt templates, our model can maintain relatively stable performance, even when processing sentences with high error density.

The discussion in this section further confirms the superiority of our model over existing models in handling sentences with multiple errors, especially in terms of an F0.5 score. It also verifies the effectiveness of the Chinese grammar-correction prompt template method we proposed, which can help the model better understand and deal with error information, thus improving the accuracy of error correction and the stability of the model. When correcting errors, traditional models may be influenced by erroneous character information, but our model can avoid this situation. Specifically, our model dynamically updates the error-correction information into the prompt template based on the error type, thus fully utilizing BERT’s masked prediction capability for more accurate prediction during the error-correction process. This makes the model perform better when dealing with complex sentences. This method endows the model with greater robustness when facing multiple errors.

To analyze the effectiveness of the model, a comparison was made with models that did not use the confusion set and models that did not employ the iterative mechanism, as shown in

Table 7. Comparative analysis of ablative performance.

Model	Precision	Recall	F0.5
Our Model—Confusion set	35.22	19.16	30.16
Our Model—Iterative mechanism	33.91	20.03	29.78
Our Model	38.39	20.08	32.47

. Table 7 shows that the proposed model exhibited relatively stable performance in terms of recall compared to the other two models, with no significant differences. However, the proposed model achieved the best performance in terms of precision. This result confirms the effectiveness of incorporating homophonic and homographic knowledge and known error-correction information into the error-correction model to improve the accuracy of character-correction predictions.

5. Conclusions

This paper proposes a method for grammar correction in Chinese text, explicitly targeting the scenario of multiple grammar errors. To mitigate the interference of error character dependencies in multi-error grammar-correction scenarios, a prompt template-based approach is employed. The prompt templates guide the model to focus more on learning the semantic information of correct characters in the sentence. Furthermore, known error-correction information is integrated into the prompt templates through iterative updates, further improving the quality of the prompt templates. Additionally, a strategy combining the masked language model (MLM) prediction and confusion sets containing homophonic and homographic knowledge is utilized to enhance the accuracy of the model’s predicted correction results in multi-error grammar-correction scenarios. Experimental results demonstrate the effectiveness of the proposed method in handling multi-error grammar-correction scenarios.

Moreover, although this model is specifically designed for Chinese grammar correction, its basic principles and methods can be extended to other languages. Our approach is a model framework not confined to Chinese. For non-Chinese languages, the error types in the target language can be defined, and the tagging system of the error-detection layer can be adjusted to fit the characteristics of the target language. Our proposed method allows the prompt template to be designed and optimized for these error types. In addition, our method employs the mask prediction capability of BERT during the error-correction stage, which is a language-independent feature. In future work, exploring how to effectively adapt the Chinese grammar-correction task to other forms of pre-training models using prompt learning methods will be investigated, along with studying the corresponding task formats.