Numerical Analysis Applying the Finite Element Method by Developing a Complex Three-Dimensional Biomodel of the Biological Tissues of the Elbow Joint Using Computerized Axial Tomography
Abstract
1. Introduction
2. Methodology
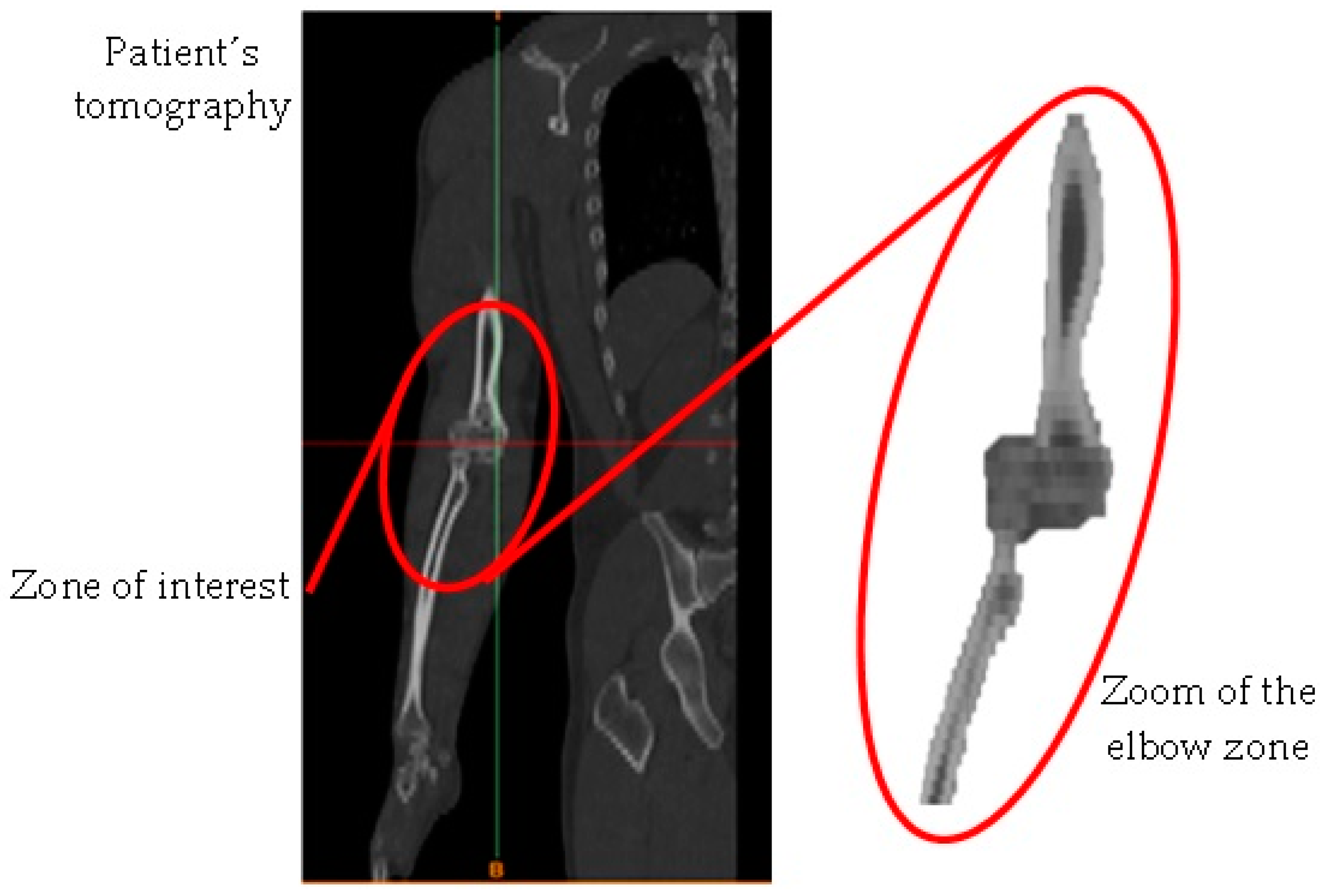
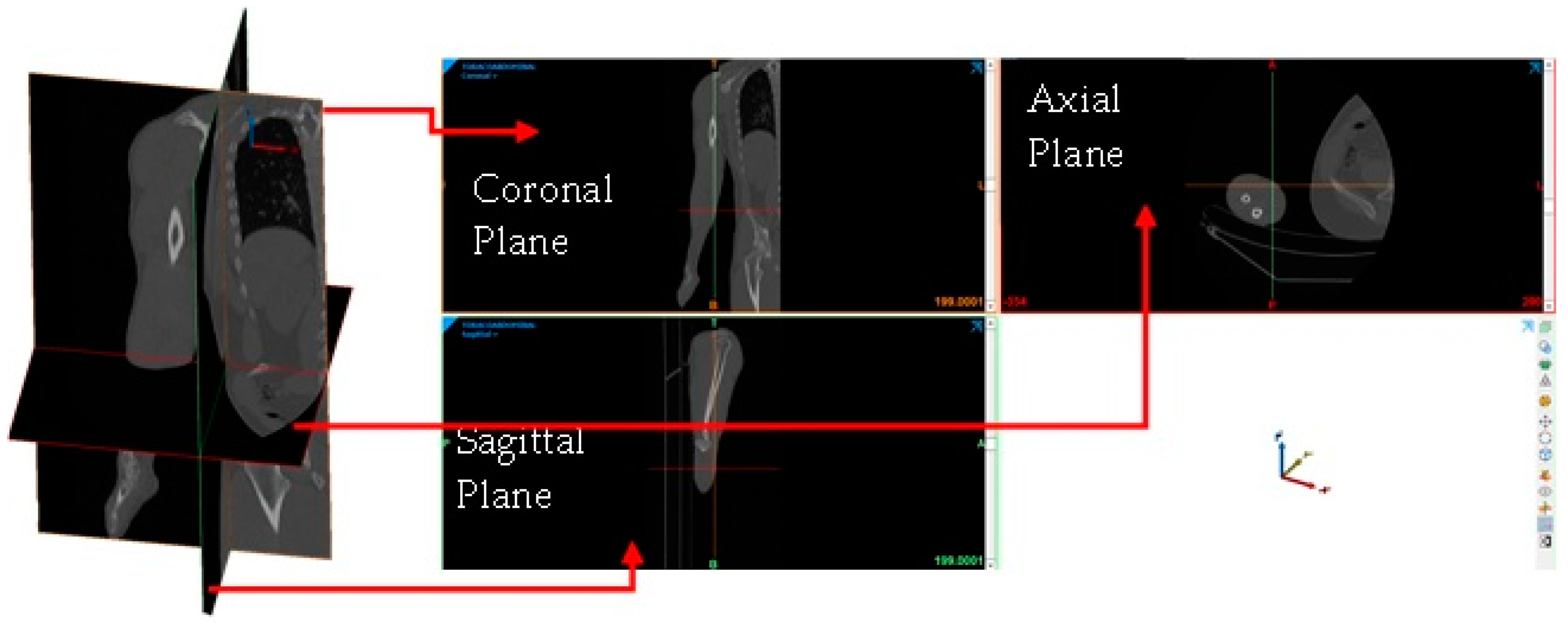
- Obtaining of the computerized axial tomography (upper limb).
- Development of images in DICOM format.
- Image importation into the Materialise Mimics® computer program.
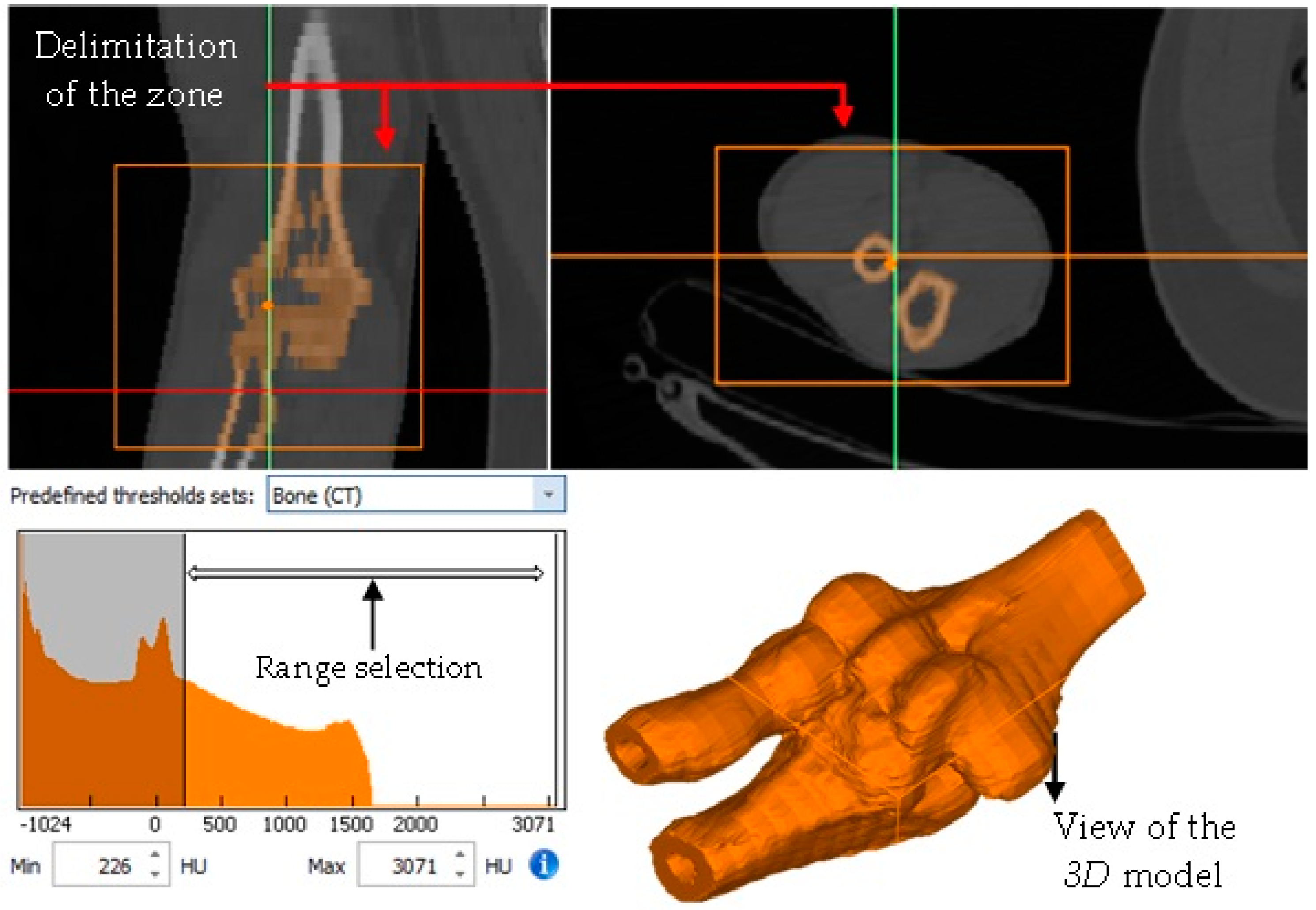
- Delimitation of the area of interest for the development of the biomodel (elbow).
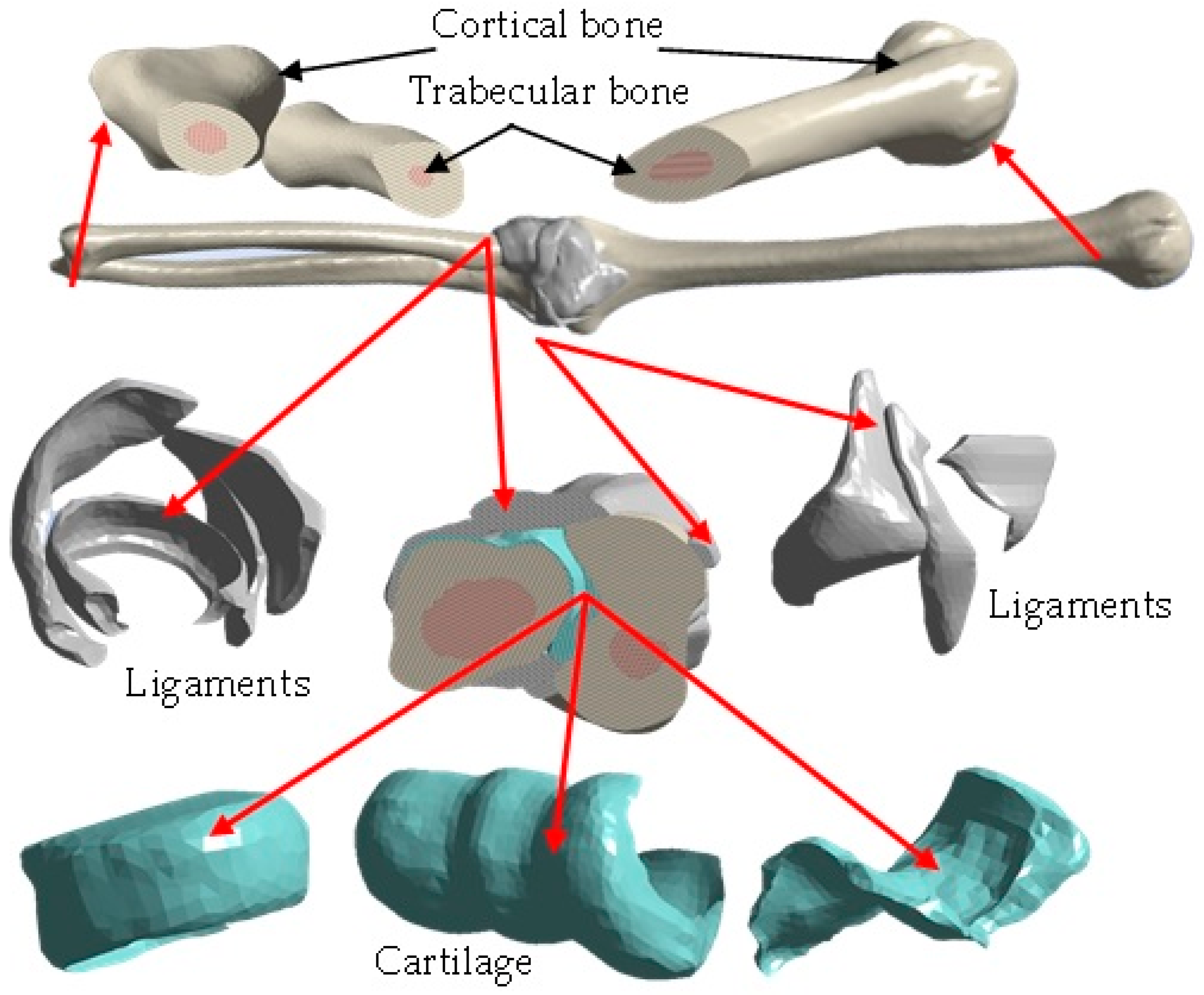
- Application of masks in the work area where the bones (cortical and trabecular) and cartilage will be represented.
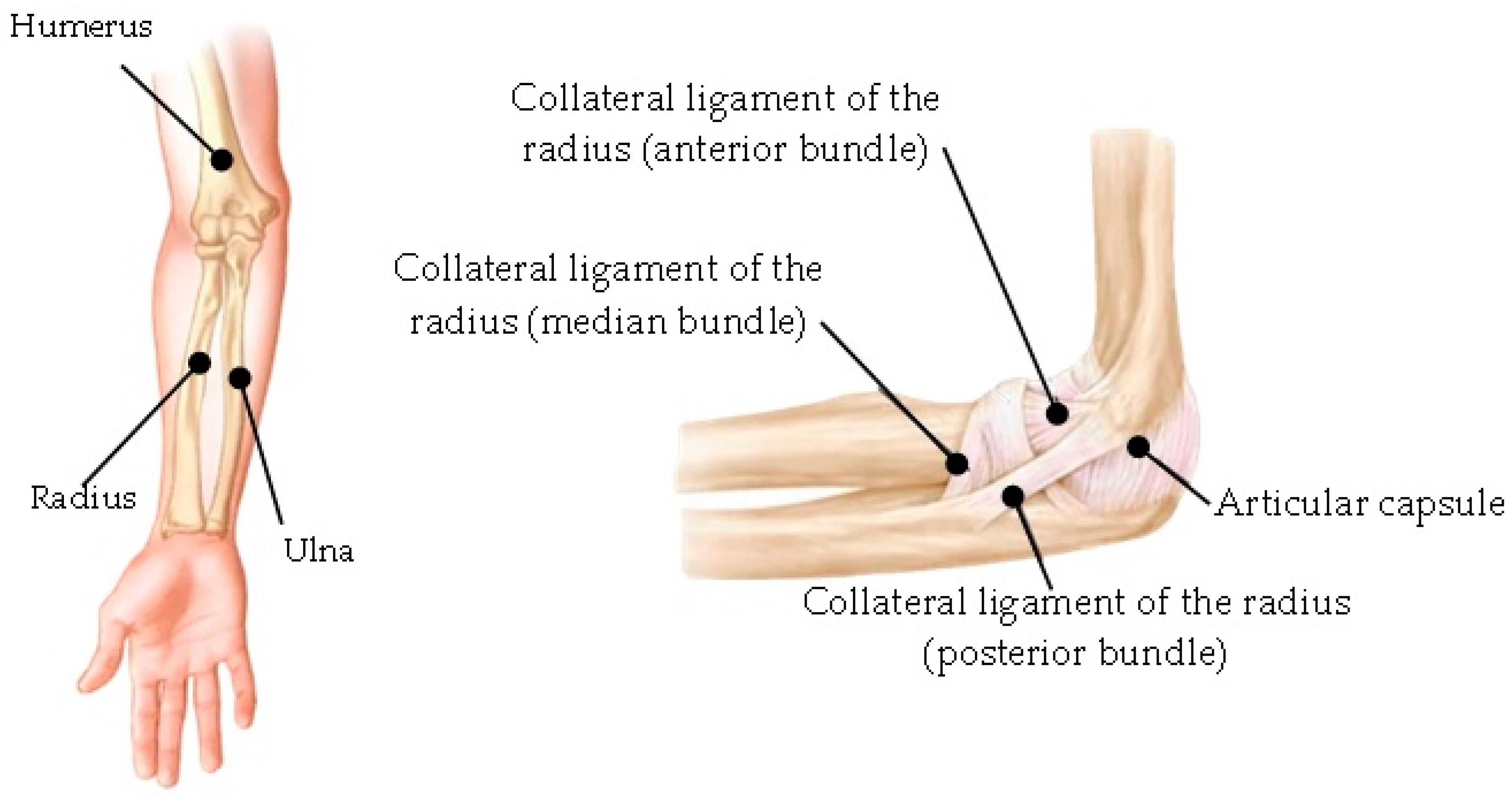
- Development of the capsule joint, implementing the mask around the contour between the bones that make up the elbow joint (humerus, radius, and ulna).
- Development of ligaments through a mask that fills the gaps between the bones.
- Application of smoothing to the surface of the biomodel.
- Export of the biomodel to the 3-Matic Medical® program for the application of a mesh to obtain elements of similar size.
- Solidification of the biomodel through re-meshing.
- Exportation of the biomodel to a format with an extension compatible with the Ansys Workbench® program, which implements the Finite Element Method, for the development of numerical analysis.
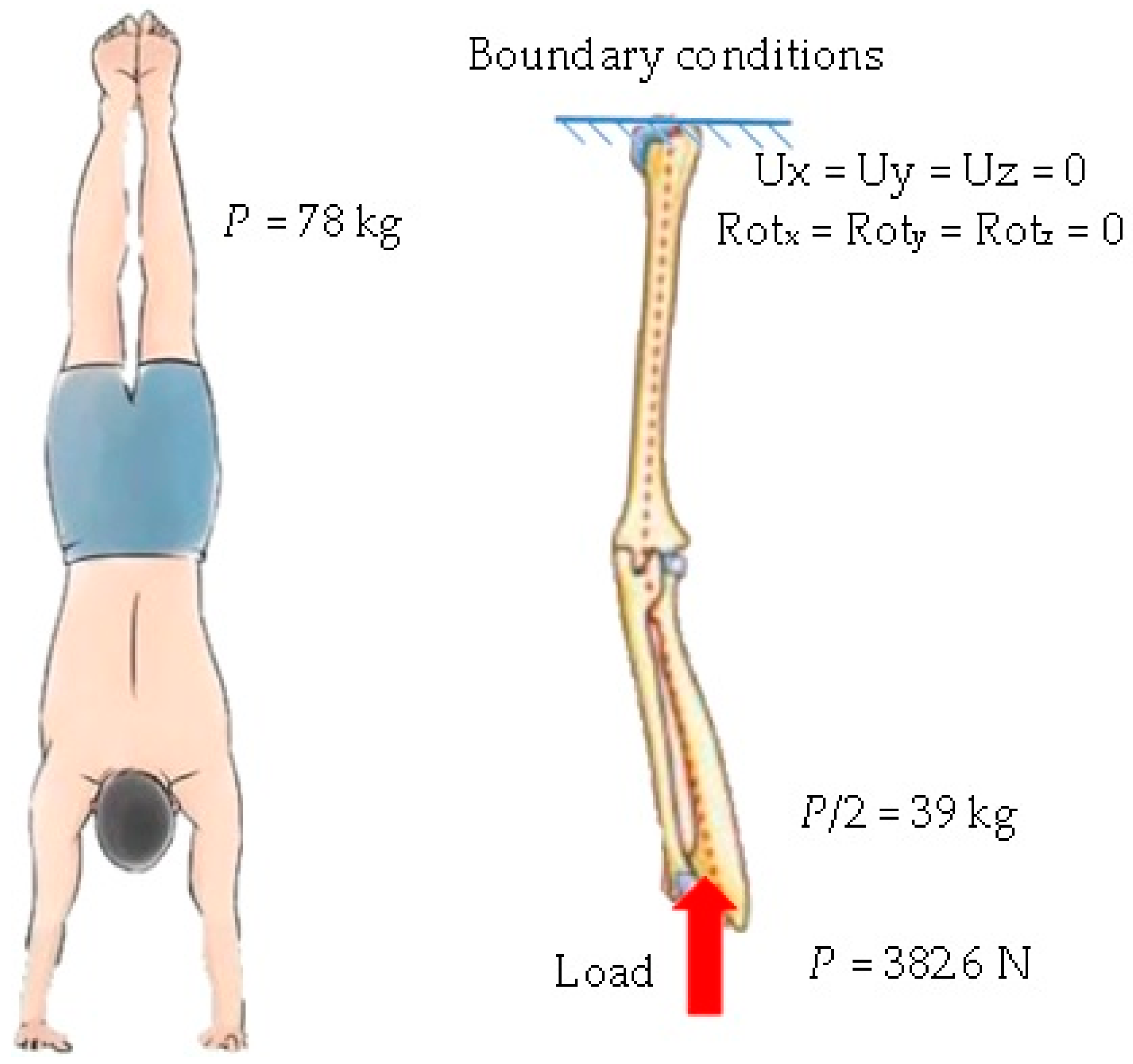
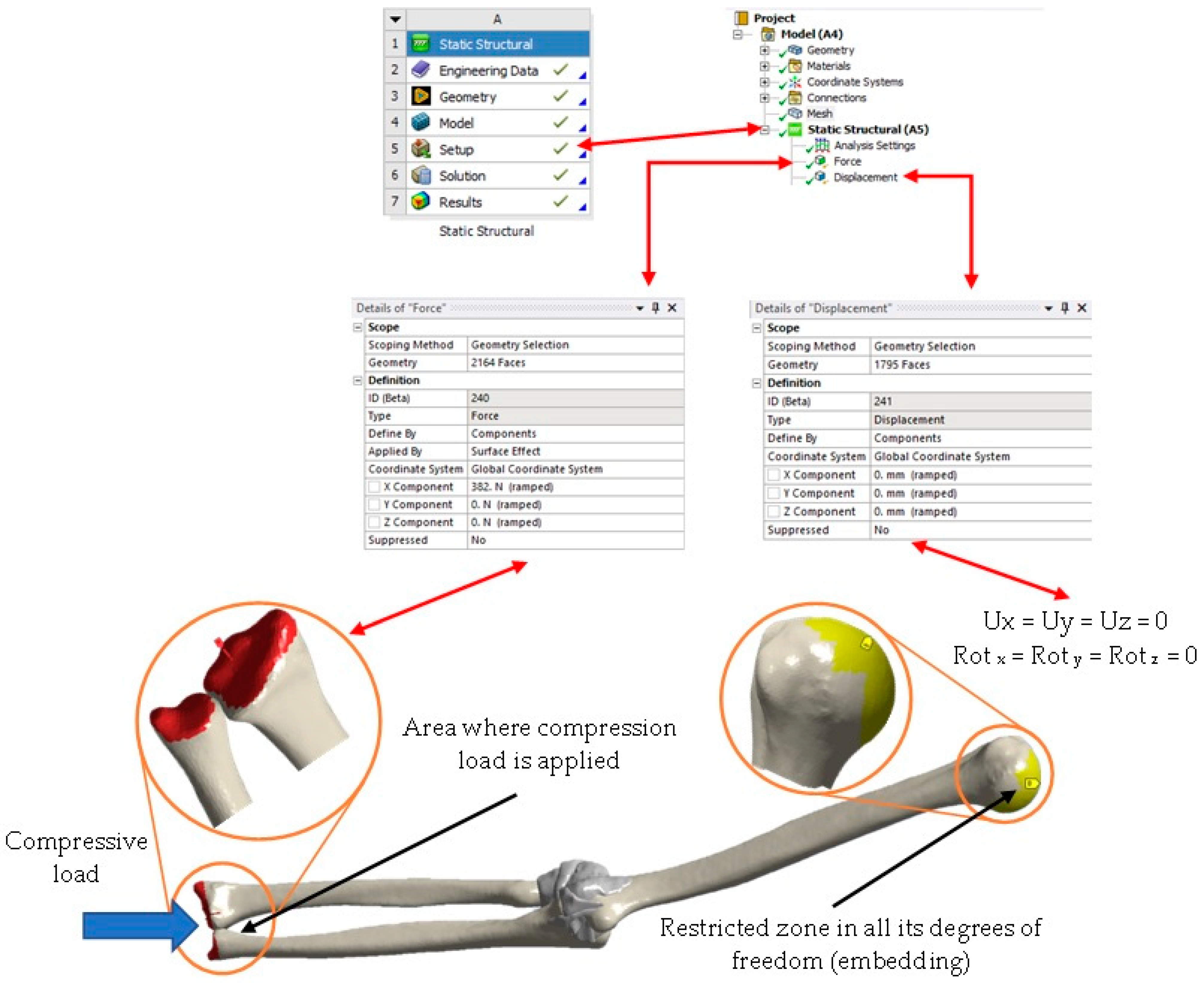
3. Numerical Analysis
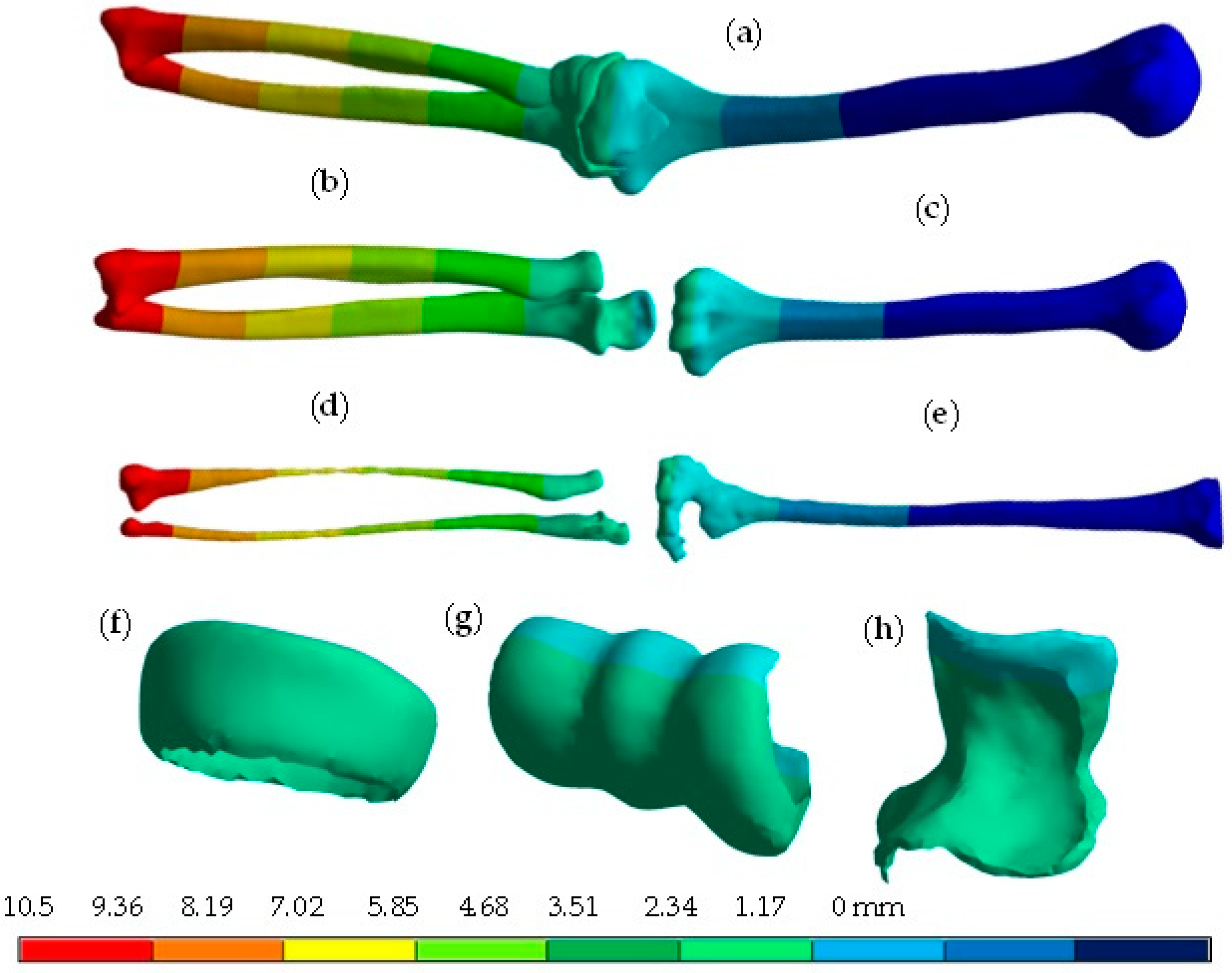
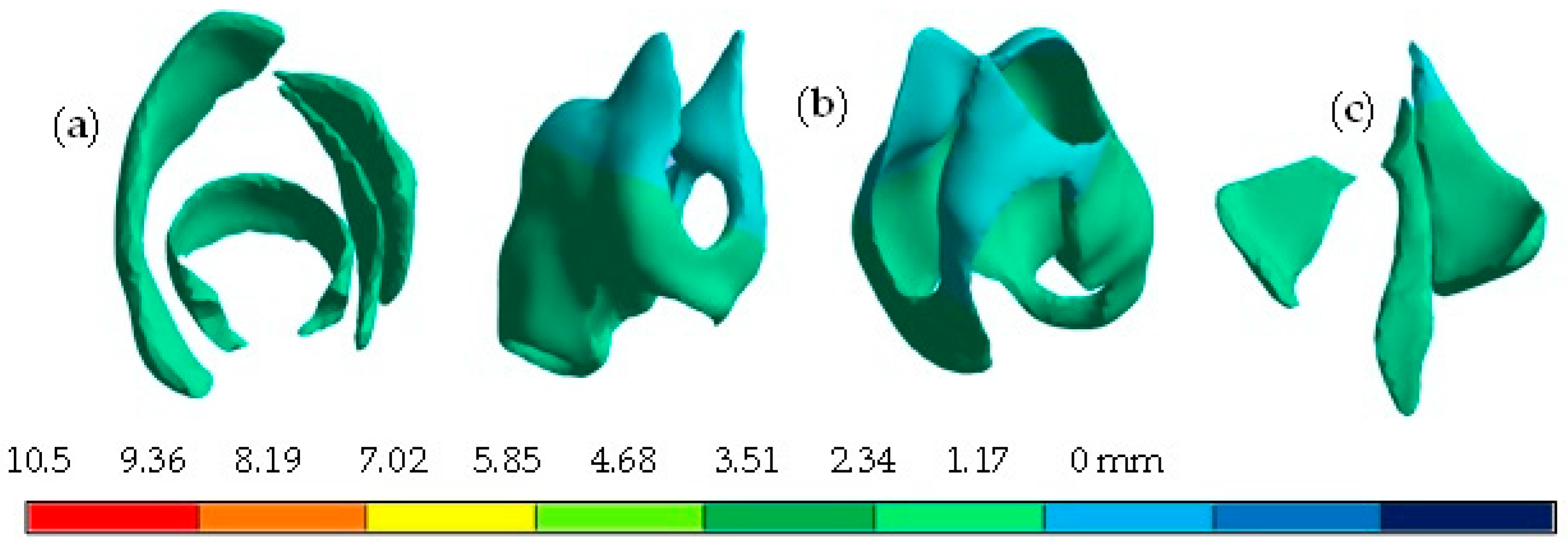
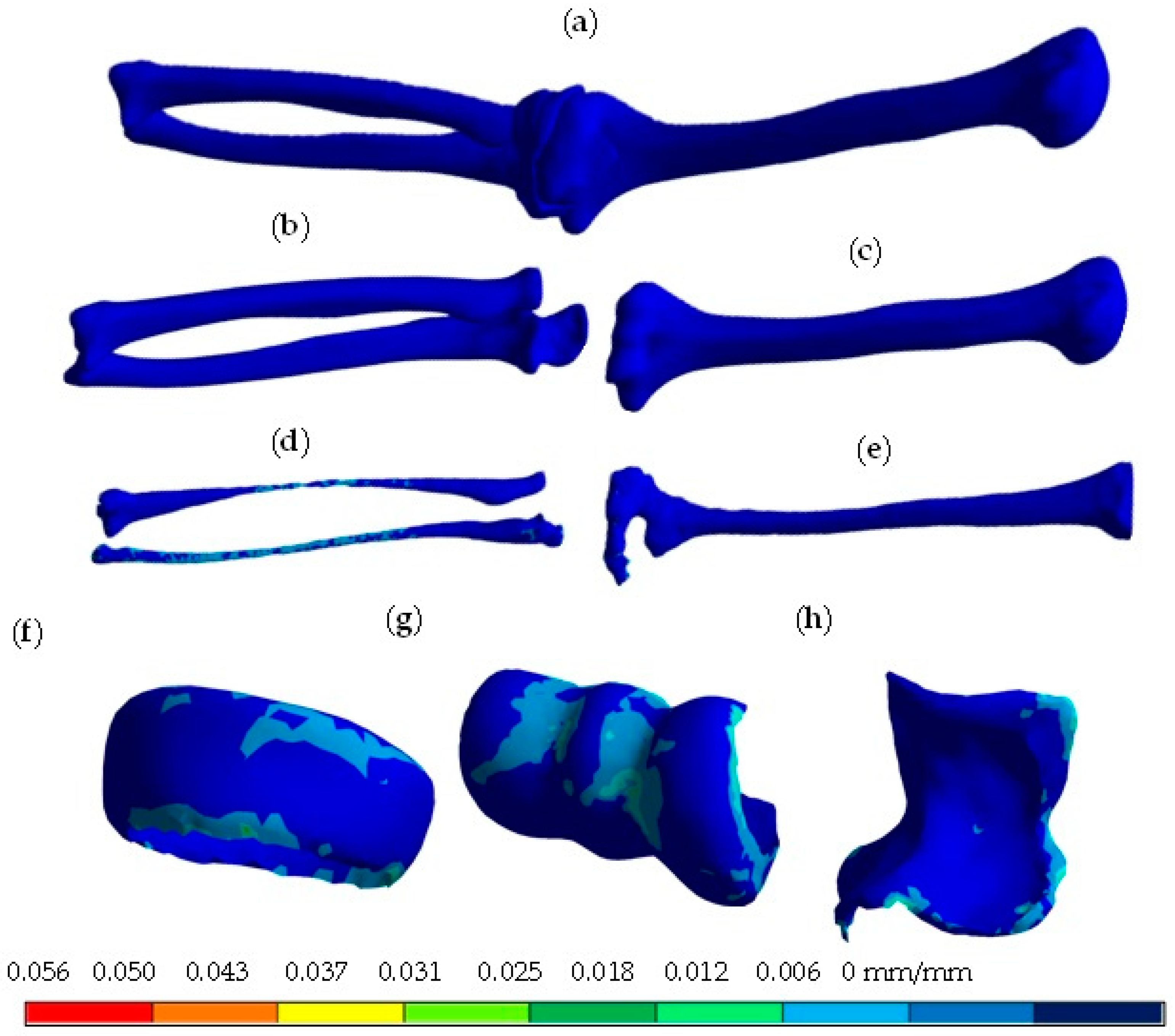
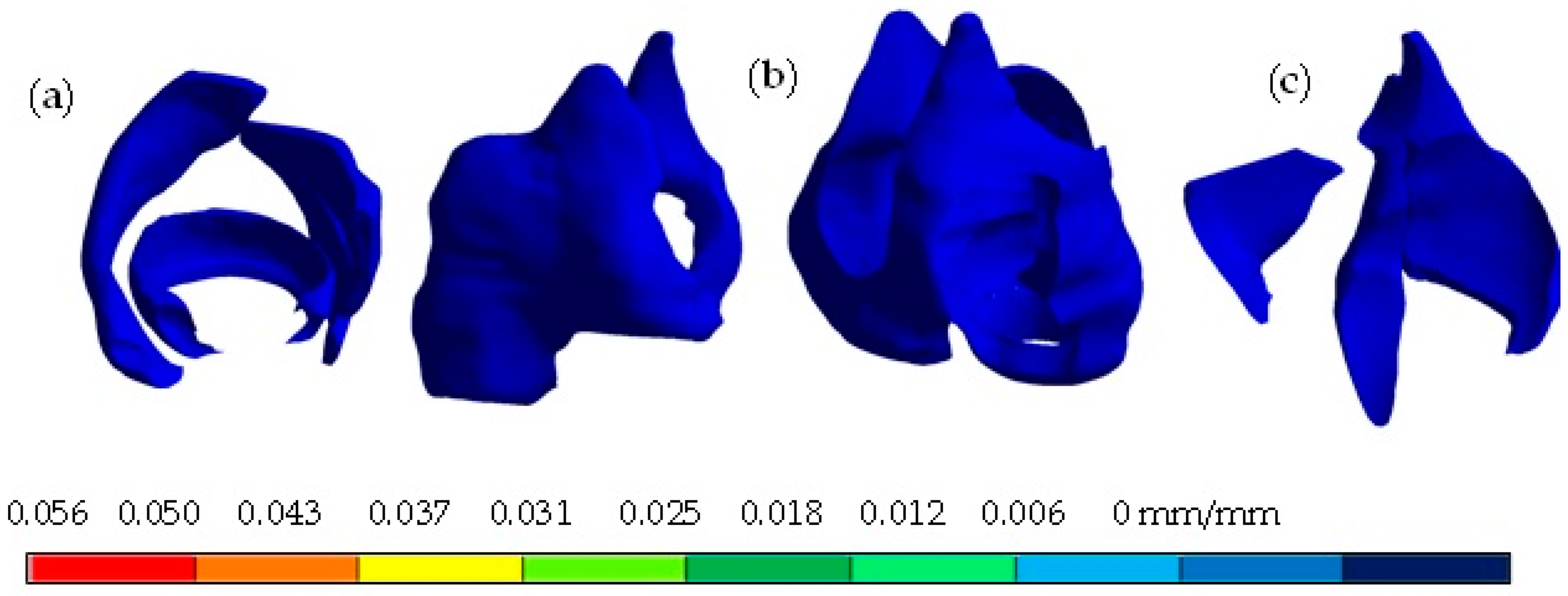
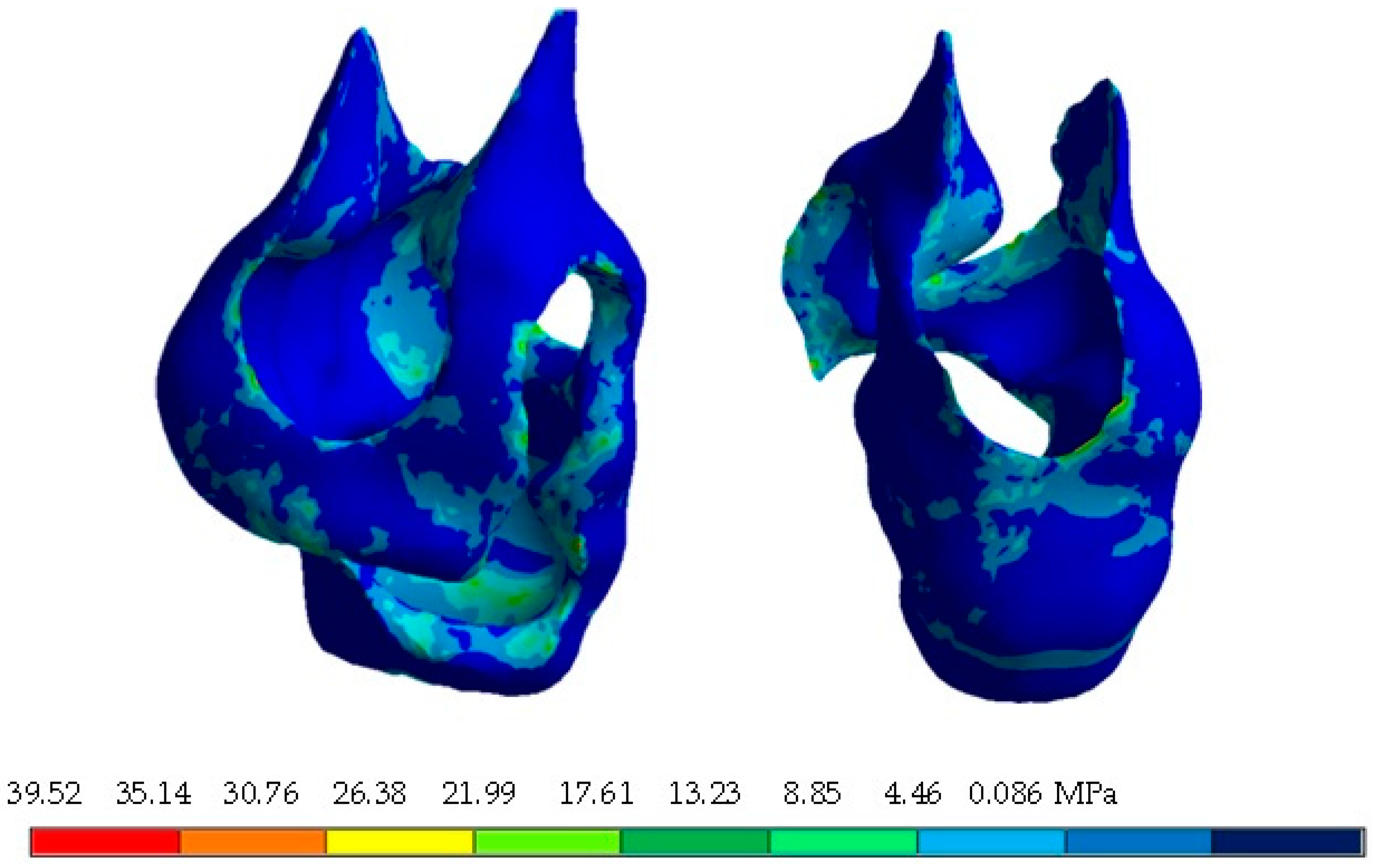
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Concept | Cortical Bone | Trabecular Bone | Cartilage | |||
|---|---|---|---|---|---|---|
| Maximum | Minimum | Maximum | Minimum | Maximum | Minimum | |
| Total displacement (mm) | 3.80 | 0 | 3.70 | 0 | 3.87 | 3.32 |
| Directional displacement, X axis (mm) | 1.16 | −0.21 | 1.02 | −0.071 | 1.03 | 0.02 |
| Directional displacement, Y axis (mm) | 0.010 | −1.57 | 0.008 | −1.51 | −1.42 | −1.58 |
| Directional displacement, Z axis (mm) | 0.002 | −3.46 | 0.007 | −3.28 | −2.97 | −3.53 |
| Elastic Strain | 0.005 | −1.85 × 10−8 | 0.015 | 5.69 × 10−5 | 0.056 | 0.0001 |
| Elastic Strain, X axis | 0.001 | −0.002 | 0.007 | −0.005 | 0.018 | −0.023 |
| Elastic Strain, Y axis | 0.0008 | −0.0006 | 0.008 | −0.006 | 0.014 | −0.005 |
| Elastic Strain, Z axis | 0.001 | −0.002 | 0.005 | −0.005 | 0.025 | −0.019 |
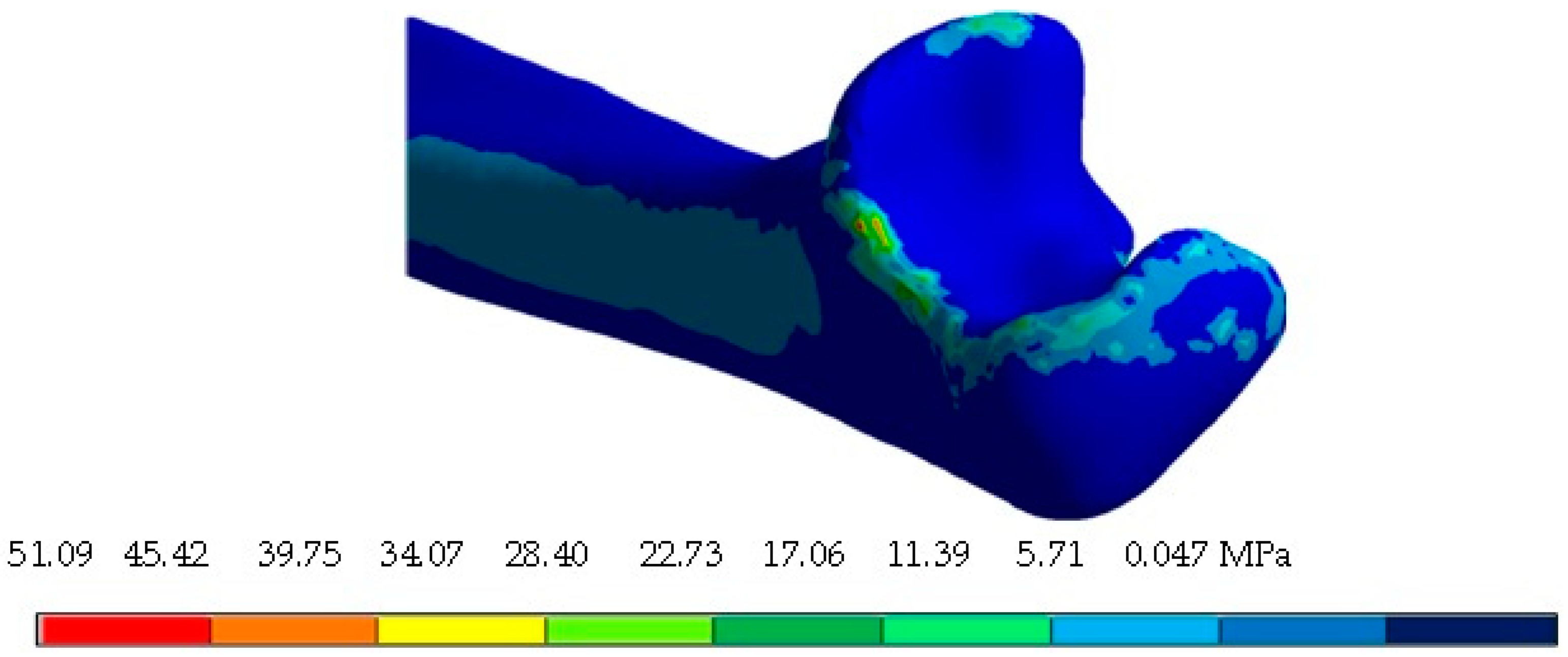
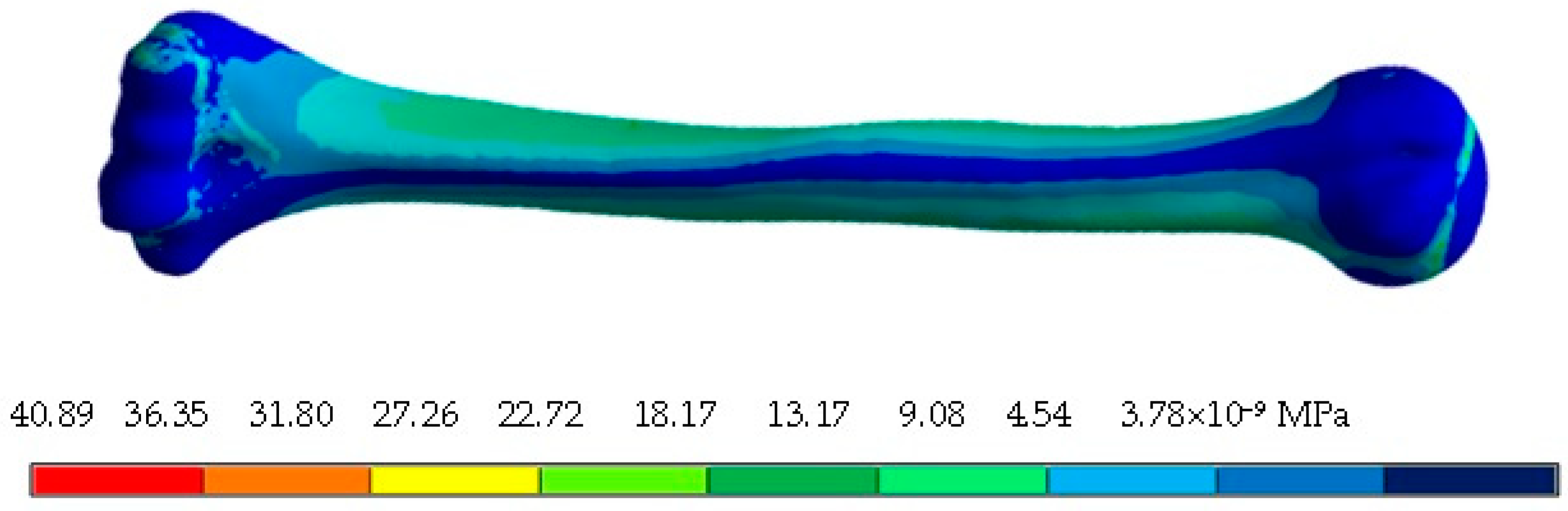
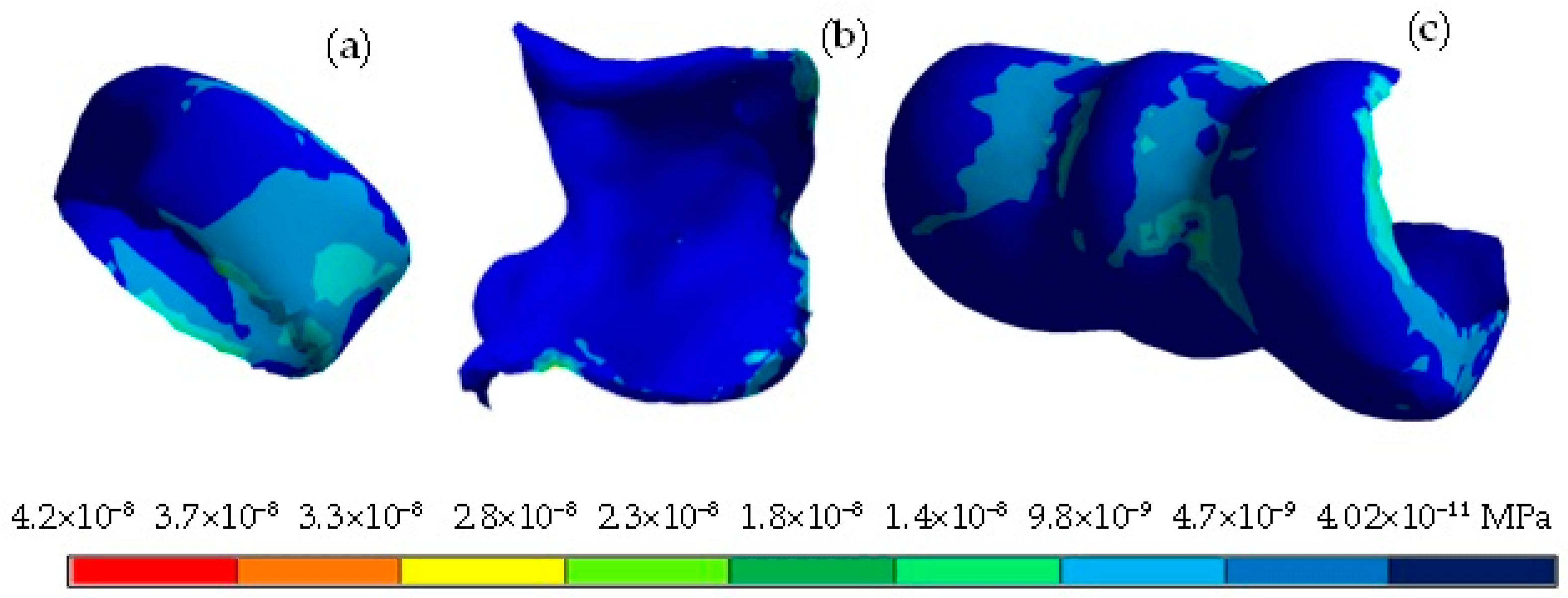
| Von Mises stress (MPa) | 33.5 | 0 | 11.65 | 0 | 4.02 × 10−8 | 3.68 × 10−11 |
| Nominal X-axis stress (MPa) | 25.46 | −36.62 | 11.28 | −8.86 | 1.35 × 10−8 | 1.69 × 10−8 |
| Nominal Y-axis stress (MPa) | 10.99 | −6.80 | 2.47 | −2.35 | 1.14 × 10−8 | −4.67 × 10−9 |
| Nominal Z-axis stress (MPa) | 15.68 | −15.85 | 4.22 | −4.24 | 1.95 × 10−8 | 1.44 × 10−8 |
| Maximum principal stress (MPa) | 27.29 | −5.50 | 12.98 | −1.27 | 2.50 × 10−8 | −8.46 × 10−10 |
| Middle principal stress (MPa) | 10.78 | −10.63 | 2.67 | −2.25 | 6.04 × 10−9 | −2.47 × 10−9 |
| Minimum principal stress (MPa) | 5.63 | −37.19 | 1.15 | −10.79 | 9.68 × 10−10 | −2.13 × 10−8 |
| XY shear stress (MPa) | 7.89 | −6.84 | 2.39 | −2.09 | 7.73 × 10−9 | −8.98 × 10−9 |
| YZ shear stress (MPa) | 6.57 | −8.47 | 1.92 | −2.45 | 5.06 × 10−9 | −7.18 × 10−9 |
| XZ shear stress (MPa) | 13.45 | −11.04 | 4.20 | −5.52 | 9.51 × 10−9 | −1.34 × 10−8 |
| Concept | Cortical Bone | Trabecular Bone | Cartilage | |||
|---|---|---|---|---|---|---|
| Maximum | Minimum | Maximum | Minimum | Maximum | Minimum | |
| Total displacement (mm) | 10.26 | 3.26 | 10.07 | 3.68 | 4.11 | 3.31 |
| Directional displacement, X axis (mm) | 1.99 | 0.08 | 1.82 | 0.37 | 0.92 | 0.07 |
| Directional displacement, Y axis (mm) | −1.41 | −2.90 | −1.52 | −2.85 | −1.43 | −1.61 |
| Directional displacement, Z axis (mm) | −2.90 | −9.69 | −3.32 | −9.50 | −2.97 | −3.68 |
| Elastic Strain | 0.006 | 5.92 × 10−6 | 0.017 | 0.0001 | 0.04 | 2.87 × 10−5 |
| Elastic Strain, X axis | 0.002 | −0.002 | 0.009 | −0.007 | 0.02 | −0.015 |
| Elastic Strain, Y axis | 0.0007 | −0.0006 | 0.001 | −0.002 | 0.004 | −0.003 |
| Elastic Strain, Z axis | 0.001 | 0.002 | 0.006 | −0.004 | 0.017 | −0.017 |
| Von Mises stress (MPa) | 48.72 | 0 | 14.41 | 0 | 3.43 × 10−8 | 1.75 × 10−11 |
| Nominal X-axis stress (MPa) | 35.08 | −47.64 | 12.72 | −9.83 | 1.73 × 10−8 | −1.15 × 10−8 |
| Nominal Y-axis stress (MPa) | 7.83 | −10.74 | 2.25 | −2.42 | 3.84 × 10−9 | −2.84 × 10−9 |
| Nominal Z-axis stress (MPa) | 11.63 | −15.83 | 3.97 | −3.55 | 1.37 × 10−8 | −1.35 × 10−8 |
| Maximum principal stress (MPa) | 37.32 | −5.19 | 13.79 | −1.34 | 2.23 × 10−8 | −2.11 × 10−10 |
| Middle principal stress (MPa) | 8.75 | −11.18 | 3.55 | −3.45 | 6.17 × 10−9 | −3.82 × 10−9 |
| Minimum principal stress (MPa) | 4.85 | −50.81 | 1.22 | −10.07 | 6.83 × 10−10 | −1.81 × 10−8 |
| XY shear stress (MPa) | 7.95 | −7.14 | 3.18 | −5.15 | 6.12 × 10−9 | −6.36 × 10−9 |
| YZ shear stress (MPa) | 9.47 | −8.48 | 2.08 | −2.78 | 7.35 × 10−9 | −4.25 × 10−9 |
| XZ shear stress (MPa) | 12.52 | −14.16 | 7.12 | −5.06 | 1.31 × 10−8 | 9.61 × 10−9 |
| Concept | Cortical Bone | Trabecular Bone | Cartilage | |||
|---|---|---|---|---|---|---|
| Maximum | Minimum | Maximum | Minimum | Maximum | Minimum | |
| Total displacement (mm) | 10.54 | 3.85 | 10.34 | 4.00 | 4.16 | 3.82 |
| Directional displacement, X axis (mm) | 2.30 | 0.66 | 2.18 | 0.80 | 1.18 | 0.64 |
| Directional displacement, Y axis (mm) | −1.54 | −3.01 | −1.57 | −2.96 | −1.53 | −1.61 |
| Directional displacement, Z axis (mm) | −3.44 | −9.88 | −3.56 | −9.69 | −3.40 | −3.67 |
| Elastic Strain | 0.005 | 5.34 × 10−6 | 0.016 | 5.34 × 10−6 | 0.03 | 0.0001 |
| Elastic Strain, X axis | 0.002 | −0.002 | 2.07 | −3.48 | 0.008 | −0.010 |
| Elastic Strain, Y axis | 0.0005 | −0.0007 | 5.83 | −5.57 | 0.006 | −0.0010 |
| Elastic Strain, Z axis | 0.002 | −0.001 | 0.009 | −0.007 | 0.011 | −0.009 |
| Von Mises stress (MPa) | 37.32 | 0 | 14.22 | 0 | 2.16 × 10−8 | 7.42 × 10−11 |
| Nominal X-axis stress (MPa) | 38.11 | 36.65 | 9.70 | −8.77 | 6.73 × 10−6 | −8.00 × 10−9 |
| Nominal Y-axis stress (MPa) | 7.01 | −7.96 | 2.07 | −3.48 | 5.22 × 10−9 | −1.65 × 10−9 |
| Nominal Z-axis stress (MPa) | 15.17 | −13.84 | 5.83 | −5.57 | 9.33 × 10−9 | −7.03 × 10−9 |
| Maximum principal stress (MPa) | 41.53 | −4.99 | 11.56 | −1.21 | 1.56 × 10−8 | −4.33 × 10−10 |
| Middle principal stress (MPa) | 8.40 | −7.45 | 2.02 | −2.37 | 4.52 × 10−9 | 4.23 × 10−9 |
| Minimum principal stress (MPa) | 5.16 | −37.00 | 0.93 | −11.2 | 9.94 × 10−10 | −1.13 × 10−8 |
| XY shear stress (MPa) | 10.83 | −5.84 | 3.87 | −2.33 | 2.72 × 10−9 | −4.05 × 10−9 |
| YZ shear stress (MPa) | 4.17 | −11.38 | 2.77 | −2.40 | 8.94 × 10−9 | −2.24 × 10−9 |
| XZ shear stress (MPa) | −11.09 | −11.09 | 7.52 | −4.36 | 3.15 × 10−9 | −1.77 × 10−8 |
| Concept | Capsule Joint | Ligaments of the Radius | Ligaments of the Ulna | |||
|---|---|---|---|---|---|---|
| Maximum | Minimum | Maximum | Minimum | Maximum | Minimum | |
| Total displacement (mm) | 4.53 | 2.76 | 4.20 | 3.51 | 4.19 | 3.36 |
| Directional displacement, X axis (mm) | 1.25 | −0.01 | 1.27 | 0.38 | 0.43 | −0.08 |
| Directional displacement, Y axis (mm) | −1.26 | −1.66 | −1.44 | −1.61 | −1.45 | −1.65 |
| Directional displacement, Z axis (mm) | −2.41 | −3.87 | −3.06 | −3.71 | 3.03 | −3.83 |
| Elastic Strain | 0.006 | 2.00 × 10−5 | 0.017 | 2.09 × 10−6 | 0.012 | 1.08 × 10−6 |
| Elastic Strain, X axis | 0.004 | −0.004 | −0.008 | −0.006 | 0.006 | −0.004 |
| Elastic Strain, Y axis | 0.002 | −0.001 | 0.008 | −0.004 | 0.001 | −0.001 |
| Elastic Strain, Z axis | 0.003 | −0.004 | 0.005 | −0.007 | 0.004 | −0.005 |
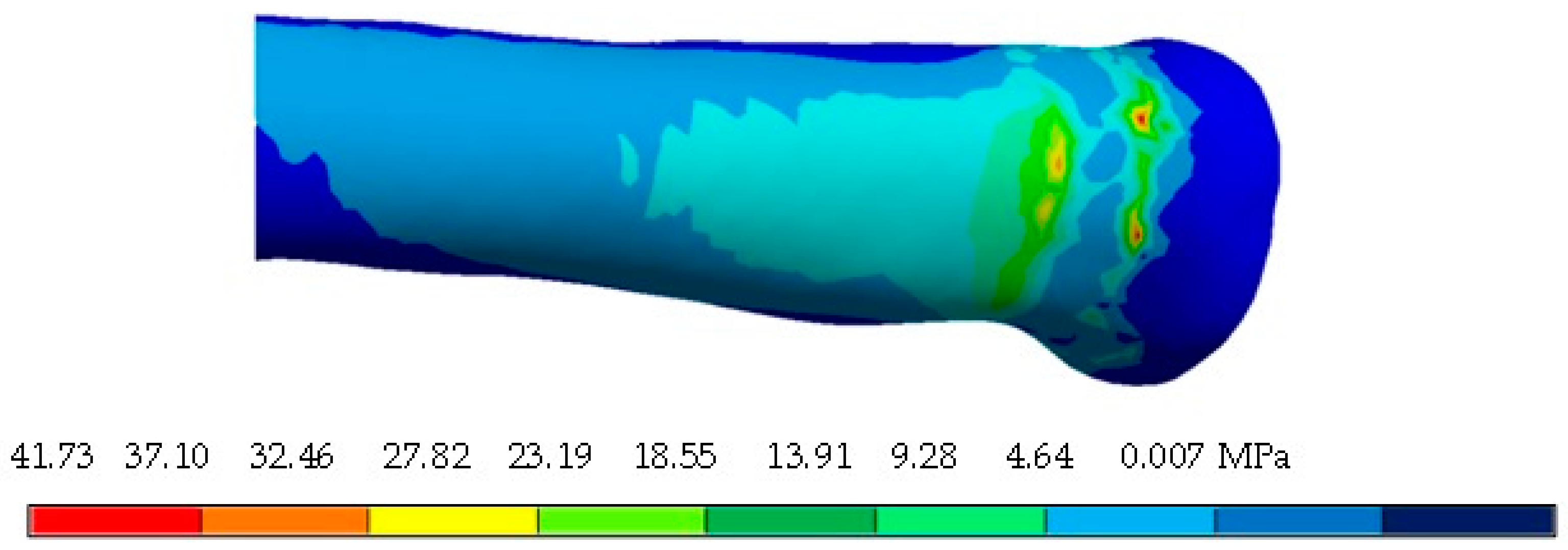
| Von Mises stress (MPa) | 37.66 | 0 | 103.3 | 0 | 73.49 | 0 |
| Nominal X-axis stress (MPa) | 34.22 | −40.48 | 102.6 | −39.28 | 30.39 | −38.10 |
| Nominal Y-axis stress (MPa) | 17.71 | −22.10 | 52.39 | −21.20 | 15.36 | −20.77 |
| Nominal Z-axis stress (MPa) | 18.15 | −25.81 | 65.00 | −62.19 | 34.97 | −20.42 |
| Maximum principal stress (MPa) | 34.32 | −12.02 | 115.19 | −15.52 | 38.52 | −7.87 |
| Middle principal stress (MPa) | 18.96 | −21.66 | 63.34 | −28.37 | 24.06 | −18.40 |
| Minimum principal stress (MPa) | 11.27 | −43.95 | 39.42 | −94.40 | 12.73 | −49.20 |
| XY shear stress (MPa) | 15.52 | −12.91 | 25.26 | −26.15 | 7.73 | −17.11 |
| YZ shear stress (MPa) | 7.54 | −9.14 | 42.17 | −5.95 | 12.38 | −28.54 |
| XZ shear stress (MPa) | 13.41 | −19.75 | 28.34 | −25.33 | 19.07 | −14.26 |
References
- Willing, R.T.; Lalone, E.A.; Shannon, H.; Johnson, J.A.; King, G.J.W. Validation of a finite element model of the human elbow for determining cartilage contact mechanics. J. Biomech. 2013, 46, 1767–1771. [Google Scholar] [CrossRef] [PubMed]
- Garzón-Alvarado, D.A.; Duque-Daza, C.A.; Ramírez-Martínez, A.M. On the emergence of biomechanics and computational mechanobiology: Computational experiments and recent findings. Rev. Cuba. Investig. Bioméd. 2009, 28, 83–101. [Google Scholar]
- Urbanowieza, E.M.; Ramíreza, E.I.; Ruiz, O.; Ortiza, A. Analysis by finite element parcel of a Thompson® hip prosthesis under four different load conditions. In Proceedings of the XXI Annual International Congress of the SOMIM, Pachuca, México, 22–24 September 2021; pp. 24–31. [Google Scholar]
- López-Liévano, A.; López-Liévano, D.R.; Caicedo-Ortiz, H.E.; González-Rebattú, A. Biomodeling of the components of the human middle ear using magnetic resonance imaging. Scientist 2017, 21, 3–8. [Google Scholar]
- Kumar, S.; Kumar, J. A review on application of finite element modelling in bone biomechanics. Perspect. Sci. 2016, 8, 696–698. [Google Scholar]
- Goel, V.K.; Singh, D.; Bijlani, V. Contact areas in human elbow joints. J. Biomech. Eng. 1982, 104, 169–175. [Google Scholar] [CrossRef]
- Lohfeld, S.; Barron, V.; McHugh, P.E. Biomodels of Bone: A Review. Ann. Biomed. Eng. 2005, 33, 1295–1311. [Google Scholar] [CrossRef]
- Ruiz-Santiago, F.; Castellano-García, M.; Guzmán-Álvarez, L.; Tello-Moreno, M. Computed tomography and magnetic resonance imaging in painful diseases of the spine; Respective contributions and controversies. Radiology 2011, 53, 116–133. [Google Scholar]
- Cristea, A.F. Mechanical stress and strain properties, regarding the elbow joint. Acta Tech. Napoc.-Ser. Appl. Math. Mech. Eng. 2014, 57, 179–188. [Google Scholar]
- Jardini, A.L.; Larosa, M.A.; Filho, R.M.; Zavaglia, C.A.D.C.; Bernardes, L.F.; Lambert, C.S.; Kharmandayan, P. Cranial reconstruction: 3D biomodel and custom-built implant created using additive manufacturing. J. Cranio-Maxillofac. Surg. 2014, 42, 1877–1884. [Google Scholar] [CrossRef]
- Oliveira, M.; Sooraj Hussain, N.; Dias, A.G.; Lopes, M.A.; Azevedo, L.; Zenha, H.; Santos, J.D. 3-D biomodelling technology for maxillofacial reconstruction. Mater. Sci. Eng. C 2008, 28, 1347–1351. [Google Scholar] [CrossRef]
- Nareliya, R.; Kumar, V. Finite element application to a femur bone: A review. J. Biomed. Bioeng. 2012, 3, 57–62. [Google Scholar]
- Cisneros-Hidalgo, Y.; González-Carbonell, R.; Ortiz-Prado, A.; Jacobo-Almendáriz, V.; Puente-Álvarez, A. Modelo mechanobiological of a human tibia to determine its response to external mechanical stimuli. Cuba. J. Biomed. Res. 2015, 34, 54–63. [Google Scholar]
- Mastache-Miranda, O.A.; Urriolagoitia-Sosa, G.; Marquet-Rivera, R.A. Three-dimensional reconstruction for use in medicine and biomechanics. MOJ Appl. Bionics Biomech. 2018, 2, 310–331. [Google Scholar]
- Marquet-Rivera, R.A.; Urriolagoitia-Sosa, G.; Romero-Ángeles, B.; Vázquez-Feijoo, J.A.; Urriolagoitia-Calderón, G. Computational biomodelling and numerical analysis as means of diagnostic and odontological prognosis. MOJ Appl. Bionics Biomech. 2018, 2, 262–263. [Google Scholar]
- Wu, D.; Isaksson, P.; Fergusson, S.J.; Persson, C. Young´s modulus of trabecular bone at the tissue level: A review. Acta Biomater. 2018, 78, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Flores-Renteria, M.A.; Ortíz-Domínguez, M.; Cruz-Avilés, A.; López-Sánchez, F. Bone mechanics: A review of bone remodeling, Ingenuity and Consciousness. Sci. Bull. Super. Sch. Ciudad. Sahagún 2018, 9, 1–15. [Google Scholar]
- Mendoza, A. Study of the mechanical properties of the bone system. J. Eng. Res. 1991, 23, 14–19. [Google Scholar]
- Martinez-Mondragon, M.; Urriolagoitia-Sosa, G.; Romero-Ángeles, B.; Maya-Anaya, D.; Martínez-Reyes, J.; Gallegos-Funes, F.J.; Urriolagoitia-Calderón, G.M. Numerical Analysis of Zirconium and Titanium Implants under the Effect of Critical Masticatory Load. Materials 2022, 15, 7843. [Google Scholar] [CrossRef]
- Hernández-Vázquez, R.A.; Romero-Ángeles, B.; Urriolagoitia-Sosa, G.; Vázquez-Feijoo, J.A.; Vázquez-López, Á.J.; Urriolagoitia-Calderón, G. Numerical analysis of masticatory forces on a lower first molar considering the contact between dental tissues. Appl. Bionics Biomech. 2018, 2018, 4196343. [Google Scholar] [CrossRef]
- Marquet-Rivera, R.A.; Urriolagoitia-Sosa, G.; Hernández-Vázquez, R.A.; Romero-Ángeles, B.; Mastache-Miranda, O.A.; Urriolagoitia-Calderón, G. High biofidelity 3D biomodel reconstruction from soft and hard tissues (knee), FEM, and 3D printing: A three-dimensional methodological proposal. BioMed Res. Int. 2021, 2021, 6688164. [Google Scholar]
- Hernández-Vázquez, R.A.; Urriolagoitia-Sosa, G.; Marquet-Rivera, R.A.; Romero-Angeles, B.; Mastache-Miranda, O.A.; Vázquez-Feijoo, J.A.; Urriolagoitia-Calderon, G. High-biofidelity biomodel generated from three-dimensional imaging (cone-beam computed tomography): A methodological proposal. Comput. Math. Methods Med. 2020, 2020, 4292501. [Google Scholar] [CrossRef] [PubMed]
- Marquet-Rivera, R.A.; Urriolagoitia-Sosa, G.; Romero-Ángeles, B.; Hernández-Vázquez, R.A.; Mastache-Miranda, O.A.; Cruz-López, S.; Urriolagoitia-Calderón, G. Numerical Analysis of the ACL, with Sprains of Different Degrees after Trauma. Comput. Math. Methods Med. 2021, 2021, 2109348. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Vázquez, R.A.; Romero-Ángeles, B.; Urriolagoitia-Sosa, G.; Vázquez-Feijoo, J.A.; Marquet-Rivera, R.A.; Urriolagoitia-Calderón, G. Mechanobiological analysis of molar teeth with carious lesions through the finite element method. Appl. Bionics Biomech. 2018, 2018, 1815830. [Google Scholar] [CrossRef] [PubMed]

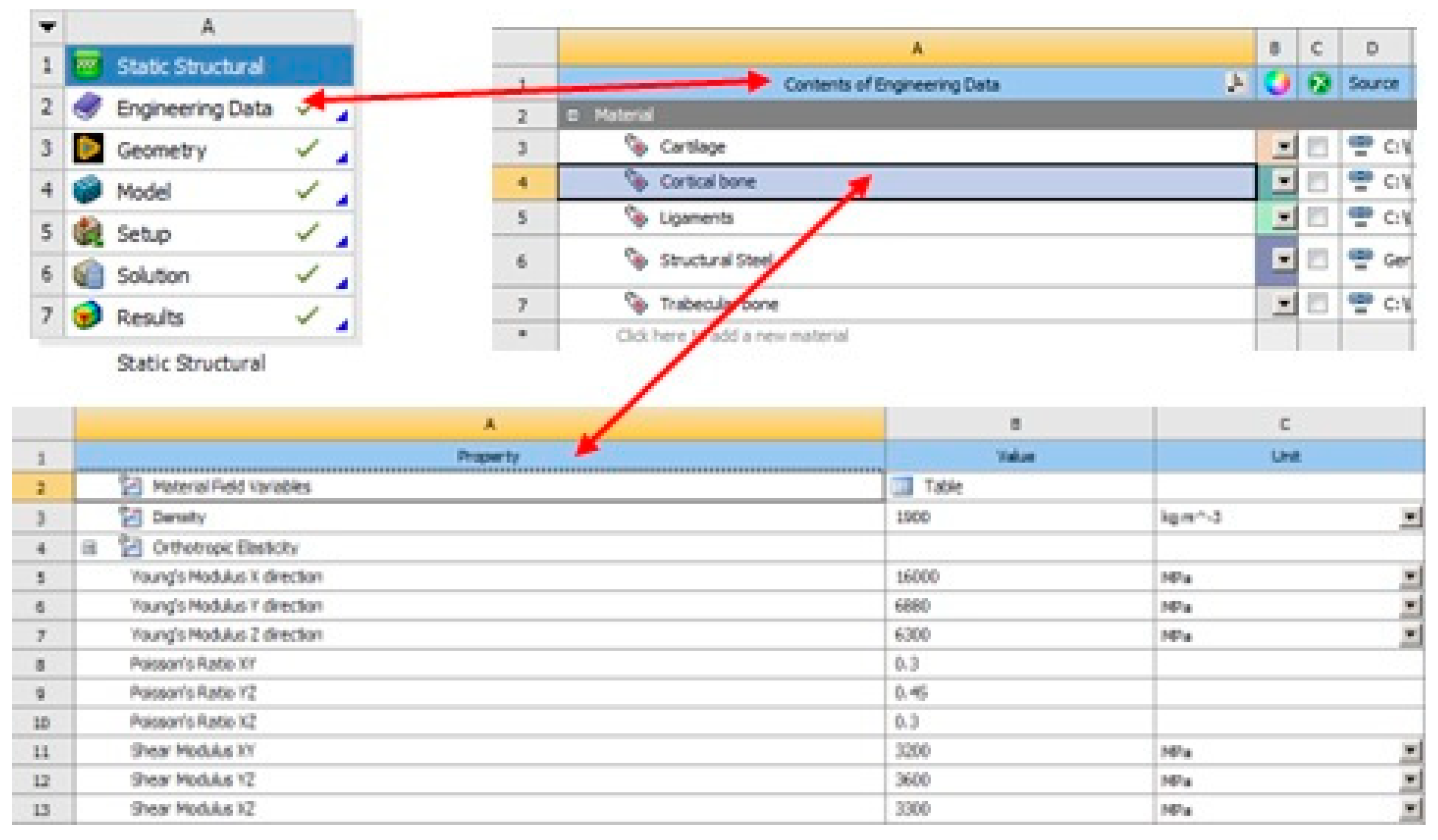



| Young’s Modulus (MPa) | Shear Modulus (MPa) | Poisson Ratio |
|---|---|---|
| E1 = 16,000 | G12 = 3200 | υ12 = 0.30 |
| E2 = 6880 | G23 = 3600 | υ23 = 0.45 |
| E3 = 6300 | G13 = 3300 | υ13 = 0.30 |
| Young’s Modulus (MPa) | Shear Modulus (MPa) | Poisson Ratio |
|---|---|---|
| E1 = 1352 | G12 = 292 | υ12 = 0.30 |
| E2 = 968 | G23 = 370 | υ23 = 0.30 |
| E3 = 676 | G13 = 505 | υ13 = 0.30 |
| Component | Young’s Modulus | Poisson Ratio |
|---|---|---|
| Ligament | 6100 MPa | 0.45 |
| Cartilage | 0.8 MPa | 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maya-Anaya, D.; Urriolagoitia-Sosa, G.; Romero-Ángeles, B.; Martinez-Mondragon, M.; German-Carcaño, J.M.; Correa-Corona, M.I.; Trejo-Enríquez, A.; Sánchez-Cervantes, A.; Urriolagoitia-Luna, A.; Urriolagoitia-Calderón, G.M. Numerical Analysis Applying the Finite Element Method by Developing a Complex Three-Dimensional Biomodel of the Biological Tissues of the Elbow Joint Using Computerized Axial Tomography. Appl. Sci. 2023, 13, 8903. https://doi.org/10.3390/app13158903
Maya-Anaya D, Urriolagoitia-Sosa G, Romero-Ángeles B, Martinez-Mondragon M, German-Carcaño JM, Correa-Corona MI, Trejo-Enríquez A, Sánchez-Cervantes A, Urriolagoitia-Luna A, Urriolagoitia-Calderón GM. Numerical Analysis Applying the Finite Element Method by Developing a Complex Three-Dimensional Biomodel of the Biological Tissues of the Elbow Joint Using Computerized Axial Tomography. Applied Sciences. 2023; 13(15):8903. https://doi.org/10.3390/app13158903
Chicago/Turabian StyleMaya-Anaya, Daniel, Guillermo Urriolagoitia-Sosa, Beatriz Romero-Ángeles, Miguel Martinez-Mondragon, Jesús Manuel German-Carcaño, Martin Ivan Correa-Corona, Alfonso Trejo-Enríquez, Arturo Sánchez-Cervantes, Alejandro Urriolagoitia-Luna, and Guillermo Manuel Urriolagoitia-Calderón. 2023. "Numerical Analysis Applying the Finite Element Method by Developing a Complex Three-Dimensional Biomodel of the Biological Tissues of the Elbow Joint Using Computerized Axial Tomography" Applied Sciences 13, no. 15: 8903. https://doi.org/10.3390/app13158903
APA StyleMaya-Anaya, D., Urriolagoitia-Sosa, G., Romero-Ángeles, B., Martinez-Mondragon, M., German-Carcaño, J. M., Correa-Corona, M. I., Trejo-Enríquez, A., Sánchez-Cervantes, A., Urriolagoitia-Luna, A., & Urriolagoitia-Calderón, G. M. (2023). Numerical Analysis Applying the Finite Element Method by Developing a Complex Three-Dimensional Biomodel of the Biological Tissues of the Elbow Joint Using Computerized Axial Tomography. Applied Sciences, 13(15), 8903. https://doi.org/10.3390/app13158903






