Skip Content
You are currently on the new version of our website. Access the old version .
MDPIMDPI
Applied SciencesApplied Sciences
Download PDF
  • Article
  • Open Access

12 August 2023

Study on the Particle Surface Fractal Characteristics of Sulfide Ores

,
,
,
,
and
1
School of Resource, Environment & Safety Engineering, Hunan University of Science & Technology, Xiangtan 411201, China
2
Work Safety Key Lab on Prevention and Control of Gas and Roof Disasters for Southern Coal Mines, Hunan University of Science & Technology, Xiangtan 411201, China
3
School of Resource & Safety Engineering, Central South University, Changsha 410083, China
*
Author to whom correspondence should be addressed.
Appl. Sci.2023, 13(16), 9199;https://doi.org/10.3390/app13169199
This article belongs to the Topic New Trends in Rock Materials Mechanics and Engineering Geology
Version Notes
Order Reprints

Abstract

The fractal dimension is widely used in many fields as a parameter to characterize the geometric complexity and geometric distribution relationship of research objects. To study the surface characteristics of sulfide ore particles, the fractal theory was applied to quantitatively characterize the surface fractal dimension Ds of sulfide ore microparticles in three particle size ranges, 60–100 mesh, 100–140 mesh and >200 mesh, based on the area–perimeter method. Using an optical microscope, grain projection images of the particles were obtained. The grain shape and characteristics of sulfide ore particles were studied by means of an image processing system. The results demonstrate that the grain shape of sulfide ore particles can be expressed by fractal dimension, and the particle surface fractal dimension ranges from 2.4392 to 2.5492. It was found that the fractal properties begin to decrease due to the increasing of the particle size. The larger the fractal dimension, the finer the particles are. The fractal dimension of sulfide ore particles can be used as an important indicator of their particle shape distribution characteristics, which can provide important information for further study of the relevant physical and chemical properties of sulfide ore particles and provide a new theoretical method and basis for the adhesion and removal of sulfide ore dust. With the quantitative description of the fractal distribution of sulfide ore particles, a new way to study the adhesive force between particles is offered for further research.

1. Introduction

A large amount of dusts are produced from mining, metal smelting and other production activities. Dust pollution is one of the world’s public hazards. With the development of the mining industry in China, especially the improvement of mechanization in mining, dust pollution is becoming a serious problem [1,2,3,4]. Workers who are exposed to high dust concentrations for an extended length of time run a serious risk to their health and safety [5,6,7,8]. China reported more than 1,012,000 cases of occupational diseases by the end of 2020, with pneumoconiosis making up over 88.6% of these cases. The status of occupational sickness in China is still dire, and pneumoconiosis is still the most dangerous occupational disease, despite the fact that many production businesses have adopted numerous effective dust protection measures. It was put forward by Chao Wu, Fu-qiang Yang, Wei Pan et al. [9,10,11,12] that sulfide ore dust is very representative in metal and nonmetal mines; it is characterized by complicated composition, hydrophobic nature and causing large and widespread damage. Sulfide ore dust, especially at the micron-level, is present in high concentrations at production sites and difficult to remove, causing widespread dust pollution and occupational hazards Therefore, it has very important meaning and practical value for sulfide ore dust research. At present, dust pollution has caused serious damage to the environment, production and life. To solve the problem of microparticle pollution, it is necessary to study the interaction mechanism of adhesion between microparticles and interfaces, so that the adhesion effect between microparticles and interfaces can be effectively controlled or utilized. The surface adhesion problem is a comprehensive subject involving physics, chemistry, biology and mechanics. The magnitude of the adhesion force between dust microparticles and the interface can measure the difficulty of dust being removed. To study the magnitude of the adhesion force, it is particularly important to study the geometric fractal shape of the dust microparticles.
It is well known that the geometry of particles is one of the most important parameters to describe their geometric features [13,14,15]. For non-cohesive soil (sand, silt), particle shape has a close relation with its mechanical properties such as compressibility and filling property [16,17]. Recent studies show that the fractal geometry theory, which was proposed and developed by Mandelbrot and Feder [18,19], provides a strong tool to describe the heterogenization of natural particulates (such as rock particles, soil particles, proteins, floes and catalyst particles). Based on the fractal geometry theory, many intensive studies on the testing method of the fractal dimension [20,21,22,23,24,25,26] have been carried out by domestic and foreign scholars. Dust control in metal and nonmetal mines is very important. Currently, many research works about sulfide ore particles mainly focus on spontaneous combustion tendency [27,28,29,30,31,32], but less work has considered the particle shape fractal of sulfide ores.
In this work, based on the area–perimeter method, the shape fractal characteristics of sulfide ore particles were analyzed and summed up, providing a new approach for studying the adhesive force between particles. By combining with numerical calculation and the fractal geometry theory, the experimental result was identified and explained, revealing that the fractal dimension of sulfide ore particles can serve as an important indicator of their particle shape distribution characteristics. Simultaneously, this provides valuable information for further studying the relevant physical and chemical properties of sulfide ore particles and establishes a new theoretical method and foundation for the adhesion and removal of sulfide ore dust.

2. Materials and Methods

2.1. Materials

The original sample of sulfide ore microparticles for testing was taken from a processed sulfide iron ore in Henan Province. The mineral composition and structural configuration of the ore samples were determined using a physical microanalysis system.
Sulfide ore is a sulfur-based polymetallic deposit. The natural types of ore are pyrite ore, pyrite-type copper ore, leached copper ore, lead–zinc ore and magnetite ore, all of which are primary ores. Ore structure is mainly dense massive, brecciated, vein-like, etc. The structure of ore is mainly self-formed semi-automorphic crystal structure, accountable fusion structure and colloidal structure, etc. The mineral composition of ore includes pyrite, colloidal pyrite, magnetite, sphalerite, galena, etc. The minor metal minerals include hematite, magnetic pyrite, speckled copper ore, pyroxene, etc.
Appropriate sulfide ore particle samples were dried and set aside before testing. The original samples were screened, and particles larger than 60 m in size were eliminated in order to regulate the test conditions and outcomes. In this experiment, three particle sizes—60–100 mesh, 100–140 mesh and greater than 200 mesh—were used.

2.2. Specimen Preparation

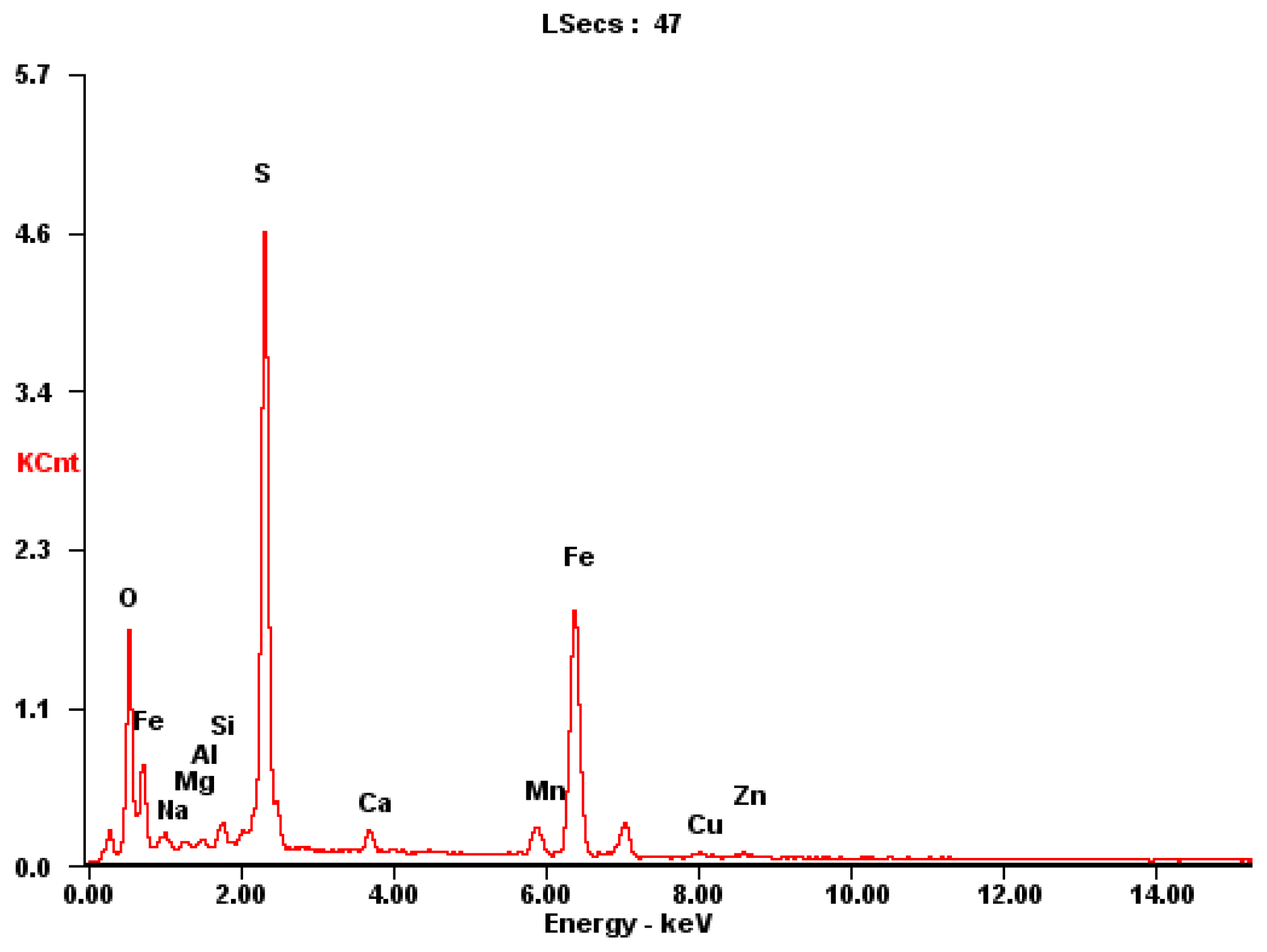
The sampling and preparation of sulfide ore particles should be representative; that is, the samples which were taken for analysis should represent the average composition of the bulk ore samples. The well-ground sulfide ore particles were screened and then dried in a programmable oven for 10 h, where the oven temperature was 80 °C. The samples of sulfide ores were examined using plasma emission spectroscopy, and the results of the chemical analysis are displayed in Figure 1 and Table 1. Sulfide minerals have an extremely complicated chemical composition; the most abundant elements are Fe, S, Mn and Zn (Table 1).
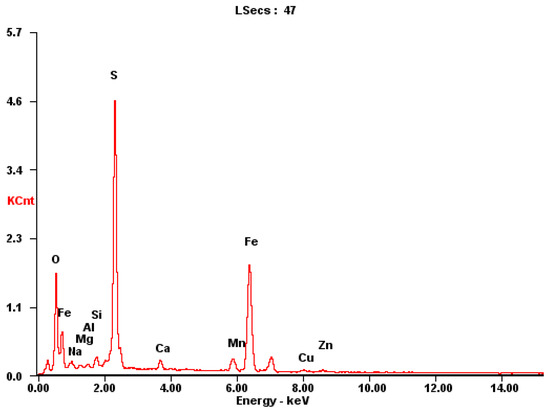
Figure 1. Typical mineralogical X-ray analysis of mineral dust.
Table 1. The main chemical composition of the sulfide ores.
The representative mineral phases are shown in Figure 2. From Figure 2, we can see that the actual sulfide ores contain a variety of minerals and the crystal particle size and shape, texture and structure are different from each other.
Figure 2. Mineralogical observation using optical microscope. (a) Brechified granular pyrite cemented by dissolution of sphalerite. (b) Euhedral pyrite particle distributed in vein quartz. (c) Fine chalcopyrite particles filling fractures of pyrite. (d) Pyrite attached with galena.
The sulfide ore particle samples that were utilized in the experiment are shown in Figure 3. From the scanning electron microscope images, it is clear that the surface of the sulfide particle was in the form of fragmented loose powder with numerous small particulate materials clinging to it. Analysis revealed that the surface structure of the sulfide ores had changed as a result of oxidation.
Figure 3. Images of the sample. (a) Ground ore sample of 60~100 mesh. (b) Ground ore sample of 100~140 mesh. (c) Ground ore sample > 200 mesh. (d) SEM photograph of the ore sample (>200 mesh ore sample).

2.3. Apparatus

The experiments were carried out using a micro-image analysis system (Beijing Tech (Beijing, China), SS3300), laser particle size analyzer (Omicron LS-800) and programmable temperature chamber (Chongqing Hanba (Chongqing, China), HT302E).

2.4. Experimental Procedure for Observing Sulfide Ore Powder

First, we took a small amount of sulfide ore powder on a glass rod and shook it gently onto the surface of a slide (slide sizes 76.2 mm × 25.4 mm × 1 mm). We labeled the slides, where the glass slide with 60~100 mesh sulfide particles was labeled as a, the glass slide with 100~140 mesh sulfide particles was labeled as b and the glass slide with 200 mesh sulfide particles was labeled as c. We clamped the sides of the slide, then put it on the table. We observed each of the slides using the microscopic analysis system. In order to improve the accuracy of the experiment, we sampled three times using the same operation mode, and then observed the samples, respectively.
Following sampling, we placed the glass slides under the microscope, chose the center of the slide’s center line as the object to be examined, magnified the object 400 times and then studied the selected area. The graphics were binarized to obtain a graphical profile of the particles, and parameters such as particle size, area and perimeter of each microparticle projection could be measured.

3. Calculation Models

The perimeter–area approach is derived in the manner described below. The perimeter L of a geometric object with a regular shape, such a circle, is proportional to the area A, so
( L ) 1 / 1 = 2 π 1 / 2 ( A ) 1 / 2
In addition, a square has an area of A and a perimeter of L, so
( L ) 1 / 1 = 4 ( A ) 1 / 2
The regular geometric figure’s perimeter L is proportionate to its area A, as can be shown from (1) and (2), which means
( L ) 1 / 1 ∝ ( A ) 1 / 2
According to our study, a geometric figure with an irregular shape would be
( L ) D L / 1 ∝ ( A ) 1 / 2
where DL is the particle’s fractal dimension.
The tiny structure of an irregular particle will continue to be discovered with the improvement in the resolution of the measuring microscope or scanning electron microscope since its center of gravity is in the most stable condition. Under various magnification circumstances, the perimeter and area that the microparticle’s projection showed were measured; the relationship between the two may be found in the following formula:
( 1 / D L ) lg L = k 0 + ( 1 / 2 ) lg A   ( k 0   is   a   plus   constant )
lg L = ( D L / 2 ) lg A + k 0   ( k 0   is   a   plus   constant )
Making a straight line based on the relationship of LgL-LgA, then DL is 2 times the line slope, that is
D L 2 = k
The method described above can be used to determine the projection profile fractal dimension of particulate materials, and the formula [13,14] that follows can be used to determine the single particle surface fractal dimension:
Ds = DL + 1 (2≤ Ds ≤3)
Through the use of microscopic analysis apparatus, the projected area A and projected perimeter L of a single particle can be determined in this study. Using the formula above, the fractal dimension of the projection of a single particle and the surface fractal dimension can then be estimated.

4. Experimental Results and Analysis

We put the glass slides under the microscope after sampling, then chose the center region of the center line on the slide as the subject of observation and analysis. The size, area, perimeter and other characteristics of the particle in the observation region were disclosed by the test analysis. The binary images of the samples are shown in Figure 4.
Figure 4. Binary images of the sulfide ore particles. (a) Ore sample of 60~100 mesh. (b) Ore sample of 100~140 mesh. (c) Ore sample of more than 200 mesh.

Analysis of Microparticles on the Surface of Slides

The samples with large and obvious data in the three experiments were taken as the study objects, and parameters such as the number of particles on the three slides were measured, respectively. The analysis results are shown in Table 2 and Table 3.
Table 2. Results of microparticle analysis on the surface of slides.
Table 3. Results of microparticle analysis on slide C.
Due to the large amount of data, only some of the analysis results of sulfide ore microparticles on slide C are listed. They are shown in Table 3.
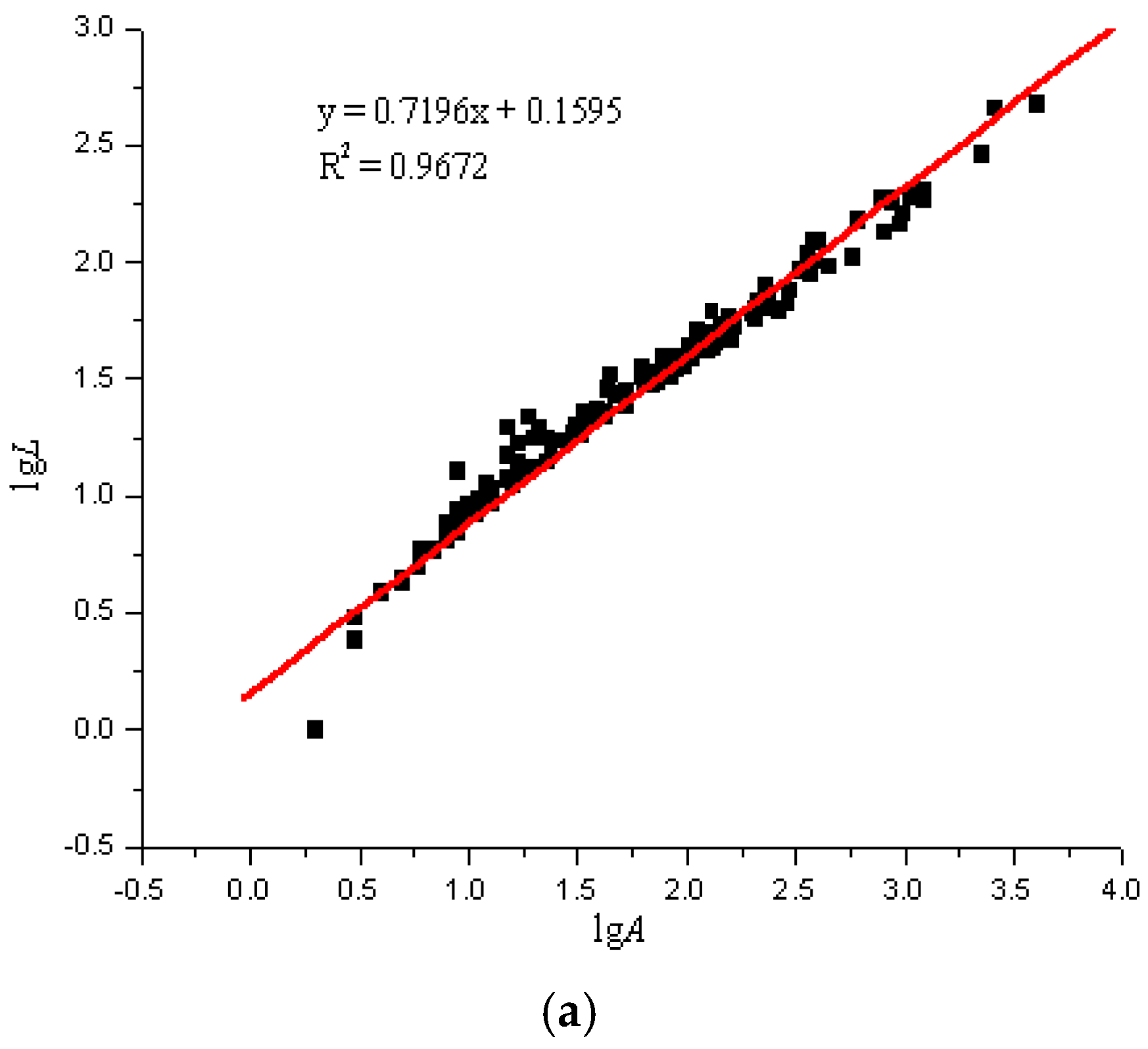
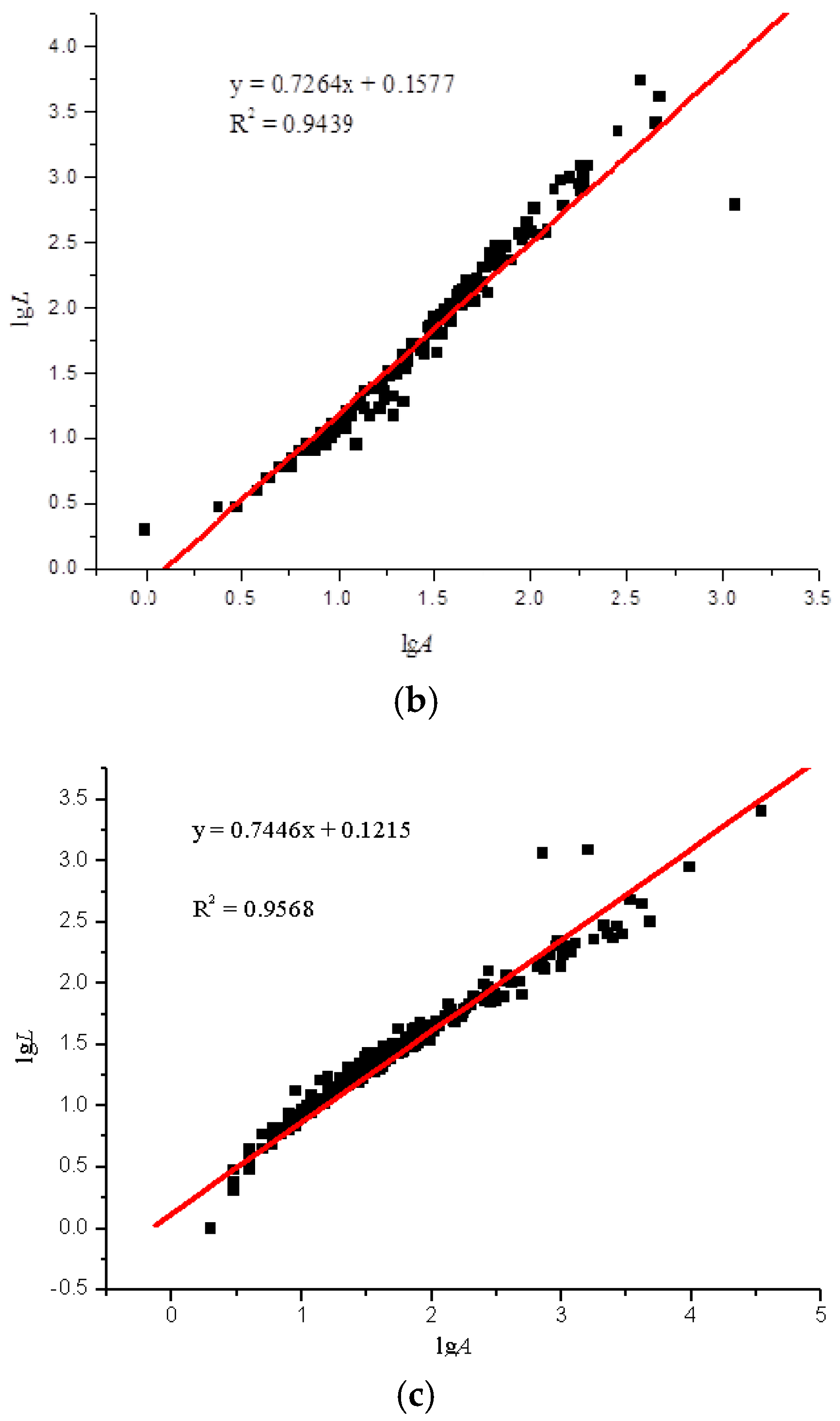
Using the image analysis technique previously described, the perimeter and area of the particle projection were computed. According to the particles in the areas on the glass slides, the LgL-LgA curves of the three slides were drawn. Due to the overwhelming amount of test data, we only selected a set of representative data for analysis, as seen in Figure 5.
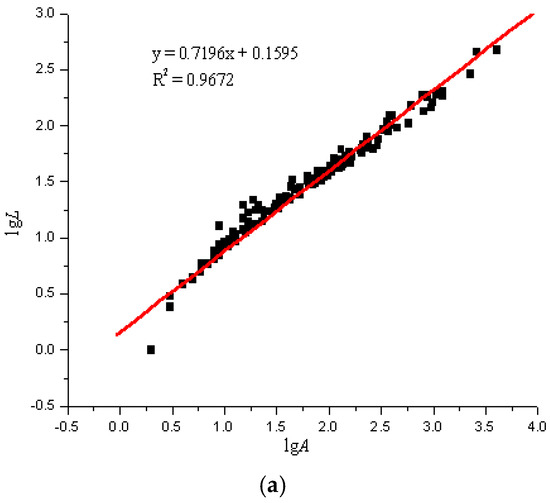
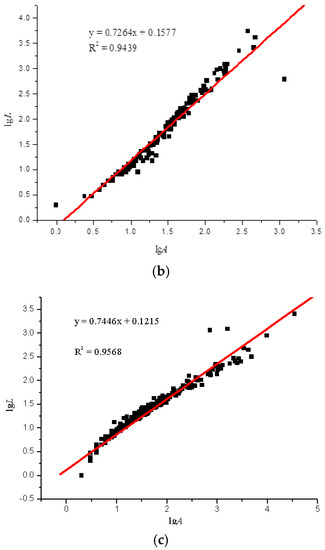
Figure 5. lgL-lgA curves of three sulfide ore microparticles. (a) Fractal curve of 60–100 mesh sulfide ore microparticles. (b) Fractal curve of 100–140 mesh sulfide ore microparticles. (c) Fractal curve of microparticles of sulfide ore larger than 200 mesh.
The fractal dimension of the projection of a single particle and the surface fractal dimension were determined by comparing the experimental results in accordance with Equations (7) and (8). The statistical results are shown in Table 4.
Table 4. Statistical results of sulfide ores’ fractal dimension.
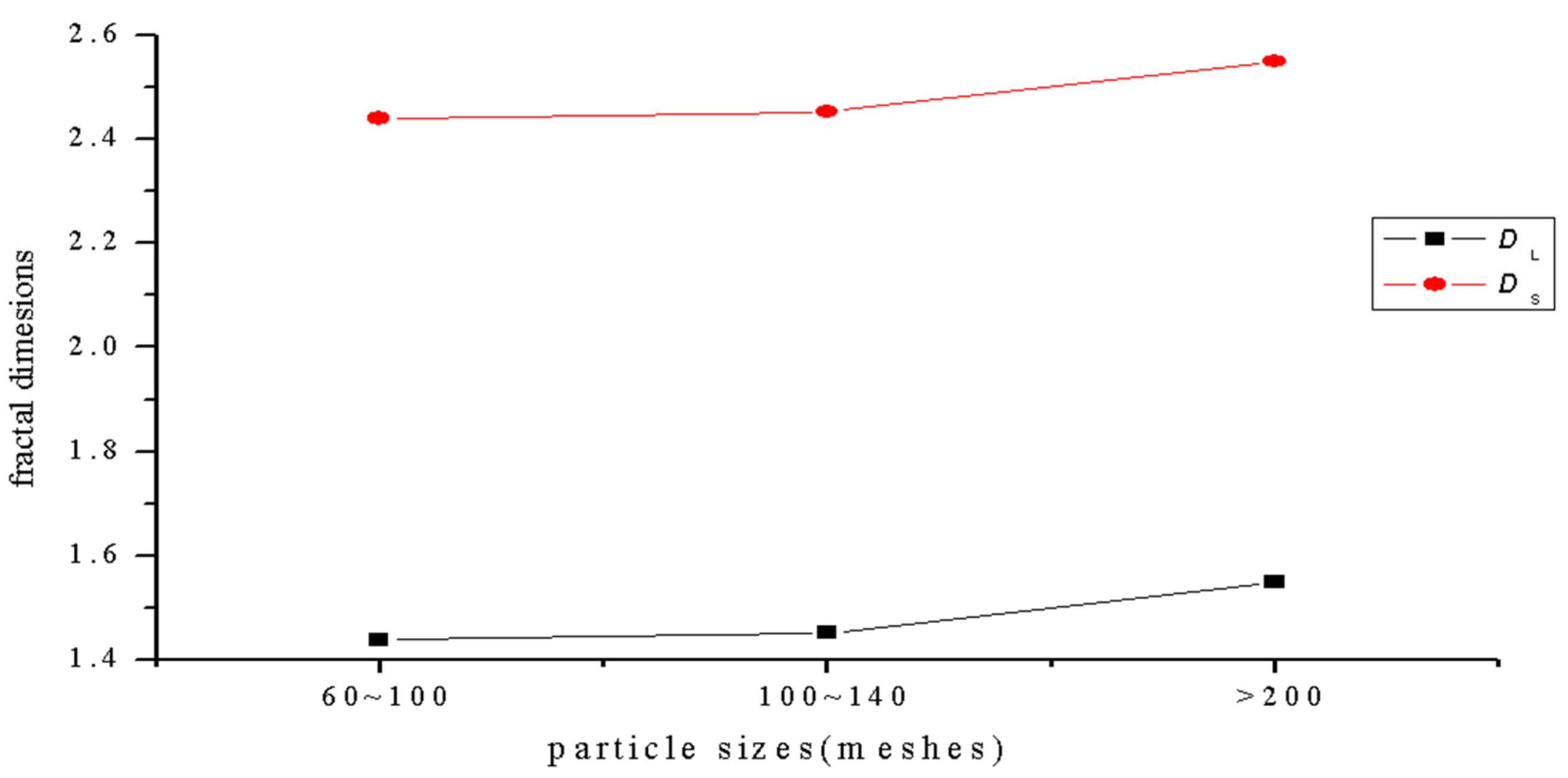
The fractal dimensions of the projection of a single particle range from 1.4392 to 1.5492, and the surface fractal dimension ranges from 2.4392 to 2.5492 for the sulfide ore particles examined in the experiment, as shown in Figure 6 and Table 4. According to the calculation results, the correlation coefficients of the three fractal dimension curves of the sulfide ore particles were all above 0.94, which shows that the differences between the fractal properties of the three different types of particle are substantial.
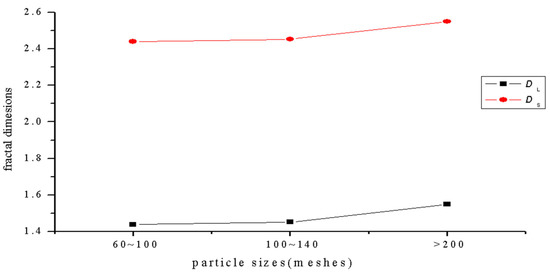
Figure 6. Curve of the relationship between particle size and fractal dimension.
The complexity of the projection profile of sulfide ores can be characterized by the various particle projection profile fractal dimensions. The greater the fractal dimension, the more irregular the shape of the particles. The projection profile fractal dimension of the particles with size greater than 200 mesh is the largest, and it reached a value of 1.5492, as shown in Figure 6 above. This indicates that the projection profile curve of the sulfide ore particles is far off the circular path. The surface fractal dimension of particles larger than 200 mesh is up to 2.5492, and it is the largest fractal dimension in the three groups. This indicates that the group of particles has a lot of multi-level fine structures on it, and it has a large degree of self-similarity. At the same time, the particles have concave convex surfaces.

5. Conclusions

(1) The particle projection profile fractal dimensions and surface fractal dimensions of the sulfide ore particles were calculated on the basis of a large amount of experimental data. We proved that the shape of sulfide ore particles in the experiment has obvious fractal characteristics.
(2) The sulfide ore particles’ projection fractal dimension is from 1.4392 to 1.5492, and the surface fractal dimension ranges from 2.4392 to 2.5492. The correlation coefficients of the three fractal dimension curves of the sulfide ore particles were all above 0.94, which indicates that the fractal characteristics of three kinds of particle are significantly different. The projection profile fractal dimension of the particles with size ranging from 60~100 mesh is the smallest, and the projection profile fractal dimension of the particles whose size is larger than 200 mesh is the largest.
(3) The particle projection profile fractal dimensions characterize the complexity of the projection contour curvature variation of sulfide ore particles. The projection profile fractal dimensions of microparticles larger than 200 mesh is the largest, with a value of 1.5492, which indicates that the projection contour curve of this group of particles deviates from the circle to the largest extent. The surface fractal dimension of particles larger than 200 mesh reaches 2.5492, which is also the largest group of fractal dimension among these three groups of sulfide ore particles, which indicates that the surface fine structure of this group of granules has many levels and a large degree of self-similarity, and at the same time, the surface concavity of this group of granules is the largest.
(4) Because the finer particles are also associated with the larger surface area, and thus the higher adsorption capacities, the shape fractal dimension value is believed to be able to reflect the adsorption capacities of other finer particles.
(5) The preliminary analysis of the geometric shape was based on the conventional statistical method and the fractal theory. How to analyze the particle shape, size and interaction between particles overall and systematically then establish models and relationships between them and the micro mechanical properties need to be further studied.

Author Contributions

Conceptualization, Y.C.; Methodology, Y.C.; Software, M.L.; Validation, J.W.; Writing—original draft, Y.C.; Writing—review & editing, J.W., C.C., B.Y., Y.L. and M.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Natural Science Foundation of Hunan grant number 2020JJ5172. This research was funded by the Scientific Research Fund of Hunan Provincial Education Department grant number 19B197.

Data Availability Statement

Data is contained within the article. The data presented in this study are available in insert article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Tatyana, G.K.; Olga, V.R.; Irina, V.M.; Artyukov, E.V. Health risk assessment of metal(loid)s exposure via indoor dust from urban area in Chelyabinsk, Russia. Int. J. GEOMATE 2019, 16, 1–7. [Google Scholar]
  2. Chen, L.J.; Li, P.C.; Liu, G.M.; Cheng, W.M.; Liu, Z.X. Development of cement dust suppression technology during shotcrete in mine of China—A review. J. Loss Prev. Process Ind. 2018, 55, 232–242. [Google Scholar] [CrossRef]
  3. Han, W.B.; Zhou, G.; Gao, D.H.; Zhang, Z.X.; Wei, Z.Y.; Wang, H.T.; Yang, H.Q. Experimental analysis of the pore structure and fractal characteristics of different metamorphic coal based on mercury intrusion-nitrogen adsorption porosimetry. Powder Technol. 2020, 362, 386–398. [Google Scholar] [CrossRef]
  4. Xie, Y.; Cheng, W.M.; Yu, H.M.; Wang, Y.H. Study on spray dust removal law for cleaner production at fully mechanized mining face with large mining height. Powder Technol. 2021, 389, 48–62. [Google Scholar] [CrossRef]
  5. Kumia, J.C.; Sasmito, A.P.; Mujumdar, A.S. Dust dispersion and management in underground mining faces. Int. J. Min. Sci. Technol. 2014, 24, 39–44. [Google Scholar]
  6. Li, Y.J.; Wang, P.F.; Liu, R.H.; Jiang, Y.D.; Han, H. Determination of the optimal axial-to-radial flow ratio of the wall-mounted swirling ventilation in fully mechanized excavation face. Powder Technol. 2020, 360, 890–910. [Google Scholar] [CrossRef]
  7. Inoka, E.P.; Marcia, L.H.; Michael, L.S. Examination of classified rock dust (treated and untreated) performance in a 20-L explosion chamber. J. Loss Prev. Proc. 2019, 62, 103943. [Google Scholar]
  8. Ji, Y.L.; Reng, T.; Peter, W.; Wan, Z.J.; Ma, Z.Y.; Wang, Z.M. A comparative study of dust control practices in Chinese and Australian longwall coal mines. Int. J. Min. Sci. Technol. 2016, 26, 199–208. [Google Scholar] [CrossRef]
  9. Wu, C. Chemical Suppression of Dust; Central University Press: Changsha, China, 2003. [Google Scholar]
  10. Wu, C.; Ou, J.C.; Wu, G.M. Experiment on Coupling of Wet Agents Composed with Anionic Surfact and Dust of Sulfide Ores. J. China Univ. Min. Technol. 2006, 35, 323–327. [Google Scholar]
  11. Yang, F.Q.; Wu, C.; Li, Z.J. Matterelement model and its application to comprehensive determination on spontaneous combustion tendency of sulfide ores. J. Cent. South Univ. 2011, 42, 3459–3464. [Google Scholar]
  12. Pan, W.; Wu, C.; Liu, H.; Yang, F. Self-heating test of sulfide ore heap and numerical simulation of temperature field. Chin. J. Nonferrous Met. 2010, 20, 149–155. [Google Scholar]
  13. Sun, X.; Wu, Z.Q. Theory and Application of Fractal; China Science & Technology University Press: Hefei, China, 2003. [Google Scholar]
  14. Wang, D.S.; Tang, H.X.; Luan, Z.K. Fractal theory and its research method. Acta Sci. Circumstantiae 2001, 21, 10–16. [Google Scholar]
  15. Jiao, H.L.; Xia, D.H.; Zhang, S.X.; Chen, Y. Fractal model for particle-size distribution of coal griding. Chin. J. Eng. 2007, 29, 1151–1153. [Google Scholar]
  16. Xie, H.P. Fractals in Rock Mechanics; Science Press: Beijing, China, 1997. [Google Scholar]
  17. Zhang, Y.L.; Xia, J.H.; Li, G.H. The Partical Shape and Fractal Dimension. J. Wuhan Univ. Technol. 1996, 18, 53–56. [Google Scholar]
  18. Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: San Francisco, CA, USA, 1982. [Google Scholar]
  19. Feder, J. Fractals; Plenum Press: New York, NY, USA, 1988. [Google Scholar]
  20. Zhao, M.K.; Kong, D.S. Study on seepage characteristics of rock fractures considering fracture surface roughness and opening fractal dimension. Chin. J. Rock Mech. Eng. 2022, 41, 1993–2002. [Google Scholar]
  21. Shen, L.F.; Zeng, Y.; Wang, Z.L.; Li, S.J. Research on seepage properties of rough fracture considering geometrical morphology. Chin. J. Rock Mech. Eng. 2019, 38 (Suppl. S1), 2704–2711. [Google Scholar]
  22. Ma, H.Y.; Shen, Z.Z. Roughness characterization of concave fracture surface and coefficient fitting of modified cubic law. J. Hydraul. Eng. 2021, 52, 420–431. [Google Scholar]
  23. Zhang, Z.H.; Wei, W.; Zhang, J.; Jia, H.B. Determining method of multiscale fractal dimesion of bed red sandstone pores based on CT scanning. Bull. Geol. Sci. Technol. 2022, 41, 254–263. [Google Scholar]
  24. Xie, B.X.; Gao, W.H.; Yi, M.H.; Zhang, Z.T.; Wu, J. Analysis of fractal dimension index and influencing factors of red sandstone coarse granular material breaking. Chin. J. Appl. Mech. 2022, 39, 1117–1124. [Google Scholar]
  25. Jia, C.J.; Lu, Y.; Wu, G.; Huang, W.H.; Qin, H.L.; Jiang, K. Fractal Features of Particle-Size Distribution of Soil Profiles in Luofu Mountain, Guangdong. Chin. J. Soil Sci. 2022, 53, 1049–1055. [Google Scholar]
  26. Azam, S.; Mishra, D.P. Effects of particle size, dust concentration and dust-dispersion-air pressure on rock dust inertant requirement for coal dust explosion suppression in underground coal mines. Process Saf. Environ. Prot. 2019, 129, 35–43. [Google Scholar] [CrossRef]
  27. Pan, W.; Yang, L.R.; Jin, H.M.; Yi, R.G.; Liao, Z.G. Experimental study on microbial desulphurization of sulfide ores and self-heating simulation of ore heaps under ultrasonic and microwave. Process Saf. Environ. Prot. 2022, 164, 435–448. [Google Scholar] [CrossRef]
  28. Pan, W.; Jin, H.M.; Liu, Z.Z.; Tang, J.H.; Cheng, S.Y. Experimental and theoretical study on strengthening leaching of sulfide ores by surfactants. Process Saf. Environ. Prot. 2020, 137, 289–299. [Google Scholar] [CrossRef]
  29. Rosenblum, F.; Nesset, J.E.; Moon, S.; Finch, J.A.; Waters, K.E. Reducing the self-heating of sulphides by chemical treatment with lignosulfonates. Miner. Eng. 2017, 107, 78–80. [Google Scholar] [CrossRef]
  30. Liu, H.; Pan, K.; Xiang, C.L.; Ye, D.; Wang, H.N.; Gou, X.Q. Mechanochemical effect of spontaneous combustion of sulfide ore. Fuel 2022, 329, 125391. [Google Scholar] [CrossRef]
  31. Liu, H.; Gou, X.Q.; Pan, K.; Huang, R.; Lang, Z.H.; Ye, D.; Wang, X.; Wang, H.N. Thermodynamics and inhibition mechanism of imidazolium-based ionic liquids for inhibiting spontaneous combustion of iron sulfide. Fuel 2023, 338, 127335. [Google Scholar] [CrossRef]
  32. Li, X.; Shang, Y.J.; Chen, Z.L.; Chen, X.F.; Niu, Y.; Yang, M.; Zhang, Y. Study of spontaneous combustion mechanism and heat stability of sulfide minerals powder based on thermal analysis. Powder Technol. 2017, 309, 68–73. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Download PDF
Parametric Integration of Multiple Criteria from a Cultural Heritage Perspective
Previous
HPLC with Post-Column Derivatization with Alizarin for Determination of OATD-02, an Anticancer Arginase Inhibitor in Clinical Development
Next