Improved Genetic Algorithm for Solving Green Path Models of Concrete Trucks
Abstract
:1. Introduction
- The vehicle fuel consumption of a concrete tanker was modeled;
- A low-carbon collaborative distribution model of multi-mixing stations was established for the current situation of concrete multi-mixing station distribution;
- Adaptive elite retention strategies, adaptive crossover, mutation operators, and immune selection have been added to the standard genetic algorithm to improve it;
- The established low-carbon co-operative distribution model for multiple mixing stations was solved using improved genetic algorithms in combination with concrete enterprise orders.
2. Fuel Consumption Models
- (1)
- Each concrete distribution truck is allowed to depart from the mixing plant to the customer’s site only once and is not allowed to return;
- (2)
- The mixing plants are able to produce different grades of concrete in time to meet the needs of each site;
- (3)
- The maximum transport time required by the site for each mixing plant is the true transport time of the truck;
- (4)
- Concrete trucks in transit will not interrupt distribution.
2.1. Vehicle Driving Fuel Consumption
- (1)
- Climbing and turning of vehicles on urban roads;
- (2)
- Acceleration and deceleration of vehicles.
2.2. Fuel Consumption of Stirring Tank
2.3. GVRP Model
2.3.1. Objective Function
2.3.2. Constraints
- (1)
- The total output of the concrete-mixing plant should meet the total demand of the total customer sites:
- (2)
- The quantity of delivery from the mixing plant to the customer’s site exceeds the customer’s demand:
- (3)
- Weight constraint:
- (4)
- Total number of trucks constraint:
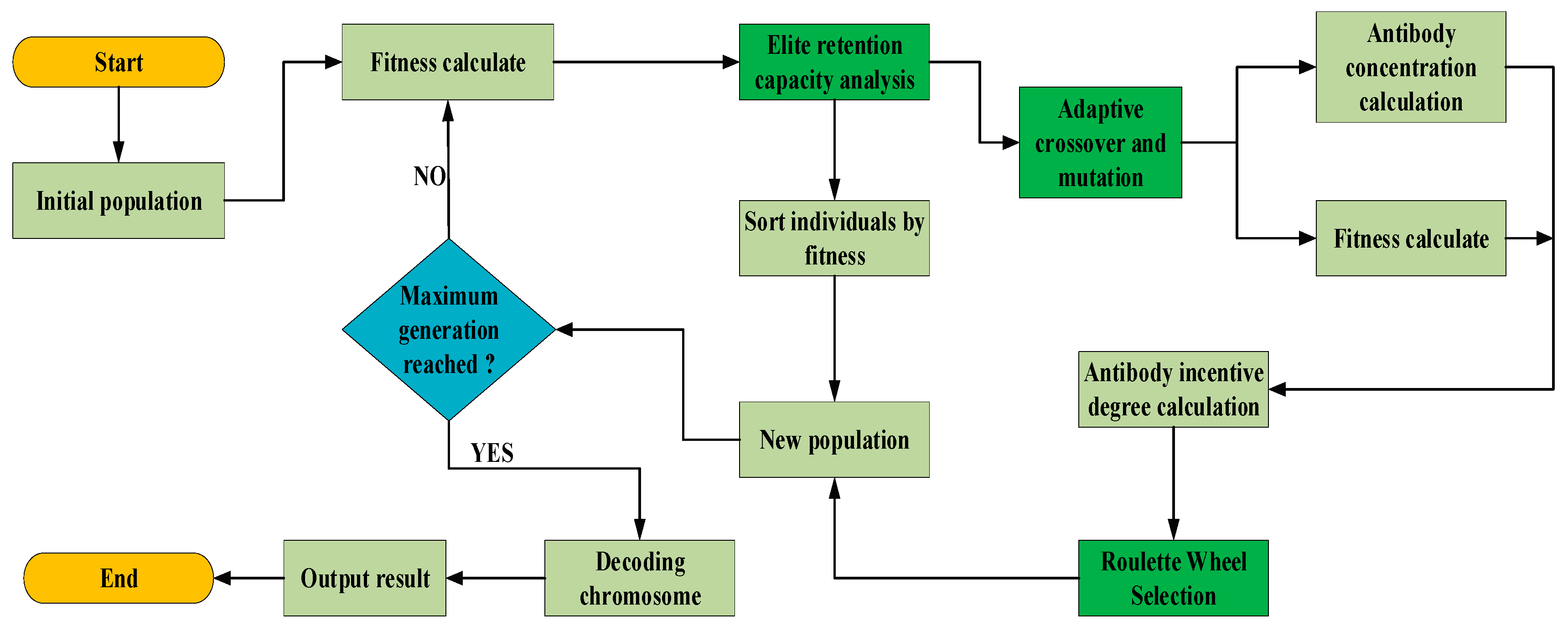
3. Model Solving
- (1)
- A new method of preserving superior individuals based on the variable capacity of population size and fitness was introduced in combination with the elite reservation strategy proposed in [33].
- (2)
- In combination with the adaptive crossover and mutation operators proposed in [34], a new method was introduced to automatically adjust the Pc (crossover probability) and the Pm (mutation probability) based on the individual fitness and the average fitness of the population.
- (3)
- The immune operator was introduced after crossover and mutation operations to improve the global search ability of the GA. Immune selection selects antibodies according to the antibody incentive degree with a roulette wheel method.
- (4)
- An adaptive elite retention strategy before crossover and mutation manipulation was introduced.
3.1. Fitness Value
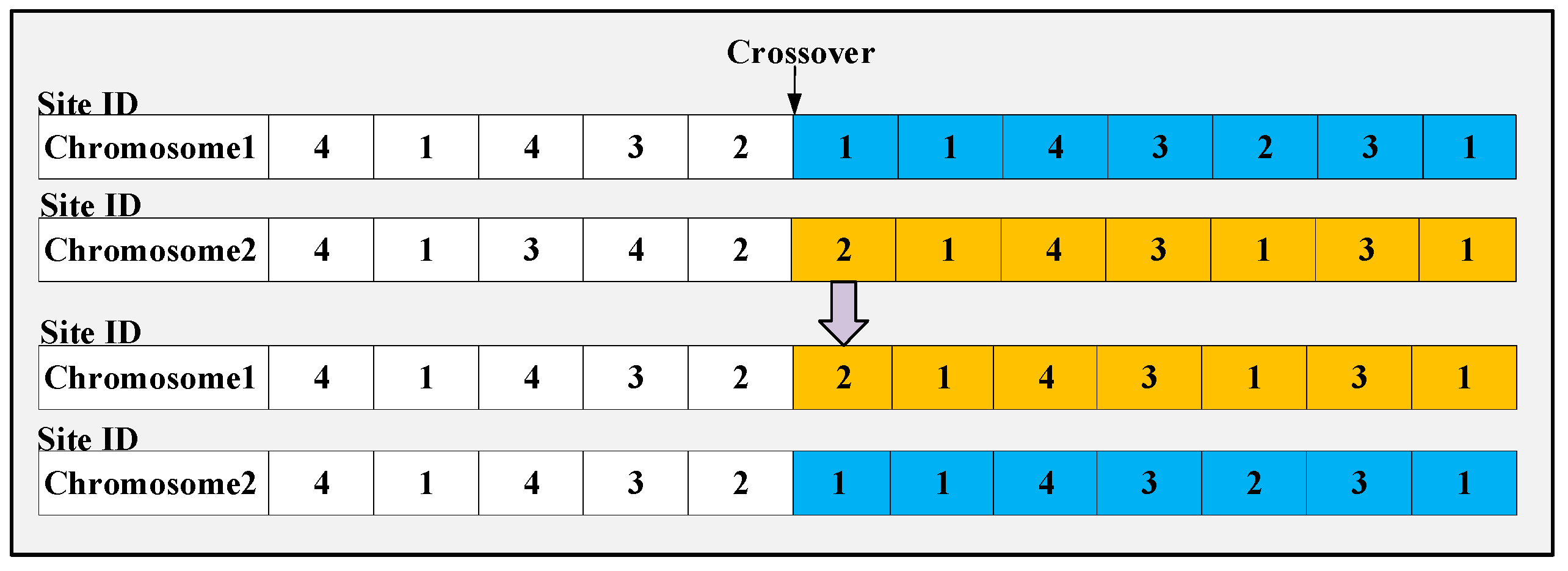
3.2. Code and Adaptive Strategy
3.2.1. Elite Retention
| Algorithm 1: Adaptive elite retention strategy |
| Input: Population fitness: fit; population size: M; population: pop; |
| Output: N_pop |
| 1: Fit = sort (fit, ‘descend’) |
| 2: Fmax = Fit (1), Fmin = Fit(end), fa = sum (Fit)/M |
| 3:(fa−fmin)] |
| 4: In = zeros (Ne,1) |
| 5: F = Fit (1: Ne) |
| 6: for i = 1: Ne |
| 7: In(i) = find(fit == F(i)) |
| 8: N_pop (i, :)=pop(index(i), :) |
| 9: end |
3.2.2. Adaptive Crossover and Mutation Operators
- (1)
- Individuals are more likely to enter the next generation when their fitness value is higher than the average, and, conversely, they are more likely to be displaced.
- (2)
- In the early stage of the algorithm, since the individuals are randomly generated and the fitness values are less, the use of a larger crossover and mutation probability facilitates the generation of better individuals.
- (3)
- In the late stages of the algorithm, individuals who have high fitness values, and adopt a smaller crossover and mutation probability are useful for reserving the good individuals and also contributing to enhancing the algorithm’s search efficiency.
3.3. Immune Operator
4. Simulation Experiment
4.1. Simulation Process
4.2. Experimental Analysis
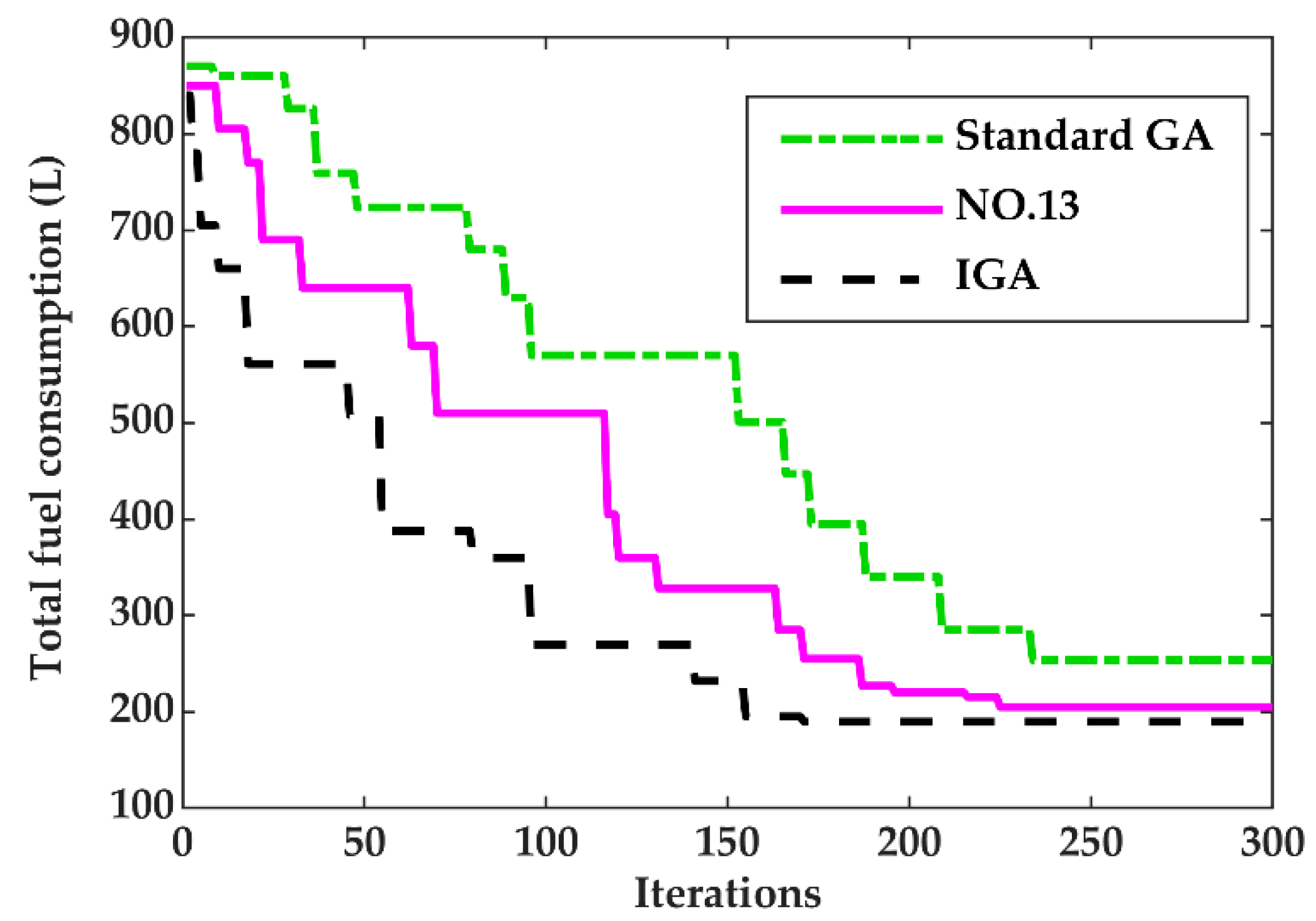
- Compared with the standard GA, the IGA has a stronger convergence ability to generate high-quality individuals in the early stage of the algorithm.
- The IGA converged the solution in 172 iterations and had a 26.45% faster convergence than the standard GA.
- Compared with the standard genetic algorithm, the final solution obtained by the improved genetic algorithm is better.
- Compared with Experiment 3, the performance of the improved genetic algorithm under the optimal horizontal combination is improved.
5. Conclusions
- The concrete tanker fuel consumption model we developed is valid;
- The distribution fuel consumption is reduced by 21.25% compared with the original scheme, which proves that our established mathematical model of the low-carbon co-operative distribution of concrete multi-mixing stations effectively reduces the overall fuel consumption of distribution vehicles;
- IGA converges 26.25% faster than GA, which proves that our proposed improved genetic algorithm can solve the established mathematical model more quickly and efficiently than the standard genetic algorithm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Tan, J. Green Traffic-Oriented Heavy-Duty Vehicle Emission Characteristics of China VI Based on Portable Emission Measurement Systems. IEEE Access 2020, 8, 106639–106647. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Ramser, J.H. The Truck Dispatching Problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Erdoğan, S.; Miller-Hooks, E. A Green Vehicle Routing Problem. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 100–114. [Google Scholar] [CrossRef]
- Lin, C.H.; Choy, K.L.; Ho, G.T.S.; Chung, S.H.; Lam, H.Y. Survey of Green Vehicle Routing Problem: Past and future trends. Expert Syst. Appl. 2014, 41, 1118–1138. [Google Scholar] [CrossRef]
- Wang, P.; Bai, J.; Meng, J. A Hybrid Genetic Ant Colony Optimization Algorithm with an Embedded Cloud Model for Continuous Optimization. J. Inf. Process. Syst. 2020, 16, 1169–1182. [Google Scholar]
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2022, 39, 2627–2651. [Google Scholar] [CrossRef]
- Arasteh, B.; Sadegi, R.; Arasteh, K.; Gunes, P.; Kiani, F.; Torkamanian-Afshar, M. A bioinspired discrete heuristic algorithm to generate the effective structural model of a program source code. J. King Saud Univ.—Comput. Inf. Sci. 2023, 35, 101655. [Google Scholar] [CrossRef]
- Peng, B.; Zhang, Y.; Gajpal, Y.; Chen, X. A Memetic Algorithm for the Green Vehicle Routing Problem. Sustainability 2019, 11, 6055. [Google Scholar] [CrossRef]
- da Costa, P.R.; Mauceri, S.; Carroll, P.; Pallonetto, F. A Genetic Algorithm for a Green Vehicle Routing Problem. Electron. Notes Discret. Math. 2018, 64, 65–74. [Google Scholar] [CrossRef]
- Rong, H.; Wenbo, C.; Bin, Q.; Ning, G.; Fenghong, X. Learning Ant Colony Algorithm for Green Multi-depot Vehicle Routing Problem. J. Syst. Simul. 2021, 33, 2095. [Google Scholar]
- Zhang, B.; Li, H.; Li, S.; Peng, J. Sustainable multi-depot emergency facilities location-routing problem with uncertain information. Appl. Math. Comput. 2018, 333, 506–520. [Google Scholar]
- Li, Y.; Soleimani, H.; Zohal, M. An improved ant colony optimization algorithm for the multi-depot green vehicle routing problem with multiple objectives. J. Clean. Prod. 2019, 227, 1161–1172. [Google Scholar] [CrossRef]
- Yao, Z.; Cao, H.; Cui, Z. Research on Urban Distribution Routes Considering the Impact of Vehicle Speed on Carbon Emissions. Sustainability 2022, 14, 15827. [Google Scholar] [CrossRef]
- Yao, Z.; Cao, H.; Cui, Z.; Wang, Y.; Huang, N. Review of green vehicle routing model and its algorithm in logistics distribution. Syst. Eng. Theory Pract. 2021, 41, 213–230. [Google Scholar]
- Elshaer, R.; Awad, H. A taxonomic review of metaheuristic algorithms for solving the vehicle routing problem and its variants. Comput. Ind. Eng. 2020, 140, 106242. [Google Scholar] [CrossRef]
- Nogareda, A.-M.; del Ser, J.; Osaba, E.; Camacho, D. On the design of hybrid bio-inspired meta-heuristics for complex multiattribute vehicle routing problems. Expert Syst. 2020, 37, e12528. [Google Scholar] [CrossRef]
- Wang, Y.D.; Lu, X.C.; Song, Y.M.; Feng, Y.; Shen, J.R. Monte Carlo Tree Search improved Genetic Algorithm for unmanned vehicle routing problem with path flexibility. Adv. Prod. Eng. Manag. 2022, 17, 425–438. [Google Scholar] [CrossRef]
- Lu, W.; Wu, M. Optimization of vehicle automatic navigation path based on remote sensing and GIS. Optik 2022, 270, 169952. [Google Scholar] [CrossRef]
- Feng, C.-W.; Cheng, T.-M.; Wu, H.-T. Optimizing the schedule of dispatching RMC trucks through genetic algorithms. Autom. Constr. 2004, 13, 327–340. [Google Scholar] [CrossRef]
- Feng, C.-W.; Wu, H.-T. Integrating fmGA and CYCLONE to optimize the schedule of dispatching RMC trucks. Autom. Constr. 2006, 15, 186–199. [Google Scholar] [CrossRef]
- Yang, J.; Zong, H.; Ma, J.; Guo, D.; Shi, J.; Wang, L. Coordinated dispatching of distribution vehicles in concrete batching plant. China Sci. Pap. 2021, 16, 06–0644-05. [Google Scholar]
- Kuo, Y. Using simulated annealing to minimize fuel consumption for the time-dependent vehicle routing problem. Comput. Ind. Eng. 2010, 59, 157–165. [Google Scholar] [CrossRef]
- Asbach, L.; Dorndorf, U.; Pesch, E. Analysis, modeling and solution of the concrete delivery problem. Eur. J. Oper. Res. 2009, 193, 820–835. [Google Scholar] [CrossRef]
- Yan, S.; Wang, W.-C.; Chang, G.-W.; Lin, H.-C. Effective ready mixed concrete supply adjustments with inoperative mixers under stochastic travel times. Transp. Lett. 2016, 8, 286–300. [Google Scholar] [CrossRef]
- Maghrebi, M.; Waller, S.T.; Sammut, C. Sequential Meta-Heuristic Approach for Solving Large-Scale Ready-Mixed Concrete–Dispatching Problems. J. Comput. Civ. Eng. 2016, 30, 04014117. [Google Scholar] [CrossRef]
- Mayteekriengkrai, N.; Wongthatsanekorn, W. Ready mixed concrete trucks scheduling for minimizing fuel cost of ready mixed concrete trucks from multiple plants to multiple sites using bee algorithm. Int. J. Oper. Res. 2017, 28, 327. [Google Scholar] [CrossRef]
- Ehsani, M.; Ahmadi, A.; Fadai, D. Modeling of vehicle fuel consumption and carbon dioxide emission in road transport. Renew. Sust. Energy Rev. 2016, 53, 1638–1648. [Google Scholar] [CrossRef]
- Hoen, K.M.R.; Tan, T.; Fransoo, J.C.; van Houtum, G.J. Effect of carbon emission regulations on transport mode selection under stochastic demand. Flex. Serv. Manuf. J. 2014, 26, 170–195. [Google Scholar] [CrossRef]
- Barth, M.; Younglove, T.; Scora, G. Development of a Heavy-Duty Diesel Modal Emissions and Fuel Consumption Model; CSU: Los Angeles, CA, USA, 2005. [Google Scholar]
- Xiao, Y.; Zhao, Q.; Kaku, I.; Xu, Y. Development of a fuel consumption optimization model for the capacitated vehicle routing problem. Comput. Oper. Res. 2012, 39, 1419–1431. [Google Scholar] [CrossRef]
- Wang, S.; Lu, Z.; Wei, L.; Ji, G.; Yang, J. Fitness-scaling adaptive genetic algorithm with local search for solving the Multiple Depot Vehicle Routing Problem. Simulation 2016, 92, 601–616. [Google Scholar] [CrossRef]
- Yao, J.; Liu, Y.; Feng, Z.; Liu, T.; Zhou, S.; Liu, H. Application of New Modified Genetic Algorithm in Inverse Calculation of Strong Source Location. Atmosphere 2022, 14, 89. [Google Scholar] [CrossRef]
- Wu, M.; Yang, D.; Liu, T. An Improved Particle Swarm Algorithm with the Elite Retain Strategy for Solving Flexible Jobshop Scheduling Problem. J. Phys. Conf. Ser. 2021, 2173, 012082. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, C.; Sun, Y. Research on Application of Improved Adaptive Genetic Algorithm in Multi-load AGV Scheduling. J. Chin. Mini-Micro Comput. Syst. 2021, 42, 2241–2245. [Google Scholar]
- Ballester-Ripoll, R.; Leonelli, M. Computing Sobol indices in probabilistic graphical models. Reliab. Eng. Syst. Safe 2022, 225, 108573. [Google Scholar] [CrossRef]
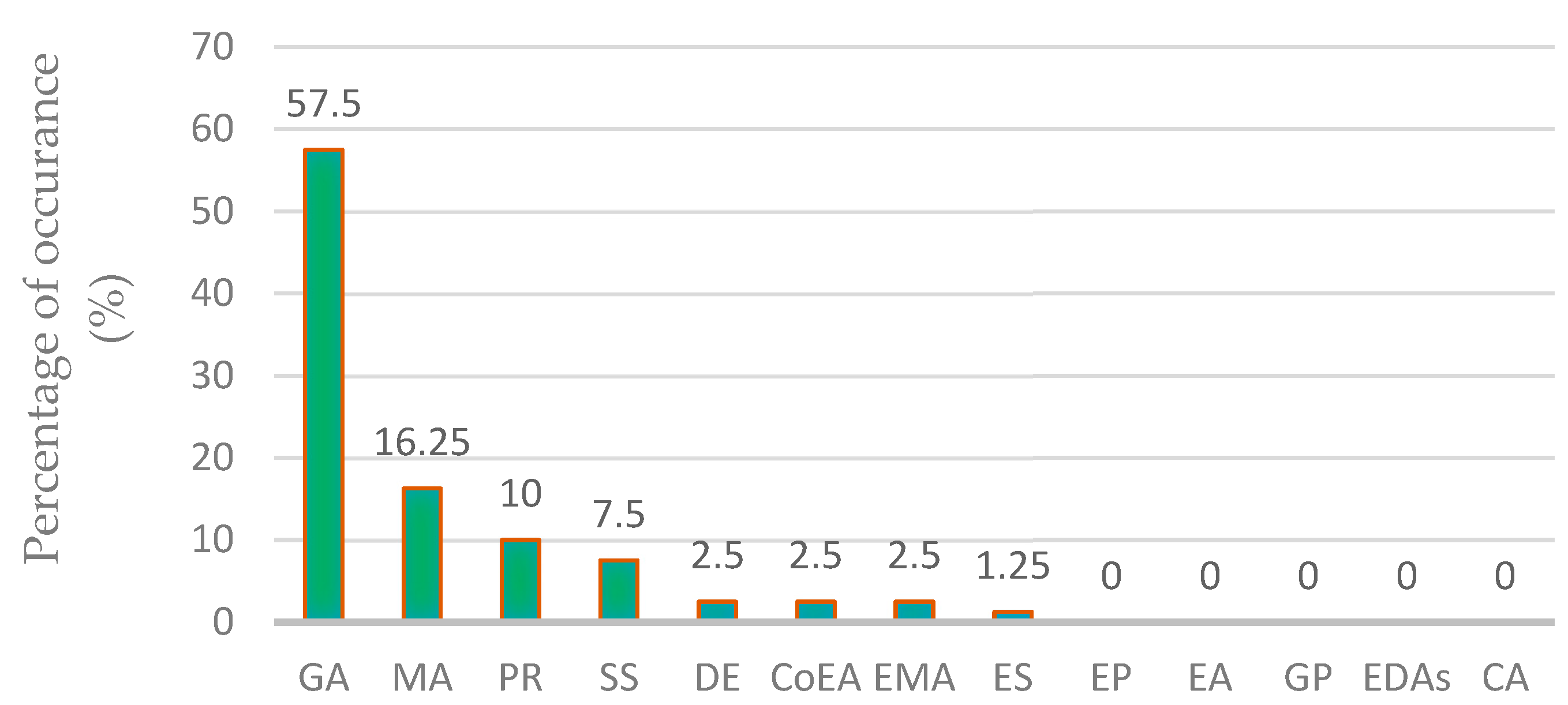


| References | Contributions | Algorithms | Disadvantages |
|---|---|---|---|
| [8] | The algorithm is improved to solve the GVRP problem. | MA | The universality of the algorithm is difficult to guarantee. |
| [10] | The GVRP model was established with the aim of minimizing total fuel consumption by considering some factors that affect vehicle fuel consumption. | ACO | The effect of road slope on fuel consumption was not considered. |
| [11] | A multi-objective MDVRP model was established with the aim of minimizing vehicle carbon emission. | GA | Other factors affecting vehicle fuel consumption are not considered. |
| [12] | A multi-objective MDVRP model was established considering the carbon emission cost and driving time. | ACO | The load of the vehicle was not taken into account. |
| [14] | The GVRP models are classified according to their objective functions. | / | The improved algorithms for solving GVRP are not compared and analyzed. |
| [19] | The factors affecting RMC delivery are analyzed, and a model is established with minimum delivery time as the target. | GA | The fuel consumption of the vehicle is not taken into account. |
| [20] | The RMC-scheduling model is established by simulation technology. | The capacity of the different tankers was not taken into account. | |
| [21] | Aiming at the minimum pouring and waiting time of mixing plant, the vehicle-scheduling model is established. | GA | The road congestion problem that may be encountered in the actual distribution of tank cars is ignored. |
| [22] | From the perspective of reducing carbon emission, the TDVRP model is established after considering the factors of vehicle speed, distance, and load. | SA | A method of estimation is used to predict vehicle fuel consumption. |
| [23] | This paper proposes a general delivery model. | / | The time window of distribution and the problem of vehicle failure in the process of distribution are ignored. |
| [24] | A model is proposed for concrete companies to adjust their plans to reduce production costs. | / | It is not conducive to the solution of the model. |
| [25] | RMC delivery is divided into two parts to reduce the difficulty of solving it. | / | The method of multi-mixing collaborative distribution is not considered. |
| [26] | The RMC distribution model is established from the perspective of multi-mixing plant co-operative distribution. | BA | The article acquiesces that the volume of all tank cars is the same without considering different models. |
| Symbol | Parameter | Symbol | Parameter |
|---|---|---|---|
| The total mass of the vehicle | Air resistance workmanship distance (km) | ||
| Gravitational constant | Engine efficiency | ||
| Travel distance (km) | Frontal area ( | ||
| Driving | Air resistance coefficient | ||
| Rolling resistance | Vehicle speed considering the influence of wind speed | ||
| Effect of temperature (℉) | Wind influence factor | ||
| Rolling resistance work distance (km) | Fuel density (kg/L) | ||
| Type of pavement | Air density ( | ||
| Fuel calorific value (MJ/kg) | Time (h) |
| Symbol | Parameter | Value |
|---|---|---|
| Effect of temperature (℉) | 46.4 | |
| Type of pavement | 0.29 | |
| Engine efficiency | 0.4 | |
| Frontal area ( | 3.27 | |
| Driving | 1 | |
| Rolling resistance | 0.01 | |
| Fuel efficiency | 0.395 |
| Algorithm | Parameter | Result | Convergence Algebra |
|---|---|---|---|
| GA | Np = 50 G= 500 Pc = 0.8 Pm = 0.1 | 64 | |
| DE | Np = 50 G = 500 F0 = 0.4 CR = 0.1 | 53 | |
| IA | Np = 50 G = 500 Pm = 0.7 Nc1 = 10 alfa = 1 belta = 1 detas = 0.2 | 26 | |
| PSO | N = 50 G = 500 C1 = C2 = 1.5 w = 0.8 xmax = 20 xmin = 20 vmax = 10 vmin = −10 | 31 | |
| IGA | Np = 50 G = 500 Pm1 = 0.01 Pm2 = 0.08 Pc1 = 0.5 Pc2 = 0.8 | 19 |
| City | Co-Ordinate | City | Co-Ordinate | City | Co-Ordinate | City | Co-Ordinate |
|---|---|---|---|---|---|---|---|
| 1 | (1304, 2312) | 9 | (3488, 1535) | 17 | (4312, 790) | 25 | (2788, 1491) |
| 2 | (3639, 1315) | 10 | (3326,1556) | 18 | (4386, 570) | 26 | (2381, 1676) |
| 3 | (4177, 2244) | 11 | (3238, 1229) | 19 | (3007, 1970) | 27 | (3715, 1678) |
| 4 | (3712, 1399) | 12 | (4196, 1004) | 20 | (2562, 1756) | 28 | (3918, 2179) |
| 5 | (4061, 2370) | 13 | (4263, 2931) | 21 | (3439, 3201) | 29 | (2778, 2826) |
| 6 | (3780, 2212) | 14 | (3429, 1908) | 22 | (2935, 3240) | 30 | (2370, 2975) |
| 7 | (3676, 2578) | 15 | (3507, 2376) | 23 | (3140, 3550) | 31 | (1332, 695) |
| 8 | (4029, 2838) | 16 | (3394, 2643) | 24 | (2545, 2357) |
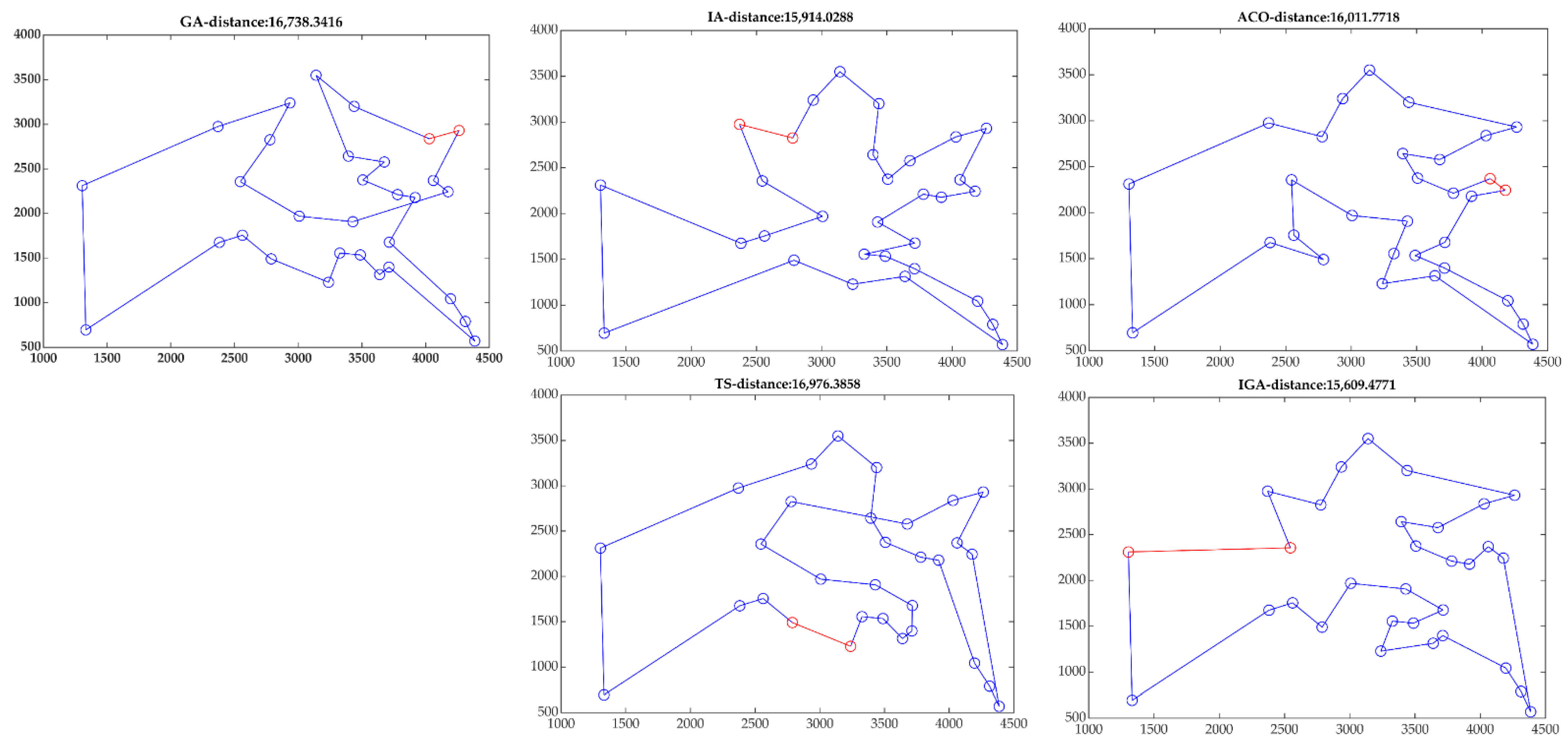
| Algorithm | Parameter | Result | Convergence Algebra |
|---|---|---|---|
| GA | Np = 200 G = 1000 | 16,738.34 | 920 |
| ACO | M = 50 G = 200 Alpha = 1 Beta = 5 Rho = 0.1 | 16,011.77 | 158 |
| IA | Np = 200 G = 1000 Nc1 = 10 | 15,914.02 | 680 |
| TS | G = 1000 TabuL = 22 Ca = 200 | 16,976.38 | 780 |
| IGA | Np = 200 G = 500 Pm1 = 0.02 Pm2 = 0.07 Pc1 = 0.4 Pc2 = 0.7 | 15,609.47 | 132 |
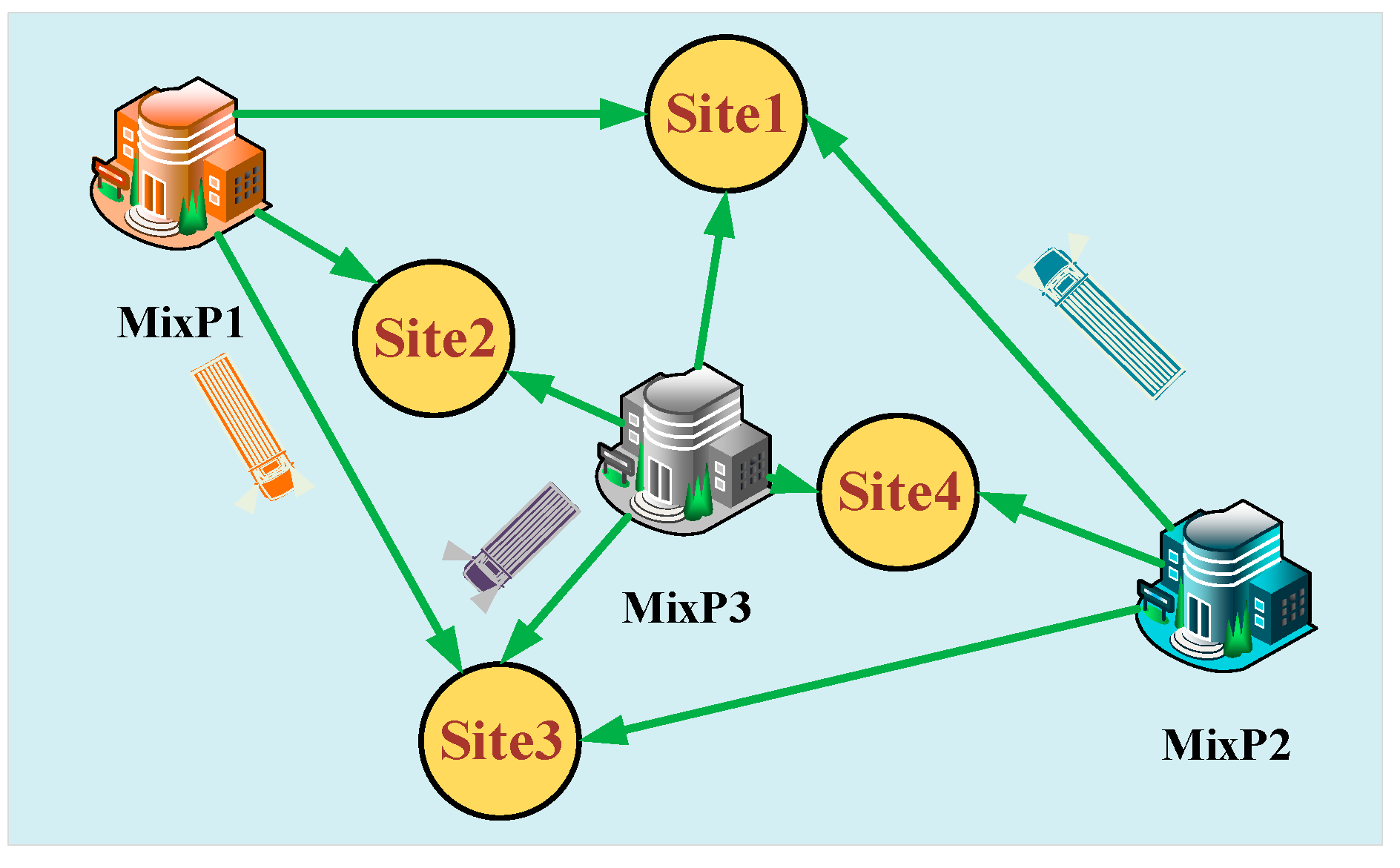
| Mixing plant | A | B | ||||
| Truck | 1 | 2 | 3 | 4 | 5 | 6 |
| Total weight (t) | 39.5 | 27 | 39.5 | 18.6 | 39.5 | 39.5 |
| Mixing plant | B | C | ||||
| Truck | 7 | 8 | 9 | 10 | 11 | 12 |
| Total weigh (t) | 18.6 | 27 | 27 | 18.6 | 39.5 | 27 |
| Mixing Plant | A | B | C | |
|---|---|---|---|---|
| Site 1 | Distances (km) | 20 | 15 | 14 |
| Time (h) | 0.47 | 0.21 | 0.38 | |
| Site 2 | Distances (km) | 38 | 30 | 25 |
| Time (h) | 0.66 | 0.75 | 0.4 | |
| Site 3 | Distances (km) | 15 | 40 | 35 |
| Time (h) | 0.51 | 0.85 | 0.76 | |
| Site 4 | Distances (km) | 23 | 20 | 45 |
| Time (h) | 0.57 | 0.35 | 0.8 | |
| NO. | ||||
|---|---|---|---|---|
| 1 | 4 | 0.55 | 0.03 | 0.8 |
| 2 | 8 | 0.6 | 0.04 | 0.85 |
| 3 | 12 | 0.65 | 0.05 | 0.9 |
| 4 | 16 | 0.7 | 0.06 | 0.95 |
| NO. | CA | FC | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 215.00 | 0.195 | 235.000 | 0.872 |
| 2 | 1 | 2 | 2 | 2 | 248.00 | 1.000 | 230.000 | 0.744 |
| 3 | 1 | 3 | 3 | 3 | 216.00 | 0.220 | 232.000 | 0.795 |
| 4 | 1 | 4 | 4 | 4 | 233.00 | 0.634 | 240.000 | 1.000 |
| 5 | 2 | 1 | 2 | 3 | 217.00 | 0.244 | 219.000 | 0.462 |
| 6 | 2 | 2 | 1 | 4 | 229.00 | 0.537 | 240.000 | 1.000 |
| 7 | 2 | 3 | 4 | 1 | 220.00 | 0.317 | 220.000 | 0.487 |
| 8 | 2 | 4 | 3 | 2 | 215.00 | 0.195 | 208.000 | 0.179 |
| 9 | 3 | 1 | 3 | 4 | 207.00 | 0.000 | 218.000 | 0.436 |
| 10 | 3 | 2 | 4 | 3 | 235.00 | 0.683 | 201.000 | 0.000 |
| 11 | 3 | 3 | 1 | 2 | 233.00 | 0.634 | 214.000 | 0.333 |
| 12 | 3 | 4 | 2 | 1 | 229.00 | 0.537 | 230.000 | 0.744 |
| 13 | 4 | 1 | 4 | 2 | 217.00 | 0.244 | 205.000 | 0.103 |
| 14 | 4 | 2 | 3 | 1 | 236.00 | 0.707 | 224.000 | 0.590 |
| 15 | 4 | 3 | 2 | 4 | 241.00 | 0.829 | 227.000 | 0.667 |
| 16 | 4 | 4 | 1 | 3 | 232.00 | 0.610 | 223.000 | 0.564 |
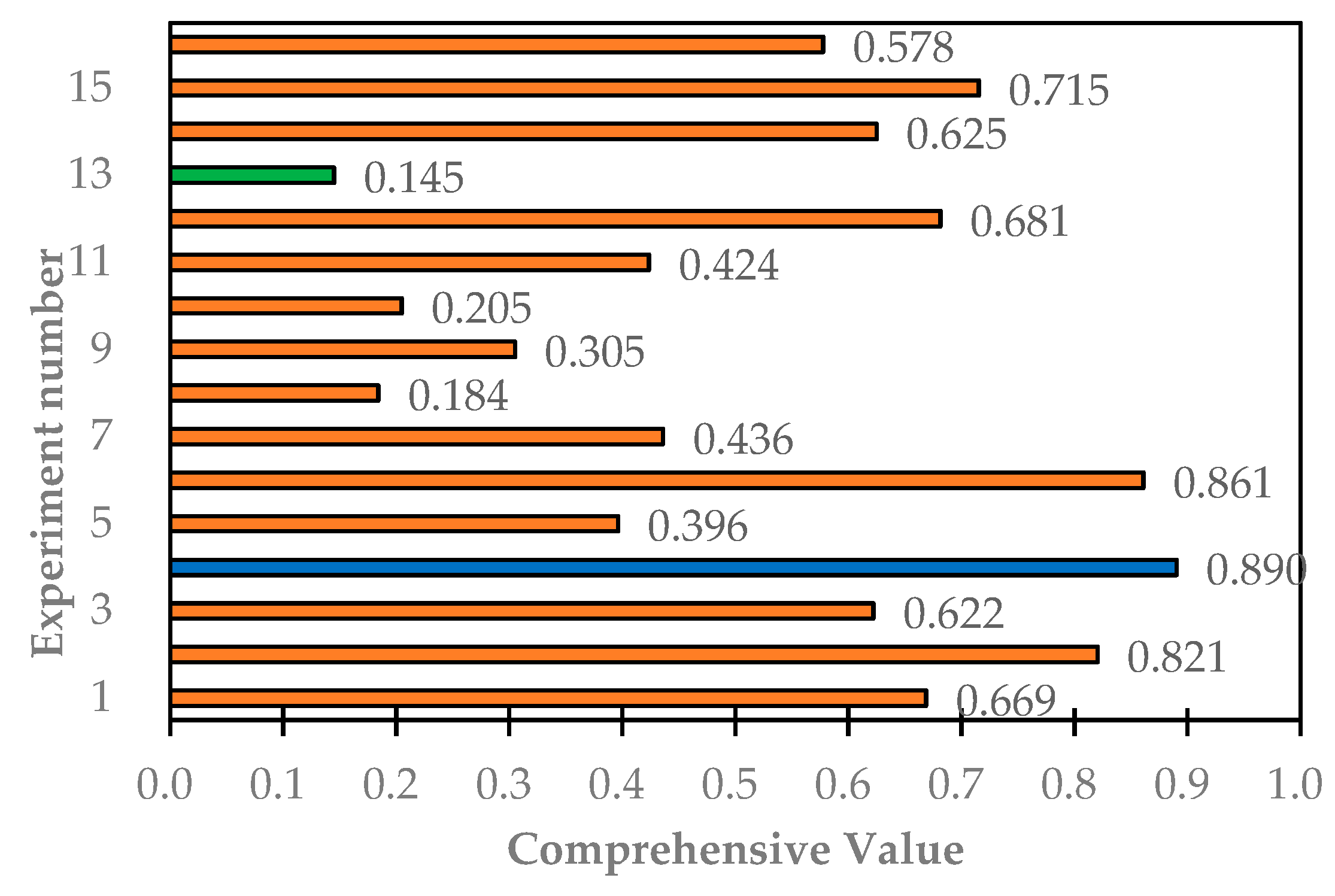
| NO. | CV | ||||
|---|---|---|---|---|---|
| 1 | 4 | 0.55 | 0.03 | 0.8 | 0.669 |
| 2 | 4 | 0.6 | 0.04 | 0.85 | 0.821 |
| 3 | 4 | 0.65 | 0.05 | 0.9 | 0.622 |
| 4 | 4 | 0.7 | 0.06 | 0.95 | 0.890 |
| 5 | 8 | 0.55 | 0.04 | 0.9 | 0.396 |
| 6 | 8 | 0.6 | 0.03 | 0.95 | 0.861 |
| 7 | 8 | 0.65 | 0.06 | 0.8 | 0.436 |
| 8 | 8 | 0.7 | 0.05 | 0.85 | 0.184 |
| 9 | 12 | 0.55 | 0.05 | 0.95 | 0.305 |
| 10 | 12 | 0.6 | 0.06 | 0.9 | 0.205 |
| 11 | 12 | 0.65 | 0.03 | 0.85 | 0.424 |
| 12 | 12 | 0.7 | 0.04 | 0.8 | 0.681 |
| 13 | 16 | 0.55 | 0.06 | 0.85 | 0.145 |
| 14 | 16 | 0.6 | 0.05 | 0.8 | 0.625 |
| 15 | 16 | 0.65 | 0.04 | 0.95 | 0.715 |
| 16 | 16 | 0.7 | 0.03 | 0.9 | 0.578 |
| k1j | 3.002 | 1.515 | 2.531 | 2.411 | |
| k2j | 1.878 | 2.511 | 2.614 | 1.573 | |
| k3j | 1.615 | 2.197 | 1.737 | 1.801 | |
| K4j | 2.063 | 2.334 | 1.676 | 2.772 | |
| Rj | 1.387 | 0.996 | 0.937 | 1.199 |
| Truck | 2 | 4 | 3 | 1 | 5 | 7 |
| Site | 3 | 3 | 4 | 3 | 2 | 4 |
| Truck | 8 | 6 | 10 | 11 | 9 | 12 |
| Site | 1 | 4 | 2 | 1 | 1 | 1 |
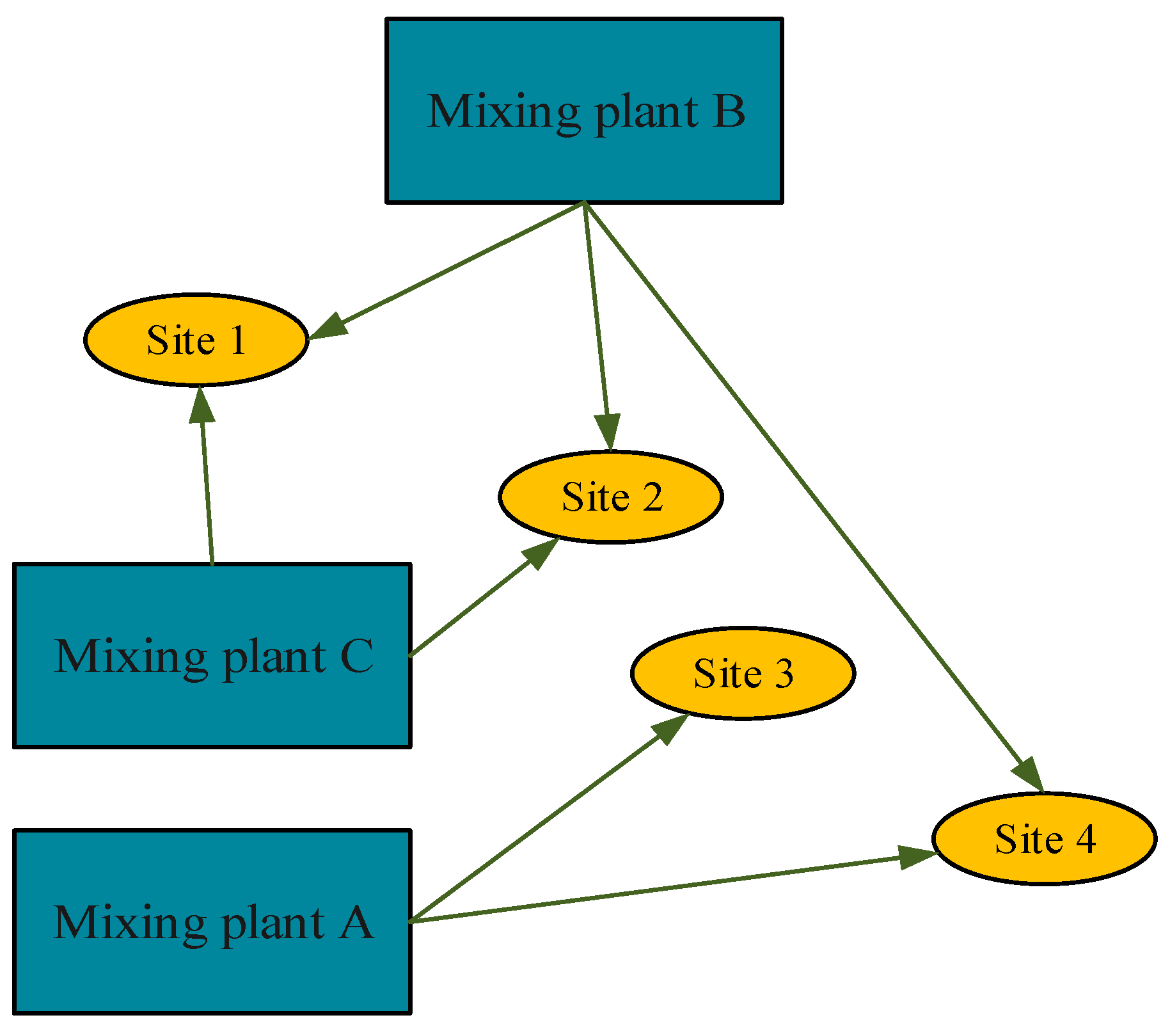
| Scheme | Distribution Route | Total Path | Concrete Volume | Fuel Consumption |
|---|---|---|---|---|
| Original | 2→1, 4→4, 3→3, 1→1 | 78km | 156 (m3) | 270 (L) |
| 5→2, 7→1, 8→1, 6→4 | 80 km | |||
| 10→2, 11→4, 9→3, 12→3 | 140 km | |||
| GA | 2→3, 4→3, 3→1, 1→1 | 70 km | 156 (m3) | 253.5 (L) |
| 5→4, 7→3, 8→4, 6→4 | 100 km | |||
| 10→1, 11→12, 9→1,12→2 | 78 km | |||
| IGA | 2→3, 4→3, 3→4, 1→3 | 68 km | 156 (m3) | 189.6 (L) |
| 5→2, 7→4, 8→1, 6→4 | 85 km | |||
| 10→2, 11→1, 9→1, 12→1 | 67 km |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Zhu, H.; Ma, J.; Yue, B.; Guan, Y.; Shi, J.; Shangguan, L. Improved Genetic Algorithm for Solving Green Path Models of Concrete Trucks. Appl. Sci. 2023, 13, 9256. https://doi.org/10.3390/app13169256
Yang J, Zhu H, Ma J, Yue B, Guan Y, Shi J, Shangguan L. Improved Genetic Algorithm for Solving Green Path Models of Concrete Trucks. Applied Sciences. 2023; 13(16):9256. https://doi.org/10.3390/app13169256
Chicago/Turabian StyleYang, Jie, Haotian Zhu, Junxu Ma, Bin Yue, Yang Guan, Jinfa Shi, and Linjian Shangguan. 2023. "Improved Genetic Algorithm for Solving Green Path Models of Concrete Trucks" Applied Sciences 13, no. 16: 9256. https://doi.org/10.3390/app13169256
APA StyleYang, J., Zhu, H., Ma, J., Yue, B., Guan, Y., Shi, J., & Shangguan, L. (2023). Improved Genetic Algorithm for Solving Green Path Models of Concrete Trucks. Applied Sciences, 13(16), 9256. https://doi.org/10.3390/app13169256






